2. 河海大学地球科学与工程学院, 南京 210098
3. 江苏省地质勘查技术院, 南京 210049
2. School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China
3. Geological Exploration Technology Institute of Jiangsu Province, Nanjing 210049, China
重力异常是由目标体与围岩在横向上存在密度差异引起的,包括区域场异常和局部场异常(曾华霖,2005).在重力资料处理过程中,如何从异常场中分离出由目标体引起的局部异常是长期困扰地球物理学家的难题之一.多年来,人们陆续提出并应用了一系列位场分离方法,包括趋势分析法(Simpson,1954;Oldham and Sutherland, 1955)、解析延拓法(栾文贵,1983;Martínez-Moreno et al., 2015)、匹配滤波法(Pawlowski and Hansen, 1990;杨辉等,1999)、插值切割法(程方道等,1987;Abdelrahman and El-Araby, 1996)、高阶导数法(Clarke,1969;Agarwal and Lal, 1971)及小波分析法(侯遵泽和杨文采,1997;Liu et al., 2015)等.这些方法由于基于不同的数学原理,在实际应用中并不是对所有位场异常的分离都行之有效.因此需要根据目标体的大小、埋深、所处地质环境等,有针对性地选择合适的方法进行位场分离.
坐落于宁芜北段的梅山铁矿区是著名的火山岩铁矿成矿区,矿床位于次火山岩体及其附近的火山岩围岩中,矿石类型多样,矿化阶段多期,铁矿物质多源的多种成因的铁矿床;该区具有矿体集中、形态规整、储量大、品味较高、易于开采等独特的赋存条件;矿山现已属中度危机矿山(陈小华,2003;孙喜华等,2014),为延长矿山服务年限,寻找主矿区深部及外围盲矿体,进一步厘清局部异常与矿体分布之间的对应关系具有十分重要的意义.
根据前人的研究成果(Grant,1972;刘东甲和程方道,1997;刘彦等,2012;Woolrych et al., 2015),笔者建立垂向叠加的长方体理论模型,分别应用趋势分析法、解析延拓法、插值切割法及匹配滤波法分离区域场和局部场并做误差分析,探讨各方法的分离效果;对梅山铁矿区重力异常进行分离,从分离出的局部场中推断该区地下深部及外围盲矿体赋存的空间形态,为寻找铁矿接替资源提供直接依据和线索.
1 位场分离的计算方法 1.1 趋势分析法趋势分析法的实质是最小二乘意义下的多项式拟合(Agocs,1951).其计算公式为:

|
(1) |

|
(2) |
式中:a0、a1、…、aN-1为N个待定系数,N=(n+1)(n+2)/2;gtre为拟合区域重力异常;g0为实测区域重力异常;SSR为最小二乘差值.
显然,当n取值不同时,上述多项式代表着不同阶次的曲面.在实际资料处理过程中需要通过比较不同阶次趋势分析的效果再确定n值.由于趋势分析法要一次性地利用全测区中所有测点的异常数据来组成线性方程组求解待定系数a0、a1、…、aN-1,大测区情况下线性方程组可能病态无解,只能运用最小二乘法求取超定方程组的近似解.这就从理论上解释了其适用于范围小的测区.
1.2 解析延拓法解析延拓是根据观测平面或剖面上的重力异常值计算高于(或低于)它的平面或剖面上异常值的过程,其理论基础是诺依曼无限平面外部问题的解,实质是一种位场的转换(Peters,1949).在某一点重力值已知的情况下,该点任意高度的重力值的计算方法为

|
(3) |
式中:Δg(ih, 0)为横坐标为ih点上的重力异常值(以取值的点距为延拓高度h的单位);Δg(ξ, 0)为区间[(i-1/2)h, (i+1/2)h]上的值,令Δg(ξ, 0)=Δg(ih, 0).
由式(3)可知,延拓后的重力场值与测区面积、测区内重力值个数n、延拓高度h有关.延拓后计算得到的异常值的幅值、宽度均发生改变.因此当两个场源体埋深相差较大时,通过延拓一定高度,其各自异常的幅值、宽度的改变速度不同,即上延有利于突出深部异常,下延相对突出浅部异常(Gupta and Ramani, 1980;郝天珧等,2002).
1.3 插值切割法插值切割法以当前计算点场值与四点圆周平均值的插值运算为切割算子,经一次或多次切割得到切割区域场,再从原始异常中减去切割区域场,从而得到切割局部场(文百红和程方道,1990).因此,异常体信号的量纲或位置经插值切割处理后未发生改变.其计算公式为:

|
(4) |

|
(5) |

|
(6) |

|
(7) |

|
(8) |
式中:G(x, y)为重力异常,(x, y)⊂D;R(x, y)为区域场;L(x, y)为局部场,(x, y) ⊂D1, D1⊂D;A为切割算子,A取决于切割半径;R1(x, y)、L1(x, y)为第一次切割区域场、局部场;R2(x, y)、L2(x, y)为第二次切割区域场、局部场.
插值切割法的关键在于确定切割半径和切割次数.在实际资料处理过程中,通过设定一系列不同切割半径和切割次数进行位场分离,并与地质和钻井资料相对比,选择与已有资料相吻合的那一组参数作为最佳的切割半径和切割次数(段本春等,1998).
1.4 匹配滤波法从频谱分析来看,区域场以低频成分为主,局部场以高频成分为主.因此,在应用匹配滤波法时应首先分析实测异常功率谱曲线,之后取功率谱变化曲线的切线,建造适宜的低通、带通滤波器,对异常波谱进行滤波,以提取不同波数成分的异常场(Spector and Grant, 1970).其计算方法为:

|
(9) |

|
(10) |
式中,
当波数较大时,1-e-l2→1,则两模型重力异常一阶垂向导数波谱为:

|
(11) |

|
(12) |

|
(13) |
其中W1、W2为匹配滤波因子,
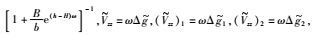

分离区域场的匹配滤波是一种低通滤波器,而提取局部场则需要一种高通滤波器,当输入滤波器的信号具有某一特殊波形时,其输出达到最大.因此在分析功率谱时,准确划分功率谱的低频段和中高频段尤为重要(刘彦等,2012;Woolrych et al., 2015).
2 模型实验数据分析为探讨上述四种方法的分离效果,建立了包含两个大小不同且垂向叠加的长方体模型(图 1a).其中:R1为理论局部场,长200 m、宽200 m、高160 m,中心坐标(1500 m, 1500 m, 100 m), 剩余密度1.0 g/cm3,重力值区间为0.0~25.8 g.u.;R2为理论区域场,长1000 m、宽1000 m、高500 m,中心坐标(1500 m,1500 m,800 m),剩余密度1.0 g/cm3,重力值区间为2.0~39.9 g.u..模型所处区域的观测网为3100 m×3100 m,网格点距、线距均为31 m.叠加重力场等值线呈同心圆状,异常值范围为2.0~65.7 g.u.(图 1b).

|
图 1 理论模型 (a)模型三维立体图;(b)模型布格重力异常. Figure 1 Superposed model (a) 3D diagram of model; (b) Bouguer gravity anomaly map of model. |
对理论异常场进行1~5阶次趋势分析(图 2).二阶趋势区域场重力等值线呈长轴为南北向的椭圆状,局部场则呈两低夹一高的特点(图 2a和2b);二阶与三阶(四阶与五阶)曲线形态相同(图 2c和2d);标准差随着阶次的增大而逐渐减小;二阶与三阶(四阶与五阶)的标准差基本相同,但均小于四阶(五阶)趋势(图 2f);局部场R1高值分布在1200~1800 m之间(图 2d),二阶、三阶趋势在此区间内相对误差基本为0(图 2e),根据Abdelrahman等(1991)采用连续两个阶次的趋势分析获得的剩余异常做相关,取相关性最好的两个阶次中的低阶作为最佳阶次,本次试验得到二阶趋势分析效果较好.

|
图 2 趋势分析及误差分析成果 (a)二阶趋势后的区域场;(b)二阶趋势后的局部场;(c)区域场剖面曲线;(d)局部场剖面曲线;(e)相对误差;(f)标准差. Figure 2 The results of trend analysis and error analysis (a) Regional field of 2 order trend analysis; (b) Local field of 2 order trend analysis; (c) Profile curve of regional field section; (d) Profile curve of local field section; (e) Relative error; (f) Standard deviation. |
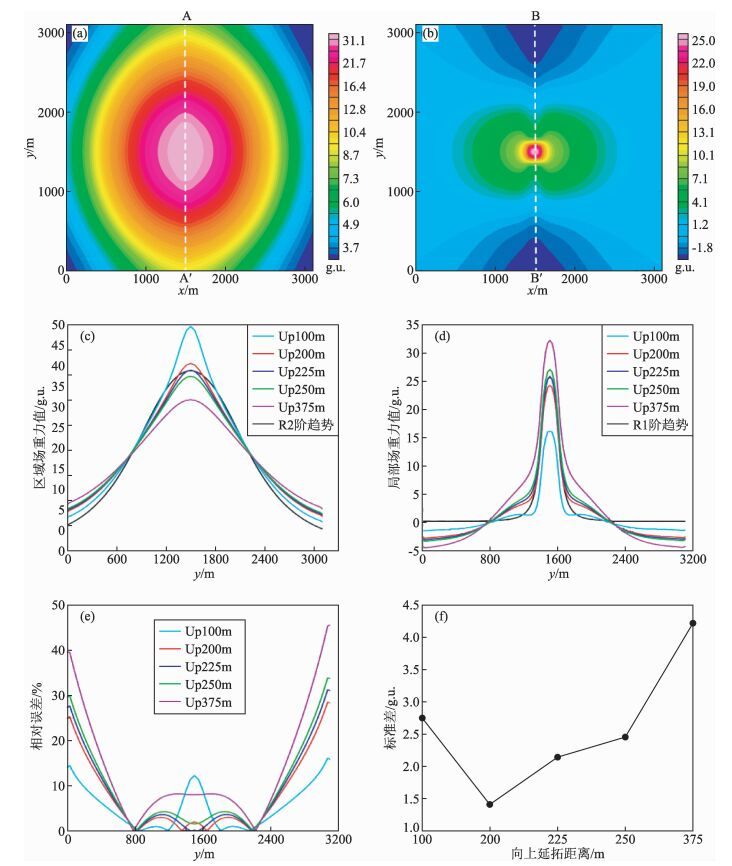
图 3给出了上延100 m、200 m、225 m、250 m及375 m的成果图.其分离结果与趋势分析法相似(图 3a和3b).剖面线拟合效果较趋势分析法好,且随着延拓高度的增加,区域场曲线变的平缓,极值减小,局部场曲线形态变化不大(图 3c和3d);相对误差曲线呈现边界附近高值、中心点附近低值的特征,在800~2200 m范围内相对误差小于5%(图 3e);标准差整体呈“V”型,在上延200 m时极值小于1.5 g.u.(图 3f),因此选取最佳上延高度为225 m.
|
图 3 解析延拓效果 (a)上延225 m后的区域场;(b)上延225 m后的局部场;(c)区域场剖面曲线; (d)局部场剖面曲线;(e)相对误差;(f)标准差. Figure 3 Analytic continuation maps (a) Regional field of 225 m upward continuation; (b) Local field of 225 m upward continuation; (c) Profile curve of regional field section; (d) Profile curve of local field section; (e) Relative error; (f) Standard deviation. |
选取切割半径r=3 m、4 m、5 m,切割次数n=1次、2次,切割成果见图 4.不同于趋势分析和解析延拓,插值切割获得的区域场和局部场重力等值线图与理论模型基本吻合(图 4a和4b);当切割次数不变、切割半径增大(或切割半径不变、切割次数增加)时,区域场重力极大值减小,局部场重力极大值增大(图 4c和4d).相对误差曲线近似“W”型,模型中心点附近的相对误差值随切割次数增多而减小,但出现明显的震荡(图 4e).标准差曲线呈‘U’型,当切割半径为4 m时,标准差最小,其值为0.725 g.u.左右,具有非常小的离散性(图 4f).整体而言,插值切割最大相对误差小于14%,标准差不超过1.025 g.u.,无论是最大相对误差还是标准差都小于趋势分析法和解析延拓法.

|
图 4 插值切割成果(r为切割半径,n为切割次数,下同) (a)切割半径4、切割2次后的区域场;(b)切割半径4、切割2次后的局部场; (c)区域场剖面曲线;(d)局部场剖面曲线;(e)相对误差;(f)标准差. Figure 4 Interpolating cut map (a) Regional field of 4 m cutting radius and 2-time iteration; (b) Local field of 4 m cutting radius and 2-time iteration; (c) Profile curve of regional field section; (d) Profile curve of local field section; (e) Relative error; (f) Standard deviation. |
通过分析异常功率谱曲线,选取合适的低频、高频率波段(图 5a中切线),建造适宜的滤波器对实测波谱进行滤波.滤波后区域场和局部场重力等值线呈同心圆状分布,与所设模型吻合,但由于局部异常体埋深浅,使得功率谱曲线高低频段不明显,导致分离结果与理论场偏差较大.

|
图 5 匹配滤波功率谱及匹配滤波效果 (a)功率谱曲线;(b)区域异常;(c)局部异常;(d)剖面曲线对比. Figure 5 Power spectrum and renderings of matched filtering (a) Power spectrum; (b) Regional anomalies; (c) Local anomalies; (d) Comparison of section curves. |
梅山铁矿床位于宁芜中生代陆相火山岩断陷盆地北段,梅山—凤凰山构造岩浆成矿带与滨江构造岩浆带的交叉部位;区内出露侏罗—白垩系陆相火山岩系、白垩系红层及新近纪及其以来沉积地层;侵入岩主要有辉长闪长玢岩—次火山岩体、石英角闪石安山玢岩、辉绿岩;与铁矿有关的梅山短轴背斜主要分布在陈家凹—大凹山一带,为辉石安山岩组成;区内断裂以302°~336°方向的张性断裂和26°~48°方向压性断裂为主,断裂交叉部位控制成矿,北西西向压扭性断裂为控岩构造.
重力数据取自1983年江苏省地质局物探队提交的《江苏省宁芜地区(北段)铁矿重磁普查工作成果报告》中的重磁数据.运用geosoft软件绘制了梅山铁矿布格重力异常平面图(图 6),重力异常高值区和重力异常低值区界限明显,测区内重力值变化范围为4.4~15.1 mGal, 整体呈西北部低值、东南部高值分布.重力异常低值区等值线较平缓,异常值不大于5.8 mGal, 在数值上明显低于其他各处,根据已有区域资料,西北部分布着数百米厚的低密度值的火山碎屑岩浦口组砂岩、砂砾岩,密度在2.4 g/cm3左右;布格重力异常低值区与高值区之间存在一条分界带,延伸范围较大,异常值为5.8~7.7 mGal, 根据区域地质资料,此处为滨江断裂带,走向北北东;东南区的重力异常变化较大,重力高值带从数据处理区的最南边开始,经大凹山、胡家山,向西北一直延伸到大茅曹(梅山铁矿主矿区所在位置).在高重力带旁侧,伴随着三个规模较大的二级重力扭曲异常,分别为喻村至梅山村西南方向重力异常带、大茅曹经萝卜山至刘家村方向重力异常带以及从陈家洼经黄林库至吴家洼北北东方向的重力异常带.结合区域综合地质图分析,本区的区域重力高异常基本反映了区内的辉石闪长玢岩岩体分布情况与赋存状态,区域重力异常最高处通常对应岩体的出露部位或埋深较浅部位,外凸处对应岩体顶面埋深较大的部位,区域异常不明显的地方通常对应岩体消失部位及深部倾伏部位.

|
图 6 梅山铁矿原始布格重力异常 Figure 6 Bouguer gravity anomaly map of the Meishan iron deposit |
对原始重力异常开展1~4阶次的趋势分析,其成果见图 7.二阶、三阶趋势相关性最好,且异常高点更集中一些(图 7c和7d).图 7a和7b分别为二阶趋势分析后得到的背景场和局部异常场.二阶趋势拟合的趋势面平缓光滑,反映了地下深部大的区域构造(图 7a).局部异常场的重力高值集中在5个区域(图中黑色虚线框,下文同),其中B区为梅山铁矿主矿区,重力异常极值为4.1 mGal, 矿体顶板标高由-34~-327 m, 底板标高由-169.4~-524 m;前述趋势分析法不适宜用于大测区,在局部场边界处趋势效果差,并根据钻井资料知,F区为假异常区;萝卜山—刘家村带(A区)、梅山村南部(D区)、黄林库—吴家洼带(C区)、主矿区(B区)深部及东南部(E区)存在剩余重力异常,极值在1.0 7 mGal左右,为梅山铁矿外围找矿前景区(图 7b).

|
图 7 梅山铁矿重力异常趋势分析效果 (a)二阶趋势后区域场;(b)二阶趋势后局部场;(c)区域场剖面比较;(b)局部场剖面比较. Figure 7 Trend analysis renderings of Meishan iron (a) Regional field anomalies; (b) Local field anomalies; (c) Section curves comparison of regional field; (d) Section curves comparison of local field. |
接着开展了解析延拓工作,将原始重力异常分别上延400 m、500 m、600 m、700 m、800 m、1000 m.布格重力异常上延至600 m时,梅山铁矿主异常圈闭等值线与泰山异常等值线一致,上延至700 m时,梅山铁矿主异常圈闭消失,高重力异常趋势反映了密度较高的辉石闪长玢岩从泰山至梅山埋深由浅入深的变化趋势,因此,选择了上延700 m的布格重力异常作为本区的区域重力异常,将原始布格重力异常数据与其差值作为本区的剩余重力异常(图 8).由于矿体的规模、埋深、走向和延深都是不一样的,因此,利用上延高度过大和过小的结果求取的剩余异常将分别给小矿体和大矿体的推断制造困难.相比于二阶趋势分析,上延700 m后的区域场形态更圆滑,局部场没有出现明显的假异常.与趋势分析相同,萝卜山—刘家村带(A区)、梅山村南部(D区)、黄林库—吴家洼带(C区)、主矿区(B区)深部及东南部(E区)存在剩余重力异常.

|
图 8 梅山铁矿重力异常解析延拓效果 (a)区域场;(b)局部场;(c)区域场剖面曲线;(d)局部场剖面曲线. Figure 8 Continuation renderings of Meishan iron (a) Regional field; (b) Local field; (c) Section curves comparison of regional field; (d) Section curves comparison of local field. |
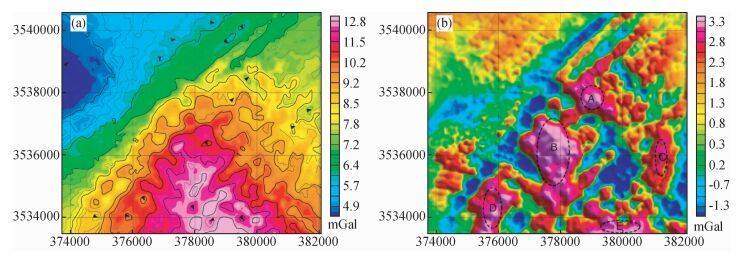
为进一步对比异常分离的效果,采用插值切割法对原始重力异常进行位场分离.通过设置一系列切割半径、连续切割,并以趋势分析、解析延拓后的局部场为参考,当切割半径为10 m、切割1次时,切割效果较好,符合现有地质情况(图 9).由于少量地质信息残留在区域异常场中,导致区域场重力等值线严重扭曲,但局部场重力异常刻画的较好,主矿区和远景成矿区的刻画与趋势分析、解析延拓的局部异常较为一致.同时,低重力值的滨江断裂带在局部异常图中能清晰的反映出来.
|
图 9 梅山铁矿切割半径为10 m、切割1次的插值切割法分离效果 (a)区域场;(b)局部场. Figure 9 Interpolation cut map of 10 m cutting radius and 1-time iteration (a) Regional field; (b) Local field. |
图 10a为实测功率谱曲线,曲线的高频、低频段明显,根据区域场功率谱以低频为主、局部场以高频为主的原则,通过选取合适的滤波段(图中切线所示),建立适宜的低通、带通滤波器来提取不同波数的异常场,图 10b和10c分别为匹配滤波后的区域场和局部场.区域场平缓光滑,局部场重力异常区域比趋势分析、解析延拓及插值切割获得的异常区域更集中,说明萝卜山—刘家村带(A区)、梅山村南部(C区)、主矿区深部(B区)及东南部(D区)均处于同一闪长玢岩的隆起带上,这与已有的物性资料相符.可能是矿体埋藏浅的缘故,局部异常图中的黄林库—吴家洼带无重力异常.

|
图 10 功率谱曲线及匹配滤波效果 (a)功率谱曲线;(b)背景场;(c)局部异常场. Figure 10 Power spectrum and renderings of matched filtering (a) Power spectrum; (b) Regional anomalies; (c) Local anomalies. |
根据已有物性资料,与重力异常分离结果进行比照.磁铁矿密度平均值大于4.44 g/cm3,一般均在3.0 g/cm3以上,它们与区内地层密度差在0.5区103 g/cm3以上,有的超过1.0×103 g/cm3;与区内次火山岩体间的密度差在0.35×103 g/cm3.闪长岩类(含磁铁矿化)在区内仅次于铁矿石,其密度平均值一般在2.70~2.80 g/cm3,与火山岩的密度差为0.1~0.4 g/cm3.第四系及第三系雨花台组地层密度一般在2.0 g/cm3左右,由于厚度不大,分布范围有限,不足引起重力异常.侏罗系—白垩系地层密度一般在2.47~2.58 g/cm3.说明铁矿体与围岩存在明显的密度差异,通过位场分离得到的局部异常应该是由矿体引起的异常.已有资料显示梅山铁矿主矿区及刘家村附近钻孔见矿.而梅山村南部、黄林库—吴家洼处,由于没有钻孔资料,所以只能推断其为潜在的找矿远景区.
4 结论 4.1本文从趋势分析法、解析延拓法、插值切割法及匹配滤波法的数学原理出发,通过模型位场分离试验发现:理论局部场重力高值主要分布在1200~1800 m区间内,二阶趋势后的局部场与理论局部场剖面线重合,远离此区间时异常场等值线形态与理论场等值线形态差异较大,说明趋势分析法适用于小测区;解析延拓法与趋势分析法同属于位场转换,异常分离结果相似,位场向上延拓225 m时,整体拟合度好于趋势分析法,但延拓高度与目标体埋深并不一一对应;插值切割法能基本保持重力等值线形态不变,即异常体信号的量纲或位置未发生改变,当切割次数较大时,易产生震荡效应;匹配滤波重力等值线呈同心圆状分布,与理论模型吻合,但分离效果较差,可能与目标体大小、形状、埋深有关.
4.2分别运用趋势分析法、解析延拓法、插值切割法及匹配滤波法对梅山铁矿重力资料进行位场分离.实践表明:二阶趋势分析、向上延拓700 m、插值切割选取切割半径为10 m切割一次、匹配滤波法的分离结果具有较好的一致性,且与钻孔资料吻合.萝卜山—刘家村带、梅山村南部、黄林库—吴家洼带、主矿区深部及东南部存在幅值较高的剩余重力异常,揭示了铁矿资源分布的一般特征.
4.3通过理论模型试验和梅山铁矿重力异常分离实践,进一步说明了各种位场分离方法都具有一定的优缺点.在实际资料处理过程中,对研究区的物性资料及各种分离方法的侧重点和局限性的了解至关重要,有利于选取合适的分离方法并准确的分离出目标体引起的局部.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Abdelrahman E M, Bayoumi A I, El-Araby H M. 1991. A least-squares minimization approach to invert gravity data[J]. Geophysics, 56(1): 115–118. DOI:10.1190/1.1442946 |
| [] | Abdelrahman E M, El-Araby T M. 1996. Shape and depth solutions from moving average residual gravity anomalies[J]. Journal of Applied Geophysics, 36(2-3): 89–95. DOI:10.1016/S0926-9851(96)00038-9 |
| [] | Agarwal B N P, Lal L. 1971. Application of rational approximation in calculation of the second derivative of the gravity field[J]. Geophysics, 36(3): 571–581. DOI:10.1190/1.1440192 |
| [] | Agocs W B. 1951. Least squares residual anomaly determination[J]. Geophysics, 16(4): 686–696. DOI:10.1190/1.1437720 |
| [] | Chen X H. 2003. Geological characteristics and genesis of siderite in Meishan iron deposit Nanjing[J]. Mineral Resources and Geology , 17(S1): 361–364. |
| [] | Cheng F D, Liu D J, Yao R X. 1987. A study on the identification of regional and local gravity fields[J]. Computing Techniques for Geophysical and Geochemical Exploration , 9(1): 1–9. |
| [] | Clarke G K C. 1969. Optimum second-derivative and downward-continuation filters[J]. Geophysics, 34(3): 424–437. DOI:10.1190/1.1440020 |
| [] | Duan B C, Xu S Z, Yan H J, et al. 1998. Application of interpolation-cut method for magnetic anomaly division to igneous mass investigation[J]. Oil Geophysical Prospecting , 33(1): 125–131. |
| [] | Grant F S. 1972. Review of data processing and interpretation methods in gravity and magnetics, 1964-1971[J]. Geophysics, 37(4): 647–661. DOI:10.1190/1.1440288 |
| [] | Gupta V K, Ramani N. 1980. Some aspects of regional-residual separation of gravity anomalies in a Precambrian terrain[J]. Geophysics, 45(9): 1412–1426. DOI:10.1190/1.1441130 |
| [] | Hao T Y, Mancheol S, Wang Q S, et al. 2002. A study on the extension of fault zones in Yellow Sea and its adjacent areas based on gravity data[J]. Chinese Journal of Geophysics , 45(3): 385–397. DOI:10.3321/j.issn:0001-5733.2002.03.010 |
| [] | Hou Z Z, Yang W C. 1997. Wavelet transform and multi-scale analysis on gravity anomalies of China[J]. Acta Geophysica Sinica , 40(1): 85–95. |
| [] | Liu D J, Cheng F D. 1997. A multiple-cut method for identification of regional and local gravity fields[J]. Computing Techniques for Geophysical and Geochemical Exploration , 19(1): 31–35. |
| [] | Liu Q S, Qiu N, Zheng J P, et al. 2015. Crustal large-scale serpentinized mantle peridotite body in the Sulu ultrahigh-pressure metamorphic belt, eastern China:Evidence from gravity and magnetic anomalies[J]. Journal of Structural Geology, 70: 190–199. DOI:10.1016/j.jsg.2014.11.009 |
| [] | Liu Y, Yan J Y, Wu M A, et al. 2012. Exploring deep concealed ore bodies based on gravity anomaly separation methods:A case study of the Nihe iron deposit[J]. Chinese Journal of Geophysics , 55(12): 4181–4193. DOI:10.6038/j.issn.0001-5733.2012.12.030 |
| [] | Luan W G. 1983. The stabilized algorithm of the analytic continuation for the potential field[J]. Acta Geophysica Sinica , 26(3): 263–274. |
| [] | Martínez-Moreno F J, Galindo-Zaldívar J, Pedrera A, et al. 2015. Regional and residual anomaly separation in microgravity maps for cave detection:The case study of Gruta de las Maravillas (SW Spain)[J]. Journal of Applied Geophysics, 114: 1–11. DOI:10.1016/j.jappgeo.2015.01.001 |
| [] | Oldham C H G, Sutherland D B. 1955. Orthogonal polynomials:their use in estimating the regional effect[J]. Geophysics, 20(2): 295–306. DOI:10.1190/1.1438143 |
| [] | Pawlowski R S, Hansen R O. 1990. Gravity anomaly separation by wiener filtering[J]. Geophysics, 55(5): 539–548. DOI:10.1190/1.1442865 |
| [] | Peters L J. 1949. The direct approach to magnetic interpretation and its practical application[J]. Geophysics, 14(3): 290–320. DOI:10.1190/1.1437537 |
| [] | Simpson S M Jr. 1954. Least squares polynomial fitting to gravitational data and density plotting by digital computers[J]. Geophysics, 19(2): 255–269. DOI:10.1190/1.1437990 |
| [] | Spector A, Grant F S. 1970. Statistical models for interpreting aeromagnetic data[J]. Geophysics, 35(2): 293–302. DOI:10.1190/1.1440092 |
| [] | Sun X H, Gao L K, Zhang L S, et al. 2014. On geological characters of gold-copper-molybdenum polymetallic deposit in Meishan iron mine periphery[J]. Journal of Geology , 38(1): 128–134. |
| [] | Wen B H, Cheng F D. 1990. A new interpolating cut method for identifying regional and local fields of magnetic anomaly[J]. Journal of Central-South Institute of Mining and Metallurgy , 21(3): 229–235. |
| [] | Woolrych T R H, Christensen A N, McGill D L, et al. 2015. Geophysical methods used in the discovery of the Kitumba iron oxide copper gold deposit[J]. Interpretation, 3(2): SL15–SL25. DOI:10.1190/INT-2014-0201.1 |
| [] | Yang H, Wang J L, Wang X M, et al. 1999. Apparent depth filter for gravity anomalies and a case study[J]. Chinese Journal of Geophysics , 42(3): 416–421. DOI:10.3321/j.issn:0001-5733.1999.03.015 |
| [] | Zeng H L. 2005. Gravity Field and Gravity Exploration [M]. Beijing: Geological Publishing House. |
| [] | 陈小华. 2003. 梅山铁矿床菱铁矿的地质特征及成因探讨[J]. 矿产与地质, 17(S1): 361–364. |
| [] | 程方道, 刘东甲, 姚汝信. 1987. 划分重力区域场与局部场的研究[J]. 物化探计算技术, 9(1): 1–9. |
| [] | 段本春, 徐世浙, 阎汉杰, 等. 1998. 划分磁异常场的插值切割法在研究火成岩体分布中的应用[J]. 石油地球物理勘探, 33(1): 125–131. |
| [] | 郝天珧, MancheolS, 王谦身, 等. 2002. 根据重力数据研究黄海周边断裂带在海区的延伸[J]. 地球物理学报, 45(3): 385–397. DOI:10.3321/j.issn:0001-5733.2002.03.010 |
| [] | 侯遵泽, 杨文采. 1997. 中国重力异常的小波变换与多尺度分析[J]. 地球物理学报, 40(1): 85–95. |
| [] | 刘东甲, 程方道. 1997. 划分重力区域场与局部场的多次切割法[J]. 物探化探计算技术, 19(1): 31–35. |
| [] | 刘彦, 严加永, 吴明安, 等. 2012. 基于重力异常分离方法寻找深部隐伏铁矿-以安徽泥河铁矿为例[J]. 地球物理学报, 55(12): 4181–4193. DOI:10.6038/j.issn.0001-5733.2012.12.030 |
| [] | 栾文贵. 1983. 场位解析延拓的稳定化算法[J]. 地球物理学报, 26(3): 263–274. |
| [] | 孙喜华, 高丽坤, 张龙生, 等. 2014. 梅山铁矿外围金、铜、钼多金属矿地质特征[J]. 地质学刊, 38(1): 128–134. |
| [] | 文百红, 程方道. 1990. 用于划分磁异常的新方法-插值切割法[J]. 中南矿冶学院学报, 21(3): 229–235. |
| [] | 杨辉, 王家林, 王小牧, 等. 1999. 重力异常视深度滤波及应用[J]. 地球物理学报, 42(3): 416–421. DOI:10.3321/j.issn:0001-5733.1999.03.015 |
| [] | 曾华霖. 2005. 重力场与重力勘探[M]. 北京: 地质出版社. |
 2017, Vol. 32
2017, Vol. 32


