地球物理学进展  2017, Vol. 32 Issue (6): 2424-2429   PDF    
引用本文
曹中林, 陈浩凡, 何光明, 等. 2017. 基于复数域混合SVD滤波方法及在随机噪声压制中的应用. 地球物理学进展, 2017, 32(6): 2424-2429, doi: 10.6038/pg20170619  
CAO Zhong-lin, CHEN Hao-fan, HE Guang-ming, et al. 2017. Hybrid SVD filtering method in complex domain and its application in random noise suppression. Progress in Geophysics (in Chinese), 32(6): 2424-2429, doi: 10.6038/pg20170619   
基于复数域混合SVD滤波方法及在随机噪声压制中的应用
曹中林1,2,3, 陈浩凡1,3, 何光明1,3, 李德珍1,3, 曾旖1, 黄晓兵1, 陈丹1,3     
1. 中国石油集团川庆钻探工程有限公司地球物理勘探公司, 成都 610213
2. 成都理工大学, 成都 610059
3. 中国石油天然气集团公司山地地震技术试验基地, 成都 610213
收稿日期：2017-04-16; 修回日期：2017-10-13.
基金项目：中国石油天然气集团公司重大科技专项课题（2013E-38-08）资助.
作者简介：曹中林, 男, 1981年生, 博士研究生, 主要从事地震资料去噪处理方面的研究.(E-mail:czlor@163.com)
摘要：在低信噪比地震资料处理中，压制随机噪声是其中的关键处理环节.传统的频率空间域预测滤波方法，容易使得去噪后高频段的有效信号严重畸变，不利于进一步提高分辨率.为此，提出了一种基于复数域混合SVD滤波法压制三维地震数据中随机干扰的方法，该方法首先在时空域对地震数据作傅里叶变换，再依据Eigenimage滤波法与Cadzow滤波法建立混合Hankel矩阵，然后对其运行奇异值分解，最后通过秩约化的方法来压制随机干扰.理论模型和实际地震数据的应用表明：该方法可有效地去除随机噪声，保护有效波，明显地改善了叠后三维地震资料的信噪比.
关键词：随机噪声    复数域    混合SVD    Hankel矩阵    
Hybrid SVD filtering method in complex domain and its application in random noise suppression
CAO Zhong-lin1,2,3 , CHEN Hao-fan1,3 , HE Guang-ming1,3 , LI De-zhen1,3 , ZENG yi1 , HUANG Xiao-bing1 , CHEN Dan1,3     
1. Geophysical Exploration Company, Chuanqing Drilling Engineering Company Limited, CNPC, Chengdu 610213, China
2. Chengdu University of Technology, Chengdu 610059, China
3. Mountain Geophysical Technology Test Center, CNPC, Chengdu 610213, China
Abstract: In the low signal-to-noise ratio seismic data, random noise suppression is one of the key processing chains. The traditional method of random noise suppression is the frequency space domain prediction filtering, which is easy to make effective signal serious distortion in the high frequency, is not conducive to further improve the resolution. Therefore, we proposed a filtering method based on the hybrid Singular Value (SVD) decomposition to suppress random noise. Firstly, the seismic data will be transformed into frequency space domain by Fourier transform method. Secondly, based on Eigenimage filtering method and Cadzow filtering method, the hybrid Hankel matrix is constructed, and then performed singular value decomposition. Finally, by means of reducing the rank of matrix, random noise will be eliminated effectively. The theoretical model and field data experiments show that the method can effectively remove random noise, and protect the effective wave, significantly improved signal-to-noise ratio of post-stack seismic data.
Key words: random noise     complex domain     hybrid singular value decomposition     Hankel matrix    
0 引言

在复杂地表地区采集的地震资料中，资料的信噪比很低，普遍存在着相当严重的随机噪声，一般情况下这类噪声严重干扰了有效反射信号，大大降低了地震资料的信噪比.目前压制随机噪声的方法主要有频率空间域预测滤波技术，该技术利用有效波在横向上的相干性和随机噪声横向上的不相干, 来压制随机噪声, 提高地震资料的信噪比.但是由于高频段的信噪比较低，求取的预测算子受噪声成分的影响较大，这就使得去噪后高频段的有效信号严重畸变，不利于进一步提高分辨率(Hornbostel, 1991; Abma and Claerbout, 1995; 王忠仁等, 1999).

基于SVD分解的滤波方法是一种非线性滤波，早在20世纪70年代末期，Andrews (1976)提出SVD方法可用于数字图像的噪声压制，Cadzow (1988)提出Cadzow滤波法，它也是一种基于奇异值分解的方法.近些年的研究对SVD滤波法作了有益的应用与改进，主要有两大类：一类是Eigenimage滤波方法；另一类是Cadzow滤波方法.Trickett(2002, 2003)将基于Eigenimage方法的SVD滤波技术用于三维叠前和叠后地震资料以提高信噪比；随后，Trickett等(2008, 2009, 2012)又提出了基于Cadzow方法的SVD滤波技术衰减三维地震数据中随机噪声；崔树果(2012)和刘志鹏(2012)在此基础上，为适应弯曲地震同相轴的处理，采用局部分块的处理策略，进一步优化了该方法的去噪效果；彭更新等(2013)进一步探讨了Cadzow滤波法的优势以及局限性.在这些研究的基础上，针对随机干扰的特点，提出了基于复数域的混合SVD滤波法压制随机干扰方法，该技术首先对地震数据进行傅里叶变换，得到复数域的数据，并结合Eigenimage滤波方法与Cadzow滤波法能充分利用维数的优势，通过对复数域数据进行高维折叠的组合，构建混合Cadzow矩阵，进一步增强有效信号的相干性，从而实现更为有效的压制随机噪声并最大限度的保护有效信号的特征.合成地震记录的理论测试和实际资料的应用结果验证了该方法的优越性.

1 方法原理

在复数域进行混合SVD滤波，首先需要对数据进行傅里叶变换到频率域，然后对每个频率切片构建矩阵，再进行SVD滤波(秩约化)，最后利用傅里叶反变换得到去噪后的有效信号.

1.1 复数域矩阵构建

设叠后三维地震数据s(x, y, t)，Inline方向有Nx道，Xline方向有Ny道，每道数据最大的采样点数为Ns，对其沿时间方向作傅里叶变换，得到复数域地震数据z(x, y, w), 并取某一频率f的切片数据，形成矩阵A，公式为

(1)

式中zi, j为第f个频率切片中第i条Inline线第j条Xline的样点值.

Cadzow滤波法(1988)可以处理高维空间数据，且滤波能力更强，但需要空间上的等距分布，而Eigenimage方法允许使用非一致空间分布.因此可以结合这两种滤波法的各自优势，对复数矩阵A采用高维折叠组合的方法，形成以下三种高维矩阵的组合方式，从而进一步增强有效信号的相干性.

(1) Eigenimage滤波法

Eigenimage方法是将频率切片直接形成矩阵，则有Eigenimage滤波法对应的Hankel矩阵B为

(2)

(2) Eigenimage-Cadzow滤波法

Cadzow方法可以处理高维空间数据，且滤波能力更强，但需要空间上的等距分布，而Eigenimage方法允许使用非一致空间分布.所谓Eigenimage-Cadzow混合滤波，即在某些空间维数使用Eigenimage方法，而在另一些空间维数上使用Cadzow方法.则有Eigenimage-Cadzow滤波法对应的Hankel矩阵C为

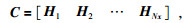
(3)

其中：

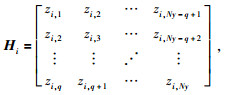
(4)

一般选择q=Ny/2，Hankel矩阵C沿Inline方向是Eigenimage滤波，沿Xline方向也是Cadzow滤波，采用的是混合Eigenimage-Cadzow滤波.

(3) Cadzow-Cadzow滤波法

Cadzow-Cadzow方法将频率切片组织成嵌套Hankel矩阵，则有Cadzow-Cadzow滤波法对应的Hankel矩阵D为

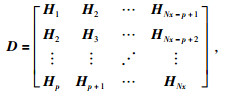
(5)

其中：

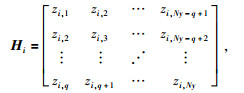
(6)

一般选择p=Nx/2，q=Ny/2，Hankel矩阵D沿Inline方向是Cadzow滤波，沿Xline方向也是Cadzow滤波，采用的是混合Cadzow滤波.

1.2 奇异值分解

SVD将矩阵分解成一系列的以矩阵奇异值为系数的特征图像的和，则矩阵的奇异值反映了信号相干能量的强弱：随机噪声由于相干性较弱，对应着奇异值较小的特征图像；有效信号的相干性较强，对应着奇异值较大的特征图像.因此，只用表征有效信号的前几个较大奇异值重构矩阵，就可去除随机干扰，恢复有效信号.公式为

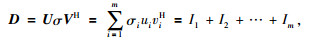
(7)

其中，m×m酉矩阵U =[u1, …, um]，n×n酉矩阵V =[v1, …, vn]，矩阵Σ由D的奇异值σi构成，奇异值σ1≥σ2≥…≥σm≥0由大到小排列在其主对角线上.

令k是矩阵D所希望的秩(信号个数)，则在2-范数或F-范数下矩阵D的最佳秩k逼近为前k个特征图像之和，公式为

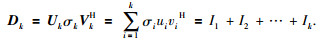
(8)
1.3 信号的重构

逼近矩阵Dk一般不是Hankel形式，因此需要对Dk沿反对角线做平均以恢复Hankel结构，并进一步从中恢复出有效信号S′k.不妨设L≤k，令n=i+j-1，N=L+k-1，则有:

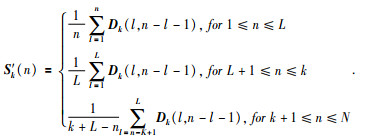
(9)
1.4 实现步骤

在地震记录中，有效信号相干性较强，而随机噪声相干性较弱.根据随机干扰的这个特征，我们建立了复数域的混合SVD滤波法去随机干扰的步骤为：

(1) 首先在时空域将地震数据划分为多个窗口，窗口与窗口之间存在一定的重叠；

(2) 再对每个窗口中地震数据进行傅里叶变换，得到复数域地震数据z；

(3) 取复数域地震数据z中每一个切片数据分别代入公式(5)~(6)中，形成Hankel矩阵D；

(4) 再将Hankel矩阵D进行奇异值分解；

(5) 然后利用公式(7)~(8)，只用表征有效信号的前k个较大奇异值重构矩阵，得到新的矩阵Dk；

(6) 再将Dk代入公式(9)中做反对角线平均，并提取重构的信号；

(7) 最后对数据进行傅里叶反变换，就可去除随机干扰，恢复时间空间域的有效信号.

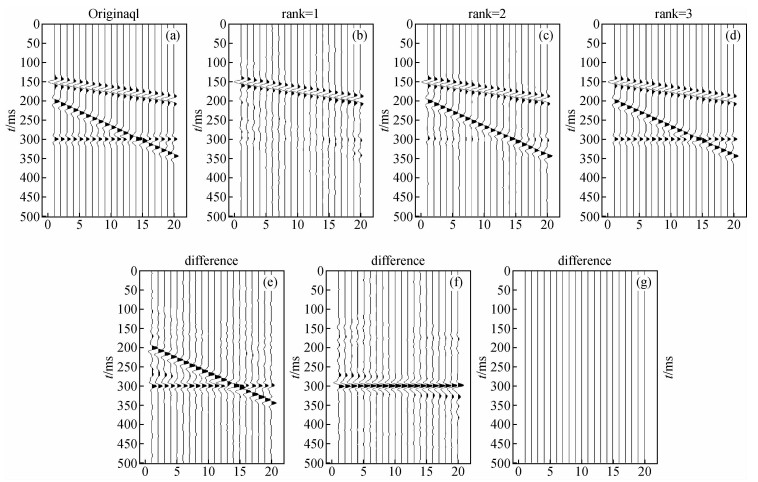
2 模型测试 2.1 信号重构测试

为了验证复数域的混合SVD重构信号的保真度，采用图 1所示的理论模型进行了测试.图 1a是用声波模拟三个倾斜同相轴，图 1b、图 1c与图 1d分别是采用复数域的混合SVD滤波法中秩为1、秩为2及秩为3重构后的结果；图 1e、图 1f与图 1g分别是采用复数域的混合SVD滤波法中秩为1、秩为2及秩为3重构后的偏差；对比重构的结果与偏差可以看出，秩为1与秩为2都不能较好重构倾斜同相轴，而秩为3则能实现有效信号的完整重构.说明了该方法只要选取的合适秩，就能够有效重构水平或者倾斜的有效信号.

图 1 不同秩重构的结果 (a)原始信号；(b)秩为1重构；(c)秩为2重构；(d)秩为3重构；(e)秩为1重构的偏差；(f)秩为2重构的偏差；(g)秩为3重构的偏差. Figure 1 The reconstructed results (a)Theoretical data; (b) The reconstructed results(Rank=1);(c)The reconstructed results (Rank=2); (d) The reconstructed results(Rank=3);(e)The subtraction by SVD Filtering(Rank=1); (f) The subtraction by SVD filtering(Rank=2);(g) The subtraction by SVD filtering(Rank=3).
2.2 随机噪声衰减测试

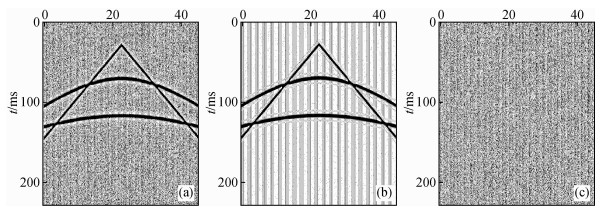
为了验证该方法去随机噪声的效果，采用图 2所示的理论模型进行了测试.图 2a是用声波模拟简单地质模型，模型的主要参数为：Riker子波的主频为25 Hz、采样率为2 ms，样点数为1500，地震道为200，图 2b、图 2c分别是采用复数域的混合SVD滤波法去噪后的结果以及差值剖面.对比去噪结果可以看出，随机噪声得到有效的衰减，而且有效信号没有任何的损失，也没有发生任何的畸变.

图 2 理论模型去噪前后的效果 (a)去噪前单炮；(b)去噪后单炮；(c)差值噪声. Figure 2 Denoising effect with theoretical model (a) Single shot before denoising; (b) Single shot after denoising; (c) Difference before and after denoising.
3 实际资料效果分析 3.1 三种SVD滤波方法应用效果

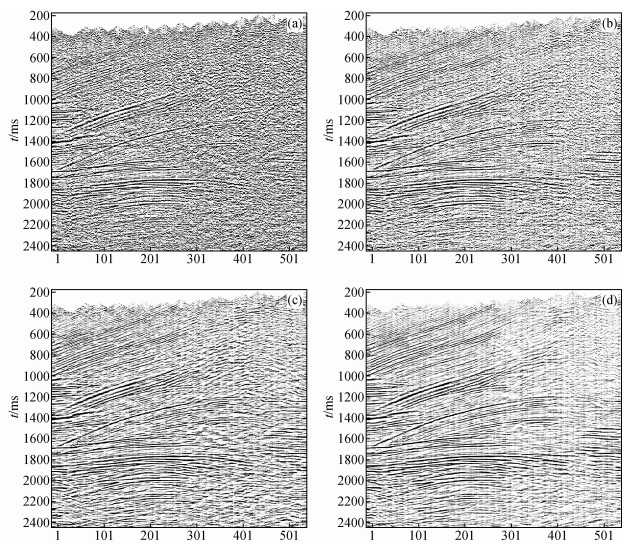
图 3a为四川某地区三维叠后地震数据，随机干扰十分发育.图 3b、图 3c以及图 3d分别为Eigenimage-Cadzow滤波法、Cadzow-Eigenimage滤波法以及Cadzow-Cadzow滤波法压制噪声后的剖面.对比这三种滤波方法的效果，可以得出Cadzow-Cadzow滤波法压制随机干扰的能力最强，其次是Cadzow-Eigenimage滤波法，而Eigenimage-Cadzow滤波法压制随机噪声的能力较弱.但是，就这三种滤波方法的效率来说，Cadzow-Cadzow滤波法的矩阵复杂度最高，其相应的计算耗时最多，而Eigenimage-Cadzow滤波法和Cadzow-Eigenimage滤波法的矩阵复杂度较低，其相应的计算耗时最少，因此在实际应用过程中，我们可以根据生产的时效需求来选择合适的滤波法.

图 3 三种混合Cadzow滤波法的噪声压制效果 (a)叠加数据；(b) Eigenimage滤波(Rank=2)；(c) Cadzow-Eigenimage滤波(Rank=2)；(d) Cadzow-Cadzow滤波(Rank=2). Figure 3 Comparison of the filtering results with different methods (a)Field data; (b)Seismic profile after denoising by Eigenimage-Cadzow filtering; (c) Denoising by Cadzow-Eigenimage filtering method; (d) Denoising by Cadzow-Cadzow filtering.
3.2 实际资料测试处理效果分析

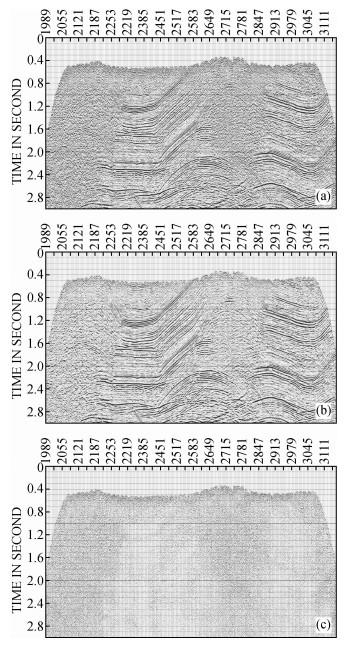
图 4a为四川某地区三维叠后地震数据，随机干扰十分发育，掩盖了部分有效反射信号；图 4b为基于复数域的混合SVD滤波法压制噪声后的剖面，随机干扰得到了有效的衰减, 被随机干扰湮没的有效信号得到了呈现，而且滤波前后的差值剖面图 4c中只有随机噪声，不含有反射波同相轴.由此可以得出，基于复数域的混合SVD滤波法能够有效的压制随机干扰，有效反射同相轴更加连续，而且不损伤曲率较大的有效信号.

图 4 去噪前后的剖面 (a)去噪前剖面；(b)去噪后剖面；(c)差值剖面. Figure 4 Denoising effect (a) Section before denoising; (b) Section after denoising; (c) Difference before and after denoising.
4 结论

本文提出了一种基于复数域的混合SVD滤波法压制随机干扰的方法.该方法充分利用了随机干扰的相干性较差，而有效信号的相干性很强的特点，在频率空间域采用混合SVD滤波法压制随机干扰，克服了频率空间域预测滤波技术压制随机干扰的不足，保真效果好，具有良好的适应性.理论模型和实际数据的处理结果表明：该方法能够最大限度地压制随机干扰，保护有效信号，使反射波同相轴更加清晰、连续性更好，为地震资料的后续处理奠定了有利基础，具有较好的推广应用前景.但是需要指出的是，该方法是通过减少秩的方法压制噪声，秩选取的不好，就有可能造成有效信号的损失，那么在实际应用中如何自适应的减秩，还需要进一步的研究.

致谢 感谢审稿专家提出的修改意见和编辑部的大力支持！
参考文献
[] Abma R, Claerbout J. 1995. Lateral prediction for noise attenuation by t-x and f-x techniques[J]. Geophysics, 60(6): 1887–1896. DOI:10.1190/1.1443920
[] Andrews HC, Patterson CL. 1976. Outer Product Expansions and Their Uses in Digital Image Processing[J]. IEEE Transactions on Computers, 25(2): 140–148.
[] Cadzow J A. 1988. Signal enhancement-a composite property mapping algorithm[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 36(1): 49–62. DOI:10.1109/29.1488
[] CUI Shu-Guo, ZHU Ling-Yan, WANG Jian-Hua. 2012. Random noise attenuation with Cadzow technique in f-x domain and its application[J]. Geophysical Prospecting for Petroleum, 51(1): 43–50.
[] Hornbostel S. 1991. Spatial prediction filtering in the t-x and f-x domains[J]. Geophysics, 56(12): 2019–2026. DOI:10.1190/1.1443014
[] LIU Zhi-Peng, ZHAO Wei, CHEN Xiao-Hong, et al. 2012. Local SVD for random noise suppression of seismic data in frequency domain[J]. Oil Geophysical Prospecting, 47(2): 202–206.
[] PENG Geng-Xin, DENG Xiao-Dong, MAN Yi-Zhi, et al. 2013. Cadzow filtering in f-x domain for random noise attenuation and Its limitation analysis[J]. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Institute), 35(1): 63–66.
[] Trickett S. 2008. F-xy Cadzow noise suppression[C].//78th Annual International Meeting. SEG. Expanded Abstracts, 2586-2590.
[] Trickett S, Burroughs L. 2009. Prestack rank-reduction-based noise suppression[C].//2009 CSPG CSEG CWLS Convention. CSEG Recorder, 34:24-31.
[] Trickett S, Burroughs L, Milton A. 2012. Robust rank-reduction filtering for erratic noise[C].//SEG Annual Meeting. Las Vegas, Nevada:SEG, 129-132. Trickett S R. 2002. F-x eigenimage noise suppression[C].//72nd Annual International Meeting. SEG. Expanded Abstracts, 2166-2169.
[] Trickett S R. 2003. F-xy eigenimage noise suppression[J]. Geophysics, 68(2): 751–759. DOI:10.1190/1.1567245
[] WANG Zhong-Ren, MA Zhong-Gao, LI Min, et al. 1999. 3-D poststack random noise attenuation technique[J]. Geophysical Prospecting for Petroleum, 38(4): 31–35.
[] 崔树果, 朱凌燕, 王建花. 2012. f-x域Cadzow技术分块压制随机噪声及其应用[J]. 石油物探, 51(1): 43–50.
[] 刘志鹏 , 赵 伟, 陈小宏, 等. 2012. 局部频率域SVD压制随机噪声方法[J]. 石油地球物理勘探, 47(2): 202–206.
[] 彭更新, 邓晓东, 满益志, 等. 2013. f-x域Cadzow滤波随机噪声衰减及其局限性分析[J]. 石油天然气学报(江汉石油学院学报), 35(1): 63–66.
[] 王忠仁, 马中高, 李敏, 等. 1999. 三维叠后随机噪声衰减技术[J]. 石油物探, 38(4): 31–35.