地球物理学进展  2017, Vol. 32 Issue (6): 2409-2414   PDF    
引用本文
张建经, 李鸿杰, 唐雅蕾, 等. 2017. 基于芦山主震及余震的地震预警参数与快速震级估算研究. 地球物理学进展, 2017, 32(6): 2409-2414, doi: 10.6038/pg20170617  
ZHANG Jian-jing, LI Hong-jie, TANG Ya-lei, et al. 2017. Research on EEW parameters and rapid magnitude estimation for Lushan earthquake and aftershocks. Progress in Geophysics (in Chinese), 32(6): 2409-2414, doi: 10.6038/pg20170617   
基于芦山主震及余震的地震预警参数与快速震级估算研究
张建经, 李鸿杰, 唐雅蕾, 王皓正     
西南交通大学交通隧道工程教育部重点实验室, 土木工程学院, 成都 610031
收稿日期：2017-05-13; 修回日期：2017-11-06.
基金项目：四川省科技计划项目“高速铁路地震监测、预警及紧急处理成套技术项目”（申报编号15ZC1687，计划编号2015SZ0068）资助.
作者简介：张建经, 男, 1970年生, 博士, 教授, 主要从事岩土工程抗震、边坡防护、路基、地震预警研究.(E-mail:jianzhang1102@swjtu.edu.cn)
摘要：我国四川地区继08年汶川地震后，在2013年再次发生了7级强烈大地震，造成了重大人员伤亡并诱发了多处灾难性滑坡灾害.地震预警系统是防震减灾中最为行之有效的方法之一，其中对地震震级的快速估算是非常重要且困难的.目前世界上提出较早、应用较为广泛的震级估计的方法主要有：基于最大卓越周期（τpmax）、特征周期（τc）和最大位移幅值（Pd）方法.本文利用2013年芦山主震及余震P波初期部分的信息，研究了地震震级快速估算中三个预警参数与震级的相关性，提出了四川地区的震级估计模型，然后对其进行验证分析，并与前人得出的震级估计模型进行对比和评价.结果表明：三种方法均能在短时间内（3 s）有效地进行震级估算，总体而言，Pd方法估算效果最优，τc方法次优，τpmax方法较弱.在震级较大的主震震级估计中，三种方法均出现明显的震级低估（震级饱和）现象.对于τpmax方法，基于芦山地震的估计模型与基于汶川地震的估计模型较为接近，但与南加州地区模型区别较大，可能与四川地区龙门山断裂带的复杂地质条件有关；而τc方法的估计模型大体均较为接近，更具有普适性和稳定性.在地震预警系统的实际应用中，由于目前我国仍处于刚起步阶段，尚未建立密集的地震监测台网系统，因此在短时间内难以得到较为准确的震源距，所以与震源距相独立的τpmax和τc两种算法则显得较为实用，其中τc方法略优于τpmax方法，同时能较好地满足地震预警系统的精度要求，因此推荐使用τc方法应用于四川地区地震预警系统中的快速震级估算.需要注意的是，地震预警参数具有一定的区域适用性，即在不同震源机制、地形和地质条件影响下，不同地方的震级估算回归模型存在一定的差别.
关键词：芦山地震    地震预警    震级估算    τpmax方法    τc方法    Pd方法    
Research on EEW parameters and rapid magnitude estimation for Lushan earthquake and aftershocks
ZHANG Jian-jing , LI Hong-jie , TANG Ya-lei , WANG Hao-zheng     
Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
Abstract: In 2013, five year after the 2008 Wenchuan earthquake, a strong earthquakes of magnitude 7.0 shocked Sichuan region again, which caused heavy casualties and induced the several devastating landslide disaster. Earthquake Early Warning system (EEWs) is one of the most effective ways for seismic hazard mitigation, in which predicting earthquake magnitude is one of the most important and difficult tasks. Currently, different empirical models have been used to estimate earthquake magnitude based on τpmax or τc or Pd methods. We studied the correlation between magnitude and three early warning parameters obtained from the early portion of P-waves for the Lushan earthquake.And we analyzed, verified, evaluated and compared the estimation models with previous studies. Results indicate that three methods can be effectively used for magnitude estimation in a short time (3 s). In general, Pd method works best in magnitude estimation, and then τc method, finally τpmax method. For large scale earthquakes, all of three methods come up the obvious magnitude underestimation (saturation) phenomenon. For τpmax method, the model built up by Lushan sequence is close to the one built up by Wenchuan sequence instead of Southern California, which might be because of the complicated geological conditions in Longmenshan Fault Zone. For τc method, the modelsare close to each other with the higher feasibility and stability.In the practical application of EEWs, at present our country is still at the fledgling stage and the seismic networks have not yet set up. Hence, it is difficult to get a relatively accurate hypocentral distance in a short time. So τpmax and τc method which are independent with distance are more practical. What is more, τc method is slightly better than τpmax method and it can well satisfies the requirement of the EEWs. To draw a conclusion, τc method is recommended to apply in rapid magnitude estimation of EEW system in Sichaun region. However, it should be noted that the earthquake early warning parameters have certain regional applicability. The parameters perform differently under the influence of different focal mechanism, the terrain and geological conditions.
Key words: Lushan earthquake     earthquake early warning     magnitude estimate     τpmax method     τc method     Pd method    
0 引言

2013年4月20日，在汶川地震发生后的第五年，四川芦山地区再次发生了MS 7.0级强烈地震，震中位置为30.3°N，103.0°E, 震源深度为13 km，位于龙门山断裂带南部.反演结果表明，此次地震以逆冲型为主，断层破裂方向长轴呈西南走向(张勇等，2013).近十余年来，龙门山断裂带十分活跃，控制着四川地区主要的大地震，尤其在08年汶川地震以及13年芦山地震两次大地震后，龙门山断裂带仍存在发生大震级地震的危险性，对其进行深入研究的意义显得尤为突出，同时应当强化对潜在地震危险性区域的监测与多学科综合研究，其中尤为重要的是针对四川地区开展地震预警研究工作.

地震预警系统(EEWs)是指在地震发生后，利用前锋P波估计地震信息，在破坏性地震波到达前，向目标区域提供数秒至数十秒的预警时间，以便人们采取紧急处置措施.目前，地震预警系统已在多国和地区应用，如日本(Nakamura, 1988; Odaka et al., 2003)、墨西哥(Espinosa-Aranda et al., 2009)、罗马尼亚(Böse et al., 2007)、土耳其(Alcik et al., 2009)、意大利(Zollo et al., 2009)、美国(Allen andKanamori, 2003; Allen et al., 2009)和中国台湾地区(Wu andKanamori, 2005; Hsiao et al., 2009)等.我国北京首都圈地震预警系统已投入使用并测试五年，2015年我国发布了为地震密集台网建设的五年计划.

地震预警系统包括地震定位(金星等，2012a；马强等，2013)、震级实时计算、预警目标区烈度估计及报警信息发布等几个功能模块(张红才等，2013).其中要准确、快速地估计实时震级是较为困难以及重要的，目前应用较为广泛的震级估计方法有：基于最大卓越周期τpmax(Allen andKanamori, 2003)、特征周期τc(Kanamori, 2005)、地震动位移幅值Pd(Wu andKanamori, 2005)或速度平方积分Ⅳ2参数(Festa et al., 2008)等地震快速震级估算方法.我国学者张红才等(2012)和金星等(2012b)对地震预警震级计算方法进行了相关综述，宋晋东和李山有(2012)对地震预警中两种利用周期估算震级(τpmax和τc)方法进行了比较，并建议在地震预警系统中优先采用3 s τc方法作为震级估算方法.为了在我国四川地区开展地震预警工作，最后利用四川地震数据建立适合于四川的地震震级估计模型.彭朝勇等(2013)则基于汶川主震及余震研究了预警参数τpmax、τc、Pd以及Ⅳ2与震级的相关性，Li等(2017)则进一步探讨了不同时间窗口以及滤波条件对相关预警参数以及震级饱和(震级低估)现象的影响.为进行进一步深入研究，本文基于2013年芦山地震主震及余震观测数据，研究了地震震级快速估算中三个预警参数与震级的相关性，建立快速震级估算回归模型，然后利用汶川地震数据进行验证，并与已有研究的震级估计模型进行对比和评价，重点评价了回归模型和数据时间窗长度对估计震级精度的影响，从而为震级快速估计模型的选择提供依据，以期能够从中推荐一种适用于四川地区地震预警的地震震级快速估计模型.

1 震级估计方法

目前，国际上已发展了一些实用的实时震级计算方法，这些方法大致可以归纳为三大类：与周期(或频率)相关的算法(如卓越周期τpmax、特征周期τc方法等)、与幅值相关的算法(如Pd方法等)及与强度相关算法(如Ⅳ2、MⅠ方法等)，本文着重研究其中τpmax、τc和Pd方法，本节对其进行简要介绍.

1.1 最大卓越周期τpmax方法

Allen和Kanamori(2003)利用式(1)实时计算地震动的卓越周期τp(i)，并认为在P波到来后数秒内卓越周期τp(i)的最大值τpmax与震级成比例关系.公式(1)为

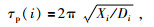
(1)

式中：Xi=αXi-1+xi2；Di=αDi-1+(dx/dt)i2；xi为竖向速度记录；α为平滑参数，一般取值为0.999.

式(1)最早由Nakamura(1988)提出，被应用于日本新干线UrEDAS地震预警系统.Allen和Kanamori(2003)将此方法改进后提出了τpmax方法，该法已被应用于美国加州地震预警测试系统(Wurman et al., 2007)和ElarmS系统(Allen andKanamori, 2003)上.

1.2 特征周期τc方法

Kanamori(2005)在Nakamura(1988)和Allen andKanamori(2003)的研究基础上对卓越周期的计算方法做了改进，用固定的积分区间代替步步积分，即特征周期τc方法，计算公式为

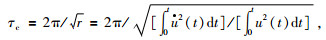
(2)

式中：u(t)为竖向位移记录；t为时间窗口长度，一般取为3 s.目前该方法已被应用于Virtual Seismologist系统(Cua et al., 2009)上.

1.3 最大位移幅值Pd方法

Wu和Kanamori(2005)发现在对地震数据采用高通滤波后，位移记录中P波触发3 s时间内的位移幅值Pd以及地震动峰值速度PGV与地震震级之间存在着良好的相关性.之后，Wu和Zhao(2006)利用发生在美国南加州地区的强震记录，提出了Pd和震中距R与震级M之间的经验关系，并把这个关系用于进行震级估算，见公式(3).目前该方法已被运用于RTMag系统(Kanamori, 2005)和PRESTo系统(LancieriandZollo, 2008; Zollo et al., 2009).Lancieri和Zollo(2008)利用震中距50 km内的强震记录对该方法进行了进一步研究，认为可用捡拾到P波后2 s或4 s时间窗内的Pd值来预测地震震级.公式(3)为

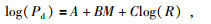
(3)

式中：Pd为采用2阶高通Butterworth滤波器(低频截止频率为0.075 Hz)滤波后的位移记录中P波触发若干秒内的峰值位移；M为事件震级；R为震源距.

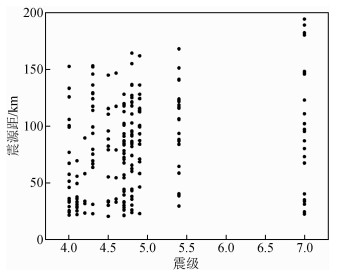
2 地震记录选择及数据处理

中国地震局工程力学研究所“国家强震动台网中心”为本研究提供了数据支持，其中经过挑选后，包括2013年芦山地震数据，共计211个地震记录，其中27条主震记录(MS 7.0)，184条余震记录(MS 4.0~5.4)，这些记录均具有发育较好的P波UD向分量.在地震记录选择中，设置了4个原则：震级大于或等于4.0；震源距在20~200 km范围内；信噪比(SNR)大于30 dB；仅采用UD向记录.此外，本研究的震级标度统一为面波震级，记为M，所用地震记录的震级和震源距分布情况如图 1所示.

图 1 本研究采用的地震记录震级与震源距分布 Figure 1 Magnitude and hypocentral distance of eventsused in this study

对强震记录进行基线校正等基本处理后，进行0.075 Hz Butterworth高通滤波，采用人工捡拾分别从竖直方向分量和水平方向分量确定P波和S波到时.本研究分别研究了P波触发后1 s、2 s和3 s时间窗长度下不同预警参数与震级的相关关系，以确定不同方法的最佳时间窗口长度.

3 震级估计模型建立

基于上述芦山地震记录，利用τpmax、τc和Pd三种方法计算地震动P波段前1s、2s和3s的周期和幅值特征参数，并分别采用公式为

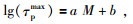
(4)
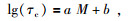
(5)
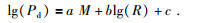
(6)

三种形式拟合，得到特征参数与地震震级间的关系，即建立特征参数与震级的经验公式.然后基于相关系数从中分别选出每种方法拟合程度最优的时间窗口及拟合公式，建立回归模型.

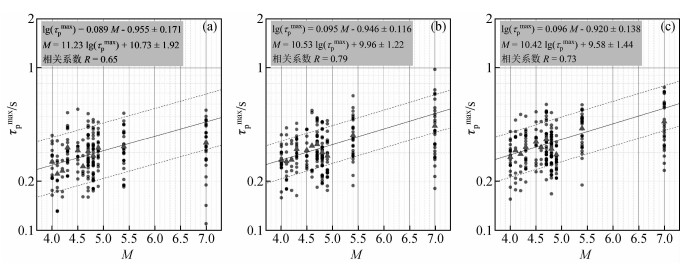
图 2和图 3分别显示了利用P波到达后不同时间窗下计算得到的τpmax与震级、τc与震级的关系，从两图中均能明显看到在主震事件M 7.0中，出现了明显了震级低估(震级饱和)现象，Wu和Zhao(2006)认为震级饱和现象会在短时窗下的大震级事件(M＞6.5)中出现.因此回归模型由余震事件的平均值进行拟合以减少离散性，给出的拟合经验公式、相关系数如图左上角所示，图中实线为最优拟合线并伴有表示±1.0标准差的虚线.基于拟合相关系数的比较可知，在τpmax方法回归模型下2 s时间窗的拟合结果最优，相关系数为0.79，最优回归公式为

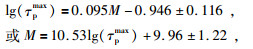
(7)
图 2 τpmax与震级在(a)1 s、(b)2 s和(c)3 s时间窗口下的相关关系 Figure 2 τpmax vs. Magnitudes in time window length of (a) 1 s, (b) 2 s and (c) 3 s

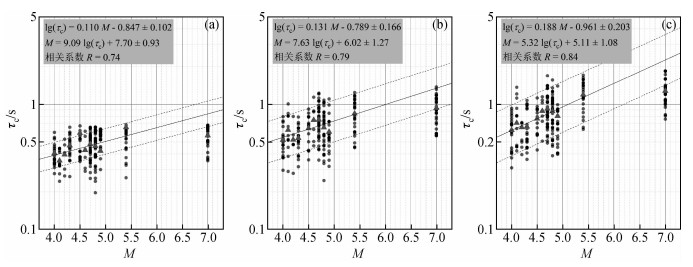
图 3 τc与震级在(a)1 s、(b)2 s和(c)3 s时间窗口下的相关关系 Figure 3 τc vs. Magnitudes in time window length of (a) 1 s, (b) 2 s and (c) 3 s

而τc方法回归模型在3 s时间窗的拟合结果最优，相关系数为0.84，最优回归公式为

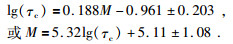
(8)

值得注意的是，τpmax方法和τc方法都属于与周期相关的算法，基于本研究数据库，短时窗内τpmax方法的最优时间窗为2 s，而τc方法的最优时间窗为3 s，在相同时间窗口下，τc方法的相关系数均略大于τpmax方法，即τc与震级的相关性略大于τpmax.我们认为出现上述结果的原因是在短时窗内地震动信号的信噪比相对而言较低，依据式(1)计算的τpmax在步步递归计算的过程中积累了噪声误差，而依据式(2)所计算的τc方法是在固定的积分区间上进行一次积分，因此受到误差积累的影响较小.

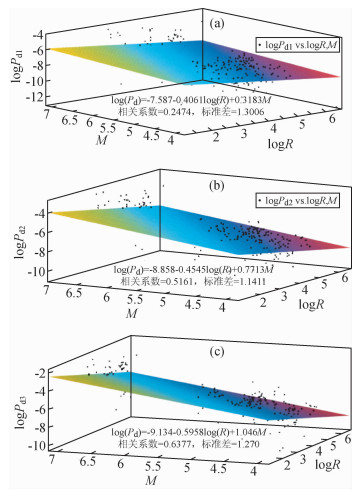
图 4显示了利用P波到达后，Pd方法回归模型式(6)下1 s、2 s和3 s时间窗计算得到的Pd与震级、震源距的关系，经验公式由数据样本总体进行拟合，给出的拟合经验公式和对应相关系数如图中所示.基于拟合相关系数的比较可知，Pd方法回归模型下3 s时间窗的拟合结果最优，相关系数为0.64，最优回归公式为

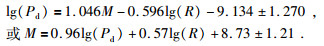
(9)
图 4 Pd与地震震级和震源距间的统计关系 (a)1 s时间窗；(b)2 s时间窗；(c)3 s时间窗. Figure 4 Relationship between Pd and hypocentraldistance in time window lengths of (a) 1 s, (b) 2 s and (c) 3 s
4 估计模型验证及对比

为使本文的工作可以做到实用化，本节通过实际应用来验证上节得出的震级估算回归模型，同时也能直观明确地比较不同方法的震级估算效果.模型验证所使用的数据库为08年汶川地震主余震数据(合计207条记录)，震级范围在4.0级以上，震源距在60 km内，与彭朝勇等(2013)的数据库大体一致.本节首先基于残差分析，在本研究数据库下，横向比较分别在最优时间窗下式(7)、式(8)和式(9)所代表的三种方法，进而评价三种估计模型的估算效果，残差分析结果如图 5所示.

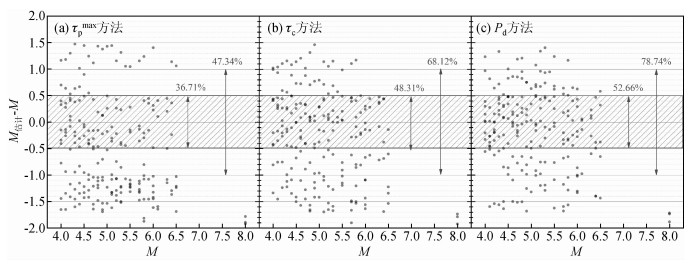
图 5 三种方法计算得到的残差值与实际震级的关系(a)τpmax方法、(b)τc方法和(c)Pd方法 Figure 5 Relationship between residualsand catalogue magnitudes for (a)τpmax, (b) τc, and (c) Pd method

图 5a、b、c分别显示利用τpmax方法、τc方法和Pd方法进行快速震级估算的残差值(估算值-实际值)与实际震级的关系，图中灰色斜线区域表示残差值在±0.5个震级单位内，同时用较短的红色双箭头表示，而较长的双箭头表示残差值在±1.0个震级单位内.即在本数据库下，对于τpmax方法，约有37%的震级估计误差在±0.5个震级单位内，有47%的震级误差在±1.0个震级单位内；τc方法精度略为提高，约有48%的震级估计误差在±0.5个震级单位内，有68%的震级误差在±1.0个震级单位内；Pd方法估算效果最优，约有53%的震级估计误差在±0.5个震级单位内，有79%的震级误差在±1.0个震级单位内.总体而言，在该数据库震级范围M 4.0~6.5下，Pd方法的准确性较高，残差值基本上在±1.0个震级单位以内，估算效果最优，τc方法次优，τpmax方法其次，同时三种方法在主震事件M 8.0中均出现了明显的震级低估(震级饱和)现象.

值得注意的是，虽然在本研究下Pd方法的估算效果最好，但是应用该方法需要已知震源距(或震中距)参数，在地震预警系统的实际应用中，我国在除了北京首都圈以外的地方尚未建立密集的地震监测台网，往往难以利用台网算法(Horiuchi et al., 2005)在短时间内得到较为准确的震源距，而与周期相关的两种算法则与震源距变量相对独立，因此目前对我国大部分地区而言τpmax和τc方法更具有实用性.两种方法相比，τc方法在精度和离散性上均略优于τpmax方法，可以较好地满足地震预警系统的精度要求.

除此以外，从图 5中还能看出，利用芦山地震所建立的模型来验证汶川地震的数据时，图 5c中Pd方法的高估值和低估值的数量大体一样，但图 5a和5b所代表τpmax和τc方法的低估值的数量显然多于高估值的数量，即出现了模型的整体低估.为探究该现象的成因，继续进一步纵向比较本研究中利用芦山地震数据所建立的τpmax和τc方法回归模型与彭朝勇等(2013)利用汶川地震数据以及南加州和其他地区的预警参数回归模型，对比结果如下图 6所示.

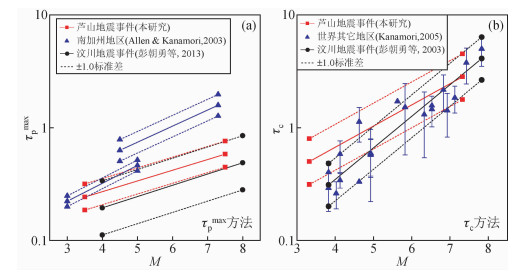
图 6 本研究和前人研究的其他地区的(a)τpmax和(b)τc模型对比 Figure 6 Comparison of (a) τpmax and (b) τc regression between this study and other regions in previous researches

如图 6a所示，对于τpmax方法，相比起南加州模型，本文中利用芦山地震数据所建立模型和彭朝勇等(2013)汶川地震所建立的模型更为接近，笔者认为其原因可能是四川地区的两次地震均发震于龙门山断裂带，且具有接近的震源机制.不过虽然两个模型的斜率十分接近，但芦山模型整体位于汶川模型的上方，因此当使用芦山模型估计汶川数据时，会出现整体的低估现象.相比较而言，图8b中τc方法在不同地区的使用则显得有较好的一致性，但芦山模型总体仍位于汶川模型的上方，同样会出现模型的整体低估.从本节模型的验证和对比中可以得出，地震预警参数具有一定的区域适用性，即在不同震源机制、地形和地质条件影响下，不同地方的震级估算回归模型存在一定的差别.

5 结论与讨论 5.1

本文利用2013年芦山地震的211条主、余震记录(最小震级MS 4.0)建立了基于τpmax、τc和Pd方法不同时间窗口下的地震震级快速估算经验公式，并基于残差分析和与前人工作对比，对建立的模型进行了评价，主要结论如下：

(1) 三种预警参数均能在短时间内(3 s内)有效地估算震级.对于芦山地震最优震级估算拟合公式分别为①lg(τpmax)=0.095M-0.946±0.116(2 s时间窗)；②lg(τc)=0.188M-0.961±0.203(3 s时间窗)；③lg(Pd)=1.046M-0.596lg(R)-9.134±1.270(3 s时间窗).

(2) 在本研究中，Pd方法与震级的相关性最高，估算误差和离散程度最小，估算效果最好，τc方法次优，τpmax方法其次.但对于主震事件(M 7.0)，三种方法均出现了明显的“震级饱和”，即震级低估现象.

(3) 在地震预警系统的实际应用中，我国目前在云南地区尚未建立密集地震台网，往往难以在短时间内得到较为准确的震源(中)距，而与震源距相对独立的τpmax和τc方法显得较为实用.在这两种方法中，τc方法精度较高、离散性和地区差别也较小，略优于τpmax方法，可基本满足地震预警系统的精度要求，因此推荐使用τc方法应用于四川地区地震预警系统中的快速震级估算.

5.2

值得注意的是，在地震震级确定的过程中还涉及到诸多复杂因素，如震源破裂过程、传播介质、场地条件、仪器响应等.从本文模型的验证和对比中可以得出，地震预警参数具有一定的区域适用性，即在不同震源机制、地形和地质条件影响下，不同地方的震级估算回归模型存在一定的差别.尤其在四川地区龙门山断裂带的复杂地质条件下，如何综合运用预警参数，或者发展新的、更可靠的预警参数方法是非常值得继续深入研究的问题.

致谢 感谢中国地震局工程力学研究所“国家强震动台网中心”为本研究提供了数据支持，同时感谢责任编辑和审稿人对本稿件的建议.本研究资金支持源于四川省科技计划项目，高速铁路地震监测、预警及紧急处理成套技术项目.
参考文献
[] Alcik H, Ozel O, Apaydin N, et al. 2009. A study on warning algorithms for Istanbul earthquake early warning system[J]. Geophys. Res. Lett., 36(5): L00B05.
[] Allen R M, Gasparini P, Kamigaichi O, et al. 2009. The status of earthquake early warning around the world:An introductory overview[J]. Seismol. Res. Lett., 80(5): 682–693. DOI:10.1785/gssrl.80.5.682
[] Allen R M, Kanamori H. 2003. The potential for earthquake early warning in Southern California[J]. Science, 300(5620): 786–789. DOI:10.1126/science.1080912
[] Böse M, Ionescu C, Wenzel F. 2007. Earthquake early warning for Bucharest, Romania:Novel and revised scaling relations[J]. Geophys. Res. Lett., 34(7): L07302.
[] Cua G, Fischer M, Heaton T, et al. 2009. Real-time performance of the Virtual Seismologist earthquake early warning algorithm in Southern California[J]. Seismol. Res. Lett., 80(5): 740–747. DOI:10.1785/gssrl.80.5.740
[] Espinosa-Aranda J M, Cuellar A, Garcia A, et al. 2009. Evolution of the Mexican seismic alert system (SASMEX)[J]. Seismol. Res. Lett., 80(5): 694–706. DOI:10.1785/gssrl.80.5.694
[] Festa G, Zollo A, Lancieri M. 2008. Earthquake magnitude estimation from early radiated energy[J]. Geophys. Res. Lett., 35(22): L22307. DOI:10.1029/2008GL035576
[] Horiuchi S, Negishi H, Abe K, et al. 2005. An automatic processing system for broadcasting earthquake alarms[J]. Bull. Seismol. Soc. Am., 95(2): 708–718. DOI:10.1785/0120030133
[] Hsiao N C, Wu Y M, Shin T C, et al. 2009. Development of earthquake early warning system in Taiwan[J]. Geophys. Res. Lett., 36(5): L00B02.
[] Jin X, Zhang H C, Li J, et al. 2012a. Research on continuous location method used in earthquake early warning system[J]. Chinese J. Geophys., 55(3): 925–936. DOI:10.6038/j.issn.0001-5733.2012.03.022
[] Jin X, Zhang H C, Li J, et al. 2012b. Research on earthquake early warning magnitude estimate[J]. Acta Seismologica Sinica, 34(5): 593–610.
[] Kanamori H. 2005. Real-time seismology and earthquake damage mitigation[J]. Annu. Rev. Earth Planet. Sci., 33(1): 195–214. DOI:10.1146/annurev.earth.33.092203.122626
[] Lancieri M, Zollo A. 2008. A Bayesian approach to the real-time estimation of magnitude from the early P and S wave displacement peaks[J]. J. Geophys. Res., 113(B12): B12302. DOI:10.1029/2007JB005386
[] Li H J, Zhang J J, Tang Y L. 2017. Testing earthquake early warning parameters, τmaxp, τc, and Pd, for rapid magnitude estimation in the Sichuan, China, region[J]. Bull. Seismol. Soc. Am., 107(3): 1439–1450. DOI:10.1785/0120160386
[] Ma Q, Jin X, Li S Y, et al. 2013. Automatic P-arrival detection for earthquake early warning[J]. Chinese J. Geophys., 56(7): 2313–2321. DOI:10.6038/cjg20130718
[] Nakamura Y. 1988. On the urgent earthquake detection and alarm system (UrEDAS)[C].//Proceedings of the 9th World Conference on Earthquake Engineering. Tokyo, Japan, 673-678.
[] Odaka T, Ashiya K, Tsukada S, et al. 2003. A new method of quickly estimating epicentral distance and magnitude from a single seismic record[J]. Bull. Seismol. Soc. Am., 93(1): 526–532. DOI:10.1785/0120020008
[] Peng C Y, Yang J S, Xue B, et al. 2013. Research on correlation between early-warning parameters and magnitude for the Wenchuan Earthquake and its aftershocks[J]. Chinese J. Geophys., 56(10): 3404–3415. DOI:10.6038/cjg20131016
[] Song J D, Li S Y. 2012. A comparison between two magnitude estimating methods using predominant period in earthquake early warning[J]. Journal of Earthquake Engineering and Engineering Vibration, 32(6): 174–181.
[] Wu Y M, Kanamori H. 2005. Experiment on an onsite early warning method for the Taiwan early warning system[J]. Bull. Seismol. Soc. Am., 95(1): 347–353. DOI:10.1785/0120040097
[] Wu Y M, Zhao L. 2006. Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning[J]. Geophys. Res. Lett., 33(16): L16312. DOI:10.1029/2006GL026871
[] Wurman G, Allen R M, Lombard P. 2007. Toward earthquake early warning in northern California[J]. J. Geophys. Res., 112(B8): B08311.
[] Zhang H C, Jin X, Li J, et al. 2012. Review on magnitude estimation methods applied to earthquake early warning systems[J]. Progress in Geophysics, 27(2): 464–474. DOI:10.6038/j.issn.1004-2903.2012.02.009
[] Zhang H C, Jin X, Li J, et al. 2013. Progress of research and application of earthquake early warning system (EEWs)[J]. Progress in Geophysics, 28(2): 706–719. DOI:10.6038/pg20130219
[] Zhang Y, Xu L S, Chen Y T. 2013. Rupture process of the Lushan 4.20 earthquake and preliminary analysis on the disaster-causing mechanism[J]. Chinese J. Geophys., 56(4): 1408–1411. DOI:10.6038/cjg20130435
[] Zollo A, Iannaccone G, Lancieri M, et al. 2009. Earthquake early warning system in southern Italy:Methodologies and performance evaluation[J]. Geophys. Res. Lett., 36(5): L00B07.
[] 金星, 张红才, 李军, 等. 2012a. 地震预警连续定位方法研究[J]. 地球物理学报, 55(3): 925–936. DOI:10.6038/j.issn.0001-5733.2012.03.022
[] 金星, 张红才, 李军, 等. 2012b. 地震预警震级确定方法研究[J]. 地震学报, 34(5): 593–610.
[] 马强, 金星, 李山有, 等. 2013. 用于地震预警的P波震相到时自动拾取[J]. 地球物理学报, 56(7): 2313–2321. DOI:10.6038/cjg20130718
[] 彭朝勇, 杨建思, 薛兵, 等. 2013. 基于汶川主震及余震的预警参数与震级相关性研究[J]. 地球物理学报, 56(10): 3404–3415. DOI:10.6038/cjg20131016
[] 宋晋东, 李山有. 2012. 地震预警中两种利用卓越周期估算震级方法的比较[J]. 地震工程与工程振动, 32(6): 174–181.
[] 张红才, 金星, 李军, 等. 2012. 地震预警震级计算方法研究综述[J]. 地球物理学进展, 27(2): 464–474.
[] 张红才, 金星, 李军, 等. 2013. 地震预警系统研究及应用进展[J]. 地球物理学进展, 28(2): 706–719.
[] 张勇, 许力生, 陈运泰. 2013. 芦山4.20地震破裂过程及其致灾特征初步分析[J]. 地球物理学报, 56(4): 1408–1411. DOI:10.6038/cjg20130435