2017, Vol. 32
完整Coriolis力作用下的二维非线性Rossby波
引用本文
尹晓军, 杨联贵, 刘全生, 等. 2017. 完整Coriolis力作用下的二维非线性Rossby波. 地球物理学进展, 2017, 32(6): 2401-2404, doi: 10.6038/pg20170615 
YIN Xiao-jun, YANG Lian-gui, LIU Quan-sheng, et al. 2017. Two-dimensional for nonlinear Rossby waves with a complete Coriolis force. Progress in Geophysics (in Chinese), 32(6): 2401-2404, doi: 10.6038/pg20170615
完整Coriolis力作用下的二维非线性Rossby波
1. 内蒙古大学数学科学学院, 呼和浩特 010021
2. 内蒙古农业大学理学院, 呼和浩特 010018
2. 内蒙古农业大学理学院, 呼和浩特 010018
摘要：本文在正压流体中，从包含完整Coriolis参数的准地转位涡方程出发，在弱非线性长波近似下，采用多时空尺度和摄动方法，推导出大气非线性Rossby波振幅演变满足带有地形强迫的非线性Zakharov-Kuznetsov（ZK）-Burgers方程.结果分析表明：地球旋转的水平分量、β效应、地形效应和耗散都是诱导二维Rossby波产生的重要因子.
关键词：科氏参数 ZK-Burgers方程 Rossby波
Two-dimensional for nonlinear Rossby waves with a complete Coriolis force
1. School of Mathematical Sciences, Inner Mongolia University, Hohhot 010021, China
2. College of Science, Inner Mongolia Agriculture University, Hohhot 010018, China
2. College of Science, Inner Mongolia Agriculture University, Hohhot 010018, China
Abstract:
In barotropic fluids, the nonlinear Zakharov-Kuznetsov(ZK)-Burgers equation in a potential vorticity equation which includes both the vertical and horizontal components of Coriolis parameter is derived to describe Rossby waves that propagate in a plane by using multiple scales and perturbation expansion method in a weakly nonlinear, long wave approximation. It is show that the horizontal component of the earth's rotation plays an important role in the structures of the Rossby waves, at the same time, beta effect, topographic and dissipation effect are also important factor to the Rossby waves.
Key words:
Coriolis parameter
Zakharov-Kuznetsov(ZK)-Burgers equation
Rossby waves
0 引言
在地球流体力学中，当非线性与色散在一个动力系统中达到平衡时，可以产生一种稳定的孤立波.1834年, 自J.S.Russell首次观察到孤立波以来，孤立波的理论就逐步成为一个重要的研究课题, 主要分布在力学、应用数学、物理学、大气以及海洋科学等交叉学科领域里(Infeld and Rowland, 2000; Belashov and Vladimirov, 2005，Yang et al., 2012).在流体孤立波中，Rossby波是其一个主要分支.因此，Rossby波研究对大气和海洋运动有着重要的研究意义，而且许多自然现象都与Rossby波有着联系，如大气阻塞高压以及北太平洋年季变化等(Latif and Barnett, 1994, 1996).自从Long(1964)在β平面近似下(即球面效应)采用摄动方法对Rossby波做了开创性的研究，许多研究者利用KdV方程来描述Rossby波(Haines and Malanotte-Rizzoli, 1991; Mitsudera, 1994; Gottwald and Grimshaw, 1999).之后, One(1981)提出一个新的积分方程(Benjamin-Ono方程)去描述Rossby孤立波，这个方程被称为代数Rossby波孤立子(Gao, 1988)，相比于mKdV方程，BO方程的非线性弱于mKdV方程.直到1993年，Helfrich和Pedlosky(1993, 1995)提出了Boussinesq方程去描述Rossby波.国内研究者，Lü和Lü(2000)采用时空伸缩变换，推导了Boussinesq方程来描述Rossby孤立子，并讨论了质量和能量守恒关系.黎爱兵等(2012)通过数值求解，分析了基本场结构和初始场对Rossby演变的影响，揭示了纬向非均匀基流对大气长波调整的作用.Yang等(2015)推导了带有地形和大气阻塞相互作用的代数Rossby孤立波.上述这些模型虽然能够解释大气阻塞、风暴形成以及木星红斑的物理机制，但是我们发现上述描述Rossby波仅是在一维方程基础上，也就是说Rossby波的传播限于在一个方向上的传播，然而在实际海洋海脊或大气山脉上的传播中，一维方程有它的局限性，不能充分揭示Rossby波孤立子的动力学特征.
另一方面，地球旋转作用的水平分量也是Rossby波一个特征，但许多研究都省略地球旋转作用的水平分量，可以说是“传统近似(White et al., 2005)”，如：宋健等(2012)通过准地转位涡方程研究了切变纬向流作用下具有β效应的赤道包络Rossby孤立波.罗德海(Luo and Ji, 1988)提出的包络Rossby孤立子来描述偶极子阻塞形成的理论.Yang等(2016)推导了非线性Rossby波振幅演变满足非线性Zakharov-Kuznetsov(ZK)-Burgers方程, 但是他们没有讨论Coriolis参数的水平分量对Rossby波动的影响.杨洁和赵强(2010)给出了在完整Coriolis力和热源影响下的超长波的解析解.赵强和于鑫(2008)在半地转近似模式(刘式适和刘式达，1987)下，得到了完整Coriolis力作用下的非线性Rossby波解，他们虽然讨论了完整Coriolis力对地球流体的影响，但作了半地转近似.然而，就动力学角度而言，一直是个有争议的问题(Phillips, 1966; Wangsness, 1970)，Burger(1991)、White和Bromley(1995)通过尺度分析表明，对于大尺度运动，保留-2Ωwcosφ是可取的.Dellar和Salmon(2005)在浅水方程模式下，给出了带有底地形的既有Coriolis参数的垂直分量又有水平分量的位涡方程.Stewart和Dellar(2011)通过分析深海洋流在跨越赤道附近时的数值解，进一步证实了完整科氏力的重要性.Tort和Dubos(2014)利用Hamilton原理，推导出了含有完整Coriolis力的浅水大气方程.
在这里，我们从包含完整Coriolis参数的准地转位涡方程出发，推导了非线性Rossby波振幅演变满足带有地形强迫的非线性Zakharov-Kuznetsov(ZK)-Burgers方程, 同时得到地球旋转的水平分量、β效应、地形效应以及耗散共同作用下的非线性Rossby波的演变规律.
1 方程的推导 1.1 控制方程已知含有科氏力水平分量的位涡方程为
|
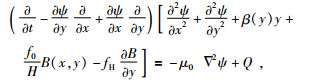
(1) |
其中，f=f0+β(y)y和fH分别表示Coriolis参数的垂直分量和水平分量，且fH为常数，B(x, y)表示底地形函数，ψ(x, y)表示流函数，而μ表示耗散强度，通常取正数，Q表示外源，∇2为二维Laplace算子，定义为
|
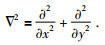
(2) |
侧边界条件为刚壁条件，公式为
|
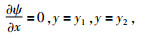
(3) |
其中y=y1、y=y2为南北方向的边界.
引入无量纲参数为
|
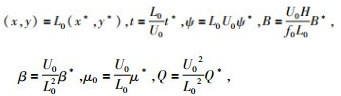
(4) |
其中无量纲的物理量带有星号，L0和H分别表示水平和垂直尺度，U0表示速度尺度.方程(1)和(3)方程分别变为
|
(5) |
|
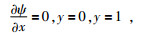
(6) |
这里为书写方便已经去掉了无量纲的星号，并引入两个无量纲参数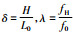
假设总的流函数ψ(x, y, t)由基本流函数和扰动流函数两部分构成，即：
|
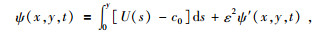
(7) |
把(7)式代入到方程(5)中变为
|
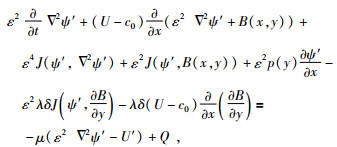
(8) |
其中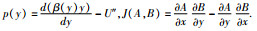
这里，我们采用如下时空伸缩变换，公式为
|
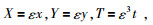
(9) |
其中X、T为缓变量, 即：
|
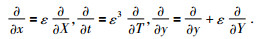
(10) |
为了使地形强迫、耗散和非线性之间达到平衡，设：
|
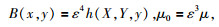
(11) |
同时令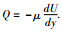
|
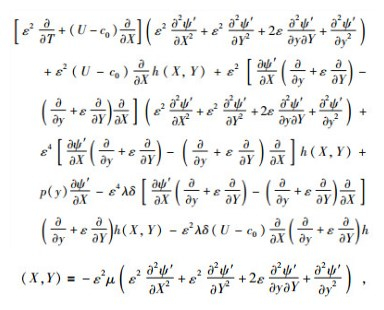
(12) |
|
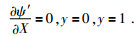
(13) |
设扰动流函数的小参数展开式为
|
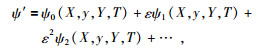
(14) |
把(14)式代入到方程(12)中，得到各阶摄动问题，考虑到最低阶问题，有：
|
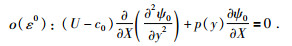
(15) |
假设ψ0的分离变量解公式为
|
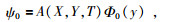
(16) |
把(16)式代入方程(12)、(13)式中，得：
|
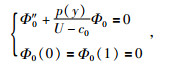
(17) |
其中U-c0≠0，方程组(17)构成一个本征值问题，从该本征值问题可以确定本征函数，但在个本征值问题只能确定Rossby波随纬度的变化规律，不能确定Rossby波振幅的演变，继续求解高阶问题.对于ο(ε)阶，有：
|
(18) |
假设ψ1= 
|
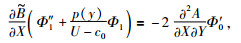
(19) |
通过分析得，
|
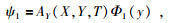
(20) |
方程(19)变为
|
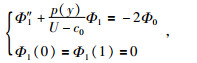
(21) |
其中U-c0≠0，方程组(21)仍是一个本征值问题，可以确定本征函数，但这个本征值问题只能确定Rossby波随纬度的变化规律，不能确定Rossby波振幅的演变，需要继续考虑求解高阶问题.
对于ο(ε2)阶，有：
|
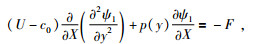
(22) |
其中：
|
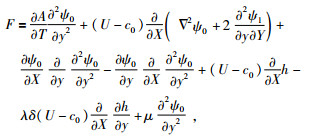
(23) |
进一步化解得：
|
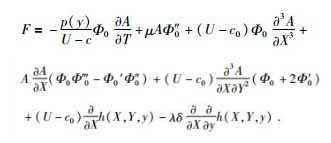
(24) |
利用本征函数的正交性，可得消奇异条件为
|
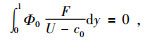
(25) |
由此得到振幅满足下列方程为
|
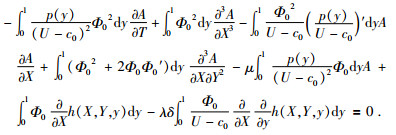
(26) |
进一步整理，得：
|
(27) |
其中系数满足条件为
|
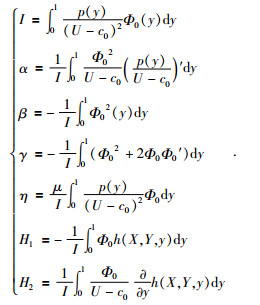
(28) |
在式(27)中，ηA表示耗散项，与标准Burgers方程中的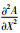
|
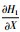
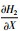
(29) |
这表示不能产生正压不稳定.
2 结论本文从包含完整Coriolis参数的准地转位涡方程出发，推导了带有地形强迫项的非线性Zakharov-Kuznetsov(ZK)-Burgers方程，同时说明在非线性、地形强迫效应、非线性β效应以及耗散相互共同作用下，Rossby波振幅满足非线性Zakharov-Kuznetsov(ZK)-Burgers方程.如果当γ=0, λ=0时，方程(27)就退化为为Yang等(2015)获得广义受迫KdV-Burgers方程；如果不考虑Coriolis参数的水平分量，即当λ=0时，方程(27)就退化为带有地形强迫的非线性Zakharov-Kuznetsov(ZK)-Burgers方程.分析结果表明，基本气流切变、非线性β效应以及耗散都是诱导二维Rossby孤立波产生的重要因子.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持！
参考文献
| [] | Belashov V Y, Vladimirov S V. 2005. Solitary Waves in Dispersive Complex Media:Theory, Simulation, Applications[M]. Berlin: Springer. |
| [] | Burger A P. 1991. The potential vorticity equation:From planetary to small scale[J]. Tellus, 43(3): 191–197. DOI:10.3402/tellusa.v43i3.11926 |
| [] | Dellar P J, Salmon R. 2005. Shallow water equations with a complete Coriolis force and topography[J]. Physics of Fluids, 17(10): 106601. DOI:10.1063/1.2116747 |
| [] | Gao S T. 1988. Nonlinear rossby wave induced by large-scale topography[J]. Advances in Atmospheric Sciences, 5(3): 301–310. DOI:10.1007/BF02656754 |
| [] | Gottwald G, Grimshaw R. 1999. The formation of coherent structures in the context of blocking[J]. Journal of the Atmospheric Sciences, 56(21): 3640–3662. DOI:10.1175/1520-0469(1999)056<3640:TFOCSI>2.0.CO;2 |
| [] | Haines K, Malanotte-Rizzoli P. 1991. Isolated anomalies in westerly jet streams:A unified approach[J]. Journal of Atmospheric Sciences, 48(4): 510–526. DOI:10.1175/1520-0469(1991)048<0510:IAIWJS>2.0.CO;2 |
| [] | Helfrich K R, Pedlosky J. 1993. Time-dependent isolated anomalies in zonal flows[J]. Journal of Fluid Mechanics, 251: 377–409. DOI:10.1017/S0022112093003453 |
| [] | Helfrich K R, Pedlosky J. 1995. Large-amplitude coherent anomalies in baroclinic zonal flows[J]. Journal of Atmospheric Sciences, 52(10): 1615–1629. DOI:10.1175/1520-0469(1995)052<1615:LACAIB>2.0.CO;2 |
| [] | Infeld E, Rowlands G. 2000. Nonlinear Waves, Solitons and Chaos[M]. Cambridge: Cambridge University Press. |
| [] | Latif M, Barnett T P. 1994. Causes of decadal climate variability over the North Pacific and North America[J]. Science, 266(5185): 634–637. DOI:10.1126/science.266.5185.634 |
| [] | Latif M, Barnett T P. 1996. Decadal climate variability over the North Pacific and North America:Dynamics and predictability[J]. Journal of Climate, 9(10): 2407–2423. DOI:10.1175/1520-0442(1996)009<2407:DCVOTN>2.0.CO;2 |
| [] | Li A B, Zhang L F, Zhang L, et al. 2012. The effects of zonal non-uniform basic flow on adjustment of atmospheric long-wave[J]. Chinese Journal of Geophysics, 55(4): 1104–1113. DOI:10.6038/j.issn.0001-5733.2012.04.005 |
| [] | Liu S K, Liu S D. 1987. Nonlinear waves with semi-geostrophic fiow[J]. Acta Meteorologica Sinica, 45(3): 257–266. |
| [] | Long R R. 1964. Solitary waves in the Westerlies[J]. Journal of Atmospheric Sciences, 21(2): 197–200. DOI:10.1175/1520-0469(1964)021<0197:SWITW>2.0.CO;2 |
| [] | Luo D H, Ji L R. 1988. Algebraic Rossby solitary wave and blocking in the atmosphere[J]. Advances in Atmospheric Sciences, 5(4): 445–454. DOI:10.1007/BF02656790 |
| [] | Lü M, Lü K L. 2000. Nonlinear long-wave disturbances excited by localized forcing[J]. Chinese Journal of Computational Physics, 17(3): 259–267. |
| [] | Mitsudera H. 1994. Eady solitary waves:A theory of type B cyclogenesis[J]. Journal of Atmospheric Sciences, 51(21): 3137–3154. DOI:10.1175/1520-0469(1994)051<3137:ESWATO>2.0.CO;2 |
| [] | Ono H. 1981. Algebraic Rossby wave soliton[J]. Physical Society of Japan, 50(8): 2757–2761. DOI:10.1143/JPSJ.50.2757 |
| [] | Phillips N A. 1966. The equations of motion for a shallow rotating atmosphere and the "traditional approximation"[J]. Journal of Atmospheric Sciences, 23(5): 626–627. DOI:10.1175/1520-0469(1966)023<0626:TEOMFA>2.0.CO;2 |
| [] | Song J, Yang L G, Liu Q S. 2012. Solitary Rossby waves with beta effect and topography effect in a barotropic atmospheric model[J]. Progress in Geophysics, 27(2): 393–397. DOI:10.6038/j.issn.1004-2903.2012.02.001 |
| [] | Stewart A L, Dellar P J. 2011. The rôle of the complete Coriolis force in cross-equatorial flow of abyssal ocean currents[J]. Ocean Modelling, 38(3-4): 187–202. DOI:10.1016/j.ocemod.2011.03.001 |
| [] | Tort M, Dubos T. 2014. Dynamically consistent shallow-atmosphere equations with a complete Coriolis force[J]. Quarterly Journal of the Royal Meteorological Society, 140(684): 2388–2392. DOI:10.1002/qj.2274 |
| [] | Wangsness R K. 1970. Comments on "the equations of motion for a shallow rotating atmosphere and the traditional approximation"[J]. Journal of Atmospheric Sciences, 27(3): 504–505. DOI:10.1175/1520-0469(1970)027<0504:COEOMF>2.0.CO;2 |
| [] | White A A, Bromley R A. 1995. Dynamically consistent, quasi-hydrostatic equations for global models with a complete representation of the Coriolis force[J]. Quarterly Journal of the Royal Meteorological Society, 121(552): 399–418. |
| [] | White A A, Hoskins B J, Roulstone I, et al. 2005. Consistent approximate models of the global atmosphere:Shallow, deep, hydrostatic, quasi-hydrostatic and non-hydrostatic[J]. Quarterly Journal of the Royal Meteorological Society, 131(609): 2081–2107. DOI:10.1256/qj.04.49 |
| [] | Yang H W, Xu Z H, Yang D Z, et al. 2016. ZK-Burgers equation for three-dimensional Rossby solitary waves and its solutions as well as chirp effect[J]. Advances in Difference Equations, 2016: 167. DOI:10.1186/s13662-016-0901-8 |
| [] | Yang H W, Yang D Z, Shi Y L, et al. 2015. Interaction of algebraic Rossby solitary waves with topography and atmospheric blocking[J]. Dynamics of Atmospheres and Oceans, 71: 21–34. DOI:10.1016/j.dynatmoce.2015.05.001 |
| [] | Yang H W, Yin B S, Dong H H, et al. 2012. Generation of solitary Rossby waves by unstable topography[J]. Communications in Theoretical Physics, 57(3): 473–476. DOI:10.1088/0253-6102/57/3/21 |
| [] | Yang J, Zhao Q. 2010. Analytical solutions to ultra-long waves with the complete Coriolis force and heating[J]. Acta Physica Sinica, 59(2): 750–753. |
| [] | Zhao Q, Yu X. 2008. Exact solutions to the nonlinear Rossby waves with acomplete representation of the Coriolis force[J]. Chinese Journal of Geophysics, 51(5): 1304–1308. DOI:10.3321/j.issn:0001-5733.2008.05.004 |
| [] | 黎爱兵, 张立凤, 张亮, 等. 2012. 纬向非均匀基流对大气长波调整的作用[J]. 地球物理学报, 55(4): 1104–1113. DOI:10.6038/j.issn.0001-5733.2012.04.005 |
| [] | 刘式适, 刘式达. 1987. 半地转近似下的非线性波[J]. 气象学报, 45(3): 257–266. DOI:10.11676/qxxb1987.032 |
| [] | 宋健, 杨联贵, 刘全生. 2012. 正压大气模式下具有β效应与地形效应的Rossby孤立波[J]. 地球物理学进展, 27(2): 393–397. |
| [] | 杨洁, 赵强. 2010. 有完整Coriolis力和热源影响下超长波的解析解[J]. 物理学报, 59(2): 750–753. DOI:10.7498/aps.59.750 |
| [] | 赵强, 于鑫. 2008. 完整Coriolis力作用下非线性Rossby波的精确解[J]. 地球物理学报, 51(5): 1304–1308. DOI:10.3321/j.issn:0001-5733.2008.05.004 |