2. 西安交通大学电子工程与信息学院, 西安 710049
2. Xi'an Jiaotong University, Xi'an 710049, China
地震波在地层中传播时,其能量、波形等特性会随传播距离发生改变,这一方面是由于球面扩散和透射损失,另一方面是由于地层的固有衰减作用,而且随着频率的升高(大于10 Hz)吸收衰减部分在两者中起主要作用(Spencer,1977).后者导致了地震波能量不可逆地转化为热能而耗散,振幅产生衰减,子波形态发生变化.它是影响地震勘探分辨率的一个重要因素,一般用品质因子Q值来描述.实验表明:地震波在地层中的衰减对岩性变化具有较高的灵敏度,尤其是对于介质内流体性质的变化具有明显反映(辛可锋等,2001).除了可以直接揭示地层特性外,Q值还可用于反Q滤波等处理,提高地震资料的质量和分辨率;另外,也可以根据不同类型波的衰减程度差异,进行裂缝检测、多波多分量的高精度解释等(Tommy,2005).正因如此,Q值的提取方法是地震勘探领域重要的研究方向.
基于在不同计算域中(如时间域、频率域等)地震波能量、振幅、波形、频率等方面的变化,人们研究和发展了多种算法来反演Q值.Tonn(1991)利用VSP数据对当时的10种方法进行了对比,Toverud和Ursin(2005)在其发表的文章中论述了8种衰减模式的对比研究.在这些方法中,应用最早的为振幅衰减法,这是由于地震波衰减最明显的表现就是时间域中振幅的减小.Ward和Young(1980)、Brzostowski和McMechan(1992)、Watanabe和Sassa(1996)等利用地震波振幅的变化作为观测数据进行了衰减成像研究.但由于地震波振幅容易受到诸多信息如几何扩散、散射、震源类型及检波器响应等干扰,一般认为利用振幅衰减法得到的衰减估计值可靠性较低(Tonn,1991).
根据反射地震资料和频率谱(时频谱)变化计算Q值的方法中,最常用的是频谱比法(Jacobson et al., 1981;Dasgupta and Clark, 1998;Jeng et al., 1999).近年来众多学者对其进行了研究改进,如Dasgupta和Clark(1998)对地面地震数据进行计算得出了Q值,并认为在经过动校正后的小偏移距道集上使用该方法效果较好;陈文爽等(2014)进一步在叠前零偏移距道集上引入广义S变换,利用时频域的谱比法寻找含气致密砂岩储层;张繁昌等(2016)基于自适应子波技术计算不同时刻的谱比值,并进行了反Q滤波衰减补偿对比.需要指出的是,该方法在计算过程中,对原始数据质量要求较高(如低噪声干扰),并且其效果依赖于求取斜率的起止值等,认为求得的Q值稳定性不够(Sams and Goldberg, 1990;Tonn,1991).
由于大地滤波作用,低频部分增加,主频向低频方向移动,这种现象于1981年在VSP资料中被发现.基于此,Quan和Harris(1997)提出了质心频率方法.该方法根据地震波吸收过程中高频成份吸收快于低频的特点,通过求取主频的偏移,估测介质的吸收系数.由于波形的质心频率(或脉冲增宽)不受远波场几何扩散和传输/反射效应的影响,因此认为该方法能够获得较为可靠的结果.王辉等(2001)曾将其作为井间地震衰减成像的主要方法之一作过阐述.严又生等(2001)利用该方法进行了井间地震Q值和速度的联合层析成像的研究;朱定等(2006)、武银婷等(2010)曾应用该方法对零偏VSP理论模型进行了试算,验证了利用质心频率量求取Q值的可靠性.在频率域运算使得该方法计算成本大大降低,不需要迭代求解,不用考虑收敛条件,因此认为具有较大的实用价值.
虽然现有方法无一具有普适性(Tonn,1991),但鉴于Q值对地层特性的揭示作用,对各方法进行影响因素分析或适用性分析具有现实意义(陈雨茂,2016).为了满足实际需求,本文选取以上三种反演方法:振幅衰减法、频谱比法、质心频率法,对零偏VSP模型及实际数据进行Q值反演分析对比.
1 质心频率法简介针对Q值的三种主要反演方法——振幅衰减法、频谱比法和质心频率法进行对比应用.由于前两种方法应用较早且广泛,分别见参考文献5和10,不再赘述,此处仅对第三种方法理论进行简要阐述.
质心频率方法是基于地震波在传播过程中,高频成分比低频成分衰减快,导致子波频谱脉冲增宽,质心频率下降的现象提出的.它通过计算震源谱和接收谱质心频率的差值,估算地层的衰减特性.
假设地震波的传播过程由线性系统理论来描述,定义输入信号S(f)的质心频率及方差为
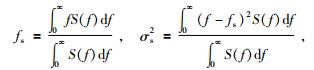
|
(1) |
同样,定义输出信号R(f)的质心频率及方差为
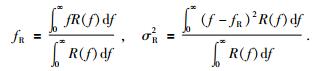
|
(2) |
当输入信号的振幅谱为高斯形状时,存在关系式为
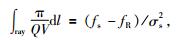
|
(3) |
其中V为地层速度.通过求解式(3) 右端,即可求出左端中地层的衰减.从推导过程可知,该方法不受几何扩散、仪器响应等干扰(Quan and Harris, 1997).需要指出的是,鉴于速度值可从VSP或测井数据中准确地得到,本文认为已知.
在具体求解时,由于VSP实际采集过程中的震源谱fs和σs2不易求.解决的办法有两个,其一:利用震源点附近的接收器.由于其距离震源点很近,故可近似为震源.其缺点在于,靠近炮点的接收器受干扰大,噪声较强,影响计算效果;其二:利用接收井中相邻的接收器,将其频谱分别看作震源谱和接收谱,可将式(3) 写为
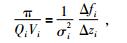
|
(4) |
其中,Δfi=fi+1-fi表示相邻深度处两个接收器的质心频率差;Δzi表示两个相邻接收器之间的距离.通过对井段上相邻检波器的计算,可得整个测量井地层的衰减情形.
图 1展示了一个八层的地质模型及其正演零偏VSP数据(道间隔25 m),各层Q值分别为15、40、60、80、350、30、60、100.从图 1可见,无论是下行波还是上行波,其能量均随着传播距离的增大而减弱,更值得注意的是,其波形展宽,频率亦发生了改变.图 2显示了下行波场的质心频率和方差曲线,可以看出,质心频率随着深度的增加而逐渐降低,从最初的125 Hz降低到了35 Hz,且在Q值越低的地层内降低越快,变化幅度非常明显.另外,震源方差也有明显的变化,变化趋势与质心频率变化一致.
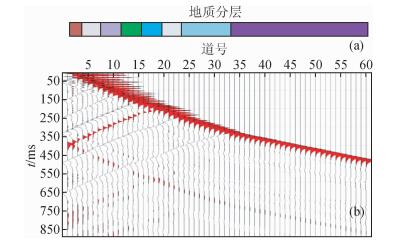
|
图 1 零偏VSP全波场记录(b)与地质模型(a)的对比 Figure 1 Zero-offset VSP data (b) and its corresponding geological model (a) |
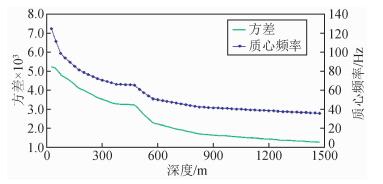
|
图 2 零偏VSP下行波场质心频率和方差曲线 Figure 2 Centroid frequency and variance curves for down-going wavefield |
以多个零偏VSP模型数据为输入,利用三种反演方法(振幅衰减法、频谱比法、质心频率法)计算不同层位的Q值,并与理论值进行对比,总结各方法在薄层、频带宽度及低衰减层、波场成分、界面干扰等不同影响因素下的反演效果.
2.1 薄层为了考察三种反演方法对于薄层的反映能力,设计含有三个相对较薄地层的四层模型,层厚分别为10 m、30 m、15 m、400 m,对应的Q值分别为25、40、50、90,并将检波点间距设定为5 m,震源点位于井口,第一个检波点位于井内5 m处.用于计算的是全波场数据.
该模型的Q值反演曲线如图 3所示.对比可以看出,三种方法均能够反映出地质模型的衰减趋势(尤其是对于最后一个厚层的反演),具有揭示地层吸收衰减特性的能力.但是,从细节来看,三者还是具有不同之处:质心频率法计算值,除了在45 m处出现一个异常点,其他计算值几乎都与理论值相重合,转折点恰好对应地层分界面且变化平缓;频谱比法计算出的第一层Q值为10,超出理论值大约40%.另外,在第一个分界面10 m处的反演值出现较大起跳为120,相对于理论值40,误差达200%;35 m处出现波动值,表明对第二层的厚度划分不够准确;振幅衰减法在15 m处出现较大的异常值,误差达250%,对第二层的厚度刻画不准确,在第四个分界面55 m处出现起跳值.分析原因为:参与计算的数据中含有上行波,频谱比法和振幅衰减法受到较大干扰.
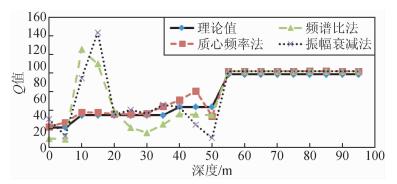
|
图 3 含有三个薄层的地质模型Q值反演曲线对比 Figure 3 Inversion Q curves for a geological model with three thin layers |
当进行Q值反演时,尤其是在频率域,一般要求震源频带要足够宽,主频要足够高,使得接收信号由于岩石衰减引起的频率变化范围足够大.为了验证这一点,利用图 1中具有不同频带宽度0~100 Hz、0~250 Hz和0~400 Hz的全波场零偏VSP记录进行反演,得出不同频率范围下三种Q值计算方法的对比结果,如图 4所示.
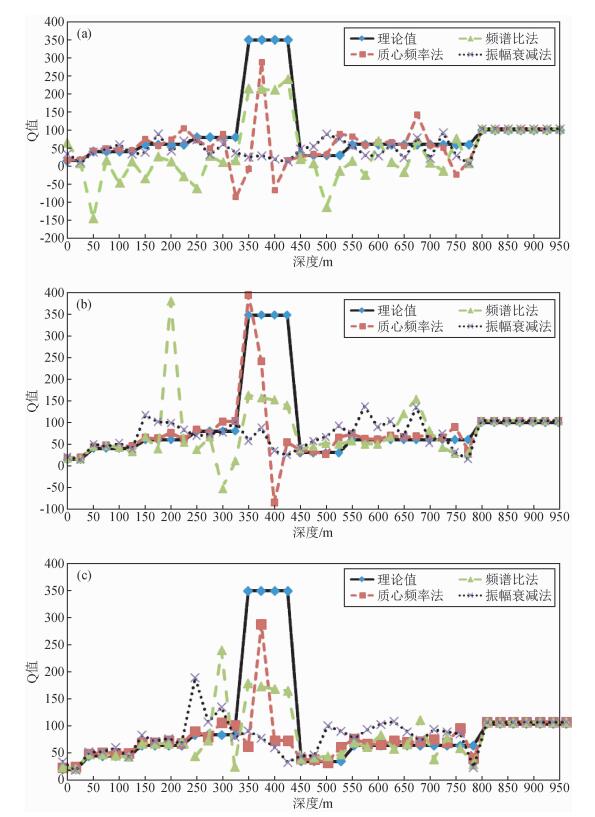
|
图 4 不同频率范围的全波场VSP数据Q值反演曲线对比 (a)频率范围0~100 Hz;(b)频率范围0~250 Hz;(c)频率范围0~400 Hz. Figure 4 Inversion Q curves based on the VSP input data in full wavefield with different frequency ranges (a) 0~100 Hz; (b) 0~250 Hz; (c) 0~400 Hz. |
对比图 4a、4b、4c,分析如下:其最大的差别在于对第五层——低衰减层(高Q层,Q=350) 的反演.在频带0~100 Hz的情况下(图 4a),频谱比法存在跳跃波动,对各个层位几乎都不能得到可靠的结果;振幅衰减法计算结果均比理论值小,并且对分界面的揭示不明显;质心频率法效果稍好,基本能够反映衰减变化趋势,但是对高Q层的计算结果与理论值存在较大偏差,尚未达到150.
相较于0~100 Hz的情况,利用频带0~250 Hz数据(如图 4b)进行反演计算时,频谱比法改善效果最明显,振幅衰减法变化不大,但两者无论是对界面位置的刻画还是地层Q值的揭示,都逊于质心频率法.
而在频带较宽(0~400 Hz)的情况下(如图 4c),三种方法的反演效果得到很大改善:三者基本都能够揭示分界面的位置,计算数值在层内波动较小,接近理论值,对浅层和基底层的反演数据均接近理论值.质心频率法和频谱比法对高Q层的反映能力得到提高,尽管该层反演值整体低于理论值,但是已经能够揭示出高Q值层位的存在,前者对高Q值揭示比较接近理论值,后者对高Q值界面位置揭示较准确.另外,频谱比法反演曲线显示,在250 m的厚层上(深度范围550~800 m),其值出现波动起伏;振幅衰减法对各层位的数值和位置的计算都得到较大改善,但是对高Q层的揭示不够好,计算值仅为75(理论值为350).
从频带范围为0~100 Hz、0~250 Hz、0~400 Hz的反演结果可以得出,频带宽度对Q值反演效果影响较大,尤其是对于高Q值层位.分析原因为:Q值较高的地层,其吸收衰减作用小,对低频段的地震波影响不明显,而对频率较高的地震波,其吸收作用相对要增强很多,衰减差异明显,反演效果能够得到改善.因此,在接收条件允许的情况下,频带应尽量保持较大的范围,尤其是高频成分,则反演效果会更接近真实值,对分界面位置的揭示也更准确.另外,频率范围较小时(0~100 Hz),尽管质心频率法和频谱比法均基于频率变化,但质心频率的计算要更稳定,有很好的反演效果.因此,在实际工作中面对该情况时,可优先选择质心频率法.
2.3 波场成分在实际应用中,通常只利用VSP记录中的下行波场来计算Q值,同时在零偏VSP资料处理中很重要的一个步骤就是波场分离,以期分别得到上行波场和下行波场.但是在实际操作中,会由于各种原因导致分离并不彻底,两者很容易互相掺杂到一起.为了测试不同波场成分的作用,对一个含有衰减的七层地质模型(正演记录频带范围为0~150 Hz)进行Q值的反演计算,见图 5.
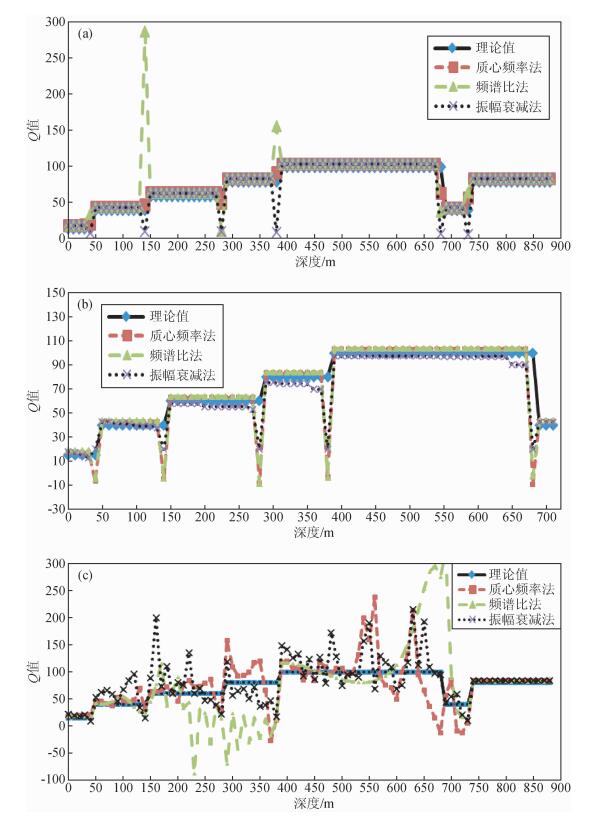
|
图 5 不同波场成分的VSP数据Q值反演曲线对比 (a)下行波场;(b)上行波场;(c)全波场. Figure 5 Inversion Q curves based on different wavefield of input VSP data (a) Down-going wavefield; (b) Up-going wavefield; (c) Full wavefield. |
图 5a是利用三种方法对下行波场求出的Q值随深度的变化曲线.除了在Q值为105的第五层底界面位置出现偏差外,三种方法均能够较好地反映各层的衰减值,对于基底层Q值的反演几乎达到完美.而三种方法的差别主要在于:质心频率法在各个分界面处出现微弱的异常值跳动,与理论值吻合相当准确;而频谱比法和振幅衰减法在各个界面处均出现高或低的异常值跳跃,存在一定的误差.
图 5b是利用三种方法对上行波场反演的Q值曲线.可以看出与利用下行波场得到的计算效果相似,三者在分界面处均出现异常值跳动,但频谱比法和振幅衰减法的反演结果在第三层至第五层界面的上方均出现了偏差.
图 5c是利用三种方法对全波场反演的Q值曲线对比.对比分析可以看出:利用质心频率法计算出的Q值曲线与理论值符合程度较好;在高Q值地层中,其反演结果表现为在该地层的顶界面和底界面出现高异常值,而在层内出现低异常值跳跃;频谱比法和振幅衰减法在250~500 m的深度范围内则出现较大的偏差,不能准确反映正演模型的衰减特性;对于浅层和基底层的反演,三种方法均能得到令人满意的结果.
2.4 界面干扰分界面的反射是反演Q值的干扰.为了说明地层分界面对地震波频散的作用,将2.3节模型各层的密度和速度均设定为同一值,分别为2.0 g/cm3和2000.0 m/s,利用下行波场计算得到的Q值曲线如图 6所示.对比于图 5a可以看出,在这种情况下,频谱比法和振幅衰减法均有显著的改善,分界面处的异常值基本消失,能够准确反映地层的衰减特性;而质心频率法则依然保持其良好的反演效果,没有更进一步的变化.
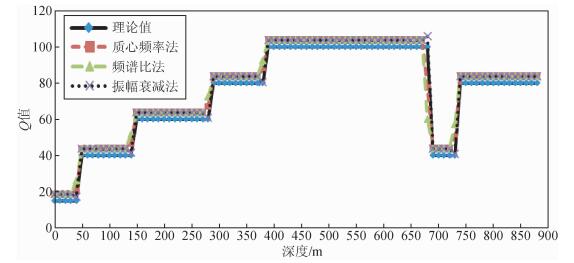
|
图 6 不含反射界面的地质模型Q值反演曲线对比(各地层具有相同的速度和密度) Figure 6 Inversion Q curves based on the model with the same velocity and density for each layer |
由此可以推断,质心频率法对界面的干扰能力要优于频谱比法和振幅衰减法,抗界面干扰能力强,在下行波场的分界面处不出现突跳点,直接反映真实Q值.
3 实际应用对比分析引用某地区一零偏VSP资料,图 7是其原始采集记录.从图中可以明显看出,在地下30 m和20 m深度处,分别出现下行波和反射波的交汇,揭示了反射界面的位置.图 8是检波点深度2 m和7 m的时频分析结果,对比可以看出,频率范围从0~180 Hz降低到0~100 Hz,高频吸收严重,揭示该地层衰减特性突出,符合此地区采集条件——近地表疏松地层.
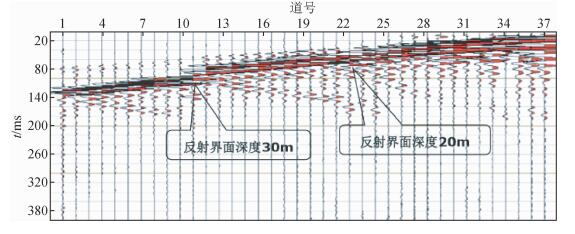
|
图 7 某地区实际零偏VSP记录 Figure 7 A field zero-offset VSP data |
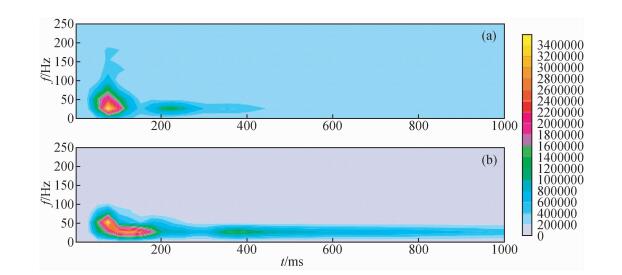
|
图 8 某地区两道零偏VSP记录时频分析对比 (a)对应检波点深度2 m;(b)对应检波点深度7 m. Figure 8 The time-frequency analysis for the field data (a)From the receiver depth of 2 m; (b)From the receiver depth of 7 m. |
图 9是利用三种方法对该零偏VSP资料进行反演得到的Q值曲线与地质取芯分层、层速度的对比:在已知的反射分界面深度上,Q值出现了强的起跳,在古土壤的地层处,Q反演值较大,而在黄土的地层处,Q值反演较小,这符合岩性特征——相对而言,古土壤压实性强,结构致密,土质坚硬,其衰减作用要小些,对应较大的Q值;而黄土疏松、压实性差,因此其对地震波的衰减能力强,Q值较低.
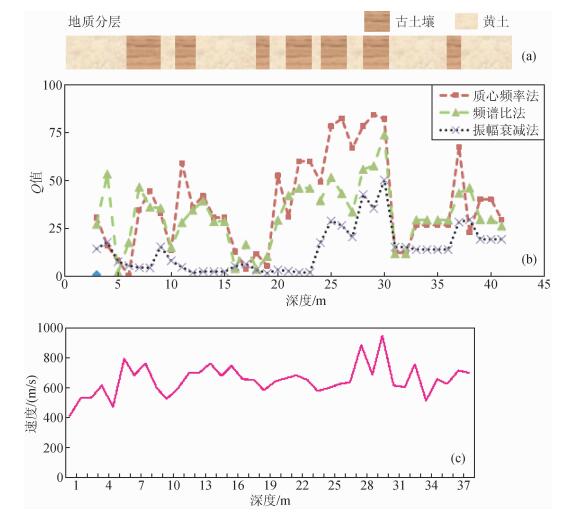
|
图 9 Q值反演曲线(b)与地质分层(a)、速度曲线(c)对比 Figure 9 Comparison inversion Q curves (b) with geological layers (a) and velocity curve (c) |
在三种方法中,质心频率法与地层的吻合程度是最好的:从层速度曲线来看,其变化在分界面处并没有较好地反映岩性的变化,而质心频率法揭示了地层的衰减特性, 能够更为准确地反映出地质层位的位置,Q值分层比速度更为敏感、准确;频谱比法可以得到Q值的主要变化趋势;振幅衰减法得到的反演效果较差.其原因在于,实际资料受多种外界因素干扰,而质心频率方法具有较好的抗干扰能力.
4 结论 4.1本文基于多个零偏VSP数据,对比分析了质心频率法与振幅衰减法、频谱比法在Q值反演计算中的差异.针对多个影响因素(薄层、频带宽度及低衰减层、不同波场成分、反射界面干扰),重点分析了不同方法对衰减值与层位位置揭示的准确性及差异性.算例与文献表明,振幅衰减法的稳定性较差.频谱比法较为稳定,在高Q值层位位置揭示方面表现优异,但对其他层位的揭示欠佳,不适于实际地震记录成像.从现有的论述来看,一般情况下质心频率法表现更为稳定,对高Q值层的反演值较为接近理论值,对各个层位(甚至是薄层)的揭示准确.因此,认为该方法具有较大实际应用价值.
4.2另外,本文未涉及信号在不满足高斯假设时的质心频率法前期处理,已有学者对其进行了研究讨论(高静怀和杨森林,2007;王宗俊,2015),相信这会使得该方法应用范围更广.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Brzostowski M A, McMechan G A. 1992. 3-D tomographic imaging of near-surface seismic velocity and attenuation[J]. Geophysics, 57(3): 396–403. DOI:10.1190/1.1443254 |
| [] | Chen W S, Guan L P, Li Z C, et al. 2014. Prestack Q-inversion based on generalized S transform[J]. Geophysical Prospecting for Petroleum, 53(6): 706–712. DOI:10.3969/j.issn.1000-1441.2014.06.011 |
| [] | Chen Y M. 2016. Full combinatorial optimization Q value calculation method[J]. Process in Geophysics, 31(4): 1557–1561. DOI:10.6038/pg20160419 |
| [] | Dasgupta R, Clark R A. 1998. Estimation of Q from surface seismic reflection data[J]. Geophysics, 63(6): 2120–2128. DOI:10.1190/1.1444505 |
| [] | Gao J H, Yang S L. 2007. On the method of quality factors estimation from zero-offset VSP data[J]. Chinese Journal of Geophysics, 50(4): 1198–1209. DOI:10.3321/j.issn:0001-5733.2007.04.029 |
| [] | Jacobson R S, Shor Jr G G, Dorman L M, et al. 1981. Linear inversion of body wave data-Part Ⅱ:Attenuation versus depth using spectral ratios[J]. Geophysics, 46(2): 152–162. DOI:10.1190/1.1441185 |
| [] | Jeng Y, Tsai J Y, Chen S H. 1999. An improved method of determining near-surface Q[J]. Geophysics, 64(5): 1608–1617. DOI:10.1190/1.1444665 |
| [] | Quan Y L, Harris J M. 1997. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 62(3): 895–905. DOI:10.1190/1.1444197 |
| [] | Sams M, Goldberg D. 1990. The validity of Q estimates from borehole data using spectral ratios[J]. Geophysics, 55(1): 97–101. DOI:10.1190/1.1442776 |
| [] | Spencer T W, Edwards C M, Sonnad J R. 1977. Seismic wave attenuation in nonresolvable cyclic stratification[J]. Geophysics, 42(5): 939–949. DOI:10.1190/1.1440773 |
| [] | Tonn R. 1991. The determination of the seismic quality factor Q from VSP data:A comparison of different computational methods[J]. Geophysical Prospecting, 39(1): 1–27. DOI:10.1111/gpr.1991.39.issue-1 |
| [] | Toverud T, Ursin B. 2005. Comparison of seismic attenuation models using zero-offset vertical seismic profiling (VSP) data[J]. Geophysics, 70(2): F17–F25. DOI:10.1190/1.1884827 |
| [] | Wang H, Chang X, Gao F. 2001. Several methods of crosswell seismic attenuation tomography[J]. Progress in Geophysics, 16(1): 104–109. DOI:10.3969/j.issn.1004-2903.2001.01.014 |
| [] | Wang Z J. 2015. Quality factor estimation by centroid frequency shift of spectrum fitting[J]. Geophysical Prospecting for Petroleum, 54(3): 267–273. DOI:10.3969/j.issn.1000-1441.2015.03.004 |
| [] | Ward R W, Young C Y. 1980. Mapping seismic attenuation within geothermal systems using teleseisms with application to the Geysers Clear Lake region[J]. J. Geophys. Res., 85(B10): 5227–5236. DOI:10.1029/JB085iB10p05227 |
| [] | Watanabe T, Sassa K. 1996. Seismic attenuation tomography and its application to rock mass evaluation[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 33(5): 467–477. |
| [] | Wu Y T, Zhu G M, Liu Y K, et al. 2010. Study on CFS method in Q inversion using zero-offset VSP data[J]. Progress in Geophysics, 25(6): 1897–1904. DOI:10.3969/j.issn.1004-2903.2010.06.003 |
| [] | Xin K F, Li Z C, Wang Y G, et al. 2001. Formation equivalent absorption coefficient inversion[J]. Geophysical Prospecting for Petroleum, 40(4): 14–20. |
| [] | Yan Y S, Yi M L, Wei X, et al. 2001. Joint tomographic imaging for cross-hole seismic velocity and Q value[J]. Oil Geophysical Prospecting, 36(1): 9–17. |
| [] | Zhang F C, Zhang X X, Zhang L Q, et al. 2016. Extraction method for quality factor Q based on adaptive wavelet decomposition[J]. Geophysical Prospecting for Petroleum, 55(1): 41–48. DOI:10.3969/j.issn.1000-1441.2016.01.006 |
| [] | Zhu D, Min X G, Gu H M. 2006. Inversion of attention coefficient based on frequency shift[J]. Process in Exploration Geophysics, 29(1): 30–33. |
| [] | 陈文爽, 管路平, 李振春, 等. 2014. 基于广义S变换的叠前Q值反演方法研究[J]. 石油物探, 53(6): 706–712. DOI:10.3969/j.issn.1000-1441.2014.06.011 |
| [] | 陈雨茂. 2016. 全组合最优化Q值计算方法[J]. 地球物理学进展, 31(4): 1557–1561. DOI:10.6038/pg20160419 |
| [] | 高静怀, 杨森林. 2007. 利用零偏移VSP资料估计介质品质因子方法研究[J]. 地球物理学报, 50(4): 1198–1209. DOI:10.3321/j.issn:0001-5733.2007.04.029 |
| [] | 王辉, 常旭, 高峰. 2001. 井间地震波衰减成像的几种方法[J]. 地球物理学进展, 16(1): 104–109. DOI:10.3969/j.issn.1004-2903.2001.01.014 |
| [] | 王宗俊. 2015. 基于谱模拟的质心法品质因子估算[J]. 石油物探, 54(3): 267–273. DOI:10.3969/j.issn.1000-1441.2015.03.004 |
| [] | 武银婷, 朱光明, 刘伊克, 等. 2010. 零偏VSP反演Q值CFS方法及影响因素研究[J]. 地球物理学进展, 25(6): 1897–1904. DOI:10.3969/j.issn.1004-2903.2010.06.003 |
| [] | 辛可锋, 李振春, 王永刚, 等. 2001. 地层等效吸收系数反演[J]. 石油物探, 40(4): 14–20. |
| [] | 严又生, 宜明理, 魏新, 等. 2001. 井间地震速度和Q值联合层析成像及应用[J]. 石油地球物理勘探, 36(1): 9–17. |
| [] | 张繁昌, 张汛汛, 张立强, 等. 2016. 基于自适应子波分解的品质因子Q提取方法[J]. 石油物探, 55(1): 41–48. DOI:10.3969/j.issn.1000-1441.2016.01.006 |
| [] | 朱定, 闵小刚, 顾汉明. 2006. 基于主频偏移反演地层的吸收系数[J]. 勘探地球物理进展, 29(1): 30–33. |
 2017, Vol. 32
2017, Vol. 32

