波动方程数值模拟中的有限差分法、传统有限元法、谱元法、间断有限元法具有各自的优势,在高精度逆时偏移和波形反演中已得到广泛的应用.谱元法结合Legendre或Chebyshev伪谱法与有限元法的优点,允许不同的单元大小,且在不同单元中用不同阶基函数逼近波场值, 谱元法能够采用较稀疏单元划分达到有限元法相同精度,高阶插值不出现Runge现象且并行计算容易实现(Tromp, et al., 2008; Komatitsch, et al., 2010).严珍珍等(2009)利用谱元法结合高性能并行计算,分别对人工点源和复合源激发的汶川大地震地震波的全球传播过程进行数值模拟.王秀明等(2007)完整推导了谱元法中Legendre和Chebyshev展开的有关计算公式,通过引入空间域中在预先条件下的共轭梯度的元到元算法和时间域中时间积分的交错网格的预期/多次校正算法,不需要形成有限元中的全局矩阵和有效载荷矢量,从而提高了谱元法计算精度和计算效率.二维波动方程Legendre谱元法程序包SPECFEM2D采用四边形单元对各向同性或各向异性介质进行弹性波场模拟、伴随波场模拟以及全波形反演(Komatitsch and Vilotte, 1998; Tromp, et al., 2008),谱元法将GLL积分节点取为插值点,在GLL点上构造基函数,生成的质量矩阵为对角矩阵.刘有山等(2014)通过波动方程谱元法数值模拟表明,与经典的四边形网格谱元法相比,三角网格谱元法能更好适应剧烈起伏地形,但波场模拟精度较低.
四边形网格谱元法波场模拟通常采用贴体网格(贾艳艳等, 2014;李振春等, 2016)和非贴体网格剖分方式,每个单元称为谱单元.本文将四边形谱元法波场模拟中属性建模方式归纳为单元属性建模和节点属性建模两种方式.单元属性建模是根据单元号和属性号对谱单元属性(密度、波速和弹性参数)赋值,在谱单元内属性为常数;节点属性建模方式是利用插值方法对所有谱单元的GLL点进行属性赋值,在单元内属性可以不是常数,比单元属性建模方式更具灵活性.
GLL节点属性建模可以采用双线性插值(马德堂等, 2014)和快速径向基函数插值法(Yokota et al., 2010)实现.双线性插值需要四边形网格分布的属性控制点实现所有谱单元GLL点属性插值,如果属性控制点是散乱的,双线性插值会失效.针对N个离散控制点插值问题,Yokota等(2010)提出计算复杂度和内存需求量均为O(N)的Gauss径向基函数插值并行算法,称为快速径向基函数插值,能处理控制点个数N=103~106,且其迭代收敛速度快.魏亦文和王彦春(2012)实现了薄板样条(TPS)径向基函数插值重构近地表模型,TPS插值需要O(N3)运算量和O(N2)的内存.Gumerov和Duraiswami(2010)提出改进的迭代求解法(如FGP05) 使径向基函数插值过程计算复杂度达到O(NlogN),但仍然需要O(N2)的存储量.
1 波动方程Legendre谱元法中的GLL点关于波动方程谱元法的理论公式推导和求解过程(Komatitsch and Vilotte, 1998; Tromp et al., 2008; Komatitsch et al., 2010; Cupillard et al., 2012),此处不赘述.在谱元法中,Lagrange多项式插值节点常取为GLL(Gauss-Labotto-Legendre)积分点(李孝波等, 2014).正方形参考单元(母单元)区域为Λ[-1, 1],其上任意点ψ(ξ, η)都满足-1≤ξ, η≤1.母单元使用n阶Lagrange插值多项式作为基函数,共有(n+1)2个GLL点,在ξ或η方向上各有n+1个GLL点.在ξ方向上,GLL点坐标ξα满足方程:
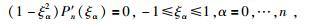
|
(1) |
其中P′n(ξ)是n阶Legendre多项式的导数,n阶Legendre多项式为
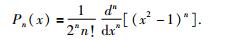
|
在ξ方向上,通过n+1个GLL点ξα(-1≤ξα≤1, α=0, …, n)构造n+1个Lagrange插值基函数,公式为
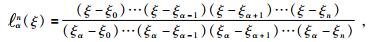
|
(2) |
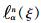
|
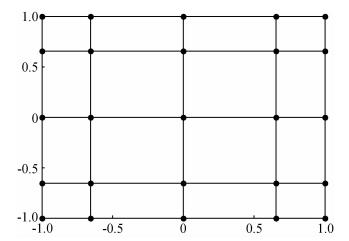
图 1 单元内GLL点 Figure 1 GLL points of an element |
|
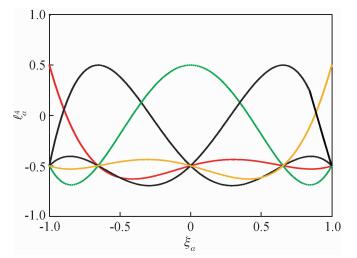
图 2 Lagrange插值基函数 Figure 2 Lagrange interpolation basis function |
SPECFEM2D程序包可将Gmsh创建的1阶或2阶四边形单元贴体网格转换成内部格式的4阶单元,即谱单元默认为4阶单元,每个谱单元包含25个GLL点.SPECFEM2D程序包也可以直接创建内部格式的规则矩形网格.为了保证谱元法计算结果的精度,要求每个波长内至少包含5个GLL点(Cupillard et al., 2012),应满足条件为
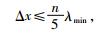
|
(3) |
式中Δx为单元边长,n为Lagrange多项式的阶数,默认n=4,λmin为传播介质的最短波长,当震源为Ricker子波时,横波最短波长λmin=[Vs/fc]min,为介质中横波波速,fc为截止频率,fc=2.5fp,fp为峰值频率.刘有山等(2014)利用7阶谱单元精确模拟面波,提出三角网格谱元法在每个最短的面波波长内至少有11个采样点,然而经典的四边形谱元法只需要4个采样点.实际上最短波长可以是纵波、横波、面波的最短波长,由式(3) 可以得到三种波最短波长内样点数计算公式为
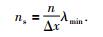
|
(4) |
谱元法若采用Newmark积分方法,为保证计算稳定性,时间步长必须满足CFL条件为
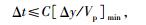
|
(5) |
其中Δy是相邻GLL点之间的距离,Vp是介质中纵波波速,C为CFL条件数,通常在0.3和0.4之间.
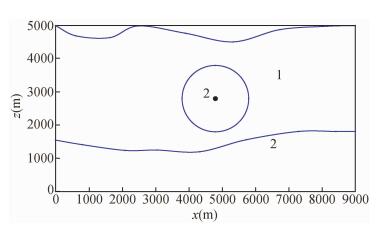
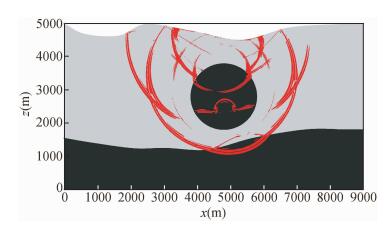
2 单元属性建模单元属性建模方式是对于已经剖分好的四边形网格,根据单元号和属性号对单元属性进行赋值,适合块状贴体网格的属性建模.通过Gmsh建立带起伏地形的块状几何模型,属性号如图 3所示,密度、纵横波速度如表 1所示,最大纵波波速6000 m/s,最小横波波速2000 m/s.为保证计算精度,根据式(3) 单元边长Δx与最小波长λmin存在约束关系,设置单元边长Δx=50 m,Ricker子波峰值频率fp=30 Hz.由式(4) 计算得到最短横波波长内有5.3个样点,最短纵波波长内有10.7个样点.在SPECFEM2D程序中利用属性号对已编号的谱单元进行属性赋值后,根据式(5) 设置时间采样间隔Δt=1×10-4 s进行谱元法波场模拟,t=0.72 s时的波场快照如图 4所示,结果表明以上参数设置能较好压制数值频散.
|
图 3 块状几何模型 Figure 3 Block geometry model |
|
|
表 1 块体属性 Table 1 Block attribute |
|
图 4 0.72 s波场模拟快照 Figure 4 Snapshot of wave field simulation at 0.72 s |
单元属性建模方式对于块状分布的地质结构特别适用,但是对于复杂非均匀地质体的属性建模在单元内属性为常数是不精确的.节点属性建模方式在单元内部的GLL点上对属性赋值,从而能更好建立非均匀介质模型.谱元法波场正演模拟程序包SPECFEM2D对于Gmsh软件所建立四边形贴体网格的质量合格判定标准为,必须满足每个单元上Jacobi行列式的值大于0以及单元最大偏度小于0.75的条件,这会导致复杂构造模型贴体网格过程耗时过长.例如常用的Marmousi模型很难建立准确的几何模型和贴体网格,此时只需要矩形单元非贴体网格,虽然几何模型缺失但存在一些属性控制点数据.如果这些属性控制点分布在规则的矩形网格控制点上,可以采用双线性插值所有GLL点属性值.如果这些属性控制点是散乱的可以采用快速径向基函数插值所有GLL点属性值.在快速径向基函数插值法中,规则分布属性控制点也可以当成散乱控制点进行插值计算.本文针对稠密网格控制点个数N>104情况,主要研究双线性插值和快速Gauss径向基函数插值属性建模方式.
3.1 双线性插值双线性插值将规则属性网格节点作为控制点,将谱单元的GLL点作为待插值点.双线性插值公式为
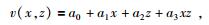
|
(6) |
通过式(6) 建立线性方程组,可以快速求解系数ai, i=1、2、3、4,从而内插单元内GLL点上属性值.
3.2 快速Gauss径向基函数插值快速Gauss径向基函数节点属性插值建模方式,利用Krylov子空间法(KSP)有效完成算法的并行计算(Yokota et al., 2010).采用基于径向基函数插值建模流程,控制点是散乱点,有序节点可以当作散乱点进行处理.在二维地下介质属性插值建模中,已知散乱点x及属性函数为f(x),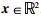
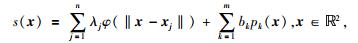
|
(7) |
φ为径向基函数,‖·‖为欧氏范数或L2范数,{p1, p2, …, pm}是次数小于m的所有双变量多项式空间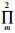
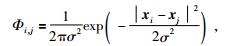
|
(8) |
其中,σ为高斯基函数的标准偏差.当σ不变,Gauss函数值随着距离衰减很快,当|xi-xj|>8σ时,高斯函数对于双精度计算的影响可以被忽略.矩阵Φ中的元素Φi, j可以近似为0.式(7) 可简写为AX=b,如果计算区域大小远远大于σ,那么矩阵A是非常稀疏的.设计算点之间的平均距离为h,h/σ越小插值越具全局性,显然h/σ决定了Gauss径向基函数插值的精度.
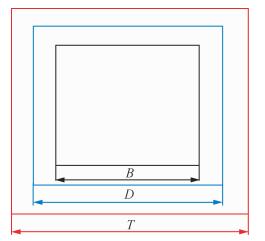
快速Gauss径向基函数插值算法使用Petsc中GMRES求解器,采用限制可加性Schwarz方法作为预条件子(Balay et al., 2004; Abhyankar, et al., 2013),利用区域分解法将区域Ω分解成多个子区域后进行并行求解.随着计算区域内节点数N的增加,快速Gauss径向基函数插值计算量为O(N).基于域分解和PC集群的并行计算不但可以节约存储,还能提高收敛速度.设区域重叠度为h/σ,D是重叠区域尺度,B是非重叠区域尺度,T表示矩阵向量积中非0元素范围尺度,如图 5所示.为确保快速Gauss径向基函数插值算法具有适当的收敛速度和精度,实际应用中应该合理选取B、T、D的值.
|
图 5 重叠单元中的参数关系 Figure 5 The relationship of parameters in overlapping element |
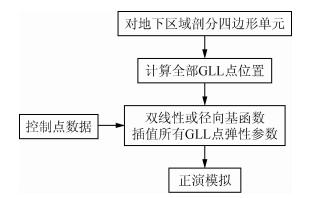
节点属性建模方式直接对GLL点进行属性赋值,适合SPECFEM2D软件包自带规则矩形网格建模.与单元属性建模方式相比,节点属性建模方式可使单元内每个GLL点上属性值不一致,从而确保复杂非均匀介质属性建模的高精度性.GLL点属性赋值可以通过双线性插值和快速Gauss径向基函数插值两种插值方式来实现.基于节点属性建模技术的谱元法波场模拟技术路线,如图 6所示.
|
图 6 波场模拟技术路线图 Figure 6 Technology roadmap for wave field simulation |
以Marmousi复杂速度模型为例,x方向长度lx=9200,z方向深度lz=3000 m,属性控制点分布于均匀网格节点上,在各方向上节点间距为4 m,属性控制点总数N=2301×751=1728051>106.对于Marmousi模型,如果采用贴体网格剖分方式,必须得到该模型的精确几何模型,会相当困难,此时若采用非贴体网格剖分方式具有更大灵活性.首先对整个区域进行均匀四边形网格剖分,然后利用稠密的属性控制点采用双线性插值或者快速Gauss径向基函数插值GLL点的属性完成建模.
考虑到内存需求和模拟速度,本次设置Marmousi模拟谱单元数为460×150=69000,单元边长Δx=20 m,每个谱单元内GLL点为25个,因此整个区域中GLL点总数为1725000.对于稠密属性控制点N>106,采用双线性插值建模耗时55 s.为了测试快速Gauss径向基函数插值效率,首先,对区域按最小方向长度lz=3000 m进行归一化,在h/σ=1,B/σ=10,T/B=1.9固定不变的前提下,设置不同的σ.然后,对原始属性网格进行抽稀得到新的属性控制点个数N.最后,在相同KSP迭代误差终止条件下,采用快速Gauss基函数插值GLL点属性,参数设置如表 2所示.表 2中控制点数N=17556对应抽稀网格间隔数为10,控制点数N=108288对应抽稀网格间隔数为4.表 2说明在参数h、B、D、T与σ的比值不变的情况下,快速Gauss径向基函数插值的收敛速度随着σ的减小而加快.
|
|
表 2 快速径向基函数插值参数 Table 2 Parameters of fast radial basis function interpolation |
选择N=108288(104≤N < 106)个属性控制点进行快速Gauss基函数插值建模,纵横波速度比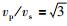
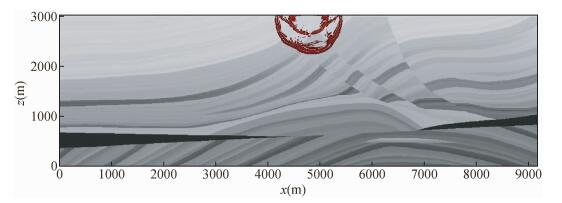
|
图 7 t=0.442 s波场快照 Figure 7 Snapshot of wave field simulation at 0.442 s |
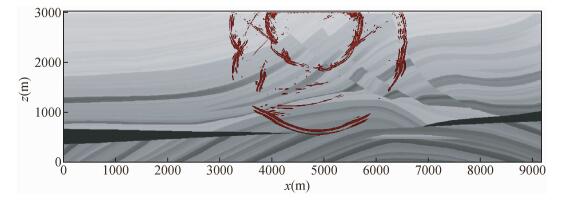
|
图 8 t=1.02 s波场快照 Figure 8 Snapshot of wave field simulation at 1.02 s |
通常谱元法属性建模需要建立几何模型进行贴体网格剖分,单元属性建模方式比较适合贴体网格属性建模.在实际属性建模流程中,往往缺少几何模型,或者难以建立复杂的几何模型,而属性控制点是已知的.利用双线性插值和快速径向基函数插值方法原理,分析了控制点个数N>106的双线性插值和104≤N < 106快速Gauss基函数插值效率.将以上双线性插值和快速Gauss径向基函数插值方法集成到SPECFEM2D中,在属性建模的基础上设置震源、观测系统等参数进行谱元法波动方程模拟,证明了两种属性建模方式的有效性,得出如下结论:
(1) 当介质属性在各个单元内为常数时,单元属性建模方式较为方便,特别是对于简单块状几何模型可以建立贴体网格以提高谱元法波场模拟精度.当存在复杂非均匀介质且几何模型未知时,已知一系列散乱分布的属性控制点,可采用基于插值算法的节点属性建模方式,对模型范围进行矩形网格剖分可提高属性建模效率.
(2) 在节点属性建模方式中,对于复杂非均匀介质模型,控制点个数越多,插值建模精度越高.双线性插值特别适合规则分布的稠密网格控制点高精度插值建模,在控制点个数N>106时,插值效率依然很高;快速Gauss插值针对稠密控制点(104≤N < 106),依然能够建立高精度的属性模型.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Abhyankar S, Smith B, Constantinescu E. 2013. Evaluation of overlapping restricted additive Schwarz preconditioning for parallel solution of very large power flow problems[C].//Proceedings of the 3rd International Workshop on high Performance Computing, Networking and Analytics for the Power Grid. Denver, Colorado:ACM, Article No.5, doi:10.1145/2536780.2536784. |
| [] | Balay S, Buschelman K, Eijkhout V, et al. 2004. PETSc users manual[R]. Technical Report ANL-95/11-Revision 2.1.5. Argonne National Laboratory, 206-207. |
| [] | Cupillard P, Delavaud E, Burgos G, et al. 2012. RegSEM:A versatile code based on the spectral element method to compute seismic wave propagation at the regional scale[J]. Geophysical Journal International, 188(3): 1203–1220. DOI:10.1111/j.1365-246X.2011.05311.x |
| [] | de Basabe J D, Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations[J]. Geophysics, 72(6): T81–T95. DOI:10.1190/1.2785046 |
| [] | Gumerov N A, Duraiswami R. 2010. Fast radial basis function interpolation via preconditioned Krylov iteration[J]. SIAM Journal on Scientific Computing, 29(5): 1876–1899. |
| [] | Jia Y Y, Xing X J, Shi J A, et al. 2014. The application of the maximum criteria optimizing technique in generation of body-fitted grids[J]. Chinese J. Geophys., 57(4): 1275–1283. DOI:10.6038/cjg20140424 |
| [] | Komatitsch D, Erlebacher G, G ddeke D, et al. 2010. High-order finite-element seismic wave propagation modeling with MPI on a large GPU cluster[J]. Journal of Computational Physics, 229(20): 7692–7714. DOI:10.1016/j.jcp.2010.06.024 |
| [] | Komatitsch D, Vilotte J P. 1998. The spectral-element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures[J]. Bulletin of the Seismological Society of America, 88(2): 368–392. |
| [] | Li X B, Bo J S, Qi W H, et al. 2014. Spectral element method in seismic ground motion simulation[J]. Progress in Geophysics, 29(5): 2029–2039. DOI:10.6038/pg20140506 |
| [] | Li Z C, Xiao J E, Qu Y M, et al. 2016. The review of irregular free-surface forward modeling in time domain[J]. Progress in Geophysics, 31(1): 300–309. DOI:10.6038/pg20160135 |
| [] | Liu Y S, Teng J W, Xu T, et al. 2014. Numerical modeling of seismic wavefield with the SEM based on Triangles[J]. Progress in Geophysics, 29(4): 1715–1726. DOI:10.6038/pg20140430 |
| [] | Ma D T, Yang C Y, Li X X. Preliminary waves ray tracing by linear travel-time interpolation method in 3-D transversely isotropic medium[J]. Progress in Geophysics, 29(3): 1201–1205. DOI:10.6038/pg20140327 |
| [] | Tromp J, Komatitsch D, Liu Q Y. 2008. Spectral-element and adjoint methods in seismology[J]. Communications in Computational Physics, 3(1): 1–32. |
| [] | Wei Y W, Wang Y C. 2012. A hybrid interpolation for Reconstructing near-surface model[J]. Journal of Computer-Aided Design & Computer Graphics, 24(4): 466–470. |
| [] | Yokota R, Barba L A, Knepley M G. 2010. PetRBF-A parallel O(N) algorithm for radial basis function interpolation with Gaussians[J]. Computer Methods in Applied Mechanics and Engineering, 199(25-28): 1793–1804. DOI:10.1016/j.cma.2010.02.008 |
| [] | 贾艳艳, 邢学军, 史基安, 等. 2014. 最大准则优化技术在贴体网格中的应用[J]. 地球物理学报, 57(4): 1275–1283. DOI:10.6038/cjg20140424 |
| [] | 李孝波, 薄景山, 齐文浩, 等. 2014. 地震动模拟中的谱元法[J]. 地球物理学进展, 29(5): 2029–2039. DOI:10.6038/pg20140506 |
| [] | 李振春, 肖建恩, 曲英铭, 等. 2016. 时间域起伏自由地表正演模拟综述[J]. 地球物理学进展, 31(1): 300–309. DOI:10.6038/pg20160135 |
| [] | 刘有山, 滕吉文, 徐涛, 等. 2014. 三角网格谱元法地震波场数值模拟[J]. 地球物理学进展, 29(4): 1715–1726. DOI:10.6038/pg20140430 |
| [] | 马德堂, 杨春雨, 李绪宣. 2014. 基于双线性插值的三维横向各向同性介质初至波射线追踪[J]. 地球物理学进展, 29(3): 1201–1205. DOI:10.6038/pg20140327 |
| [] | 王秀明, SerianiG, 林伟军. 2007. 利用谱元法计算弹性波场的若干理论问题[J]. 中国科学G辑:物理学力学天文学, 37(1): 41–59. |
| [] | 魏亦文, 王彦春. 2012. 混合插值法重构近地表模型[J]. 计算机辅助设计与图形学学报, 24(4): 466–470. |
| [] | 严珍珍, 张怀, 杨长春, 等. 2009. 汶川大地震地震波传播的谱元法数值模拟研究[J]. 中国科学D辑:地球科学, 39(4): 393–402. |
 2017, Vol. 32
2017, Vol. 32

