0 引言

大尺度地球物理流体中，Rossby波具有至关重要的地位，Rossby波是指生命史很长结构上有组织的前后一致的大尺度永久性波动，并且这些波动具有稳定的、大振幅孤立波特征.Rossby波理论是建立在地转适应理论基础上的，并且Rossby指出加热外源和地形对于大气长波有着重要的影响.Charney等(1949, 1980) 通过β-平面近似模式处理线性正压大气运动方程组，定量分析了超大尺度的定常波，得出地形对定常大气长波有重要的影响. Redekopp和Weidman(1978)、Wadati(1973) 从正压流体和分层流体的模式推导了Rossby孤立波振幅演变的方程分别满足KdV方程和改进的KdV(mKdV)方程的结论.Redekopp和Weidman (1978) 研究了切变气流中Rossby孤立波的产生，指出在纬向流中Rossby孤立波存在的必要条件.Long(1964) 年对正压流体模式做了模拟分析，创始性的得出在β平面模式下Rossby波的振幅随时间的变化满足KdV方程，Benney(1966) 在Long的研究基础上进行扩展，得到了Rossby孤立波的波速与其振幅之间的相关结论.Luo(2005)、达朝究和丑纪范(2008)和宋健等(宋健和杨联贵, 2010；宋健等, 2012a, b )研究了地形对Rossby孤立波的影响，发现大气运动中大气长波受地形的强迫作用，从理论上验证了地形是诱导Rossby孤立波产生重要因素之一.Redekopp(1977)、Redekopp和Weidman(1978) 利用连续模式讨论了Rossby孤立波，并给出了两种基本孤立波型.蒋后硕和吕克利(1998)、Lu和Lü(2000)利用摄动展开法和时空伸长变换导出了包括地形等因素可以强迫Rossby孤立波的产生，显示出地形对扰动具有明显的增幅作用，说明了大气中大尺度非线性运动的一些特征.赵强(1997) 讨论了地形对热带大气超长尺度Rossby波的影响，指出了地形随纬度的变化能够导致热带大气超长尺度Rossby波波动的不稳定.赵强(赵强和刘式适, 2004;赵强和于鑫, 2008)、刘全生等(2014) 对完整Coriolis力下的Rossby波进行了详细研究，说明在中高纬地区Coriolis力水平分量对Rossby孤立波的作用不能忽视.Hukuda(1979) 利用两层模式对两种基本孤立波型进行了讨论，进而指出垂直切变的重要性.但是，经过验证发现，两层模式只能给出基流简单的线性垂直变化，而多层模式能够更好的拟合实际的基本气流，更好的反映大气的实际斜压性.吕克利(1991) 通过约化摄动法给出了多层模式大气中的KdV方程，讨论了基本气流的垂直切变和水平切变对Rossby孤立波的影响，以及它们对多层模式中的正压模态和斜压模态的作用.本文在以上的研究基础上，讨论了在N层大气模式中地形效应对Rossby孤立波产生的影响.

1 方程的推导 1.1 控制方程

由l位面上的涡度方程和位面上的热流量方程消去ω，利用上、下边界上ω=0的条件，并引入尺度(王斌和翁衡毅，1981)，公式为

其中L是水平特征尺度长度；V特征速度；无量纲化，且在N位面上考虑地形得到各位面上的涡度方程为

(1)

式中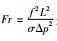是内旋转Froude数, 二维Laplace算子，算子, h(x′, y′)为无量纲形式的地廓线，边界条件为

(2)

1.2 约化摄动法推导KdV方程

用Clarke的方法(Clarke，1971)，考虑恒定波的形式解，即设：

(3)

利用变换(3)，由(1) 式得：

(4)

为了得到KdV方程，对式(4) 做以下变换，即对x′、y′引入缓变量坐标为

(5)

其中ε < < 1，且为振幅小参数，将(5) 式代入(4) 式，得：

(6)

(7)

将ψ和c展成ε的幂级数得(Hukuda，1979)：

(8)

式中是第l层上的纬向气流，c₀是Rossby孤立波在切变纬向流中的波速，将(8) 式代入(6) 式之后，可得出各阶近似方程.由于ε¹阶方程对ξ、y是可以分离的，故可以设(吕克利，1991)：

(9)

代入ε¹阶方程，得到关于ψ_l的特征值问题为

(10)

(11)

其中：

第(10) 式所描述的是斜压Rossby孤立波的经向结构，为确定A(ξ)，需要用到ε²阶方程，同时，把(9) 式代入，并利用(10) 可得：

(12)

在N层模式大气中含有地形效应的KdV方程为

(13)

其中：

(14)

其中(13) 式在ξ→±∞时，A→0的特解为孤立子解(刘式适和刘式达，2000)，即为

(15)

其中：

(16)

它表示孤立Rossby波的陡度.

2 弱水平切变气流下的Rossby孤立波

将各层基本气流取为(吕克利，1991)：

(17)

其中S_l表示基流的垂直切变，取为常值，且都取为常数，k取为+1或-1，δ < < 1，是表征基流弱水平切变强度的小参数.

将变量Φ和参数c₀用小参数δ展开得：

(18)

代入(10)、(11) 式，得零阶定解问题为

(19)

一阶定解问题为

(20)

(19) 式的解可以写为(吕克利，1991)：

(21)

将(21) 式代入(19) 式得到：

(22)

由A_l有非零解，可得到关于的N次代数方程，Pedlosky(1979) 指出，这个N次代数方程决定了N个Rossby波模态，其中一个是正压模态，其余N-1个是斜压模态，为了以下的运算方便，令，(吕克利，1991) 由(22) 式能够得到：

(23)

其中：

由一阶问题(20) 式的可解性条件，易得，再由(20) 式的解可设为(Hukuda，1979；吕克利，1991)：

(24)

代入(20) 式，得：

(25)

由(14) 式得KdV方程(13) 的系数近似为

(26)

其中：

因此，可得出计算N层模式大气中地形效应下的Rossby孤立波解为

(27)

3 结论

在人类生活的环境中，地形对大气有着重要的作用.在N层模式中，弱水平切变气流上的Rossby孤立波与基本气流密切相关.本文在前人研究的基础上用约化摄动法，导出了N层模式中地形效应下的Rossby孤立波满足KdV方程，说明地形可以激发Rossby孤立波，而且在N层模式中地形效应对Rossby孤立波有着非常重要的影响，地形效应是斜压Rossby孤立波产生的重要因子.

致谢 感谢审稿专家提出的修改意见和编辑部的大力支持！