磁共振探测(Magnetic Resonance Sounding,MRS)是目前唯一直接找水的地球物理方法,近年来常被用于估算含水层导水系数.与传统的抽水试验方法相比,MRS估算导水系数具有快速、密集、低成本、非侵入等优点,围绕如何提升估算的准确性已成为应用地球物理学与水文地质学共同关注的科学问题(Legchenko et al., 2004;高辉等,2011;林君等,2011;Vouillamoz et al., 2014).
MRS估算导水系数研究,早期集中于通过室内试验及理论分析建立渗透率计算公式,并以此为基础推求导水系数.典型的为Seevers(1966)基于Kozeny-Carman(K-C)模型及Kenyon等(Kenyon et al., 1988;Kenyon,1997)基于Schumberger-Doll Research(SDR)模型建立的公式. 20世纪90年代至今,随着MRS仪器的发展,特别是法国IRIS公司NUMIS仪器的市场化,更多研究转为该技术的野外应用,并提供了较多的实际案例(Lubczynski and Roy, 2003;Chalikakis et al., 2008;Boucher et al., 2009;Vouillamoz et al., 2014).假定通过钻探及抽水试验得到的导水系数为“相对真值”,则MRS估算的导水系数与抽水试验计算值相比,仍存在较大“误差”.如:Vouillamoz等(2007, 2008)在尼日尔及马来西亚的误差分别为9%及45%;Plata和Rubio(2008)在西班牙的误差在40%~200%之间;Nielsen等(2011)在丹麦的平均误差为40%.为提升估算结果的准确性,前人进行了少量研究,主要为探讨选择哪种计算公式及计算公式中关键参数的合理取值. Dlubac等(2014)比较了两种典型公式的室内试验条件及推导过程,并从理论上分析了两种公式的适用条件;Dlugosch等(2013)总结了两种公式在不同地质条件下的适用性;Nielsen等(2011)结合丹麦地区的实例重点探讨了计算公式中关键参数CP的合理取值.上述研究均建立在已采集的MRS数据的基础上,很少涉及对前期数据如何采集更为合理的相关讨论.
笔者经近年在内蒙古及蒙古国等地应用MRS发现,以已知的地质及水文地质信息(包括勘探孔介质岩性及导水系数、地层电阻率分布)为基础,通过合理布设MRS测点,不仅可提高解译数据的可靠性,还可为计算公式中关键参数的取值提供重要参考,能够明显提升估算结果的准确性,而现有研究在该方面鲜见报道.为此,本文以蒙古国伊和塔拉盆地的MRS应用为具体案例,仍假定通过钻探及抽水试验得到的导水系数为“相对真值”,通过比较常用计算公式不同参数取值下MRS估算的导水系数与抽水试验计算值的差异,分析多种因素对估算结果的影响,并在原有方法基础上提出一种提升估算准确性的改进方法.
1 原理与方法 1.1 MRS原理MRS利用人工激发的电磁场使地下水中氢核形成宏观磁矩,用线圈拾取宏观磁矩运动产生的磁共振信号,进而探测地下水是否存在,可得到含水量(单位体积含水量)和衰减时间随深度的变化(潘玉玲和张昌达,2000;林君等,2013;陈斌等,2014).其一般表达式为
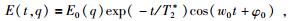
|
(1) |
式中,E(t, q)为自由感应电动势(nV);t为电流脉冲持续时间(ms);q为激发脉冲矩(A·ms);E0(q)为初始振幅(nV);T2*为平均衰减时间(ms);w0为Larmor角频率;φ0为信号初始相位(rad). MRS主要揭示3方面信息:E0(q)反映含水介质的含水量;T2*反映含水介质的平均有效孔隙度,可推断介质岩性;φ0反映含水介质的导电性.
1.2 MRS估算导水系数方法现阶段,常用的MRS估算导水系数方法均为借鉴核磁共振测井中的渗透率估算方法得到.
核磁共振测井的渗透率估算,大致经历了先由室内试验建立经验公式,再到野外应用中逐渐修正公式的过程.以典型的Kenyon等(1988)的试验为例,主要分3部分:(1) 选取了60个不同的岩样,测试岩样饱水状态下的磁共振响应,主要得到含水量和纵向弛豫时间T1;(2) 测定岩样饱水状态下的渗透率,并建立渗透率与含水量及纵向弛豫时间的最佳拟合关系,即经验公式;(3) 野外状态下的MRS与实验室有2点基本不同:存在死区时间及较低的信噪比,因此需将经验公式与实际测井数据对照,对公式不断调整.
渗透率计算公式转化为导水系数计算仍需经历2步:(1) 考虑孔隙内液体性质的影响,转化为计算渗透系数;(2) 将渗透系数值与含水层厚度相乘,转化为计算导水系数.Legchenko等(2002)总结多种公式,给出了统一的表达形式,这也是目前国内外学者普遍采用的公式(张昌达和潘玉玲,2006;Mohnke and Yaramanci, 2008;Vilhelmsen et al., 2014):
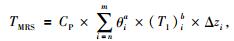
|
(2) |
式中,TMRS为MRS估算的导水系数;CP、a、b为经验值;θi为第i个脉冲对应的含水量(i=n, n+1, …m),n为含水层潜水面(或顶板)对应的脉冲,m为含水层底板对应的脉冲;(T1)i为第i个脉冲对应的纵向弛豫时间;Δzi为第i个脉冲对应的反演模型设置的地层厚度(对应含水层厚度).
假定MRS估算的导水系数与抽水试验计算值相等,可得到每个测点对应的CP最优值.公式为
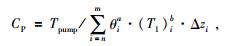
|
(3) |
式中,Tpump为抽水试验计算的导水系数,其他同上.
MRS估算导水系数的准确性主要取决于3方面因素:(1) MRS推断含水层深度的准确性;(2)CP的取值;(3) 指数a、b的取值,常用Seevers公式的参数设置a=1、b=2,也有少量研究采用Kenyon公式的参数设置a=4、b=2.
2 数据采集与处理 2.1 案例所在区域概况案例区位于蒙古国中戈壁省伊和塔拉盆地,面积约203.24 km2(图 1).盆地四周基岩出露,区内地形相对平坦,总体为西南高、东北低.主要出露为白垩系地层,地下水主要为浅部的白垩系承压水.多年平均降水量177.63 mm,平均蒸发量2882.9 mm,无常年地表水系.

|
图 1 案例区位置及磁共振探测点、勘探孔分布 Figure 1 Case zone position and magnetic resonance sounding point, drilling point distribution |
进行MRS前,应用电剖面法初步查明区内基岩起伏、断层及裂隙带的分布状况.共布设160个MRS测点(图 1),所用仪器为法国IRIS公司生产的NUMISPLUS核磁共振找水仪,线圈采用100 m×100 m方形布设,最大探测深度100 m,设置16个脉冲,叠加次数均在48次以上.
数据解译采用Samovar V6.6软件,并根据地层电阻率重新编译反演核函数.解译结果显示采集数据信噪比(singer-to-noise)均在3.0以上,质量较好.
2.3 钻探共布设8个勘探孔.为尽可能减少介质非均质性对探测结果的影响,勘探孔严格布设在对应的MRS铺设线圈中心.采用取芯钻进,每个勘探孔配置一个观测孔.需特别指出,部分勘探孔承压含水层内部存在薄的隔水层,考虑到其隔水性能较弱且非连续分布,将整个含水岩组概化为一个承压含水层.
抽水试验采用定流量非稳定流抽水,导水系数计算适用承压完整井非稳定流对应的泰斯公式.应用Aquifer Test软件的配线法及直线图解法计算并综合确定导水系数值(表 1).
|
|
表 1 勘探孔及对应的MRS基本信息 Table 1 Drilling and the corresponding MRS basic information |
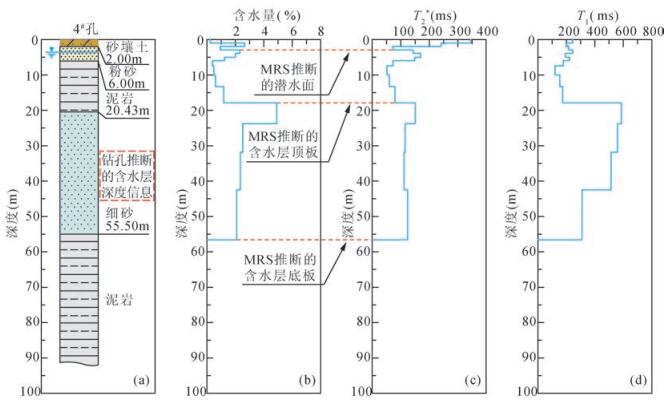
MRS推断的含水层深度表现为相对较高的含水量和平均衰减时间,如图 2显示了4#勘探孔与SJ6-5测点推断的含水层深度的对比情况.针对传统地球物理方法难以解决的非水低阻问题,MRS既可提供含水量信息,又可提供介质有效孔隙度信息,可相对容易地划分含水层.
|
图 2 4#勘探孔与SJ6-5测点推断的含水层深度的对比 (a) 4#勘探孔柱状图及推断的含水层深度;(b)-(d)分别表示SJ6-5测点含水量、平均衰减时间(T2*)、纵向弛豫时间(T1)随深度的变化. Figure 2 The aquifer position inferred from 4# drilling contrast with SJ6-5 magnetic resonance sounding (a) The exploration hole column of 4# and its aquifer depth inferred; (b)-(d) Represent SJ6-5 MRS point the water content, average decay relaxation time (T2*), longitudinal relaxation time (T1) varies with depth, respectively. |
全部勘探孔与MRS推断的含水层深度(不区分含水层顶、底板)对比结果(图 3)显示,MRS推断含水层深度的误差为-18.30~3.77 m,平均为4.85 m(误差绝对值的平均值).结果与Vouillamoz等(2005, 2008)在尼日尔及西非地区相近信噪比条件下的分析基本一致,表明在信噪比较高的情况下,MRS在推断含水层深度方面的性能较可靠.

|
图 3 勘探孔与MRS推断的含水层深度的对比 Figure 3 Comparisons of aquifer depth from drilling and MRS inferred |
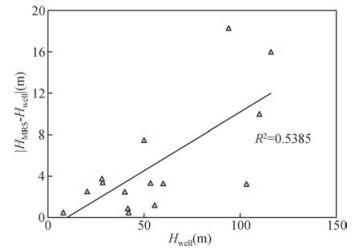
MRS推断的含水层深度还表现出随探测深度增加误差增大的趋势(图 4),最大误差出现在含水层底板深度在94.00 m处,而含水层顶、底板深度小于40.00 m,误差均在5.00 m范围内.产生上述现象的主要原因为受地层导电性影响,MRS信号随探测深度增加分辨率逐渐降低(翁爱华等,2007).
|
图 4 MRS推断含水层深度的误差随深度变化情况 Figure 4 MRS inferred aquifer depth error varies with depth |
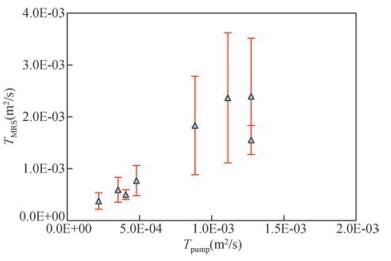
CP取值对估算结果准确性有重要影响. NUMIS仪器市场化初期,Lenbchenco根据其与Schirov等(1991)在前苏联的经验,建议此值为10-8数量级.随着后期案例增多,该值不断调整,现阶段,普遍认为10-9数量级更能代表大多数地层的特点(Plata and Rubio, 2008).现阶段,常用的取值为7.00×10-9,CP取该值(本节在a=1、b=2的情况下讨论CP的取值影响),导水系数估算误差为22.02%~112.93%,平均为69.34%(图 5).
|
图 5 CP取常用值MRS估算的导水系数与抽水试验计算值的对比 Figure 5 Comparisons of transmissivity values from pumping test and MRS estimates for CP common parameter settings |
假定MRS估算的导水系数与抽水试验计算值相等,应用式(3) 计算每个勘探孔对应的CP值,介于3.29×10-9~5.74×10-9之间. CP取最小值3.29×10-9,误差为-42.70%~0%,平均为-20.47%;Cp取最大值5.74×10-9,误差为0.00%~74.51%,平均为38.79%.
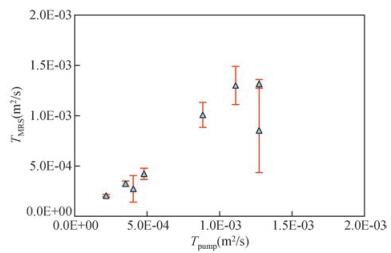
将CP作为未知数,应用最小二乘法计算全部勘探孔对应的MRS估算的导水系数与抽水试验计算值残差平方和最小对应的CP值,该值为适用于全部勘探孔的最优值,为3.85×10-9. CP取最优值,误差为-32.93%~17.05%,平均为15.53%(图 6).
|
图 6 CP取最优值MRS估算的导水系数与抽水试验计算值的对比 Figure 6 Comparisons of transmissivity values from pumping test and MRS estimates for CP optimal value |
通过上述计算可知:
(1) CP取最优值,平均误差较小且整体误差相对平均,没有出现极大值或极小值,表明MRS估算导水系数表现出较高的准确性及稳定性.
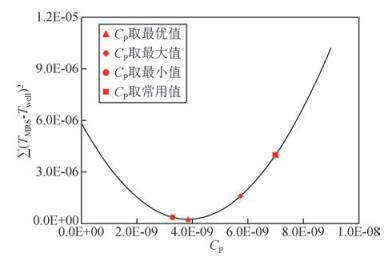
(2) 比较CP取不同值的误差(图 7)可知,即使CP取最小值或最大值,误差也小于取常用值.由此可知,CP值未知的情况下,在测点布设环节,通过搜集勘探区内及附近的钻孔及其导水系数信息,并设计在已知导水系数的钻孔附近进行MRS,从而得到一个具体的CP值或区间(区间对应多个CP值,可整体取最优),应用该值估算导水系数的准确性高于CP取现阶段的常用值.
|
图 7 CP不同取值对应的MRS估算的导水系数与抽水试验计算值残差平方和的变化 Figure 7 The varies of residual squares sum for transmissivity values between Pumping tests and MRS estimates corresponding to differen CP |
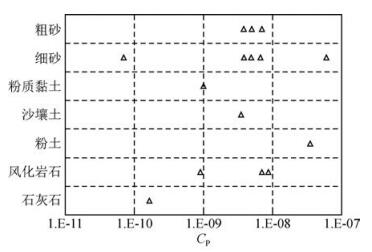
(3) Chalikakis等(2009)及Baroncini等(2014)指出,可根据已知的介质岩性信息推断合理的CP值.根据前人资料及本案例成果总结CP值与介质岩性的对应关系(图 8),CP值与介质岩性并不具有明显的对应关系.事实上,尽管导水系数与介质岩性直接相关,但其内在关联已经体现在式(2) 中的含水量及衰减时间变化上.
|
图 8 CP值与钻孔岩性的对应关系 Figure 8 Correspondence between CP value and the borehole lithology |
比较Seevers公式(a=1、b=2) 与Kenyon公式(a=4、b=2) 不同的参数设置引起的估算误差.由a=4、b=2情况下CP不同取值的误差(表 2)可知,a=4、b=2各项误差均大于a=1、b=2对应的误差,表明Seevers公式相比Kenyon公式具有更好的适用性.
|
|
表 2 CP不同取值的估算误差 Table 2 The estimation error for using the Kenyon formula different values of CP |
根据Seevers公式及Kenyon公式建立的原始文献(Seevers,1966;Kenyon et al., 1988;Kenyon,1997),Kenyon公式依据的SDR模型基于两个基本假设:(1) 表面弛豫起主要作用,从而认为块状水弛豫的贡献可以忽略;(2) 表面弛豫快速发生.事实上,上述假设主要发生在孔隙较小的介质中,对较为普遍的孔隙较大的含水介质(砂砾或粗砂),一旦孔径大于临界尺度,这些假设是不成立的. Dlugosch等(2011)指出,当孔隙较大时,应合理限定表面弛豫与块状水弛豫的关系.另外,据Dlubac等(2014)的研究,当孔隙尺度较大时,表面弛豫并不快速发生,而是缓慢扩散.与之相比,Seevers公式依据的K-C模型则是从总表面积与总孔隙的比率的角度推算导水系数,具有更好的适用性.上述分析佐证了本案例的结论.
3.2 原有方法与改进方法对比分析前文探讨了3个主要因素对MRS估算导水系数准确性的影响,在此基础上对原有方法作改进:(1) 在采集数据信噪比较高的情况下,MRS推断含水深度的性能较可靠,其对估算结果的影响较小.(2)CP取值对估算结果有重要影响,现阶段,原有方法常将其取为7.00×10-9.而通过本案例发现,在CP值未知的情况下,借助在已知导水系数的钻孔附近进行MRS,从而得到一个具体的CP值或区间,应用该值估算的导水系数准确性高于CP取常用值.改进方法建议采用此取值方法. (3) 原有方法,指数a、b存在两种取值方法,即a=1、b=2或a=4、b=2,通过本案例发现,a=1、b=2具有更好的适用性,改进方法采用此取值.
比较原有方法与改进方法的估算结果,原有方法的估算误差为22.02%~112.93%,平均69.34%,对于改进后的方法,通过已知钻孔可获得8个参考值,即使CP取其中的最小值或最大值,误差均小于原有方法,如果取整体最优值,误差更小,为-32.93%~17.05%,平均15.53%,说明改进方法具有很好的适用性.
4 结论 4.1本文分析了3个主要因素对MRS估算导水系数准确性的影响,并根据分析结果对原有方法进行了改进.取得以下主要认识:
(1) 在采集数据信噪比较高的情况下,MRS推断含水深度的性能较可靠,平均为4.85 m,其对估算结果准确性的影响较小.
(2) 关键参数CP,在能够获得最优值的情况下,MRS估算结果表现出较高的准确性及稳定性.而在CP值未知的情况下,建议在测点布设环节,设计在已知导水系数的钻孔附近进行MRS,从而得到一个具体的CP值或区间,应用该值估算导水系数的准确性高于CP取原有方法的常用值.
(3) 指数a、b取为a=1、b=2具有更好的适用性,改进方法采用此值.
4.2相比原有方法,改进后的方法误差更小,能明显提升估算结果的准确性,具有很好的适用性.
致谢 吉林大学蒋川东博士、北京师范大学翟远征博士认真审阅了本文初稿,审稿专家提出了宝贵建议,在此表示诚挚谢意.| [] | Baroncini-Turricchia G, Francés A P, Lubczynski M W, et al. 2014. Integrating MRS data with hydrologic model-Carrizal Catchment (Spain)[J]. Near Surface Geophysics, 12(2): 255–269. |
| [] | Boucher M, Favreau G, Vouillamoz J M, et al. 2009. Estimating specific yield and transmissivity with magnetic resonance sounding in an unconfined sandstone aquifer (Niger)[J]. Hydrogeology Journal, 17(7): 1805–1815. DOI:10.1007/s10040-009-0447-x |
| [] | Chalikakis K, Nielsen M R, Legchenko A. 2008. MRS applicability for a study of glacial sedimentary aquifers in Central Jutland, Denmark[J]. Journal of Applied Geophysics, 66(3-4): 176–187. DOI:10.1016/j.jappgeo.2007.11.005 |
| [] | Chalikakis K, Nielsen M R, Legchenko A, et al. 2009. Investigation of sedimentary aquifers in Denmark using the magnetic resonance sounding method (MRS)[J]. Comptes Rendus Geoscience, 341(10-11): 918–927. DOI:10.1016/j.crte.2009.07.007 |
| [] | Chen B, Hu XY, Liu DH, et al. 2014. The development history and new progress of magnetic resonance sounding technique[J]. Progress in Geophysics, 29(2): 650–659. DOI:10.6038/pg20140224 |
| [] | Dlubac K, Knight R, Keating K. 2014. A numerical study of the relationship between NMR relaxation and permeability in sands and gravels[J]. Near Surface Geophysics, 12(2): 219–230. |
| [] | Dlugosch R, Günther T, Müller-Petke M, et al. 2013. Improved prediction of hydraulic conductivity for coarse-grained, unconsolidated material from nuclear magnetic resonance[J]. Geophysics, 78(4): EN55–EN64. DOI:10.1190/geo2012-0187.1 |
| [] | Dlugosch R, Mueller-Petke M, Günther T, et al. 2011. Assessment of the potential of a new generation of surface nuclear magnetic resonance instruments[J]. Near Surface Geophysics, 9(2): 89–102. |
| [] | Gao H, Sun W, Tian Y H, et al. 2011. Application of NMR technique in evaluation of micro-pore structure in extra-low permeability sandstone[J]. Progress in Geophysics, 26(1): 294–299. DOI:10.3969/j.issn.1004-2903.2011.01.034 |
| [] | Kenyon W E. 1997. Petrophysical principles of applications of NMR logging[J]. The Log Analyst, 38(2): 21–43. |
| [] | Kenyon W E, Day P I, Straley C, et al. 1988. A three-part study of NMR longitudinal relaxation properties of water-saturated sandstones[J]. SPE Formation Evaluation, 3(3): 622–636. DOI:10.2118/15643-PA |
| [] | Legchenko A, Baltassat J M, Beauce A, et al. 2002. Nuclear magnetic resonance as a geophysical tool for hydrogeologists[J]. Journal of Applied Geophysics, 50(1-2): 21–46. DOI:10.1016/S0926-9851(02)00128-3 |
| [] | Legchenko A, Baltassat J M, Bobachev A, et al. 2004. Magnetic resonance sounding applied to aquifer characterization[J]. Groundwater, 42(3): 363–373. DOI:10.1111/gwat.2004.42.issue-3 |
| [] | Lin J, Duan Q M, Wang Y J, et al. 2011. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and its Applications[M]. Beijing: Science Press. |
| [] | Lin J, Jiang C D, Lin T T, et al. 2013. Underground magnetic resonance sounding (UMRS) for detection of disastrous water in mining and tunneling[J]. Chinese Journal of Geophysics, 56(11): 3619–3628. DOI:10.6038/cjg20131103 |
| [] | Lubczynski M, Roy J. 2003. Hydrogeological interpretation and potential of the new magnetic resonance sounding (MRS) method[J]. Journal of Hydrology, 283(1-4): 19–40. DOI:10.1016/S0022-1694(03)00170-7 |
| [] | Mohnke O, Yaramanci U. 2008. Pore size distributions and hydraulic conductivities of rocks derived from magnetic resonance sounding relaxation data using multi-exponential decay time inversion[J]. Journal of Applied Geophysics, 66(3-4): 73–81. DOI:10.1016/j.jappgeo.2008.05.002 |
| [] | Nielsen R M, Hagensen T F, Chalikakis K, et al. 2011. Comparison of transmissivities from MRS and pumping tests in Denmark[J]. Near Surface Geophysics, 9(2): 211–223. |
| [] | Pan Y L, Zhang C D. 2000. Nuclear Magnetic Resonance Theory and Method[M]. Wuhan: China University of Geosciences Press. |
| [] | Plata J L, Rubio F M. 2008. The use of MRS in the determination of hydraulic transmissivity:The case of alluvial aquifers[J]. Journal of Applied Geophysics, 66(3-4): 128–139. DOI:10.1016/j.jappgeo.2008.04.001 |
| [] | Schirov M, Legchenko A, Creer G. 1991. A new direct non-invasive groundwater detection technology for Australia[J]. Exploration Geophysics, 22(2): 333–338. DOI:10.1071/EG991333 |
| [] | Seevers D O. 1966. A nuclear magnetic method for determining the permeability of sandstones[C].//SPWLA 7th Ann. Logging Symposium.Tulsa, Oklahoma:Society of Petrophysicists, Well Log Analysts, 923-943. |
| [] | Vilhelmsen T N, Behroozmand A A, Christensen S, et al. 2014. Joint inversion of aquifer test, MRS, and TEM data[J]. Water Resources Research, 50(5): 3956–3975. DOI:10.1002/2013WR014679 |
| [] | Vouillamoz J M, Chatenoux B, Mathieu F, et al. 2007. Efficiency of joint use of MRS and VES to characterize coastal aquifer in Myanmar[J]. Journal of Applied Geophysics, 61(2): 142–154. DOI:10.1016/j.jappgeo.2006.06.003 |
| [] | Vouillamoz J M, Descloitres M, Toe G, et al. 2005. Characterization of crystalline basement aquifers with MRS:Comparison with boreholes and pumping tests data in BurkinaFaso[J]. Near Surface Geophysics, 3(3): 205–213. |
| [] | Vouillamoz J M, Favreau G, Massuel S, et al. 2008. Contribution of magnetic resonance sounding to aquifer characterization and recharge estimate in semiarid Niger[J]. Journal of Applied Geophysics, 64(3-4): 99–108. DOI:10.1016/j.jappgeo.2007.12.006 |
| [] | Vouillamoz J M, Lawson F M A, Yalo N, et al. 2014. The use of magnetic resonance sounding for quantifying specific yield and transmissivity in hard rock aquifers:The example of Benin[J]. Journal of Applied Geophysics, 107: 16–24. DOI:10.1016/j.jappgeo.2014.05.012 |
| [] | Weng A H, Wang X Q, Liu G X, et al. 2007. Nonlinear inversion of surface nuclear magnetic resonance over electrically conductive medium[J]. Chinese Journal of Geophysics, 50(3): 890–896. DOI:10.3321/j.issn:0001-5733.2007.03.030 |
| [] | Zhang C D, Pan Y L. 2006. Some views on petrophysical interpretation of SNMR data[J]. Chinese Journal of Engineering Geophysics, 3(1): 1–8. DOI:10.1088/1742-2132/3/1/001 |
| [] | 陈斌, 胡祥云, 刘道涵, 等. 2014. 磁共振测深技术的发展历程与新进展[J]. 地球物理学进展, 29(2): 650–659. DOI:10.6038/pg20140224 |
| [] | 高辉, 孙卫, 田育红, 等. 2011. 核磁共振技术在特低渗砂岩微观孔隙结构评价中的应用[J]. 地球物理学进展, 26(1): 294–299. DOI:10.3969/j.issn.1004-2903.2011.01.034 |
| [] | 林君, 段清明, 王应吉, 等. 2011. 核磁共振找水仪原理与应用[M]. 北京: 科学出版社. |
| [] | 林君, 蒋川东, 林婷婷, 等. 2013. 地下工程灾害水源的磁共振探测研究[J]. 地球物理学报, 56(11): 3619–3628. DOI:10.6038/cjg20131103 |
| [] | 潘玉玲, 张昌达. 2000. 地面核磁共振找水理论和方法[M]. 武汉: 中国地质大学出版社. |
| [] | 翁爱华, 王雪秋, 刘国兴, 等. 2007. 导电性影响的地面核磁共振反演[J]. 地球物理学报, 50(3): 890–896. DOI:10.3321/j.issn:0001-5733.2007.03.030 |
| [] | 张昌达, 潘玉玲. 2006. 关于地面核磁共振方法资料岩石物理学解释的一些见解[J]. 工程地球物理学报, 3(1): 1–8. |
 2017, Vol. 32
2017, Vol. 32

