随着国家发展,我国工程建设已进入高峰期,对工程三维地震勘探技术有迫切需求.目前工程三维地震勘探在工程中的应用研究尚处于起步阶段,其在工程领域的开展几近空白,国内浙江大学的石战结(2013)等人在上海市某公路上对地下隧道进行了超浅层三维地震探测试验,长江设计院的熊永红(2013)等人进行了三维地震勘探在工程中的应用性研究,提出了适合浅层三维地震勘探的野外工作程序及数据处理流程.工程三维地震一般在山区、丘陵等地形展开,面临着地表条件复杂、起伏较大等因素的影响,这样就造成了测线不能按照常规的正交型等三维观测系统进行布置,即道间距(或线间距)不能保持等距,如果为了追求相等的道间距(线间距)而盲目的增大道间距(线间距),势必会影响采集资料的质量,产生混叠效应.
近几年兴起的压缩感知理论认为:如果采样数据是欠采样的,那么进行随机采样可以很好的降低混叠效应(Moldoveanu,2010).该已经应用到一些领域的应用科学和工程中,如信号处理,信息理论,医疗成像,编码理论,模拟数字转换等等.这个理论的基本概念(Donoho,1995):如果采样不满足奈奎斯特采样条件,最好进行随机采样,而不是规则化的采样.随机采样这个概念对于地震领域也是非常有吸引力的,这个理论可以应用到地震信号处理(噪声衰减、插值和数据正则化等)(Abma and Kabir, 2006)、地震成像(Lustig et al., 2007)、伪随机蒙托卡洛抽样三维偏移(Zhou and Schuster, 1995),随机采样数据比有规律的欠采样数据能更好的进行波场重建(Zwartjes and Sacchi, 2007;李鹏等, 2015).在SEG(2009)年会上,有学者(Herrmann,2009)提出了其他方面的应用.随机采样在环绕型观测系统采集中也有广泛的应用前景,环绕采集的一个特殊方面是激发和检波点的分布是没有规律的,采集圆中心网格点的设计决定了激发和检波点的分布,它可以被设计成规则的或随机的(Wong et al., 1997),无论采集圆中心网格点是规则分布的还是随机分布的,激发和检波点的分布都是不规则的.压缩感知理论在工程三维地震中的应用有天然的优势,复杂地形使得检波点的布置具有随机性,本文将这一理论应用到浅层三维地震的采集设计中,探讨随机采样在浅层三维地震采集上的实现,对于浅层三维地震勘探的采集设计和数据处理具有重要的指导意义
1 基本理论 1.1 奈奎斯特定理奈奎斯特采样定理说,对于一个连续函数h(t),设其最高频率为fmax,那么函数h(t)的样本值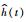
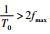
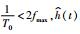
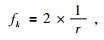
|
(1) |
其中:r为子波波长.
当空间采样频率f>fk时,不会产生空间假频,即空间采样间隔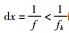
最近几年出现的压缩感知理论的基本思想是:如果采样不能满足奈奎斯特条件或者说是在采样不足的情况下,最好进行随机采样,而不是规则化的采样.随机欠采样数据比有规律的欠采样数据能更好的进行波场重建,同时随机采样可以降低采集脚印的影响.目前野外地震采集激发点和接收点的分布是沿平行线的,如果忽略环境的影响,理论上是非常有规律的,如果考虑地形、障碍物等因素的影响,那么炮点和检波点的分布将是非规则的,满足一定的随机性.
然而,采用完全随机策略采集的数据存在着数据点的空间位置过于集中或过于稀疏的情况,不利于波场重建取得理想的效果,同时也不利于灵活应对野外的实际地质条件(张华和陈小宏,2013),而jittered可以更好的控制采样间隔,更加有利于波场重建和适应野外的地质条件.
假设在采样区间中等间隔采集n个点不能满足奈奎斯特采样定律,那么就需要对采样区间中的采样点进行随机采样,其中jittered随机采样方式是将采样区间等分为n个待采样区域,并保证在每个待采样区域强制采集一个点,这种采样策略不仅保证了采样的随机性,也使得采样间隔不至于过密和过疏.为了说明jittered随机欠采样的基本思想,假设采样空间的最佳采样点数为N,欠采样因子为γ,γ为奇数(γ=1, 3, 5, …)或偶数(γ=2, 4, 6, …),N与γ成倍数关系,比值为n=N/γ,n即为实际的欠采样点数,从而可以计算出实际的采样点为
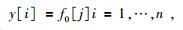
|
(2) |
其中:
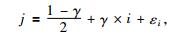
|
(3) |
公式(3) 中的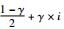
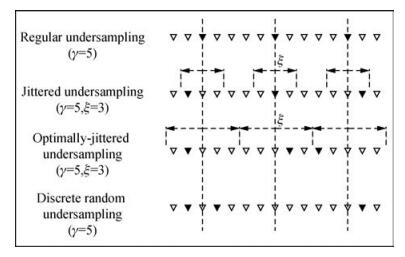
如图 1所示分别为规则欠采样和随机欠采样示意图,其中空心倒三角形和实心倒三角形的集合表示最佳采样点,实心倒三角形为实际采样点,图中从上往下分别表示规则欠采样、一般jittered欠采样、最优jittered欠采样和离散随机欠采样.jittered欠采样的最大样点间隔(相对于最佳采样)不超过(γ-1)+2×[(ξ-1)/2],规则欠采样的样点间隔均为γ-1,离散随机欠采样的样点间隔最大为N-n.
|
图 1 不同欠采样示意图 (Hennenfent and Herrmann, 2008) Figure 1 Diagram showing the different undersampling schemes(Hennenfent and Herrmann, 2008) |
随机采样得到二维地震数据X(x, t),X(x, t)在t方向为规则采样,在x方向为随机采样.对随机采样得到的地震数据X(x, t)进行频谱分析需要采用随机采样二维傅里叶变换,常规所使用的二维数据频谱分析均为均匀采样二维傅里叶变换,其与随机采样二维傅里叶变换的区别在于积分时间上的不同(汪安民等,2005;赵贻玖,2008;郭东亮等,2012).
计算机上实现随机采样的傅里叶变换需要采用非均匀二维离散傅里叶变换,连续时间的二维傅里叶变换为
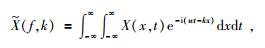
|
(4) |
式中w为傅里叶变换变量;k为傅里叶变换变量;i为虚数单位;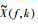
将公式(3) 进行离散化,可以得到均匀采样的二维离散傅里叶变换表达式为
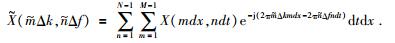
|
(5) |
非均匀二维离散傅里叶变换与均匀采样二维离散傅里叶变换类似,其表达式为
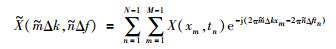
|
(6) |
式中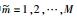
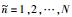
表达式(5) 中包含时间采样间隔(tn+1-tn)和空间采样间隔(xm+1-xm),体现了公式的非均匀性,表达式(5) 可以描述为时间、空间的非均匀采样和频率、波数的均匀采样.
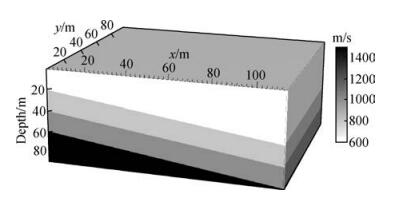
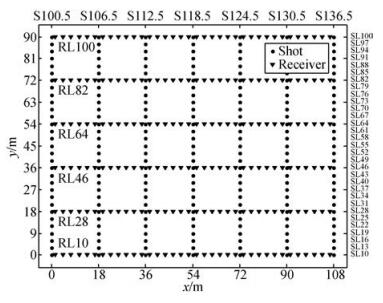
2 模型分析为了分析不同采样方式得到的浅层三维地震记录的频谱特征及三维成像效果,设计了如图 2所示的简单三维倾斜层模型,采用如图 3所示的观测系统进行三维数值模拟.图 3中倒三角形为检波点,实心圆点为炮点.观测系统参数为:3 m道间距,18 m线间距,6条接收线,每线36道,3 m炮点距,18 m炮线距,7条炮线,每线31炮.模型覆盖层速度为600 m/s,地震波的主频大概为30 Hz,可以计算出满足Nyquist采样定理的空间采样间隔为10 m,即道间距小于10 m时的规则采样不会产生空间假频.而当道间距大于10 m时,则会产生明显的空间假频.模型采用观测系统的道间距为3 m,远小于采样定理规定的最大10 m道间距,因此模型三维数值模拟得到的原始记录在空间上采样充分.
|
图 2 简单模型 Figure 2 Simple model |
|
图 3 简单模型三维地震观测系统 Figure 3 3D geometry of simple model |
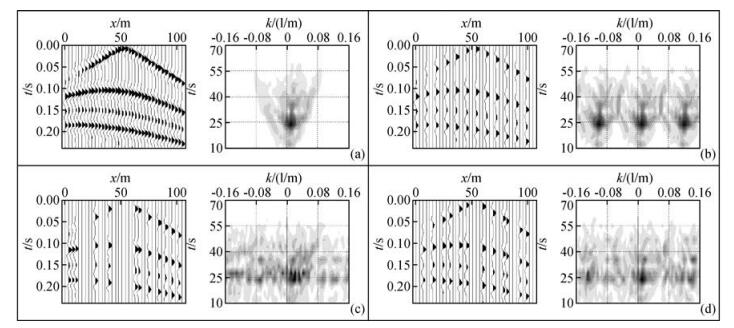
对原始记录每炮接收道进行三分之一的采样,分别得到规则欠采样、随机欠采样和jittered随机欠采样数据.图 4为四种不同采样方式的合成数据及其频谱图, 其中图 4a为原始合成记录及其频谱,图 4b为规则欠采样合成记录及其频谱,存在着严重的相干噪声,图 4c和图 4d分别为普通随机欠采样及jittered随机欠采样合成记录及其频谱图,图中可见,随机欠采样将规则欠采样数据的相干噪声转换成了不相干随机噪声,有效压制了假频的干扰,而jittered随机欠采样的效果又要优于普通随机欠采样.
|
图 4 简单模型合成地震记录及频谱图 (a)原始记录及其频谱;(b)规则欠采样记录及其频谱;(c)随机欠采样记录及其频谱;(d)jittered随机欠采样记录及其频谱. Figure 4 Simple model synthetic record and corresponding amplitude spectrum (a)Original record and corresponding amplitude spectrum; (b)Regularly sampled sub-Nyquist record and corresponding amplitude spectrum; (c)Randomly sampled sub-Nyquist record and corresponding amplitude spectrum; (d) Jittered sampled sub-Nyquist record and corresponding amplitude spectrum. |
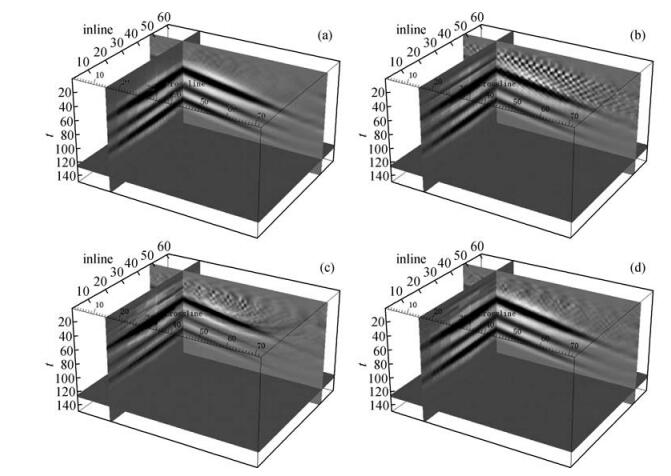
前面对原始地震记录每炮接收道进行了三分之一的抽样,通过数据处理得到四种数据的三维偏移成像图(图 5),图 5a为原始记录偏移成像图,由于原始记录在空间进行了充分的采样,因此偏移成像结果层位显示清晰,图 5b、图 5c和图 5d分别为规则欠采样记录偏移成像图、随机欠采样记录偏移成像图和jittered随机欠采样记录偏移成像图,其中规则欠采样数据的成像效果最差,存在着严重的相干干扰,随机欠采样记录有效压制了相干干扰,偏移成像图中只存在一定的随机噪声,而jittered随机欠采样记录几乎不存在相干干扰和随机噪声的影响,偏移成像效果与完全采样数据成像效果相当.
|
图 5 简单模型不同采样方式偏移成像图 (a)原始记录偏移成像图; (b)规则欠采样记录偏移成像图; (c)随机欠采样记录偏移成像图; (d)jittered随机欠采样记录偏移成像图. Figure 5 Simple models of different sampling methods migration imaging (a)Image of original record; (b)Image of regularly sampled sub-Nyquist record; (c)Image of randomly sampled sub-Nyquist record; (d)Image of jittered randomly sampled sub-Nyquist record. |
为了定量说明不同欠采样方式得到偏移成果图的效果, 定义信噪比PSNR=10×log10‖S0‖2/‖S-S0‖2,其中S0表示原始记录偏移成果数据体,S表示待计算信噪比的欠采样记录偏移成果数据体,信噪比越高,代表偏移成果越好.通过计算得到各欠采样记录偏移成果数据体的信噪比(表 1),通过信噪比分析可以明显看出随机欠采样记录的成像效果要好于规则欠采样记录,同时jittered随机欠采样记录的成像效果又远远优于普通随机欠采样记录的成像效果.
|
|
表 1 简单模型不同采样方式偏移成果数据体信噪比 Table 1 SNRs of simple model different sampling methods migration imaging |
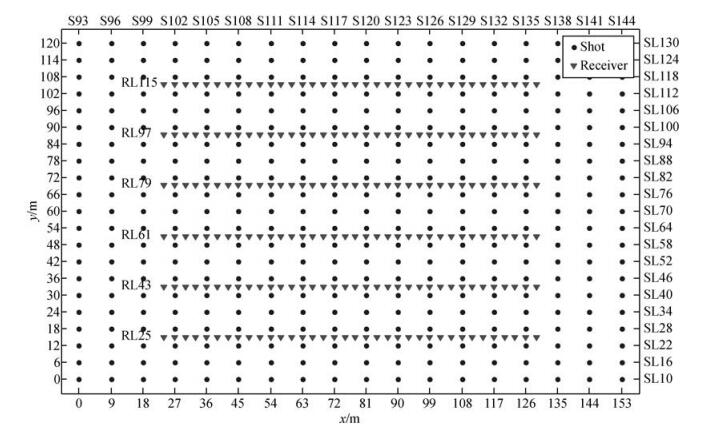
如图 6所示为某工区三维观测系统设计图,图中倒三角形为检波点,实心圆点为炮点.观测系统参数为:3 m道间距,18 m线间距,6条接收线,每线36道,6 m炮点距,9 m炮线间距,18条炮线,每线23炮.从图 6中可以看出,传统三维地震观测系统的炮点和检波点的分布是均匀规则的.
|
图 6 某工区三维观测系统设计图 Figure 6 3D geometry of the study area |
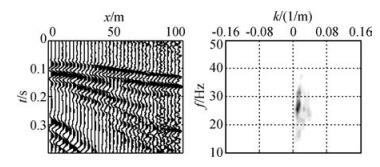
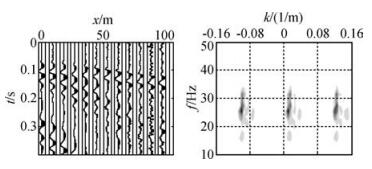
如图 7所示为实际浅层三维地震数据中某炮的原始地震记录及其频谱图,工区覆盖层速度为700 m/s,地震波的主频大概为40 Hz,可以计算出满足Nyquist采样定理的空间采样间隔为8.7 m,即道间距小于8.7 m时的规则采样不会产生空间假频.而当道间距大于8.7 m时(如图 8为等间隔抽取三分之一的地震记录及其频率波数图,其道间距为9 m),会产生空间假频.
|
图 7 原始地震记录及其频率波数图 (3 m道间距) Figure 7 Filed record and its frequency-wavenumber diagram(trace interval 3m) |
|
图 8 等间隔抽取地震记录及其频率波数图 (9 m道间距) Figure 8 Regularly sampled sub-Nyquist record and its frequency-wavenumber diagram(trace interval 9m) |
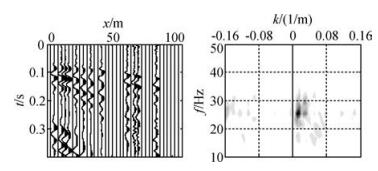
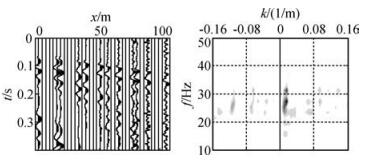
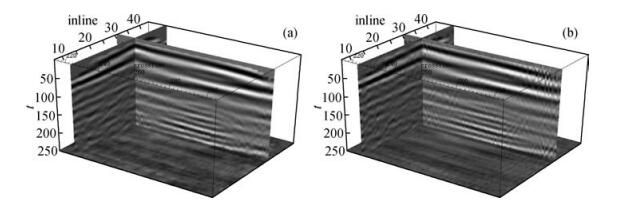
随机欠采样地震记录(图 9和图 10)与图 8具有相同的道数,其频率波数图中的有效信号反映清晰,相干噪声的压制效果比较明显,同时jittered随机欠采样地震记录(图 10)不仅有效压制了相干噪声,背景噪声的干扰也要小于随机欠采样地震记录,图 11是使用实际采集的三维地震记录处理得到三维偏移成果数据体,其中图 11a为使用原始地震记录偏移得到的成果图,图 11b为使用jittered随机采样抽取三分之一数据体偏移得到的成果图,jittered欠采样数据体偏移成果清晰,通过计算得到jittered欠采样偏移数据体信噪比(PSNR)达到了9.567,充分证明了jittered采样在浅层三维地震勘探中使用的有效性.
|
图 9 随机欠采样地震记录及其频率波数图 (与图 8的道数相等) Figure 9 Randomly sampled sub-Nyquist record and corresponding amplitude spectrum |
|
图 10 jittered随机欠采样地震记录及其频率波数图 (与图 8的道数相等) Figure 10 Jittered randomly sampled sub-Nyquist record and corresponding amplitude spectrum |
|
图 11 原始地震记录偏移成像图(a)和jittered随机欠采样记录偏移成像图(b) Figure 11 (a)Image of original record; (b)Image of jittered randomly sampled sub-Nyquist record |
通过数值模拟合成记录和采集实际地震数据,进行规则欠采样、普通随机欠采样和jittered随机欠采样,分析其频率-波数域特征和三维偏移成果,结果表明:
(1) 在陆上浅层三维地震道间距无法满足奈奎斯特采样条件的情况下,检波点随机分布所采集的地震数据可以有效降低地震资料的混叠效应.
(2) 普通随机欠采样和jittered随机欠采样均可以将规则欠采样的相干混叠转换成不相干随机噪声,而jittered随机欠采样的效果又要优于普通随机欠采样.
(3) 在野外进行浅层三维地震数据采集时,如采用jittered随机欠采样方式进行检波器的布置,可以实现以较少的检波器布置较大范围的观测系统,从而大大提高了野外数据采集工作的效率,同时,这种随机的布线可以较灵活地适应野外的工作环境,在采用规则布线时,尽量希望测区足够平坦、开阔,无大尺度障碍物,而随机的布线可以适应有障碍物的地形地貌,在遇到障碍物或不能跨越的地形时,可适当增大道间距,在开阔位置减小道间距进行数据补偿.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Abma R, Kabir N. 2006. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 71(6): E91–E97. DOI:10.1190/1.2356088 |
| [] | Donoho L L. 2006. 1995. Compressed sensing[J]. IEEE Transactions on Information Theory, 52(4): 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [] | GUO Dong-Liang, ZHANG Tie-Jun, DAI Xian-Hua. 2012. Methods of signal frequency, amplitude and phase measurement based on non-uniform sampling[J]. Systems Engineering and Electronics (in Chinese), 34(4): 662–665. |
| [] | Hennenfent G, Herrmann F J. 2008. Simply denoise:Wavefield reconstruction via jittered undersampling[J]. Geophysics, 73(3): V19–V28. DOI:10.1190/1.2841038 |
| [] | Herrmann F J. 2009. Sub-Nyquist sampling and sparsity:How to get more information from fewer samples[C].//79th Annual International Meeting, SEG. Extended Abstracts, 3410-3413. |
| [] | LI Peng, GU Han-Ming, MA Sheng-Min, et al. 2015. Marine towed streamer random sampling of spectral analysis[J]. Geological Science and Technology Information(in Chinese), 34(1): 179–184. |
| [] | Lustig M, Donoho D, Pauly J M. 2007. Sparse MRI:The application of compressed sensing for rapid MR imaging[J]. Magnetic Resonance in Medicine, 58(6): 1182–1195. DOI:10.1002/(ISSN)1522-2594 |
| [] | Moldoveanu N. 2008. Circular geometry for wide-azimuth towed-streamer acquisition[C].//70th EAGE Conference and Exhibition incorporating SPE EUROPEC 2008, EAGE. Extended Abstracts. |
| [] | Moldoveanu N, Kapoor J. 2009. What is the next step after WAZ for exploration in the Gulf of Mexico?[C].//79th Annual International Meeting, SEG. Extended Abstracts, 41-45. |
| [] | Moldoveanu N. 2010. Random sampling:A new strategy for marine acquisition[C].//80th Annual International Meeting, SEG. Extended Abstracts, 51-55. |
| [] | Shannon C E. 1949. Communication in the presence of noise[J]. Proc. IRE, 37(1): 10–21. |
| [] | WANG An-Min, WANG Shu, CHEN Ming-Xin. 2005. A novel spectrum analysis method for nonuniform periodically sampling[J]. Signal Processing, 21(3): 240–243. |
| [] | Wong T T, Luk W S, Heng P A. 1997. Sampling with Hammersley and Halton points[J]. Journal of Graphics Tools, 2(2): 9–24. DOI:10.1080/10867651.1997.10487471 |
| [] | ZHANG Hua, CHEN Xiao-Hong. 2013. Seismic data reconstruction based on jittered sampling and curvelet transform[J]. Chinese J. Geophys. (in Chinese), 56(5): 1637–1649. DOI:10.6038/cjg20130521 |
| [] | ZHAO Yi-Jiu. 2008. Study on compressive sampling and recovery algorithm of sparse analog signal (in Chinese)[Ph. D. thesis]. Chengdu:University of Electronic Science and Technology of China. |
| [] | Zhou C X, Schuster G T. 1995. Quasi-random migration of 3-D field data[C].//65th Annual International Meeting, SEG. Expanded Abstracts, 1145-1148. |
| [] | Zwartjes P M, Sacchi M D. 2007. Fourier reconstruction of nonuniformly sampled, seismic data[J]. Geophysics, 72(1): V21–V32. DOI:10.1190/1.2399442 |
| [] | 郭东亮, 张铁军, 戴宪华. 2012. 基于非均匀采样的信号频率、幅值和相位检测[J]. 系统工程与电子技术, 32(4): 662–665. |
| [] | 李鹏, 顾汉明, 马圣敏, 等. 2015. 海上拖缆随机采样抗混叠机理分析[J]. 地质科技情报, 34(1): 179–184. |
| [] | 汪安民, 王殊, 陈明欣. 2005. 一种抗混叠的非均匀周期采样及其频谱分析方法[J]. 信号处理, 21(3): 240–243. |
| [] | 张华, 陈小宏. 2013. 基于jitter采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 56(5): 1637–1649. DOI:10.6038/cjg20130521 |
| [] | 赵贻玖. 2008. 稀疏模拟信号压缩采样与重构算法研究[博士论文]. 成都: 电子科技大学. http://cdmd.cnki.com.cn/Article/CDMD-10614-1012473969.htm |
 2017, Vol. 32
2017, Vol. 32

