2. 北京吉奥博锐科技有限公司, 北京 102200
2. Beijing GeoBrain Technology Limited Company, Beijing 102200, China
随着油气勘探和开发技术的不断发展,富集的油气储层日趋紧缩,海洋深层油气藏、剩余油气藏和边缘油气资源逐渐受到人们的重视.由于这类油气资源储层的物理性质表现差,分布复杂,需要更加可靠的开采和勘探方法,由此使得地质导向钻井方式得到极大的发展.地质勘探测井公司通过地质导向钻井技术设计和布置大位移井,水平井以及多底井、多分支井的方式,有效地解决了复杂油气藏的勘探和开发问题,极大地提高了海洋深层及滩海油气资源和剩余油气资源的开发成本和采收率(魏宝君等, 2010; 张克等, 2014; 刘乃震等, 2015).作为指导地质导向钻井的关键技术之一——定向电磁波测井通过倾斜线圈天线测量地层电阻率差异,高效率、高准确度显示了油水界面的分布和走向,提高了导向钻井技术对未钻地层界面和方位的钻前预测能力,并通过磁场交叉耦合分量和共面耦合分量的测量提供地层的电各向异性特征、地层倾角信息实现了复杂地层的初步评估,为大斜度井和水平井的井位设计提供可靠资料(Seydoux et al., 2004; Omeragic et al., 2005).
由于定向电磁波测井主要应用于导向钻井方式,其测井环境主要是大斜度井和水平井,然而由于重力,地质情况等因素导致仪器在井眼中处于偏心位置的情况十分常见.这种仪器偏心对定向电磁波测井的测量信号影响严重(尤其共面耦合分量),混淆了仪器对油水界面的方位和距离的识别和评估.针对仪器偏心的影响可以通过多种数值计算方法进行研究,包括有限差分方法(Wang and Fang, 2001; Hue et al., 2005; 杨守文等, 2009)、有限元方法(Pardo et al., 2006, 2008; 孙向阳等, 2008)、半解析方法(Hue et al., 2006; 汪宏年等, 2008; 张雷等, 2012)和解析方法(Liu et al., 2012; Moon et al., 2016).前两类数值方法虽然可以分析更加复杂的介质模型,但是相对而言,计算消耗十分严重,不利于现场应用.第三种方法将三维模型简化成二维模型,在一定程度上提高了算法的精度和效率,然而它的计算效率仍然比不上解析算法.解析算法在井眼因素的快速分析上具有不可忽略的优势,为实时校正测井数据、快速反演井眼环境提供极为便利的条件.Lovell和Chew在柱坐标条件下,通过并矢格林函数的谱分解形式描述了点偶极子和线流源在仪器居中和偏心条件下对地层的响应特征(Lovell and Chew, 1987).Hagiwara建立具有任意倾斜方向的线流源在井眼中响应的伪解方程(Pseudoanalytic Formulation),模拟研究了定向电磁波测井受到井眼,钻铤,侵入等因素的影响(Hagiwara et al., 2005).而后,Hue考虑了均匀各向同性介质中,计算了仪器偏心对测井响应的影响(Hue et al., 2006).Liu在此基础上推导了复杂的伪反射矩阵,使得伪解方程能够计算多偏心模型,但是复杂的伪反射矩阵的引进也导致积分收敛速度非常慢.Moon同时考虑磁导率单轴各向异性和电导率单轴各向异性介质,建立了双单轴各向异性的伪解模型,这种双单轴各向异性模型的考虑为更加详细地分析地层电各向异性对测井响应的影响奠定基础,然而Moon并没有分析双单轴地层中,井中仪器偏心对定向电磁波测井的影响(Moon et al., 2016).
本文在同时考虑磁导率单轴各向异性和电导率单轴各向异性介质的基础上,推导了定向电磁波测井仪器在仪器偏心条件下的广义反射矩阵,建立了定向电磁波测井井中偏心响应的伪解模型.伪解模型不但能够同时考虑电导率单轴各向异性和磁导率单轴各向异性,而且避免了伪反射矩阵复杂的求解步骤(Liu et al., 2012),提高了运算速度,使得算法能够应用到随钻电磁波测井的实时井眼评价中,而后通过对比数值模式匹配方法验证算法的精度.本文计算定向电磁波测井仪器在偏心条件下的旋转测量结果,分析仪器偏心对测井响应的影响(Bittar et al., 2011; Bittar and Wu, 2013),并提取耦合电压矩阵,分析不同偏心条件下,九个电压分量对地层各向异性的响应规律,为精确解释定向电磁波测井数据提供依据.
1 方法原理 1.1 伪解模型柱坐标条件下的MAXWELL’s方程,考虑时间变化因子eiωt.公式为

|
(1) |

|
(2) |

|
(3) |

|
(4) |
E和H表示电场(V/m)和磁场(A/m),JT表示电流密度(A/m2),μ为磁导率张量(H/m),下角标‘h’表示横向,‘v’表示纵向,μ=diag(μh, μh, μv),

任意倾斜方向线圈系的电流密度,IT发射电流(A),ρT表示线圈投影半径(m),θT表示线圈倾斜角度(°),ψT表示线圈方位角度(°),表达式为
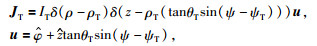
|
发射线圈的位置zT=0,倾斜线圈结构如图 1所示(Hagiwara et al., 2003).

|
图 1 倾斜线圈结构在径向分层介质中的模型 激励线圈的倾斜角度为θT,方位角度为ψT, 激励线圈套在钻铤(-1) 上,i=0表示井眼,i=1表示地层. Figure 1 Geometry of a tilted-coil antenna in a cylindrically multilayered formation The coil antenna with tilt angle(θT) and azimuthal angle(ψT) is located on the metallic mandrel (i=-1 layer), the i=0 layer stands for borehole and the i=1 layer stands for formation. |
对(1)(2) 式分别求旋度,公式为

|
(5) |

|
(6) |
场分解为轴向场(下标为z)和横向场(下标为s),公式为

|
考虑无源条件下,联立(3)(4) 式,将(5) 和(6) 式化简为

|
(7a) |

|
(7b) |
提取z方向的电场和磁场,公式为

|
(8a) |

|
(8b) |
通过Fourier变换,对电场和磁场进行谱分解,可以得:
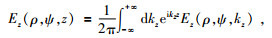
|
(9a) |

|
(9b) |
将

|
(10a) |

|
(10b) |
其中k表示波数,


对于(10) 式的解可以表示成Bessel函数形式,公式为

|
(11) |
其中,Gv表示第一类Bessel函数Jv或者第一类Hankel函数Hv(1),上标“=”表示矩阵,av或bv者表示幅度系数,通过层边界之间的连续性条件求解.
无源条件下的横向场Es和Hs表示为

|
(12a) |

|
(12b) |
通过(11)(12) 式,横向场表示为

|
(13) |
当仪器在井眼内处于偏心位置如图 2所示,仪器轴距离井轴d,与井轴的偏心角度为ψE,图中含有两个坐标系,一个是以井轴为z轴的坐标系(z, ρ, ψ),为辅坐标系,一个是以仪器轴为z′轴的坐标系(z′,ρ′,ψ′),为主坐标系,井眼内泥浆为各向同性介质.

|
图 2 偏心井模型的横剖面图 以井轴为中心的(ρ, ψ)辅坐标系相对于以仪器轴为中心的(ρ, ψ)主坐标系的偏心角度ψE,偏心距离为d,虚线线圈表示主坐标系的伪边界. Figure 2 Cross section view of an eccentric borehole geometry The nonprime coordinate system(ρ, ψ) is concentric to the borehole and has a displacement of (d, ψE) with respect to the primed coordinate system(ρ, ψ) which is concentric to logging tool. The fictitious circular boundary show by a dashed circle is concentric to the primed coordinate system. |
主坐标系中,井内线圈内侧的电场和磁场可以为

|
(14) |
仪器含有钻铤时,钻铤表面形成广义反射矩阵


|
为了保证线圈处电场和磁场的连续性条件,ρ′≥ρ′T的井内电场和磁场方程可以写为

|
(15) |
其中:

|
辅坐标系中电场和磁场的方程表示为,

|
(16) |

采用Bessel函数的Graf’s加法原理(Liu et al., 2012):

|
ϕ表示Bessel方程.(16) 式变为

|
(17) |
在“伪边界处”匹配(15) 和(17) 式,公式为

|
(18a) |

|
(18b) |
通过(18a)(18b)式求得:

|
上述线性方程转化成矩阵方程为

|
(19) |
其中:
求解上述矩阵方程,可得a0j,


|
(20) |
将(20) 式带入(15) 式可得主坐标系内的电场和磁场方程.而电场和磁场的横向分量可以由(13) 求解.
接收端的感应电动势为

|
(21) |
式中,
径向非均匀介质中,电磁波在径向界面上形成反射和透射,单次界面的反射和透射可以用狭义反射矩阵和狭义透射矩阵表示,多次反射和透射的累加可以通过广义反射矩阵表示如图 3所示.

|
图 3 驻波和外行波在界面处的反射和透射 驻波由i层在界面ρi-1入射,反射在i层形成外行波和透射在i-1层形成驻波, 外行波由i层在界面ρi入射,反射在i层形成驻波和透射在i+1层形成外行波,P为狭义反射矩阵,T为狭义透射矩阵和R为内边界上的广义反射矩阵,N为外边界上的广义反射矩阵. Figure 3 Boundary condition in terms of reflection and transmission coefficients for standing and outgoing waves A standing wave is incident from layer i onto boundary ρi-1, an outgoing wave is reflected and a standing wave is transmitted into layer i-1.An outgoing wave is incident from layer i onto boundary ρi, a standing wave is reflected and an outgoing wave is transmitted into layer i+1. P stands for local reflection coefficient, T stands for local transmission coefficient. R is general reflection coefficient on the inner boundaries and N is general reflection coefficient on the outer boundaries. |
考虑双单轴各向异性介质地层模型,内行波是从i+1介质中入射到介质中,在边界ρi形成发射和透射,


|
(22) |
外行波从i介质入射到i+1介质中,在边界ρi处形成的反射和透射,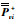


|
(23) |
广义反射矩阵可以通过叠加形式求得,公式为

|
(24) |

|
(25) |
其中,



计算定向电磁波测井在井眼内处于偏心位置的响应模型,模型1:井内泥浆电阻率为0.1 Ω·m,地层水平电阻率为10 Ω·m,垂直电阻率为50 Ω·m;模型2:井内泥浆电阻率为10 Ω·m,地层水平电阻率为0.1 Ω·m,垂直电阻率为0.5 Ω·m.地层模型如图 4a所示,仪器偏心等于90°,井眼半径12 in(1 in=0.0254 m),仪器轴距离井轴为d(d=0,1,2,3,4,5) in.定向电磁波测井仪器为单发双收结构如图 4b所示,每个线圈的倾斜角度均为45°,钻铤半径为4 in,发射线圈在xoy平面内投影为4.5 in,TR1的线圈距离为24 in,TR2的线圈距离为30 in,计算接收线圈(R1和R2) 的电压实部和虚部,与数值模式匹配方法进行对比(如图 4c, d),伪解方法的偏心模型的结果精度很高,而且速度非常快(计算一次偏心模型需要11 s,采用8核3.6 GHz的CPU,内存32 GB的计算机).

|
图 4 井眼内仪器偏心模型及伪解方法与数值模式匹配方法对比结果 (a)为井眼内仪器偏心模型;(b)为仪器模型;(c)为电压实部对比结果;(d)为电压虚部对比结果,“/”左侧为泥浆电阻率,右侧为地层电阻率. Figure 4 Comparsion of the real part and image part of measured voltages in eccentric borehole computed by Pseudoanalytical method and NMM respectively (a) Eccentric borehole model; (b) Geometry of directional electromagnetic logging tool; (c) Results of real parts; (d) Results of image parts. |
定向电磁波测井仪器如图 5所示,仪器采用倾斜角度为45°角的线圈系发射和接收电磁信号,激发频率为500 kHz.通过旋转测量方式记录周向360°的方位信息,并在此基础上分析获得地层与井眼轨迹的相对倾角,地层的各向异性以及油气层界面距离等信息.旋转360°测量记录32个数据点,每个点的电压值可以分解成如式(26)(Bittar et al., 2011; Bittar and Wu, 2013),公式为

|
(26) |

|
图 5 定向电磁波测井的仪器模型 T为激励线圈,R为接收线圈,T3up、R1、R2、T2dn倾斜角度均为45°,T2up,T3dn倾斜角度均为-45°. Figure 5 Configurations of Directional electromagnetic logging tool T stands for transmitter coil antenna. R stands for receiver coil antenna. The tilt angle of T3up, R1, R2, T2dn is 45°, and The tilt angle of T2up, T3dn is -45°. |
其中:

|
θT为发射线圈的倾斜角度,θR为接收线圈的倾斜角度,β为仪器的旋转角度,β′表示仪器的x轴(Highside)与目标层指示方位的夹角(Bittar et al., 2011;Bittar and Wu, 2013),Vij为耦合电压,表示法线方向为i的发射线圈在法线方向为j的接收线圈处产生的耦合电压,VRT为一对接收R和发射线圈T随着方位角度变化的电压值,A和C主要由直接耦合分量(包括共面分量Vxx,Vyy和共轴分量Vzz)组成,B由交叉耦合分量组成.以下选取其中一对组合测量单元(T2upR1和T2dnR1)进行分析.
图 6为仪器在井中处于偏心位置时的旋转测量结果,仪器偏心如图 4a所示,记录接收线圈的实部和虚部.由图看出,仪器响应的实部和虚部由于受到仪器偏心的影响出现了余弦形式的变化,响应幅度随着偏心距离的增大呈现增强趋势.图中,T2upR1呈现cos(β)变化,T2dnR1呈现cos2(β)变化,根据(26) 式,发现对于VR1T2up而言,B分量的比重较大,而对于VR1T2dn而言,A分量的比重较大.因此,具有正交结构的T2upR1更加容易提供方位信息.将余弦函数cos(β-β′)与图 6拟合,得出β′=270°,这与仪器沿着井眼-y轴偏心的模型(图 4a)相符合,说明仪器对目标层的指示角度同时也指示了仪器相对于井眼的偏心角度,也意味着仪器在井眼内偏心情况直接影响仪器对目标层的方位确定.公式为

|
(27) |

|
图 6 T2upR1和T2dnR1在井眼偏心模型中的旋转测量 (a)为实部;(b)为虚部,“/”左侧为发射线圈倾斜角度,右侧为接收线圈倾斜角度. Figure 6 Measurement signals of T2upR1 and T2dnR1 according to different azimuth angles from 0 degree to 360 degree (a) Real parts of signals. (b) Imag parts of signals. The left part of"/"is the tilt angle of transmitter. The right part of"/"is the tilt angle of receiver. |
(26) 式中A、B、C可以通过32个数据点的电压合成计算得到.
对于每个测量单元(VR1T2up或者VR1T2dn等)均可以提取交叉耦合分量B,而由于分量随着方位角度呈cos(β)变化,因此B分量对目标层具有唯一指向性.然而图 7中,交叉耦合分量B由于偏心的影响而产生余弦变化,将Bcos(β-β′)和图 7拟合,得出β′=270°,与仪器相对于井眼的偏心角度相符合,因此交叉耦合分量对目标层方位的指示受到井眼内仪器偏心的影响,这点与VR1T2up的规律类似.

|
图 7 交叉耦合分量B随着方位角度的旋转测量结果 (a)为实部; (b)为虚部.“/”左侧为发射线圈倾斜角度,右侧为接收线圈倾斜角度. Figure 7 Measurement signals of cross-component B according to different azimuth angles from 0 degree to 360 degree (a) Real parts of signals; (b) Imag parts of signals. The left part of "/"is the tilt angle of transmitter. The right part of"/"is the tilt angle of receiver. |
对于定向电磁波测井仪器来说,交叉耦合分量B主要提供目标层的方位信息,但是由于B信号较为微弱,不如A信号对目标层的响应幅值变化明显.因此,定向电磁波测井仪器通过A测量目标层与仪器的距离,一般来说,A随着目标层逐渐接近仪器,其幅度值呈近线性增大(Bittar et al., 2011).然而,本文通过计算发现直耦分量A也会受到井眼内部仪器偏心的影响,其幅度值随着偏心距离增大而增大.这点可以通过将仪器偏心的模型等效成井侧出现目标层的响应模型进行解释(如图 8b),因此随着仪器的偏心距离增大,相当于仪器与目标层的距离逐渐缩短,其直耦分量A的幅度也随之增大.仪器在井眼内偏心的情况混淆了直耦分量A对目标层边界的响应,使得我们无法准确地通过直耦分量A确定油气储层与井眼的距离,尤其当仪器的偏心方向与油气储层边界相反时.因此,对于井眼内的仪器偏心校正是提高定向电磁波测井精确评价油气储层方位和距离的主要途径.当然,随着源距的增长和频率的降低,偏心影响将逐渐减弱.另外,非对称性侵入带(如Teardrop invasion)对仪器的边界响应特征也会产生类似的影响(Omeragic et al., 2009).

|
图 8 直耦分量A的幅度值随着偏心距离的变化(a)及偏心模型等效图(b) Figure 8 Amplitude ratios of directional-component A with different offset distance in eccentric borehole (a) and equivalent diagram of eccentric borehole model(b) |
由于定向电磁波测井仪器的旋转测量模式,可以对测量单元(T2upR1和T2dnR1)中提取类似三分量感应测井的耦合电压矩阵.本文计算各耦合电压矩阵受到偏心距的影响(如图 9)(Bittar and Wu, 2013).

|
图 9 耦合电压矩阵实部随着偏心距离的变化 Figure 9 Coupling voltage matrix with different offset distance in eccentric borehole |
图 9中,对比井内外地层电阻率差异极大时,各耦合电压受偏心的影响.由图 9,无论井内外电阻率如何分布,直耦电压分量Vzz均随着偏心距离的增大而降低,这是因为此时Vzz分量不但受井内外电阻率分布的影响,也受到由于偏心的存在导致涡流形状改变的影响,其规律与阵列感应测井中的中等源距子阵列受偏心影响的变化规律类似,由于Vzz随着偏心变化的规律较为稳定,因此可以用于反演井眼的偏心情况.对比不同井眼环境的Vxx、Vyy,看出由于井筒内涡流的影响使得Vxx、Vyy产生符号的变化,然而在不同的泥浆环境中,Vxx、Vyy随着偏心的变化规律相似,均随着偏心距离的增大,电压实部的幅度值降低.交叉耦合电压Vyz、Vzy在高阻泥浆的时候,实部响应随着偏心变化程度很大,甚至比Vzz分量变化更加明显,而在低阻泥浆的时候则变化很小,说明交叉耦合分量受偏心的影响程度与井内泥浆的电阻率大小有关.由于仪器沿着-y轴偏心的原因,其余交叉耦合分量Vxy、Vyx和Vxz、Vzx响应幅度非常小.
耦合电压矩阵是判断地层各向异性特征的主要参考,主要通过Vzz确定地层的水平电阻率,然后通过Vxx和Vyy分量确定地层的电各向异性,但是由于偏心的影响,Vzz分量也会受到仪器偏心的影响发生一定的变化(如图 9),而且由于偏心的存在,Vzz也会随着各向异性比率发生一定的变化.同样,Vxx和Vyy对各向异性比率的变化规律也会受到偏心的影响.具体见下图 10.考虑仪器居中或者偏心条件下,耦合电压随着各向异性比率变化(Rv/Rh)的响应.

|
图 10 不同偏心条件下,耦合电压矩阵对各向异性的响应 Figure 10 Coupling voltage matrix with different anisotropic formation in eccentric borehole |
当仪器处于居中位置时,只有直耦电压分量Vxx、Vyy、Vzz有一定的幅度值,其他交叉耦合分量均为零.其中Vzz并不随着各向异性比率变化,Vxx、Vyy随着各向异性比率变化,因此,Vzz可以不受地层各向异性的影响真实反映地层的水平电阻率,而Vxx、Vyy能够反映地层的各向异性特征,即获得地层的垂直电阻率.当仪器在井眼中处于偏心位置时,不但直耦电压分量Vxx、Vyy随着各向异性比率变化,Vzz也会随着各向异性比率的增大而增大,说明偏心情况下的Vzz会受到地层各向异性的影响.交叉耦合分量Vyz、Vzy相比居中条件下,不但出现了一定的响应值,而其值也随着各向异性比率发生明显的变化,甚至Vyz、Vzy对各向异性的响应规律相同.由于仪器沿着-y轴偏心,仅有Vyz、Vzy随着地层各向异性比率变化,但如果沿x轴偏心或者与x轴成一定的角度(不等于90°),其他交叉耦合分量也会随着各向异性比率变化.上述结论也适用于三分量感应测井在偏心井眼中的响应规律(Davydycheva et al., 2009).总之,当仪器处于偏心位置时,各耦合电压均会对地层各向异性产生响应,只不过响应规律会受到仪器偏心的影响,给识别地层的各向异性特征带来一定的困难,因此基于解析模型建立的实时井眼校正是定向电磁波测井实施地质导向过程中十分重要的步骤.
3 结论和讨论本文在柱坐标条件下,基于并矢格林函数的谱表达式建立了井中仪器偏心条件下,定向电磁波测井对双单轴各向异性地层响应的伪解模型.文章推导了仪器对双单轴各向异性介质的广义反射矩阵,在“伪边界”处匹配电磁场建立了幅度系数的求解矩阵,提高了伪解方法在求解井中偏心问题上的运算速度,有利于算法在实时井眼校正方面的应用,并通过对比数值模式匹配算法验证算法的精度.本文基于伪解模型分析了定向电磁波测井仪器在偏心井眼中的周向测井响应,通过数值方法分析发现仪器偏心严重影响了定向电磁波测井仪器对目标层的方位和距离判断能力.本文认为对于定向电磁波测井来说,井内仪器偏心和非对称侵入等情况是影响仪器判断目标层边界的主要因素.本文也分析了定向电磁波测井仪器的耦合电压矩阵随着仪器偏心距离的变化,并在不同偏心条件下,分析其对地层各向异性的响应能力.总之,由于定向电磁波测井识别地层边界和评价各向异性地层的能力受到仪器偏心的严重影响,而且这种偏心影响不但与井眼状况和仪器偏心程度有关,也与地层的电各向异性特征有关.因此基于快速解析方法分析电各向异性地层中仪器偏心的影响规律,建立高效可靠的井眼校正方案,是提高仪器识别和精确评价油气储层的重要途径.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Bittar M, Beste R, Li S J, et al. 2011. Field testing of a new LWD triaxial sensor for anisotropy and dip measurement in vertical and deviated wells[C].//SPWLA 52nd Annual Logging Symposium. Colorado Springs, Colorado:Society of Petrophysicists and Well-Log Analysts. |
| [] | Bittar M, Wu H. 2013. New logging while drilling ranging and formation evaluation technique[C].//Offshore Mediterranean Conference and Exhibition. Ravenna, Italy:Offshore Mediterranean Conference. |
| [] | Chew W C. 1990. Waves and Fields in Inhomogeneous Media[M]. New York: Van Nostrand Reinhold. |
| [] | Davydycheva S, Homan D, Minerbo G. 2009. Triaxial induction tool with electrode sleeve:FD modeling in 3D geometries[J]. Journal of Applied Geophysics, 67(1): 98–108. DOI:10.1016/j.jappgeo.2008.10.001 |
| [] | Hagiwara T, Banning E J, Ostermeier R M, et al. 2005. Effects of mandrel, borehole, and invasion for tilt-coil antennas[J]. SPE Reservoir Evaluation & Engineering, 8(3): 255–263. |
| [] | Hue Y K. 2006. Analysis of electromagnetic well-logging tools[Ph. D. thesis]. Columbus:The Ohio State University. |
| [] | Hue Y K, Teixeira F L, Martin L E S, et al. 2005. Modeling of EM logging tools in arbitrary 3-D borehole geometries using PML-FDTD[J]. IEEE Geoscience and Remote Sensing Letters, 2(1): 78–81. DOI:10.1109/LGRS.2004.840637 |
| [] | Liu G S, Teixeira F L, Zhang G J. 2012. Analysis of directional logging tools in anisotropic and multieccentric cylindrically-layered earth formations[J]. IEEE Transactions on Antennas and Propagation, 60(1): 318–327. DOI:10.1109/TAP.2011.2167907 |
| [] | Liu N Z, Wang Z, Liu C. 2015. Theories and key techniques of directional electromagnetic propagation resistivity tool for geosteering applications while drilling[J]. Chinese Journal of Geophysics, 58(5): 1767–1775. DOI:10.6038/cjg20150526 |
| [] | Lovell J R, Chew W C. 1987. Response of a point source in a multicylindrcally layered medium[J]. IEEE Transactions on Geoscience and Remote Sensing, GE-25(6): 850–858. DOI:10.1109/TGRS.1987.289757 |
| [] | Moon H, Donderici B, Teixeria F L. 2016. Stable evaluation of Green's functions in cylindrically stratified regions with uniaxial anisotropic layers[J]. Journal of Computational Physics, 325: 174–200. DOI:10.1016/j.jcp.2016.08.019 |
| [] | Omeragic D, Habashy T, Chen Y H, et al. 2009. 3D reservoir characterization and well placement in complex scenarios using azimuthal measurements while drilling[C].//SPWLA 50th Annual Logging Symposium. The Woodlands, Texas:Society of Petrophysicists and Well-Log Analysts. |
| [] | Omeragic D, Li Q M, Chou L, et al. 2005. Deep directional electromagnetic measurements for optimal well placement[C].//SPE Annual Technical Conference and Exhibition. Dallas, Texas:Society of Petroleum Engineers, DOI:10.2118/97045-MS. |
| [] | Pardo D, Demkowicz L, Torres-Verdín C, et al. 2006. Two-dimensional high-accuracy simulation of resistivity log ging-while-drilling (LWD) measurements using a self-adaptive goal-oriented &hp& finite element method[J]. SIAM Journal on Applied Mathematics, 66(6): 2085–2106. DOI:10.1137/050631732 |
| [] | Pardo D, Torres-Verdín C, Nam M J, et al. 2008. Fourier series expansion in a non-orthogonal system of coordinates for the simulation of 3D alternating current borehole resistivity measurements[J]. Computer Methods in Applied Mechanics and Engineering, 197(45-48): 3836–3849. DOI:10.1016/j.cma.2008.03.007 |
| [] | Seydoux J, Tabanou J, De Laet Y, et al. 2004. A deep resistivity logging-while-drilling device for proactive geosteering[J]. The Leading Edge, 23(6): 581–586. DOI:10.1190/1.1766233 |
| [] | Sun X Y, Nie Z P, Zhao Y W, et al. 2008. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method[J]. Chinese Journal of Geophysics, 51(5): 1600–1607. DOI:10.3321/j.issn:0001-5733.2008.05.036 |
| [] | Wang H N, Tao H G, Yao J J, et al. 2008. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method[J]. Chinese Journal of Geophysics, 51(5): 1591–1599. DOI:10.3321/j.issn:0001-5733.2008.05.035 |
| [] | Wang T, Fang S. 2001. 3-D electromagnetic anisotropy modeling using finite difference[J]. Geophysics, 66(5): 1386–1398. DOI:10.1190/1.1486779 |
| [] | Wei B J, Tian K, Zhang X, et al. 2010. Physics of directional electromagnetic propagation measurements while drilling and its application formation boundaries[J]. Chinese Journal of Geophysics, 53(10): 2507–2515. DOI:10.3969/j.issn.0001-5733.2010.10.024 |
| [] | Yang S W, Wang H N, Chen G B, et al. 2009. The 3-D finite difference time domain(FDTD)algorithm of response of multi-component electromagnetic well logging tool in a deviated and layered anisotropic formation[J]. Chinese Journal of Geophysics, 52(3): 833–841. |
| [] | Zhang K, Wei B J, Chang X L. 2014. Preliminary geo-steering method of directional electromagnetic wave resistivity logging-while-drilling tools[J]. Progress in Geophysics, 29(1): 462–469. DOI:10.6038/pg20140167 |
| [] | Zhang L, Chen H, Wang X M. 2012. Numerical modeling of responses to a tilted-coil antenna in a transversely isotropic formation[J]. Chinese Journal of Geophysics, 55(10): 3493–3505. DOI:10.6038/j.issn.0001-5733.2012.10.033 |
| [] | 刘乃震, 王忠, 刘策. 2015. 随钻电磁波传播方位电阻率仪地质导向关键技术[J]. 地球物理学报, 58(5): 1767–1775. DOI:10.6038/cjg20150526 |
| [] | 孙向阳, 聂在平, 赵延文, 等. 2008. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应[J]. 地球物理学报, 51(5): 1600–1607. DOI:10.3321/j.issn:0001-5733.2008.05.036 |
| [] | 汪宏年, 陶宏根, 姚敬金, 等. 2008. 用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应[J]. 地球物理学报, 51(5): 1591–1599. DOI:10.3321/j.issn:0001-5733.2008.05.035 |
| [] | 魏宝君, 田坤, 张旭, 刘坤. 2010. 定向电磁波传播随钻测量基本理论及其在地层界面预测中的应用[J]. 地球物理学报, 53(10): 2507–2515. DOI:10.3969/j.issn.0001-5733.2010.10.024 |
| [] | 杨守文, 汪宏年, 陈桂波, 等. 2009. 倾斜各向异性地层中多分量电磁波测井响应三维时域有限差分(FDTD)算法[J]. 地球物理学报, 52(3): 833–841. |
| [] | 张克, 魏宝君, 常欣莉. 2014. 定向随钻电磁波电阻率测井仪器地质导向方法初探[J]. 地球物理学进展, 29(1): 462–469. DOI:10.6038/pg20140167 |
| [] | 张雷, 陈浩, 王秀明. 2012. 横向各向同性地层中倾斜线圈系响应特征的数值模拟[J]. 地球物理学报, 55(10): 3493–3505. DOI:10.6038/j.issn.0001-5733.2012.10.033 |
 2017, Vol. 32
2017, Vol. 32

