地球表面所见到的一系列地球物理场异常、地质构造格局、地球化学组分变异,无一不受到地球内部物质与能量交换的制约,而这些现象和深层动力学过程密不可分(滕吉文,2003).越来越多的研究表明,在研究大陆动力学乃至全球动力学中,对岩石圈、软流圈和地幔结构以及它们之间相互作用和耦合关系的认识是非常必要的(赵国泽等,2001;魏文博等,2003).因此全球范围的地幔性质一直以来都是各国专家学者们研究的一个重要课题.目前,人们对地幔的认知主要来自于岩石学、地球化学、实验室中对地球矿物物理和化学性质的研究以及通过地震、电磁感应、重力和天文学等技术获得的观测数据直接对地幔结构进行的研究,其中地震层析成像技术已经较为成熟(Kawakatsu and Watada, 2007;French and Romanowicz, 2015).与地震学关注岩石的弹性性质不同,电磁感应研究主要关注岩石的电导率变化.地下岩石的电导率对地球内部温度、流体、熔融和挥发物的存在以及它们的体积、含量等比较敏感(Karato,1990;Bai and Kohlstedt, 1992;赵国泽等,2001),是揭示地球内部状态的重要物理参数.因此深部电磁感应研究对于探索地幔的结构构造、物质组成、物质的物理化学性质、热力学状态并由此正确认识地球的构造、演化、地球动力学等具有十分重要的意义.
深部电磁感应是通过长周期的天然电磁场来研究大范围以及全球性的地幔构造,旨在得到地幔的电导率分布(从几百千米到核幔边界),发现其中的异常带并分析其起因,为地球内部构造分析提供信息,如果结合地震层析成像和岩石物理实验数据等,可以更好的研究地幔性质.深部电磁感应的基本原理为:受太阳活动的影响,地球外部电离层和磁层中产生的电流体系经常发生变化,会在地球内部激发出感应电流,而不均匀分布的地球内部介质,会在该电流的作用下产生感应磁场,深部电磁感应正是通过研究地表变化的地磁场和地电场来得到地球内部的电导率结构(Banks,1969).由于电磁感应的趋肤效应,不同周期的电磁场包含不同深度的电性信息,对于地幔深度的研究,需要非常长周期的观测数据(几小时到几年).但是长周期的电场强度很弱,容易受到地表及浅层电导率的影响,而且观测方式困难,导致可靠的长期地电场数据量远远少于地磁场的观测数据量,因此在研究地幔的电导率分布时,通常单独使用磁场数据(Tarits,1994).
国外从20世纪60年代就开始根据地表电磁场的变化研究地幔电导率.半个多世纪以来,他们对北太平洋、欧洲、澳大利亚、印度洋等地区以及全球范围的电磁场数据进行处理和解释,得到了不同地区和全球的地幔电导率剖面图和3-D分布图(Banks,1969;Schultz and Larsen, 1990;Olsen,1992;Utada,2003;Kelbert et al., 2009b;Shimizu et al., 2010b;Kuvshinov,2012;Kuvshinov and Semenov, 2012;Semenov and Kuvshinov, 2012).国内学者从20世纪80年代末开始,根据国内不同地区的地磁和地电数据,对我国深部电导率结构进行了研究,取得了丰硕的成果,对认识我国地幔性质、地质构造演化等具有重要意义(张贵宾,1998;汤吉和赵国泽,2005;徐光晶等,2015).进入21世纪之后,随着越来越多低地球轨道卫星的发射,其搭载的磁场测量装置提供了大量精度高、覆盖广、数据质量统一的观测数据,进一步促进了全球深部电磁感应研究的发展(Velímsky et al., 2006;Olsen et al., 2014;Püthe and Kuvshinov, 2014).
本文以深部电磁感应研究中的地磁测深(geomagnetic depth sounding/GDS)为重点,从其基本理论、正演模拟、数据处理及反演等方面总结了几十年来国内外深部电磁感应的研究进展.本文第一章为地磁测深法的基本理论,第二章主要介绍不同的3-D正演模拟方法,在第三章中对不同反演方法的结果进行总结和对比,第四章则重点介绍低地球轨道卫星(low earth orbit satellite)的观测数据处理及其反演结果,最后一章为总结和展望.
1 地磁测深的基本理论在地球深部电磁感应的研究过程中,我们通常将地球外部磁层和电离层中激发电流产生的场称为外源场,将其在地球内部导电介质中引起的感应场称为内源场.很明显内源场既与外源场有关,也与地球内部介质导电性及其分布有关,地磁测深正是通过观测地表不同周期的地磁场变化来研究地球内部介质电性结构的一种方法.
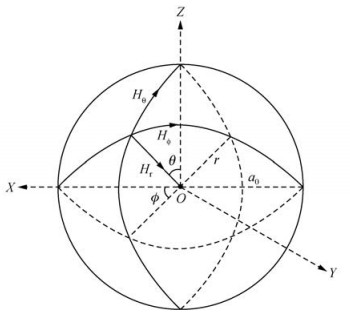
假设地球是一个半径a0=6371 km、导电率为σ的导电球体,取原点位于地心的球坐标系.Z轴为地理轴,XY平面为赤道面,X轴通过格林尼治子午线,ϕ为经度,θ为余纬度(图 1).Banks(1969)将地磁场按照球坐标系分解为三个方向的分量Hr,Hθ,Hϕ(垂直指向地心,水平北方向,水平东方向).在地球外部时,由于σ=0,并且地磁场随时间的变化非常缓慢,可以忽略位移电流的影响.所以地磁场可以表示为标量磁势Ω的梯度,公式为

|
(1) |
|
图 1 球坐标系下的磁场三分量 Figure 1 The three components of magnetic field in spherical coordinates |
考虑到∇·H=0,可以得到Ω满足拉普拉斯方程(k=0时的亥姆霍兹方程),公式为

|
(2) |
在球坐标系下,取时谐因子eiwt,公式为

|
(3) |
其中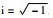

|
(4) |
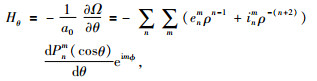
|
(5) |
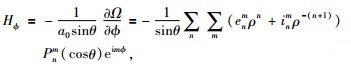
|
(6) |
式中ρ=r/a0,由此我们很容易得到地表处(ρ=1) 的磁场分量.
Banks(1969)用相同频率内源场系数和外源场系数的比值作为描述地磁测深的响应函数,即
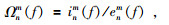
|
(17) |
并提出当地磁场的变化周期为2天~1年时,可以认为其是由磁层中的环形电流感应所引起(该假设一直沿用至今,变化的电流源主要是由太阳风暴时Dst变化的弛豫相位引起,此时n=1、m=0),通过对分布全球的地磁台站数据分析可以提供地下200~2000 km的地幔信息(Roberts,1986).Banks通过实测数据和不同模型响应进行比对的方法来研究地球内部电导率的分布结构,得到了只随深度变化的地球电导率分布.C-响应作为地磁测深研究中用到的传统转换函数,通常是由磁场的垂直分量和水平分量得到.Schmucker(1964)提出了计算C-响应的地磁梯度法:C(ω)=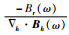
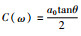

Schultz和Larsen(1987)将地磁测深的磁变化响应

|
(8) |
与大地电磁的阻抗响应

|
(9) |
进行比较得到比例因子

|
(10) |
进而提出将地磁响应函数转化为等效标量MT阻抗来进行反演的方法.Olsen(1992)提出Z:Y法,利用单一台站的垂直分量和所有地磁台站按照球谐展开得到的全球水平分量计算C-响应,这是对Schmucker(1964)提出方法的一种完善,但其缺点是需要大量分布全球且同时观测的磁场数据.Fujii和Schultz(2002)提出D-响应: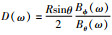
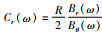
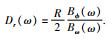
相较于理想的1-D地球深部结构,已经有很多地球物理的探测证据,尤其是一些地震层析成像结果表明深部物性存在明显的横向变化(Jordan,1975;Su and Dziewonski, 1992;Romanowicz,2003),很多C-响应的计算也证明了这一点(Schultz and Larsen, 1987;Lizarralde et al., 1995;Neal et al., 2000),这说明地幔是一个多维的结构,简单的一维结构并不足以对其描述.这些不均匀性可分成两种基本类型:(1) 地表异常:由地球表层(如陆地、海洋等)电导率不均匀引起,主要对短周期(小于几天)的地磁场变化有明显的影响;(2) 深部异常:与地壳、地幔的电导率不均匀性有关,直接影响长周期的地磁场变化.
用C-响应进行研究时通常假设引起磁场变化的源近似为一个大范围的对称磁层环电流,可以由单一的球谐函数(P10)来表示.但是越来越多的证据表明实际的源,尤其是短周期(小于几天)时激发源为电离层的电流体系,P10并不足以准确地表示源的结构(Kuvshinov et al., 1999;Kuvshinov,2008),因此在进行地磁测深研究时通常选择较大周期的磁场数据,避免电离层及其他复杂源的影响.对于激发源的复杂性,本文不进行过多的介绍,但这仍是进行全球电磁感应分析时的一大挑战.
2 三维数值模拟无论是对地面台站数据还是卫星测量数据进行反演,要得到真实可靠的地球深部电性结构模型,都是以对不均匀球状地球模型的电磁感应进行精确、高效的求解为基础的.众所周知,在3-D球体模型下,麦克斯韦方程的解析解很难求得,虽然能得到针对特定3-D模型,比如不均匀的无限薄层(Kuvshinov el al.,1999),离心嵌套球体(Everett and Schultz, 1995;Martinec,1999)的半解析解,但通常是通过数值模拟的方法来进行求解.过去的十多年内,国内外学者提出了多种3-D正演数值模拟的求解方法,包括有限差分法、积分方程法、有限元法、球谐有限元法等.下文将分别对这些方法进行简单介绍.
2.1 有限差分法(FD)交错网格有限差分法(staggered-grid FD)是结构化网格数值模拟中最容易实现的一种.球坐标系中的交错网格有限差分法最早由Uyeshima和Schultz(2000)用于全球电磁感应问题的研究(图 2),他们通过求解矢量亥姆霍兹方程来解得磁场H.取时谐因子为

|
(11) |

|
图 2 球坐标系中交错网格有限差分法的网格剖分 图中黑色和灰色实线所组成的曲边六面体分别为磁场和电场网格单元.以磁场网格单元为例,其节点处的三个棱边分别为纬度方向、经度方向和径向(θ、ϕ、r)的磁场分量,该单元内的电导率值是相同的.而与该磁场单元交错的电场单元,其节点位于磁场单元的中心,棱边被磁场的曲面边界均分.在图中的电场坐标表示中,‘-’表示位于磁场单元的外部,‘+’表示位于磁场单元的内部.摘自Uyeshima和Schultz(2000). Figure 2 The mesh division geometry for the staggered-grid finite difference formulation in spherical coordinates This primary prism (H-prism drawn with solid curves on the left-hand side and at the bottom on the right-hand side)is bounded by latitudinal, longitudinal and radial edges along which H field components are defined. Conductivity values are defined to be uniform in the respective H-prisms. Staggered prisms (E-prisms drawn with shaded curves on the left-hand side and at the top on the right-hand side) are also defined whose nodes are located at the center of the respective H-prisms and whose edges cut halfway through H-surfaces. In coordinate indices for the E field components, '-' means outside the H-prism of uniform conductivity and '+' means inside that prism. After Uyeshima and Schultz (2000). |
式中的H为磁场,ρ为电阻率,ω为角频率,μ0为真空磁导率.其计算范围包括高阻空气层、导电的地壳和地幔.上下边界分别为空气层的顶部和核幔边界.求解采用双共轭梯度稳定解法,并在迭代中进行散度矫正.Uyeshima和Schultz通过与半解析解的对比验证了SGFD方法的正确性,并被以后的学者不断优化.Kelbert等(2008, 2009b)提出当右端项不为零时,可以求解地球内部的磁场,并由此实现了全球电磁感应反演.在3-D条件下,假设ρ为地球内部1-D分布的背景电阻率,电阻率的扰动变化为δρ,那么通过下式可以得到电阻率变化产生的场δH,公式为

|
(12) |
由于1-D模型的解析解容易求得,将其解作为背景场H,然后计算右端项,就可以通过上式求得δH,进而得到3-D电阻率ρ+δρ对应的总场H+δH.(12) 式的下边界并不受限于磁场在核幔边界处衰减为0的条件,因此在一定程度上能提供更加精确的解,也能用于解决下地幔之上的深部磁场感应问题.(12) 式也适用于更加复杂的外部源正演求解,而且并不需要对正演求解程序进行太大的改动.需要指出的是外部场源结构只对背景场影响较大,对扰动的异常场影响很小.
在有限差分网格中,对麦克斯韦方程的离散近似可以写成一种对称的形式而且很容易达到收敛.但是在全球电磁感应的球坐标系中,南北两极是结构化网格的两个奇点,在计算中需要特殊处理.如果收敛性判别标准过于宽松,会在两极处造成较大误差,而且会一直累加,影响中纬度地区的计算精度.
2.2 有限元法(FE)和球谐有限元法(SHFE)Martinec(1999)首次将球谐-有限元法(spherical harmonic-FE)用于频率域中球体的电磁感应研究,之后Velímsky和Martinec(2005)将其应用于时间域.SHFE法主要有两个优点:(1) 在1-D条件下,由于复杂性较低,将电磁场的解展开为球谐函数很大程度上对解进行了简化.这样就将问题分解为仅与球谐函数的阶数有关的径向常微分方程.这种快速的1-D求解可以为频率域的3-D电磁感应迭代求解提供理想的预处理,有效提高计算效率(Martinec,1999),或者实现时间域中积分的半隐式方法求解(Velímsky and Martinec, 2005);(2) 在3-D模型中,地球周围为绝缘的大气层,将SHFE的解进行耦合可以很容易的得到标量磁势的解析解.
SHFE法以球谐函数为基础,整体具有相同的分辨率,难以提高局部的分辨率.因此当横向电导率差异较大时,SHFE法不能精确地表示这种不连续性,并会产生边缘振荡效应.
时间域中的SHFE法主要用于低地球轨道卫星观测数据的处理.由于卫星的高速运动,对其记录的数据进行时间和空间变化分离就显得尤为重要,在时间域中通过积分的方法求解电磁感应问题较之频率域中会容易很多.将矢量球谐函数和1-D有限元法结合对空间进行离散化,这一点与频率域类似,对时间的积分采用半隐式的方法,横向电阻率变化产生的影响则用由前一个时间步长得到的已知解进行计算.这种方法有效避免了大型矩阵的存储,而且可以采用基于快速傅里叶变换和高斯-勒让德公式的高效矩阵矢量乘法进行计算.需要注意的是,球谐函数的截断阶数以及层数、时间步长的选择对解的精度都有很重要的影响.
Ribaudo等(2012)将商业有限元软件FlexPDE用于进行全球地磁感应问题的研究,可以建立任意地核、地幔的电导率模型,获得任意空间分布和时间特性的一次磁场.他们将海洋和地壳看做一个横向不均匀的薄层,并将其作为地球-空气界面的边界条件.频率域中的感应方程写成关于一次场和二次场的复矢量磁场势A和标量电场势V的形式,公式为

|
(13) |
模型域包括地壳、地幔、地核以及10倍于地球半径的高阻真空层.Ribaudo等(2012)成功的实现了2-D和3-D地球理论模型的地磁感应模拟,并通过与解析解的对比验证了其准确性.其中时间域的解考虑了地球的自转和卫星的运动,因此可以用来研究复杂源对地面和卫星观测数据的影响.
2.3 积分方程法(IE)Fainberg和Zinger(1980)首先将积分方程法用于不均匀球状地球模型(表层为不均匀的薄层,下方电导率呈球对称分布)的电磁感应研究,他们由地球表层的边界条件推导得到了一组包含两个积分-微分形式的特殊方程,并证明这组方程用简单的迭代方法就能得到收敛解.他们将这种方法称为迭代耗散方法(iterative dissipative method-IDM),认为IDM中的最优收敛率与电导率分布的横向对比成反比.Singer(1995)提出压缩积分方程法(contracting IE-CIE),在迭代中使用新得到的积分方程,此时最优收敛率与电导率分布横向对比的平方根成反比.他将这种算法称为改进的迭代耗散方法(modified IDM-MIDM).以上两种方法的共同点为:(1) 都忽略了位移电流,只考虑电导率的不均匀性;(2) 他们的最优收敛率都是通过特定的1-D参考模型实现,而且不必和背景场一致.Pankratov等(1995)指出用于求解CIE的简单迭代法可以认为是该方程收敛Neumann级数的部分和,并将其命名为改进的Neumann级数(modified Neumann series-MNS).Kuvshinov等(1999)将MIDM-MNS的思想用于计算地表为不均匀薄层时的地磁响应,虽然只是理论分析,但这种方法明显的提高了计算速度.
Koyama等(2002)和Kuvshinov等(2002a)分别独立地提出了可以对真正3-D地球电磁场进行模拟的CIE方法,并从2012年开始,陆续对积分方程求解中最重要的格林函数张量的推导和计算进行了详细介绍.Avdeev等(2002)对CIE方法进行了更深入的研究,他们认为不论电导率如何变化,都可以很好地约束CIE积分算子,并建议在计算CIE时用Krylov子空间迭代代替Neumann级数求和.之后Kuvshinov等(2005)、Singer(2008)都实现了在Krylov子空间的迭代求解,此时收敛率与横向变化的自然对数成反比,进一步减少了所需的迭代次数,这也是现在CIE求解的主流方法.
2.4 正演方法总结全球深部电磁感应研究逐渐成为近些年来的热点,不同的研究小组及学者提出了各自独立的正演模拟算法,并在此基础上展开了反演工作.Kelbert等(2014)对不同的3-D正演模拟方法进行了对比研究,用七种正演程序(三种CIE、两种SHFE、一种规则交错网格FD、一种自适应网格FE,详见表 1)模拟了不同地球模型的响应,结果表明,尽管这些程序的数值实现方法不同,但他们的结果十分吻合,都可以用于全球电磁感应模拟,也都可以用于全球地磁反演研究(图 3).
|
|
表 1 目前主流的全球电磁感应正演模拟程序(Kelbert et al., 2014) Table 1 List of numerical codes for global EM induction modelling (Kelbert et al., 2014) |

|
图 3 (a)、(b)、(c)不同球谐扰动下的理论模型;(d)模型(b)的磁场θ分量的实部和虚部(周期为4天) (d)的垂直第一列为各方法计算得到的磁场分量的实部,对应左上角的色标,水平第一行为各方法计算得到的磁场分量的虚部,对应右下角的色标;对角线部分是空的,下部三角区域为不同程序计算的实部差异,上部三角区域为虚部差异. Figure 3 (a), (b), (c) Synthetic model: spherical harmonic perturbations; (d) Real and imaginary parts of the θ-component of the magnetic field for model (b) at a single period (4 days) (d) The first (vertical) column corresponds to the real part of the magnetic fields. The colourbar at the top corresponds to the real part. The first (horizontal) row is the imaginary part. The colourbar at the bottom corresponds to the imaginary part. The diagonal is empty. The lower triangle are the differences between the real parts from different codes. The upper triangle are the differences between the imaginary parts from different codes. |
Kelbert等发现,目前的FE解在不均匀模型的计算过程中会产生比较大的误差,而且是对计算机要求最高的方法.自适应FE提供了前所未有的模型自由度,用户可以自己调整建模设置,但通常不能进行最优化的选择,因此花费的时间可能会更多.
FD在求解变化剧烈和复杂结构模型时需要很精细的网格,这会增加对内存的需求并降低计算速度.而且在两极地区,网格粗糙时FD收敛性较差,需要对网格进行加密.
三种基于CIE的程序在模拟试验中具有最高的效率.CIE的关键是格林张量函数的计算和CIE的数值求解.而且,如果背景场模型不变,只需要计算一次格林张量函数就可以用于变化的源和电导率的正演模拟.与FE和FD求解稀疏矩阵不同,CIE法虽然是求解稠密矩阵,但是矩阵更紧凑,而且不需要进行预处理,可以不考虑频率、离散化和电导率变化.因此在地球的局部范围内计算时,FD所占用的计算资源更多;而当进行全球范围的计算时,CIE计算的模型域迅速增大,所需要的计算时间和SGFD相差不多,而且在计算格林函数张量时对内存和存储空间要求都很高.
SHFE方法在处理变化剧烈模型时的精确度最高,和CIE一样,不用考虑极点的离散化问题.SHFE最适于源场和感应场都由球谐函数进行全球范围的离散化的情形,因此该方法是处理低地球轨道卫星时间域数据时的首选.
3 地面数据反演深部电磁感应研究可以提供地下几百千米直到核幔边界(2900 km)的电导率分布信息,在最近几十年内一直是国内外学者研究的热点,这主要是由于以下几个原因:
1) 全球范围内越来越多地磁台站的建立和低地球轨道卫星的发射以及观测技术的不断发展提供了更多、更精确、更大范围的磁场观测数据.由海底电缆两端的电压变化等得到的地电数据与地磁数据结合也可以用于深部电磁感应的研究(Lizarralde et al., 1995;Utada et al., 2003).
2) 目前对全球范围地幔性质的研究,地震层析成像技术已经较为成熟,并在地幔动力学的研究中发挥着重要的作用.但是地震层析成像只能确定地幔的弹性性质,并不能有效区分异常的起因是矿物成分变化还是温度变化等.而电导率对地球内部的温度、孔隙流体、熔融物质和挥发成分的存在以及它们的体积、含量等异常敏感(赵国泽等,2001),因此可以由电导率变化分析地幔异常的起因.
3) 地幔过渡带的主要矿物瓦兹利石和尖晶橄榄石都具有很高的水溶性,最近的很多高温高压试验表明这些矿物的电导率对水含量非常敏感(Hae et al., 2006).极少量的水就能在很大程度上影响地幔矿物质的物理性质,包括降低固相线、减小有效黏度以及地震波速等(Kelbert et al., 2009b).因此地幔的总含水量及其分布对地球动力学和地球化学演化有重要的启示作用.由深部电磁感应研究得到的地幔过渡带电导率可以很好地对过渡带中的含水量进行约束.
在深部电磁感应研究中,将观测到的磁场数据转换为球坐标系中的磁场三分量,经过数据校正之后得到不同周期的C-响应,对其反演就可以得到不同地区以及全球范围的电导率1-D剖面或3-D分布图.
3.1 1-D、拟1-D反演 3.1.1 1-D反演近年来,世界各国学者根据不同的观测数据(主要是地面测站的磁场和海底电缆的电场)对地幔电导率分布做了大量的研究工作,得到了很多地区的1-D电导率剖面,其中大部分都是采用Constable等(1987)提出的正则化Occam方法.
Olsen(1998)用欧洲24个地磁台站的观测数据按照Z:Y法,得到了周期为3小时~30天的C-响应.他得到的C-响应被很多学者用于地幔结构的研究.Neal等(2000)对北美和北太平洋不同地区的长周期大地电磁和地磁测深数据进行分析,得到的1-D电导率剖面显示不同地区之间存在明显的电导率横向变化,反映了地幔的不均匀性.Ichiki等(2001)通过对中国东北地区长周期MT和地磁数据的反演分别得到了上地幔和过渡带的1-D电导率模型,其中电场数据是由长距离电话线连接的电极测得.Tarits等(2004)由长周期MT响应得到了法国阿尔卑斯山下方200~1000 km的电导率剖面.Semenov和Jozwiak(2006)重新整理了欧洲35个台站周期为6小时~11年的数据,得到了地表到地下800 km深度的电导分布图,并认为电导反演比电导率反演更加稳定.Khan等(2006)用Olsen得到的响应数据直接反演地球的化学组成和热状态,结果与之前的电导率和地震波速模型吻合.Medin等(2007)也反演了Olsen的数据,他们采用一种非传统的反演方法——“all-at-once”(不需要正则化),得到了所有电导率剖面都必须满足的地球平均电导率范围.他们将反演结果与实验室结果结合,对上地幔和过渡带的温度和水含量进行了约束,并认为完全由瓦兹利石组成或者只含有很少量尖晶橄榄石的过渡带,其水含量 < 0.27 wt%(weight percent);在410 km的地震波不连续处,只有 < 0.4 wt%的水含量才能满足熔融的条件.Khan等(2011)对全球范围内六个具有不同地质背景的台站(Fürstenfeldbrück (FUR),欧洲;Hermanus (HER),南非;Langzhou (LZH),中国;Alice Springs (ASP),澳大利亚;Tucson (TUC),北美和Honolulu (HON),北太平洋)数据进行了电导率结构研究,得到了各地区500~1200 km深度的1-D电导率剖面.他们认为在整个研究深度内,电导率存在剧烈的径向和横向变化,比如600 km处的平均电导率在0.1~0.4 S/m之间,而在800 km处明显增大到1.3~2.0 S/m,并且这种径向的递增趋势一直延续到1200 km.
3.1.2 拟1-D反演Kuvshinov等(2002b)通过数值模拟与观测数据对比的方法发现,当周期小于20天时,海洋对沿海地区电磁感应的影响不能忽略,并提出采用下式对海洋造成的影响进行校正,公式为

|
(14) |
式中Cobs和Cobs,corr分别为观测和校正后的C-响应;CID和CID+shell为1-D地球模型但表层分别为均匀层和不均匀的海洋和陆地时的响应,其中正演模拟基于Singer(1995)提出的迭代离散方法.Utada等(2003)将北太平洋地区地面台站的磁场数据和海底电缆测得的电场数据结合,选取周期为1~8天的MT响应和5~27天的地磁测深响应,采用迭代反演的方法得到了该地区的1-D电导率剖面图.之后Kuvshinov等(2005)和Shimizu等(2010a)用相同的方法对北太平洋下方的1-D电导率分布进行了研究.
Shimizu等(2010a)认为,地球的电导率结构σ(r)可以写为

|
(15) |
式中的r为位置矢量,r是距地心的距离,是1-D参考模型的电导率分布,δσmantle(r)和δσocean(r)分别是地幔和地表海陆分布导致的电导率异常.在δσmanrle(r)和δσocean(r)存在的条件下精确求解σID(r)是问题的关键,这个过程主要分为四步:(1) 由不同的观测数据得到电磁响应;(2) 对响应进行地表异常不均匀性造成影响的校正;(3) 将校正后的响应进行平均,得到拟1-D响应;(4) 对拟1-D响应进行反演,得到1-D电导率参考模型.
假设激发源的结构可以由P10表示,反演中所用的地磁测深C-响应和等效MT的阻抗响应可以表示为

|
(16) |
式中Bz(ω;r)和Bx(ω;r)分别为地磁坐标系中在位置r和角频率ω时的垂向和水平北方向的地磁场分量,Rcable(ω;k)是电缆的等效MT响应,μ0为真空磁导率,V21是海底电缆两侧的电压,Zcable(ω;k)是转换后的等效MT响应,Bxref(ω;r0)是参考台站r0处的水平北方向磁场;Lk为第k条电缆的长度,qk是电缆相对于地磁北的方位角,θ0和θc分别为参考台站和电缆中点的地磁余纬度.Shimizu等(2010a)选用北太平洋地区周期为1.7~113天的响应数据(等效MT响应和GDS响应的最小周期分别为1.7天和5.33天),并针对不同的模型约束进行了反演:(1) 模型没有任何的电导率突变,(2) 模型在400和650 km的深度出现电导率突变,(3) 模型在400、500和650 km的深度出现电导率突变(为了模拟在这几个深度存在的矿物相变).图 4为第二种模型的反演结果与其他研究中反演结果的对比.作者还提出,由模型(2) 反演出的电导率比实验室中测得的干瓦兹利石和尖晶橄榄石的电导率要高,并且认为如果这种差别完全是由过渡带中的水造成的,那么水含量约为0.5 wt%.但是如果在500 km处也存在一个电导率的突变,过渡带上层100 km的电导率值会降低,此时该处瓦兹利石的水含量约为0.1 wt%.

|
图 4 (a)Shimizu等(2010a)给出的北太平洋地区及附近的表层电导分布;(b)Shimizu等(2010a)由两次跳跃模型得到的1D反演结果(蓝线)与Utada等(2003)(黑线)和Kuvshinov等(2005)(红线)结果的对比 Figure 4 (a) Supposed conductance distribution of the surface layer in North Pacific Ocean area by Shimizu et al.(2010a); (b) Comparison of the two-jump model obtained by Shimizu et al.(2010a) (blue line) and that obtained by previous studies by Utada et al. (2003) (black line) and by Kuvshinov et al. (2005) (red line) |
国内从20世纪80年代左右开始了对我国部分地区的深部电导率分布研究,并取得了丰硕的成果.陈伯舫(1986、1989) 采用地磁梯度法对我国东南部地区的地幔高导层埋藏深度进行了研究.他用武汉、佘山、广州、泉州、仑坪等5个地磁台站的静日变资料,采用二次曲面法计算磁场梯度,计算周期为24、12、8 h和6 h的地磁响应,以简单的Monte-Carlo法反演推断可能的电性结构模型,得到地表至1000 km左右深度的四层电导率模型,并认为在315 km附近出现电导率约0.3 S/m、厚度约28 km的高导薄层,在740 km以下为1 S/m的高导层.陈伯舫(1987)用类似的方法对华北地区地幔高导层埋深进行了研究,得到的四层模型中高导薄层埋深约334 km,电导率约0.325 S/m,厚度约24.5 km,与东南地区的深部结构有较大差异.杜兴信等(杜兴信等,1994;杜兴信和鲁秀玲,1995)利用陕西地磁台网近10年记录的春秋季磁静日资料和单台Z/H磁测深法研究了陕西地区深部电导率状况,并发现陕西地区的高导层位于250 km附近,小于全球的地幔高导层埋深350 km,也小于东南和华北地区的结果.范国华等(1997)利用梯度法,对我国地震局系统一、二类地磁台中25个台站1992年的数据进行处理,寻找磁变化在平面上的最佳多项式拟合形式,获得了各台站周期为24 h、12 h、8 h和6 h的C值,通过非线性不适定问题反演方法探讨各台站地下的导电率结构,给出了各地区地表至地下1000 km的电导率分布1-D模型图,并指出在我国的西南部、北部及其他地区之间C值和地下深部导电率结构存在差异.
张贵宾(1998)详细介绍了地磁测深方法,采用Z:Y法对资料整理、频谱分析、场源特征、正演计算、反演解释等一系列问题进行了系统研究,并将其用于处理东北地区地磁台磁照图资料得到了地下电导率分布,对认识该地区深部电性结构,进而推断深部地质构造具有实际意义.
赵国泽等(2001)使用长周期大地电磁测深网等技术,在长春和三岔河等地对太平洋板块弧后的上地幔结构进行了探测.他们用陆地电话线或电缆接收长基线的电场,由设置在长春地磁台站的三分量磁通门磁力仪记录磁场变化,得到的观测资料最长周期可达105~106 s,反演深度可达1000 km.他们的研究表明我国东北地下的地幔内存在不连续界面和电导率的横向不均匀性,对于认识板块消减带的深部结构和动力学问题、研究东北地区的构造演化以及了解地震和火山活动的深部背景等有重要的意义.汤吉等(2007)收集了我国东部地区地磁台网30个台站的观测数据,采用远参考和Robust技术,对其中20个较为理想的地磁台站的资料进行处理,得到了高置信度周期为105~107 s的地磁响应函数,并用等效MT标量阻抗的方法进行研究.他们利用Occam反演方法得到了1500 km以上的地幔电性结构.由不同台站下方地幔过渡带电导率对比发现,从南到北过渡带电导率逐渐增强,东北地区最高.他们认为这也许和东北地区过渡带中的西太平洋俯冲板块在东北地区变为停滞板块且含水有关.徐光晶等(2015)采用与汤吉等(2007)相似的方法处理了华北地区14个地磁台站的资料,反演得到1-D最光滑的Occam模型,并与前人在其他地区的研究结果进行了对比,发现华北地区地幔过渡带的电导率在大兴安岭-太行山重力梯度带东西两侧表现不同,过渡带东部的电导率是西部地区的2~5倍,这可能和太平洋板块的俯冲携带了岩石圈的水到地球深部、深部物质脱水后上涌使水进入上地幔有关,从电磁学的角度印证了太平洋板块俯冲是华北地区首要的动力学背景.
3.2 3-D反演Schultz和Pritchard(1999)第一次对全球范围的电磁感应数据进行了3-D反演,他们提出的模型是假设在1-D参考模型的基础上只有较小的扰动变化.但是后来人们发现,除了欧洲下方地幔的电导率横向变化较小,全球其他地方的电导率变化并不满足这一假设.之后,日本东京大学地震研究所、美国俄勒冈州立大学和瑞士地球物理所等分别提出了更为严格的频率域3-D全球电磁反演方法,用来处理地面台站的磁场数据.尽管他们的方法在细节处理上有很多不同,但仍然具有很多共同点:(1) 反演问题转化为求解正则化最小二乘反演的最优解,可以写为
Koyama(2001)率先在对半全球范围地面台站得到的C-响应进行解释时采用了严格的3-D反演方法.其反演采用拟牛顿法,正演响应计算用体积分方程法.这种反演方法后来用于长周期电磁数据解释,研究北太平洋地区的深部电性结构(Fukao et al., 2004;Koyama et al., 2006;Utada et al., 2009).在上述研究中,为强调过渡带及其附近的电性分布,通常假设地幔的横向不均匀是位于350~850 km的深度.
Fukao等(2004)对北太平洋地区分别进行了电磁感应反演和地震反演,并比较了过渡带四个不同的深度处电导率异常和P-波异常图.他们选用地磁测深和海底电缆的观测数据进行3-D反演,结果表明在菲律宾海南部和夏威夷下方存在高导异常、在太平洋西北部存在低导异常.通过两种方法的对比,作者发现了高(低)波速和低(高)电导率间的相关性,但这种相关性并不是绝对的.他们认为如果两者之间存在这种相关性,那么就可以考虑是热力学原因引起的波速和电导率异常,并给出了温度变化和两者之间的关系.通过理论计算和实际反演结果的对比,他们判断出菲律宾海下方的波速和电导率异常并不能仅靠热力学变化解释.Koyama等(2006)对这一问题进行了深入研究,指出菲律宾海地幔过渡带的高导异常是由于瓦兹利石中含水(或者氢)造成的,并基于Hae等(2006)的氢扩散实验数据进一步推断在西太平洋地区地幔过渡带的水含量约为0.3 wt%,而过渡带中的水可能是板块俯冲至地幔时带入的.
Utada等(2009)对欧洲和北太平洋地区的3-D电导率模型进行了对比.他们选取欧洲12个地磁台站周期为5~50天的C-响应数据进行反演.北太平洋地区的电导率模型选择Fukao等(2004)得到的3-D反演结果.结合地震波速异常,他们认为引起欧洲下方地幔过渡带的滞留俯冲板块呈现低导、高波速特征的最可能原因是高温异常.通过两个地区模型的对比,作者认为如果两个地区具有类似的矿物和化学成分,电导率的差异是由水含量引起,那么欧洲地区的地幔过渡带水含量要比北太平洋西部地区的水含量低约1 wt%.
Shimizu等(2010b)使用北太平洋地区13个地磁台站新测得的C-响应和8条长基线海底电缆数据对地幔过渡带电导率再次进行了反演.较之以前的反演研究,他们有更长时间序列的数据,并以Shimizu等(2010a)得到的1-D模型为初始模型,得到了新的3-D反演结果.对比Fukao等(2004)的结果,Shimizu等(2010b)同样认为在夏威夷和菲律宾海下方的地幔过渡带存在高导异常,日本北部及其附近地区也存在高阻异常,但菲律宾海550 km之下的高阻异常并不明显.作者认为这些高导异常可以一直延伸到过渡带底部,更深处则表现为略微高阻.Shimizu等(2010b)进一步对上述三个地区温度和电导率异常的关系进行了研究,他们认为仅仅是温度变化并不足以解释菲律宾海下方的高导异常,如果考虑水含量的作用,那么过渡带的水含量要大于1 wt%.
上文所列举都是半全球(北太平洋)甚至是区域范围(欧洲)的反演.Kelbert等(2008)提出了基于非线性共轭梯度的全球3-D电磁反演方法.正演响应和灵敏度矩阵的计算采用Uyeshima和Schultz(2000)提出的球坐标系交错网格有限差分和伴随矩阵的解法.他们用球谐函数对每一个不均匀层进行参数化,并对由棋盘模型得到的一系列模拟数据进行反演以得到垂向和水平分辨率.Kelbert等(2008)认为周期为5~107天的地磁测深响应数据可以有效的解决地下深度为670~1600 km时大尺度(垂向300~500 km,水平几千千米)的电导率异常.
Kelbert等(2009b)用之前提出的反演方法(Kelbert等,2008)得到了第一个全球地幔电导率分布模型(图 5a).他们将地表到1600 km深度之间的地球分为8个不均匀层,其层厚分别为100、150、160、110、150、230、300、400 km,每一层的横向电导率变化都按照Kuvshinov和Olsen(2006)的1-D参考模型进行球谐展开,并且在410、520、670 km深度处允许电导率发生跳跃,1600 km以下假设为电导率均匀且固定的层.Kelbert等(2009b)一共选取了中纬度地区59个台站的C-响应数据,并对海洋的影响进行校正.他们的反演结果表明过渡带电导率在环太平洋地区有一个较为明显的升高,日本、中国东部、伊豆-小笠原和汤加板块尤为明显;太平洋中部盆地的电导率较其周围地区的电导率低一个数量级以上;过渡带及其下方的高导与低温、高波速、俯冲板块有较好的对应关系.基于该全球电导率模型,他们通过与实验室测得的地幔主要矿物水含量变化时的电导率(Yoshino et al., 2008)对比得到了过渡带的水含量变化,并且认为要达到过渡带(比如日本下方)的最高电导率(0.5~2.0 S/m),水含量应为0.5~1.0 wt%;在一些高阻地区(比如欧洲中部和南部)则对应较为干燥的地幔环境,其水含量不足0.1%(图 5d).Kelbert等提出的全球3-D电导率分布模型对地幔过渡带的水含量进行了很好地约束,有助于我们更好的研究地幔对流等动力学问题以及地球化学演化.Kelbert等(2009a)采用相同的反演方法对中纬度( < 60°)地区118个测站、周期范围更大(2.1~102.4天)的地磁测深C-响应进行了反演.他们采用10年(1995-2004) 地磁数据每小时的平均值来计算电磁响应,剔除偏差较大的5个台站数据,并对海洋和极光电流的影响进行了校正.反演结果如图 5b.

|
图 5 不同3-D反演方法的结果对比和Kelbert等(2009b)给出的全球和区域电导率剖面 (a)Kelbert等(2009b)反演结果;(b)Kelbert等(2009a)反演结果;(c)Semenov和Kuvshinov(2010)反演结果; (d)虚线对应不同测站下方的剖面,蓝线为全球平均电导率剖面,红线为反演所用的1-D初始模型,四个黄线分别为不同水含量(从下往上依次为:0、0.1、0.5、1.0 wt%)时的矿物电导率. Figure 5 Comparison of the results obtained by different 3-D inversion methods and global and regional electrical conductivity profiles obtained by Kelbert et al. (2009a) (a)result obtained by Kelbert et al. (2009b); (b) result obtained by Kelbert et al. (2009a); (c) result obtained by Semenov and Kuvshinov (2010); (d) the dashed lines correspond to the profiles beneath a set of locations, representative of geographical regions. The blue solid line is the global average. The red solid line represents the prior one-dimensional model used for the inversion. The four yellow lines indicate the existing mineral physics constraints as a function of water content (from the bottom up, in wt%: 0, 0.1, 0.5, 1.0). |
另一种频率域的全球3-D反演由Kuvshinov(2008)提出,他们采用有限内存拟牛顿法(limited memory QN—LMQN)进行最优化,正演模拟基于积分方程解.他们充分考虑了磁层电流、电离层电流(静日变化、极光电流和赤道电射流)、海洋潮汐、全球海洋环流和海啸等的3-D影响.为加快反演速度,在正演中最为耗时的格林函数张量只需要在反演前进行一次计算并保存.文中的模型试验表明,这样单独计算格林函数能提高反演速度一个数量级以上.除此之外,因为不同频率的正演计算是完全互不干扰的,在积分方程的求解中采用并行技术,还能进一步提高计算速度.Semenov和Kuvshinov(2010)对中纬度地区133个地磁台站的51年(1957-2007) 周期为3.9~109.2天的数据每小时平均值求得C-响应,并用Kuvshinov(2008)的方法进行了反演(图 5c).
3.2.2 时间域的全球3-D反演和Mandéa(2010)提出了时间域的全球3-D反演,并对120个地磁台站32年(1958-1990) 的月平均磁场数据进行反演,得到了下地幔的电导率分布.时间域反演首先对地磁台站数据进行全球分析,得到外部场源随时间变化的稳定值;然后用内源场和外源场的响应函数(Q或者C)进行1-D反演,通过得到的1-D剖面分析所选数据对反演深度的分辨率,并将该1-D剖面作为3-D反演的初始模型;最后对分辨率最高的目标层在时间-空间域中进行3-D反演.
在地球表面及外部空间内,磁场的计算与频率域中类似,可以由标量磁势V的梯度求得,只不过表示为时间域的形式,公式为

|
(17) |
其中,Vlm为标量势V的球谐系数,lmax为球谐展开的最高阶数,a为地球半径,i和e分别表示内源场和外源场.作者采用正则化最小二乘的方法得到了阶数为1~3的外源和内源系数,但在1-D反演中只选取了与P10相应的C-响应,然后进行非线性反演就可以得到1-D电导率剖面.在3-D反演中,作者建立的罚函数为

|
(18) |
式中No为观测台站的总个数,t为所有的时间步长,Bo和Bc分别为观测和计算出的矢量磁场,Σ是标准差(设为1nT),Wo为权重系数,下标i和j表示不同的单元或者层,λ为阻尼系数.时间-空间域的3-D正演响应是通过先计算各个观测点上不同球谐系数的多个频率域响应,然后将计算结果叠加到外场上得到总场,最后采用Fourier和Legendre变换得到.反演采用最速下降法对目标函数进行最小化.反演中只假设900~1400 km为横向不均匀层,其他各层均认为与1-D反演得到的初始模型具有相同且固定的电阻率值.他们的反演结果表明,在澳大利亚、西非、日本附近以及美国中部和北部为低导异常,东非、亚洲东南部以及欧亚大陆为高导异常.该时间域反演结果与频率域3-D反演结果(Kelbert et al., 2009;Semenov and Kuvshinov, 2010)相比,最明显的特征就是电导率变化幅度更大(时间域:2~3个对数单位,频率域:小于1个对数单位);与层析成像的结果对比后,作者认为下地幔的电导率变化可能是由温度和铁含量的变化引起.
4 卫星数据反演近地球轨道卫星提供的大量高精度数据为进行真正全球范围的地幔电导率分布研究提供了可能.第一台为电磁感应研究提供高精度数据的是1979/80运行的Magsat,尽管该卫星的使用期仅有7个月,但它证明了由太空进行地幔电导率研究的可行性.目前主要的低地球轨道卫星组包括Ørsted、CHAMP、SAC-C以及Swarm.相比于覆盖范围小、分布不规律,尤其是在南半球和海洋较少存在的地磁台站,由卫星搭载的测量装置提供了覆盖范围广、质量统一的高精度数据,为地磁测深研究提供了大量的可靠数据.用卫星测量数据进行感应研究主要有以下几个优点:
1) 卫星观测是对整个地球进行的采样,可以得到真正的全球响应,而不是像地面台站那样以北半球陆地响应为主.
2) 覆盖全球的卫星数据可以用来研究不同区域的电导率差异,比如海洋和陆地.
3) 近地球轨道卫星的飞行高度约为400 km,因此其观测数据为一个地区的平均值,减少了局部不均匀性的影响,得到的区域响应受局部异常影响较小.
4) 卫星观测是由同一个观测装置进行不断的测量,这有效地减少了由观测仪器不同造成的误差.
但在处理卫星观测数据时,存在如下问题:
1) 卫星时刻以约8 km/s的速度飞行,很难确定观测的磁场变化是时间还是空间变化引起的,数据的时空分离是必须面对的问题.
2) 必须得到高精度的磁场变化数据,这并不是单指分辨率,对磁场方向和绝对值都有高精度的要求.
3) 由于地球的自转,大约一天之后卫星会重新观测一个特定的区域,容易出现混淆的重复采样.
4) 卫星记录的是轨道处的磁场变化,而我们需要的是地表的磁场变化,因此二者之间必须进行转换.在假设卫星和地面之间的空间是与一次场和二次场均无关的情况下,这种转换较易实现;但卫星的运行轨迹为椭圆,其焦点之一为地球的质心,不断变化的卫星高度使这种转换变得复杂,如果忽略高度变化则会引入静态误差.
5) 在对地面观测数据处理时通常将卫星轨道下方的所有电流都看做是地球感应产生的二次场,这一点在处理卫星观测数据时并不成立,比如轨道下方电离层的Sq电流,既有一次场的感生电流也有二次场的感应电流.但如果和地面数据结合,可以有效的解决这一问题.
6) 地表和卫星轨道之间必须假设为不导电的.即使忽略电离层电流,电导率不为零的电离层依旧会产生二次场,影响响应函数.但Olsen(1999)的研究表明了这种影响很小,可以忽略.
卫星观测到的磁场的


Kuvshinov和Olsen(2006)对Ørsted,CHAMP,SAC-C卫星组5年(2001-2005) 的磁场数据进行分析得到了全球1-D电导率模型.他们根据最新的地磁场模型移除地核和地壳磁场得到剩余场.然后通过磁势的球谐展开得到外源和内源系数间的传输函数,计算周期为14小时到120天的全球平均C-响应,当周期小于7天时进行海洋影响的3-D校正.由校正后的数据反演得到1-D电导率模型,该模型与地面测站数据反演结果非常接近.
Püthe和Kuvshinov(2013)、(2014) 提出了在频率域中对卫星处的磁场模拟数据进行3-D电导率反演的方法.这种方法基于对Q矩阵(其元素为磁层电流源产生的磁势进行球谐展开的外源和内源系数)的多变量分析,采用LMNQ的最优化方法以及伴随法计算灵敏度矩阵,基于Pankratov等(1995)提出的CIE方法进行正演模拟,并按照频率进行并行以提高速度.他们通过对3-D电导率模型的模拟数据反演认为周期为2~30天时,可以很好地解决地下100~1200 km的3-D结构,且分辨率最好的深度为500~900 km.
Püthe等(2015)进一步联合了Ørsted,CHAMP,SAC-C以及Swarm卫星组测量的磁场数据和全球地磁观测台站网的数据反演得到了径向对称的地幔电导率结构.他们将周期为1.5~150天的C-响应进行关于地表海陆分布的3-D校正,用概率性和确定性的方法分别进行反演.通过对Hessian矩阵的分析,他们认为所选周期范围对800~1200 km深度的电性结构最为敏感.
4.2 时间域反演Velímsky等(2006)第一次对CHAMP卫星的观测数据直接进行时间域反演得到了1-D电导率模型.他们假设卫星轨道近似为一个极轨道,其飞行速度远大于环电流随时间的变化速度.对卫星数据记录的2001-2003年间11个风暴事件一一追踪,得到时间序列的球谐系数,对这些数据进行反演解释.正演响应的计算基于球谐有限元法(Velímsky和Martinec,2005),反演通过对模型参数空间的全搜索来求得最优的电导率模型.
Martinec和Velímsky(2009)采用共轭梯度法对CHAMP卫星观测的1年(2001) 数据进行时间域反演,得到地球的1-D和2-D电导率结构模型(图 6).正演同样采用球谐有限元法,反演中提出伴随方法(类似于频率域中所用),使得伴随灵敏度矩阵可以不用考虑电导率参数的个数,只需要一次额外的正演计算就能得到.他们认为,上地幔电导率沿纬度有相对于平均电导率约20%的变化,下地幔电导率则有约4%的变化.

|
图 6 Martinec和Velímsky(2009)对2001年CHAMP数据进行反演的结果模型 (a)1-D反演的结果模型;(b)、(c)分别为下地幔和上地幔电导率随地磁余纬度变化图(2-D反演).图中红线为拟合最好的模型,蓝线为共轭梯度法的初始模型,黑色点线为第一次迭代后的模型. Figure 6 The conductivity model best fitting the 2001-CHAMP data, after Martinec and Velímsky (2009). (a)1-D conductivity model; (b), (c) Latitudinally dependent conductivity model of the upper part of the lower mantle and the upper mantle (2-D). Red lines are the model best fitting the data, blue lines are the starting model for the CG minimization and dotted line is the model after the first iteration. |
几十年来,国内外学者利用地磁台站和卫星观测的磁场数据以及可测量的电场数据对地球深部电导率分布进行了深入的研究,尤其是最新的一些结果表明地幔电导率存在明显的横向不均匀性,需要精细的3-D结构才能表示.将得到的地幔电导率模型与地震层析成像、实验室高温高压试验的测量数据等结合,可以对地幔的物质组成、含量、状态进行很好的约束,对地球的演化和全球动力学研究有重要意义.但地球深部电导率的研究同样面临很多的难点,需要我们去不断克服:
1) 在进行深部电磁感应研究时通常都将源近似为磁层环电流,其变化可以由单一的球谐函数来表示,但实际的源要复杂很多,如果能处理好短周期时复杂的源问题,可以很好地解决上地幔电性结构,因此如何处理复杂的源问题以及利用其所包含的信息,是进行深部电磁感应研究所面临的一个重要课题.
2) 人们很早就发现极地电流和赤道喷射电流等对地表磁场有明显的影响,如何精确、高效的去除它们的影响,同样是一个难点.
3) 目前,不同的小组往往采用不同的反演技术以及正演模拟方法,不论是数据选择、参数设置、网格大小、精度范围还是阻尼系数的选择等都对反演结果有明显的影响,也就使得反演结果之间往往具有不同的特征,因此得到一个准确度较高的模型是非常必要的.
4) 地面测站数据与卫星测量数据的联合分析往往可以取得比单个反演更好地结果,将二者联合可以有效地提高对横向不均性的探测能力,但现有的尝试仍然较少.
5) 在国内开展大范围甚至全国性的深部电磁感应研究以及在3-D条件下进行更加细致的研究对于探索我国地幔的物理、化学状态、物质组成和结构转变及相关地球动力学过程具有重要意义.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Avdeev D B, Kuvshinov A V, Pankratov O V, et al. 2002. Three-dimensional induction logging problems, Part Ⅰ:An integral equation solution and model comparisons[J]. Geophysics, 67(2): 413–426. DOI:10.1190/1.1468601 |
| [] | Bai Q, Kohlstedt D L. 1992. Substantial hydrogen solubility in olivine and implications for water storage in the mantle[J]. Nature, 357(6380): 672–674. DOI:10.1038/357672a0 |
| [] | Banks R J. 1969. Geomagnetic variations and the electrical conductivity of the upper mantle[J]. Geophysical Journal International, 17(5): 457–487. DOI:10.1111/j.1365-246X.1969.tb00252.x |
| [] | Chen B F. 1986. Buried depth of the high conductivity layer beneath the region of south-east China[J]. Acta Seismologica Sinica, 8(2): 172–178. |
| [] | Chen B F. 1987. Investigations of the deep electrical conductivity beneath northern China using the spatial gradient method[J]. Acta Seismologica Sinica, 9(2): 193–200. |
| [] | Chen B F. 1989. Further study of the electrical conductivity beneath the region of south-east China[J]. Journal of Seismological Research, 12(4): 348–352. |
| [] | Constable S C, Parker R L, Constable G. 1987. Occam's inversion:A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 52(3): 289–300. DOI:10.1190/1.1442303 |
| [] | Du X X, Lu X L. 1995. Research on the geomagnetic deep sounding in Shaanxi region by single station Z/H method[J]. Seismological and Geomagnetic Observation and Research, 16(1): 27–34. |
| [] | Du X X, Lu X L, Ji J Z. 1994. Investigation on deep electroconductibility of Shaanxi region by means of Z/H method with single station[J]. Inland Earthquake, 8(4): 333–338. |
| [] | Everett M E, Schultz A. 1995. Geomagnetic induction in eccentrically nested spheres[J]. Physics of the Earth and Planetary Interiors, 92(3-4): 189–198. DOI:10.1016/0031-9201(95)03036-6 |
| [] | Fainberg E B, Zinger B S. 1980. Electromagnetic induction in a non-uniform spherical model of the Earth[J]. Annales De Geophysique, 36: 127–134. |
| [] | Fan G H, Yao T Q, Gu Z W, et al. 1997. Research on mantle conductivity of China with gradient method[J]. Acta Seismologica Sinica, 19(2): 164–173. |
| [] | French S W, Romanowicz B. 2015. Broad plumes rooted at the base of the Earth's mantle beneath major hotspots[J]. Nature, 525(7567): 95–99. DOI:10.1038/nature14876 |
| [] | Fujii I, Schultz A. 2002. The 3D electromagnetic response of the Earth to ring current and auroral oval excitation[J]. Geophysical Journal International, 151(3): 689–709. DOI:10.1046/j.1365-246X.2002.01775.x |
| [] | Fukao Y, Koyama T, Obayashi M, et al. 2004. Trans-Pacific temperature field in the mantle transition region derived from seismic and electromagnetic tomography[J]. Earth and Planetary Science Letters, 217(3-4): 425–434. DOI:10.1016/S0012-821X(03)00610-1 |
| [] | Hae R, Ohtani E, Kubo T, et al. 2006. Hydrogen diffusivity in wadsleyite and water distribution in the mantle transition zone[J]. Earth and Planetary Science Letters, 243(1-2): 141–148. DOI:10.1016/j.epsl.2005.12.035 |
| [] | Ichiki M, Uyeshima M, Utada H, et al. 2001. Upper mantle conductivity structure of the back-arc region beneath northeastern China[J]. Geophysical Research Letters, 28(19): 3773–3776. DOI:10.1029/2001GL012983 |
| [] | Jordan T H. 1975. Lateral heterogeneity and mantle dynamics[J]. Nature, 257(5529): 745–750. DOI:10.1038/257745a0 |
| [] | Karato S. 1990. The role of hydrogen in the electrical conductivity of the upper mantle[J]. Nature, 347(6290): 272–273. DOI:10.1038/347272a0 |
| [] | Kawakatsu H, Watada S. 2007. Seismic evidence for deep-water transportation in the mantle[J]. Science, 316(5830): 1468–1471. DOI:10.1126/science.1140855 |
| [] | Kelbert A, Egbert G D, Schultz A. 2008. Non-linear conjugate gradient inversion for global EM induction:Resolution studies[J]. Geophysical Journal International, 173(2): 365–381. DOI:10.1111/j.1365-246X.2008.03717.x |
| [] | Kelbert A, Egbert G D, Schultz A. 2009a. Spatial variability of mantle transition zone water content:Evidence from global electromagnetic induction data[C].//Abstracts of AGU Fall Meeting, San-Francisco. |
| [] | Kelbert A, Kuvshinov A, Velímsky J, et al. 2014. Global 3-D electromagnetic forward modelling:A benchmark study[J]. Geophysical Journal International, 197(2): 785–814. DOI:10.1093/gji/ggu028 |
| [] | Kelbert A, Schultz A, Egbert G. 2009b. Global electromagnetic induction constraints on transition-zone water content variations[J]. Nature, 460(7258): 1003–1006. DOI:10.1038/nature08257 |
| [] | Khan A, Connolly J A D, Olsen N. 2006. Constraining the composition and thermal state of the mantle beneath Europe from inversion of long-period electromagnetic sounding data[J]. Journal of Geophysical Research:Solid Earth, 111(B10). DOI:10.1029/2006JB004270 |
| [] | Khan A, Kuvshinov A, Semenov A. 2011. On the heterogeneous electrical conductivity structure of the Earth's mantle with implications for transition zone water content[J]. Journal of Geophysical Research:Solid Earth, 116(B1). DOI:10.1029/2010JB007458 |
| [] | Koyama T. 2001. A study on the electrical conductivity of the mantle by voltage measurements of submarine cables[Ph. D. thesis]. Tokyo:University of Tokyo. |
| [] | Koyama T, Shimizu H, Utada H. 2002. Possible effects of lateral heterogeneity in the D″ layer on electromagnetic variations of core origin[J]. Physics of the Earth and Planetary Interiors, 129(1-2): 99–116. DOI:10.1016/S0031-9201(01)00263-1 |
| [] | Koyama T, Shimizu H, Utada H, et al. 2006. Water content in the mantle transition zone beneath the North Pacific derived from the electrical conductivity anomaly[M].//Jacobsen S D, Van Der Lee S eds. Earth's Deep Water Cycle. New York:John Wiley & Sons, Inc., 171-179. |
| [] | Kuvshinov A V. 2012. Deep electromagnetic studies from land, sea, and space:Progress status in the past 10 years[J]. Surveys in Geophysics, 33(1): 169–209. DOI:10.1007/s10712-011-9118-2 |
| [] | Kuvshinov A V. 2008. 3-D global induction in the oceans and solid earth:Recent progress in modeling magnetic and electric fields from sources of magnetospheric, ionospheric and oceanic origin[J]. Surveys in Geophysics, 29(2): 139–186. DOI:10.1007/s10712-008-9045-z |
| [] | Kuvshinov A, Avdeev D B, Pankratov O V, et al. 2002. Modelling electromagnetic fields in a 3D spherical earth using a fast integral equation approach[J]. Methods in Geochemistry and Geophysics, 35: 43–54. DOI:10.1016/S0076-6895(02)80085-3 |
| [] | Kuvshinov A, Avdeev D B, Pankratov O V. 1999. Global induction by Sq and Dst sources in the presence of oceans:Bimodal solutions for non-uniform spherical surface shells above radially symmetric earth models in comparison to observations[J]. Geophysical Journal International, 137(3): 630–650. DOI:10.1046/j.1365-246X.1999.00827.x |
| [] | Kuvshinov A, Olsen N. 2006. A global model of mantle conductivity derived from 5 years of CHAMP, Ørsted, and SAC-C magnetic data[J]. Geophysical Research Letters, 33(18): L18301. DOI:10.1029/2006GL027083 |
| [] | Kuvshinov A, Olsen N, Avdeev D B, et al. 2002. Electromagnetic induction in the oceans and the anomalous behaviour of coastal C-responses for periods up to 20 days[J]. Geophysical Research Letters, 29(2): 36-1–36-4. DOI:10.1029/2001GL014409 |
| [] | Kuvshinov A, Utada H, Avdeev D, et al. 2005. 3-D modelling and analysis of DstC-responses in the north Pacific Ocean region, revisited[J]. Geophysical Journal International, 160(2): 505–526. DOI:10.1111/j.1365-246X.2005.02477.x |
| [] | Kuvshinov A, Semenov A. 2012. Global 3-D imaging of mantle electrical conductivity based on inversion of observatory C-responses-Ⅰ.An approach and its verification[J]. Geophysical Journal International, 189(3): 1335–1352. DOI:10.1111/j.1365-246X.2011.05349.x |
| [] | Lizarralde D, Chave A, Hirth G, et al. 1995. Northeastern Pacific mantle conductivity profile from long-period magnetotelluric sounding using Hawaii-to-California submarine cable data[J]. Journal of Geophysical Research:Solid Earth, 100(B9): 17837–17854. DOI:10.1029/95JB01244 |
| [] | Martinec Z. 1999. Spectral-finite element approach to three-dimensional electromagnetic induction in a spherical earth[J]. Geophysical Journal International, 136(1): 229–250. DOI:10.1046/j.1365-246X.1999.00713.x |
| [] | Martinec Z, Velímsky J. 2009. The adjoint sensitivity method of global electromagnetic induction for CHAMP magnetic data[J]. Geophysical Journal International, 179(3): 1372–1396. DOI:10.1111/j.1365-246X.2009.04356.x |
| [] | Medin A E, Parker R L, Constable S. 2007. Making sound inferences from geomagnetic sounding[J]. Physics of the Earth and Planetary Interiors, 160(1): 51–59. DOI:10.1016/j.pepi.2006.09.001 |
| [] | Neal S L, Mackie R L, Larsen J C, et al. 2000. Variations in the electrical conductivity of the upper mantle beneath North America and the Pacific Ocean[J]. Journal of Geophysical Research:Solid Earth, 105(B4): 8229–8242. DOI:10.1029/1999JB900447 |
| [] | Olsen N. 1992. Day-to-day C-response estimation for Sq from 1 cpd to 6 cpd using the Z:Y-method[J]. Journal of Geomagnetism and Geoelectricity, 44(6): 433–447. DOI:10.5636/jgg.44.433 |
| [] | Olsen N. 1998. The electrical conductivity of the mantle beneath Europe derived from C-responses from 3 to 720 hr[J]. Geophysical Journal International, 133(2): 298–308. DOI:10.1046/j.1365-246X.1998.00503.x |
| [] | Olsen N. 1999. Induction studies with satellite data[J]. Surveys in Geophysics, 20(3-4): 309–340. DOI:10.1023/A:1006611303582 |
| [] | Olsen N, Lühr H, Finlay C C, et al. 2014. The CHAOS-4 geomagnetic field model[J]. Geophysical Journal International, 197(2): 815–827. DOI:10.1093/gji/ggu033 |
| [] | Pankratov O, Avdeyev D, Kuvshinov A. 1995. Electromagnetic field scattering in a heterogeneous earth:A solution to the forward problem[J]. Physics of the Solid Earth, 31(3): 201–209. |
| [] | Püthe C, Kuvshinov A. 2013. Determination of the 3-D distribution of electrical conductivity in Earth's mantle from Swarm satellite data:Frequency domain approach based on inversion of induced coefficients[J]. Earth, Planets and Space, 65(11): 1247–1256. DOI:10.5047/eps.2013.09.004 |
| [] | Püthe C, Kuvshinov A. 2014. Mapping 3-D mantle electrical conductivity from space:A new 3-D inversion scheme based on analysis of matrix Q-responses[J]. Geophysical Journal International, 197(2): 768–784. DOI:10.1093/gji/ggu027 |
| [] | Püthe C, Kuvshinov A, Khan A, et al. 2015. A new model of Earth's radial conductivity structure derived from over 10 yr of satellite and observatory magnetic data[J]. Geophysical Journal International, 203(3): 1864–1872. DOI:10.1093/gji/ggv407 |
| [] | Ribaudo J T, Constable C G, Parker R L. 2012. Scripted finite element tools for global electromagnetic induction studies[J]. Geophysical Journal International, 188(2): 435–446. DOI:10.1111/j.1365-246X.2011.05255.x |
| [] | Roberts R G. 1986. Global electromagnetic induction[J]. Surveys in Geophysics, 8(3): 339–374. DOI:10.1007/BF01904064 |
| [] | Romanowicz B. 2003. Global mantle tomography:Progress status in the past 10 years[J]. Annual Review of Earth and Planetary Sciences, 31(1): 303–328. DOI:10.1146/annurev.earth.31.091602.113555 |
| [] | Schmucker U. 1964. Anomalies of geomagnetic variations in the southwestern United States[J]. Journal of Geomagnetism and Geoelectricity, 15(4): 193–221. DOI:10.5636/jgg.15.193 |
| [] | Schultz A, Larsen J C. 1987. On the electrical conductivity of the mid-mantle-Ⅰ.Calculation of equivalent scalar magnetotelluric response functions[J]. Geophysical Journal International, 88(3): 733–761. DOI:10.1111/j.1365-246X.1987.tb01654.x |
| [] | Schultz A, Larsen J C. 1990. On the electrical conductivity of the mid-mantle:Ⅱ.Delineation of heterogeneity by application of extremal inverse solutions[J]. Geophysical Journal International, 101(3): 565–580. DOI:10.1111/j.1365-246X.1990.tb05571.x |
| [] | Schultz A, Pritchard G. 1999. Three-dimensional inversion for large-scale structure in a spherical domain[M].//Oristaglio M, Spies B eds. Three-Dimensional Electromagnetics. Tulsa, OK:SEG, 451-473, doi:10.1190/1.9781560802154.ch29. |
| [] | Semenov A, Kuvshinov A. 2010. Spatial distribution of the mantle conductivity as seen from the 3-D inversion of ground-based C-responses[C].//EGU General Assembly Conference. Expanded Abstracts, 607-620. |
| [] | Semenov A, Kuvshinov A. 2012. Global 3-D imaging of mantle conductivity based on inversion of observatory C-responses-Ⅱ.Data analysis and results[J]. Geophysical Journal International, 191(3): 965–992. DOI:10.1111/j.1365-246X.2012.05665.x |
| [] | Semenov V Y, Jozwiak W. 2006. Lateral variations of the mid-mantle conductance beneath Europe[J]. Tectonophysics, 416(1-4): 279–288. DOI:10.1016/j.tecto.2005.11.017 |
| [] | Shimizu H, Koyama T, Baba K, et al. 2009. Three-dimensional geomagnetic response functions for global and semi-global scale induction problems[J]. Geophysical Journal International, 178(1): 123–144. DOI:10.1111/j.1365-246X.2009.04150.x |
| [] | Shimizu H, Koyama T, Baba K, et al. 2010a. Revised 1-D mantle electrical conductivity structure beneath the north Pacific[J]. Geophysical Journal International, 180(3): 1030–1048. DOI:10.1111/j.1365-246X.2009.04466.x |
| [] | Shimizu H, Utada H, Baba K, et al. 2010b. Three-dimensional imaging of electrical conductivity in the mantle transition zone beneath the North Pacific Ocean by a semi-global induction study[J]. Physics of the Earth and Planetary Interiors, 183(1-2): 252–269. DOI:10.1016/j.pepi.2010.01.010 |
| [] | Singer B S. 1995. Method for solution of Maxwell's equations in non-uniform media[J]. Geophysical Journal International, 120(3): 590–598. DOI:10.1111/j.1365-246X.1995.tb01841.x |
| [] | Singer B S. 2008. Electromagnetic integral equation approach based on contraction operator and solution optimization in Krylov subspace[J]. Geophysical Journal International, 175(3): 857–884. DOI:10.1111/j.1365-246X.2008.03930.x |
| [] | Su W J, Dziewonski A M. 1992. On the scale of mantle heterogeneity[J]. Physics of the Earth and Planetary Interiors, 74(1-2): 29–54. DOI:10.1016/0031-9201(92)90066-5 |
| [] | Sun J, Egbert G D. 2012. A thin-sheet model for global electromagnetic induction[J]. Geophysical Journal International, 189(1): 343–356. DOI:10.1111/j.1365-246X.2012.05383.x |
| [] | Tang J, Zhao G Z. 2005. Extension of long-period electromagnetic sounding by GDS equivalent MT response function[C].//Chinese Geophysical Society Twenty-first Annual Meeting Proceedings (in Chinese). Changchun:Chinese Geophysical Society, 634-636. |
| [] | Tang J, Zhao G Z, Chen X B, et al. 2007. Study on the mantle electrical structure in eastern China by geomagnetic station[C].//Chinese Geophysical Society Twenty-third Annual Meeting Proceedings (in Chinese). Chinese Geophysical Society, 710. |
| [] | Tarits P. 1994. Electromagnetic studies of global geodynamic processes[J]. Surveys in Geophysics, 15(2): 209–238. DOI:10.1007/BF00689860 |
| [] | Tarits P, Hautot S, Perrier F. 2004. Water in the mantle:Results from electrical conductivity beneath the French Alps[J]. Geophysical Research Letters, 31(6). DOI:10.1029/2003GL019277 |
| [] | Tarits P, Mandéa M. 2010. The heterogeneous electrical conductivity structure of the lower mantle[J]. Physics of the Earth and Planetary Interiors, 183(1-2): 115–125. DOI:10.1016/j.pepi.2010.08.002 |
| [] | Teng J W. 2003. Dynamic process of substance and energy exchanges in depths of the Earth and formation of mineral resources[J]. Geotectonica et Metallogenia, 27(1): 3–21. |
| [] | Utada H, Koyama T, Obayashi M, et al. 2009. A joint interpretation of electromagnetic and seismic tomography models suggests the mantle transition zone below Europe is dry[J]. Earth and Planetary Science Letters, 281(3-4): 249–257. DOI:10.1016/j.epsl.2009.02.027 |
| [] | Utada H, Koyama T, Shimizu H, et al. 2003. A semi-global reference model for electrical conductivity in the mid-mantle beneath the north Pacific region[J]. Geophysical Research Letters, 30(4). DOI:10.1029/2002GL016092 |
| [] | Uyeshima M, Schultz A. 2000. Geoelectromagnetic induction in a heterogeneous sphere:A new three-dimensional forward solver using a conservative staggered-grid finite difference method[J]. Geophysical Journal International, 140(3): 636–650. DOI:10.1046/j.1365-246X.2000.00051.x |
| [] | Velímsky J, Martinec Z. 2005. Time-domain, spherical harmonic-finite element approach to transient three-dimensional geomagnetic induction in a spherical heterogeneous Earth[J]. Geophysical Journal International, 161(1): 81–101. DOI:10.1111/j.1365-246X.2005.02546.x |
| [] | Velímsky J, Martinec Z, Everett M E. 2006. Electrical conductivity in the Earth's mantle inferred from CHAMP satellite measurements-Ⅰ.Data processing and 1-D inversion[J]. Geophysical Journal International, 166(2): 529–542. DOI:10.1111/j.1365-246X.2006.03013.x |
| [] | Wei W B, Jin S, Ye G F, et al. 2003. Methods to study electrical conductivity of continental lithosphere[J]. Earth Science Frontiers, 10(1): 15–23. |
| [] | Xu G J, Tang J, Huang Q H, et al. 2015. Study on the conductivity structure of the upper mantle and transition zone beneath North China[J]. Chinese Journal of Geophysics, 58(2): 566–575. DOI:10.6038/cjg20150219 |
| [] | Yoshino T, Manthilake G, Matsuzaki T, et al. 2008. Dry mantle transition zone inferred from the conductivity of wadsleyite and ringwoodite[J]. Nature, 451(7176): 326–329. DOI:10.1038/nature06427 |
| [] | Zhang G B. 1998. Geomagnetic Gradient Sounding and Inversion of Potential Field[M]. Beijing: Metallurgical Industry Press. |
| [] | Zhang L T, Wei W B, Jin S, et al. 2011. Studies on the temperature dependence of electrical conductivity of upper mantle rocks[J]. Progress in Geophysics, 26(2): 505–510. DOI:10.3969/j.issn.1004-2903.2011.02.015 |
| [] | Zhao G Z, Tang J, Liang J G, et al. 2001. Measuement of network-MT in two areas of NE China for study of upper mantle conductivity structure of the back-arc region[J]. Seismology and Geology, 23(2): 143–152. |
| [] | 陈伯舫. 1986. 中国东南部地幔高导层的埋藏深度[J]. 地震学报, 8(2): 172–178. |
| [] | 陈伯舫. 1987. 华北地区地幔高导层埋藏深度的研究[J]. 地震学报, 9(2): 193–200. |
| [] | 陈伯舫. 1989. 中国东南地区深部电导率分布的进一步研究[J]. 地震研究, 12(4): 348–352. |
| [] | 杜兴信, 鲁秀玲. 1995. 陕西地区单台Z/H地磁测深研究[J]. 地震地磁观测与研究, 16(1): 27–34. |
| [] | 杜兴信, 鲁秀玲, 姬建中. 1994. 用单台Z/H法研究陕西地区深部电导率[J]. 内陆地震, 8(4): 333–338. |
| [] | 范国华, 姚同起, 顾左文, 等. 1997. 利用磁梯度法研究我国地幔导电率[J]. 地震学报, 19(2): 164–173. |
| [] | 汤吉, 赵国泽. 2005. 利用GDS的等效MT响应函数扩展长周期电磁测深研究[C]. //中国地球物理学会第二十一届年会论文集. 长春: 中国地球物理学会, 634-636. |
| [] | 汤吉, 赵国泽, 陈小斌, 等. 2007. 地磁台资料研究中国东部地幔电性结构[C]. //中国地球物理学会第二十三届年会论文集. 中国地球物理学会, 710. |
| [] | 滕吉文. 2003. 地球深部物质和能量交换的动力过程与矿产资源的形成[J]. 大地构造与成矿学, 27(1): 3–21. |
| [] | 魏文博, 金胜, 叶高峰, 等. 2003. 大陆岩石圈导电性的研究方法[J]. 地学前缘, 10(1): 15–23. |
| [] | 徐光晶, 汤吉, 黄清华, 等. 2015. 华北地区上地幔及过渡带电性结构研究[J]. 地球物理学报, 58(2): 566–575. DOI:10.6038/cjg20150219 |
| [] | 张贵宾. 1998. 地磁梯度测深与位场反演[M]. 北京: 冶金工业出版社. |
| [] | 张乐天, 魏文博, 金胜, 等. 2011. 上地幔岩石的电性-温度依赖关系研究[J]. 地球物理学进展, 26(2): 505–510. DOI:10.3969/j.issn.1004-2903.2011.02.015 |
| [] | 赵国泽, 汤吉, 梁竞阁, 等. 2001. 用大地电磁网法在长春等地探测上地幔电导率结构[J]. 地震地质, 23(2): 143–152. |
 2017, Vol. 32
2017, Vol. 32

