2. 海底科学与探测技术教育部重点实验室, 青岛 266100
2. Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Qingdao 266100, China
远震初至拾取按照实施方式可以分为人工手动拾取和计算机拾取两类方法.人工手动拾取实施过程简单,容易广泛应用.然而,手动拾取的存在拾取效率低、人工工作量大、容易引入系统的人为误差等缺点(江国明等,2012;陈金焕等,2015).而且,对于低信噪比地震资料,手动拾取难以实施、精度较低(Zeiler and Velasco, 2009).计算机拾取法则可以较好避免上述问题,它基于对地震波初至的不同解释,利用了地震波的振幅、相位、波形相似性等信息,使得初至拾取可以半自动或者自动完成,极大节省了人工工作量.
按照参与拾取的地震道个数,计算机拾取法可以分为单道拾取和多道拾取两类方法(Akram and Eaton, 2016).单道拾取方法长期以来被用于快速识别和拾取远震波形起跳位置,以进行震源定位和地震速报.目前较为常用的是长短时平均比法(Short-Term Average and Long-Term Average ratio,简称STA/LTA法)及其改进方法(Stevenson,1976;Allen,1978;Baer and Kradolfer, 1987;Sleeman and van Eck,1999;马强等,2013).单道拾取方法在信噪比较高的情况下具有较高的拾取精度,但是,当地震资料的信噪比较低时,单道初至拾取方法较易受干扰而产生拾取不准确的问题(Baer and Kradolfer, 1987).
多道拾取方法多数利用了不同台站记录的地震信号的相似性.对于台站间距小、分布密集的台网,不同台站接收到的同一远震初至波形具有较高相似度(Langston,1979).前人研究也表明,当台站的间距小于10km时,不同台站记录的远震波形的相似性较好(Archambeau et al., 1965;Husebye and Jansson, 1966;Jansson and Husebye, 1968;Bungum and Husebye, 1971).由于具有一定间距台站处的背景噪声的相似程度较差,基于波形相似性的远震初至拾取方法在抗噪性和拾取精度等方面都具有较好的表现.
不同台站远震记录的相似程度可以通过互相关来衡量,信号的相似度越高,其互相关系数就越大.两个台站远震记录的互相关系数最大值的相对时移量显示了地震波先后到达两台站的时差(王彩霞等,2013).Peraldi和Clement(1972)基于各道与参考道波形相似的假设提出用相邻道的互相关来寻找初至间的延迟时间.VanDecar和Crosson(1990)运用多道互相关(Multi-Channel Cross-Correlation,简称MCCC方法)和最小二乘法检测初至震相的相对到时.Molyneux和Schmitt(1999)提出直接相关法,将初至起跳脉冲附近波形与挑选的参考波形之间的相关系数最大值作为初至时间的判定准则.Bear和Pavlis(1999)利用模拟退火方法计算宽频带地震记录的走时残差.Rawlinson和Kennett(2004)选用叠加道作为参考道,利用波形叠加技术提取参考信号以计算初至时间,提出了自适应叠加方法(Adaptive Stacking,简称AS方法).王继等(2006)利用单台Akaike信息准则(AIC)和多台多道互相关方法确定远震震相初至时间.潘树林等(2010)提出通过不断优化相关模型道来提高初至拾取精度的优化相关法等.Pavlis和Vernon(2010)采用加权叠加方式计算叠加道,计算台网远震体波的初至时间,提出了台网远震体波处理方法(Array Processing of teleseismic body waves,简称AP方法).江国明等(2012)对多道互相关方法加以改进,将相位一致性信息引入多道互相关中,提升了初至拾取的精度,提出了改进多道互相关方法(Modified Multi-Channel Cross-Correlation,简称MMCCC方法).Lou等(2013)对多道互相关方法进行改进,用迭代互相关和叠加的方法代替多道互相关方法中的初始震相的标定过程,提出了迭代互相关叠加方法(Iterative Cross-Correlation and Stack,简称ICCS方法).近几年,地震初至拾取方法不断发展和完善,在提高精度的基础上实现了自动拾取(刘劲松等,2013).何先龙等(2016)利用地震波能量变化率时程曲线拾取P波和S波的初至时间.谭玉阳等(2016)利用信噪在振幅、偏振、统计特征等方面的差异,借助SLPEA算法拾取微地震事件的初至.许银波等(2016)根据初至波能量比确定初至时间,并利用相邻初至波的波形相似性对拾取的初至进行评价,实现了初至波的自动拾取.
本文以五种方法为例(多道互相关方法、迭代互相关叠加方法、自适应叠加方法、台网远震体波处理方法、改进多道互相关方法),对比和分析了基于波形相似性的远震初至拾取方法.首先,介绍各方法的基本原理和实施流程,并分析其优缺点;然后,通过实际资料应用效果来比较各个方法,并对比和总结了参数取值、时窗选取等因素对各方法的影响;最后,总结对比分析结果,并针对不同的应用目的提出了远震初至拾取方案的建议.
1 方法概述 1.1 多道互相关方法VanDecar和Crosson(1990)提出了一种拾取远震相对到时的方法即多道互相关方法(Multi-Channel Cross-Correlation),简称MCCC方法.MCCC方法基本原理是先用互相关计算任意两地震道间直达波的相对时差,然后采用最小二乘法反演得到去平均的相对到时.互相关提取相对到时的具体过程如下:
设同一个地震被n个台站接收到,获得n道波形记录,对于其中任意的两道i和j,其互相关函数可以表示为
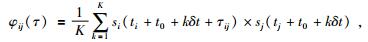
|
(1) |
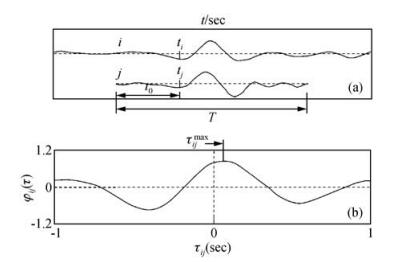
如图 1所示,K=T/δt表示时窗内的采样点数;si和sj分别是第i道和第j道的波形数据;ti和tj分别是第i道和第j道的远震地震波到时;τij为两道相对于到时估计的相对延迟时间;T是时窗长度,k是时窗内的第k个采样点,t0是地震波到时与时窗起点的时差,δt为时间采样间隔.
|
图 1 波形互相关示意图 (a)是用于互相关的地震数据; (b)是对应的互相关系数. (据VanDecar和Crosson,1990) Figure 1 Schematic diagram showing cross-correlation of waveforms (a) The portions of trace data used for cross-correlation; (b) The corresponding cross-correlation coefficients. (After VanDecar and Crosson, 1990) |
将第i道和第j道的远震波形作互相关后,两道的相对延迟时间Δtij为
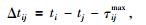
|
(2) |
其中,τijmax是互相关系数φij(τ)取最大值时对应的相对延迟时间,理论到时ti和tj可以根据台站与震源的位置信息借助地球一维速度模型AK135、IASP91(Kennett and Engdahl, 1991;Kennett et al., 1995)等计算出来.在实际拾取中,噪声会造成τijmax值的误差,导致各台站之间的到时不完全遵循求和关系,如Δt12+Δt23≠Δt13.因此需要建立反演格式来求取各台站的相对到时.在互相关获取各道的相对时差后,需要采取最小二乘法反演得到所有台站的相对到时.
MCCC方法的具体步骤如下:
首先,设ti和tj分别是第i道和第j道的远震到时,对于n道地震记录,两道之间的相对时差可由互相关求出,公式为
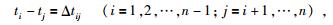
|
(3) |
上式构成了一个包含n(n-1)/2个方程的超定方程组.
其次,施加约束,公式为
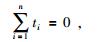
|
(4) |
增加这一约束是为了使方程组非奇异且有最小二乘解.式(4) 的约束条件使得反演得到的相对到时的平均值为0.
之后,把式(3) 和(4) 合并,写成矩阵相乘的形式即
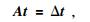
|
(5) |
式中,解向量t代表每一道波形的最优化相对到时,A是[n(n-1)/2+1]×n维的稀疏矩阵,Δt是n(n-1)/2+1维的相对延迟时间向量,它可由互相关函数计算得出.
最后,使用最小二乘反演获得相对延迟时间,即test=(ATA)-1ATΔt.其解析表达式为
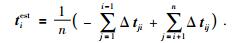
|
(6) |
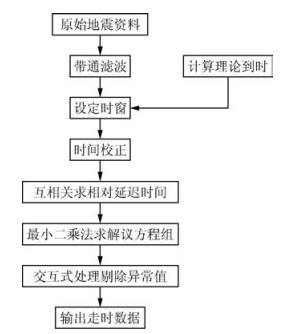
综上,MCCC方法的具体实施过程可以总结为图 2中的流程.
|
图 2 MCCC方法实施流程 Figure 2 Flow chart of MCCC method |
MCCC方法基于远震波形的相似性实现了远震初至的计算机自动拾取,降低了人工成本,提升了拾取效率.此外,该方法受不相干噪声的影响相对较小,具有一定的抗噪性(左国平,2006),被广泛应用于远震初至到时的拾取(Pavlis and Vernon, 2010).
尽管MCCC方法提升了拾取效率,但还是存在一定的问题.例如,需要人工设定时窗、剔除坏道;定位每两道间互相关系数的极大值时,存在周期跳跃:较大的相对延迟时间离群值也会降低最小二乘解的准确度(Rawlinson and Kennett, 2004).此外,该方法在计算走时数据时需要用最小二乘法求解超定方程组,求解过程还会产生计算误差,影响拾取的精度(江国明等,2012).
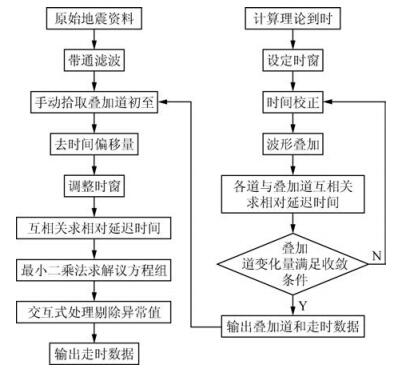
1.2 迭代互相关叠加方法MCCC方法中最小二乘反演要求初至不能有较大离群值,而且互相关需要预知较为准确的时窗位置,这要求人为设定时窗以获得准确初至.处理海量远震数据和多震相拾取时,标定过程工作量大,拾取效率低.针对上述问题,Lou等(2013)用迭代互相关与叠加相结合的方式代替MCCC方法中的目标震相的标定过程,提出了迭代互相关叠加(Iterative Cross-Correlation and Stack)方法,简称ICCS方法.应用ICCS方法将各道波形记录初步排齐,可以更好的应用MCCC方法拾取初至.
ICCS方法的具体步骤如下:
(1) 根据各道的理论到时tn0,(n=1, …, N),确定一个包含该到时的相对大的时窗W0.通过各道与叠加道迭代互相关的方式更新各道目标震相的初至时间tn,至满足收敛条件,经过迭代计算出各道的初至时间记作Tn.
(2) 由于Tn是相对于理论到时获得的,相对于绝对到时有恒定的时间偏移量,为了将该偏移量消除,需要在最后一次迭代的叠加道中手动拾取初至记作Tman,根据公式Tnabs=Tn-(Tn-Tman)计算各道的绝对到时,其中Tn是各道Tn取平均的结果.
(3) 根据Tnabs调整时窗的位置,选用比W0更短的时窗W1,锁定目标震相,作为MCCC方法的输入,计算相对走时残差.
具体实施流程见图 3.该方法是一种人机交互式的半自动初至拾取方法,可以计算出目标震相的绝对到时和相对走时残差.减少了人为干预,一定程度上提高了拾取的效率.不过该方法依然需要人为拾取绝对到时,不能实现初至时间的全自动拾取.
|
图 3 ICCS方法实施流程 Figure 3 Flow chart of ICCS method |
不同于MCCC方法,自适应叠加方法(Adaptive Stacking,简称AS方法)在计算任意两道波形记录的延迟时间时,使用波形叠加技术生成参考地震道,选定的某一震相到时为参考时间,并以波形时移叠加的方式取代互相关来获取最优化的相对到时(Rawlinson and Kennett, 2004).
设某一远震发出的地震波同时被N个台站接收到.台站记录到的波形为si(t),(i=1, …, N),理论到时ti0.对各台站的波形分别按照其理论到时校正后,得到时间校正后的波形si(t-ti0).对此远震实施AS方法的具体步骤如下:
首先,将校正后的波形叠加形成参考道Sn(t)(其中n是迭代次数),公式为
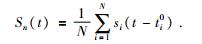
|
(7) |
其次,对每个台站的波形施加一个时间偏移量τ,使用包含目标震相的时窗内的地震波计算si(t-ti0-τ)与Sn(t)的L3范数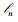
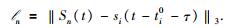
|
(8) |
之后,不断更新τ值.范数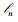
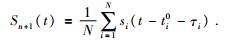
|
(9) |
最后,重复(8) 式计算L3范数及时间偏移量,并继续根据(9) 式对参考道进行更新.这样循环迭代直至叠加道的变化量满足用户定义的条件或走时残差趋于稳定为止(张风雪等,2013).
AS方法的具体实施流程如图 4所示.
|
图 4 AS方法实施流程 Figure 4 Flow chart of AS method |
相比于多道互相关方法,AS方法不用求解超定方程组,也不用对道集中所有波形对做互相关,计算效率和精度有所提升.此外,在自适应叠加过程中,选用叠加道作为参考道有利于将各道的波形平均化,因而该方法同样适用于信噪比低的地震记录.然而,该方法在对各道波形进行叠加时,仅仅是对波形的简单叠加,没有考虑各道波形的差异.当道集中存在坏道或波形差异特别大的道时,拾取的精度也会降低.
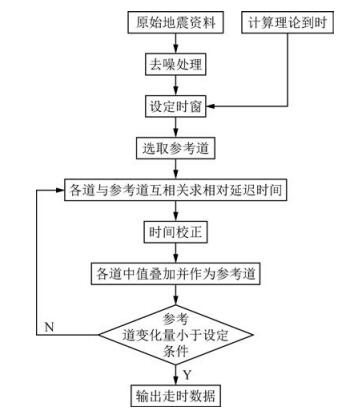
1.4 台网远震体波处理方法台网远震体波处理方法(Array Processing of teleseismic body waves,简称AP方法),利用各道与叠加道互相关求相对延迟时间,提取相对到时.该方法与ICCS方法的不同之处在于,在计算叠加道时,该方法采用加权叠加的方式计算各道的叠加中值作为参考地震道.
AP方法的基本步骤如下:
首先,对于记录到同一远震事件的N个台站的波形记录.根据目标震相的理论到时分别在各个台站的地震记录中截取时长为T的一段含有目标震相的波形,选取其中的某一道作为参考道,计算各道波形与参考道波形的互相关系数.
其次,根据互相关系数的最大值求取各道与参考道的相对延迟时间,并根据该延迟时间对各道波形进行第一次时移排齐(时间校正),并叠加获得地震道的中值,记作b0.叠加操作如(10) 式所示,其中的权重根据(11) 式和(12) 式计算.公式为
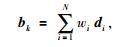
|
(10) |
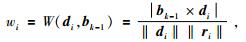
|
(11) |
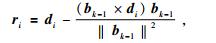
|
(12) |
其中bk和bk-1是第k和第k-1次迭代产生的参考道.ri是第i道的残差向量,反映的是第i道地震波形di与中值道波形b的差异程度.wi表示的是第i道的叠加权重,di与b的差异程度越大,则(10) 式中的残差向量ri越大;wi越小,第i道数据对叠加值b贡献越小.可见,加权叠加的过程对不相关强噪声信号有一定的压制作用.
最后,计算叠加道的变化量并判断其是否满足设定的条件.迭代的停机条件取决于b值是否满足收敛条件,即:
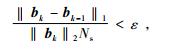
|
(13) |
其中,Ns是时窗内的样点数;ε是设定的收敛值,与地震资料的信噪比有关,在本文实例中,在2~4次迭代后就降到了10-4.满足条件则输出走时数据,否则继续执行循环.
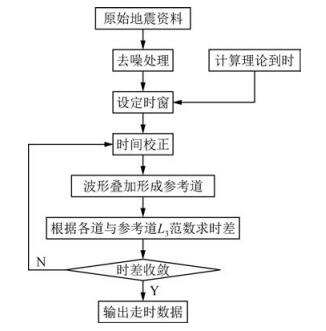
AP方法的具体实施流程如图 5所示.AP方法由于不采用互相关,节省了处理所用的时间,具有较高的拾取效率(Pavlis and Vernon, 2010).因此,AP方法比较适用于处理大尺度地震台网(例如USArray)数据.然而,该方法在实际应用中存在周期跳跃的问题,易产生离群值(Pavlis and Vernon, 2010).
|
图 5 AP方法实施流程 Figure 5 Flow chart of AP method |
上述几种方法在对波形数据进行叠加时,仅仅利用了到时和振幅的一致性,而没有考虑地震波相位一致性.根据相位加权叠加(Phase weighted stack)原理,对于低信噪比的远震记录,在波形叠加过程中考虑相位一致性,可以在一定程度上改善互相关效果(Schimmel and Paulssen, 1997).
江国明等(2012)将相位一致性信息引入多道互相关中,提出了一种改进多道互相关方法(Modified multi-channel cross-correlation),简称MMCCC方法.具体实现步骤如下:
首先,在远震道集中计算任意两条波形si(t)和sj(t)的互相关系数时引入波形瞬时相位角,并对互相关系数进行归一化,得到了改进后的互相关系数计算公式为
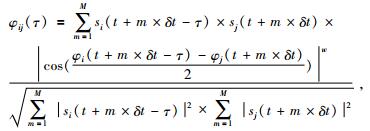
|
(14) |
其中,M是时窗内的采样点数;τ是偏移时间;δt是采样间隔;ϕi和ϕj分别是第i道和第j道波形的瞬时相位角,瞬时相位角表达式为ϕ=arctan[H(t)/s(t)],H(t)为波形数据s(t)的希尔伯特变换.φij(τ)是改进的互相关系数;w是相位权重因子,通常取2或3.
其次,对于第i个远震同时被N个台站接收到的情形,利用改进的互相关求第k道波形相对于第j道波形的延迟时间,计算得到所有N个台站波形相对于第j道波形的延迟时间(其中,第j道波形相对于自身的到时差为0),记为
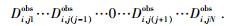
|
(15) |
同样,N道波形相对于第j道波形的理论到时的相对延迟时间可以表示为
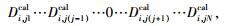
|
(16) |
其中:
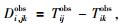
|
(17) |
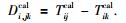
|
(18) |
最后,取相对延迟时间的平均并作差,公式为
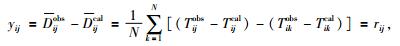
|
(19) |
这样就求出了相对走时残差rij.
改进多道互相关方法的具体实施流程见图 6.在用改进的互相关函数计算延迟时间时,由于引入了波形的相位信息,从时间、振幅和相位三方面区分信号和噪声,有效提高了震相初至到时的识别能力.
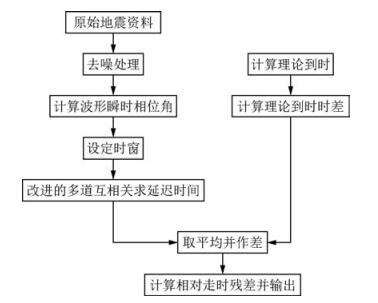
|
图 6 MMCCC方法实施流程 Figure 6 Flow chart of MMCCC method |
本文以山东省中部地区的远震波形资料为例,对比了五种初至拾取方法的应用效果.研究时窗参数对不同拾取方法结果的影响,并分析不同初至拾取方法的精度.
2.1 实测远震数据的初至拾取效果对比我们于2015年夏季在山东省中部布设了29个便携式地震仪连续采集了一个月地震数据.地震仪采用自然频率4.5 Hz的动圈式检波器(GS11D)和TEXAN(RefTek125A)微型记录仪.台站布设大致沿东西向横跨郯庐断裂带,构成总长度约80 km的地震测线,台站自西向东编号为1~29,如图 7所示.

|
图 7 地震台站分布.测线沿近东西向展布,实心三角代表台站 Figure 7 Locations of seismic stations (triangles). Survey line distributes nearly east-west |
图 8列出了台网记录到的两个地震事件的波形记录,表 1中的事件5和事件6.从记录中可以看出,对于相同地震事件,各台站记录的波形相似度较高,可以识别出初至波的同相轴.地震测线中西侧的1~20号台站下方基岩较浅,且检波器与大地的耦合较好,地震记录的信噪比比较高.测线东测的21~29号台站布设在松散的沉积层上,而且此区频繁的人类活动产生了大量噪声,导致地震记录的信噪比偏低.图 8显示:事件5地震子波稍长,事件6的子波能量较集中.后文将针对这两个远震事件的地震记录讨论时窗参数对各方法拾取精度和稳定性的影响.
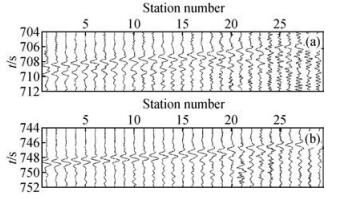
|
图 8 两个典型地震事件的波形.(a)和(b)分别显示表 1中的事件5和事件6的初至波形 Figure 8 Seismic records of two typical earthquake events. Panels (a) and (b) show the seismic first-arrival waveforms of events 5 and 6, respectively |
|
|
表 1 本文用到的地震事件信息(根据USGS发布的地震列表) Table 1 Parameters of earthquake events (according to USGS earthquake catalog) |
|
|
表 2 五种初至拾取方法特点对比 Table 2 Performance comparison of five onset time picking methods |
在经过了低通滤波和归一化等预处理后,我们分别使用上述五种初至拾取方法计算各道波形的相对延迟时间,并以29号台站为参考对各道数据进行延迟时间校正.理论上,移除各道之间的相对时差后,各台站记录的地震波形应该排齐在相同时刻,形成相干叠加.如图 9所示.
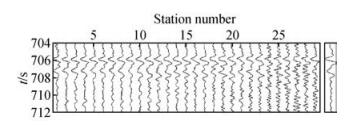
|
图 9 时差校正后的地震记录.时差由MCCC方法估计.右侧方框中的波形是所有数据的叠加 Figure 9 Seismic records after the correction of relative arrival time, which is estimated by MCCC method. Right panel shows the stack trace |
为了对比拾取效果,分别对两个地震事件进行手动拾取,以同样的方式对各道波形进行时间校正,提取时间校正后各道波形的叠加记录,五种拾取方法和手动拾取方法对应的叠加记录见图 10.图 10对比了五种计算机初至拾取方法和手动拾取的叠加记录.从图中可以看出,六种方法的叠加记录初至部分的波形基本对齐.可以从叠加记录波形中提取参考到时(用竖线表示),后文将以该到时为参考时刻进行滑动时窗测试.
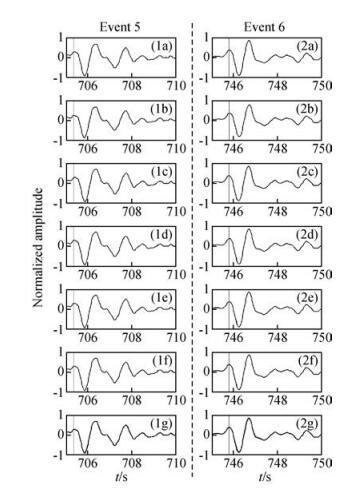
|
图 10 叠加记录对比图 序号1和2分别对应事件5和事件6. (a)~(f)分别是利用MCCC方法、AS方法、AP方法、MMCCC方法、ICCS方法和手动拾取的初至排齐叠加后的远震初至波形;(g)中灰线是六种方法的计算结果,黑线是取平均的结果. Figure 10 Comparison chart of stacked records Panel numbers 1 and 2 refer to event 5 and event 6, respectively. (a)~(f) correspond to the MCCC method、the AS method、the AP method、the MMCCC method、the ICCS method and picking method of manual. In panel; (g) the grey line represents the stacked traces for the 6 methods, and the black line represents the average of them. |
图 11显示,五种初至拾取方法得到的相对走时残差差异较小,这与图 10中应用各方法获得的叠加道差异很小相一致.这表明,本文讨论的这五种初至拾取方法在恰当信噪比的情况下会得到相似的结果.这种一致性可能是这几种方法都基于波形相似性的互相关来获得相对到时所致.
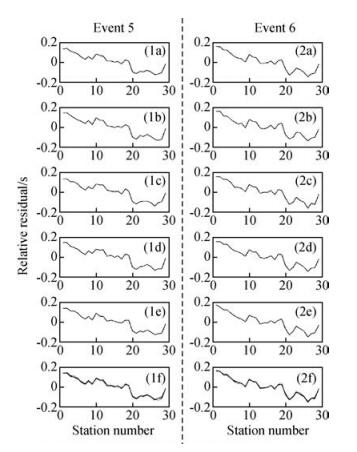
|
图 11 相对走时残差对比图 序号1和2分别对应事件5和事件6. (a)~(e)分别对应MCCC方法、AS方法、AP方法、MMCCC方法、ICCS方法;(f)中灰线是五种计算机拾取方法计算结果,黑线是取平均的结果. Figure 11 Comparison chart of relative residua Panel numbers 1 and 2 refer to event 5 and event 6, respectively. (a)~(e) correspond to the MCCC method、the AS method、the AP method、the MMCCC method and the ICCS method. In panel; (f) the grey line represents the stacked traces for the 5 methods, and the black line represents the average of them. |
由于上述五种初至拾取方法都利用互相关提取固定时窗内相似波形的相对时差,时窗的位置和长度对于所拾取初至的精度和稳定性至关重要.为了研究时窗参数对拾取精度的影响,以事件5和事件6的地震记录(图 12)为例对五种拾取方法进行滑动时窗测试.计算各道理论到时的平均值与图 10f叠加记录中手动提取的绝对到时的差值.将该时差施加到各道的理论到时上,作为滑动时窗的零值点(虚线),如图 12所示.取各道零值点前后0.1 s作为时窗的边界,并以0.1 s的时间间隔分别沿时间轴的正反方向(箭头方向)移动时窗的边界(实线),直至所有数据均包含在时窗内.
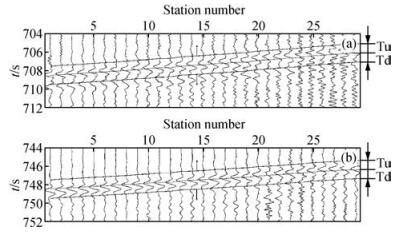
|
图 12 滑动时窗示意图 实线之间的波形被用于互相关.(a)事件5的记录,(b)事件6的记录.箭头代表时窗滑动方向,虚线代表时窗滑动零值点,实线是时窗的边界Tu和Td是时窗零值点分别与时窗起点和时窗终点的时差. Figure 12 Schematic diagram showing the sliding of time window The waveforms between the solid lines are used in cross correlation. Panels (a) and (b) show records of event 5 & 6. Arrows represents the time window sliding direction; dotted lines are the starting point of sliding window; solid lines are the border of the window. Tu & Td are the time ahead and after the zero point of time window, respectively. |
对于各种时窗长度取值,分别用五种初至拾取方法拾取初至时间,提取时间校正后各道波形的叠加记录,并计算最大振幅值.初至拾取的准确度越高,用该初至进行时间校正后的地震波形对齐程度越高,叠加道的最大振幅值越大.因而,叠加道的最大振幅值可以反映拾取的精度.设时窗的起点时刻和终点时刻分别为Tu和Td,分别以Tu和Td作为纵坐标和横坐标,可以获得时窗长度变化对叠加道最大振幅的影响(如图 13所示),它反映了时窗长度与初至拾取精度的关系.
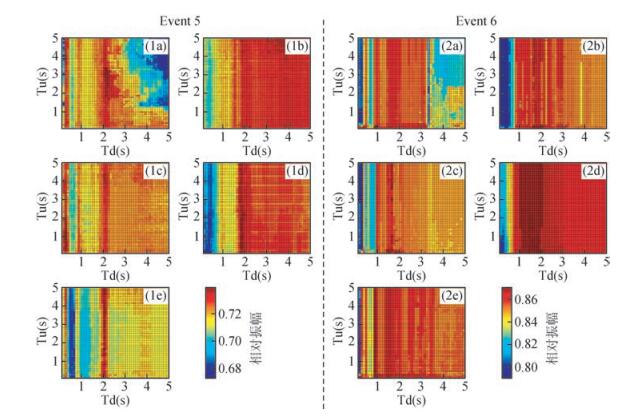
|
图 13 叠加记录最大振幅与时窗长度的关系 序号1和2分别对应事件5和事件6. (a)~(e)分别对应MCCC方法、AS方法、AP方法、MMCCC方法、ICCS方法.图中颜色代表叠加记录的归一化最大振幅值.Tu和Td与图 12中含义相同. Figure 13 Relation of maximum amplitude of stacked records and length of time window No.1 and No.2 corresponding to event 5 and event 6, respectively. (a)~(e) corresponding to the MCCC method、the AS method、the AP method、the MMCCC method and the ICCS method. Color map represents the normalized maximum amplitude of the stacked traces. Tu & Td has the same meaning as those in Figure 12. |
图 13表明,对于子波较长的地震记录(事件5),MCCC方法在时窗起点时间取2~3 s,时窗终点时间取2~2.5 s时,叠加记录的振幅值较大;对于AS方法、AP方法和MMCCC方法,当时窗的终点时间大于2 s,时窗起点的位置对拾取结果影响不大,即这三种方法对时窗长度的敏感度小,稳定性较高;ICCS方法在时窗终点取2 s左右时,叠加记录的振幅值较大.对于子波能量集中的地震记录(事件6),当时窗的终点时间取2~3 s时,时窗起点的位置对五种初至拾取方法的拾取结果影响不大.可见,对于本文选择的两个远震事件,最佳的时窗长度是2 s左右.对比事件5和事件6叠加记录的最大振幅可以看出:ICCS方法对时窗长度的敏感度最高,MCCC方法次之,AS方法、AP方法和MMCCC方法最低.当时窗完全覆盖初至波子波波形的整个相位时,叠加记录的振幅值较大.频谱分析显示,5、6两个远震事件的波形记录的主频分别为0.8 Hz和1 Hz,主频恰好是最佳时窗长度的1/2.考虑到时窗太长会增加计算量,建议时窗中点取在初至震相的起跳点,长度取初至震相信号主周期的1~2倍,在实际应用时可以对初至拾取方法施加人机交互环节,手动调整时窗位置,以获得较高的拾取精度和稳定性.
2.3 初至拾取方法的拾取精度分析为了测试五种拾取方法精度的高低,本文以手动精细拾取获得的相对走时残差为参考,计算其他五种方法相对走时残差的计算误差.其中,远震波形传播到各个台站的理论到时是根据震源与台站的位置信息借助地球的一维速度模型IASP91计算得来.对于同一地震资料,每种方法的时窗位置和长度都是相同的.本文共统计了174道波形(所有远震事件的信息如表 1所示)的相对走时残差的拾取误差,并参照Akram和Eaton(2016)的方法,分区间对各方法的拾取误差进行了统计(图 14).
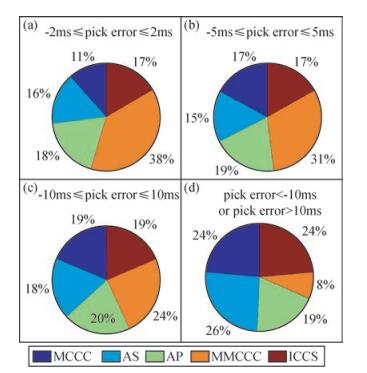
|
图 14 各方法拾取误差分布 拾取误差的分布区间分别为:(a)[2 ms,2 ms]; (b)[-5 ms,5 ms]; (c)[-10 ms,10 ms]; (d)(-∞,-10 ms) & (10 ms,+∞). Figure 14 Picking error pie charts showing the error distribution Picking errors are divided into different intervals:(a) [-2 ms, 2 ms]; (b) [5 ms, 5 ms]; (c) [-10 ms, 10 ms]; (d) (-∞, -10 ms) & (10 ms, +∞). |
从图 14中可以看出,在±2 ms误差范围内,MMCCC方法所占比重最大,其次是AP、AS和ICCS方法所占比重相近,MCCC方法比重最小.在±5 ms误差范围内,MMCCC方法比重最大,其他四种方法所占比重相近,在±10 ms误差范围内,本文所讨论五种方法的拾取精度接近.在误差大于10 ms的范围内,AS方法所占比重最大,其次是MCCC方法和ICCS方法和AS方法比重相近,MMCCC方法所占比重最小.分析五种初至拾取方法的误差可以看出:MMCCC方法精度最高,AP方法次之,MCCC和ICCS方法中等,AS方法最低.
3 结论与讨论 3.1基于波形相似性的初至拾取方法具有较高的精度,但互相关波形的选取差异会造成初至拾取结果的较大差异,这使得时窗位置和长度以及波形的相似程度等因素对初至拾取的精度具有一定影响.对比分析表明,五种初至拾取方法在拾取精度、效率和对时窗的依赖程度方面存在差异,具体体现是:当时窗选取合适时,在拾取精度方面,改进多道互相关方法精度最高,台网远震体波处理方法次之,再次是改进多道互相关方法和迭代互相关叠加方法,自适应叠加方法最低;在拾取效率方面,自适应叠加方法效率最高,其次是台网远震体波处理方法,再次是多道互相关方法和迭代互相关叠加方法,改进多道互相关方法最低.对于相同的地震资料,各方法对时窗的依赖程度方面,自适应叠加方法、台网远震体波处理方法和改进多道互相关方法最小,多道互相关方法次之,迭代互相关叠加方法最大.时窗长度取初至震相信号主周期的1~2倍,互相关时窗恰好覆盖初至震相起跳部分的波形时,拾取的稳定性和精度较高.
3.2鉴于不同方法在拾取精度、效率和稳定性方面的差异,针对不同的应用目的,应选用不同的拾取方法.例如,对于地震速报等需要快速获取初至时间但对走时精度要求不高的情形,可以采用效率较高、拾取绝对到时的自适应叠加方法(AS方法);对于层析反演等对走时精度要求比较高的情形,建议选用改进多道互相关方法(MCCC方法)或台网远震体波处理方法(AP方法);对于密集台网和大量远震事件的情形,建议采用台网远震体波处理方法(AP方法).
致谢 感谢审稿专家提出的宝贵意见和编辑部的大力支持!| [] | Akram J, Eaton D W. 2016. A review and appraisal of arrival-time picking methods for downhole microseismic data[J]. Geophysics, 81(2): KS71–KS91. DOI:10.1190/geo2014-0500.1 |
| [] | Allen R V. 1978. Automatic earthquake recognition and timing from single traces[J]. Bulletin of the Seismological Society of America, 68(5): 1521–1532. |
| [] | Archambeau C B, Bradford J C, Broome P W, et al. 1965. Data processing techniques for the detection and interpretation of teleseismic signals[J]. Proceedings of the IEEE, 53(12): 1860–1861. DOI:10.1109/PROC.1965.4457 |
| [] | Baer M, Kradolfer U. 1987. An automatic phase picker for local and teleseismic events[J]. Bulletin of the Seismological Society of America, 77(4): 1437–1445. |
| [] | Bear L K, Pavlis G L. 1999. Multi-channel estimation of time residuals from broadband seismic data using multi-wavelets[J]. Bulletin of the Seismological Society of America, 89(3): 681–692. |
| [] | Bungum H, Husebye E S. 1971. Errors in time delay measurements[J]. Pure and Applied Geophysics, 91(1): 56–70. DOI:10.1007/BF00879557 |
| [] | CHEN Jin-Huan, CAO Yong-Sheng, SUN Cheng-Long, et al. 2015. The algorithm for automatic first-breaks picking on seismic traces based on Dichotomy[J]. Progress in Geophysics, 30(2): 688–694. DOI:10.6038/pg20150228 |
| [] | HE Xian-Long, SHE Tian-Li, GAO Feng. 2016. A new method for picking up arrival times of seismic P and S waves automatically[J]. Chinese Journal of Geophysics, 59(7): 2519–2527. DOI:10.6038/cjg20160717 |
| [] | Husebye E S, Jansson B. 1966. Application of array data processing techniques to the Swedish seismograph stations[J]. Pure and Applied Geophysics, 63(1): 82–104. DOI:10.1007/BF00875160 |
| [] | JanssonB, Husebye E S. 1968. Application of array data processing techniques to a network of ordinary seismograph stations[J]. Pure and Applied Geophysics, 69(1): 80–99. DOI:10.1007/BF00874907 |
| [] | JIANG Guo-Ming, ZHANG Gui-Bin, XU Yao. 2012. A fast method for calculating relative residuals of teleseismic data and its application[J]. Chinese Journal of Geophysics, 55(12): 4097–4105. DOI:10.6038/j.issn.0001-5733.2012.12.022 |
| [] | Kennett B L N, Engdahl E R. 1991. Traveltimes for global earthquake location and phase identification[J]. Geophysical Journal International, 105(2): 429–465. DOI:10.1111/gji.1991.105.issue-2 |
| [] | Kennett B L N, Engdahl E R, Buland R. 1995. Constraints on seismic velocities in the Earth from traveltimes[J]. Geophysical Journal International, 122(1): 108–124. DOI:10.1111/gji.1995.122.issue-1 |
| [] | Langston C A. 1979. Structure under Mount Rainier, Washington, inferred from teleseismic body waves[J]. Journal of Geophysical Research, 84(B9): 4749–4762. DOI:10.1029/JB084iB09p04749 |
| [] | LIU Jing-Song, WANG Yun, YAO Zhen-Xing. 2013. On micro-seismic first arrival identification:A case study[J]. Chinese Journal of Geophysics, 56(5): 1660–1666. DOI:10.6038/cjg20130523 |
| [] | Lou X T, van der Lee S, Lloyd S. 2013. AIMBAT:A python/matplotlib tool for measuring teleseismic arrival times[J]. Seismological Research Letters, 84(1): 85–93. DOI:10.1785/0220120033 |
| [] | MA Qiang, JIN Xing, LI Shan-You, et al. 2013. Automatic P-arrival detection for earthquake early warning[J]. Chinese Journal of Geophysics, 56(7): 2313–2321. DOI:10.6038/cjg20130718 |
| [] | Molyneux J B, Schmitt D R. 1999. First-break timing:Arrival onset times by direct correlation[J]. Geophysics, 64(5): 1492–1501. DOI:10.1190/1.1444653 |
| [] | PAN Shu-Lin, Gao Lei, Chen Hui, et al. 2010. Study on methods for picking up first break of seismic record acquired by vibroseis[J]. Geophysical Prospecting for Petroleum, 49(2): 209–212. |
| [] | Pavlis G L, Vernon F L. 2010. Array processing of teleseismic body waves with the USArray[J]. Computers & Geosciences, 36(7): 910–920. |
| [] | Peraldi R, Clement A. 1972. Digital processing of refraction data study of first arrivals[J]. Geophysical Prospecting, 20(3): 529–548. DOI:10.1111/gpr.1972.20.issue-3 |
| [] | Rawlinson N, Kennett B L N. 2004. Rapid estimation of relative and absolute delay times across a network by adaptive stacking[J]. Geophysical Journal International, 157(1): 332–340. DOI:10.1111/gji.2004.157.issue-1 |
| [] | SchimmelM, Paulssen H. 1997. Noise reduction and detection of weak, coherent signals through phase-weighted stacks[J]. Geophysical Journal International, 130(2): 497–505. DOI:10.1111/gji.1997.130.issue-2 |
| [] | Sleeman R, van Eck T. 1999. Robust automatic P-phase picking:An on-line implementation in the analysis of broadband seismogram recordings[J]. Physics of the Earth and Planetary Interiors, 113(1-4): 265–275. DOI:10.1016/S0031-9201(99)00007-2 |
| [] | Stevenson P R. 1976. Microearthquakes at Flathead Lake, Montana:A study using automatic earthquake processing[J]. Bulletin of the Seismological Society of America, 66(1): 61–80. |
| [] | TAN Yu-Yang, YU Jing, FENG Gang, et al. 2016. Arrival picking of microseismic events using the SLPEA algorithm[J]. Chinese Journal of Geophysics, 59(1): 185–196. DOI:10.6038/cjg20160116 |
| [] | VanDecar J C, Crosson R S. 1990. Determination of teleseismic relative phase arrival times using multi-channel cross-correlation and least squares[J]. Bulletin of the Seismological Society of America, 80(1): 150–169. |
| [] | WANG Cai-Xia, BAI Chao-Ying, WANG Xin. 2013. Review of automatic onset time picking for seismic arrivals[J]. Progress in Geophysics, 28(5): 2363–2375. DOI:10.6038/pg20130518 |
| [] | Wang J, Chen J H, Liu Q Y, et al. 2006. Automatic onset phase picking for portable seismic array observation[J]. Acta Seismologica Sinica, 28(1): 42–51. |
| [] | XU Yin-Po, YANG Hai-Shen, YANG Jian, et al. 2016. Iteration pickup method of first break using energy ratio[J]. Progress in Geophysics, 31(2): 845–850. DOI:10.6038/pg20160246 |
| [] | Zeiler C, Velasco A A. 2009. Seismogram picking error from analyst review (SPEAR):Single-analyst and institution analysis[J]. Bulletin of the Seismological Society of America, 99(5): 2759–2770. DOI:10.1785/0120080131 |
| [] | ZHANG Feng-Xue, WU Qing-Ju, LI Yong-Hua, et al. 2013. Pick up the teleseismic relative traveltime residuals by wave form correlation based on the GUI[J]. Seismological and Geomagnetic Observation and Research, 34(3): 58–64. |
| [] | ZUO Guo-Ping. 2006. The contrast and study of first arrivals detecting on seismic record (in Chinese)[MSc thesis]. Beijing:China University of Geosciences (Beijing). |
| [] | 陈金焕, 曹永生, 孙成龙, 等. 2015. 基于二分法的地震波初至自动拾取算法[J]. 地球物理学进展, 30(2): 688–694. DOI:10.6038/pg20150228 |
| [] | 何先龙, 佘天莉, 高峰. 2016. 一种地震P波和S波初至时间自动拾取的新方法[J]. 地球物理学报, 59(7): 2519–2527. DOI:10.6038/cjg20160717 |
| [] | 江国明, 张贵宾, 徐峣. 2012. 远震相对走时数据快速计算方法及应用[J]. 地球物理学报, 55(12): 4097–4105. DOI:10.6038/j.issn.0001-5733.2012.12.022 |
| [] | 刘劲松, 王赟, 姚振兴. 2013. 微地震信号到时自动拾取方法[J]. 地球物理学报, 56(5): 1660–1666. DOI:10.6038/cjg20130523 |
| [] | 马强, 金星, 李山有, 等. 2013. 用于地震预警的P波震相到时自动拾取[J]. 地球物理学报, 56(7): 2313–2321. DOI:10.6038/cjg20130718 |
| [] | 潘树林, 高磊, 陈辉, 等. 2010. 可控震源地震记录初至拾取方法研究[J]. 石油物探, 49(2): 209–212. |
| [] | 谭玉阳, 于静, 冯刚, 等. 2016. 微地震事件初至拾取SLPEA算法[J]. 地球物理学报, 59(1): 185–196. DOI:10.6038/cjg20160116 |
| [] | 王彩霞, 白超英, 王馨. 2013. 地震震相初至自动检测技术综述[J]. 地球物理学进展, 28(5): 2363–2375. DOI:10.6038/pg20130518 |
| [] | 王继, 陈九辉, 刘启元, 等. 2006. 流动地震台阵观测初至震相的自动检测[J]. 地震学报, 28(1): 42–51. |
| [] | 许银坡, 杨海申, 杨剑, 等. 2016. 初至波能量比迭代拾取方法[J]. 地球物理学进展, 31(2): 845–850. DOI:10.6038/pg20160246 |
| [] | 张风雪, 吴庆举, 李永华, 等. 2013. 基于图形界面的波形相关法拾取远震相对走时残差[J]. 地震地磁观测与研究, 34(3): 58–64. |
| [] | 左国平. 2006. 地震记录初至拾取方法对比和研究[硕士论文]. 北京: 中国地质大学(北京). |
 2017, Vol. 32
2017, Vol. 32


