2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
地球重力场通常用球谐函数进行表达,而求解球谐系数需要全球范围内足够均匀的重力观测值,这就必须对原始数据进行格网化,但在格网化的同时也会引入插值误差;另外,由于球谐函数缺乏空域局部性, 任何局部的变化都会导致所有的球谐系数发生改变(宁津生等,2004),不适于局部重力场模型的构建和更新.作为球谐函数模型的补充,径向基函数模型,由于其在空域及频域范围内都有很好的局部化特性,尤其适合于描述局部重力场.利用径向基函数的球面展开,可将重力场信号表达为多个依赖于频率的细节信号,径向基函数的这种频率局部化特性,构成了重力场多尺度分析的基础.
近些年来,径向基函数在局部重力场建模方面得到越来越广泛的应用,德国Kaiserskautern大学的地学研究小组提出了运用径向基函数对重力场进行多尺度分析的理论(Freeden et al., 1998; Freeden, 1999).随后,该理论得到了长足的发展.Kusche(2002)就重力场的确定和多分辨率分析的概念做了简要的概括总结;Schmidt等(2002, 2005)利用模拟数据采用两种不同的径向基函数方法(小波基函数法和小波球谐函数组合法)对全球重力异常/大地水准面进行了多尺度分解,证明了多尺度分析方法的可行性. Chambodut等(2005)提出了径向基函数多尺度框架的概念,通过实际多尺度分析表明,在输入数据较为稀疏的情况下,径向基函数模型比球谐函数模型更具优势.Roland和Denker(2005)对比了利用径向基函数多尺度分析方法和斯托克斯方法构建局部大地水准面模型的差异,指出了相比于斯托克斯多尺度分析法不再需要内区改正,但同时存在计算量过大的劣势.Freeden和Schreiner(2006)研究了利用垂线偏差数据对大地水准面进行多尺度建模的相关理论,并指出多尺度方法的优势在于它可以充分利用径向基函数的局部化特性;Schmidt等(2006)对径向基函数局部重力场多尺度分析的方法做了详细描述,并给出了其在诸如构建高分辨率融合模型、时空统一模型等方面的具体应用实例.Fehlinger等(2008)在多尺度框架的基础上利用格林函数的球面积分公式,提出了运用垂线偏差数据模型化扰动位的新方法.Freeden等(2009)将多尺度分析运用于探测夏威夷和冰岛的地幔羽流中,其所得关于地幔羽流位置的结论与地震学结果相当.Freeden等(2010)又将该方法运用于GRACE和水文数据中,并在局部化的时空范围内比较了两种数据结果的差异.Peidou和Vergos(2015)在对近几年的GOCE/GRACE卫星重力场资料进行多尺度分析的基础上,使得重力场模型的精度得到了一定的改善.
上述多尺度算法大多基于离散积分法,即在求解尺度基函数和小波基函数系数时采用积分方程离散化来对其进行估计,这需要确定合适的积分权重.但是,不同的积分权重会对多尺度估计的效果产生不同的影响,当定权方案不恰当时,会引起平滑函数和细节函数间的信号泄露,进而影响多尺度分析的效果.为了减弱上述定权策略对多尺度分析的影响,本文中提出对所有尺度系数和细节系数均采用最小二乘的方法直接求解(简称直接法),并针对具体多尺度分析实例对这两种方法做简要的分析比较.
1 方法原理 1.1 重力场信号的多尺度表示多尺度表示,又称多分辨率表示,其基本思想是通过逐次滤波,将输入信号逐步分解为一个平滑信号和若干个细节信号的过程;这个不断得到的不同尺度上的一系列估值信号的过程被称为多尺度分析(多分辨率分析).(Schmidt et al., 2006).
重力场信号也具有多尺度特征,实际上,对地球重力场的认识就是一个不断从粗略到精细的多分辨分析过程(宁津生等,2004).基于上述多尺度分析理论,重力场信号可表示为式
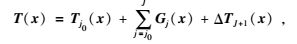
|
(1) |
式(1) 中,x为球面上任一点坐标,j为尺度,j=j0, …, J,T(x)为重力场泛函,Tj0(x)为j0尺度下的平滑信号,Gj(x)为j尺度下的重力场细节信号,ΔTJ+1为多尺度分析误差.
平滑信号和细节信号分别通过尺度基函数、小波基函数与输入重力场信号的卷积得到,公式为

|
(2) |
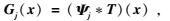
|
(3) |
其中,*为卷积,Sj+1为尺度基函数,Ψj为小波基函数.
Sj+1、Ψj均为径向基函数,它们具有良好的空间局部化特性,其具体表达形式为
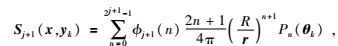
|
(4) |

|
(5) |
yk为第k个基函数格网点坐标,R为地球半径,r为向径,n为径向基函数阶次,Pn(·)为n阶勒让德多项式,θk为x、yk之间的球面角距, φj+1(n)、ωj(n)分别为尺度基函数和小波基函数的基函数核,也称为勒让德系数,它们决定了径向基函数在频率域内的表现.
小波基函数核ωj(n)与尺度基函数核φj(n)存在如(6) 式的线性关系,公式为

|
(6) |
由于ωj(n)由相邻尺度的基函数核φj+1(n)、φj(n)作差而来,因此小波基函数、尺度基函数的类型均由φj(n)决定.φj(n)的类型有多种选择,如Abel-Poisson核、Smoothed Shannon核等,本文中φj(n)取如(7) 式Abel-Poisson核的形式,公式为

|
(7) |
式中,p为带宽参数,本文取p=0.5.
图 1绘出了不同尺度下的Abel-Poisson尺度基函数和小波基函数在空间域和频率域的表现情况.从图 1a、b可以看出,Abel-Poisson基函数确实具有良好的空间局部化特性,尺度越大,基函数形状越狭窄,能量越集中.图 1c、d中,尺度越大,核函数覆盖的频率范围越广,越能分解高阶次高分辨率的重力场信号;在相同尺度上,尺度核函数φj(n)主要覆盖低频信息,而小波核函数ωj(n)除了覆盖低频部分,还包含一定范围的高频信息.例如,在j=7的尺度上,尺度核函数φ7(n)>0的频率范围约为0≤n<1000,而小波核函数ω7(n)>0的频率覆盖范围约为0≤n<2800,小波核函数ω7(n)主要包含了尺度核函数φ7(n)所没有的部分高频信息(1000<n<2800).因此,小波基函数可以提取重力场信号的高频信息,而尺度基函数只能提取低频重力场信息,将两者结合起来,便可实现对重力场信号的多尺度分解.

|
图 1 不同尺度下Abel-Poisson基函数在空域和频域的表现 (a)尺度基函数;(b)小波基函数;(c)尺度基函数核;(d)小波基函数核. Figure 1 Performance of Abel-Poisson basis functions in the spatial and frequency domain (a)Scaling basis function; (b) Wavelet basis function; (c) Scaling basis function kernel; (d) Wavelet basis function kernel. |
多尺度分析方法的关键在于求解各尺度基函数系数dj,通常的算法采用离散积分法.它的基本思想是先通过积分离散化求解出最高尺度上的基函数系数dJ,然后依据尺度间的递推关系,依次求解其余尺度上的基函数系数(Freeden and Windheuser, 1996;Schreiner, 1999).
对于满足可容许条件的基函数格网点系统(Schreiner, 1999, Driscoll and Healy, 1994),卷积公式(2)、(3) 可离散化表示为
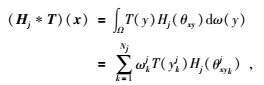
|
(8) |
式(8) 中,Hj表示尺度基函数或小波基函数,θxy为球面角距,T(ykj)表示j尺度下的重力场值,y为基函数格网点坐标,ω为积分权重.令:
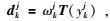
|
(9) |
则dkj即为待求的基函数系数.由于实际上只有最高尺度的重力场参量T(ykJ)是已知量,所能直接得到的只有该尺度上的基函数系数,公式为
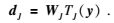
|
(10) |
但是,运用公式(8),相邻尺度之间还可以推导出如(11) 式的递推关系(Schreiner, 1999),这样基函数系数可依次求解,这也正是离散积分法的基本原理,公式为
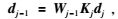
|
(11) |
式(10)、(11) 中,Kj是维数为Nj-1×Nj的转换矩阵,Wj-1=diag{wj-11, wj-12, …, wj-1Nj-1}, 它是Nj-1×Nj-1维的积分权阵.
不同的基函数格网点系统的定权策略不尽相同,常用的基函数格网有标准经-纬度格网权和Reuter格网权.
标准经-纬度格网的权为
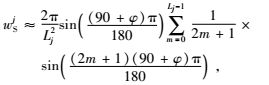
|
(12) |
上式中,φ为格网点的纬度,Lj为格网密度参数(Schmidt et al.,2006).
Reuter格网的权为
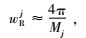
|
(13) |
其中,Mj为尺度j的基函数格网点总数(Freeden,1999).
这样可依据(10)、(11),先求出各基函数系数dj,再依据(14)、(15) 两式,便可计算出各个尺度的平滑信号和细节信号.公式为
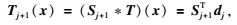
|
(14) |
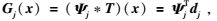
|
(15) |
注意到(14)、(15) 两式中尺度基函数和小波基函数的系数dj是相同的.
离散积分多尺度分析方法自提出以来,因其求解系数方便直观,得到了广泛的应用.但是,由于它是对球面积分的近似估计,分解后得到的各尺度信号(细节信号和平滑信号)会出现信号损失(即信号泄露),致使最后所得的重构信号与输入重力场信号之间有较大差异.因此,为了减弱信号泄露,有必要寻求新的解算方法.
直接法由本文提出,它是在最小二乘算法的基础上,采用方差分量估计法,对每一尺度的基函数系数直接进行求解,它的主要依据是(14)、(15) 式中相邻尺度的平滑信号和细节信号具有相同的基函数系数以及(16) 式的相邻尺度间的信号分解关系(Schmidt et al.,2006),公式为
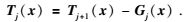
|
(16) |
另外,考虑到求解基函数系数可能出现病态性的问题,本文采用方差分量估计法对法方程进行正则化,依次对各个尺度基函数系数进行求解.计算时,使用逆递推法,先从最高尺度起算,即令j=J,主要计算步骤如下:
1) 依据(14) 式利用最小二乘法求解出dj,公式为
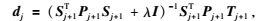
|
(17) |
式中Pj+1为平滑信号Sj+1的权重,λ为正则化因子.具体求解过程参考Koch和Kusche(2002);
2) 利用(15) 式求解细节信号Gj(x);
3) 利用(16) 式求解平滑信号Tj(x);
4) 降低尺度,重复1)、2)、3) 过程直到求解至最低尺度j0.
图 2给出了两种基函数求解方法的计算流程差异.图 2a为离散积分方法,其基函数系数dj、平滑信号Tj和细节信号Gj的求解平行进行.每一尺度上都是先求解出基函数系数dj,再依据该系数求出平滑信号Tj和细节信号Gj,最后将求解的一系列的细节信号和最低尺度的平滑信号相加,即为重构信号

|
图 2 多尺度分析计算流程
(a)离散积分法;(b)直接法.
→代表尺度系数转换过程; 表示可计算,但不必要.
Figure 2 Flow chart of multi-scale analysis
(a) Discrete integral method; (b)Direct method.
→Scale coefficients conversion process; 表示可计算,但不必要.
Figure 2 Flow chart of multi-scale analysis
(a) Discrete integral method; (b)Direct method.
→Scale coefficients conversion process;  Can be calculated, but not necessary. Can be calculated, but not necessary.
|
基于上述两种多尺度分析理论,搜集了南海局部地区(北纬8° N~18° N,东经108° E~116° E)、丹麦空间研究所提供的2′×2′的DTU13自由空气重力异常数据(共72000个,图 3a), 作为本文的研究对象.为了保证多尺度建模的有效性、充分利用卫星重力场模型可靠的中低阶信息,运用“移去恢复法”,从原始数据中移去了EIGEN-GL04S模型前36阶重力异常贡献,作为输入数据,如图 3b.表 1给出了原始数据和输入数据的统计情况.表 1中,移去EIGE-GL04S的重力异常贡献后,重力异常均值由3.42 mGal降低为-0.26 mGal,标准差从±22.84 mGal变为±21.94 mGal.

|
图 3 南海地区DTU13重力异常输入数据 (a)原始数据;(b)输入数据(单位:mGal). Figure 3 DTU13 gravity anomaly of the South ChinaSea (a) Raw gravity data; (b) Input data(unit: mGal). |
|
|
表 1 南海局部地区DTU13重力场数据统计(mGal) Table 1 Statistics of the DTU13 gravity field in the South China Sea (mGal) |
多尺度分析必须先确定出尺度的范围. DTU13输入数据的空间分辨率为2′×2′,对应的球谐阶次约为5400阶,在图 1中,当尺度j=10时,尺度核函数(图 1c)覆盖频率范围超过5400阶,因此可将该尺度作为多尺度分析的最高尺度J(J=10);至于最低尺度,为了避免过多过细的分解低尺度信号,将最低尺度取为j0=6.故本文中,多尺度分析的尺度范围6至10.
为了比较两种多尺度算法的差异,本文选取Abel-Poisson径向基函数,在Reuter基函数格网的基础上,分别采用离散积分法和直接法,对南海地区重力异常进行多尺度分析,图 4绘出了两种多尺度分析算法后的重力异常分布情况,相关的数据统计见表 2.
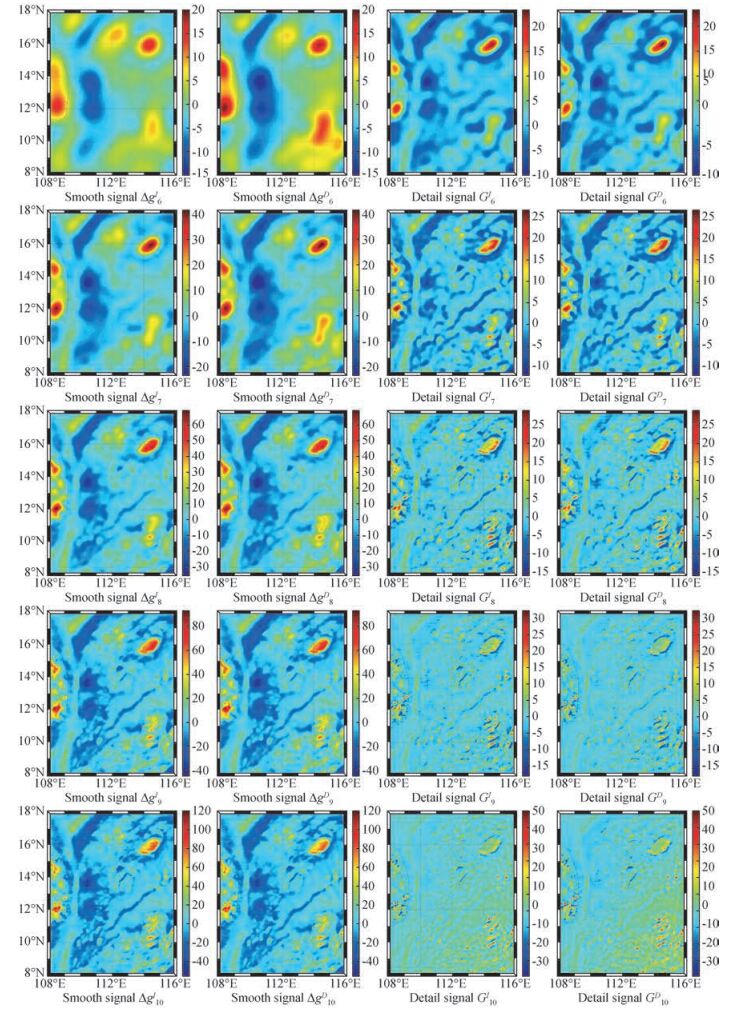
|
图 4 南海地区DTU13重力异常的多尺度分析(单位:mGal) ΔgjI表示离散积分法得到的j尺度平滑重力异常信号; ΔgjD表示直接法得到的j尺度平滑重力异常信号;GjI表示离散积分法得到的j尺度细节重力异常信号; GjD表示直接法得到的j尺度细节重力异常信号. Figure 4 Multi-scale analysis of the DTU13 gravity anomaly in the South China Sea(unit: mGal) ΔgjI Smooth signal obtained by discrete integral method; ΔgjD Smooth signal obtained by direct method; GjI Detail signal obtained by discrete integral method; GjD Detail signal obtained by direct method. |
|
|
表 2 离散积分法和直接法各尺度信号及两者差异统计(单位:mGal) Table 2 Signal statistics for each scale of the two methods and their difference(unit: mGal) |
从图 4可以看出,离散积分法和直接法都有效的对重力场(重力异常)进行了多尺度分解,且所得结果比较相近.随着尺度水平的降低,平滑信号Δg10、Δg9、Δg8、Δg7、Δg6的最大最小值的绝对值逐渐减小,标准差从Δg10的±17.14 mGal/±16.72 mGal降低至Δg6的±4.23 mGal/±5.47 mGal(表 2),表明重力异常的起伏变化越来越小.这与实际情况相符,因为平滑信号Δg10、Δg9、Δg8、Δg7、Δg6是对原始重力场信号的低通滤波过程(图 1c),随着尺度水平的降低,平滑信号所对应的重力异常频谱范围也越来越小,所得信号也越来越平滑.同样,由于细节信号G10、G9、G8、G7、G6是对重力场信号的带通滤波(图 1d),它所对应的是某一段频谱的重力异常信息,尽管标准差在数值上并无显著差异(表 2),随着分解程度的加深(G10至G6),复杂琐细的重力异常信号变得越来越简单平滑,重力异常在不同频段内的重力场阶信息也逐渐凸显出来,这一方面可以为重力场的频谱分析提供新的思路,另一方面可为研究地球内部的质量分布提供新的借鉴.
另外,尽管图 4的分布情况非常相似,离散积分方法和直接法得到的多尺度分析结果还存在些许细微差别,这主要体现为各尺度信号的强弱上(表 2,差异统计).多尺度分解后,两种方法在平滑信号上的最严重差异出现在Δg7上,其标准差为±2.07 mGal;而细节信号上这一数值出现在G10上,为±0.82 mGal,整体上平滑信号的差异标准差要大于细节信号的对应值.造成上述差异的主要原因,就是本文提到的信号泄露.
依据式(16),高尺度的平滑信号应等于低尺度平滑信号和细节信号之和,但由于信号泄露,实际分解后的信号并不满足这一条件.为了探测两种方法是否存在信号泄露及其数值大小,对多尺度分析后的各尺度信号(平滑信号和细节信号)分别进行如(18) 式的做差处理,公式为
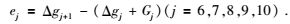
|
(18) |
图 5绘出了两种方法在不同尺度下信号的泄露情况,表 3列出了各尺度信号泄露误差大小及总的累计误差.
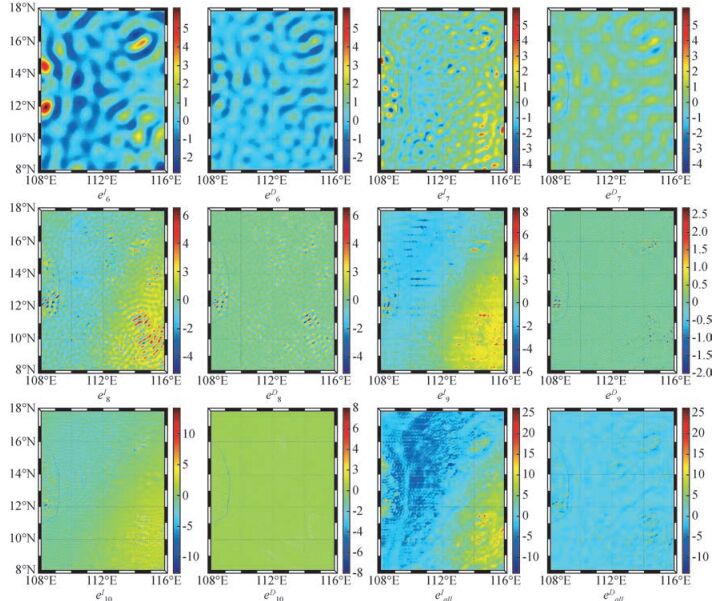
|
图 5 信号泄露误差分布(单位:mGal) ejI表示离散积分法j尺度泄露误差; ejD表示直接法j尺度泄露误差; eallI表示离散积分法总的泄露误差; eallD表示直接法总的泄露误差. Figure 5 The distribution of the signal leakage error ejI Leakage error of the discrete integral method; ejD Leakage error of the direct method; eallI The total leakage error of the discrete integral method; eallD The total leakage error of the direct method. |
|
|
表 3 多尺度分析信号泄露误差统计(单位:mGal) Table 3 Statistics of signal leakage after multi-scale decomposition(unit:mGal) |
结合图 5和表 3,两种分析方法都存在信号泄露现象,由于采用的基函数系数求解方法不同,两种分析算法的各个尺度信号泄露误差分布均不一致,但在每一个尺度上,离散积分法的泄露误差都比直接法要大.离散积分方法中,6、7、8、9、10尺度上的均方根误差分别为±0.90 mGal、±0.85 mGal、±1.00 mGal、±1.39 mGal和±1.45 mGal,误差最大最小值均出现在第10尺度上,分别为14.07 mGal和-11.97 mGal;5个尺度上信号重构后总的泄露误差均方差(eall)为±4.04 mGal,最大值达到了26.07 mGal.而直接法,其在各个尺度的泄露误差均方根值分别为±0.45 mGal、±0.49 mGal、±0.61 mGal、±0.30 mGal和±0.43 mGal, 比离散积分法各尺度信号泄露误差减少了50%、42%、39%、79%、71%;单个尺度的泄露误差最大最小值分别为5.24 mGal和-4.04 mGal(尺度8),5个尺度上总的泄露误差均方根为±1.12 mGal,其中最大误差为9.47 mGal,分别比离散积分法信号误差减少约72%和63%,明显小于离散积分法的各对应值.因此,直接法更适用于高精度高分辨率的重力场多尺度分析.
造成离散积分法泄露误差的主要原因,在于积分权重估计的不够准确.离散积分法的权重是根据基函数格网满足可容许条件的情况下对全球积分离散化得到的,但它与基函数格网的分布间隔密切相关.当基函数数格网分布间隔不是足够小,即使满足可容许条件,离散积分得到的尺度和细节信号仍然会产生误差.积分权重出现误差,不仅会导致各尺度基函数系数估计不准,而且随着多尺度分解的进行,基函数系数的误差会越来越大,以致于出现多尺度分析泄露误差较大的情况.
直接法也有少许信号泄露,这与最小二乘算法本身有关.在求解各尺度基函数系数时,由于重力场信号起伏变化剧烈、基函数格网数选择不当等原因,所得基函数系数便不能完全的拟合该尺度信号,这在利用径向基函数模型化重力场的过程中是常见的情况.如果基函数系数解算存在误差,利用其恢复的平滑信号也会有所偏差,进而也会导致一定的信号泄露现象,但相对于积分法信号泄露误差明显减少了许多.
3 结论 3.1针对离散积分多尺度分析中容易被忽视的信号泄露现象,本文在最小二乘算法和方差分量估计的基础上,提出了一种新的多尺度分析算法(直接法),有效的减少了重力场分解过程中的信号泄露.以南海地区DTU13重力异常数据为例,分别运用离散积分法和直接法对重力异常进行多尺度分解,结果显示:直接法的5个尺度的信号泄露误差分别为±0.45 mGal、±0.49 mGal、±0.61 mGal、±0.30 mGal和±0.43 mGal,离散积分法的各对应值为±0.90 mGal、±0.85 mGal、±1.00 mGal、±1.39 mGal和±1.45 mGal;在不同尺度上,直接法比离散积分法的泄露误差减少了约39%~79%,直接法总的泄露误差为±1.12 mGal,明显小于离散积分法的±4.04 mGal,因此可将直接法应用于高精度高分辨率的重力场多尺度分析中.
3.2离散积分法基函数系数的求解依赖于卷积积分方程离散化,但由于积分权重估的估计存在误差,导致其计算的基函数系数不够准确,随着多尺度分析的深入,信号累计泄露误差越来越大;而直接法在求解各尺度基函数系数会产生拟合误差,同样导致少量信号泄露.但是,如果操作得当,直接法的泄露误差均能控制在较小的范围内.
3.3作为球谐函数的补充,多尺度分析方法有多种用途,例如探测地幔羽流的位置和大小,融合多源重力数据,构建时空统一重力场模型等,可以为高分辨率重力场模型的构建提供借鉴.
致谢 感谢丹麦技术大学空间研究所提供的DTU13自由空气重力异常数据.| [] | Chambodut A, Panet I, Mandea M, et al. 2005. Wavelet frames:an alternative to spherical harmonic representation of potential fields[J]. Geophysical Journal International, 163(3): 875–899. DOI:10.1111/gji.2005.163.issue-3 |
| [] | CuiJ J, Freeden W. 1997. Equidistribution on the sphere[J]. SIAM Journal on Scientific Computing, 18(2): 595–609. DOI:10.1137/S1064827595281344 |
| [] | Driscoll J R, Healy D M. 1994. Computing Fourier transforms and convolutions on the 2-sphere[J]. Advances in Applied Mathematics, 15(2): 202–250. DOI:10.1006/aama.1994.1008 |
| [] | Fehlinger T, Freeden W, Mayer C, et al. 2008. On the local multiscale determination of the Earth's disturbing potential from discrete deflections of the vertical[J]. Computational Geosciences, 12(4): 473–490. DOI:10.1007/s10596-008-9086-x |
| [] | Fengler M J, Freeden W, Gutting M. 2005. Multiscale modeling from EIGEN-1S, EIGEN-2, EIGEN-GRACE01S, UCPH2002_0.5, EGM96[A].//Reigber C, Lühr H, Schwintzer P, et al. Earth Observation with CHAMP[M]. Berlin Heidelberg:Springer, 145-150. |
| [] | Freeden W. 1999. Multiscale Modelling of Spaceborne Geodata[M]. Leipzig, Stuttgart: Teubner. |
| [] | Freeden W. 1980. On integral formulas of the (unit) sphere and their application to numerical computation of integrals[J]. Computing, 25(2): 131–146. DOI:10.1007/BF02259639 |
| [] | Freeden W, Fehlinger T, Klug M, et al. 2009. Classical globally reflected gravity field determination in modern locally oriented multiscale framework[J]. Journal of Geodesy, 83(12): 1171–1191. DOI:10.1007/s00190-009-0335-0 |
| [] | Freeden W, Glockner O, Schreiner M. 1998. Spherical panel clustering and its numerical aspects[J]. Journal of Geodesy, 72(10): 586–599. DOI:10.1007/s001900050197 |
| [] | Freeden W, Mayer C. 2003. Wavelets generated by layer potentials[J]. Applied and Computational Harmonic Analysis, 14(3): 195–237. DOI:10.1016/S1063-5203(03)00003-4 |
| [] | Freeden W, Schreiner M. 2006. Local multiscale modelling of geoid undulations from deflections of the vertical[J]. Journal of Geodesy, 79(10-11): 641–651. DOI:10.1007/s00190-005-0017-5 |
| [] | Freeden W, Windheuser U. 1996. Spherical wavelet transform and its discretization[J]. Advances in Computational Mathematics, 5(1): 51–94. DOI:10.1007/BF02124735 |
| [] | Koch K R, Kusche J. 2002. Regularization of geopotential determination from satellite data by variance components[J]. Journal of Geodesy, 76(5): 259–268. DOI:10.1007/s00190-002-0245-x |
| [] | Mayer C. 2003. Wavelet modelling of ionospheric currents and induced magnetic fields from satellite data[Ph. D. thesis]. Kaiserslautern:University of Kaiserslautern. |
| [] | Ning J S, Wang H H, Luo Z C. 2004. Applications of wavelet analysis in geodesy and its progress[J]. Geomatics and Information Science of Wuhan University (in Chinese), 29(8): 659–663. |
| [] | Nutz H, Wolf K. 2008. Time-space multiscale analysis by use of tensor product wavelets and its application to hydrology and GRACE data[J]. Studia Geophysica et Geodaetica, 52(3): 321–339. DOI:10.1007/s11200-008-0024-0 |
| [] | Panet I, Kuroishi Y, Holschneider M. 2011. Wavelet modelling of the gravity field by domain decomposition methods:an example over Japan[J]. Geophysical Journal International, 184(1): 203–219. DOI:10.1111/gji.2010.184.issue-1 |
| [] | Peidou A C, Vergos G S. 2015. Wavelet multi-resolution analysis of recent GOCE/GRACE GGMs[C].//Jin S, Barzaghi R. IGFS 2014. International Association of Geodesy Symposia. Cham:Springer. |
| [] | Roland M, Denker H. 2005. Stokes integration versus wavelet techniques for regional geoid modelling[C].//Sansò F. A Window on the Future of Geodesy. International Association of Geodesy Symposia. Berlin Heidelberg:Springer, 368-373. |
| [] | Schmidt M, Fengler M, Mayer-Gürr T, et al. 2007. Regional gravity modeling in terms of spherical base functions[J]. Journal of Geodesy, 81(1): 17–38. |
| [] | Schmidt M, Fabert O, Shum C K. 2005a. On the estimation of a multi-resolution representation of the gravity field based on spherical harmonics and wavelets[J]. Journal of Geodynamics, 39(5): 512–526. DOI:10.1016/j.jog.2005.04.007 |
| [] | Schmidt M, Fabert O, Shum C K. 2005b. Towards the estimation of a multi-resolution representation of the gravity field based on spherical wavelets[C].//Sansò F. A Window on the Future of Geodesy. International Association of Geodesy Symposia. Berlin Heidelberg:Springer, 362-367. |
| [] | Schmidt M, Fabert O, Shum C K, et al. 2004. Gravity field determination using multiresolution techniques[C].//Proceedings of the 2nd International GOCE User Workshop. Frascati:ESA-ESRIN. |
| [] | Schmidt M, Han S C, Kusche J, et al. 2006. Regional high-resolution spatiotemporal gravity modeling from GRACE data using spherical wavelets[J]. Geophysical Research Letters, 33(8). DOI:10.1029/2005GL025509 |
| [] | Schmidt M, Kusche J, van Loon J P, et al. 2005c. Multiresolution representation of a regional geoid from satellite and terrestrial gravity data[C].//Jekeli C, Bastos L, Fernandes J. Gravity, Geoid and Space Missions. International Association of Geodesy Symposia. Berlin Heidelberg:Springer, 167-172. |
| [] | Schmidt M, Martínez W, Florez J. 2002. General scheme for the computation of regional geoid undulations using spherical wavelets[C].//Drewes H, Dodson A H, Fortes L P S, et al. Vertical Reference Systems. International Association of Geodesy Symposia. Berlin Heidelberg:Springer, 209-214. |
| [] | Schreiner M. 1999. A pyramid scheme for spherical wavelets[R]. AGTM Report No. 170. Kaiserslautern:Technische Universität Kaiserslautern. |
| [] | Wang H H. 2005. Research on applications of wavelet multiscale analysis in the earth's gravity field (in Chinese)[Ph. D. thesis]. Wuhan:Wuhan University. |
| [] | 宁津生, 汪海洪, 罗志才. 2004. 小波分析在大地测量中的应用及其进展[J]. 武汉大学学报·信息科学版, 29(8): 659–663. |
| [] | 汪海洪. 2005. 小波多尺度分析在地球重力场中的应用研究[博士论文]. 武汉: 武汉大学. http://cdmd.cnki.com.cn/Article/CDMD-10486-2006031340.htm |
 2017, Vol. 32
2017, Vol. 32


