2. 中国地质大学(北京), 信息工程学院, 北京 100083
3. 中南大学 地球科学与信息物理学院, 长沙 410083
2. School of Information Engineering, University of Geosciences (Beijing), Beijing 100083, China
3. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China
电法和电磁法是应用地球物理学科最为活跃的分支之一(Zhdanov, 2010).主动源电法及电磁法已形成频率域和时间域两大技术体系(Zhdanov, 2009; Kaufman et al., 2014),在大深度金属矿及油气勘查中得到广泛应用(Edwards, 2005; 滕吉文,2006;Ziolkowski et al., 2006, 2007; Constable and Srnka., 2007; Ziolkowski, 2009;何继善,2010;Zhdanov, 2015).在激发波形选择方面,频率域可控源电磁法供电波形多采用占空比为100%的双极性方波,时间域可控源电磁法多采用占空比为50%的双极性方波.采用方波易实现大功率发送,但工作效率及抗干扰能力较低.为了提高频率域电法及电磁法勘查效率,提高观测精度及深部信息的分辨率,地球物理学家们在主动源激励波形选择上进行了卓有成效的探索.中国工程院院士、中南大学教授何继善先生提出的2n系列伪随机组合波,通过编码组合,形成包含多个主频率波形,勘查效率比方波谐波法大大提高,形成了2n系列伪随机激电法及广域电磁法(何继善,2010).之前,Duncan等尝试了基于伪随机二进制序列(PRBS)为信号源的宽频带电磁测深法,表明采用编码源信号波形,实现小能量激发获得较大探测深度的技术路线是可行的(Duncan et al., 1980).后来,Anton Ziolkowski等基于PRBS编码源开发了多道瞬变电磁法(multitransient electro-magnetic,MTEM),对大深度的油气薄层有较高的分辨力,已在陆地和海洋油气勘查中商业化应用.与何继善院士所提2n系列伪随机电磁法不同,基于PRBS编码源电磁法通过同步采集输入电流信号及大地电磁响应输出信号,解卷积获得地电系统的冲激响应,由冲激响应峰值时刻计算视电阻率等电磁解释参数(Ziolkowski et al., 2006, 2007; Ziolkowski, 2009).
近几年国内也涌现出对于PRBS编码源电磁法的研究热情.赵璧如等介绍了基于CDMA技术的地电阻率高精度测量方法(赵璧如等,2006);汤井田和罗维斌提出了基于逆重复M序列伪随机电磁勘探方法原理(汤井田和罗维斌,2008;罗维斌等,2012);李梅等基于PRBS编码源提出了基于相关辨识的谱激电法(Li,2013);淳少恒等综述了编码源电磁法的若干进展(淳少恒等,2014).基于PRBS编码源电法和电磁法方法原理及观测系统研究取得进展并开展方法试验(罗先中等,2014;张建国等,2014;罗延钟等,2015).目前国内基于最长线性反馈m序列(PRBS)信号源的电法主要思想还是跟踪MTEM的观测原理,先获取待探测大地系统的冲激响应,由冲激响应得到阶跃响应和频率响应,进而计算视电阻率,频散率或相位等电磁反演解释参数.
本文在此基础上提出了一种直接获取待探测大地系统频率响应的方法,并应用于谱激电法.基于循环互相关法利用输入、输出时间序列恢复出待探测大地系统频率响应,在收发同步采样条件下,可高精度获得大地的幅度谱和相位谱;在收发不同步采样条件下,也可高精度获得大地的频率响应幅度谱,且有很高的频率分辨率和较强的抗干扰能力.在白银矿区应用本文所提方案开展实验,得到了较好的勘查效果.
1 理论和方法采用PRBS或逆重复M序列为激励信号波形,利用互相关法辨识待辨识系统的频率响应是一种应用广泛的系统辨识方法(Roinila et al., 2009; 高晋占,2011;刘金琨等,2013;刘立超等,2014;夏正武,2014;Tangirala, 2014).由互相关法系统辨识理论,系统输入、输出的互相关,与系统输入信号自相关有关系式为

|
(1) |
式中,hs(τ)是观测系统的冲激响应,he(τ)是待辨识系统的冲激响应,Ru(τ)是输入信号的自相关,Ryu(τ)系统输入与输出信号的互相关.在复数域有:

|
(2) |
式中Syu(s)和Su(s)分别是互相关Ryu(τ)和自相关Ru(τ)的拉普拉斯变换,Hs(s)和He(s)分别是观测系统自身冲激响应函数hs(τ)和待辨识大地系统冲激响应函数he(τ)的拉普拉斯变换.将拉氏变量s用jω代换,则待辨识大地系统的频率传递函数为
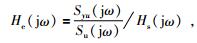
|
(3) |
由式(3) 可获得大地(或其他待辨识系统)的频率特性.观测系统本身的频率响应传递函数Hs(jω)也能够应用本文提出的方法辨识出,将其校正为1,所以式(3) 变为
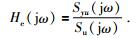
|
(4) |
本文提出的基于循环互相关法辨识频率响应的方法,是在式(4) 的计算中引入了一个参考信号SS,设置产生PRBS或逆重复M序列的寄存器位数N及固定反馈位后,产生的序列模态是固定的;不同的寄存器初始状态产生延时不同的时间序列,但具有相同的频谱分布.选取时钟频率Fc,采样率fs,软件生成与激发波形码长相同的整数周期的PRBS或逆重复M序列时间序列作为参考信号SS.用这个参考信号SS,分别与系统输入信号u(t)(信号产生参数与SS相同),系统输出信号yout(t)做循环互相关(处理时将输入、输出时间序列截取为激发序列周期的整数倍),由循环互相关时间序列的FFT变换得到互功率谱,由式(9) 和(10) 恢复出系统的频率响应.公式为

|
(5) |

|
(6) |

|
(7) |

|
(8) |

|
(9) |

|
(10) |
式中,cxcorr表示循环互相关运算,FFT为快速傅立叶变换,mod是模运算符.u(t)为系统输入信号时间序列(包含噪声V1(t)),yout为系统输出信号时间序列(包含噪声V2(t)),SS为软件产生的参考信号,PCys(ω)为参考信号SS与输出信号yout的互谱,PCus(ω)为参考信号SS与输入信号u(t)的互谱,φ(ω)为相位.这样处理,即使输入、输出两端都存在工频噪声,也有极强抗干扰能力.
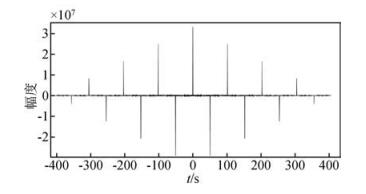
1.1 循环互相关法对于两个时间序列的互相关计算,采用非循环互相关法计算时,在序列移位过程中需要在序列头部和尾部补零,使参与计算的两个序列长度相等,计算结果中在相关脉冲峰两侧就会产生不需要的干扰信号,采用多周期信号计算可以压制相关脉冲峰两侧的干扰,但干扰仍然会存在.图 1是4个周期的逆重复M序列非循环自相关计算结果.相关峰两侧的干扰比单周期自相关减小很多,但仍有一定幅度.且相关峰幅度随时间延迟增大而衰减.
|
图 1 4个周期逆重复M序列非循环自相关时间序列 Figure 1 Non-circular autocorrelation time series of 4 periods of inverse repeated M sequences |
采用循环互相关法可以有效压制相关峰两侧的干扰.循环互相关法在计算时,将每个时间序列首尾环状相连,这样在计算中序列循环移位,无需补零(Roinila et al., 2009).图 2是4个周期的逆重复M序列循环自相关计算结果.相关峰两侧的干扰平稳很多,且相关峰幅度是等幅的.这个特性在多周期信号功率谱叠加中有优势.

|
图 2 4个周期逆重复M序列循环自相关时间序列 Figure 2 Circular autocorrelation time series of 4 periods of inverse repeated M sequences |
多次仿真计算证实,序列产生参数选择对辨识精度有直接影响,对于基于系统辨识的地球物理实用观测系统,移位时钟频率Fc、寄存器位数N以及采样率fs等参数应可选择.对于不同地电条件的勘查区,应通过实验选择产生信号参数.下面,用仿真计算方法研究叠加周期数和采样率对辨识结果的影响.
用式(11) 给定一个已知系统,式中s为拉普拉斯变量,s=iω.固定采样率fs为200 Hz,逆重复M序列产生参数寄存器位数N为7,移位寄存器时钟频率Fc为4 Hz,激励式(11) 仿真模型.在输入和输出端均加了工频干扰,从低频0.007874~2.905512 Hz,统计了150个频点辨识得到的频率响应与理论模型频率响应幅度的均方相对误差,如表 1统计结果,随采样叠加周期数增加,均方相对误差变小,叠加30个周期均方相对误差减小量已达到叠加50个周期均方相对误差改善的94%.公式(11) 为

|
(11) |
|
|
表 1 均方误差随叠加周期数变化表 Table 1 Mean square error with superposition period number |
固定采样叠加周期数为30个周期,在输入和输出端均加工频干扰,从低频0.007874~2.905512 Hz,统计了150个频点辨识得到的频率响应与理论模型频率响应幅度的均方相对误差.如表 2统计结果,随采样率增加,均方相对误差变小,采样率为128 Hz时均方相对误差减小量已达到采样率为512 Hz时均方相对误差改善的86.4%.
|
|
表 2 均方误差随采样率变化表 Table 2 Mean square error with sampling rate change |
由以上计算表明,在有干扰条件下,基于循环相关法相关辨识的频率响应获取方法中,时间序列采样率和叠加周期对于辨识结果有很大影响.在低频激电法测量中,视干扰情况,采样率设为200~500 Hz,叠加周期数30个周期为宜.
获取的频率响应频率分辨率很高.在以上所述条件下,在1e-3 Hz以下获取了1个频点,在1e-2~1e-1 Hz间获取了5个频点,在1e-1~1 Hz间获取了57个频点,在1~2 Hz间获取了48个频点,在2~3 Hz间获取了44个频点(图 3),由于激发时钟频率为4 Hz,获取的频率响应频带较低,要获得系统的高频带响应,用一个较高时钟频率激发就可获得,如移位寄存器时钟频率Fc选用2540 Hz,可获得高频段频率响应,这里不再详述.

|
图 3 基于循环相关法辨识的幅度谱 Figure 3 Retrieved amplitude spectrum based on circular correlation method |
甘肃省白银厂铜多金属矿是我国“一五”期间建成的156个重点建设项目之一,也是我国最早建成的大型铜硫生产基地、重要的有色金属生产基地之一.现在面临资源枯竭.近几年在新一轮找矿勘查中,在折腰山、火焰山矿床和小铁山矿床之间的结合部四方山矿区,实施深部钻探揭露,其中在四方山ZK0-1、ZK4-2在500 m深度以下分别见到块状铜、铅锌矿体,找矿效果显著.ZK0-1孔在661.5~678.5 m见铜铅锌多金属硫化物块状矿,穿矿厚度17 m,在927.1~937.1 m见浸染状铅锌矿,穿矿厚度10 m;ZK4-2孔在915~1067 m井段见7层矿,累积厚度65 m.
我们在四方山ZK0-1东侧约95 m处布置频率域激电法实验剖面.仪器选用湖南强军科技有限公司研制的频率域激电仪.剖面长2000 m,点距20 m,用了25个4通道接收机首尾相连,一次布置100个并行测量通道.从测线中间开始供电.AB/2最小10 m,最大为2600 m,共设34个供电极距.每次供电,100个并行测量通道同时测量,并同时采集发送电流信号.见矿孔四方山ZK0-1和四方山ZK4-2与测线相对位置见图 4.图中‘四’字为四方山地名的简称.

|
图 4 实验剖面与钻孔ZK0-1相对位置(红色+为供电点,蓝色★为接收点) Figure 4 The relative position of profile and borehole Si-ZK0-1 (red+are current electrodes and blue ★ are the receiving electrodes) |
从34个供电电极距测量数据中,选择最大AB=5200 m供电时采集的电流时间序列(电流强度8 A),及100个接收道同时采集的Ex时间序列,应用本文提出的处理方法截取54个周期数据进行处理.
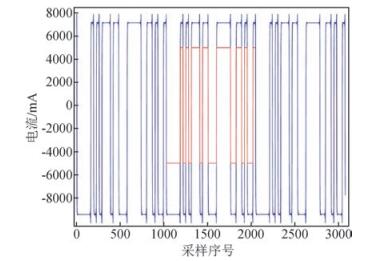
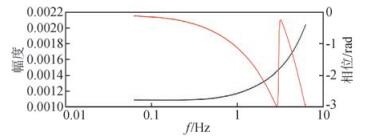
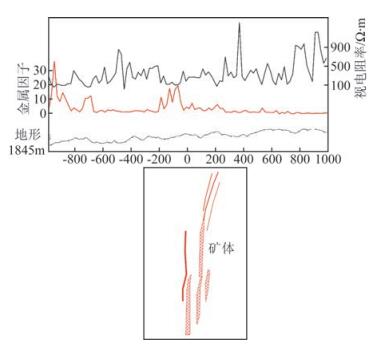
为验证算法,从采集的电流时间序列中恢复出发送激励波形(图 5),将其扩展为p=54个整数周期的时间序列(与输入、输出时间序列长度相同)作为参考信号SS.结果在0.0625~6.4375 Hz间获得了100个频率的系统响应,幅度谱和相位谱曲线光滑(图 6).在测线中部-120~240点间获得了明显的视电阻率(0.0625 Hz)、相对相位(0.0625 Hz,0.125 Hz)和金属因子MF(0.0625 Hz,0.125 Hz)异常(图 7,图中中间2条虚线对应深部矿体位置),而钻孔揭露矿体分布在-80~210点间,小号点矿体埋深1000多米,大号点埋深300多米,向南西向陡倾斜,如图 8剖面曲线与钻孔揭露矿体产出简图可以看出,金属因子异常明显.在-70号点,视电阻率为101 Ω·m,相对相位约为233 mrad,金属因子为19,与钻孔揭露深部矿体位置有很好对应.幅度谱随频率增大说明测量中存在激电效应和较强的电磁感应耦合.
|
图 5 发送电流波形(蓝)及恢复的1个周期参考信号(红) Figure 5 Transmission current waveform (blue) and recovered one cycle reference signal (red) |
|
图 6 在810点获得的幅度谱(黑)和相位谱(红) Figure 6 Retrieved amplitude spectra (black) and phase spectra(red) at 810 points |

|
图 7 供电极距AB=5200 m剖面曲线,(上)金属因素,(中)相对相位,(下)视电阻率 Figure 7 Profile curve of current dipole AB=5200 m, apparent resistivity(top), the relative phase(middle), metal factors (bottom) |
|
图 8 金属因子及视电阻率剖面曲线与矿体产出简图 Figure 8 The metal factor and apparent resistivity profile curve and orebody diagram |
实验选用m序列(PRBS)为供电波形.选择线性反馈移位寄存器位N=5,将产生的31位PRBS序列补1位,变成32位,存储为激励波形.选择驱动时钟频率,使32位序列周期为16 s.选择采样率,每1个序列位采32个样,一个周期的输入和输出时间序列长度为1024位.
在频率域,金属因子MF定义为

|
(12) |
式中ρL是低频视电阻率,ρH是低频视电阻率.
选择干扰较大的-70号和干扰较小的810号点做误差统计.将采集的输入电流信号和电场响应输出信号,分别截取20、30、40和54个整周期,将数据按不同延时分为两组,统计低频段50个频率的幅度和相位均方相对误差.按本文所提方案进行带参考循环互相关处理,与输入、输出直接循环互相关法处理结果进行比较.从表 4误差统计表可以看出:有参考处理结果的幅度和相位均方误差小于无参考直接互相关法处理结果,说明加参考信号有助于提高获取系统频率响应的精度;幅度和相位均方相对误差均随周期数增加而减小,获取的谱线随周期数增加,频率越低,频带越宽.说明在干扰较大时,增加叠加次数,延长采样时间是提高数据精度的切实有效措施.
|
|
表 3 误差统计表 Table 3 Error statistics |
仿真计算和矿区实验结果表明:基于编码源信号激励,循环互相关法辨识地电系统频率响应有良好的应用前景,且有较好的抗干扰能力,较高的采样率和叠加次数可显著提高测量精度.
在信号处理中引入参考信号可提高辨识结果精度,计算还表明:在收、发同步采样条件下,可高精度辨识出待辨识系统的频率响应;在收、发不同步采样条件下,可高精度辨识出待辨识系统的频率响应的幅度谱.
勘查实例中采用编码源波形激发,中间梯度装置,AB供电极距5200 m,接收极距MN=20 m,供电电流8 A条件下,获得了可靠的剖面异常.通过对实测资料的处理,统计频率响应幅度和相位的均方相对误差,结果表明:加参考信号有助于提高频率响应的辨识精度,在干扰严重条件下结果尤为明显,增加采样周期是提高抗干扰能力、获取高精度观测结果的切实有效措施.观测时间越长,获得的结果精度越高.
实验中在强干扰情况下,进行了质量控制,多周期测量叠加后满足精度要求才停止测量.但设计采样率稍低,如提高采样率,测量结果会更好.
5 结论 5.1基于系统辨识原理,将采集的系统输入、输出信号时间序列分别与参考信号应用基于快速傅立叶变换(FFT)的循环互相关法处理,得到输出与参考信号互相关时间序列和输入与参考信号互相关时间序列,运用快速傅立叶变换(FFT)计算互相关时间序列的互功率谱,分别获取输出信号与参考信号的互谱的谱线峰值及对应频率,及输入信号与参考信号的互谱的谱线峰值及对应频率,筛选出频率相同的谱线峰值对应相除,可恢复出待辨识系统的频率响应.由观测电场响应和输入电流信号辨识得到的地电系统频率响应,反映待探测大地系统的阻抗信息,可直接用于反演解释,也可反算出系统的传递函数,并进而获得系统的阶跃响应及冲激响应,可得到地球物理解释所需要的复电阻率、阻抗、频散率、金属因子及Cole-Cole模型参数.
5.2在观测场分量方面,可接收电场、垂直磁场分量,根据地电条件合理选择;可提取频率域或时间域地球物理电磁解释参数.这种观测方法有很高的频率分辨率,运用于激电或电磁测深,有助于对大深度高阻薄层的探测.
致谢 研究工作得到国家自然基金项目:相关辨识技术在谱激电中的应用研究(41374185) 的资助.实测数据采集运用了中南大学陈儒军博士研发的观测系统,论文工作还得到中南大学肖建平博士的支持,在此表示衷心感谢.对论文评阅人对本文提出的中肯意见一并表示衷心感谢!| [] | Chun S H, Chen R J, Geng M H. 2014. Review of the pseudo-random m sequence and its application in electrical prospecting of exploration geophysics[J]. Progress in Geophysics , 29(1): 439–446. DOI:10.6038/pg20140164 |
| [] | Constable S, Srnka L J. 2007. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration[J]. Geophysics, 72(2): WA3–WA12. DOI:10.1190/1.2432483 |
| [] | Di Paolo Emilio M. 2013. Data Acquisition Systems: From Fundamentals to Applied Design[M]. New York: Springer-Verlag. |
| [] | Duncan P M, Hwang A, Edwards R N, et al. 1980. The development and applications of a wide band electromagnetic sounding system using a pseudo-noise source[J]. Geophysics, 45(8): 1276–1296. DOI:10.1190/1.1441124 |
| [] | Edwards N. 2005. Marine controlled source electromagnetics: Principles, methodologies, future commercial applications[J]. Surveys in Geophysics, 26(6): 675–700. DOI:10.1007/s10712-005-1830-3 |
| [] | Gao J Z. 2011. Detection of Weak Signals [M]. 2nd ed. Beijing: Tsinghua University Press. |
| [] | He J S. 2010. Wide Band Electromagnetic Method and Pseudo Random Signal Electrical Method [M]. Beijing: Higher Education Press. |
| [] | Kaufman A A, Alekseev D, Oristaglio M. 2014. Principles of Electromagnetic Methods in Surface Geophysics[M]. Amsterdam: Elsevier. |
| [] | Li M, Wei W B, Luo W B, et al. 2013. Time-domain spectral induced polarization based on pseudo-random sequence[J]. Pure and Applied Geophysics, 170(12): 2257–2262. DOI:10.1007/s00024-012-0624-z |
| [] | Liu J K, Shen X R, Zhao L. 2013. Theory of System Identification and Simulation with MATLAB [M]. Beijing: Publishing House of Electronics Industry. |
| [] | Liu L C, Ding K L, Lin J, et al. 2014. Instrument calibration with electromagnetic method based on pseudorandom system identification[J]. Chinese Journal of Scientific Instrument , 35(8): 1721–1728. |
| [] | Luo W B. 2007. Study on pseudorandom marine controlled-source electromagnetic sounding with multi-offsets (in Chinese)[Ph. D. thesis]. Changsha: Central South University. |
| [] | Luo W B, Li Q C, Tang J T. 2012. Coded source electromagnetic sounding method[J]. Chinese J. Geophys. , 55(1): 341–349. DOI:10.6038/j.issn.0001-5733.2012.01.035 |
| [] | Luo X Z, Li D W, Peng F P, et al. 2014. Implementation and applications of an coded electrical instrument with anti-interference ability[J]. Progress in Geophysics , 29(2): 944–951. DOI:10.6038/pg20140263 |
| [] | Luo Y Z, Lu Z G, Sun G L, et al. 2015. New generation of instruments for electrical and electromagnetic prospecting-instruments using pseudo random signal[J]. Progress in Geophysics , 30(1): 411–415. DOI:10.6038/pg20150159 |
| [] | Roinila T, Helin T, Vilkko M, et al. 2009. Circular correlation based identification of switching power converter with uncertainty analysis using fuzzy density approach[J]. Simulation Modelling Practice and Theory, 17(6): 1043–1058. DOI:10.1016/j.simpat.2009.03.006 |
| [] | Tang J T, Luo W B. 2008. Pseudo-random electromagnetic exploration based on invert-repeated m-sequence correlation identification[J]. Chinese J. Geophys. , 51(4): 1226–1233. DOI:10.3321/j.issn:0001-5733.2008.04.034 |
| [] | Tangirala A K. 2014. Principles of System Identification: Theory and Practice[M]. Boca Raton: CRC Press. |
| [] | Teng J W. 2006. Where is the contemporary geophysics of China going[J]. Progress in Geophysics , 21(2): 327–339. DOI:10.3969/j.issn.1004-2903.2006.02.001 |
| [] | Trauth M H. 2015. MATLAB® Recipes for Earth Sciences[M]. 4th ed. Berlin Heidelberg: Springer. |
| [] | Xia Z W, Liu G Q, Li S Q, et al. 2014. A controlled source frequency domain electromagnetic sounding system with automatic synchronization[J]. Progress in Geophysics , 29(2): 952–957. DOI:10.6038/pg20140264 |
| [] | Zhang J G, Wu X, Qi Y Z, et al. 2014. Investigation on time domain coded electromagnetic exploration method[J]. Journal of Radars , 3(2): 158–165. |
| [] | Zhang Y, Wang L W, Zhang X G, et al. 2014. Application of correlation detection technology in low-frequency AC geo-resistivity observation[J]. Progress in Geophysics , 29(4): 1973–1979. DOI:10.6038/pg20140468 |
| [] | Zhao B R, Zhao J, Zhang H K, et al. 2006. The PS100 high precision earth-electrictity instrument system (IP to IP) with controllable source-application of CDMA technology to the measurement of earth-resistivity for the first time[J]. Progress in Geophysics , 21(2): 675–682. DOI:10.3969/j.issn.1004-2903.2006.02.053 |
| [] | Zhdanov M S. 2009. Geophysical Electromagnetic Theory and Methods[M]. Amsterdam: Elsevier. |
| [] | Zhdanov M S. 2010. Electromagnetic geophysics: Notes from the past and the road ahead[J]. Geophysics, 75(5): 75A. |
| [] | Zhdanov M S. 2015. Inverse Theory and Applications in Geophysics[M]. 2nd ed. Amsterdam: Elsevier. |
| [] | Ziolkowski A, Hobbs B, Dawes G, et al. 2006. True amplitude transient electromagnetic system response measurement: WO, 2006114561 A2[P]. 2006-11-02. |
| [] | Ziolkowski A, Hobbs B, Wright D. 2007. Multitransient electromagnetic demonstration survey in France[J]. Geophysics, 72(4): F197–F207. DOI:10.1190/1.2735802 |
| [] | Ziolkowski A. 2009. Optimisation of MTEM parameters: US, 20090230970 A1[P]. 2009-09-17. |
| [] | 淳少恒, 陈儒军, 耿明会. 2014. 伪随机m序列及其在电法勘探中的应用进展[J].地球物理学进展, 29(1): 439–446. DOI:10.6038/pg20140164 |
| [] | 高晋占. 2011. 微弱信号检测[M]. 2版.北京: 清华大学出版社. |
| [] | 何继善. 2010. 广域电磁法和伪随机信号电法[M]. 北京: 高等教育出版社. |
| [] | 刘金琨, 沈晓蓉, 赵龙. 2013. 系统辨识理论及MATLAB仿真[M]. 北京: 电子工业出版社. |
| [] | 刘立超, 丁凯来, 林君, 等. 2014. 基于伪随机系统辨识的电磁法仪器标定[J].仪器仪表学报, 35(8): 1721–1728. |
| [] | 罗维斌. 2007. 伪随机海洋可控源多道电磁测深法研究[D]. 长沙: 中南大学. |
| [] | 罗维斌, 李庆春, 汤井田. 2012. 编码电磁测深[J].地球物理学报, 55(1): 341–349. DOI:10.6038/j.issn.0001-5733.2012.01.035 |
| [] | 罗先中, 李达为, 彭芳苹, 等. 2014. 抗干扰编码电法仪的实现及应用[J].地球物理学进展, 29(2): 944–951. DOI:10.6038/pg20140263 |
| [] | 罗延钟, 陆占国, 孙国良, 等. 2015. 新一代电法勘查仪器-伪随机信号电法仪[J].地球物理学进展, 30(1): 411–415. DOI:10.6038/pg20150159 |
| [] | 汤井田, 罗维斌. 2008. 基于相关辨识的逆重复m序列伪随机电磁法[J].地球物理学报, 51(4): 1226–1233. DOI:10.3321/j.issn:0001-5733.2008.04.034 |
| [] | 夏正武, 刘国强, 李士强, 等. 2014. 一种自动同步的可控源频率域电磁探测系统[J].地球物理学进展, 29(2): 952–957. DOI:10.6038/pg20140264 |
| [] | 张建国, 武欣, 齐有政, 等. 2014. 时间域编码电磁勘探方法研究[J].雷达学报, 3(2): 158–165. |
| [] | 张宇, 王兰炜, 张兴国, 等. 2014. 相关检测技术在低频交流地电阻率观测中的应用[J].地球物理学进展, 29(4): 1973–1979. DOI:10.6038/pg20140468 |
| [] | 赵璧如, 赵健, 张洪魁, 等. 2006. PS100型IP到端可控源高精度大地电测仪系统-CDMA技术首次在地电阻率测量中的应用[J].地球物理学进展, 21(2): 675–682. DOI:10.3969/j.issn.1004-2903.2006.02.053 |
| [] | 滕吉文. 2006. 当代中国地球物理学向何处去[J].地球物理学进展, 21(2): 327–339. DOI:10.3969/j.issn.1004-2903.2006.02.001 |
 2017, Vol. 32
2017, Vol. 32





