复杂地表具有地表起伏剧烈、近地表速度低和速度变化范围大等特征,为保证数值计算模拟的精度,利用波动方程有限差分计算时若采用均匀网格有限差分法,则在低速介质区域网格步长必须取得比较小,空间网格步长的选取必须要满足采样定理,小于半个最小波长,最小波长与模型中最小速度(低速层的速度)成正比,若在一个波长上的采样点数过少会产生数值频散现象.而网格空间小步长采样会造成对高速介质区域出现过采样问题,增加计算量和计算机内存的消耗,同时小步长均匀网格要求有较小的时间步长,计算时间会增加,高速层区域的稳定性条件约束着时间步长的选择.受限于空间步长与模型最大速度的比值,空间步长越小,或者模型速度分布范围越大,相应的时间步长也要变得更小才能满足稳定性条件,否则会引起数值计算的不稳定.
为了能够有效解决这一问题,国内外学者做了许多研究,比如在模拟声波的传播和起伏地表条件下弹性波的传播过程中采用网格纵向步长变换法(Jastram and Tessmer, 1994).但该方法只考虑了地下介质速度随深度增加而增大的情况,对于横向介质速度的变化并不能处理好,同时此方法对于在介质区域内存在局部的高速或低速介质时也不适用.后来学者提出相似的不规则网格的方法.采用变网格方法一个不可避免的问题就是在网格相邻区域网格结点的计算(Opršal and Zahradník, 1999; Pitarka, 1999; Wang et al., 2001).早期的研究对这一问题的解决方法主要是采用插值法进行处理,但插值法容易加强算法的不稳定性,同时在实际应用时不能够较好的选取到合适的步长,插值方法的选取也没有一个完整的理论分析依据.后来有学者从波动方程出发,利用高阶有限差分方法,通过改进高阶有限差分系数的求解方法,消除在步长变化处由于步长的不一致而产生的计算不稳定,同时相对的减少计算量.有学者曾利用高阶差分方法模拟地震波在复杂介质条件下的传播.他们采用变网格方法依然只是纵向空间步长变化的单向变网格方法,而且这种通过改进高阶差分系数的方法需要在每个计算结点确定差分格式中每个相邻结点的步长,同时,这种方法虽然在低速层可以减小网格步长,但不能避免下层高速介质层水平方向出现过采样,该方法同样的对于近地表起伏及速度横向变化的模型依然不能很好的处理(孙成禹等,2008;张慧和李振春,2011;孙成禹和丁玉才,2012).亦有学者采用自适应网格,利用小波函数的多尺度分解的特性模拟地震波的传播(裴正林,2005;宓铁良等,2009), 该方法通过判定在初始网格点处的小波系数与阈值之间的大小决定是否对网格细化,但是利用小波函数会产生较大的计算量,同时该方法中对于粗细网格相邻处依然使用的是插值法来处理.非规则网格有限差分法将是提高复杂地震波模拟精度的主要方法(王庆等,2015).
在地震波有限差分数值模拟中不可避免的会出现数值频散现象,究其原因是用有限差分法求解波动方程时,偏导数用泰勒级数展开得到,空间导数算子的计算精度和准确性不仅依赖于近似的阶数还取决于离散化网格间距的大小,即使在各向同性的介质中,波动方程的有限差分解也有数值相速度和群速度,它们不同于波在真实介质中传播的相速度和群速度,随着波的传播,波前形状会发生变化并逐渐扩散开导致波形失真,称为数值频散现象(Sun and Trueman, 2005).后来将通量校正传输法,应用到声波和弹性波有限差分数值模拟和逆时偏移中来消弱数值频散,但这种方法会使不需要校正的地方分辨率降低,同时还会增加一定的计算量(李文杰等,2011;周竹生,2012);对有限差分的差分系数和波动方程进行优化来压制数值频散,取得了良好的效果,然而压制数值频散的优化参数需要凭借经验才能选取合适的值,给数值计算带来了很大难度(Etgen, 2007; Liu et al., 2009).
通过上面的分析,当介质区域的速度变化范围较大时,在不同速度的介质区域采用不同的空间网格步长进行处理就显得比较合理.本文在早期学者研究的基础上,提出一种步长自适应的矩形网格生成法,在给定介质速度模型的条件下,随着速度的不同在网格划分时空间步长自动增加或减少,实现了对介质速度模型的精细化网格划分.利用有限差分在不均匀网格上模拟计算的一个关键问题就是网格过渡处的结点如何计算,本文从二元函数的泰勒展开式出发,结合相邻的几个结点,直接计算过渡处结点的拉普拉斯算子,通过分析求解得到一组相邻结点系数的计算公式,这些公式在四个方向上具有通用性,避免在相邻区域进行插值计算的同时,保持了算法的稳定性.对于频散现象,本文提出了一种新的方法,在使用有限差分法求解波动方程时,采用中值定理与有限差分法相结合构造新的离散化波动方程来处理数值频散问题,并经过推导给出了确切的频散校正参数值,我们称这种方法为抗频散有限差分法.
1 基本原理本文中的算法基于二阶声波方程,公式为
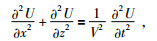
|
(1) |
其中U=U(x, z, t)为标量波场,V为介质速度.
1.1 自适应步长划分本文中对模型中不同速度区域自适应网格步长的划分是由模型中速度的分布范围决定.设模拟区域为Ω,区域中速度V∈(Vmin, Vmax),Vmin和Vmax分别为区域中介质速度的最小值和最大值,在模拟区域Ω中进行网格划分时,可以划分的网格类型有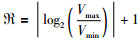
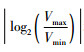
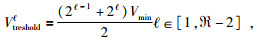
|
(2) |
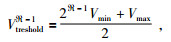
|
(3) |
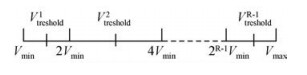
图 1为速度阈值的选取示意图.
|
图 1 速度阈值选取示意图 Figure 1 A schematic view of the speed threshold |
假设在Vtreshold1内的速度区域网格步长为Δh, 那么其他的速度阈值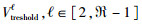
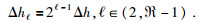
|
(4) |
各个速度区域步长的取值与速度阈值之间的对应关系为
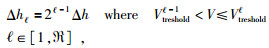
|
(5) |
其中在速度的分布范围内,取Δh时,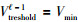
|
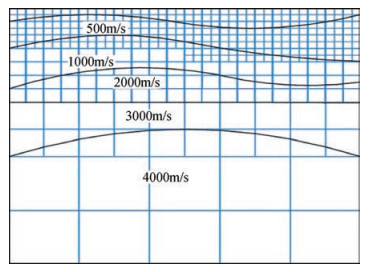
图 2 自适应网格划分示意图 Figure 2 Adaptive meshing schematic |
|
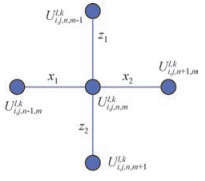
图 3 五点差分格式 Figure 3 Five point finite difference |
一般的用有限差分法计算波场的空间导数项时,在低波数区域的有限差分法可以近似的符合,在高波数区域会产生频散(朱生旺等,2007).为了在数值计算时能够尽可能地减少数值频散的产生,在空间网格步长的选取时应满足一定的条件.设地震波场的最大波数为kmax,它由子波的最高频率fmax和介质的最低速度Vmin决定,即:
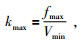
|
(6) |
设kα为可以忽略频散的最高波数,即有k < kα.一般的取kα=1/(2Δh)(朱生旺等,2007),若使得数值计算的结果不受频散的影响,则Δh的选择必须满足:kα>kmax,即:
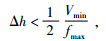
|
(7) |
上式(7) 就是细网格步长Δh在选取时应该满足的条件.同理,对于其他速度区域的介质,其最小速度就是速度阈值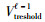
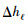
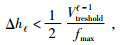
|
(8) |
因此在网格步长的选取时满足式(7) 和式(8) 即可.
假设在计算区域Ω中,各个空间步长对应的介质区域在Ω中所占比例为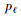
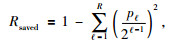
|
(9) |
如图 2所示的模型,三种不同步长网格所占比例分别是0.158、0.158、0.2、0.484,由(9) 式可以计算得到,利用自适应步长法可以节省的计算网格结点比例为96.27%.
同时,在利用有限差分法计算时,时间步长及空间步长的选择应该满足一定的稳定性条件.由Courant-Friedrichs-Lewy(CFL)条件有:
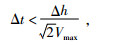
|
(10) |
由上(10) 式可以推知,利用自适应步长法在不同网格区域,计算时满足的稳定性条件为
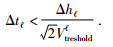
|
(11) |
将(2) 和(4) 式代入到(11) 式中,不同步长区域对应的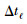

|
(12) |
由(12) 式可见,本文提出的自适应步长方法,对时间步长的要求降低,只要低速区域时间步长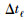
设计算区域中步长为ΔhR-1的网格结点有I×J个,波场可以表示为:Ui, jk,采用其他步长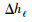
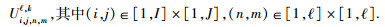
|
(1) 考虑到在低速层处的网格采用细网格步长进行划分,这种精细的划分在模拟中已然能够准确描述地质的特征,因此在细网格的内部结点处,采用五点有限差分格式.
步长为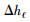
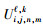
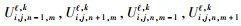
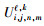
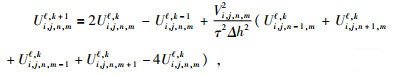
|
(13) |
(2) 对于在不同网格类型相邻处的结点波场值,其中细网格结点与其相邻的粗网格,在某一方向上会缺失其相应的一些细网格结点的波场值,这对计算这些结点造成困难.对于这种情形,本文利用二元函数的泰勒展开式,通过与计算结点相邻的几个结点在计算结点处的二元泰勒展开式的组合,构建一个方程组,由这个方程组直接求解在相邻处细网格结点波场值的拉普拉斯算子,然后使用时间二阶差分迭代计算相邻处结点在每一时刻的波场值,这种方法不需要求解那些缺失的结点波场值,通过方程的推导,这种方法在不同方向上的相邻结点处,其构成的方程组中的方程只是在方程的排列顺序和正负号上有着轻微的改变,对于相邻的结点,按照一定的顺序排列则与其相乘的系数的计算公式具有统一的形式.
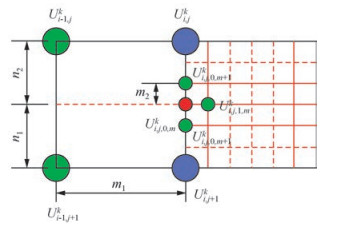
假设步长为Δh的细网格与其相邻的粗网格步长为ΔhR-1.以左边界处的相邻网格结点计算为例,设在一个细网格的左边是一个粗网格如图 4所示.
|
图 4 相邻网格左边界处 Figure 4 Left border of different grid step |
当前计算结点为边界结点Ui, j, 0, mk,若使用传统的方法求解则缺失Ui, j, 0, mk左边相邻结点的波场值,为此利用Ui, j, 0, mk周围的五个点求解,在左边界时用到的五个结点分别为:左下粗网格Ui-1, j+1k,下边细网格Ui, j, 0, m+1k,左上粗网格Ui-1, jk,上边细网格Ui, j, 0, m+1k,右边细网格Ui, j, 1, mk,各点的位置如图 4中所示.上述五个点在Ui, j, 0, mk处的二元泰勒展开式,舍去三阶及以上的高阶偏导数项有:
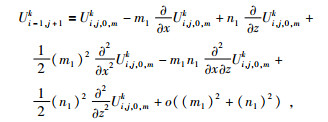
|
(14) |
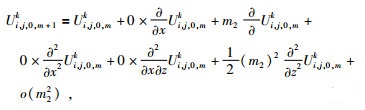
|
(15) |
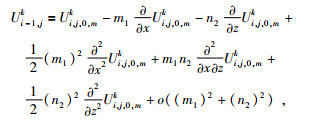
|
(16) |
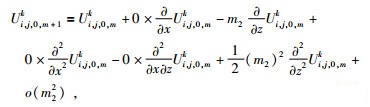
|
(17) |
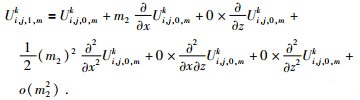
|
(18) |
公式(14) 至(18) 分别乘以系数ai(i=1, …5),使得它们满足公式为
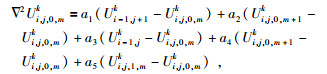
|
(19) |
将式(19) 写为方程组形式有:
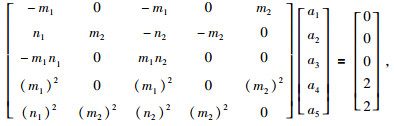
|
(20) |
解方程得各系数的计算公式为
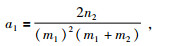
|
(21) |
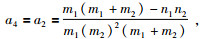
|
(22) |
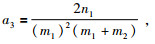
|
(23) |
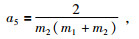
|
(24) |
然后在时间上采用二阶中心差分,则Ui, j, 0, mk的迭代计算公式为
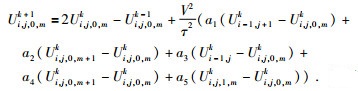
|
(25) |
其余三个方向上的边界结点计算式各结点的分布如图 5所示,图 5a至图 5c分别为右、上、下三个方向,相应的也可以得到这三个方向上系数的求解方程组,式(25) 至(27) 分别为右、上、下三个边界系数的方程组.公式为
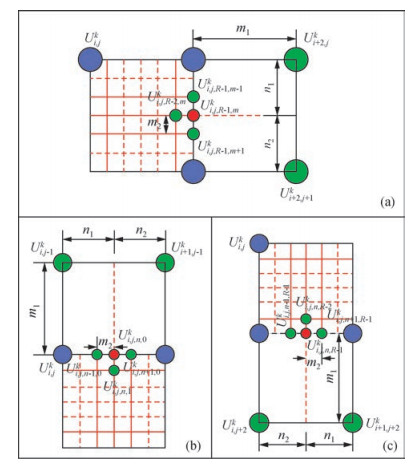
|
图 5 粗细网格右、上、下边界处 Figure 5 Right, top and bottom border of different grid step |
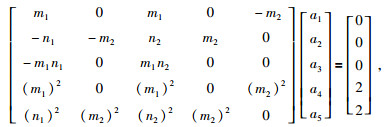
|
(26) |
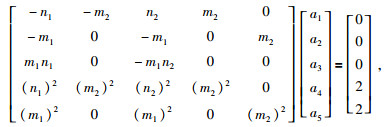
|
(27) |
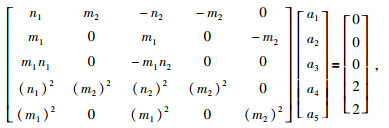
|
(28) |
(26) 和(20) 两个方程组的区别只是在于前两个方程的符号发生变化,但由于右边项为零,因此这两个方程组是相同的,和式(20) 相比较,式(27) 和(28) 是第一个和第二个方程的位置进行了调换,并且正负号发生变化,但是由于右边项为零,因此前两个方程实际并没有变化,仅仅改变了位置,同时方程位置改变的还有第四个和第五个方程,所以整体的上面的两个式子和式(20) 是相同的,因此它们求解系数ai(i=1, …5) 的计算公式不变.
(3) 对于网格过渡处的细网格四个角点,在差分计算时需要单独计算,对于角点处结点本文采用与计算细网格内部结点相同的差分格式,即式(12).但不同的是在计算每个角点时需要判断角点周围的网格类型,从而确定x1、x2、z1及z2的值.
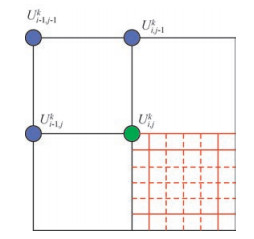
如图 6所示若要计算其左上角节点Ui, jk=Ui, j, 0, 0k处波场值则需要判断Ui-1, j-1k、Ui, j-1k以及Ui-1, jk点的速度所属区间.假设步长为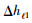
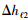
|
图 6 细网格角点示意图 Figure 6 Fine grid corner schematic diagram |
利用五点差分格式求解左上角点Ui, j, 0, 0k时,x2与z2为细网格步长,即x2=z2=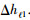
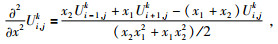
|
(29) |
同理,z方向上的二阶导数可表示为
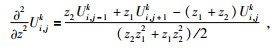
|
(30) |
最终一般的五点差分格式为
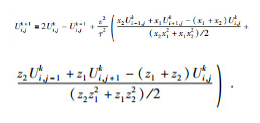
|
(31) |
在已知x2与z2的情况下,利用(31) 式进行计算需要得到x1与z1的值.而x1的取值需要通过判断Ui-1, j-1k、Ui-1, jk结点速度所属区间确定:
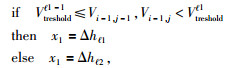
|
(32) |
而z1的值需要通过判断Ui-1, j-1k、Ui, j-1k结点的类型确定,其判断方法与x1的方法相似,如下:
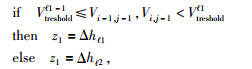
|
(33) |
假设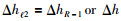
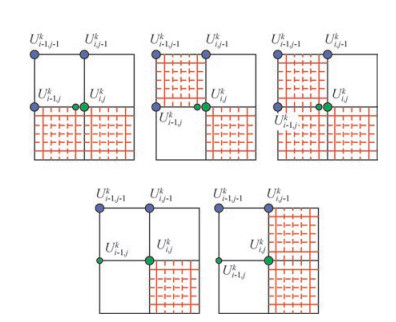
|
图 7 左边结点分布情形 Figure 7 The left node distribution |
式(33) 对应的z1取值的网格分布情况如图 8所示,图中绿色小圆圈表示左上角点Ui, j, 0, 0k在计算时用到的上边结点.
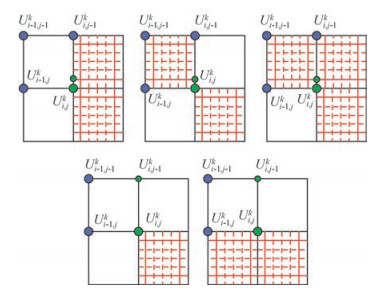
|
图 8 上边结点分布情形 Figure 8 The top node distribution |
(4) 对于步长为ΔhR网格结点,本文采用偶数阶精度的高阶有限差分格式,公式为
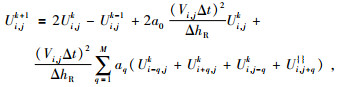
|
(34) |
其中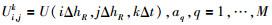
一般的在进行地表低速层进行模拟时,会产生比较严重的数值频散现象,这对地震波模拟的记录产生严重的干扰,为此如何在近地表模拟时很好的消除数值频散现象也是地震波数值模拟的一个重点.为本文利用中值定理的原理,提出一种能够很好的消除数值频散现象的有限差分格式.
首先来考虑下面这个初值问题,公式为
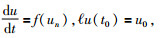
|
(35) |
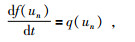
|
(36) |
现用显式欧拉方法将(34) 式和(35) 式在时间上用中值定理加权近似表示为
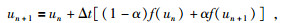
|
(37) |
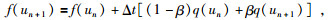
|
(38) |
式中Δt为时间步长,0 < α < 1,0 < β < 1分别为加权系数.将(37) 式代入(36) 式,经整理可得:
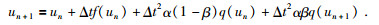
|
(39) |
对(38) 式中Δtf(un)和q(un+1)分别用Taylor展开法近似,公式为
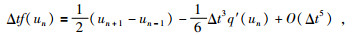
|
(40) |
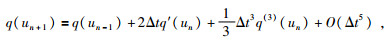
|
(41) |
将(39) 式和(40) 式分别带入到(38) 式中经整理忽略高阶导数项可得:
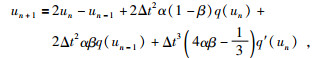
|
(42) |
现将q(un-1)运用中心差分法近似为
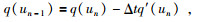
|
(43) |
将(42) 式带入到(41) 式中得:
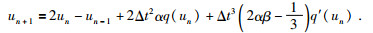
|
(44) |
假设u=u(x, y, z, t)表示波场,那么(43) 式中的q(un)= 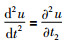
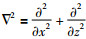
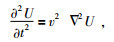
|
(45) |
对波场进行正演外推时,将(44) 式代入(43) 式中对时间做离散处理可得:
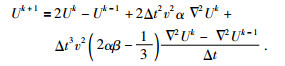
|
(46) |
现在令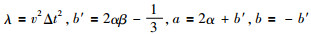
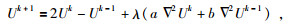
|
(47) |
数值频散主要是因相速度与群速度不一致造成的,那么当相速度和群速度近似相等时,数值频散就会明显地消弱,这样可以解出抗频散的优化校正参数,在空间二阶近似下:
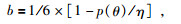
|
(48) |
其中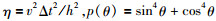
在波动方程的数值模拟中,一个关键的问题就是边界条件,因为在实际的地震波的传播是在地下无限区域中传播的,而在模拟计算时计算区域是有限的,这样就人为的增加了边界.这种人为增加的边界会产生边界反射波,干扰波场中的有效地震波信息,因此在对地震波进行数值模拟时需要消除这些人工边界反射波.
本文中采用二阶傍轴近似边界和衰减边界条件相结合的吸收边界条件(Liu and Sen, 2010),使用二阶傍轴近似能够吸收部分的边界反射,其余的反射能量通过衰减边界条件吸收,这样可以在增加少量计算量的同时很好的消除人工边界反射.
傍轴近似边界条件是在边界网格点处用单向波动方程代替原波动方程,从而达到边界吸收的效果.一般的,在某一传播方向上较小的范围内用单向波动方程可以正确的表示波在该方向上的吸收,而在其他方向上的波仍会被反射.实际上,由于对单向波动方程的有限差分离散化方法以及其误差项等,可能使得在这些边界网格点处计算的波场值是不正确的.而且,傍轴近似条件在边界处采用单向波动方程,使得边界与内部网格点由于采用的波动方程不同,引起比较尖锐的变化.为此本文通过将傍轴近似边界条件和衰减边界条件相结合,在边界与内部网格点之间增加一些过渡层,减小由于波动方程不同而引起的波场的变化.
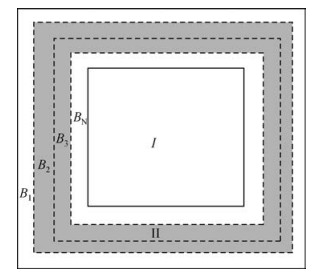
将扩充边界后的计算区域Ω划分为如图 9所示三部分:(Ⅰ)内部区域Ωiner;(Ⅱ)过渡区域Ωtrans;(Ⅲ)边界Γ.在三个区域,分别采用不同的波动方程计算,区域Ωiner内各点的波场值采用原二阶波动方程计算,其具体的差分格式由区域内网格的类型决定.
|
图 9 计算区域示意图 Figure 9 The calculation area schematic diagram |
边界Γ上各点的波场值采用单向波动方程B2计算,以下边的区域为例, 公式为
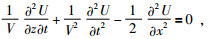
|
(49) |
区域Ωtrans内各点的波场值是两种波场值的加权平均,其他方向的过渡区域方程可以通过将式(1) 与其他方向上的B2方程相结合得到.
区域Ωtrans减小了内部区域Ωiner与边界Γ之间由于波动方程的不同产生的突变,随着区域Ωtrans层数的增加,边界的反射波会逐渐的减小.当吸收层数N=1时,就退化为传统的傍轴近似吸收边界.
对某计算时刻,整个波场的计算分为三个步骤:
(1) 利用原波动方程(1) 式计算区域Ωiner和Ωtrans的波场值Ui(1);
(2) 利用单向波动方程(49) 式计算Ωtrans和Γ的波场值Ui(2);
(3) 对区域Ωtrans处的波场值进行加权平均,公式为
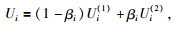
|
(50) |
其中Ui(1)和Ui(2)分别为在层Bi处原波动方程和单向波动方程的波场值,βi为在层Bi处的加权系数,其取值范围为0, 1,Ui为层Bi处的最终波场值.
权值βi的取值方式可有多种形式:指数型、抛物线型、线性型等,在本文中选取βi指数变化,即:
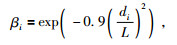
|
(51) |
其中,di为Bi距离区域(I)Ωiner的边界的距离,L为增加的层的厚度.
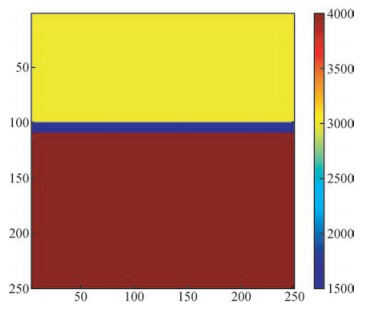
4 模型试算为验证上述算法的正确性、有效性,设计如图 10所示的低速夹层模型,震源位于水平地表的中心处.
|
图 10 低速夹层模型 Figure 10 Velocity Layers Model |
对于上述模型分别采用常规网格和本文方法进行模拟计算.模型大小为2500 m×2500 m,采用常规网格计算时步长为10 m,利用本文方法时网格步长的取值有两种5 m和10 m,采集时间均为1.5 s.震源为主频30 Hz的雷克子波,差分长度M=4,在计算区域外层增加10层的衰减层.
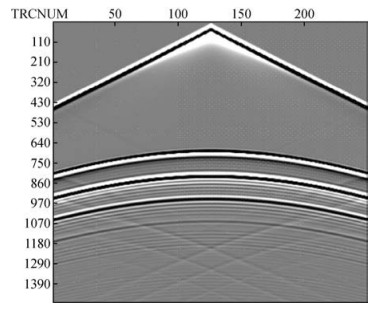
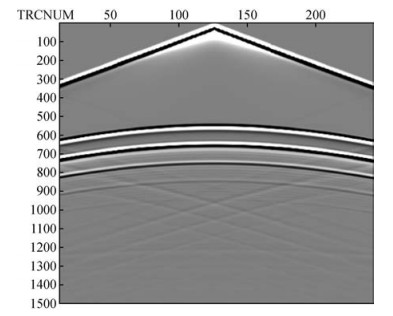
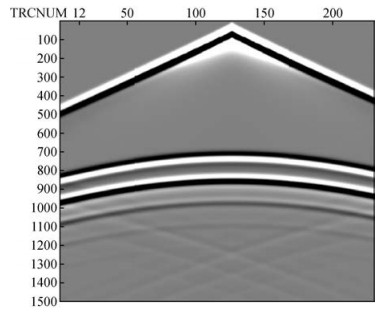
上图 11、图 12和图 13分别为采用常规粗网格方法、本文方法以及常规细网格法得到的单炮道集记录.由图 11可以看出,采用常规10 m步长网格得到的道集记录中,在低速夹层的界面放射波存在严重的数值频散现象,而且夹层下界面的频散程度要强于上界面的频散,究其原因是在低速夹层的空间采样过低造成.与图 11相比较,图 12中采用本文方法得到的道集记录中各界面的反射波清晰整洁,基本不存在频散现象,因此本文方法能够提高模拟的精度,有效压制数值频散.图 12和图 13相比较可以看出,本文方法得到的模拟结果与细网格方法得到的结果具有相近的精度和效果,可见本文方法是可以几乎达到常规细网格方法的结果的.本文采用的方法其内存需求量仅为常规5 m步长小网格的75%,计算时间节省约33%,相比较采用10 m步长的常规网格,内存的需求增加约15%,计算时间增加了约5%.
|
图 11 常规网格10 m步长单炮记录 Figure 11 Conventional grid step length of 10 m single shot records |
|
图 12 自适应网格步长为5 m和10 m单炮记录 Figure 12 Adaptive grid spacing of 5 m and 10 m single shot records |
|
图 13 常规细网格网格步长为5 m单炮记录 Figure 13 Conventional fine mesh grid spacing of 5 m single shot records |
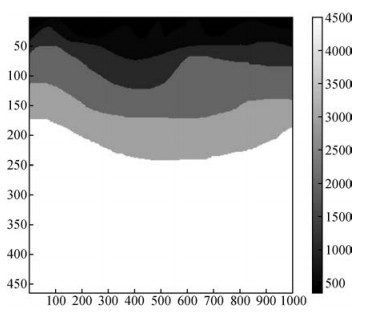
为验证本文方法对复杂地表的处理能力,构建图 14为复杂地表两层介质模型.速度模型网格结点大小为:1001×465,地表上层速度填充以声速340 m/s,地下介质速度从上至下分别为:500 m/s、1000 m/s、2000 m/s、3000 m/s和4500 m/s, 空间网格步长分别为1 m和4 m,时间步长为0.1 ms,共采集1.5 s时长.震源采用主频30 Hz的雷克子波,位于网格(254, 36) 处,采用的差分长度为M=4,在计算区域外增加10层的衰减层.
|
图 14 复杂地表模型 Figure 14 Complex surface model |
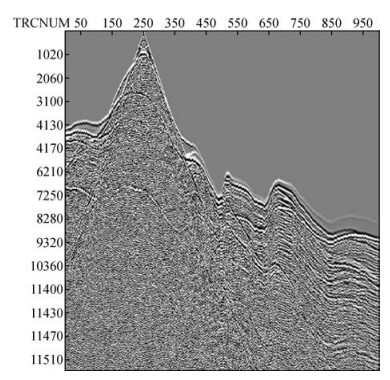
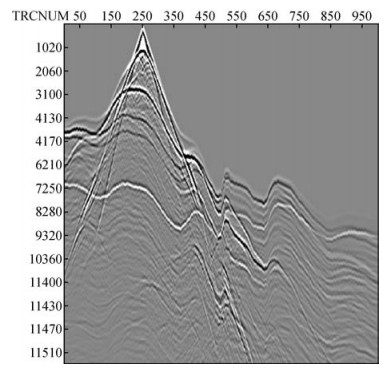
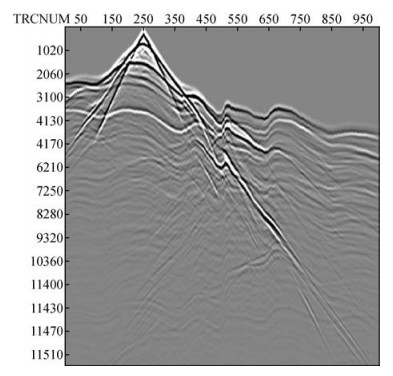
图 15为常规4 m粗网格得到的单炮道集记录.从图 15中可以看出,由于近地表存在低速层,对模型采用大网格计算时,在低速层产生的了非常严重的数值频散现象,以至于掩盖了下层介质的反射波信息.图 16为本文方法得到的道集记录,从图 16中可以看出,相比较于常规粗网格方法,本文方法得到的道集记录中能够正确的记录地下各个界面的反射波.从图 16可以看出,由于地表起伏,下层界面的反射波及地表直达波的同相轴发生剧烈的扭曲.而图 17为常规1m细网格方法得到的道集记录,由图可见采用细网格划分能够很好的抑制近地表低速层产生的频散现象.比较图 16和图 17可知,本文方法得到的道集记录与常规细网格方法得到的道集记录有着相似的精度,但比之常规粗网格方法有着明显的优势.
|
图 15 常规4 m粗网格道集记录 Figure 15 Conventional 4 m coarse grid gather records |
|
图 16 本文方法得到的道集记录 Figure 16 Gather records obtained by this method |
|
图 17 常规1m细网格道集记录 Figure 17 Conventional 1m fine grid gather records |
由图 15至图 17可以看出,利用本文方法模拟复杂地表条件下的地震波传播,也可以得到比较精确的模拟结果,基本不存在数值频散.在复杂地表条件下一般的模拟时均采用小步长网格进行划分,利用本文方法计算时,内存的需求减少了约67%,而计算时间减少约45%.上面两个模型的计算环境均为:Windows 7操作系统,CPU为Intel Core2 Extreme X7800 2.6GHz,内存:2 GB,IDE为Code::Block 12.11.由上面的两个实验可以验证采用本文方法能够节省计算时间,提高计算效率同时计算机内存也有很好的节省.
5 结论本文通过构建一种自适应网格划分方法,提升了对模型的划分精度.同时在不同网格类型相邻区域采用二元函数泰勒展开式的组合,直接求解相邻区域结点的空间拉普拉斯算子,避免使用插值法,减少了计算量.同时对采用有限差分模拟易产生数值频散的缺点,本文提出一种能够抑制频散的差分格式,并给出在不同差分阶数时,抗频散校正参数的最优取值.通过不同的模型实验结果分析可得,本文提出的方法用于地震波的模拟是正确有效的,起伏地表模拟说明本文方法能够很好的处理地表起伏条件.实验结果表明,相比较于细网格方法,本文方法在提升模拟精度的同时,能够有效的减少内存需求以及减少计算时间.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Etgen J T. 2007. A tutorial on optimizing time domain finite-difference schemes: "Beyond Holberg"[J]. Stanford Exploration Project, 129(9): 33–42. DOI:10.6038/cjg20160121 |
| [] | Feng Y, Zhou Z S, Sha C. 2012. Numerical dispersion correction method and cases analysis in numerical modeling of Rayleigh surface wave[J]. Journal of Central South University (Science and Technology) (in Chinese), 43(6): 2231–2237. DOI:10.6038/cjg20130832 |
| [] | Jastram C, Tessmer E. 1994. Elastic modelling on a grid with vertically varying spacing[J]. Geophysics Prospecting, 42(4): 357–370. DOI:10.3969/j.issn.1004-2903.2007.06.023 |
| [] | Li W J, Zhang G L, Jiang D J, et al. 2011. Suppressing numerical dispersion in finite difference modeling based on acoustic and elastic equation using FCT scheme[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 33(3): 248–251. |
| [] | Liu F G, Zhang G Q, Morton S A, et al. 2009. An optimized wave equation for seismic modeling and reverse time migration[J]. Geophysics, 74(6): WCA153–WCA158. DOI:10.6038/pg20150222 |
| [] | Liu Y, Sen M K. 2009. A new time-space domain high-order finite-difference method for the acoustic wave equation[J]. Journal of Computational Physics, 228(23): 8779–8806. DOI:10.1016/j.jcp.2009.08.027 |
| [] | Liu Y, Sen M K. 2010. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation[J]. Geophysics, 75(2): A1–A6. DOI:10.1190/1.3295447 |
| [] | Mi T L, Sun B B, Yang H Z. 2009. Adaptive mesh based on second generation wavelet simulation wave propagation for 2D acoustic wave equation[J]. Chinese Journal of Geophysics (in Chinese), 52(11): 2862–2869. |
| [] | Opršal I, Zahradník J. 1999. Elastic finite-difference method for irregular grids[J]. Geophysics, 64(1): 240–250. DOI:10.1190/1.1444520 |
| [] | Pei Z L. 2005. Finite-difference numeric modeling of wavelet adaptive network of seismic scalar equation[J]. Oil Geophysical Prospecting (in Chinese), 40(3): 267–272. |
| [] | Pitarka A. 1999. 3D elastic finite-difference modeling of seismic motion using Staggered grids with nonuniform spacing[J]. Bull. Seismol. Soc. Am, 89(1): 54–68. |
| [] | Sun C Y, Ding Y C. 2012. Accuracy analysis of wave equation finite difference with dual-variable grid algorithm[J]. Oil Geophysical Prospecting (in Chinese), 47(4): 545–551. |
| [] | Sun C Y, Li S J, Ni C K, et al. 2008. Wave equation numerical modeling by finite difference method with varying grid spacing[J]. Geophysical Prospecting for Petroleum (in Chinese), 47(2): 123–127. DOI:10.3321/j.issn:0001-5733.2004.01.012 |
| [] | Sun G L, Trueman C W. 2005. Numerical dispersion and numerical loss in explicit finite-difference time-domain methods in lossy media[J]. IEEE Transactions on Antennas and Propagation, 53(11): 3684–3690. DOI:10.1109/TAP.2005.858846 |
| [] | Wang Q, Zhang J Z, Huang Z L. 2015. Progress in the time-domain full waveform inversion[J]. Progress in Geophysics (in Chinese), 30(6): 2797–2806. |
| [] | Wang Y, Xu J, Schuster G T. 2001. Viscoelastic wave simulation in basins by a variable-grid finite-difference method[J]. Bull. Seismol. Soc. Am., 91(6): 1741–1749. DOI:10.1785/0120000236 |
| [] | Zhang H, Li Z C. 2011. Seismic wave simulation method based on dual-variable grid[J]. Chinese Journal of Geophysics (in Chinese), 54(1): 77–86. |
| [] | Zhang S W, Qu S L, Wei X C, et al. 2007. Numeric simulation by grid-various finite-difference elastic wave equation[J]. Oil Geophysical Prospecting (in Chinese), 42(6): 634–639. |
| [] | 丰赟, 周竹生, 沙椿. 2012. 瑞雷波数值模拟中的数值频散校正策略及实例分析[J].中南大学学报(自然科学版), 43(6): 2231–2237. |
| [] | 李文杰, 张改兰, 姜大建, 等. 2011. 利用FCT方法压制弹性波数值模拟中的数值频散[J].物探化探计算技术, 33(3): 248–251. |
| [] | 宓铁良, 孙兵兵, 杨慧珠. 2009. 基于第二代小波自适应网格的二维声波方程波传模拟[J].地球物理学报, 52(11): 2862–2869. |
| [] | 裴正林. 2005. 地震波标量方程的小波自适应网格有限差分法数值模拟[J].石油地球物理勘探, 40(3): 267–272. DOI:10.6038/cjg20160121 |
| [] | 孙成禹, 丁玉才. 2012. 波动方程有限差分双变网格算法的精度分析[J].石油地球物理勘探, 47(4): 545–551. DOI:10.6038/cjg20130832 |
| [] | 孙成禹, 李胜军, 倪长宽, 等. 2008. 波动方程变网格步长有限差分数值模拟[J].石油物探, 47(2): 123–127. DOI:10.3969/j.issn.1004-2903.2007.06.023 |
| [] | 王庆, 张建中, 黄忠来. 2015. 时间域地震全波形反演方法进展[J].地球物理学进展, 30(6): 2797–2806. DOI:10.6038/pg20150645 |
| [] | 张慧, 李振春. 2011. 基于双变网格算法的地震波正演模拟[J].地球物理学报, 54(1): 77–86. DOI:10.6038/pg20150222 |
| [] | 朱生旺, 曲寿利, 魏修成, 等. 2007. 变网格有限差分弹性波方程数值模拟方法[J].石油地球物理勘探, 42(6): 634–639. |
 2017, Vol. 32
2017, Vol. 32


