当前，波动方程数值模拟在地震资料采集、处理和解释等方面都发挥着极其重要的作用.目前用于波动方程数值模拟的方法主要有Fourier伪谱法、有限元法、有限差分法等(马在田, 1997)、边界元法等.其中，Fourier伪谱法虽然精度高，内存需求小，但是计算速度较慢.有限元法适宜于模拟任意形态的地质体，可以任意三角形逼近地层界面，精确模拟复杂地层形态；而不足之处则是会占用大量的内存和运算量.目前，最常用的数值模拟方法还是有限差分法，其与其他方法相比之下，有计算速度快、占用内存小、高效性等优点；而且有限差分法在地震领域的应用研究已经相当成熟，计算过程中必须考虑的初始条件、边界条件等问题已经相当的完善，故有限差分法在勘探地震学中的应用具有较大的优越性及广泛性.Alterman和Karal(1968)首先将有限差分法应用于层状介质弹性波的模拟中，到20世纪70年代中后期，它的应用更加广泛，与差分方法相关的诸如频散现象、边界条件等技术也逐渐成熟完善(Kelly et al., 1976；Reynolds，1978).1984年，Virieux对有限差分法进行了交错网格改进，极大地提高空间微分的求解精度Robertsson等(1994)将Virieux(1984)和Levander(1988)的交错网格有限差分发展到黏弹性介质中.而董良国等(1999, 2000)发展了交错网格有限差分算法的高阶形式，取得了比以往大步长短算子情况下更精确的模拟结果.近年来，一些研究者在起伏地表正演模拟过程中，引入贴体网格并取得了较好的模拟效果，Zhang等(2012)实现了贴体同位网格下的一阶速度-应力方程有限差分正演模拟，并在自由边界条件下提出了牵引力镜像法，取得了较好的模拟效果.

有限差分模型的缺点是构建实际模型时将消耗巨大的计算资源，为了解决单机单进程的内存和计算速度的限制，前人对于有限差分正演模拟的并行优化做了许多工作.比如，近年来多使用集群来解决科学计算问题.首先是利用MPI实现多进程的并行，比如王德利等(2007)基于MPI对黏弹介质中的三维波动方程进行了有限差分的并行及验证(奚先和姚姚，2001；Zhang and Chen, 2006；李振春等，2007；王春燕，2007；朱军，2007；杨尚琴和罗省贤，2009；杨莹，2009；杨尚琴等，2012；周洲，2013；李庆洋等，2015；杨尚琴等，2015).随着GPU等协处理器的流行，Micikevicius(2009)给出了利用GPU实现高阶有限差分的算法.2011年龙桂华等(2011)将交错网格有限差分应用GPU实现三维地震波模拟计算，在单GPU和多GPU上实现加速.2016年谭嘉言等(2016)基于GPU计算的地震波场高阶有限差分正演研究介绍了对于二维及三维GPU正演程序的测试.这些研究都极大地提高了数值求解波动方程的计算效率.但是，更多倾向于发挥GPU的功效，而本文吸取前人的研究经验，重在充分发挥多核CPU的性能，基于对波动方程的有限差分模拟算法的研究，通过对程序的智能监控，针对性选取采用减少同步、边界重划、线程和处理器绑定、零复制，空间局部性、时间局部性及Pthreads多线程编程模型等一系列并行优化设计方法，实现二维波动方程正演模拟的性能优化，从而提高计算效率.

各向同性弹性介质中弹性波方程组可表示为如下的一阶方程组，公式为

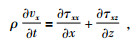
(1)

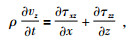
(2)

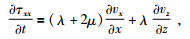
(3)

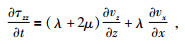
(4)

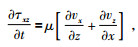
(5)

其中，τ_xx=τ_xx(x, z, t), τ_zz=τ_zz(x, z, t), τ_xz=τ_xz(x, z, t)，均为应力张量值；ρ=ρ(x, z)为密度；v_x=v_x(x, z, t), v_z=v_z(x, z, t)均为速度向量值；λ=λ(x, z), u=u(x, z)为拉梅系数.用有限差分法求解式(1)~式(5) 即可.

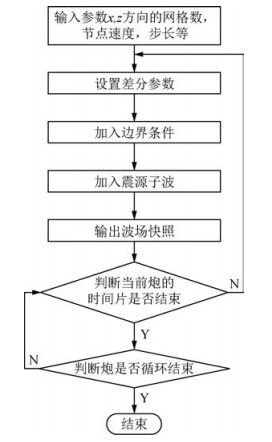
通过分析得到二维波动方程的算法流程如图 1所示.通过比对图 1所示的流程结合Intel专门的程序分析工具VTune对正演模拟程序进行热点分析，得到二维波动方程正演模拟中单炮内时间片循环即是程序的热点所在，包括了上图指出的设置差分参数、边界条件计算、加入震源子波及输出波场快照这几个计算步骤.因此需要着重对单炮内计算进行代码的深入并行化，加快单炮模拟速度，实现实时仿真模拟，从而满足采集和解释平台对正演模拟实时性的需求.

图 1

Figure 1

图 1 二维波动方程的算法流程图 Figure 1 The flowchart of two-dimensional wave equation algorithm

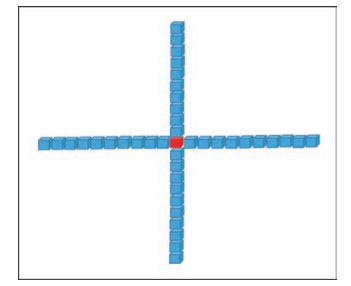
现有弹性波有限差分正演程序的单炮模拟采用Stencil计算模式.如图 2所示，在Stencil计算模式中，每个数据点的更新需要使用周围相邻若干点的值，这样的计算和访问数据的模式对并行化带来一定的困难.在对Stencil计算模式进行并行化时需要开辟边界交换存储空间，且在每个时间步交换边界数据，在并行优化时要特别注意边界通讯和同步对性能的影响.此外，本文的弹性波正演模拟主要计算核心使用的是十阶有限差分格式，即空间上每个方向每次推导需要计算10个点的有限差分，因此其主要计算核心是访存密集型的，即单位计算量对应的访存量较大，因此在很多计算平台上Stencil计算模式的访存会成为瓶颈，故本文将优化重点放在访存优化上.

图 2

Figure 2

图 2 Stencil计算示意图 Figure 2 Stencil computing schematic

整体把握影响程序性能的主要方面，并将这些优化有机结合起来达到全局性能最优，具体而言需要考虑程序特性、访存、计算和通讯四个方面，各方面需要重点考虑的优化方法如下：

(1) 程序特性方面：震源影响的空间与时间局部性；

(2) 访存优化方面：消除不必要的访存操作，减少实际访存量；

(3) 计算优化方面：消除冗余计算；使用Pthreads多线程编程模型充分利用计算机多核架构；

(4) 通讯优化方面：通讯和计算覆盖，包括了减少同步，边界重划及将线程和处理器进行绑定，防止线程迁移等方式.

下面结合二维正演数值模拟的核心算法就以上提到的并行优化设计方法分别进行阐述.

程序的局部性原理是指程序在执行时呈现出局部性规律，即在一段时间内，整个程序的执行仅限于程序中的某一部分.相应地，执行所访问的存储空间也局限于某个内存区域.局部性原理又表现为：时间局部性和空间局部性.对应于二维正演数值模拟来说，空间局部性即震源只影响一定空间范围内的点，时间局部性即震源影响随着时间增长迅速衰减.考虑局部性原理获知一个震源只在激发后一定时间段内对附近一定范围之内的区域有影响，只需要计算有效区域的震源影响且将这些值保存下来在以后的时间片循环中复用，且只有在震源发生过后的一小段时间内才使用该震源的影响值.这个优化对大模型特别有用，因为每增加一个震源需要计算并存储的震源影响值个数为较小的常数，不随模型的增大而增加，可以大大减少计算和访存.下表展示了使用此原理对代码优化的改造示例.

在二维正演数值模拟计算核心中的数组轮换尽量都使用指针复制实现，从而消除数据交换，提高效率.因此使用零复制机制，即复制指针而不是数组本身.下表为零复制在正演模拟中的优化应用示例.

表 1 (Table 1)

表 1 局部性原理在正演模拟中的优化应用示例 Table 1 The example of locality principle in forward modelling optimization

表 1 局部性原理在正演模拟中的优化应用示例 Table 1 The example of locality principle in forward modelling optimization

表 2 (Table 2)

表 2 零复制在正演模拟中的优化应用示例 Table 2 The example of zero copying in forward modelling optimization

表 2 零复制在正演模拟中的优化应用示例 Table 2 The example of zero copying in forward modelling optimization

从二维波动方程的算法流程中我们获悉二维正演数值模拟算法中，每一炮之间的计算是相互独立且没有数据依赖的，因此可以使用Pthreads多线程编程模型进行优化，从而充分发挥当今多核机器架构的性能.

Pthreads即POSIX Threads，是基于POSIX标准的多线程API，它的使用灵活，且合理的应用可以达到高效的并行.但同时它的灵活性也给编程带来了复杂性，所以本文的实现是基于自己实现的线程池上进行的算法并行化，既降低了编程的难度，也提高了以后代码的可移植性.下表为二维正演数值模拟并行化中使用Pthreads多线程编程模型的伪代码.

表 3通过控制和计算线程，实现了算法的并行化，控制线程又利用计算线程计算的时间去读取下一炮的数据，实现了读数据和计算的重叠，最后在线程池动态负载平衡的控制下，高效地发挥了多核系统的性能.

表 3 (Table 3)

表 3 正演数值模拟多线程并行化算法的伪代码 Table 3 The pseudocode of multithreading parallelization in forward modelling

表 3 正演数值模拟多线程并行化算法的伪代码 Table 3 The pseudocode of multithreading parallelization in forward modelling

二维正演数值模拟核心算法中在每个时间片下都需要进行相邻计算点之间模型数据的交换，涉及到的通讯量也相当可观，因此需要进行通讯优化.分别采取了如下的方式进行通讯优化.

(1) 减少同步

由于使用了炮间的多核Pthreads编程模型进行并行化，前期的炮内并行同步，已经得到了消除.在优化的后期，本文通过减少和合并循环中跳转语句，来消除多级CPU流水线被打断，而造成大的多级流水线不同步所带来的时间消耗.表 4及表 5为优化前后的例子，优化后，去掉了if语句.

表 4 (Table 4)

表 4 正演数值模拟减少同步优化前示例 Table 4 The example before reducing synchronization in forward modelling

表 4 正演数值模拟减少同步优化前示例 Table 4 The example before reducing synchronization in forward modelling

表 5 (Table 5)

表 5 正演数值模拟减少同步优化后示例 Table 5 The example after reducing synchronization in forward modelling

表 5 正演数值模拟减少同步优化后示例 Table 5 The example after reducing synchronization in forward modelling

(2) 边界重划

在处理边界时如果还是按照处理主体数据时的数据划分方式并行，会发生少量线程承担了主要计算任务，其他线程闲置的状况，因此在处理边界的时候考虑重新划分数据，让每个线程获得大致相等的工作量，达到更好的负载均衡.

(3) 线程和处理器绑定技术

上海超算中心的徐磊等(2009)指出，STREAM Benchmark使用OpenMP绑定比不绑定性能提升5.34%~28.22%，Intel公司也做过线程绑定方面的测试研究.通过对CPU线程亲缘性的研究，同理可以在Pthreads编程模型下将线程和处理器进行绑定，防止线程的迁移，每个线程将数据分配在与绑定的处理器核心直接相连的物理存储上，增加访存带宽.通过将处理器核心与特定线程绑定，在防止线程迁移的同时可以保证每个线程访问的数据分配在与绑定的处理器核心直接相连的物理存储上，从而增加访存带宽.优化代码示例如表 6所示.

表 6 (Table 6)

表 6 线程绑定在正演模拟中的应用示例 Table 6 The example of threads binding in forward modelling optimization

表 6 线程绑定在正演模拟中的应用示例 Table 6 The example of threads binding in forward modelling optimization

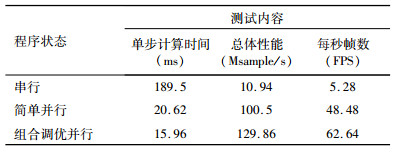
本文采用的测试环境如表 7所示.对于十阶有限差分弹性波正演核心在1920×1080模型下进行上述并行优化设计的调优性能与串行及简单并行之间的效率比较见表 8所示.其中，单位每步计算时间即每个时间片计算需要的时间数(单位：毫秒)；Msample/s即每秒钟可以计算多少M(10的6次方)的网格点数；每秒帧数(FPS)即每秒计算的时间片数，也即每秒输出的波场快照数；表中的简单并行是指一开始的炮内并行方式，组合调优并行是运用了上述一系列并行优化设计方法后的组合并行方式.

表 7 (Table 7)

表 7 测试环境参数 Table 7 Test environment parameters

表 7 测试环境参数 Table 7 Test environment parameters

表 8 (Table 8)

表 8 十阶有限差分弹性波正演在1920×1080模型下优化效果表 Table 8 The optimization results of elastic wave forward modeling with 10-order finite difference based on the 1920×1080 model

表 8 十阶有限差分弹性波正演在1920×1080模型下优化效果表 Table 8 The optimization results of elastic wave forward modeling with 10-order finite difference based on the 1920×1080 model

通过表 8可以看出，十阶有限差分弹性波正演在1920×1080模型下的调优性能得到大幅提升，其中，并行调优后单步计算时间是串行计算时的11.8倍；并行调优后每秒钟可以计算多少的网格点数是串行计算时的11.8倍；并行调优后每秒计算的时间片数是串行计算的11.8倍.表 8中得到1920×1080模型下优化后每秒帧数(FPS)大于24，即其在1 s内得到大于24个波场快照输出，尤其是组合调优并行后，FPS甚至大于60，表明其分辨率越来越高，因此并行后正演模拟达到了实时仿真的效果.

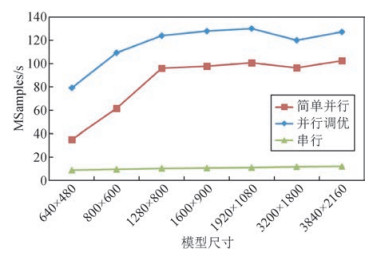
图 3为十阶有限差分弹性波正演模拟不同模型尺寸对于总体性能(Msample/s)这项优化内容的效果比较图.

图 3

Figure 3

图 3 十阶有限差分弹性波正演模拟不同模型尺寸的优化效果比较 Figure 3 The comparison of optimization results of elastic wave forward modeling with 10-order finite difference based on different model

通过图 3可以看出，十阶有限差分弹性波正演模拟在不同模型尺寸下进行的简单并行比串行的效率有大的提升，而通过一系列的并行优化方法的调优后，使得每秒钟可以计算多少的网格点数又得到一次提升.

表 9为十阶有限差分弹性波正演在1920×1080模型下各种并行优化设计方法对每秒帧数(FPS)的优化效果.

表 9 (Table 9)

表 9 十阶有限差分弹性波正演在1920x1080模型下各并行优化对FPS的效果 Table 9 The parallel optimization effects in FPS of elastic wave forward modeling with 10-order finite difference based on the 1920×1080 model

表 9 十阶有限差分弹性波正演在1920x1080模型下各并行优化对FPS的效果 Table 9 The parallel optimization effects in FPS of elastic wave forward modeling with 10-order finite difference based on the 1920×1080 model

通过表 9可以看出，程序由简单并行状态到通过减少同步、边界重划、线程和处理器绑定、零复制、空间局部性及时间局部性这一系列的并行优化设计方法后，每秒帧数(FPS)这项测试内容的性能得到了近30%的提升.

以下用于十阶有限差分弹性波正演模拟模块的实际测试模型采用的是BP2004标准网格模型的一部分.其中，模型规模为1920×1080，单元网格间距为6.25 m×12.5 m.

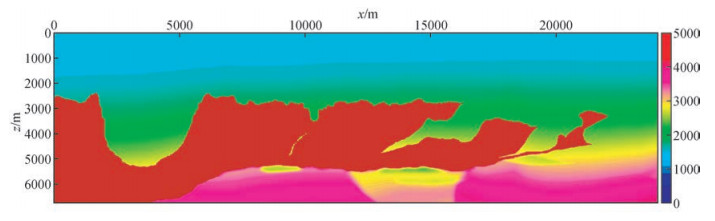
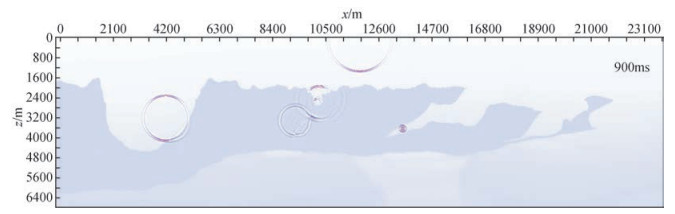
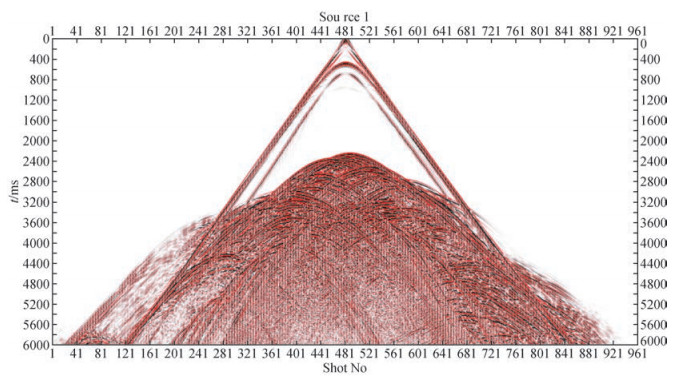
图 4为该测试模型在正演模拟软件中的显示效果截图.以上述网格模型实现的十阶有限差分弹性波正演模拟，获得了如图 5所示的多震源模拟时的快照截图，并且获得了如图 6所示的十阶有限差分弹性波正演模拟的炮记录.

图 4

Figure 4

图 4 BP2004标准网格模型在正演模拟软件中的显示效果截图 Figure 4 The screenshot of the 2004 BP velocity model benchmark in forward modeling software

图 5

Figure 5

图 5 十阶有限差分弹性波正演模拟的波场快照 Figure 5 The wave field snapshot of elastic wave forward modeling with 10-order finite difference

图 6

Figure 6

图 6 十阶有限差分弹性波正演模拟的炮记录 Figure 6 The shot records of elastic wave forward modeling with 10-order finite difference

二维地震波动方程正演模拟的数据通讯量及计算量较大，本文通过分析二维正演数值模拟程序的特性，在重点针对访存进行优化的前提下，综合使用局部性原理、零复制、Pthreads多线程编程模型并行化算法及通讯优化等一系列的并行优化设计方法对十阶有限差分正演数值模拟进行调优.通过模型数据的一系列性能测试说明了组合的并行优化方法能更大限度地提高数值模拟的计算效率；通过提高每秒帧数(FPS)的性能，从而提高了正演数值模拟的分辨率，实现了实时仿真计算的效果，进而能够更好地为勘探中的采集、处理及解释流程做出决策服务.