2. 新疆维吾尔自治区地质调查院, 乌鲁木齐 830000
3. 中国水利水电科学研究院, 北京 100038
4. 中国国土资源航空物探遥感中心, 北京 100083
2. Geological Survey Academe of Xinjiang, Vrümqi 830000, China
3. China Institute of water resource and Hydropower Research, Beijing 100038, China
4. China Aero Geophysical Survey & Remote Sensing Center for Land and Resources, Beijing 100083, China
瞬变电磁(TEM)法在金属矿产勘探、油气勘探、隧道超前探、矿井老空水探测等领域有广泛的应用(李术才等,2014;殷长春等,2015;于景邨等,2015).目前,瞬变电磁一维正反演问题已经有比较成熟的解决方法(薛国强等,2008),三维问题仍需加以研究.三维瞬变电磁场数值计算方法主要有:积分方程法、有限元法和有限差分法.时域有限差分(FDTD)法直接对麦克斯韦方程组进行差分离散,简单、有效,是三维TEM正演常用的方法.Wang和Hohmann(1993)对有限差分法做了重要改进,采用Yee单元格式和改进的Du fort-Frankel差分形式建立了TEM三维正演算法,引入虚拟介电常数,扩大了时间迭代步长.基于Wang的工作,肖怀宇(2006)、陈丹丹(2008)分别实现了TEM三维正演.李建慧等(2013)基于电场异常场的Helmholtz方程实现了回线源TEM的三维正演.许洋铖等(2012)将发射电流等效为若干脉冲元的叠加,实现了全波形时间域航空电磁响应三维正演.上述文献需要假设地下浅层为均匀模型,认为在电流关断后的极短时间内二次场只扩散到浅层,没有达到目标体,这样可以利用均匀半空间解析公式计算浅层电磁场,以此作为初始值计算二次场.孙怀凤等(2013)将矩形回线源电流密度加入麦克斯韦方程组的安培环路定理方程,采用均匀网格的有限差分法,实现回线源瞬变电磁三维正演.此方法初始值不再依赖均匀半空间解析解,不需要假设地下浅层为均匀模型,能适用更复杂的情况.有限差分法的不足之处是,对计算速度和内存要求较高.对于均匀网格有限差分法,为了达到精度要求,需要将整个模型剖分得足够细,网格剖分越细,计算需要的时间越多,程序占用的内存越大,甚至有可能超出电脑的内存无法计算.为了解决这个问题,可取的做法是,在回线和异常体周围精细剖分,其他较远的地方粗略剖分,这就需要非均匀网格有限差分算法.另外,瞬变电磁的理论基础是阶跃波,尤其是视电阻率的计算就是以阶跃波响应与电阻率之间的关系反推出来的,可是实际测量达不到阶跃波,仪器常使用的是梯形波,所以有必要对梯形波响应和阶跃波响应的区别加以研究.
综上:(1) 本文基于均匀网格的有源有限差分算法,采用非均匀网格有限差分法对瞬变响应进行三维正演,并分析其响应特征规律;(2) 本文对比了梯形波响应和阶跃波响应的区别,进一步分析了梯形波发射脉宽对瞬变响应结果的影响.
1 瞬变电磁有源有限差分法原理 1.1 控制方程在均匀、有耗、非磁性、有源介质中麦克斯韦方程组为
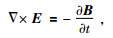
|
(1a) |
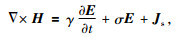
|
(1b) |
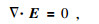
|
(1c) |
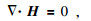
|
(1d) |
其中,E为电场强度,H为磁场强度,B为磁感应强度,Js为源电流密度,无源区Js=0.σ为电导率,γ为虚拟介电常数,t为时间.
利用式(1b)计算电场的三个分量,公式为
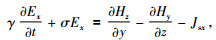
|
(2a) |
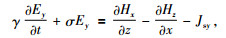
|
(2b) |
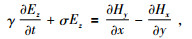
|
(2c) |
其中Ex、Ey、Ez,Hx、Hy、Hz,Jsx、Jsy、Jsz分别为电场、磁场和源电流密度的三个分量.
磁场Hx、Hy分量由式(1a)给出,而Hz分量则通过式(1d)计算.磁感应强度分量计算公式为
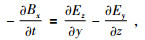
|
(2d) |
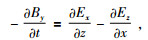
|
(2e) |
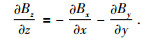
|
(2f) |
对公式(2a)~(2f)进行离散,包括时间离散和空间离散两部分.用中心差分格式对时间离散,用向前差分格式对空间离散.磁场的离散公式和Wang和Hohmann(1993)的相同不再赘述,电场不同,仅以Ex为例,公式为
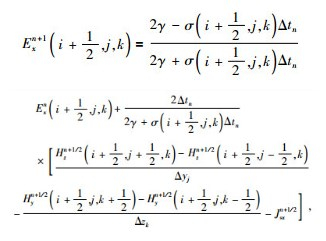
|
(3) |
式(3) 中Δxi、Δyj、Δzk为单元的三个边长,Δtn为时间步长,σ为电导率,取邻近四个单元电导率的加权平均值.
1.3 源的加入和边界条件在有源区,用导线中的电流和相邻两个网格面积的比值来表示此网格处的源电流密度,只要已知电流的波形就可以正演通电过程及关断后的过程.
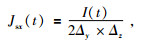
|
(4a) |
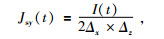
|
(4b) |
其中,I(t)为t时刻的电流,Δx、Δy、Δz分别为源所在的网格单元的大小.
地下五个边界采用狄里赫利边界条件,地空边界采用向上延拓的方式得到.延拓过程涉及三次样条插值,插值方法见许小勇和钟太勇(2006)的文章.本文改进了何光渝和高永利(2002)的双三次样条插值算法,特点是一次计算可以输出一条测线上所有插值点的值,显著提高了计算效率.
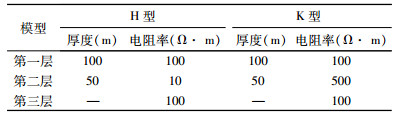
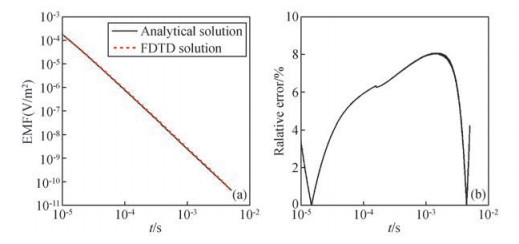
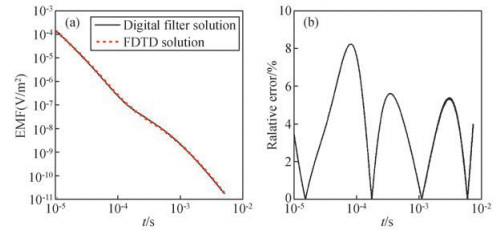
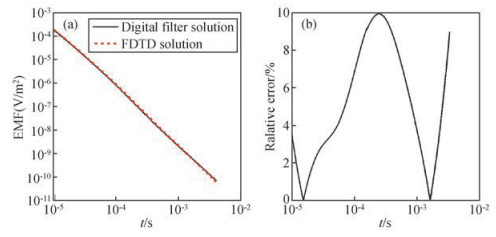
2 精度验证本文通过一维模型的理论解,来验证非均匀网格有限差分解的准确性.设均匀半空间模型电阻率为100 Ω· m,层状模型的地电参数见表 1.模型的网格剖分方式为:中间网格大小为10 m,然后以1.1的倍率向两边逐渐扩大,最大网格不超过100 m.模型x、y、z方向的网格数为85×85×80,实际模拟的大地尺寸为3000 m×3000 m×2000 m.发射源为70 m×70 m的方形回线,通电时间为7 ms,大小为1 A.图 1是均匀半空间模型回线中心点解析解和FDTD解的对比,图 2、图 3分别为H型和K型层状模型的数字滤波解和FDTD解对比结果.因为均匀半空间和层状模型都较容易计算出回线中心点的感应电动势(EMF)理论值,所以本文采用EMF作为对比量,EMF的单位V/m2表示对接收回线进行面积归一化后的值.对比结果显示有限差分解和理论解的最大相对误差小于10%,平均相对误差小于5%,满足精度要求.其误差主要来源于有限差分理论本身,有限差分法的实质是用差分代替微分,差分的误差与差分格式、迭代步长有关,步长越小误差越小.
|
图 1 均匀半空间解析解和有限差分解的对比 (a)感应电动势衰减曲线;(b)相对误差曲线. Figure 1 Comparison between the FDTD solution and the a analytical solution of a homogenous half-space model (a)Decay curves of the EMF; (b)Relative error of the EMF decaycurves. |
|
图 2 H型层状模型数字滤波解和有限差分解的对比 (a)感应电动势衰减曲线;(b)相对误差曲线. Figure 2 Comparison between the FDTD and digital filter solution for H-layered model (a)Decay curves of the EMF; (b)Relative error of the EMF decay curves. |
|
图 3 K型层状模型数字滤波解和有限差分解的对比 (a)感应电动势衰减曲线;(b)相对误差曲线. Figure 3 Comparison between the FDTD and digital filter solution for K-layered model (a)Decay curves of the EMF; (b)Relative error of the EMF decay curves. |
|
|
表 1 层状模型的地电参数 Table 1 The parameters of layered models |
本节使用非均匀网格和均匀网格有限差分法对同一个三维模型进行正演,说明两种算法的正演结果相同,并且非均匀网格算法使用的网格更少.
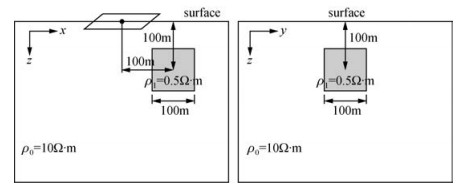
三维低阻体的模型参数如图 4所示,均匀网格有限差分法剖分单元大小为10 m,模型x、y、z方向的网格数为129×129×120,模拟的大地尺寸为1300 m×1300 m×1200 m;非均匀网格剖分方式为:中间网格大小为10 m,然后以1.1的倍率向两边逐渐扩大,最大网格不超过100 m,模拟相同尺寸的大地非均匀算法只需65×65×70个网格.
|
图 4 低阻异常模型示意图 Figure 4 Schematic diagram of low resistivity body |
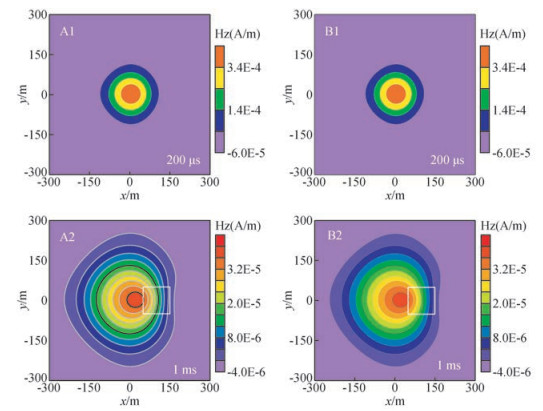
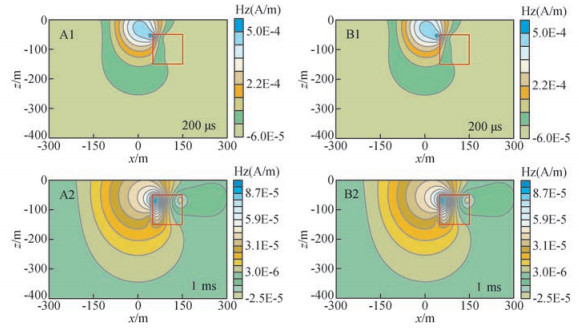
有限差分法的优势在于可以直观的反映电磁场的扩散现象,本文使用磁场垂直分量(Hz)显示二次场的变化.图 5、图 6分别为地面和X-Z剖面磁场强度等值线分布图,从中看出在200 μs和1 ms时刻非均匀网格算法和均匀网格算法正演结果完全一致.图 6中红线表示低阻体所在位置,图 5白线表示异常体在地面的投影位置,200 μs时二次场刚到达低阻体位置,此时地面场值分布并没有发生异常,而1 ms时刻二次场已经到达低阻体位置,从图 6看出磁场等值线发生畸变,低阻体位置等值线密集,说明二次场在低阻介质中扩散速度慢,相应变化也反映在地面场值分布图中,地面磁场等值线在低阻体上方聚集.
|
图 5 两种算法得到的地面Hz等值线图 A1和A2为非均匀网格FDTD解;B1和B2为均匀网格FDTD解. Figure 5 The contour maps of Hz at surface A1 and A2 are the FDTD solution of non-uniform grid; B1 and B2 are the FDTD solution of uniform grid. |
|
图 6 两种算法得到的X-Z剖面Hz等值线图 A1和A2为非均匀网格FDTD解;B1和B2为均匀网格FDTD解. Figure 6 The contour maps of Hz at X-Z profile A1 and A2 are the FDTD solution of non-uniform grid; B1 and B2 are the FDTD solution of uniform grid. |
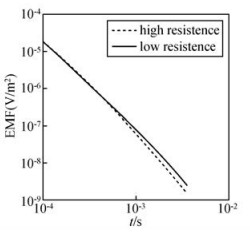
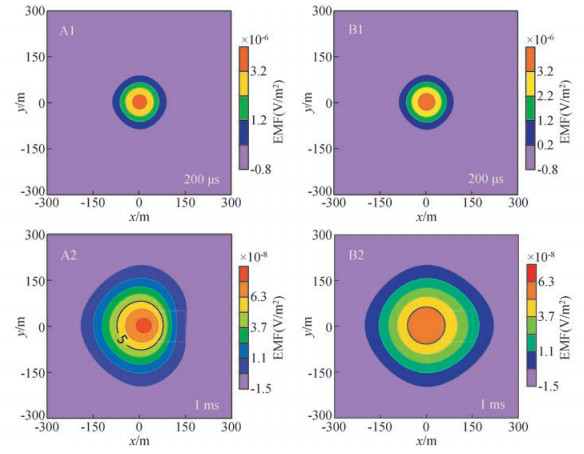
模型几何参数如图 4所示,背景电阻率为10 Ω·m,高阻体电阻率为200 Ω·m,低阻体电阻率为0.5 Ω·m.发射源为70 m×70 m的方形回线,通电时间为1 ms,大小为1 A.回线中心点感应电动势(EMF)衰减曲线如图 7所示,在早期二次场还未到达异常体,此时高阻体和低阻体EMF衰减曲线一致,在0.5 ms以后曲线发生明显分化,说明二次场到达异常体位置,异常体导致电磁场发生畸变并且地下电磁场的畸变影响到了地面场值的变化,表现在感应电动势上为低阻体响应幅值比高阻体大,说明低阻介质二次场衰减速度慢,这符合瞬变电磁的响应规律.为了更直观地对比高阻异常和低阻异常的响应特征,将200 μs和1 ms时刻地面感应电动势的分布绘于图 8,200 μs时EMF分布几乎一致,1 ms时低阻体使EMF等值线在异常体上方集中,高阻体使EMF等值线在异常体上方分散.由此可以根据地面感应电动势分布图推断异常体在水平方向上的位置,而某点的感应电动势衰减曲线可以推断异常体所在的垂向位置.
|
图 7 感应电动势衰减曲线 Figure 7 Decay curves of the EMF |
|
图 8 感应电动势分布图 A1和A2为低阻异常;B1和B2为高阻异常. Figure 8 The contour maps of EMF at surface A1 and A2 are the Low resistance anomaly; B1 and B2 are the High resistance anomaly. |
通常,地面TEM仪器的发射波形为梯形波,而瞬变电磁的理论基础是阶跃波,比如视电阻率定义就是基于均匀半空间下的阶跃波响应,为此,本文研究了梯形波响应与阶跃波响应的区别.梯形波分为上升沿、电流稳定阶段、下降沿三个部分.下降沿的影响孙怀凤等(2013)已经指出:关断时间(下降沿)越小,早期计算结果越接近阶跃波的理论解.下文的分析将证明脉宽越小,梯形波响应越早偏离阶跃波响应的理论值.
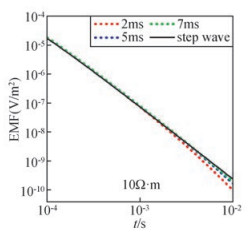
为了研究梯形波脉宽对响应的影响,本文使用非均匀网格的有源有限差分法对包括一次场在内的整个瞬变响应过程进行正演.以电阻率为10 Ω·m均匀半空间为例,对其施加脉宽分别为2 ms、5 ms和7 ms的发射电流.图 9为不同脉宽的梯形波激发的瞬变响应与阶跃波响应理论值的对比.从图 9可以看出:
|
图 9 不同脉宽的梯形波响应-10 Ω·m Figure 9 Result of different pulse duration |
(1) 在早期阶段,不同脉宽的梯形波响应与阶跃波理论响应相近.
(2) 在晚期,不同脉宽的梯形波响应明显不同,脉宽越小,响应幅值衰减越快,越早偏离阶跃波响应的理论值.
(3) 将梯形波响应与阶跃波响应理论值之间的偏差不超过10%的时间称为有效时间,即此时间段内梯形波响应和阶跃波响应一致,大量的模型试验表明,脉宽和有效时间的比值为1:0.8.
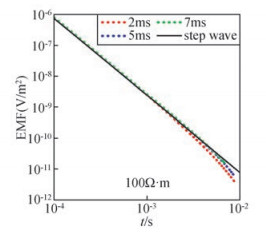
由于感应电动势与大地电阻率有关,为了排除电阻率对计算结果的影响,本文又对电阻率为100 Ω·m的均匀半空间模型进行了通电脉宽为2 ms、5 ms和7 ms的瞬变响应正演计算.正演结果如图 10,结果显示对100 Ω·m的半空间进行正演,结果仍然符合上述结论.
|
图 10 不同脉宽的梯形波响应-100 Ω·m Figure 10 Result of different pulse duration |
本文基于有源麦克斯韦方程组,使用非均匀剖分的有限差分法,实现了任意发射波激发的回线源瞬变响应三维正演.通过模型计算得出结论:非均匀网格有限差分算法计算稳定,精度可靠,效率更高.均匀半空间模型,最小网格间距为10 m的情况下,10 ms内二次场的平均相对误差小于5%,满足精度要求.通过与均匀网格有限差分法对比,在回线中心点精度不变的情况下,非均匀网格算法耗时减少75%.
4.2对高阻异常和低阻异常响应特征进行研究发现,可以利用某点的感应电动势衰减曲线推断异常体所在的垂向位置,根据地面感应电动势分布图推断异常体所在的水平位置.
4.3针对实测中常用的梯形波,研究了不同脉宽的梯形波响应与阶跃波响应的理论值的差别.在早期阶段,不同脉宽的梯形波响应与阶跃波响应的理论值一致,但是,脉宽越小,梯形波响应幅值衰减越快,结果越早偏离阶跃波响应的理论值.
致谢 感谢孙怀凤老师提供了均匀剖分的有限差分正演程序.| [] | Chen D D. 2008. Study of three-dimensional forward of TEM (in Chinese)[Master thesis]. Beijing: China University of Geoscience. |
| [] | He G Y, Gao Y L. 2002. Visual Fortran commonly used numerical algorithm set(in Chinese)[M]. . |
| [] | Li J H, Hu X Y, Zeng S H, et al. 2013. Three-dimensional forward calculation for loop source transient electromagnetic method based on electric field Helmholtz equation[J]. Chinese J. Geophys. (in Chinese), 56(12): 4256–4267. DOI:10.6038/cjg20131228 |
| [] | Li S C, Sun H F, Li X, et al. 2014. Advanced geology prediction with parallel transient electromagnetic detection in tunnelling[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 33(7): 1309–1318. |
| [] | Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time[J]. Chinese J. Geophys. (in Chinese), 56(3): 1049–1064. DOI:10.6038/cjg20130333 |
| [] | Wang T, Hohmann G W. 1993. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling[J]. Geophysics, 58(6): 797–809. DOI:10.1190/1.1443465 |
| [] | Xiao H Y. 2006. Three-dimensional numerical modeling considering the topography of TEM (in Chinese)[M]. . |
| [] | Xu X Y, Zhong T Y. 2006. Construction and realization of cubic spline interpolation function[J]. Ordnance Industry Automation (in Chinese), 25(11): 76–78. |
| [] | Xu Y C, Lin J, Li S Y, et al. 2012. Calculation of full-waveform airborne electromagnetic response with three-dimension finite-difference solution in time-domain[J]. Chinese J. Geophys. (in Chinese), 55(6): 2105–2114. DOI:10.6038/j.issn.0001-5733.2012.06.032 |
| [] | Xue G Q, Li X, Di Q Y. 2008. Research progress in TEM forward modeling and inversion calculation[J]. Progress in Geophysics (in Chinese), 23(4): 1165–1172. |
| [] | Yin C C, Zhang B, Liu Y H, et al. 2015. 2.5-D forward modeling of the time-domain airborne EM system in areas with topographic relief[J]. Chinese J. Geophys. (in Chinese), 58(4): 1411–1424. DOI:10.6038/cjg20150427 |
| [] | Yu J C, Chang J H, Su B Y, et al. 2015. Study on whole space transient electromagnetic method prospect three dimensional numerical modeling of gob water[J]. Coal Science and Technology (in Chinese), 43(1): 95–99, 103. |
| [] | 陈丹丹. 2008. 瞬变电磁法三维正演研究[硕士论文]. 北京: 中国地质大学. |
| [] | 何光渝, 高永利. 2002. Visual Fortran常用数值算法集[M]. . |
| [] | 李建慧, 胡祥云, 曾思红, 等. 2013. 基于电场Helmholtz方程的回线源瞬变电磁法三维正演[J].地球物理学报, 56(12): 4256–4267. DOI:10.6038/cjg20131228 |
| [] | 李术才, 孙怀凤, 李貅, 等. 2014. 隧道瞬变电磁超前预报平行磁场响应探测方法[J].岩石力学与工程学报, 33(7): 1309–1318. |
| [] | 孙怀凤, 李貅, 李术才, 等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演[J].地球物理学报, 56(3): 1049–1064. DOI:10.6038/cjg20130333 |
| [] | 肖怀宇. 2006. 带地形的瞬变电磁法三维数值模拟[硕士论文]. 北京: 中国地质大学. |
| [] | 许小勇, 钟太勇. 2006. 三次样条插值函数的构造与Matlab实现[J].兵工自动化, 25(11): 76–78. DOI:10.3969/j.issn.1006-1576.2006.11.034 |
| [] | 许洋铖, 林君, 李肃义, 等. 2012. 全波形时间域航空电磁响应三维有限差分数值计算[J].地球物理学报, 55(6): 2105–2114. DOI:10.6038/j.issn.0001-5733.2012.06.032 |
| [] | 薛国强, 李貅, 底青云. 2008. 瞬变电磁法正反演问题研究进展[J].地球物理学进展, 23(4): 1165–1172. |
| [] | 殷长春, 张博, 刘云鹤, 等. 2015. 2.5维起伏地表条件下时间域航空电磁正演模拟[J].地球物理学报, 58(4): 1411–1424. DOI:10.6038/cjg20150427 |
| [] | 于景邨, 常江浩, 苏本玉, 等. 2015. 老空水全空间瞬变电磁法探测三维数值模拟研究[J].煤炭科学技术, 43(1): 95–99, 103. |
 2017, Vol. 32
2017, Vol. 32