2. 中国石化石油物探技术研究院, 南京 211103
2. Sinopec Geophysics Research Institute, Nanjing 211103, China
地下储集层岩石物理特征研究,对于地震勘探技术和油气的开发都具有十分重要的意义(徐文俊和郭建,1994).在实际地层中,大部分岩石均含有孔隙,所以,油气储集层是由岩石骨架和填充流体组成,即双相介质(Parra, 1997;杨顶辉等,2000).由于孔隙结构和各种充填介质存在性质差异,利用地震和声波测井资料难以满足储层声学特征的研究需求(王东等,2006),因此,研究双相介质中部分饱和的多种孔隙介质中声波的传播规律,定量分析不同含水饱和度的岩心弹性参数变化规律,对油气田声波和地震波勘探有着十分重要的意义.
双相介质中声波传播已经有大量的理论和实验研究,Gassmann(1951)提出的模型考虑了岩石中孔隙流体的随机分布特点以及固体骨架的组成结构特点,分析了在低频条件下,岩石颗粒、骨架体积和流体体积模量与不用流体饱和度之间的平均关系.Biot(1956)提出了流体饱和孔隙固体的弹性波传播相关理论,在泊肃叶流动的假设前提下,从低频段到高频段分析了孔隙中含有的黏弹性流体对弹性波相速度和逆品质因子的影响.巴晶等(2008) 提出了双孔介质中观流动的理论,并且双孔介质模型在地震勘探频带内产生了巨大的衰减.
目前,实验室一般采用天然岩心进行岩心孔隙流体对声学参数的影响的岩石物理实验(李维新等,2007;马中高和伍向阳,2007;李东会等,2011;席道瑛等,2011),双相介质对声学参数的影响机理的研究至今还没有明确的理论阐述,为了建立岩心含水饱度对波速和弹性参数的影响的认识,我们采取参数可控的人造岩心样品进行相应的实验研究.实验在常温常压条件下进行,根据饱水岩心和干燥岩心的重量之差确定人造岩心的含水饱和度,并且,通过示波器采集到的波形的初至时间确定波速,从而计算出不同含水饱和度条件下的人造岩心的弹性参数.
在石油领域中的科学研究中,利用天然岩心进行岩石物理实验的重要手段,但是天然岩心组成成分具有多样性,孔隙结构复杂,且不同地区的岩心差异较大.为了研究含水饱和度对声学参数影响规律,按照天然岩心的矿物组分和孔隙结构特征,定量控制其孔隙度和渗透率,有效的解决物理模型的相似性问题,人造岩心因其定量控制实验参数、性能稳定、重复性好,所以在岩心含水饱和度对声学参数影响的研究的理论和实验方面研究中有着重要指导作用(皮彦夫,2010;徐洪波等,2011).
1 双相介质人造岩心的制作工艺研究 1.1 胶结剂人造岩心通常有石英砂环氧树脂胶结、石英砂填砂管和石英砂磷酸铝胶结三种,其中石英砂环氧树脂胶结模型稳定性较高,并且更加适合用于制备双相介质物理模型(皮彦夫,2010),所以,本文采取环氧树脂作为胶结剂,制备具有定量孔隙度的工程材料双相介质物理模型.
环氧树脂作为胶结剂,最好选取中等环氧值的环氧树脂,一般采取0.25~0.45的树脂,由于环氧树脂的强度和交联度的大小有关,所以,环氧值高的环氧树脂固化后交联度高,环氧值低的环氧树脂固化后交联度低,故引起强度上的差异,但是,如果采取环氧值过高的环氧树脂,虽然制备出的人造岩心强度很大,但是较脆,不利于人造岩心的切割,所以,选取中等环氧值的环氧树脂作为交联剂,既能够保证人造岩心的硬度,又可以使得人造岩心可以完成钻、切、磨等加工程序.
人造岩心的制作过程中,环氧树脂的用量直接影响着模型的强度、孔隙度、渗透率和颗粒分布均匀程度,因此,选取合理的环氧树脂胶结剂用量,对于制备具有定量孔隙度的工程材料双相介质物理模型十分重要.
1.2 石英砂颗粒在理论上,环氧树脂胶结剂的用量应与石英砂的表面积成正比例关系,通过这种方式制备的人双相介质人造岩心物理模型,可以有效的控制人造岩心的强度和胶结方式更为接近.
如图 1所示,我们选取的石英砂颗粒为基本为球形,并且颗粒大小均匀,本文共选取9种不同颗粒大小的石英砂,分别为30~50目、40~70目、60~70目、60~120目、100~200目、200目、400目、600目和800目,通过不同颗粒大小的石英砂以一定的比例进行混合,从而形成不同的石英砂颗粒堆积系统.不同颗粒堆积系统中的石英砂颗粒尺寸分布在人造岩心的制备工艺起着重要的作用,堆积颗粒系统不仅影响着人造岩心的性质,如孔隙度、密度、强度等,而且许多工艺性质也取决于颗粒尺寸分布,如流体的渗透速度、孔隙连通性等.

|
图 1 石英砂颗粒 (a)30~50目石英砂颗粒;(b)40~70目石英砂颗粒;(c)60~70目石英砂颗粒;(d)60~120目石英砂颗粒;(e)100~200目石英砂颗粒;(f)200目石英砂颗粒;(g)400目石英砂颗粒;(h)600目石英砂颗粒;(i)800目石英砂颗粒. Figure 1 Quartz particles of (a) 30~50 mesh; (b) 40~70 mesh; (c) 60~70 mesh; (d) 60~120 mesh; (e) 100~200 mesh; (f) 200 mesh; (g) 400 mesh; (h) 600 mesh; (i) 800 mesh. |
首先,将纯环氧树脂加热至60 ℃左右,从而去除环氧树脂中可能的结晶部分,并且降低环氧树脂的黏度;然后,将不同颗粒大小的石英砂颗粒与环氧树脂共混,并且按照一个方向充分搅拌,然后,在石英砂颗粒与环氧树脂的混合物进行研磨,为了是环氧树脂与石英砂颗粒不产生团聚现象,并且通过最大的目数的石英砂颗粒标准筛进行筛选,从而保证环氧树脂与单个石英砂颗粒进行均匀包裹,将配比好的实验原料浇注至如图 2a所示的模具中,并且通过不同的压力将实验原料压制成型,完全干燥后得到直径为25 mm的圆柱形双相介质人造岩心.图 2b为石英砂与环氧树脂产生团聚现象制备的双相介质人造岩心切片,由图可知,如果环氧树脂与石英砂没有充分混合均匀,制备的双相介质人造岩心会产生各向异性性质,并且孔隙连通性不好,从而使得流体不能够进行充填,不利于双相介质物理模型的研究.图 2c为改进工艺后的双相介质人造岩心切片,由图可知,将石英砂与环氧树脂充分混合,并且进行研磨,通过标准筛进行筛选等制备工艺后,制备的双相介质人造岩心样品不会产生局部环氧树脂团聚现象,颗粒分布均匀,孔隙连通性良好,有利于双相介质物理模型的流体填充,并且如图 2d所示,将双相介质人造岩心进行分层切割,可见整个岩心的石英砂与环氧树脂颗粒分布十分均匀,并且整个岩心从顶部到底部孔隙大小均匀,没有上层孔隙度小,底部孔隙度大的现象,从而保证流体在双相介质人造岩心中分布状态统一,孔隙形态一致,从而有利于双相介质物理模型实验研究.选取直径25 mm、高50 mm的孔隙度为19.1%的圆柱体砂岩进行微米尺度CT低分辨率扫描,分辨率为27 μm,共获取1200张二维图像.由二维扫描图像图 2e所示,在微米尺度下,微孔结构在空间分布上均匀,颗粒分布均匀,孔隙连通性良好.

|
图 2 a)双相介质人造岩心制备模具;(b)石英砂与环氧树脂产生团聚现象制备的双相介质人造岩心切片;(c)改进工艺双相介质人造岩心切片;(d)双相介质人造岩心分层切片;(e)双相介质人造岩心微米尺寸CT二维扫描图像 Figure 2 (a) the mould and accessories for the preparation of artificial core samples; (b) and (c) the cross-sectional images of the artificial core samples with/without aggregation; (d) Images of different sections of the artificial core samples; (e) 2-D CT scanning images of the artificial core sample |
选取双相介质人造岩心样品中微孔部分区域区域(二维切片数据440~891),在微米CT扫描尺度下,利用360°二维图像进行三维数值模拟,分析双相介质人造岩心骨架、孔隙结构及其相互连通关系等三维结构特征(见图 3),图 3a为双相介质人造岩心的CT扫描图片,图中橘黄色部分为双相介质人造岩心骨架,即石英砂颗粒,蓝色部分为孔隙,即为空气,图 3b为双相介质人造岩心石英砂骨架的CT扫描俯视图,图 3c双相介质人造岩心孔隙CT扫描俯视图,由图可知,本文制备的双相介质人造岩心孔隙连通性良好,有利于流体的填充实验研究.

|
图 3 (a)双相介质人造岩心的CT扫描图片,(b)双相介质人造岩心石英砂骨架的CT扫描俯视图,(c)双相介质人造岩心孔隙CT扫描俯视图 Figure 3 (a) 3-D CT scanning image of the artificial core sample; (b) Top-view CT scanning image of the quartz framework; (c) Top-view CT scanning image of the pores in the sample |
通过环氧树脂作为胶结剂,将不同颗粒大小的石英砂颗粒进行胶结成型,并且给予一定的制备压力,从而控制双相介质人造岩心的孔隙度大小,本文选取10个双相介质人造岩心进行弹性参数和物性参数的测试分析工作,其孔隙度分别为39.8%、30.2%、26.31%、21.12%、19.1%、16.82%、15.93%、10.19%、9.81%、4.45%,本文将双相介质人造岩心按照孔隙度的大小进行划分,将孔隙度小于10%的双相介质人造岩心样品定义为低孔隙度-样品,孔隙度介于10%和25%之间的双相介质人造岩心样品定义为中孔隙度-样品,孔隙度大于25%的双相介质人造岩心样品定义为高孔隙度-样品,由于孔隙度10.19%的双相介质人造岩心样品更加接近10%,所以我们将其归纳为低孔隙度双相介质人造岩心样品.
Cadoret等(1955, 1988)为调查流体的空间分布规律对弹性波传播的影响,分布采用了两种方式改变岩石中的含水饱和度:干燥排水法与减压排水法.干燥法中,岩石中每单位时间损失的水正比于样本与气体接触的表面积,且与气体的热力学状态有关,而与岩石的弹性参数无关.减压法中,将干燥岩石置于水中浸泡以自发吸水,最终样本能达到的水饱和度上限与岩石的物性及颗粒的润湿性有关,一般在60%~80%之间,然后将水压恢复为大气压,并反复重复“减压-恢复”这一过程,从而使含水饱和度不断上升,含气饱和度不断下降.
本文采取的是自然吸水法,将不同孔隙度的双相介质人造岩心置于水中浸泡,并且根据双相介质人造岩心的孔隙度计算其含水饱和度,由于制备的样品孔隙连通性较好,自然吸水方式可以使含水饱和度达到60%~80%左右,当双相介质人造岩心样品达到自然吸水上限时,则采取抽真空减压方式,直至达到完全水饱和的状态.
2.2 双相介质人造岩心速度测试设备本文测量人造岩石的声速主要以超声穿透法为主, 所谓超声穿透法就是向平整光滑的双相介质人造岩心样品的末端施加超声波, 然后测量到达样品另一端的声波所经历的时间.将超声发射换能器和超声接收换能器固定在双相介质人造岩心样品两端, 表面涂抹适量的耦合剂进行耦合, 换能器分别接于脉冲发生器的超声穿透法接口的发射端和接收端,通过脉冲发生器产生的脉冲在发射端换能器产生超声波, 测量接收端的波形, 通过对比同步信号和接收的信号时间差, 计算出声波在岩石中的传播速度.
超声波换能器每次只能选择一种(纵波或横波)模式进行发射, 接收时示波器两个信道可以同时接收纵波、横波, 实际有用的信号是与发射模式一致的波形, 本次实验是常温常压条件下的测量双相介质人造岩心声学测试系统(如图 4所示),其中脉冲信号发生器采用奥林巴斯5077设备, 设定实验采用的纵波声波频率为500 kHz, 横波声波频率为500 kHz; 示波器采用Agilent(安捷伦)TDS2014数字存储示波器, 带宽300 MHz, 最大采样率达2 Gsa/s.

|
图 4 测量双相介质人造岩心声学测试系统 Figure 4 The acoustic testing system for two-phase medium based artificial cores |
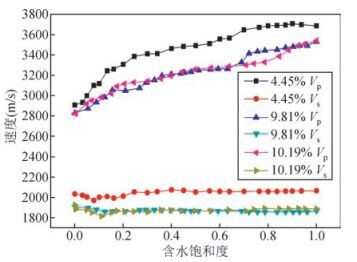
本文将双相介质人造岩心按照孔隙度小于10%,10%~25%,大于25%进行划分,图 5为孔隙度小于10%的双相介质人造岩心速度随含水饱和度的变化关系,由图可知,当双相介质人造岩心孔隙度小于10%时,含水饱和度由0增加至0.3时,纵波速度以较快的速率增长,含水饱和度由0.3增加至0.7时,纵波速度增长速率减缓,当含水饱和度大于0.7时,纵波速度变化趋于恒定,由此可见,孔隙度小于10%的双相介质人造岩心样品纵波速度随含水饱和度的增加总体呈现线性上升的趋势.横波速度随含水饱和度增加基本上没有变化,一直保持一个恒定的速度,在含水饱和度由0增加至0.1时,横波速度有略微的降低.
|
图 5 孔隙度小于10%的双相介质人造岩心速度随含水饱和度的变化关系 Figure 5 The evolution of the velocities of elastic waves when the water saturation of the samples (porosity of < 10%) increased |
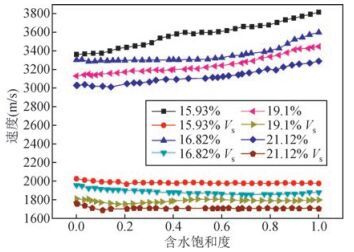
图 6为孔隙度10%~25%的双相介质人造岩心速度随含水饱和度的变化关系,由图可知,当双相介质人造岩心孔隙度介于10%至25%之间时,含水饱和度由0增加至0.6时,纵波速度增长速率较缓,当含水饱和度大于0.6时,纵波速度增长速率增大但仍保持线性增长规律,呈明显的二段近线性增长模式,由此可见,孔隙度介于10%至25%之间的双相介质人造岩心样品纵波速度随含水饱和度的增加总体呈现先平稳后上升的趋势.横波速度随含水饱和度增加基本上没有变化,一直保持一个恒定的速度,在含水饱和度由0增加至0.1时,横波速度有略微的降低.
|
图 6 孔隙度10%~25%的双相介质人造岩心速度随含水饱和度的变化关系 Figure 6 The evolution of the velocities of elastic waves when the water saturation of the samples (porosity of 10%-25%) increased |
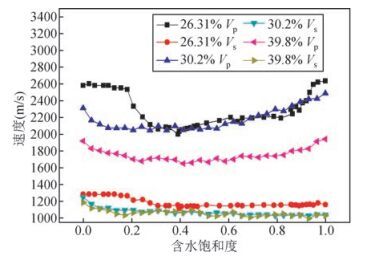
图 7为孔隙度大于25%的双相介质人造岩心速度随含水饱和度的变化关系,由图可知,当双相介质人造岩心孔隙度大于25%时,含水饱和度由0增加至0.3时,纵波速度以较快的速率降低,含水饱和度由0.3增加至0.7时,纵波速度趋于恒定,当含水饱和度大于0.7时,纵波速度呈现出线性快速回升的变化趋势,由此可见,孔隙度大于25%的双相介质人造岩心样品纵波速度随含水饱和度的增加总体呈现先下降后上升的趋势.横波速度随含水饱和度增加基本上没有变化,一直保持一个较为恒定的速度,在含水饱和度由0增加至0.2时,横波速度有略微的降低.
|
图 7 孔隙度大于25%的双相介质人造岩心速度随含水饱和度的变化关系 Figure 7 The evolution of the velocities of elastic waves when the water saturation of the samples (porosity of >25%) increased |
将不同孔隙度的双相介质人造岩心纵波速度随含水饱和度的变化关系进行数据拟合,按照小于10%,10%~25%,大于25%三个类型进行分类,分别对每条曲线进行归一化,设最大速度为Vpmax,各数据点速度为Vp,则有:
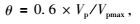
|
(1) |
我们称θ为归一化参数,则所有数据都被整理为一组0~0.6之间分布的数值.对每组数据进行拟合可得各条曲线对应的曲线表达式为
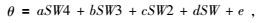
|
(2) |
其中SW为样品含水饱和度.对组内的表达式求取算术平均,可得组内所有曲线算数平均曲线(如图 5和图 6所示),我们认为这样的曲线可以代表该组样品的客观趋势.
如图 8所示,总体来说,当双相介质人造岩心样品为低孔隙度,即孔隙度小于10%时,纵波波速会随样品含水饱和度的增加而呈现上升趋势;而当双相介质人造岩心样品为中孔隙度,即孔隙度介于10%至25%之间时,在含水饱和度在0至0.5之间时,纵波速度以缓慢的增长速率上升,含水饱和度大于0.5时,纵波速度呈现出加速线性上升的趋势;当双相介质人造岩心样品为大孔隙度时,即孔隙度大于25%时,纵波波速并不随双相介质人造岩心样品含水饱和度的增加而呈现简单的上升趋势,而是先下降,在含水饱和度在0.4~0.5时达到最低值,然后开始上升,逐渐恢复到比含水饱和度为0略高的范围.
|
图 8 不同孔隙度的双相介质人造岩心纵波速度随含水饱和度的变化关系 Figure 8 The evolutions of the average velocities (different porosities) of P waves when the water saturation of the samples increased |
当流体与双相介质人造岩心接触时,单位面积的流体与石英砂骨架表面黏附时,对外所做的功称为黏附功,黏附功是流体能够润湿石英砂骨架的一种量度,黏附功越大,流体越能够润湿石英砂骨架,固-液结合的越牢,在润湿过程中,消失了单位流体表面和固体表面,产生了单位固体和液体界面,单个石英砂颗粒表面包裹了3至4层水分子,从而颗粒之间的紧密接触结合变弱,双相介质人造岩心样品的刚度变小,导致体积模量降低,纵波速度也降低.
当双相介质人造岩心样品为小孔隙度时,孔喉半径较小的孔隙由于毛细管作用流体比较容易进行充填,少量流体即可填充大量孔隙,双相介质人造岩心样品体积模量快速增大,从而纵波速度随含水饱和度的增大明显升高,并且流体填充引起的弹性模量影响大于润湿作用的影响,所以,低孔隙度的双相介质人造岩心速度随含水饱和度的增加呈现出线性增大的趋势;而中等孔隙度的双相介质人造岩心样品,其流体填充对孔隙填充带来的影响和润湿作用相互抵消,所以在含水饱和度在0至0.5之间时,纵波速度以缓慢的增长速率上升,含水饱和度大于0.5时,纵波速度呈现出线性上升的趋势;当双相介质人造岩心样品为大孔隙度时,孔隙孔喉半径较大的孔隙较多,在含水饱和度较低时,润湿作用大于孔隙纵横比的影响,所以,纵波波速并不随双相介质人造岩心样品含水饱和度的增加而呈现简单的上升趋势,而是先下降,在含水饱和度在0.4~0.5时达到最低值,然后开始上升,逐渐恢复到比含水饱和度为0略高的范围.而三者在最后都有迅速的增大,我们则认为是由于本身被封在岩石内部的大量分散气泡被排出,固液分界面减少导致了最后速度的迅速增大.
2.4 双相介质人造岩心弹性参数分析图 9为双相介质人造岩心饱水前后弹性模量变化示意图,由图可知,双相介质人造岩心由完全干燥的情况充填流体,直至完全饱水时,体积模量K在双相介质人造岩心饱水前后没有重叠部分,并且由于流体的影响,体积模量增加较大,说明体积模量K是识别流体的敏感因子,杨氏模量E和剪切模量μ在饱水前后几乎重叠,但是总体呈现出增大的趋势,说明杨氏模量和剪切模量对流体不敏感,由于双相介质人造岩心随着样品含水饱和度的增加,纵波速度比横波速度变化率大,从波速纵横比增加,泊松比v变大,并且泊松v增大的幅度最大,说明泊松比v是识别流体的最敏感指示因子.
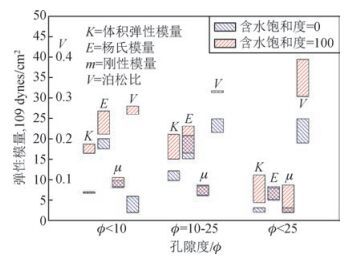
|
图 9 双相介质人造岩心饱水前后弹性模量变化示意图 Figure 9 The elastic parameters of the samples with different porosities before and after water penetration. |
随着我国油气勘探开发工作的不断深入,扩大油气发现的焦点已逐渐向复杂地区延伸.由于孔隙结构和各种充填介质的性质差异,利用地震和声波测井资料难以满足储层声学特征的研究需求,因此,研究双相介质中部分饱和的多种孔隙介质中声波的传播规律,通过人造岩心模型定量分析不同含水饱和度的岩心弹性参数变化规律,对油气田声波和地震波勘探有着十分重要的意义.本文通过双相介质人造岩心的方法,探索双相介质人造岩心不同含水饱和度对声学参数的影响变化规律,并且得到了一定的理论认识:
(1) 通过控制石英砂颗粒大小与环氧树脂的配比比例,调节制备压力有效的控制双相介质人造岩心的孔隙度,并且通过CT扫描进行微观结构表征,表明双相介质人造岩心微孔结构在空间分布上均匀,颗粒分布均匀,孔隙连通性良好.
(2) 当双相介质人造岩心样品为低孔隙度,即孔隙度小于10%时,纵波波速会随样品含水饱和度的增加而呈现上升趋势;而当双相介质人造岩心样品为中孔隙度,即孔隙度介于10%至25%之间时,在含水饱和度在0至0.5之间时,纵波速度以缓慢的增长速率上升,含水饱和度大于0.5时,纵波速度呈现出加速线性上升的趋势;当双相介质人造岩心样品为大孔隙度时,即孔隙度大于25%时,纵波波速并不随双相介质人造岩心样品含水饱和度的增加而呈现简单的上升趋势,而是先下降,在含水饱和度在0.4~0.5时达到最低点,然后开始上升,逐渐恢复到比含水饱和度为0略高的范围,而横波速度随含水饱和度增加基本上没有变化.
(3) 通过对比双相介质人造岩心饱水前后弹性模量变化特征,随着双相介质人造岩心样品含水饱和度的增加,纵波速度比横波速度变化率大,从而波速纵横比增加,泊松比v变大,相比于其他弹性参数,泊松v变化的幅度最大,说明泊松比v是识别流体的最敏感指示因子.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Ba J, Nie J X, Cao H, et al. 2008a. Mesoscopic fluid flow simulation in double-porosity rocks[J]. Geophysical Research Letters, 35(4): L04303. |
| [] | Ba J, Yang H Z, Xie G Q. 2008b. AGILD seismic modeling for double-porosity media[C].//Progress in Electromagnetics Research Symposium. Hangzhou, China: PIERS. |
| [] | Ba J, Cao H, Yao F C, et al. 2008c. Double-porosity rock model and squirt flow in the laboratory frequency band[J]. Applied Geophysics, 5(4): 261–276. DOI:10.1007/s11770-008-0036-0 |
| [] | Biot M A. 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. Low-frequency range[J]. The Journal of the Acoustical Society of America, 28(2): 168–178. DOI:10.1121/1.1908239 |
| [] | Biot M A. 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid[J]. Ⅱ. Higher frequency range[J]. The Journal of the Acoustical Society of America, 28(2): 179–191. DOI:10.1121/1.1908241 |
| [] | Cadoret T, Marion D, Zinszner B. 1955. Influence of frequency and fluid distribution on elastic wave velocities in partially saturated limestones[J]. Journal of Geophysical Research, 100(B6): 9789–9803. |
| [] | Cadoret T, Mavko G M, Zinszner B. 1988. Fluid distribution effect on sonic attenuation in partially saturated limestones[J]. Geophysics, 63(1): 154–160. |
| [] | Gassmann F. 1951. Elastic waves through a packing of spheres[J]. Geophysics, 16(4): 673–685. DOI:10.1190/1.1437718 |
| [] | Li D H, Dong S H, Zhao X C, et al. 2011. Seismic wave simulation of biphase EDA medium in coal-bed media[J]. Progress in Geophysics (in Chinese), 26(2): 654–663. DOI:10.3969/j.issn.1004-2903.2011.02.034 |
| [] | Li W X, Shi G, Wang H, et al. 2007. The study on the relationships of elastic properties of rock physics[J]. Progress in Geophysics (in Chinese), 22(5): 1380–1385. DOI:10.3969/j.issn.1004-2903.2007.05.007 |
| [] | Ma Z G, Wu X Y. 2007. Experimental study on elastic properties of oil[J]. Geophysical Prospecting for Petroleum (in Chinese), 46(1): 94–99. |
| [] | Parra J O. 1997. The transversely isotropic poroelastic wave equation including the Biot and the squirt mechanisms: Theory and application[J]. Geophysics, 62(1): 309–318. DOI:10.1190/1.1444132 |
| [] | Pi Y F. 2010a. Technology and application of making artificial cores by the cementation of quartzite and colophony[J]. Science Technology and Engineering (in Chinese), 10(28): 6998–7000. |
| [] | Pi Y F. 2010b. Type and application of special artificial cores[J]. Science Technology and Engineering (in Chinese), 10(31): 7724–7727. |
| [] | Wang D, Zhang H L, Wang X M. 2006. A numerical study of acoustic wave propagation in partially saturated poroelastic rock[J]. Chinese J. Geophys. (in Chinese), 49(2): 524–532. DOI:10.3321/j.issn:0001-5733.2006.02.027 |
| [] | Xi D Y, Xu S L, Xi J, et al. 2011. Experimental research on viscoelastic behavior for saturated rocks[J]. Chinese J. Geophys. (in Chinese), 54(9): 2302–2308. DOI:10.3969/j.issn.0001-5733.2011.09.013 |
| [] | Xu H B, Liu L, Li J G. 2011. The manufacturing methods of artificial sandstone core in Daqing oilfield[J]. Science Technology and Engineering (in Chinese), 11(30): 7344–7348. |
| [] | Xu H B, Sun L W, Hu J L, et al. 2009. Research and evaluation of the manufacturing methods of the mineral-wide simulated core in sandstone reservoir[J]. Offshore Oil (in Chinese), 29(3): 19–25. |
| [] | Xu W J, Guo J. 1994. Numerical simulation of elastic waves in fluid-saturated porous media[J]. Acta Geophysica Sinica (in Chinese), 37(S2): 424–433. |
| [] | Yang D H, Zhang Z J, Teng W J, et al. 2000. The study of two-phase anisotropy, questions and applied prospects[J]. Progress in Geophysics (in Chinese), 15(2): 7–21. DOI:10.3969/j.issn.1004-2903.2000.02.002 |
| [] | 李东会, 董守华, 赵小翠, 等. 2011. 煤储层双相EDA介质的地震波场模拟[J].地球物理学进展, 26(2): 654–663. DOI:10.3969/j.issn.1004-2903.2011.02.034 |
| [] | 李维新, 史謌, 王红, 等. 2007. 岩石物理弹性参数规律研究[J].地球物理学进展, 22(5): 1380–1385. DOI:10.3969/j.issn.1004-2903.2007.05.007 |
| [] | 马中高, 伍向阳. 2007. 石油流体弹性参数的实验研究[J].石油物探, 46(1): 94–99. |
| [] | 皮彦夫. 2010a. 石英砂环氧树脂胶结人造岩心的技术与应用[J].科学技术与工程, 10(28): 6998–7000. |
| [] | 皮彦夫. 2010b. 特殊人造岩心的类型及应用[J].科学技术与工程, 10(31): 7724–7727. |
| [] | 王东, 张海澜, 王秀明. 2006. 部分饱和孔隙岩石中声波传播数值研究[J].地球物理学报, 49(2): 524–532. DOI:10.3321/j.issn:0001-5733.2006.02.027 |
| [] | 席道瑛, 徐松林, 席军, 等. 2011. 饱和砂岩的黏弹行为的实验研究[J].地球物理学报, 54(9): 2302–2308. DOI:10.3969/j.issn.0001-5733.2011.09.013 |
| [] | 徐洪波, 刘莉, 李建阁. 2011. 大庆油田砂岩人造岩心制作方法[J].科学技术与工程, 11(30): 7344–7348. DOI:10.3969/j.issn.1671-1815.2011.30.005 |
| [] | 徐洪波, 孙良伟, 胡景新, 等. 2009. 砂岩储层全岩矿物模拟岩心的制作方法研究与评价[J].海洋石油, 29(3): 19–25. |
| [] | 徐文俊, 郭建. 1994. 流体饱和多孔介质中弹性波的数值模拟[J].地球物理学报, 37(S2): 424–433. |
| [] | 杨顶辉, 张中杰, 滕文吉, 等. 2000. 双相各向异性研究、问题与应用前景[J].地球物理学进展, 15(2): 7–21. DOI:10.3969/j.issn.1004-2903.2000.02.002 |
 2017, Vol. 32
2017, Vol. 32

