2. 连云港杰瑞自动化有限公司, 江苏 连云港 222000
2. JARI AUTOMATION Co., Ltd, Jiangsu Lianyungang 222000, China
构造应力是造成地层岩石各向异性的主要原因之一,由于应力造成孔隙空间中柔性部分的闭合(Nur and Simmons, 1969;Shapiro,2003;Shapiro and Kaselow, 2005),一般考虑裂隙的闭合,使得岩石弹性性质发生变化,同时影响了弹性波的传播.许多学者假设岩石随机分布硬币型裂隙(Nur,1971;Sayers,1988),并以此裂隙模型为基础研究应力诱导各向异性.Rasolofosaon(1998)和Prioul等(2004)应用三阶弹性理论来描述弹性特征和各向异性的应力相关,但一些模型参数很难从实验中获得,Sayers(2002, 2005, 2006)在没有考虑具体裂隙结构的基础上研究应力诱导速度各向异性,然而模型需要数值计算来获得各向异性的模式.基于若干假设,Gurevich等(2009, 2010, 2011)研究了小单轴应力诱导各向异性模型,模型将应力介质的弹性特征表示为有物理意义的若干参数,这些参数可以从静水压力实验中获得.
但是上述应力模型多是研究干燥岩石情况,而实际岩石需要考虑充填流体情况,弹性波扰动则会诱导流体在孔隙尺度上产生“局部流动”效应,即“挤喷流”效应,极大影响了岩石的弹性性质.Dvorkin和Nur(1993)指出,孔隙尺度上“局部流动”效应会造成岩石中弹性波速度相当可观的频散和衰减.唐晓明将Biot理论与挤喷流机制统一起来,提出了“含孔隙、裂隙介质弹性波动理论”(唐晓明,2011;Tang et al., 2012),该理论能很好地解释波在实际岩石中的衰减和频散,并被用来模拟孔、裂隙地层中的井孔声场和解释致密性砂岩和页岩地层声波测井数据中的油气显示.
唐理论同样考虑岩石中的裂隙在三维空间随机取向,岩石在宏观尺度上可以认为是均匀各向同性的,但唐理论考虑的是围压加载的情况,未考虑单轴应力加载下的情况,而实际地层往往由于应力造成岩石各向异性,因此本文将描述孔隙结构下流体局部流动的挤喷流引入至Gurevich等(2011)干燥岩石应力诱导各向异性模型中,建立了岩石弹性模量的频率相关性,本文模型同时考虑了单轴应力和充填流体的影响,可以更加真实、准确地描述实际岩石中弹性波的传播特征和衰减特征,在本文模型的基础上,我们理论模拟应力诱导含流体岩石介质弹性波各向异性的传播特征,并总结和解释弹性波传播受应力和流体影响的变化规律.
1 含流体介质应力诱导各向异性模型 1.1 干燥岩石应力诱导各向异性模型假设无应力状态时,裂隙随机分布,宏观上弹性介质为各向同性,当介质受到较小的单轴应力作用,垂直应力方向的裂隙优先闭合,平行应力方向的裂隙没有影响,因此介质呈现横观各向异性(TI).Sayers和Kachanov(1995)基于裂隙间无相互作用的假设研究了干燥裂隙对介质弹性性质的影响,Gurevich在此基础上研究了干燥岩石中应力诱导各向异性的模型,他建立了干燥介质的顺度张量Sijdry与单轴应力σ0间的关系(Gurevich等,2011),公式为
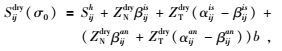
|
(1) |
其中,ZNdry和ZTdry分别为无应力状态干燥裂隙的法向和切向顺度,定义裂隙的法向和切向顺度比为B=ZNdry/ZTdry,加载单轴应力和裂隙闭合压力比为b=-σ0/Pc,Pc为裂隙闭合压力.张量Sijh为无裂隙各向同性孔隙介质的干燥体积模量,张量αijis和βijis描述无应力状态随机分布裂隙的贡献,张量αijan和βijis描述单轴应力下裂隙闭合对介质各向异性的影响.介质的刚度C与顺度S互为倒数,即刚度C=S-1.
1.2 各向异性Gassmann流体替换Gassmann将各向同性的流体替换方程推广至各向异性孔隙介质情况,他给出了各向异性饱和岩石的刚度张量Cijklsat与干燥岩石刚度张量Cijkldry的关系为
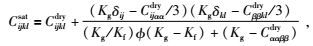
|
(2) |
其中,重复下标(αα,ββ,ααββ)采用爱因斯坦求和约定,狄拉克函数δij定义:i=j, δij=1;i≠j, δij=0.由于刚度张量具有特殊的对称性,采用Voigt标记可将各向异性流体替换方程写成类似各向同性的形式,公式为

|
(3) |
其中,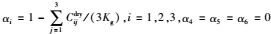
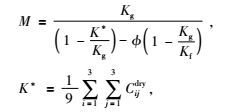
|
(4) |
其中,K*表示广义的干燥岩石的体积模量.
运用上述各向异性流体替换可以将应力诱导各向异性模型推广至低频饱和流体情况.
1.3 裂隙流体造成的附加有效模量地层往往是孔隙和裂隙并存(如图 1),前人对干燥岩石应力诱导各向异性的进行研究时,一般不考虑裂隙的具体形状,但是本文建立“挤喷流效应”下弹性模量的频率相关性则需要考虑具体的裂隙几何结构.为了分析任意加载频率下流体造成的附加模量,本文研究具体的硬币型裂隙模型(如图 2).

|
图 1 地层孔隙、裂隙示意图 Figure 1 Schematic diagram of pores and cracks in the formation |

|
图 2 硬币型裂隙挤喷流模型 Figure 2 Squirt flow model of penny-shaped crack |
附加模量K*可定义为弹性波动态加载下流体施加在裂隙表面的压力ΔF与裂隙形变ε的比值,公式为
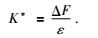
|
(5) |
图 2模型中孔隙和裂隙空间均含流体,δP为小振幅弹性波动引起的挤压,上下平面的平均位移为W,由此就在流体中产生压力变化δPC,由唐晓明(2011)裂隙模型和边界条件可以得到裂隙压力场的解为
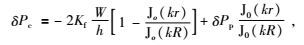
|
(6) |
其中,Jn(n=0,1) 是第一类n阶贝塞尔函数;R为裂隙半径;r为流体的流动方向;K是波数.
当孔隙干燥仅裂隙充填流体时,即式(6) 中孔隙压力δPp=0,模型退化为Murphy裂隙模型(Murphy et al., 1986).式(6) 中裂隙压力场变为
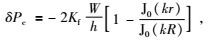
|
(7) |
式(7) 的结果与Gurevich基于Murphy裂隙模型求解的裂隙压力场结果一致(Gurevich等,2010).
裂隙被模拟为硬币型扁平充流体空间,外加压力扰动δP在孔隙、裂隙中产生的压力变化分别为δPP和δPC,压力作用下裂隙的张缩产生裂隙与孔隙间的挤喷流效应.
唐晓明等人(唐晓明,2011;Tang et al., 2012)给出了描述裂隙和孔隙间局部流动的挤喷流函数Sw与孔隙、裂隙间流体流量q的关系,公式为
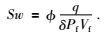
|
(8) |
挤喷流Sw的表达形式为
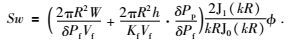
|
(9) |
考虑到裂隙的体积远小于孔隙体积,因此介质中流体体积近似为孔隙体积,即Vf~Vp.正因为如此,裂隙挤入孔隙空间的流体体积很小,不足以改变孔隙中的压力,故δPf~δPp.硬币型裂隙“孔隙度”φc=πR2h/V,总孔隙度φ=Vf/V,对于我们考虑的介质而言,裂隙体积远小于孔隙体积,即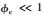
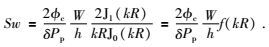
|
(10) |
由此可得到孔隙压力δPp与挤喷流Sw的关系为
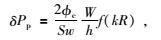
|
(11) |
其中,频率变化因子f(kR)=2J1(kR)/(kRJ0(kR)),宗量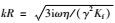
将式(11) 代入式(6),并对裂隙表面积分可得到裂隙表面的压力ΔF表达式为

|
(12) |
化简后得到ΔF为
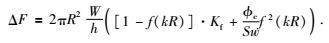
|
(13) |
将式(13) 代入式(5),根据裂隙形变ε=W/h,可得到硬币型裂隙模型中流体挤喷效应造成的附加模量K*为
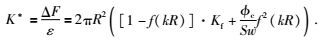
|
(14) |
低频情况(ω→0),频率因子f(kR)→1,挤喷流量q达到最大,并且裂隙、孔隙流体压力逐渐平衡,裂隙压力等于孔隙压力δPp,此时K*→2πR2φc/Swmax;高频情况(ω→∞),频率因子f(kR)→0,裂隙中流体没有足够时间流入孔隙空间,流体锁闭在裂隙空间,则K*→2πR2Kf.由式(14) 与低频、高频情况对比可知:在任意给定频率,未弛豫流体体积模量可以修正为
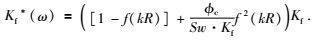
|
(15) |
Mavko和Jizba(1991)考虑了裂隙流体未弛豫对裂隙形变刚性的影响,但是受裂隙充填流体可压缩性的影响较大.Gurevich等(2009)将高频(未弛豫)模量推广至不受流体压缩性限制的一般表达式为

|
(16) |
Gurevich建立干燥、高频(未弛豫)情况裂隙垂向顺度与介质体模量的关系为

|
(17) |
将式(17) 代入式(16) 可得到无应力状态高频情况裂隙垂向顺度ZNuf与干燥裂隙垂向顺度ZNdry的关系为
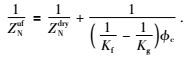
|
(18) |
高频情况裂隙垂向顺度ZNuf考虑了流体充填对于裂隙刚度的影响,且不受裂隙形状的影响.但为了考虑介质弹性模量的频率相关性,即裂隙垂向顺度ZNuf的频率相关性,我们需要考虑具体的微观裂隙形状,本文采用硬币裂隙模型,根据前面讨论的硬币型裂隙中流体未弛豫状态下的影响,可将式(18) 中Kf替换为式(15) 中Kf*,从而得到频率相关的裂隙垂向顺度ZNuf(ω),公式为
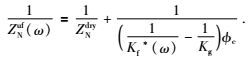
|
(19) |
考虑流体仅对裂隙垂向顺度ZN的影响,因此将式(6) 中的ZNdry替换为式(19) 的ZNuf,并结合各向异性流体替换方程,即可得到频率相关的应力诱导各向异性模型.
1.5 弹性波速度和衰减基于上述得到的频率相关的饱和岩石刚度张量,可以计算应力诱导各向异性介质的复速度,公式为
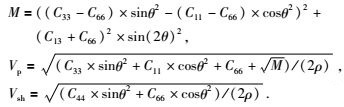
|
(20) |
由于孔隙介质的渗透率产生的孔隙流体与固体骨架之间的相对运动,纵波和快横波都有一定程度的衰减和频散,计算公式为
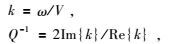
|
(21) |
其中,V为式(20) 中纵波和快横波任何之一的相速度,k为所对应波的波数,Q为品质因子,Re{k}和Im{k}分别取k的实部和虚部.
为了更清楚地看到应力和流体对介质弹性性质的影响,下面我们基于推广的模型来研究弹性波的传播特征.
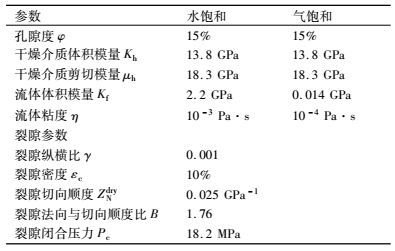
2 弹性波传播特征的数值模拟我们用上述方法和步骤来计算含流体介质应力诱导弹性波各向异性的特征,相对于Gurevich等干燥模型,饱和流体模型增加了裂隙密度和纵横比这两个重要的裂隙参数.表 1中列出了本文模型计算所用的基本参数.
|
|
表 1 应力诱导各向异性模型输入参数 Table 1 Input parameters of anisotropy model induced by stress |
图 3分别给出了饱和水(a)和饱和气(b)情况下不同压力下(0 MPa、10 MPa、20 MPa和30 MPa)弹性波随入射角的传播特征,弹性波的加载频率为10 kHz.首先需要说明的是本文入射角的方位是相对于单轴应力下而言的,0°入射方向为平行单轴应力的方向,90°入射方向即为垂直单轴应力的方向,Vp为纵波速度,Vsh为快横波速度.
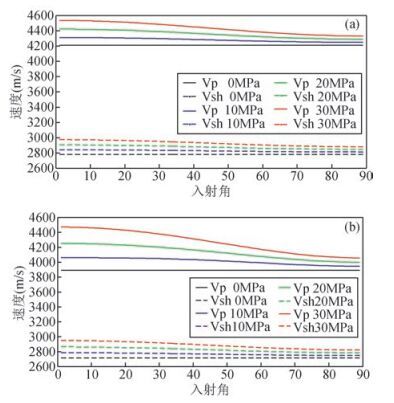
|
图 3 饱和水(a)和饱和气(b)情况下不同压力下弹性波随入射角的传播特征 Figure 3 The change of elastic wave propagation characteristics of water saturation (a) and gas saturation (b)with incidence angle under different stress |
如图 3所示,无应力加载时,纵波和横波速度不随入射角变化,即纵波和横波均没有方向性,这与我们无应力状态下各向同性模型一致;存在应力加载时,纵波和横波速度在不同入射方向上不再相同,说明地层性质由各向同性变为各向异性,且0°至90°入射方向,纵波和横波速度逐渐降低,即沿着应力方向传播的波速最快,垂直应力方向传播的波速最慢,这主要是由于垂直应力方向裂隙优先闭合,而平行裂隙方向的裂隙不受影响,因此垂直应力方向的弹性波受裂隙影响最大,挤喷流作用最强,造成了垂直应力方向弹性波的显著衰减,速度慢,而平行应力方向的弹性波受裂隙影响较小,挤喷流造成的衰减最小,因此速度快;加载应力逐渐增大时,由于地层裂隙逐渐闭合,受裂隙影响减小,介质刚性增大,弹性波速度也随着应力增大而增加,并且由于垂直应力方向的裂隙逐渐闭合,平行应力方向裂隙不受影响,造成纵波和横波各向异性程度逐渐增大.
此外,由(a)和(b)对比可知,相对可压缩性大的含气介质,含水介质中挤喷流影响显著,弹性波受挤喷流的影响,速度变化范围较窄,并且纵波速度受流体类型影响较大,横波速度基本不受流体类型的影响,因此相对于纵波而言,横波对于介质中流体不敏感,这与横波为剪切波的性质一致.
图 4分别给出了饱和水(a)和饱和气(b)情况下不同入射角下(0°、45°和90°)弹性波随加载应力的传播特征,弹性波的加载频率为10 kHz.
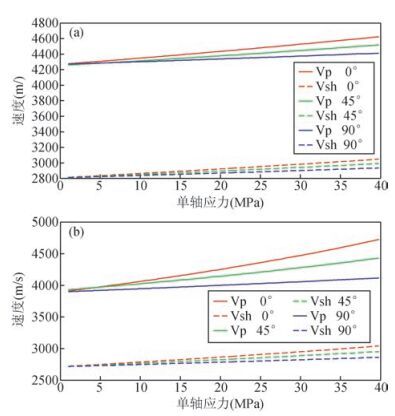
|
图 4 饱和水(a)和饱和气(b)情况下不同入射角下弹性波随压力的传播特征 Figure 4 The change of elastic wave propagation characteristics of water saturation (a) and gas saturation (b)with stress under different incidence angle |
图 4更直观地给出了弹性波速度随加载应力的变化规律:随着加载应力增大,纵波和横波速度增加,并且平行应力方向波的速度最大,垂直应力方向波的速度最慢.图 4同样反映了纵波受挤喷流的影响较大,横波对于流体类型不敏感.这些规律与图 3一致,彼此相互验证.
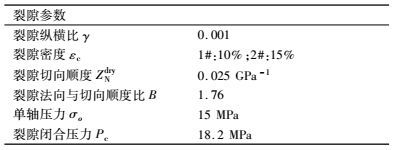
基于文章模型,我们研究了饱和水介质中弹性波的频散和衰减特征,表 2给出了裂隙输入参数.
|
|
表 2 裂隙输入参数 Table 2 Crack input parameters |
图 5分别给出了饱和水情况下加载应力为15MPa时不同入射角下(0°、45°和90°)弹性波(纵波P、快横波Sh)随加载频率的传播特征,频率范围100~108 Hz,用对数坐标给出.图 5(a)和(b)表明纵波和快横波在平行应力方向(0°方向)入射,频散最小,垂直应力方向(90°方向)入射,频散最大,这是由于垂直应力方向的裂隙优先闭合,平行应力方向的裂隙不受影响,因此垂直应力方向裂隙较发育,纵波和快横波能量衰减最大,平行应力方向相当于平行裂隙发育方向,能量衰减最小;图 5表明了由于高频时流体锁闭在裂隙中,造成了裂隙介质刚性增大,因此高频时弹性波速度快.
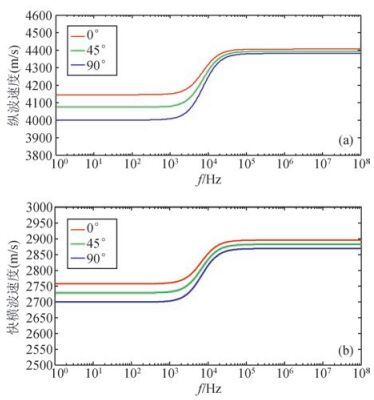
|
图 5 饱和水情况下、外加压力15 MPa时不同入射角下弹性波随加载频率的传播特征 Figure 5 The change of elastic wave propagation characteristics of water saturation with loading frequency under the stress of 15 MPa |
图 6~图 8分别给出了在平行加载应力方向(0°)和垂直加载应力方向(90°)加载应力由0 MPa变化至15 MPa时弹性波(纵波P、快横波Sh)随着加载频率的衰减特征.
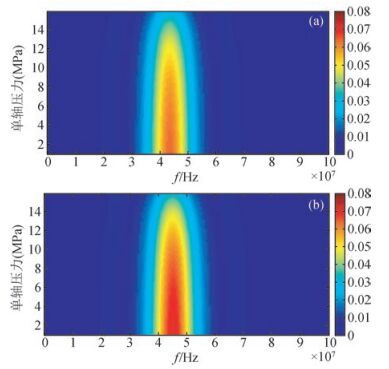
|
图 6 裂隙密度为0.1(a)和0.15(b)时0°入射纵波在不同压力和频率下的衰减特征 Figure 6 The change of P-wave attenuation of crack density of 0.1(a) and 0.15(b)of incidence angle 0 with stress and frequency |
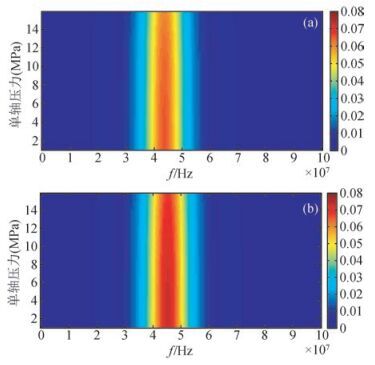
|
图 7 裂隙密度为0.1(a)和0.15(b)时90°入射纵波在不同压力和频率下的衰减特征 Figure 7 The change of P-wave attenuation of crack density of 0.1(a) and 0.15(b)of incidence angle 90 with stress and frequency |

|
图 8 0°(a)和90°(b)入射时Sh波在不同压力和频率下的衰减特征 Figure 8 The change of Sh-wave attenuation of incidence angle 0(a) and 90(b)with stress and frequency |
由前面的模拟结果可知:弹性波速度随加载应力的增大而增大,随加载频率的增大而增大;纵波和快横波速度在平行应力方向快,垂直应力方向慢.图 6~图 8弹性波衰减特征谱图则对上述规律的合理性给出了直观地解释和验证:随着加载应力的增大,弹性波的衰减减小,因此速度增大;纵波和快横波垂直应力方向的衰减比平行应力方向的衰减大,因此垂直应力方向速度低.
图 6~图 7还分别给出了在平行加载应力方向(0°)和垂直加载应力方向(90°)裂隙密度为10%(a)和15%(b)时纵波的衰减特征谱图.我们可以很清楚看到:由于裂隙密度增大造成挤喷流效应的增强,裂隙密度为15%的纵波衰减要大于裂隙密度为10%的纵波衰减,这也表明了裂隙的发育对于弹性波传播影响显著.
3 结论和认识本文研究的裂缝介质简化为各向同性的双孔隙介质模型,其中静态单轴应力和动态弹性波扰动都会对裂隙介质的弹性性质产生显著影响.因此,本文考虑了充填流体和应力诱导各向异性的影响,建立了含流体介质应力诱导各向异性模型,在此基础上,本文模拟了加载应力、流体性质和加载频率对于裂隙介质弹性特征的影响,对裂隙介质中弹性波传播规律及应力、流体的影响研究发现:
(1) 单轴应力造成垂直应力方向的裂隙优先闭合,使得应力方向弹性波速度显著增大,同时裂隙的闭合造成了挤喷流效应的减小,也使得应力方向弹性波的频散和衰减减小,单轴应力增大也造成了介质各向异性程度的增大.
(2) 纵波和横波速度随单轴应力变化明显,同时纵波传播受介质中流体影响显著,而横波几乎不受流体类型的影响,因此,纵波对于应力和流体敏感,横波对应力敏感,但对流体不敏感.
(3) 裂隙密度增大,即岩石裂隙发育,使得流体的挤喷效应显著增强,会造成弹性波的频散和衰减增大.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Dvorkin J, Nur A. 1993. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms[J]. Geophysics, 58(4): 524–533. DOI:10.1190/1.1443435 |
| [] | Gurevich B, Brajanovski M, Galvin R J, et al. 2009. P-wave dispersion and attenuation in fractured and porous reservoirs-poroelasticity approach[J]. Geophysical Prospecting, 57(2): 225–237. DOI:10.1111/gpr.2008.57.issue-2 |
| [] | Gurevich B, Makarynska D, de Paula O B, et al. 2010. A simple model for squirt-flow dispersion and attenuation in fluid-saturated granular rocks[J]. Geophysics, 75(6): N109–N120. DOI:10.1190/1.3509782 |
| [] | Gurevich B, Pervukhina M, Makarynska D. 2011. An analytic model for the stress-induced anisotropy of dry rocks[J]. Geophysics, 76(3): WA125–WA133. DOI:10.1190/1.3567950 |
| [] | Mavko G, Jizba D. 1991. Estimating grain-scale fluid effects on velocity dispersion in rocks[J]. Geophysics, 56(12): 1940–1949. DOI:10.1190/1.1443005 |
| [] | Murphy W F, Winkler K W, Kleinberg R L. 1986. Acoustic relaxation in sedimentary rocks: Dependence on grain contacts and fluid saturation[J]. Geophysics, 51(3): 757–766. DOI:10.1190/1.1442128 |
| [] | Nur A. 1971. Effects of stress on velocity anisotropy in rocks with cracks[J]. Journal of Geophysical Research, 76(8): 2022–2034. DOI:10.1029/JB076i008p02022 |
| [] | Nur A, Simmons G. 1969. Stress-induced velocity anisotropy in rock: An experimental study[J]. Journal of Geophysical Research, 74(27): 6667–6674. DOI:10.1029/JB074i027p06667 |
| [] | Prioul R, Bakulin A, Bakulin V. 2004. Nonlinear rock physics model for estimation of 3D subsurface stress in anisotropic formations: Theory and laboratory verification[J]. Geophysics, 69(2): 415–425. DOI:10.1190/1.1707061 |
| [] | Rasolofosaon P. 1998. Stress-induced seismic anisotropy revisited[J]. Revue De L'Institut Francais du Pétrole, 53(5): 679–692. DOI:10.2516/ogst:1998061 |
| [] | Sayers C M. 1988. Stress-induced ultrasonic wave velocity anisotropy in fractured rock[J]. Ultrasonics, 26(6): 311–317. DOI:10.1016/0041-624X(88)90028-5 |
| [] | Sayers C M. 2002. Stress-dependent elastic anisotropy of sandstones[J]. Geophysical Prospecting, 50(1): 85–95. DOI:10.1046/j.1365-2478.2002.00289.x |
| [] | Sayers C M. 2005. Sensitivity of elastic-wave velocities to stress changes in sandstones[J]. The Leading Edge, 24(12): 1262–1266. DOI:10.1190/1.2149646 |
| [] | Sayers C M. 2006. Sensitivity of time-lapse seismic to reservoir stress path[J]. Geophysical Prospecting, 54(3): 369–380. DOI:10.1111/gpr.2006.54.issue-3 |
| [] | Sayers C M, Kachanov M. 1995. Microcrack-induced elastic wave anisotropy of brittle rocks[J]. Journal of Geophysical Research, 100(B3): 4149–4156. DOI:10.1029/94JB03134 |
| [] | Shapiro S A. 2003. Elastic piezosensitivity of porous and fractured rocks[J]. Geophysics, 68(2): 482–486. DOI:10.1190/1.1567215 |
| [] | Shapiro S A, Kaselow A. 2005. Porosity and elastic anisotropy of rocks under tectonic stress and pore-pressure changes[J]. Geophysics, 70(5): N27–N38. DOI:10.1190/1.2073884 |
| [] | Tang X M. 2011. A unified theory for elastic wave propagation through porous media containing cracks—an extension of Biot's poroelastic wave theory[J]. Sci. China Earth Sci., 54(9): 1441–1452. DOI:10.1007/s11430-011-4245-7 |
| [] | Tang X M, Chen X L, Xu X K. 2012. A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations[J]. Geophysics, 77(6): D245–D252. DOI:10.1190/geo2012-0091.1 |
| [] | 唐晓明. 2011. 含孔隙、裂隙介质弹性波动的统一理论——Biot理论的推广[J].中国科学:地球科学, 41(6): 784–795. |
 2017, Vol. 32
2017, Vol. 32