2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266061
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266061, China
在地震勘探中,复杂的近地表覆盖层通常制约着地下构造的精确成像,为了避免覆盖层的影响,需要建立精确的近地表速度模型,而在目前的地震勘探技术中这仍是一个难题.虚源法通过逆时重构将井下检波器变为虚拟震源从而避免复杂近地表的影响,为解决这一问题提供了新的途径.
壳牌石油公司的Calvert(2004)提出了一种地表激发井中检波器接收的观测方式的新成像方法,并申请了专利,这就是后来的虚源法.Bakulin和Calvert(2004, 2006)首先提出虚源法的概念,利用逆时不变原理对虚源法的理论基础进行了详细阐述,并将虚源法应用到复杂覆盖层地区的成像和储层监控.常规虚源法的观测方式是震源放置在地表而在覆盖层之下的井中分布检波器,优点是可以避开复杂覆盖层对地震记录的污染,并且覆盖层越复杂,虚源重构的质量越好,这是因为复杂覆盖层通过散射增加了地表震源的有效孔径,与声学中的超分辨率概念(Tsogka and Papanicolaou, 2002)类似.而且由于仅在地表激发地震波,使得虚源能量主要向下辐射,避免了井下真实震源勘探所造成的地表反射成像.地震勘探中,剪切波的接收(三分量检波器)要比剪切波的激发容易得多,这使得重构虚拟剪切源成为一种非常有实用价值的技术,Bakulin等(Bakulin and Calvert, 2005; Bakulin et al., 2007a)实现了虚拟剪切源地震勘探,得到了地下的SS波成像以及沿井的S波速度剖面.Korneev和Bakulin (2006)对虚源法的理论基础进行了研究,指出虚源法是修正Kirchhoff-Helmholtz积分的一种应用.大多数有关虚源法的文章焦点都集中在虚源的几何特征,van der Neut和Bakulin(2009)对虚源的振幅特征进行了研究,提出了一种校正虚源记录振幅的方法.常规虚源法是将检波器转换为虚拟震源,Broggini等(2012)、Wapenaar等(2014a, b)和van der Neut等(2015)提出一种新的重构方法,称为Marchenko成像,其核心在于将地下某位置(没有检波器放置)转化为虚拟震源,其理论基础不再是逆时不变原理.
虚源法一个重要的理论要求是震源沿围绕检波器的封闭曲面分布,实际应用中一般不能满足,这就会在虚源记录中引入假象.为了压制这种假象,Mehta等(2007a, b)提出利用上下行波分离来提高虚源法的成像质量,并在OBC数据上进行了应用.另外,有限的震源孔径会造成互相关道集中的边界效应,不同的研究人员提出了不同的方法来压制:Mehta等(2007)与Snieder等(2006)通过对互相关道集进行边缘道衰减来压制端点震源造成的虚假同相轴,这是一种简单易行的办法.Melo等(2010)利用奇异值分解来增强稳相位区域的能量,得到压制虚假同相轴的效果,这与边缘道衰减的出发点是相反的.Jeong和Byun(2014)提出利用f-k滤波来压制虚假同相轴.
虚源法理论应用到不同的观测方式上有不同的成像优势,包括估计沿井速度(Bakulin et al., 2007b)、盐丘侧翼成像(Willis et al., 2006)、井间地震(Mehta et al., 2008; Byun et al., 2010)、储层监控、OBS成像(Carrière and Gerstoft, 2013)等.将虚源法应用到垂直井中的检波器记录上构建虚源检验炮,可以进一步估计沿井速度.常规地表地震勘探很难对陡峭的盐丘侧翼进行精确成像,而将虚源法应用到Walkaway VSP上可以对盐丘侧翼进行高精度的成像,而且可以在现场采集时同步进行.利用虚源法构建的虚拟井间记录与真实井间记录相比有很多优势,不仅可以控制虚拟震源的辐射方向和震源类型,而且可以直接通过不同波场成分来构建仅仅包含直达波或反射波的虚源记录,分别用于层析成像和反射地震成像.除了成像之外,虚源法的另一个主要用途是储层监控,复杂近地表以及近地表的季节变化给时移信号对比带来困难,虚源记录可以消除这些因素的影响,而且更好地满足观测系统的可重复性,有助于实现高保真度的时移地震勘探.
由于虚源法展现的独特魅力,最近几年国内很多研究人员(吴世萍等,2011;许卓等,2012;陈国金等,2013;Wang et al., 2014)对虚源法进行了初步研究,侧重于虚源法的数值模拟,对理论部分研究不多.本文通过逆时原理和扰动理论对虚源法的理论基础进行阐述,对比分析了虚源法的三种实现形式,利用数值模拟验证了边缘道衰减压制互相关道集边界效应的有效性.
1 方法原理 1.1 逆时不变原理虚源法(Virtual source method)是Fink等(Fink, 1992; Fink and Prada, 2001)研究的逆时声学在地震勘探上的应用,理论基础为波动方程的逆时不变性(Wapenaar et al., 2005),概念上与逆时声学又存在差异.逆时声学是震源激发的波场经散射介质传播被接收排列记录,将这个记录的波场进行逆时传播,最终波场能量会重新聚集在震源点位置,整个过程是通过实验装置完成的.与逆时声学相比,虚源法概念上有三点不同(Saul et al., 2007):① 在逆时传播的能量聚集在震源点之后,波场从这个震源点继续传播;② 应用互易理论使得地表震源与井中接收器的观测方式代替井中震源与地表接收器;③ 虚源法的逆时传播过程是通过数值计算实现的.
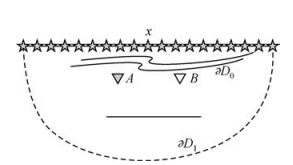
考虑如图 1所示的二维模型,地表∂D0上分布震源,近地表的曲线表示复杂覆盖层,介质内有A和B两个接收点,虚线∂D1和地表∂D0组成包围地下介质的封闭曲线∂D.为了利用逆时不变原理对虚源法进行物理解释,首先假设震源连续分布在封闭曲线∂D上.
|
图 1 虚源法示意图(A、B表示接收点,x表示地表震源,∂D0表示地表,∂D1表示地下介质边界) Figure 1 Virtual source method diagram |
接收点A记录沿∂D分布的真实震源激发的地震波,应用互易理论将A点变为激发点而∂D上分布接收点x.将所有x接收到的波场进行逆时处理,将此逆时波场作为震源信号在x上重新激发,零时刻波场能量重新聚集在A点,然后波场继续传播,此时的波场相当于是由A点处的震源激发,即接收点A变成了虚源.对介质内的接收点B而言,零时刻以后接收的波场相当于A点激发的波场,同样零时刻以前波场也会经过B点,这相当于A点处虚源激发的非因果响应.因此B点处的虚源波场可以写为
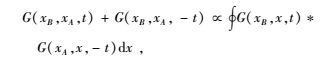
|
(1) |
式中,G(xB, xA, t)和G(xB, xA, -t)分别表示A点处虚源激发的因果响应和非因果响应,G(xB, x, t)表示∂D上真实震源激发在B点接收的波场.对一道记录进行逆时处理然后与另一道记录褶积等价于两道记录的互相关,上式可以理解为:将B点与A点接收到的波场进行互相关后沿震源位置x积分得到A点处虚源激发的因果响应和非因果响应的叠加.
上面假设震源连续分布于封闭曲线∂D上,实际上震源一般沿地表分布,并且有一定的震源间距,这两个原因限制了介质内两个接收点之间真实波场响应的提取.虚源记录可以用式(2) 进行计算,公式为
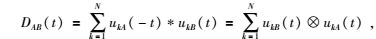
|
(2) |
式中,ukA(t)表示A点记录的震源k激发的地震道,ukA(-t)表示地震道ukA(t)的逆时记录,叠加是沿地表N个震源进行的,DAB(t)表示虚源A激发而B点记录的地震道,*表示褶积,⊗表示互相关.
1.2 扰动理论Vasconcelos和Snieder(2008)通过扰动理论对相关型干涉法进行了分析,指出不同波场成分在互相关过程中有不同的作用,这有助于虚源记录构建过程的理解与虚源法实现方法的选择.
将s点激发A点接收的波场表示为非扰动和扰动格林函数的叠加与震源子波的褶积,公式为
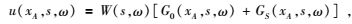
|
(3) |
式中,G0表示非扰动格林函数; GS表示扰动格林函数; W表示震源子波.A点与B点记录波场的互相关在频率域表示为
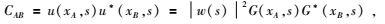
|
(4) |
式中,GxA, s表示s点激发A点接收的格林函数,G=G0+Gs.将CAB沿封闭曲线∂D积分可以得到B点激发A点接收的波场响应,表示为
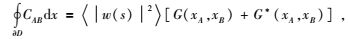
|
(5) |
式中,〈〉表示震源谱的平均,G(xA, xB)与G*(xA, xB)分别表示B点激发A点接收的因果与非因果格林函数.将式(3) 代入式(4) 可得:
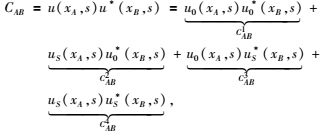
|
(6) |
式中,u0=WG0,uS=WGS.可以看出,全波场的互相关由四项不同波场成分的互相关组成.将式(6) 代入式(5) 可得:
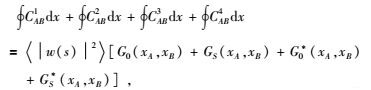
|
(7) |
式(7) 左边非扰动波场的互相关叠加得到右边B点与A点之间的因果与非因果非扰动波场的叠加.而B点处非扰动波场与A点处扰动波场的互相关叠加得到B点与A点之间的因果扰动波场,表示为
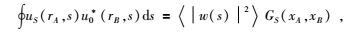
|
(8) |
式中,GS正是成像需要的波场成分.依据经典扰动理论使G0表示直达波,GS表示所有的散射波,将式(8) 应用到虚源法上,即虚源B点处接收的直达波与接收点A点处接收的散射波互相关叠加得到B激发而接收点A记录的散射波.
1.3 实现方法由于实际中震源不可能沿某一封闭曲线分布,使得虚源法有不同的实现方法.最简单的方法是将虚源位置与接收点位置记录的全波场进行互相关叠加得到虚源道集,这是理论推导的结果,但由于有限的震源孔径,这种方法重构的虚源波场存在大量的虚假同相轴.常规方法是对虚源位置记录的直达波与接收点位置记录的全波场进行互相关叠加,这种实现方式可以部分压制来自覆盖层的响应,更重要的是在实际应用中取直达P波使得虚源表现为向下辐射的P波震源.
上述两种方法都不能得到真实的地下响应,原因有两方面:有限的震源孔径会引入虚假同相轴;两种方法得到的波场响应中包含来自覆盖层和自由地表的响应,这是因为在接收点位置处利用的是全波场,其中下行波除了直达波之外,还存在来自覆盖层和自由地表的反射波.对波场记录进行上下行波分离,将虚源位置处的下行波与接收点位置处的上行波进行互相关叠加,可以压制上述两种原因造成的波场响应.
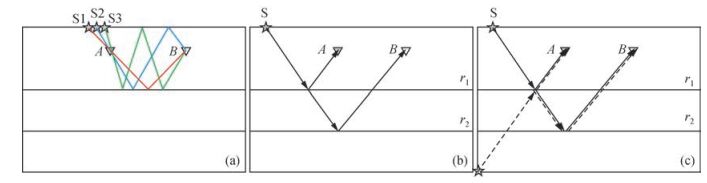
考虑图 2a所示的三层介质模型,震源位于地表,五角星表示稳相位震源点,倒三角表示井中两个接收点.对图 2a中S1稳相位点而言,虚源A与接收点B的互相关得到两点之间的物理走时,如图 2中红线所示.当震源路径如图 2b所示传播时,这时A点与B点接收到的波场均为主反射波,震源点s同样是稳相位点,这时A与B的互相关并没有对应两点之间任何物理走时,Snieder等(2006)称其为虚假多次波.如果存在如图 2c所示的震源,由于从界面r1的下界面发生反射时反射系数变为相应的负值,沿虚线路径传播的两点记录之间的互相关会与图 2b中记录的互相关抵消,由此可见虚假多次波是由震源孔径不完全造成的.从图 2b可以看出,到达A和B点的波场是上行波,如果在互相关之前限制虚源A点处的波场为下行波,虚假多次波就得到压制.
|
图 2 虚源法实现方法对比示意图 Figure 2 Comparison of implementation ways of virtual source method |
即使将虚源处的波场限制为下行波,如果接收点处取全波场,虚源记录中仍然会出现来自覆盖层及自由地表的反射波.对图 2a中S2稳相位点而言,A点与B点记录均为下行波,这时两点之间的互相关有明确的物理走时,如图 2a中蓝线所示,如果限制接收点B处的波场为上行波,这种类型的地表反射会得到压制.然而这种方法仍不能完全压制来自地表的反射,对图 2a中S3稳相位点而言,A点记录为下行波,B点记录为上行波,两者互相关有明确的物理走时,如图 2a中绿线所示.实际应用中,一般把上下行波分离与取时窗结合使用,将虚源位置处下行波的直达波部分与接收点位置处的上行波进行互相关,波场分离的作用是使虚源具有向下的辐射模式,取时窗使得虚源表现为P波震源,消除虚源的剪切能量(Bakulin and Calvert, 2006).
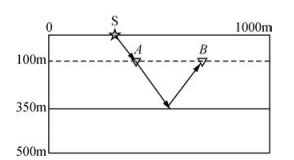
2 数值模拟 2.1 成分分析考虑如图 3所示的两层模型,模型大小为1000 m×500 m,反射界面位于地下350 m处,201个震源分布于地表,震源间隔5 m,A点(350 m,100 m)与B点(650 m,100 m)为两个接收点位置,利用声波有限差分进行模拟,不考虑自由地表的影响.
|
图 3 两层模型 Figure 3 Two-layer model |
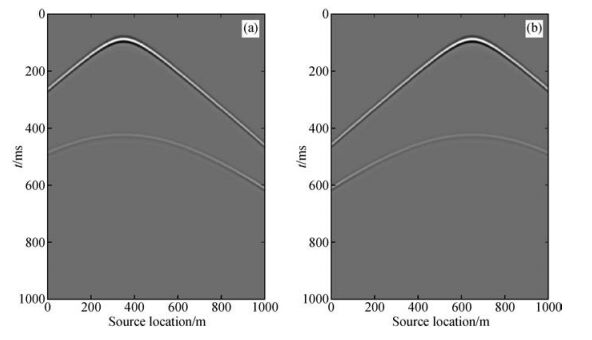
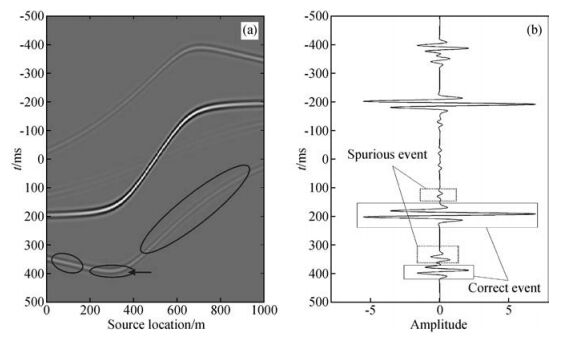
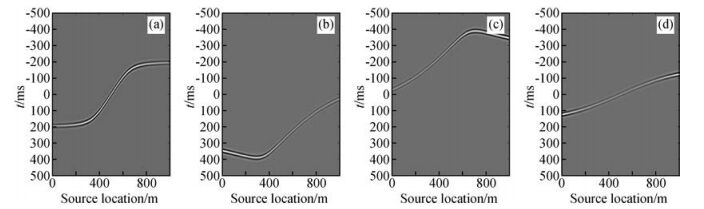
图 4a和b分别为A点与B点的共接收点道集.将B点与A点接收的记录互相关得到A点为虚源的相关道集,由四个不同的部分组成,如图 5a所示.将两点共接收点记录的不同波场成分进行互相关,结果如图 6所示,其中d表示直达波,s表示反射波.可以看出,图 5a中不同部分对应图 6中不同波场成分的互相关,即对应于扰动理论分析中的CAB1、CAB2、CAB3、CAB4.
|
图 4 共接收点道集 Figure 4 Common receive gather |
|
图 5 A点与B点全波场的互相关结果 Figure 5 Cross-correlation result of full wave field of A and B |
|
图 6 互相关成分分析 Figure 6 Cross-correlation component analysis |
图 5b为图 5a沿震源位置叠加得到的虚源记录,由沿零时刻对称的因果与非因果波场记录组成,实方框内为直达波与反射波.对简单模型而言,稳相位理论(Snieder et al., 2006)是解释虚源记录形成的有力工具,当震源位于图 3中地表S上时,其对应于互相关道集中的箭头位置,对应的时间与虚源记录中反射波的到时一致,称S点为稳相位点.稳相位点及其周围菲涅尔带内的相关道集称为稳相位区域,如图 5a中实线椭圆所示,虚线椭圆为非稳相位区域,稳相位区域对虚源记录的形成有主要贡献.在图 3所示的观测系统下,对虚源记录中的直达波而言没有对应的稳相位点,这是因为A点和B点位于同一个深度,其直达波对应的稳相位点位于地表无限远处.
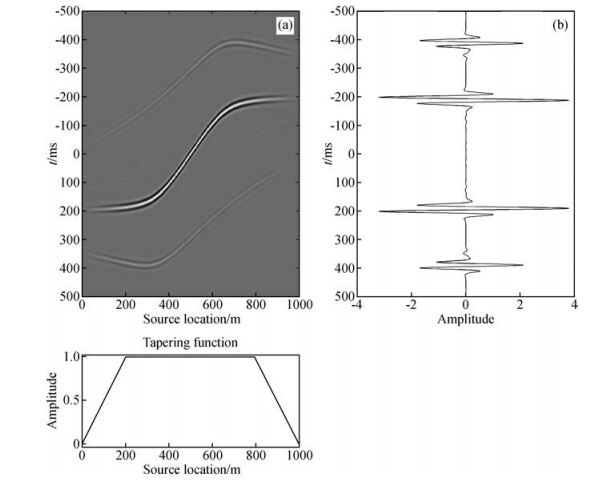
2.2 边界效应压制在图 5b中,虚方框内为明显的虚假波形,这是互相关道集端点处的记录在虚源记录中的反映,称为互相关道集的边界效应.压制这种边界效应的一种方法是对互相关道集进行边缘道衰减(Mehta et al., 2007),本文采用将互相关道集与梯形镶边函数对应相乘,梯形坡度的大小根据观测系统来试验确定,原则是不能伤害稳相位区域内的道集.图 7a为对图 5a进行边界效应压制后的相关道集,其虚源记录如图 7b所示,图 5b中虚方框内的波形得到了压制.
|
图 7 互相关道集的边界效应压制 Figure 7 Edge effect suppression of cross-correlation gather |
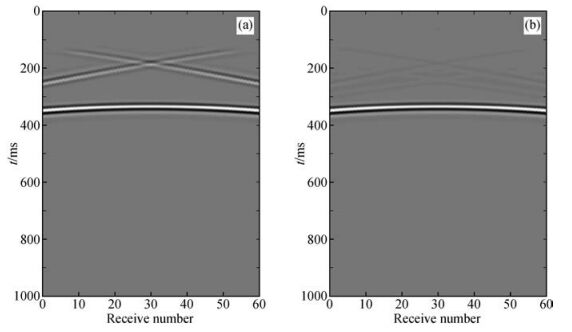
为了更明显地观察边界效应的影响,在接收点A与B之间间隔5 m分布接收点,共61个.图 8a为将中间位置的接收点作为虚源的炮集记录,上部的两个线性同相轴是边界效应造成的,图 8b是镶边后的虚源炮集,边界效应的影响得到很好地压制,图 8a和b均进行直达波切除.
|
图 8 虚源炮集的边界效应压制 Figure 8 Edge effect suppression of virtual shot gather |
考虑图 2所示的两层模型,这时考虑自由地表的影响,A点与B点之间间隔5 m分布接收点,将中间位置处的接收点作为虚源.
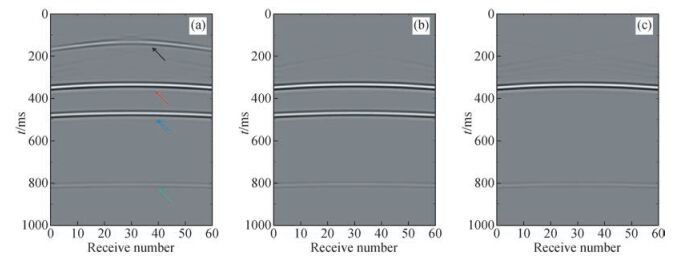
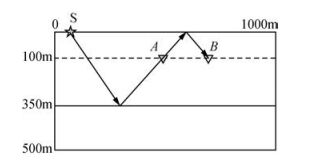
图 9a为将虚源与接收点的全波场进行互相关(方法一)得到虚源炮集,进行了直达波切除.黑色箭头所指同相轴的传播路径如图 10所示,红色箭头为地下界面的反射波,其传播路径与图 2a中红线路径类似,蓝色(绿色)箭头的传播路径与图 2a中蓝线(绿线)路径类似.图 9b为将虚源处的直达波与接收点的全波场互相关(方法二)得到的虚源炮集,同样进行了直达波切除.图 9a中黑色箭头表示的来自地表的反射波在图 9b中不存在,这是因为虚源处利用的是直达波所以不存在图 10所示的传播路径.图 9c为将虚源处下行波的直达波部分与接收点处的上行波互相关(方法三)得到的虚源炮集,图 9a中蓝色箭头指向的假象同相轴不存在,但绿色箭头指向的假象同相轴同样存在于图 9c中,这与理论证明是一致的.与图 9a和b不同,图 9c中本身就不存在直达波.
|
图 9 不同实现方法的虚源炮集 Figure 9 Virtual shot gathers of different implementation methods |
|
图 10 虚源处地表反射波的传播路径 Figure 10 The surface reflection's propagation path on virtual source position |
上述分析表明:在选择虚源法的实现方法时,可以进行上下行波分离的情况下(如OBC)应选择波场分离与加时窗相结合来实现波场重构,不能进行上下行波分离时应采用方法二来实现.
3 结论 3.1本文通过逆时不变原理给出了虚源法的理论基础,利用扰动理论分析了不同波场成分在重构道集中的作用,通过数值模拟进行了实现方法对比的讨论,得出结论如下:
(1) 虚源处的直达波与接收点处的反射波通过互相关叠加得到虚源位置激发的反射波;
(2) 利用波场分离和取直达波时窗可以极大地压制出现在虚源记录中的虚假同相轴;
(3) 边缘道衰减是压制互相关道集中边界效应的有效方法.
3.2虚源法以其特有的性质可以避开复杂近地表对地震成像的影响,并且在时移地震、井间地震勘探等方面有独特的优势,可以期望虚源法在地震勘探领域会发挥越来越重要的作用.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Bakulin A, Calvert R. 2004. Virtual source: New method for imaging and 4D below complex overburden[C].//SEG Technical Program Expanded Abstracts. Society of Exploration Geophysicists, 2477-2480. |
| [] | Bakulin A, Calvert R. 2005. Virtual shear source: A new method for shear-wave seismic surveys[C].//SEG Technical Program Expanded Abstracts. Society of Exploration Geophysicists, 2633-2636. |
| [] | Bakulin A, Calvert R. 2006. The virtual source method: Theory and case study[J]. Geophysics, 71(4): SI139–SI150. DOI:10.1190/1.2216190 |
| [] | Bakulin A, Mateeva A, Calvert R, et al. 2007a. Virtual shear source makes shear waves with air guns[J]. Geophysics, 72(2): A7–A11. DOI:10.1190/1.2430563 |
| [] | Bakulin A, Mateeva A, Mehta k, et al. 2007b. Virtual source applications to imaging and reservoir monitoring[J]. The Leading Edge, 26(6): 732–740. DOI:10.1190/1.2748490 |
| [] | Broggini F, Snieder R, Wapenaar K. 2012. Focusing the wavefield inside an unknown 1D medium: Beyond seismic interferometry[J]. Geophysics, 77(5): A25–A28. DOI:10.1190/geo2012-0060.1 |
| [] | Byun J, Yu J, Seol S J. 2010. Crosswell monitoring using virtual sources and horizontal wells[J]. Geophysics, 75(3): SA37–SA43. DOI:10.1190/1.3427175 |
| [] | Calvert R W. 2004. Seismic imaging a subsurface formation: US, US6747915[P]. 2004-06-08. |
| [] | Carrière O, Gerstoft P. 2013. Deep-water subsurface imaging using OBS interferometry[J]. Geophysics, 78(2): Q15–Q24. DOI:10.1190/geo2012-0241.1 |
| [] | CHEN Guo-Jin, CAO Hui, WU Yong-Shuan, et al. 2013. The seismic virtual source method and numerical experiments[J]. Progress in Geophysics (in Chinese), 28(5): 2725–2733. DOI:10.6038/pg20130556 |
| [] | Fink M. 1992. Time reversal of ultrasonic fields. I. Basic principles[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 39(5): 555–566. DOI:10.1109/58.156174 |
| [] | Fink M, Prada C. 2001. Acoustic time-reversal mirrors[J]. Inverse Problems, 17(1): R1–R38. DOI:10.1088/0266-5611/17/1/201 |
| [] | Jeong S, Byun J. 2014. Effective suppression of spurious events when generating reflected P-and PS-wave data using seismic interferometry[J]. Journal of Applied Geophysics, 106: 14–22. DOI:10.1016/j.jappgeo.2014.04.002 |
| [] | Korneev V, Bakulin A. 2006. On the fundamentals of the virtual source method[J]. Geophysics, 71(3): A13–A17. DOI:10.1190/1.2196868 |
| [] | Mehta K, Bakulin A, Kiyashchenko D, et al. 2008. Comparing virtual versus real crosswell surveys[C].//SEG Technical Program Expanded Abstracts, Society of Exploration Geophysicists, 1372-1376. |
| [] | Mehta K, Bakulin A, Sheiman J, et al. 2007a. Improving the virtual source method by wavefield separation[J]. Geophysics, 72(4): V79–V86. DOI:10.1190/1.2733020 |
| [] | Mehta K, Sheiman J, Snieder R, et al. 2007b. The virtual-source method applied to Mars field OBC data for time-lapse monitoring[C].//SEG Technical Program Expanded Abstracts. Society of Exploration Geophysicists, 2914-2918. |
| [] | Melo G, Malcolm A, Mikessel D, et al. 2010. Using SVD for improved interferometric Green's function recovery[C].//SEG Technical Program Expanded Abstracts. Society of Exploration Geophysicists, 3986-3990. |
| [] | Saul M J, Hartley B, Evans B. 2007. The virtual source method-verifying the concept using numerical and physical modelling[C]//ASEG Extended Abstracts 2007: 19th Geophysical Conference. Australian Society of Exploration Geophysicists, 1-6. |
| [] | Snieder R, Wapenaar K, Larner K. 2006. Spurious multiples in seismic interferometry of primaries[J]. Geophysics, 71(4): SI111–SI124. DOI:10.1190/1.2211507 |
| [] | Tsogka C, Papanicolaou G C. 2002. Time reversal through a solid-liquid interface and super-resolution[J]. Inverse Problems, 18(6): 1639–1657. DOI:10.1088/0266-5611/18/6/314 |
| [] | van der Neut J, Bakulin A. 2009. Estimating and correcting the amplitude radiation pattern of a virtual source[J]. Geophysics, 74(2): SI27–SI36. DOI:10.1190/1.3073003 |
| [] | van der Neut J, Wapenaar K, Thorbecke J, et al. 2015. An illustration of adaptive Marchenko imaging[J]. The Leading Edge, 34(7): 818–822. DOI:10.1190/tle34070818.1 |
| [] | Vasconcelos I, Snieder R. 2008. Interferometry by deconvolution: Part 1-Theory for acoustic waves and numerical examples[J]. Geophysics, 73(3): S115–S128. DOI:10.1190/1.2904554 |
| [] | WANG Le, HAN Li-Guo, LIU Yan-Qiu, et al. 2014. Study on virtual source method under complex overburden in horizontal well[J]. Global Geology, 17(2): 115–119. |
| [] | Wapenaar K, Fokkema J, Snieder R. 2005. Retrieving the Green's function in an open system by cross correlation: A comparison of approaches (L)[J]. J. Acoust. Soc. Am., 118(5): 2783–2786. DOI:10.1121/1.2046847 |
| [] | Wapenaar K, Thorbecke J, van der Neut J, et al. 2014a. On the focusing conditions in time-reversed acoustics, seismic interferometry, and Marchenko imaging[C].//SEG Technical Program Expanded Abstracts. Society of Exploration Geophysicists, 4613-4619. |
| [] | Wapenaar K, Thorbecke J, van der Neut J, et al. 2014b. Marchenko imaging[J]. Geophysics, 79(3): WA39–WA57. DOI:10.1190/geo2013-0302.1 |
| [] | Willis M E, Lu R R, Campman X, et al. 2006. A novel application of time-reversed acoustics: Salt-dome flank imaging using walkaway VSP surveys[J]. Geophysics, 71(2): A7–A11. DOI:10.1190/1.2187711 |
| [] | Wu S P, Peng G X, Huang L Z, et al. 2011. Seismic interferometry imaging based on virtual source estimation with complex overburden[J]. Chinese J. Geophys. (in Chinese), 54(7): 1874–1882. DOI:10.3969/j.issn.0001-5733.2011.07.021 |
| [] | XU Zhuo, HAN Li-Guo, WANG Li-Ming. 2012. Virtual source method for detecting subsurface steep structure[J]. Global Geology (in Chinese), 31(3): 554–560. DOI:10.3969/j.issn.1004-5589.2012.03.012 |
| [] | 陈国金, 曹辉, 吴永栓, 等. 2013. 虚源法地震技术及数值模型试验[J].地球物理学进展, 28(5): 2725–2733. DOI:10.6038/pg20130556 |
| [] | 吴世萍, 彭更新, 黄录忠, 等. 2011. 基于虚源估计的复杂上覆地层下地震相干成像[J].地球物理学报, 54(7): 1874–1882. DOI:10.3969/j.issn.0001-5733.2011.07.021 |
| [] | 许卓, 韩立国, 王立明. 2012. 虚拟震源方法用于探测地下陡倾角地质构造[J].世界地质, 31(3): 554–560. DOI:10.3969/j.issn.1004-5589.2012.03.012 |
 2017, Vol. 32
2017, Vol. 32


