2. 新疆财经大学网络与实验教学中心, 乌鲁木齐 830011
3. 长安大学计算地球物理研究所, 西安 710054
2. Xinjiang University of Finance and Economic, Vrümqi 830011, China
3. Institute of Computing Geophysics, Chang'an University, Xi'an 710054, China
层析成像始于医学中的CT技术,1976年Aki和Lee(1976)将其首次应用于地震学的研究中.经过三十多年的发展和完善,地震层析成像已成为目前研究地球内部结构行之有效的主要技术途径之一,并且出现了多种成像方法技术(成谷等,2002).
传统射线类走时成像方法一般采用规则网格单元(例如:2D中的矩形网格单元,3D中的立方体网格单元)模型参数化的方式,这种简单模型参数化可以很容易地通过网格节点的编号来确定该节点的空间坐标,从而节约内存空间.然而这种简单的模型参数化形式也存在比较多的问题.例如:若要对复杂区域进行较为精确的描述,则必须进行网格单元的精细剖分,从而增加计算时间.更为重要的是规则网格单元参数化对不规则起伏地表、以及地下不规则波阻抗界面无法进行准确的拟合,从而造成不必要的正演计算误差,进而导致反演过程中出现成像中的假象.
另一方面,从反演的角度来说,规则网格的精细剖分,意味着更多的未知模型参数要参与反演,理论上来说,则需要更多的射线进行覆盖, 故而求解的方程组的维数也将大大增加,数据对模型的约束也就越差.此外更多的未知参数意味着参数矢量中欠定的和位于零空间的分量数目更多, 性态大大变坏, 层析反演的难度增加, 通常需要加入正则化约束改变方程组的病态,而这又增加了存储量和计算量(成谷和张宝金,2006).
上述问题的解决方案之一则是采用不规则网格单元(较为理想的则是三角网格单元)进行模型参数化,便可以使上述诸多问题得到改善.例如可根据模型中不同区域物性的复杂程度来选择三角网格单元的大小,同时三角网格单元剖分对不规则起伏地表和地下波阻抗界面(含不规则异常体)的描述更加精确,从而确保了正演计算所需的计算精度.反演中由于未知模型参数相对较少,因此需要射线也相对较少, 故而待求解的方程组维数大大减小,总体上减少了反演的存储量(成谷和张宝金,2006).
基于不规则网格单元模型参数化下的射线追踪已取得了一些成果,例如:李波涛等(2009)将三角剖分和波前重建法相结合,实现了初至波射线路径和走时的快速计算;于师建和刘润泽(2010)实现了三角网射线追踪全局算法,为了对复杂区域进行精确描述,引入单元密度控制函数,进而可对一些复杂区域进行网格加密;兰海强和张忠杰(2013) 借助于流体力学中的贴体网格和坐标变换,引入了Lax-Friedrichs快速扫描法来求解与地形有关的程函方程以获取地震波初至走时场.上述几位学者的研究主要是解决了三角网格单元模型参数化下初至波走时的计算与射线追踪问题. Vinje等(1999)在开放模型的波前构造法中将三角网格应用到了反射界面的描述和波前面的描述上,并实现了反射波射线的追踪.Bai等(2011)提出了一种基于三角(2D)或四面体(3D)单元剖分下的最短路径射线追踪算法(Triangular Shortest-path Method, 以下简称TSPM),并实现了多震相地震射线路径的追踪与走时计算.
不规则网格的层析成像研究最早可追溯到20世纪80年代.Tarantola和Nercessian(1984)意识到在地震层析成像中使用固定的均匀网格的一些局限性并提出了“block-less”模型参数化方法;Sambridge等(1995)首次提出了Delaunay四面体和Voronoi多面体在地震层析成像方面的应用;Gudmundsson和Sambridge(1998)利用Delaunay四面体和Voronoi多面体进行模型参数化,使用直达P波层析成像改进了区域上地幔地球参考模型;Curtis和Snieder(1997)通过对给定的一组点进行用Delaunay三角化来描述模型的速度结构并用此方法研究了2D情况下的井间反演问题;Böhm等(2000)用Delaunay三角形和Voronoi多面体在3D反射层析成像中发展了一种自适应的反演方法;Sambridge和Faletič(2003) 使用自适应Delaunay四面体网格单元进行了全球的P波层析成像.国内对不规则网格层析成像的研究较少,成谷和张宝金(2006)对三角网格层析成像和矩形网格层析成像的优缺点进行了比较.于师建和刘润泽(2013)做了基于三角网格模型参数化的层析成像研究.上述学者所做的研究主要是不规则网格参数化下初至波走时层析成像问题.
本文所做的工作主要是用三角网格单元参数化的方式进行了层析成像研究,并引入反射波进行了多震相联合反演及同时反演.本文基于Multistage TSPM正演算法(Bai et al., 2011),结合共轭梯度求解带约束的阻尼最小二乘解反演算法,同时得到了三角网格单元下走时关于速度、走时关于反射界面的偏导计算公式,讨论并实现了三角网格单元模型参数化下二维复杂模型中地震多震相走时同时反演成像技术,本文的研究内容主要包括:(1) 反射界面已知时地震多震相走时联合成像技术;(2) 多震相走时联合同时反演速度模型和反射界面的方法技术.井间和深地震测深数值模拟实验结果表明,三角网格单元模型参数化下的多波成像、以及同时反演成像结果较为可信,可作为复杂介质中速度场和反射界面重建的一种有效方法.
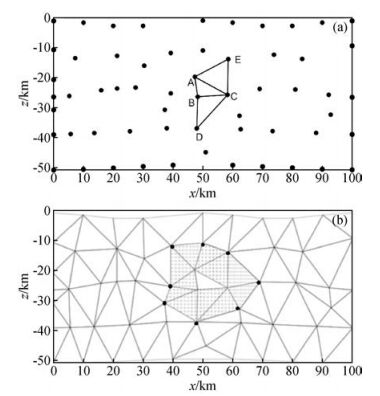
1 多震相射线追踪算法简介 1.1 三角网格单元的形成目前根据形成三角网格的步骤,可以将生成三角网格单元的方法大体上分为三大类:(1) 分而治之算法, 它的优点是时间效率较高,但是需要大量的递归运算;(2) 数据点渐次插入Lawson算法,这种算法虽然容易实现,但效率很低;(3) 改进的三角网生长算法,最初由Michael等(1980) 人提出,江剑霞等(2006)对该算法进行了改进,较大程度上提高了计算的速度, 而且比较容易实现.通过比较上述三种算法,我们采用第三种算法.此算法形成三角网格单元的过程如下(见图 1a所示,Bai et al, 2011):
|
图 1 三角网格生成与波前扩展示意图 (a)三角网格生成示意图;(b)不规则波前扩展(图中为清晰起见, 未标次级节点.灰色三角形即为第一次网格扩展的结果). Figure 1 Reconstruction of the triangular network and the propagation of the wavefront (a)Reconstruction of the triangular network; (b)The propagation of the irregular wavefront (In Figure for clear presentation, the secondary nodes are not shown. The grey triangle is the result of the first expansion). |
(1) 输入主节点坐标信息并对其进行编号;
(2) 在离散数据点集Qi中任取一点A,以点A为基点寻找与它距离最短的一点B.连接AB,即得到了三角形的一条基边,把该边作为扩展基边;
(3) 在扩展基边的顺时针方向在点集中寻找与该边两端点连成直线组成的夹角为最大的C点,作为第三个点,就组成了第一个三角形;
(4) 生成Delaunay三角形,对其编号并储存三角形的三个顶点的编号,再以三角形的两条新边(从基线起始点到第三点以及第二点到基线终止点) AC、BC作为新的基线;
(5) 重复3、4直至所有的基线处理完毕.
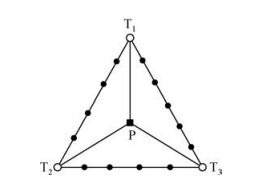
1.2 模型参数化利用Multistage TSPM进行射线追踪之前,首先要对模型进行三角网格单元参数化(如图 1所示),采用不规则三角单元进行模型参数化时,定义三角单元的三个角点为主节点.为了增加射线出射角的覆盖率(即:保证正演的计算精度),在三角单元的三条边上等间距插入节点(该节点称之为次级节点),三角网格单元内部没有节点,但炮点和检波点可置于其中(见图 2).模型中速度的采样在主节点上进行,次级节点上的速度则是通过速度插值得到(见1.3节).
|
图 2 速度插值示意图 (白色圆点是主节点, 黑色圆点是次级节点) Figure 2 The interpolation of the velocity (In figure white and black circles indicate primary and secondary nodes, respectively) |
下面给出最小走时和速度插值的计算方法.从炮点开始计算,节点走时的计算公式为
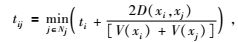
|
(1) |
其中,i是波前点当前的次级震源,j为需要计算的节点,Nj为需要计算的节点的集合. ti为炮点到达i节点射线的最小走时,D(xi, xj)是节点i和j之间的距离,V(xi)与V(xj)是i及j节点上的速度值.当i节点不是主节点时,可以通过以下方法求得i节点的速度值,公式为

|
(2) |
其中,vj表示i节点所在单元各主节点的速度值,在二维模型中k=3,uj为点在三角形中的面积坐标,举例来说,图 2中P点在三角形T1T2T3内的面积坐标uj可以表示为:

|
(3) |
(3) 式中S(ΔPT1T3)、S(ΔPT2T3)等表示各三角形的面积,当三点共线时三角形的面积为零.
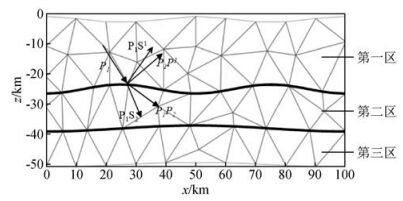
1.4 分区多步计算原理完成模型参数化和速度插值之后,根据反射界面的起伏形态将模型分成若干区域.从震源点开始计算,根据给定的震相种类对特定的射线进行追踪并计算节点的走时.这种对特定区域的计算可以避免对“无用区域”的计算,从而减少了计算时间.例如:从震源所在区域开始,逐区进行波前扫描.具体做法是,自震源所在的网格开始计算各节点的最小走时,等当前网格所有节点的走时计算结束后进行波前扩展,直到该区域内所有网格的节点都计算完毕,此时波前停留在离散速度界面上,保存离散速度界面上的走时和相应的射线路径.然后按照所要追踪的射线类型进行下一区的计算,直至追踪到检波器为止.举例说明(如图 3所示),如果是追踪P1P2或P1S2(下标代表下行波,上标代表上行波,数字为分区号),则应该首先调用1区的速度模型,从震源所在网格计算各网格节点的走时,然后进行网格扩展. 1区内所有网格计算完毕时,此时波前停留在离散速度界面上,从离散速度界面中走时最小的节点开始,对2区进行计算,若计算透射转换波P1S2,则调用2区S波速度模型.如果是计算反射波P1P1(或者P1S1),则从离散速度界面中走时最小的节点开始,调用1区相应的速度模型,这样便可以实现各种震相射线的追踪计算.
|
图 3 含有起伏界面的二维层状模型中, 计算反射、透射、转换波的示意图 Figure 3 A schematic explanation for computing the transmitted, reflected and converted arrivals using the Multistage TSPM in 2-D layered media with irregular interfaces involved |
双参数的同时反演是一项较困难的工作.对于速度和界面的同时反演问题,本文采用不同参数归一化的反演方法,并引入等权射线密度的概念.多震相走时同时反演问题可归结为下列带约束的阻尼最小二乘最优化问题,其目标函数为

|
(4) |
(4) 式中,m=[λ1(δv1, δv2, …, δvN1); λ2(δz1, δz2, …, δzN2)]是模型参数的相对变化量,其中:(δv1, δv2, …, δvN1)为速度模型的相对变化量,(δz1, δz2, …, δzN2)则为离散反射点位置的相对变化量,(λ1, λ2)为速度与反射界面深度的归一化因子.d=[p1(δt11, δt21, …, δtM11); p2(δt12, δt22, …, δtM22), …, pn(δt1n, δt2n, …, δtMnn)]为n种实际观测数据和理论数据的残差向量,其中p1, p2, …, pn是反演中所考虑的各震相所占的权重大小. M1, M2, …, Mn为各震相的射线条数;μ为阻尼因子;A是雅可比矩阵;a和b是反演解中速度模型的约束值,而c和d则为离散反射点深度的约束值.Menke(1984) 得到公式(4) 的解的一般形式为:
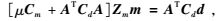
|
(5) |
(5) 式是对非线性问题局部线性化的基本反演公式.其中(Cm, Cd)为模型和数据空间的协方差矩阵.上式的解具有局域解的特征,为了得到具有实际物理意义的解,可采用Zm,Cm,及Cd的先验信息.因此,选择不同组合的(Cm,Cd)可得到不同形式的反演解;若μ=0,Cd=I,则(5) 式变为经典的最小二乘问题;若Cd=Cm=I,Zm=W,A=GW,这里W是表征射线宽度的带宽矩阵,则(5) 式变为Meyerholtz和Szpakowski(1989) 提出的卷积压制法;本文主要采用Tarantola和Valette(1982)提出的广义带约束的阻尼最小二乘反演解,即(Cm,Cd)分别为模型和数据空间的协方差矩阵的逆矩阵,其解为
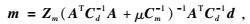
|
(6) |
上述解的约束条件为
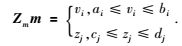
|
上述方程可以用迭代的共轭梯度法进行求解(Zhou et al., 1992).目前的关键是如何求解三角网格中具有偏导性质的Jacobi矩阵中的元素.
2.2 Jacobi矩阵的求解根据射线理论可知,二维情况下沿某一射线路径Rj的走时tj可表示为:

|
(7) |
(7) 式中Vc(x, z)为三角单元内速度函数;ds是通过某三角单元格的射线的长度;模型参数化后,射线路径Rj上的走时可写为:
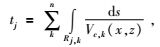
|
(8) |
式中n为该射线所穿过的三角单元总数,Rj, k表示穿过第k个三角单元的射线长度,Vc, k(x, z)表示该三角单元的速度分布.
速度与界面同时反演时的Jacobi矩阵包括两部分:走时对速度变化的偏导数和走时对反射点深度变化的偏导数,公式为:
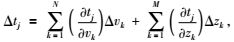
|
(9) |
式中,vk是第k个三角单元的速度分布;tj是第j条射线的走时;zk是第k反射点的深度值.
射线穿过某个三角单元时,其走时对速度的一阶偏导可用通过该三角单元射线两端点的平均值来代替(Bai and Greenhalgh, 2005),公式为:
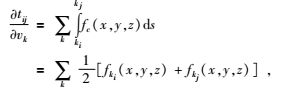
|
(10) |
(10) 式中:
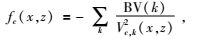
|
ki,kj是穿过第k个三角单元内射线的两个端点;BV(k)是第k个三角单元内主节点的速度值.
我们用(10) 式求出穿过第k个三角单元的射线的走时tij对该单元内速度的一阶偏导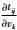
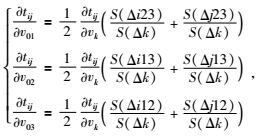
|
(11) |
其中,等号左边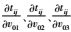
|
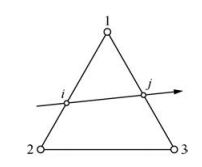
图 4 穿过某一个三角网格的射线示意图 Figure 4 A schematic diagram of the ray path which cross a triangle |
反射及透射情形时,二维情况下走时对界面位置的一阶偏导数的计算公式推导如下,界面处p点走时关于界面位置的导数为(周龙泉等,2006):
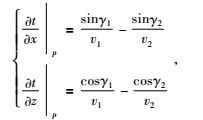
|
(12) |
其中v1和v2则分别是界面p点入射和透射时的速度(反射时v1=v2),γ1和γ2分别为p点的入射角和透射角(反射波情况下有γ1=γ2).
当只考虑z方向,且仅仅有反射波时,可以将(12) 式简化为Bishop等推导的反射波走时对反射点深度的偏导数公式(Bishop et al, 1985):
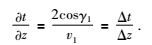
|
(13) |
本文采用(11) 式计算走时对速度的一阶偏导,用(13) 式计算走时对深度的偏导.走时对深度的偏导可通过加辅助界面来计算(Bai and Greenhalgh, 2006).具体做法是在正演的初始反射界面上或下附近加入一条与该反射界面平行的辅助界面,这样便可以利用反射界面与辅助界面上下两点的走时差通过(13) 式来计算反射波走时对界面深度的偏导数,即
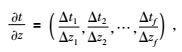
|
上式中f为离散反射界面点的总数.
在速度与界面的同时反演中,为了避免由于反射界面的更新而引起某些区域的过度(或欠)更新,我们用等权射线密度来对与速度有关的Jacobi矩阵元素进行归一化处理.具体做法是:每次正演完后统计通过每个三角网格单元的射线条数ni,在计算和某个三角网格单元有关的Jacobi矩阵元素时,对其乘以通过该三角网格单元的射线条数分之一(1/ni) (黄国娇和白超英,2010).
3 数值模拟分析本文的数值模拟实验主要讨论了常见的两种人工地震勘探模型:井间和深地震测深.井间模型我们采用检验板模型,讨论了初至波成像、以及初至波和反射波联合成像问题;而在深地震测深模型中讨论了多波联合成像、重点讨论了同时反演速度与反射界面问题.
3.1 井间检验板实验井间检验板实验是对反演算法进行评价的一种方法.由于检验板方法简单直观、实用、便于分析对比,所以目前大多数层析成像的结果都用此方法来对反演解进行评价.
本文中的检验板模型的参数为:模型大小为500 m×1300 m,模型的速度背景值为3.0 km/s.
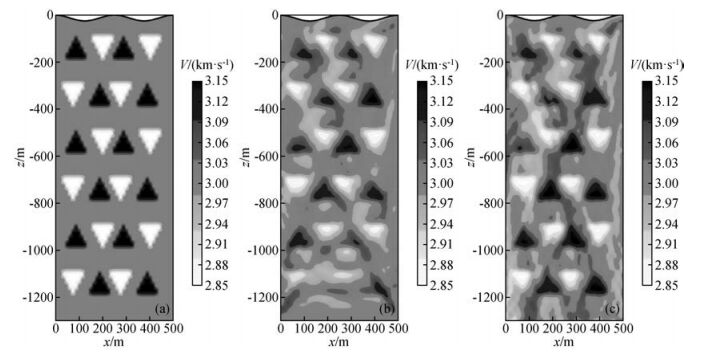
为了显示三角单元模型参数化的优势,我们将检验板实验中的高、低相间的异常体设计成三角形状,高、低三角异常体的速度值则由背景速度扰动±5%得到(图 5a所示).模型底界面为水平的反射界面,模型的上界面为起伏地表(以余弦函数变化),起伏幅度约为25.0 m.x方向主节点间距约为25.0 m,z方向上主节点的间距约为12.5 m,次级节点的间距为1.5 m.总共有2173个主节点(也即未知速度参数),所有节点共计90077个.33个炮点均匀地排列在右侧井中,33个检波点均匀地排列在左井中,21个检波器均匀地分布在地表.反演初始模型为速度值为背景值的均匀模型.图 5b则是采用初至波走时反演得到的结果,而图 5c则是联合初至波和反射波走时反演的结果.从图 5b和c中可以看出,加入了底界面的反射波后,增加了射线交错的概率,同时提高了射线密度,因此,无论是三角异常体形状的恢复,还是异常体幅度的恢复均得到了相应的改善,特别是底界面附近的异常体的恢复更为显著.这一实验的结果表明,无论是从提高射线密度或覆盖率,或是增加射线的交错概率(引入不同震相地震射线),都可以达到提高成像分辨率的目的.
|
图 5 检验板速度模型(a), 以及直达P波的反演结果(b)和直达P波和底界面反射波P1P的联合反演结果(c) Figure 5 The velocity model of the checkerboard (a), and inverted result with direct P arrivals (b) and with combined direct P and reflected P1P arrivals (c) |
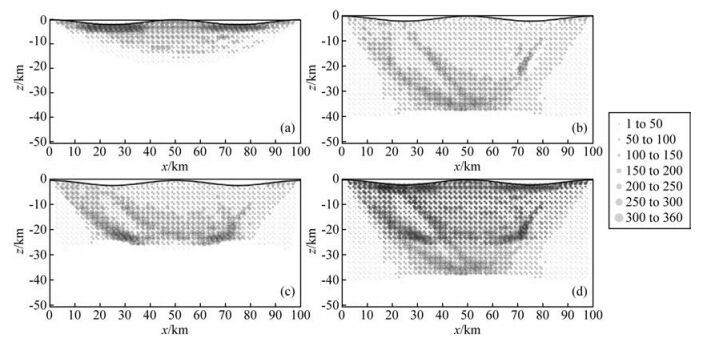
本文采用了比较复杂的模型(图 7a),模型大小为100 km×50 km.地表以余弦函数变化,起伏约2 km.速度在Z方向随深度线性增加,在模型中我们引入了两个反射界面.上反射界面是一个以正弦函数变化的反射界面,界面起伏约为3 km;下反射界面为一个界面中部略微突起的反射界面,其界面起伏约为1.5 km.在模型左上部有一不规则低速异常体,模型右上部有一不规则高速异常体.高、低异常体的速度由背景速度扰动±5%得到.三角网格单元划分后主节点的间距约为2 km,共计1122个主节点,总共剖分出2500个三角形.次级节点间距为0.15 km,所有节点总共有56819个.炮检排列如下:35个炮点,50个检波点均匀排列在地表.下面我们给出了四种震相的射线密度统计图(图 6所示).
|
图 6 三种震相的射线密度示意图 (a)直达P波;(b)反射P1P;(c)反射P2P;(d)直达P波+反射P1P+反射P2P. Figure 6 A ray density schematic diagram of three different arrivals (a)Direct P arrival; (b)Reflected P1P arrival; (c)Reflected P2P arrival; (d)Direct P arrival+reflected P1P arrival +reflected P2P arrival. |
|
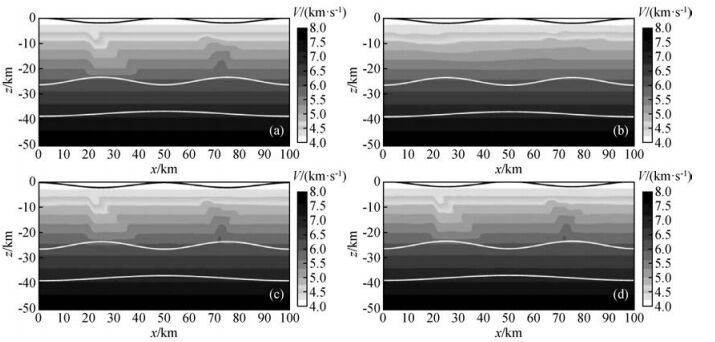
图 7 利用三种不同震相进行反演的结果(图中白线代表界面) (a)含异常体线性增加速度模型(白线为反射界面); (b)仅用直达P波的反演结果;(c)直达P波+P1P反射波联合反演结果;(d)直达P波+P1P+P2P反射波联合反演结果. Figure 7 Seismic tomography with three different arrivals (a)The true velocity model with two reflected interfaces (white lines); (b)Inverted result by direct P arrivals only; (c)Inverted result by combined direct P and reflected P1P arrivals; (d)Inverted result by combined direct P, reflected P1P and P2P arrivals. |
从图 6中可以看出,射线密度在一界面和二界面的峰值处和高速异常体处要明显高于其他区域.
3.2.1 初至波与反射波联合反演成像为了讨论多震相联合反演的分辨率和优越性,数值模拟实验中进行了三种不同震相走时单独或联合的反演成像.该实验中假设反射界面已知,反演仅更新速度模型.初始速度模型则为不含异常体的线性增加模型.图 7a为真实速度模型.图 7b、c和d分别是仅用直达P波的反演结果,直达P波和反射P1P波联合反演的结果,以及直达P波、反射P1P和P2P联合反演的结果.从图 7b中可以看出,由于受直达P波穿透深度的影响,只能在反演结果(图 7b)中隐约看到异常体的存在,异常体的边界和形状均不明显.对于联合反演,无论是P+P1P联合,还是P+P1P+P2P联合,异常体的形状已基本恢复(图 7c, d).
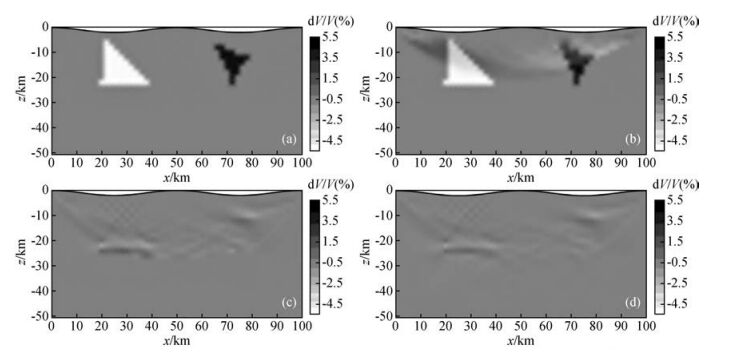
从图 7c, d中来说,两种震相走时联合反演和三种震相走时联合反演的结果相差不大.为了讨论两者间的细微差别,图 8中给出了反演速度与真实速度的百分比误差,该百分比越小说明反演结果越接近真实模型.从真实速度与初始速度模型的百分比误差来看(图 8a),异常体相对于背景速度(或初始模型)的百分比误差大约在±5.5%之间,这也是我们所要反演的异常幅度.
|
图 8 反演速度与真实速度的百分比误差 (a)真实速度模型与初始模型的百分比误差;(b)直达P波的结果;(c)直达P波+P1P反射波的结果;(d)直达P波+P1P+P2P反射波的结果. Figure 8 The percentage residual between the inverted and the real velocity model (a)Percentage residual between the real and the initial velocity model; (b)Result for direct P arrival; (c)Result for direct P arrival+reflected P1P arrival; (d)Result for direct P arrival+reflected P1P arrival+reflected P2P. |
从图 8b中可以看出,由于受直达波穿透深度的影响,成像深度只能达到15km左右.并且只有异常体顶部的残差有所减少.而且其残差的最大值也达到了4.5%左右.引入P1P反射波时,残差的分布区域大大减少,而且其残差的最大值减小到了1.6%左右(图 8c).引入P2P后,残差分布的区域进一步减少,其残差的最大值又进一步减小到了1.0%左右(图 8d).因此,可以得出结论,直达P波+P1P+P2P反射波反演的结果最好.s
3.2.2 速度与界面的同时反演一般而言,所要研究的地区的速度分布和界面起伏,以及界面位置都是未知的.先验信息只能给出粗略的结果.因此有必要进行速度与界面的同时反演.
为了压制同时反演中某些区域速度的过度更新(或欠更新),我们引入了等权射线密度的概念.初始速度模型(图 9a)与3.2.1相同,为不含异常体线性增加速度模型.上下初始反射界面位于真实反射界面之下且为水平界面(图 9a).下面给出同时反演的结果(图 9b),
|
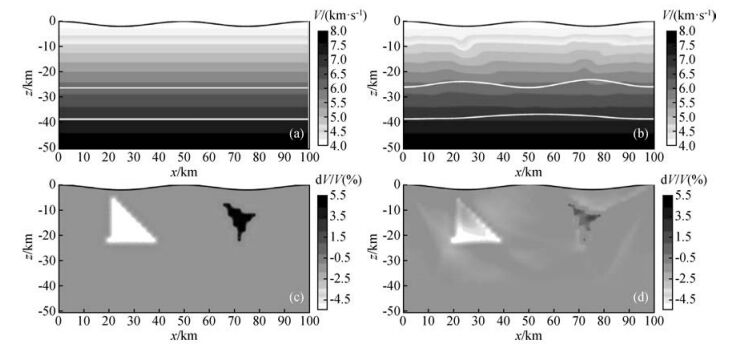
图 9 速度与界面同时反演的结果 (a)反演的初始速度模型与界面位置(图中白线为初始反射界面); (b)速度反演结果与界面反演结果, 图中白线为界面的反演结果; (c)真实速度模型与初始模型的百分比误差; (d)反演速度与真实速度的百分比误差. Figure 9 Result in simultaneous inversion (a)The initial velocity model and interfaces, in figure the white lines are the initial interfaces; (b)Result for velocity and interface, in figure the white lines are the inverted interfaces; (c)Percentage residual between the real and the initial velocity model; (d)The percentage residual between the inverted and the real velocity model. |
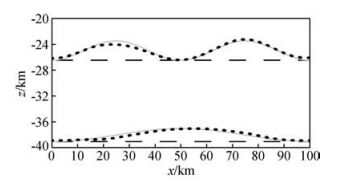
从图 9b中可以看出,同时反演已基本恢复异常体的形状.从图 9d可以看到,异常体的幅度恢复也比较好,在高速体附近,残差从原来的5.5%下降到3%左右;在低速体的上部反演效果较好,残差从-5.5%变到了-1.5%左右,中部从-5.5%变到了-3%左右.为了更加清楚地知道界面的恢复情况,我们对同时反演的界面反演结果单独作图.从图 10中看,界面的恢复情况已基本与真实界面相差无几.从而可以得出结论,三角模型参数化下的速度与界面的同时反演结果是可信的.
|
图 10 界面更新结果(图中灰色实线为真实界面,长虚线为初始反射界面,短虚线为界面更新结果) Figure 10 The updated reflected interface, in figure the grey line are the true interfaces, the long dash line are the inverted interfaces, the short dash line are the initial interfaces |
本文基于三角模型参数化下的多震相射线追踪技术,结合共轭梯度法求解带约束的阻尼最小二乘问题反演算法,实现并讨论了三角模型参数化下多震相走时联合及同时反演技术.几种数值模拟实验表示,三角模型参数化下的多震相走时联合成像技术具有较好的反演能力,能很好地反演出不规则异常体的速度分布.对于速度与界面同时反演,可以较好地反演出速度分布,恢复异常体的形状,并可以基本恢复反射界面的几何形状.由于三角网格单元在对不规则起伏地表和异常体的拟合上明显优于矩形网格,该算法具有广泛的实际应用价值.下一步的工作重点是,将该算法推广至三维四面体单元参数化情形,从而更好地利用天然地震资料来研究地球内部速度结构和Moho面起伏细节.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Aki K, Lee W H K. 1976. Determination of three dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes: 1. A homogeneous initial model[J]. J. Geophys. Res., 81(23): 4381–4399. DOI:10.1029/JB081i023p04381 |
| [] | Bai C Y, Greenhalgh S. 2005. 3-D non-linear travel-time tomography: Imaging high contrast velocity anomalies[J]. Pure Appl. Geophys., 162(11): 2029–2049. DOI:10.1007/s00024-005-2703-x |
| [] | Bai C Y, Greenhalgh S. 2006. 3D local earthquake hypocenter determination with an irregular shortest-path method[J]. Bulletin of the Seismological Society of America, 96(6): 2257–2268. DOI:10.1785/0120040178 |
| [] | Bai C Y, Li X L, Tang X P. 2011. Seismic wavefront evolution of multiply reflected, transmitted, and converted phases in 2D/3D triangular cell model[J]. Journal of Seismology, 15(4): 637–652. DOI:10.1007/s10950-011-9242-y |
| [] | Bishop T N, Bube K P, Cutler R T, et al. 1985. Tomographic determination of velocity and depth in laterally varying media[J]. Geophysics, 50(6): 903–923. DOI:10.1190/1.1441970 |
| [] | Böhm G, Galuppo P, Vesnaver A. 2000. 3D adaptive tomography using Delaunay triangles and Voronoi polygons[J]. Geophysical Prospecting, 48(4): 723–744. DOI:10.1046/j.1365-2478.2000.00211.x |
| [] | Cheng G, Ma Z T, Geng J H, et al. 2002. A review on the growth of seismic tomography[J]. Progress in Exploration Geophysics (in Chinese), 25(3): 6–12. |
| [] | Cheng G, Zhang B J. 2006. Application of triangle cell parameterization in travel-time tomography of reflection seismic data[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni (in Chinese), 45(5): 128–132. |
| [] | Curtis A, Snieder R. 1997. Reconditioning inverse problems using the genetic algorithm and revised parameterization[J]. Geophysics, 62(5): 1524–1532. DOI:10.1190/1.1444255 |
| [] | Huang G J, Bai C Y. 2010. Simultaneous inversion with multiple traveltimes within 2-D complex layered media[J]. Chinese J. Geophys. (in Chinese), 53(12): 2972–2981. DOI:10.3969/j.issn.0001-5733.2010.12.021 |
| [] | Jiang J X, Liu S H, Yan H Y. 2006. Algorithm designing and realizing of TIN in VB[J]. Surveying and Mapping of Sichuan, 29(2): 64–67. |
| [] | Li B T, Yang C C, Chen Y H, et al. 2009. 3D wavefront construction method ray tracing based on triangular grids layout on wavefront[J]. Progress in Geophys. (in Chinese), 24(2): 507–512. DOI:10.3969/j.issn.1004-2903.2009.02.019 |
| [] | McCullagh M J, Ross C G. 1980. Delaunay triangulation of a random data set for isarithmic mapping[J]. The Cartographic Journal, 17(2): 93–99. DOI:10.1179/caj.1980.17.2.93 |
| [] | Sambridge M, Braun J, McQueen H. 1995. Geophysical parametrization and interpolation of irregular data using natural neighbours[J]. Geophysical Journal International, 122(3): 837–857. DOI:10.1111/gji.1995.122.issue-3 |
| [] | Sambridge M, Faletič R. 2003. Adaptive whole Earth tomography[J]. Geochemistry, Geophysics, Geosystems, 4(3). DOI:10.1029/2001GC000213 |
| [] | Tarantola A, Nercessian A. 1984. Three-dimensional inversion without blocks[J]. Geophysical Journal International, 76(2): 299–306. DOI:10.1111/j.1365-246X.1984.tb05047.x |
| [] | Vinje V, Åstebøl K, Iversen E, et al. 1999. 3-D ray modeling by wavefront construction in open models[J]. Geophysics, 64(6): 1912–1919. DOI:10.1190/1.1444697 |
| [] | Yu S J, Liu R Z, Cheng J L. 2010. A minimum traveltime ray tracing global algorithm on a triangular net for propagating plane waves[J]. Applied Geophysics, 7(4): 348–356. DOI:10.1007/s11770-010-0263-z |
| [] | Yu S J, Liu R Z. 2013. Tomography of a minimum travel time ray tracing on a triangular net[J]. CT Theory and Applications (in Chinese), 22(3): 401–408. |
| [] | Zhou B, Greenhalgh S A, Sinadinovski C. 1992. Iterative algorithm for the damped minimum norm, least-squares and constrained problem in seismic tomography[J]. Explor. Geophys, 23(3): 497–505. DOI:10.1071/EG992497 |
| [] | Zhou L Q, Liu F T, Chen X F. 2006. Simultaneous tomography of 3-D velocity structure and interface[J]. Chinese J. Geophys. (in Chinese), 49(4): 1062–1067. DOI:10.3321/j.issn:0001-5733.2006.04.018 |
| [] | 成谷, 马在田, 耿建华, 等. 2002. 地震层析成像发展回顾[J].勘探地球物理进展, 25(3): 6–12. |
| [] | 成谷, 张宝金. 2006. 三角网格参数化在反射地震走时层析成像中的应用[J].中山大学学报(自然科学版), 45(5): 128–132. |
| [] | 黄国娇, 白超英. 2010. 二维复杂层状介质中地震多波走时联合反演成像[J].地球物理学报, 53(12): 2972–2981. DOI:10.3969/j.issn.0001-5733.2010.12.021 |
| [] | 江剑霞, 刘少华, 严汉英. 2006. VB环境下不规则三角网的算法设计与实现[J].四川测绘, 29(2): 64–67. |
| [] | 李波涛, 杨长春, 陈雨红, 等. 2009. 基于波前面三角形网格剖分的波前重建法三维射线追踪[J].地球物理学进展, 24(2): 507–512. DOI:10.3969/j.issn.1004-2903.2009.02.019 |
| [] | 于师建, 刘润泽. 2013. 三角网最小走时射线追踪层析成像[J].CT理论与应用研究, 22(3): 401–408. |
| [] | 周龙泉, 刘福田, 陈晓非. 2006. 三维介质中速度结构和界面的联合成像[J].地球物理学报, 49(4): 1062–1067. DOI:10.3321/j.issn:0001-5733.2006.04.018 |
 2017, Vol. 32
2017, Vol. 32


