2. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
3. 中国科学院深海科学与工程研究所, 三亚 572000
2. School of Geophysics and Information Technology, China University of Geoscience (Beijing), Beijing 100083, China
3. Institute of Deep-sea Science and Engineering, Chinese Academy of Sciences, Sanya 572000, China
传统的地震勘探只利用了纵波信息,但是随着实际地震勘探精细程度的不断提高,单一的纵波信息已无法满足勘探需求.多分量地震勘探技术能够同时获得纵波和转换波资料,与常规的纵波勘探相比,能够提供更多的地下介质信息.且转换波对于埋深较浅的小断层、小幅度构造有更高的分辨率,能够提供更详细的构造形态、内部变形等特点,显示出更好的储层构造成像,因此充分利用多分量地震资料可以有效的提高地震勘探的精度.多分量地震资料偏移成像技术是多分量勘探在油气开发应用中的关键技术之一,高精度的多分量叠前成像方法,能够获取地下储层准确的位置和构造形态,为后续的多分量地震勘探解释提供准确的基础资料.因此,如何对多分量地震数据更好的偏移成像是多分量地震勘探技术的关键.
此外,地下介质中广泛存在着各向异性(Thomsen, 1986; Ball, 1995; Wang, 2002),地震偏移成像过程中忽略各向异性的影响,会引起反射波归位不准确,绕射波收敛不彻底,能量不聚焦,甚至扭曲构造形态的现象(Larner and Cohen, 1993; Alkhalifah and Larner, 1994; Zhang et al., 2001).因此,随着地震勘探精度要求的不断提高,各向异性对地震偏移成像的影响越来越不可忽略.研究各向异性介质的偏移成像方法,对于剔除地震波传播过程中各向异性的影响,实现复杂构造的准确偏移归位以及油气储层的高精度成像具有重要的应用价值.各向异性对S波的影响相比于P波更严重(Thomsen, 1999),因此各向异性对于转换PS波偏移成像的影响更加不能忽略.目前,对于各向异性介质中转换PS波叠前时间偏移的研究已经较为成熟,且已获得了较好的生产应用(Wang et al., 2002; Sun and Martinez, 2003; Dai and Li, 2006; Li et al., 2007; Miao and Zuk, 2007; Zhang and Liu, 2008),但各向异性介质转换PS波的叠前深度偏移方法尚需进一步深入研究.
高斯束偏移方法是近年来发展的一种优秀的偏移算法,它不仅具有接近于波动方程偏移的成像精度,同时还保留了Kirchhoff偏移方法灵活、高效的优点以及对复杂地表条件良好的适应性,且能够有效的解决多值走时问题.在地震学领域,利用高斯束方法进行波场计算(Červeny et al., 1982, 2007; Popov, 1982)最早应用于地震波场的正演模拟(Červeny, 1985; Nowack, 2003),之后一些国外学者对高斯束偏移成像进行了研究(Hill, 1990, 2001; Hale, 1992a, b; Gray, 2005; Gray and Bleistein, 2009; Popov et al., 2010; El Yadari, 2015).在国内,虽然高斯束方法的研究起步较晚,但对高斯束偏移方法进行了大量的研究,在角度域、保幅、复杂地表以及多波高斯束偏移方法上取得了很多优秀的研究成果(李振春等,2010;Yue et al., 2010; 岳玉波等, 2011, 2012;Han et al., 2013, 2014;Cai et al., 2013;黄建平等, 2015a, b;Li, 2015; 栗学磊和毛伟建,2016).
本文基于前人研究成果,给出了一种适用于二维各向异性介质的多波高斯束叠前深度偏移方法.首先基于各向异性射线追踪理论,导出了适用于二维各向异性介质的射线追踪方程组,实现了二维各向异性介质中P波和S波的射线追踪.其次将各向异性射线追踪理论引入到高斯束偏移方法中,分别给出适用于二维各向异性介质的PP波和PS波高斯束叠前深度偏移成像方法.最后分别利用各向同性以及各向异性高斯束叠前深度偏移方法对不同各向异性介质数值模型进行偏移成像对比分析,验证本文方法的有效性.
1 基本原理各向异性高斯束叠前深度偏移采用与各向同性高斯束叠前深度偏移相同的成像原理,由震源处正向延拓的波场与束中心点处反向延拓波场进行互相关获得.而且各向异性介质中高斯束采用与各向同性介质中相同的表达形式,同样由复值时间和复值振幅表示.最大的不同在于各向异性介质中的高斯束需要各向异性射线追踪求取复值时间和复值振幅.
1.1 各向异性射线追踪通过特征值法求解程函方程,可以得到适用于任意各向异性介质任意波型的射线追踪方程组为(Červeny, 1972, 2001)
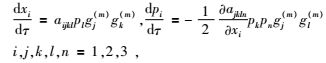
|
(1) |
式中,τ是沿射线的走时,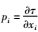
对于二维各向异性介质,不存在SH波,只需要考虑P波和SV波.消除所有下标为2的分量,即p2=0,g2(m)=0.则射线追踪方程组(1) 在二维情况下可以写为

|
(2) |
根据弹性参数矩阵元素下标表示方式的对应关系:11→1,22→2,33→3,23=32→4,13=31→5,12=21→6,对于密度单位化的弹性参数可以用两个下标的形式表示,则二维各向异性介质的射线追踪方程组可以写为
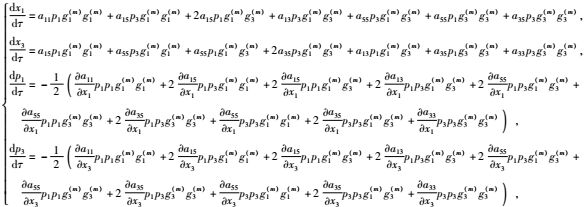
|
(3) |
其中
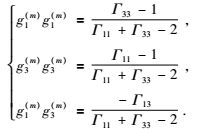
|
(4) |
射线追踪方程组(3) 对于各向异性介质中P波和SV波具有相同的形式,对哪种波型进行射线追踪必须通过初始条件进行说明.因此,对于各向异性介质,射线追踪的初始条件相比于各向同性介质更重要.各向异性介质射线追踪的初始条件不仅给定了初始位置和射线的初始方向,而且决定了射线追踪的波型.在初始时间τ=t0时,射线追踪方程组(3) 的初始条件为
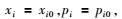
|
(5) |
且必须满足相应波型的程函方程为
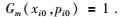
|
(6) |
对哪种波型进行计算,初始条件(5) 就必须满足相应波型的程函方程(6).而且一旦初始条件(6) 成立,则射线追踪方程组(3) 将保证沿射线满足程函方程,即沿射线的xi和pi都满足Gm(xi, pi)=1,所以满足初始条件(5) 和(6) 对各向异性介质射线追踪具有重要作用.
射线追踪方程组(3) 利用密度归一化的弹性参数表示,但对于各向异性介质的研究一般采用Thomsen参数来表征介质的各向异性.横向各向同性(TI)介质是实际应用中经常采用的各向异性介质模型,当TI介质的对称轴为垂直取向时称为VTI介质.根据弹性参数与Thomsen参数的关系,可以得到VTI介质密度归一化弹性参数的Thomsen表征形式为
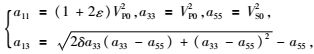
|
(7) |
式中,VP0、VS0分别为P波和SV波的垂向速度;ε和δ是表示VTI介质各向异性强度的无量纲因子.在倾斜地层中,TI介质的对称轴与垂直方向呈一定夹角,用倾斜对称轴的横向各向同性(TTI)介质模型描述更符合实际.TTI介质弹性矩阵可以由VTI介质弹性矩阵经过Bond变换获得.
1.2 各向异性多波高斯束叠前深度偏移原理将各向异性射线追踪理论引入到高斯束偏移方法中,利用震源处正向延拓的波场与束中心点处反向延拓波场进行互相关的成像条件,分别实现各向异性介质中PP波以及PS波高斯束叠前深度偏移.在二维介质中,假设xs=(xs, 0) 和xr=(xr, 0) 分别为震源和接收点,则各向异性介质中PP波和PS波对应的共炮域高斯束叠前深度偏移成像公式分别为
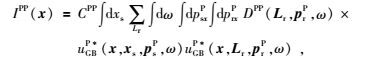
|
(8) |
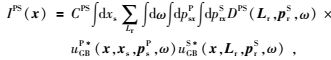
|
(9) |
式中,IPP(x)和IPS(x)分别为PP波和转换PS波对应的地下x处最终的成像值,CPP和CPS为相应的常数,ω为角频率,uGBP*(x, xs, psP, ω)是从震源出射对应的P波高斯束表达式,uGBP*(x, Lr, prP, ω)和uGBS*(x, Lr, prS, ω)为束中心点Lr=(Lr, 0) 出射,分别对应的P波和S波高斯束波场计算公式.DPP(Lr, prP, ω)和DPS(Lr, prS, ω)分别为各向异性介质中PP波和PS波地震记录经过局部倾斜叠加得到的局部平面波分量,局部倾斜叠加公式分别为
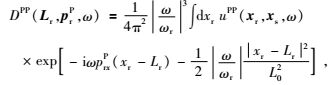
|
(10) |
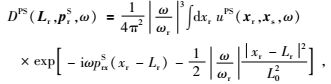
|
(11) |
式中,ωr为参考频率,uPP(xr, xs, ω)和uPS(xr, xs, ω)分别为PP波和PS波地震记录频谱.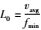
各向异性介质中高斯束的表达式同样由复值时间和复值振幅表示,用A和T分别表示高斯束的复振幅值和时间,则各向异性介质中高斯束表达式可以表示为
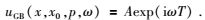
|
(12) |
将P波和S波对应的高斯束表达式分别代入式(8) 和(9),则各向异性介质中PP波和PS波对应的高斯束叠前深度偏移公式可以写为
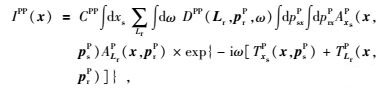
|
(13) |
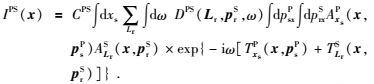
|
(14) |
对于PP波偏移,震源和束中心点均以P波延拓波场,采用适用的各向异性射线追踪计算P波高斯束的复值振幅AxsP(x, psP)和ALrP(x, prP)以及复值时间TxsP(x, psP)和TLrP(x, prP);针对PS波波场信息,震源对P波进行高斯束波场延拓求取复值振幅AxsP(x, psP)和复值时间TxsP(x, psP),而束中心点处对S波进行波场延拓求取复值振幅ALrS(x, prS)和复值时间TLrS(x, prS).相对于PP波地震记录,PS波地震记录存在极性反转现象,直接进行偏移将严重地影响偏移效果.因此,根据转换波记录的极性特征,在偏移过程中利用P波入射角的正负对其进行极性校正.
2 数值试算分析为了验证本文各向异性多波高斯束叠前深度偏移成像方法的正确性和有效性,分别设计不同各向异性介质与构造复杂程度的模型,对PP波和PS波进行数值测试.
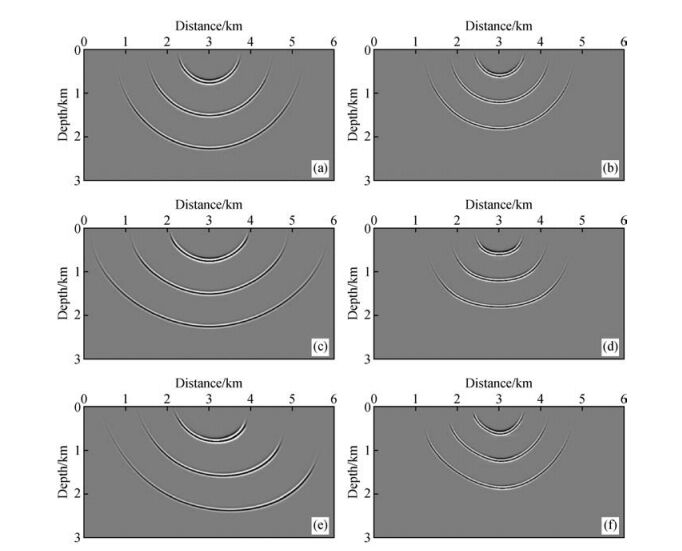
2.1 脉冲响应测试首先分别对不同介质条件下的P波和SV波进行脉冲响应对比分析.模型网格为601×301,纵横向网格间距为10 m.模型P波的垂向速度为2500 m/s,SV波的垂向速度为2000 m/s,对于P波和SV波的成像角度范围均为-80°到80°,脉冲信号位于模型中间位置.图 1a和图 1b分别为各向同性介质中P波和SV波的高斯束偏移脉冲响应结果.图 1c和图 1d分别为P波和SV波在各向异性参数ε=0.3,δ=0.15的VTI介质中的各向异性高斯束偏移脉冲响应结果.图 1e和图 1f分别为P波和SV波在对称轴倾角为30°的TTI介质中的各向异性高斯束偏移脉冲响应结果,TTI介质中各向异性参数ε=0.3,δ=0.15.从图中可以看到,对于各向同性介质、VTI介质以及TTI介质,P波和SV波的高斯束偏移脉冲响应均获得了准确的结果.
|
图 1 不同介质中P波和SV波高斯束偏移脉冲响应 (a)各向同性介质中P波的脉冲响应;(b)各向同性介质中SV波的脉冲响应;(c)VTI介质中P波的脉冲响应;(d)VTI介质中SV波的脉冲响应;(e)TTI介质中P波的脉冲响应;(f)TTI介质中SV波的脉冲响应. Figure 1 Gaussian beam migration impulse responses for P-and SV-waves in different media (a)P-wave impulse response in isotropic media; (b)SV-wave impulse response in isotropic media; (c)P-wave impulse response in VTI media; (d)SV-wave impulse response in VTI media; (e)P-wave impulse response in TTI media; (f)SV-wave impulse response in TTI media. |
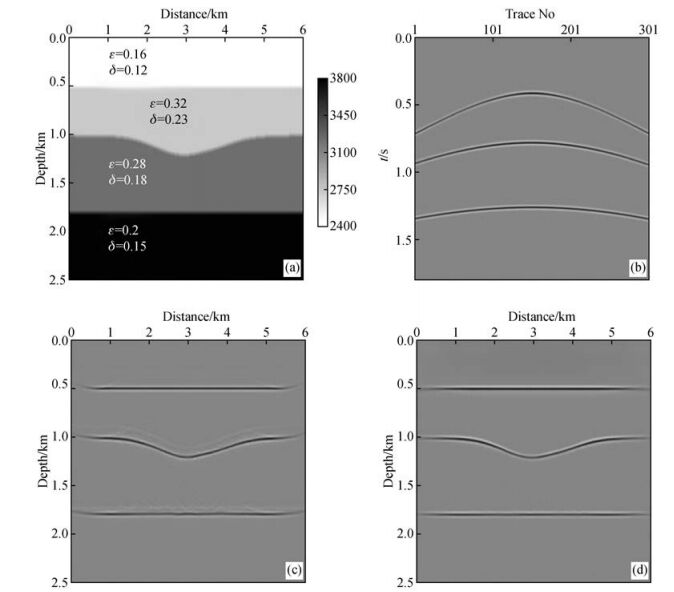
首先建立一个如图 2a所示的向斜VTI介质模型进行各向异性PP波高斯束叠前深度偏移测试,模型各向异性参数如图 2a所示.利用各向异性射线追踪方法合成PP波地震记录,震源为主频30 Hz的Ricker子波,第1炮炮点位于图 2a模型地表 600 m位置处,共模拟采集121炮,炮间距为40 m,每炮321道,道间距为10 m,采样时间为1.8 s,采样间隔为2 ms,图 2b为PP波第1炮地震记录.为了进行对比分析,分别采用各向同性以及各向异性高斯束叠前深度偏移方法对其偏移成像,各向同性高斯束偏移采用的速度为模型各层介质的垂向速度,偏移结果分别如图 2c和图 2d所示.从图中可以看到,对于各向同性高斯束偏移结果,由于忽略了各向异性的影响,导致模型中反射层归位不准确,向斜构造存在明显的成像错误,反射界面附近存在明显的发散能量.而各向异性高斯束偏移得到了准确的聚焦成像结果,消除了噪声干扰,成像效果明显优于各向同性高斯束偏移结果.通过对向斜VTI介质模型进行偏移测试,验证了本文各向异性PP波高斯束叠前深度偏移方法对于VTI介质的有效性.
|
图 2 向斜VTI介质模型PP波高斯束偏移测试 (a)向斜VTI介质模型;(b)第1炮地震记录;(c)各向同性高斯束叠前深度偏移结果;(d)各向异性高斯束叠前深度偏移结果. Figure 2 Tests of PP-wave Gaussian beam migration in syncline VTI media model (a)Syncline VTI media model; (b) The first shot seismic record; (c) Isotropic Gaussian beam prestack depth migration result; (d) Anisotropic Gaussian beam prestack depth migration result. |
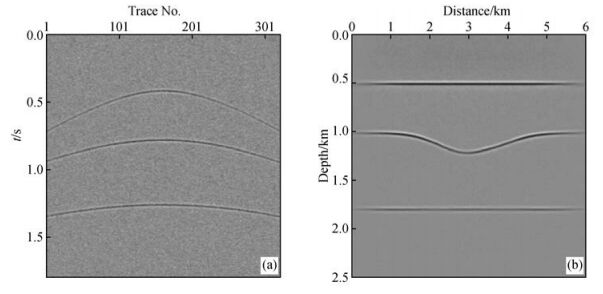
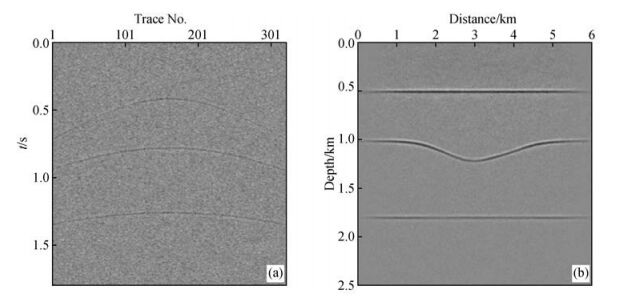
为了测试本文各向异性高斯束偏移成像方法的抗噪性,在向斜VTI介质模型的PP波地震记录中加入信噪比分别为30 db和20 db的随机噪声进行高斯束偏移测试.图 3a为地震记录中加入信噪比为30 db随机噪声后第1炮地震记录,从图中可以看到地震记录上存在明显的噪声.图 3b是对地震记录加入30 db随机噪声后进行各向异性高斯束叠前深度偏移成像的结果,从图中可以看到获得了准确的成像,并且成像结果基本没有受到随机噪声的干扰.为了进行对比分析,在地震记录中加入20 db的随机噪声,进一步减小地震记录的信噪比进行测试.如图 4a所示为地震记录中加入20 db随机噪声第1炮地震记录,可以看到地震记录中存在大量的噪声干扰,信噪比很差,反射波甚至淹没在随机噪声干扰中.对加入20 db随机噪声的地震记录进行各向异性高斯束叠前深度偏移,成像结果如图 4b所示.从图中可以看到,虽然地震记录信噪比很差,存在大量的噪声干扰,但成像剖面上噪声影响很小,获得了准确有效的偏移成像结果.通过对向斜VTI介质模型地震记录进行加噪偏移测试,验证了本文高斯束偏移成像方法具有很好的抗噪性.
|
图 3 向斜VTI介质模型PP波地震记录加入信噪比为30 db随机噪声高斯束偏移测试 (a)加入30 db随机噪声后第1炮地震记录;(b)地震记录加入30 db随机噪声后各向异性高斯束偏移结果. Figure 3 Gaussian beam migration tests of syncline VTI media model after adding 30 db random noise in PP-wave seismic record (a)The first shot seismic record with adding 30 db random noise; (b) Anisotropic Gaussian beam prestack depth migration result of PP-wave seismic record with adding 30 db random noise. |
|
图 4 向斜VTI介质模型PP波地震记录加入信噪比为20 db随机噪声高斯束偏移测试 (a)加入20 db随机噪声后第1炮地震记录;(b)地震记录加入20 db随机噪声后各向异性高斯束偏移结果. Figure 4 Gaussian beam migration tests of syncline VTI media model after adding 20 db random noise in PP-wave seismic record (a)The first shot seismic record with adding 20 db random noise; (b) Anisotropic Gaussian beam prestack depth migration result of PP-wave seismic record with adding 20 db random noise. |
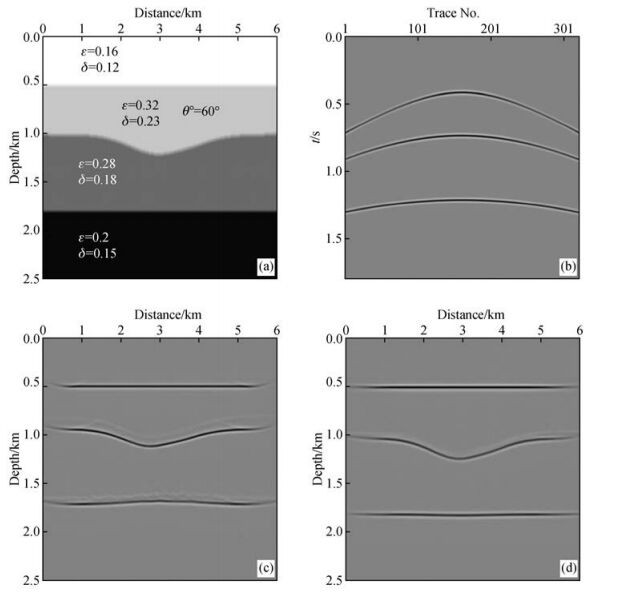
下面对上述模型进行修改,建立一个如图 5a所示的向斜TTI介质模型进行试算,验证本文各向异性高斯束叠前深度偏移方法对于TTI介质的有效性.模型各向异性参数如图 5a所示,模型第二层为TTI介质,对称轴倾角θ0为60°,其他各向异性参数不变.正演模拟采用相应的各向异性射线追踪方法,采集方式不变,图 5b为向斜TTI介质模型PP波第1炮地震记录.图 5c为采用各向同性高斯束叠前深度偏移算法得到的成像结果,各向同性高斯束偏移过程采用的速度为模型各层介质的垂向速度.从图中可以看到,向斜构造不论是在深度还是在水平方向都存在明显的成像错误,向斜构造下面的水平界面成像向上抬起,而且反射界面附近存在较强的噪声干扰.图 5d为各向异性高斯束叠前深度偏移成像结果,可以看到向斜TTI模型获得了准确的聚焦成像,且消除了噪声干扰.通过向斜TTI介质模型的偏移测试,验证了本文各向异性PP波高斯束叠前深度偏移方法对于TTI介质的有效性.
|
图 5 向斜TTI介质模型PP波高斯束偏移测试 (a)向斜TTI介质模型;(b)第1炮地震记录;(c)各向同性高斯束叠前深度偏移结果;(d)各向异性高斯束叠前深度偏移结果. Figure 5 Tests of PP-wave Gaussian beam migration in syncline TTI media model (a)Syncline TTI media model; (b) The first shot seismic record; (c) Isotropic Gaussian beam prestack depth migration result; (d) Anisotropic Gaussian beam prestack depth migration result. |
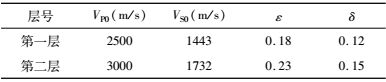
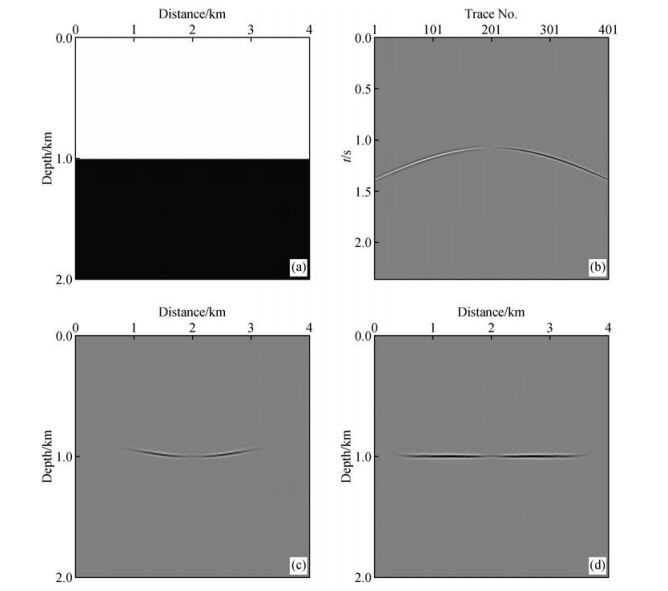
建立一个如图 6a所示的两层水平层状VTI介质模型进行单炮PS波高斯束偏移测试和分析,模型各向异性介质参数如表 1所示.模型网格为401×201,纵横向网格间距10 m.利用各向异性射线追踪方法合成PS波地震记录,震源为主频30 Hz的Ricker子波,采样时间为2.4 s,采样间隔为2 ms,单炮炮点位于模型中间位置,共401道接收,道间距为10 m,单炮地震记录如图 6b所示.为了进行对比分析,分别采用各向同性以及各向异性高斯束叠前深度偏移方法对单炮PS波地震数据进行偏移成像,偏移过程中校正了PS波极性反转现象,偏移结果分别如图 6c和图 6d所示.从图中可以看到,由于各向异性的影响,各向同性高斯束叠前深度偏移不能将VTI介质反射层准确归位,而各向异性高斯束叠前深度偏移能够使反射层完全归位,得到准确的成像结果.通过对水平层状VTI介质模型进行高斯束偏移测试,验证了本文各向异性转换PS波高斯束叠前深度偏移方法对于VTI介质的有效性.
|
图 6 水平层状VTI介质模型单炮PS波高斯束偏移测试 (a)水平层状VTI介质模型;(b)PS波单炮地震记录;(c)单炮PS波各向同性高斯束叠前深度偏移结果;(d)单炮PS波各向异性高斯束叠前深度偏移结果. Figure 6 Tests of single shot PS-wave Gaussian beam migration in horizontal layered VTI media model (a)Horizontal layered VTI media model; (b) The PS-wave single shot seismic record; (c) Isotropic Gaussian beam prestack depth migration result of single shot PS-wave; (d) Anisotropic Gaussian beam prestack depth migration result of single shot PS-wave. |
|
|
表 1 水平层状VTI介质模型各向异性参数 Table 1 Anisotropic parameters of the horizontal layered VTI media model |
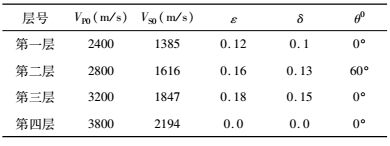
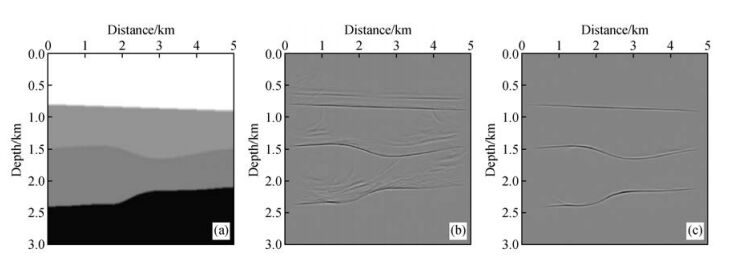
为了验证本文各向异性转换PS波高斯束叠前深度偏移方法对TTI介质的有效性,建立一个如图 7a所示的弯曲TTI介质模型进行高斯束偏移测试.模型各向异性参数如表 2所示,模型第二层为TTI介质,对称轴倾角θ0为60°.利用各向异性射线追踪方法合成PS波地震记录,震源为主频30 Hz的Ricker子波,第1炮炮点位于模型500 m位置处,共模拟采集41炮,炮间距为100 m,每炮501道,道间距为10 m,采样时间为3.6 s,采样间隔为2 ms.图 7b和图 7c分别为采用各向同性和各向异性高斯束叠前深度偏移方法对弯曲TTI介质模型PS波地震数据进行偏移的成像结果.从图中可以看到,对于各向同性高斯束偏移结果,弯曲界面成像位置不准确,且界面附近存在明显的发散能量,整个偏移剖面上噪声干扰严重.而采用各向异性高斯束进行偏移,弯曲TTI介质模型得到了准确的聚焦成像,消除了噪声干扰.通过弯曲TTI介质模型测试可以得出,对于TTI介质的转换PS波数据,采用各向异性转换PS波高斯束偏移相比于各向同性转换PS波高斯束偏移成像效果具有显著的提高.因此,本文的各向异性转换PS波高斯束叠前深度偏移方法是一种适用于TTI介质中转换PS波地震数据的准确有效的偏移方法.
|
图 7 弯曲TTI介质模型PS波高斯束偏移测试 (a)弯曲TTI介质模型;(b)PS波各向同性高斯束叠前深度偏移结果;(c)PS波各向异性高斯束叠前深度偏移结果. Figure 7 Tests of PS-wave Gaussian beam migration in curve TTI media model (a) Curve TTI media model; (b) Isotropic Gaussian beam prestack depth migration result of PS-wave; (c) Anisotropic Gaussian beam prestack depth migration result of PS-wave. |
|
|
表 2 弯曲TTI介质模型各向异性参数 Table 2 Anisotropic parameters of the curve TTI media model |
本文提出了一种适用于二维各向异性介质的多波高斯束叠前深度偏移成像方法.该方法的关键在于利用各向异性射线追踪求取各向异性介质中不同波型高斯束的复值时间和复值振幅.本文将适用于任意各向异性介质任意波型的各向异性射线追踪引入到高斯束偏移方法中,分别给出适用于二维各向异性介质的PP波和PS波高斯束叠前深度偏移成像方法.本文成像方法充分考虑各向异性因素对地震波场的影响,能够对存在各向异性介质的地下构造准确偏移归位.分别通过对不同各向异性介质的数值模型进行PP波和PS波偏移成像测试分析,验证了本文各向异性多波高斯束叠前深度偏移方法是适用于各向异性介质中PP波和转换PS波地震数据的准确有效的偏移方法,而且不受各向异性强弱限制,适应于强各向异性介质.本文不仅提出了一种适用于各向异性介质的优秀偏移算法,而且为充分利用地震资料中的多波信号,对地下各向异性介质多分量地震数据更好的进行成像提供了一种新的方法途径.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Alkhalifah T, Larner K. 1994. Migration error in transversely isotropic media[J]. Geophysics, 59(9): 1405–1418. DOI:10.1190/1.1443698 |
| [] | Ball G. 1995. Estimation of anisotropy and anisotropic 3-D prestack depth migration, offshore Zaire[J]. Geophysics, 60(5): 1495–1513. DOI:10.1190/1.1443883 |
| [] | Cai J X, Fang W B, Wang H Z. 2013. Azimuth-opening angle domain imaging in 3D Gaussian beam depth migration[J]. Journal of Geophysics and Engineering, 10(2): 025013. DOI:10.1088/1742-2132/10/2/025013 |
| [] | Červeny V. 1972. Seismic rays and ray intensities in inhomogeneous anisotropic media[J]. Geophysical Journal International, 29(1): 1–13. DOI:10.1111/j.1365-246X.1972.tb06147.x |
| [] | Červeny V. 1985. Gaussian beam synthetic seismograms[J]. Journal of Geophysics, 58: 44–72. |
| [] | Červeny V. 2001. Seismic Ray Theory[M]. Cambridge: Cambridge University Press. |
| [] | ČervenyV, KlimešL, PšenčíkI. 2007. Seismic ray method: Recent developments[J].Advances in Geophysics, 48: 1–126. |
| [] | Červeny V, Popov M M, Pšenčík I. 1982. Computation of wave fields in inhomogeneous media-Gaussian beam approach[J]. Geophysical Journal International, 70(1): 109–128. DOI:10.1111/j.1365-246X.1982.tb06394.x |
| [] | Dai H C, Li X Y. 2006. The effects of migration velocity errors on traveltime accuracy in prestack Kirchhoff time migration and the image of PS converted waves[J]. Geophysics, 71(2): S73–S83. DOI:10.1190/1.2187788 |
| [] | El Yadari N. 2015. True-amplitude vector-acoustic imaging: Application of Gaussian beams[J]. Geophysics, 80(1): S43–S54. DOI:10.1190/geo2014-0316.1 |
| [] | Gray S H. 2005. Gaussian beam migration of common-shot records[J]. Geophysics, 70(4): S71–S77. DOI:10.1190/1.1988186 |
| [] | Gray S H, Bleistein N. 2009. True-amplitude Gaussian-beam migration[J]. Geophysics, 74(2): S11–S23. DOI:10.1190/1.3052116 |
| [] | Hale D. 1992a. Migration by the Kirchhoff, slant stack, and Gaussian beam methods[R]. Colorado School of Mines Center for Wave Phenomena Report 121. |
| [] | Hale D. 1992b. Computational aspects of Gaussian beam migration[R]. Colorado School of Mines Center for Wave Phenomena Report 139. |
| [] | Han J G, Wang Y, Han N, et al. 2014. Multiwave velocity analysis based on Gaussian beam prestack depth migration[J]. Applied Geophysics, 11(2): 186–196. DOI:10.1007/s11770-014-0431-7 |
| [] | Han J G, Wang Y, Lu J. 2013. Multi-component Gaussian beam prestack depth migration[J]. Journal of Geophysics and Engineering, 10(5): 055008. DOI:10.1088/1742-2132/10/5/055008 |
| [] | Hill N R. 1990. Gaussian beam migration[J]. Geophysics, 55(11): 1416–1428. DOI:10.1190/1.1442788 |
| [] | Hill N R. 2001. Prestack Gaussian-beam depth migration[J]. Geophysics, 66(4): 1240–1250. DOI:10.1190/1.1487071 |
| [] | Huang J P, Yuan M L, Duan X Y, et al. 2015b. Decoupled elastic Gaussian beam migration for rugged topography[J]. Oil Geophysical Prospecting (in Chinese), 50(3): 460–468. |
| [] | Huang J P, Yuan M L, Li Z C, et al. 2015a. The accurate beam migration method without slant stack under dual-complexity conditions and its application[J]. Chinese Journal of Geophysics (in Chinese), 58(1): 267–276. DOI:10.6038/cjg20150124 |
| [] | Larner K L, Cohen J K. 1993. Migration error in transversely isotropic media with linear velocity variation in depth[J]. Geophysics, 58(10): 1454–1467. DOI:10.1190/1.1443360 |
| [] | Li X L. 2015. Multicomponent Gaussian beam migration in elastic medium[C].//77th EAGE Conference and Exhibition, EAGE. Extended Abstracts. |
| [] | Li X L, Mao W J. 2016. Multimode and multicomponent Gaussian beam prestack depth migration[J]. Chinese Journal of Geophysics (in Chinese), 59(8): 2989–3005. DOI:10.6038/cjg20160822 |
| [] | Li X Y, Dai H C, Mancini F. 2007. Converted-wave imaging in anisotropic media: Theory and case studies[J]. Geophysical Prospecting, 55(3): 345–363. DOI:10.1111/gpr.2007.55.issue-3 |
| [] | Li Z C, Yue Y B, Guo C B, et al. 2010. Gaussian beam common angle preserved-amplitude migration[J]. Oil Geophysical Prospecting (in Chinese), 45(3): 360–365. |
| [] | Miao X G, Zuk T. 2007. Anisotropic velocity updating for converted-wave prestack time migration[J]. Geophysics, 72(2): D29–D32. DOI:10.1190/1.2435172 |
| [] | Nowack R L. 2003. Calculation of synthetic seismograms with Gaussian beams[J]. Pure and Applied Geophysics, 160(3): 487–507. DOI:10.1007/PL00012547 |
| [] | Popov M M. 1982. A new method of computation of wave fields using Gaussian beams[J]. Wave Motion, 4(1): 85–97. DOI:10.1016/0165-2125(82)90016-6 |
| [] | Popov M M, Semtchenok N M, Popov P M, et al. 2010. Depth migration by the Gaussian beam summation method[J]. Geophysics, 75(2): S81–S93. DOI:10.1190/1.3361651 |
| [] | Sun C W, Martinez R D. 2003. 3D Kirchhoff PS-wave prestack time migration for V(z) and VTI media[C].//2003 SEG Annual Meeting, Society of Exploration Geophysicists, SEG Technical Program. Expanded Abstracts, 957-960. |
| [] | Thomsen L. 1986. Weak elastic anisotropy[J]. Geophysics, 51(10): 1954–1966. DOI:10.1190/1.1442051 |
| [] | Thomsen L. 1999. Converted-wave reflection seismology over inhomogeneous, anisotropic media[J]. Geophysics, 64(3): 678–690. DOI:10.1190/1.1444577 |
| [] | Wang W Z, Pham L D, Lou M. 2002. Converted-wave prestack time migration for isotropic and anisotropic media[C].//2002 SEG Annual Meeting, Society of Exploration Geophysicists, SEG Technical Program. Expanded Abstracts, 990-993. |
| [] | Wang Z J. 2002. Seismic anisotropy in sedimentary rocks, part 2: Laboratory data[J]. Geophysics, 67(5): 1423–1440. DOI:10.1190/1.1512743 |
| [] | Yue Y B, Li Z C, Liu W, et al. 2011. Preserved amplitude shot domain Gaussian beam migration[J]. Journal of China University of Petroleum (in Chinese), 35(1): 52–55. |
| [] | Yue Y B, Li Z C, Qian Z P, et al. 2012. Amplitude-preserved Gaussian beam migration under complex topographic conditions[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1376–1383. DOI:10.6038/j.issn.0001-5733.2012.04.033 |
| [] | Yue Y B, Li Z C, Zhang P, et al. 2010. Prestack Gaussian beam depth migration under complex surface conditions[J]. Applied Geophysics, 7(2): 143–148. DOI:10.1007/s11770-010-0238-0 |
| [] | Zhang J F, Verschuur D J, Wapenaar C P A. 2001. Depth migration of shot records in heterogeneous, transversely isotropic media using optimum explicit operators[J]. Geophysical Prospecting, 49(3): 287–299. DOI:10.1046/j.1365-2478.2001.00255.x |
| [] | Zhang L Y, Liu Y. 2008. Anisotropic converted wave amplitude-preserving prestack time migration by the pseudo-offset method[J]. Applied Geophysics, 5(3): 204–211. DOI:10.1007/s11770-008-0030-6 |
| [] | 黄建平, 袁茂林, 李振春, 等. 2015b. 一种解耦的起伏地表弹性波高斯束偏移方法[J].石油地球物理勘探, 50(3): 460–468. DOI:10.6038/cjg20150124 |
| [] | 黄建平, 袁茂林, 李振春, 等. 2015a. 双复杂条件下非倾斜叠加精确束偏移方法及应用Ⅰ—声波方程[J].地球物理学报, 58(1): 267–276. DOI:10.6038/cjg20150124 |
| [] | 栗学磊, 毛伟建. 2016. 多波多分量高斯束叠前深度偏移[J].地球物理学报, 59(8): 2989–3005. DOI:10.6038/cjg20160822 |
| [] | 李振春, 岳玉波, 郭朝斌, 等. 2010. 高斯波束共角度保幅深度偏移[J].石油地球物理勘探, 45(3): 360–365. |
| [] | 岳玉波, 李振春, 刘伟, 等. 2011. 保幅炮域高斯波束偏移[J].中国石油大学学报(自然科学版), 35(1): 52–55. |
| [] | 岳玉波, 李振春, 钱忠平, 等. 2012. 复杂地表条件下保幅高斯束偏移[J].地球物理学报, 55(4): 1376–1383. DOI:10.6038/j.issn.0001-5733.2012.04.033 |
 2017, Vol. 32
2017, Vol. 32