2. 北京矿冶研究总院, 北京 102628
3. 中国国土资源航空物探遥感中心, 北京 100083
2. Beijing General Research Institute of Mining & Metallurgy, Beijing 102628, China
3. China Aero Geophysical Survey & Remote Sensing Center for Land & Resources, Beijing 100083, China
瞬变电磁法(Transient Electromagnetic Method,TEM)是一种探测地下电导率信息的电磁勘探方法.它使用不接地回线或接地导线源作为人工场源,接收源断开之后的地下二次感应场,然后通过对地表记录的感应电磁场的研究了解地下电性结构(牛之琏, 2007).目前国内TEM数据解释主要为一维反演,基于层状介质模型假设,包括一系列快速反演(Fullagar and Reid, 2001; Christensen, 2002; Zhdanov et al., 2002; 薛国强等, 2008),以及基于一维正演程序的严格非线性反演,如Occam反演(Constable et al., 1987; 翁爱华, 2007),Levenberg-Marquardt (LM)反演(周军等,2014).然而实际的地下介质并非层状,对于复杂的电导率结构,使用一维反演必然会带来一定程度的偏差,影响最终解释结果(Goldman et al., 1994; Auken, 1995; Guillemoteau et al., 2012; Yang and Oldenburg, 2012).目前针对三维异常体的一维反演效果研究比较简略,更详细的研究极为必要.
回线源测量的两种主要方式为中心回线测量与大定源回线测量.中心回线可能获取到更大的异常幅值(梁爽, 2004),但是每次变更测点都需要同时移动发射线圈与接收线圈.而大定源回线相对中心回线只需要进行一次源的铺设便可进行多点测量(刘燚等, 2011),相对中心回线测量能够明显节约人力、资源成本,但是二者的探测效果对比却鲜有研究.从反演的角度研究二者的探测效果对于实际探测中采用何种方式具有重要的指导意义.
针对以上现状,本文将针对大定源与中心回线源三维模型数据的一维反演进行详细研究.论文首先验证采用的三维正演、一维正演的正确性以及一维反演的有效性.其中三维正演采用有限差分法实现(Wang and Hohmann, 1993; 孙怀凤等,2013),一维正演中涉及的Hankel变换以及正弦变换均采用线性滤波的方式实现(Anderson, 1979; 朴化荣, 1990),一维反演采用LM方法实现(周军等,2014).随后针对几个三维模型用三维正演分别生成大定源回线数据与中心回线数据,并对这些数据进行相应的一维反演,然后对结果进行具体分析,包括大定源数据与中心回线数据各自的反演效果以及相互之间的对比.最后对实际数据测量与解释提供一定的建议.
1 研究方法为充分保证反演结果的可靠性,本文所涉及到的一维正演均在矩形回线的基础上进行,数据处理采用基于LM反演的严格反演方法.三维正演则在时域有限差分的基础上进行(Wang and Hohmann, 1993).
1.1 矩形回线一维正演矩形回线的一维瞬变电磁响应由水平电偶极子叠加而成.常规瞬变电磁法主要记录垂直感应电压,接收面积归一化的垂直感应电压等价于垂直磁感应场的时间导数∂bz/∂t.因此本文仅考虑该分量并利用该分量进行反演.层状介质中地表点[0, 0] m处x方向水平电偶极子在点[x, y]处产生的垂直磁场可表示为(Ward and Hohmann, 1988):
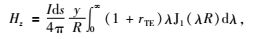
|
(1) |
其中I为偶极子电流,ds为偶极子等效长度,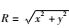
频率时间域的转换采用正弦变换实现(Newman et al., 1986),公式为
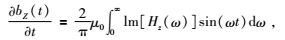
|
(2) |
其中Im(Hz)代表Hz的虚数部分.该正弦变换同样采用线性滤波的方式实现.
1.2 Levenberg-Marquardt反演本文采用Levenberg-Marquardt反演方法(周军等,2014)进行一维反演.在LM方法中,反演模型增量可表示为
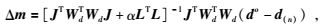
|
(3) |
其中J为敏感度矩阵,Wd为数据权重矩阵,do为原始数据,d(n)为第n次迭代所得模型m(n)对应的正演数据,L为模型约束矩阵,α为正则化因子.那么第n+1次迭代模型为m(n+1)=m(n)+Δm.本文模型约束矩阵选择最平滑约束矩阵(一阶差分) (Farquharson and Oldenburg, 1993),且不对数据人为引入误差,因此数据权重矩阵Wd均设置为单位矩阵I.拟合残差则定义为
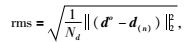
|
(4) |
以均匀半空间为初始模型,通过式建立反演迭代过程.正则化因子α采用迭代冷却的方式自适应选取(Oldenburg et al., 2013),相比一维搜索方法(刘俊峰等,2013)能够明显减小正演的次数.重复LM方法的迭代过程直到目标函数达到误差阀值或某一极小值或预先设置的最大迭代次数, 停止迭代, 得到的模型作为最终的反演结果.
2 正演与反演方法数值检验为确保研究中结论的可靠性,在对三维数据进行反演前先对研究中所涉及的正演以及反演方法进行数值检验.首先采用均匀半空间对一维线性滤波正演方法以及基于FDTD的三维正演方法进行验证,然后采用层状介质模型进行一维正演与三维正演之间的相互验证,最后利用两个典型的三层模型对LM反演方法进行验证.
2.1 一维与三维正演验证首先采用均匀半空间进行验证.均匀半空间中地表[0, 0]m处x方向水平电偶极子在点[x, y]处产生的感应场可表示为(Ward and Hohmann, 1988)
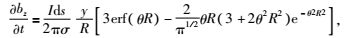
|
(5) |
其中σ为电导率,erf为误差函数,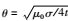
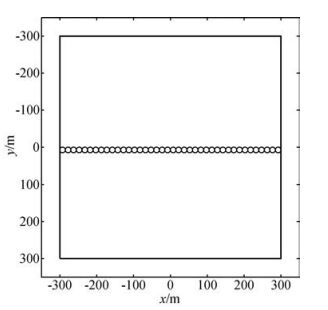
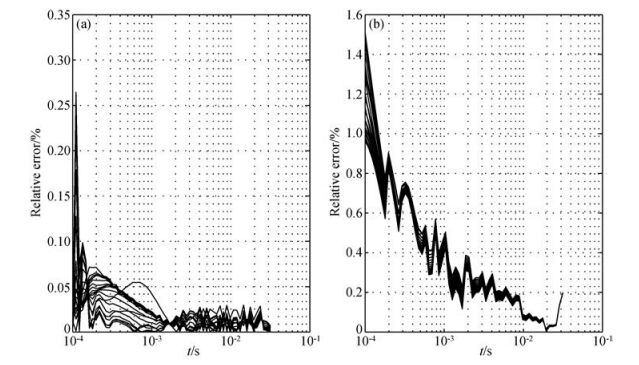
设地下电导率σ=0.02 S/m,发射线圈采用大小为600 m×600 m的矩形回线,采样时间点为t=10-4~10-1.5s范围内等对数分布的60个时间点.发射线圈以及相应的接收点如图 1所示.发射线圈中心点位于[0, 0] m位置,40个接收点采用小圆圈标记.发射电流大小为1 A.一维正演与三维正演所得结果相对由式积分所得参考解的相对误差分布分别如图 2a与图 2b所示.图 2不对具体接收点进行区分,主要考察相对误差随时间的分布.从图 2a中可以看出一维线性滤波的相对误差始终在0.5%以下,精度非常高.从图 2b中可以看出,由于线圈较大的原因,在0.1 ms时相对误差最高为1.5%左右,但是迅速衰减到1%以下,在10-3.9 s后都处于1%以下.
|
图 1 地表发射线圈(实线大正方形)与相应的数据采集测点(空心小圆圈)分布图 Figure 1 The size and position of the source loop (solid line square) and distribution of the corresponding receiving points (small hollow circles) |
|
图 2 电导率为0.02 S/m的均匀半空间一维线性滤波正演结果与参考解的相对误差(a)以及三维正演结果相对参考解的相对误差(b).本图不对接收点进行区分,主要考察相对误差随时间的分布 Figure 2 The relative errors of the 1D forward modeling using linear filter (a) and the relative errors of the 3D forward modeling (b) compared to the reference solution of a homogeneous model with a conductivity of 0.02S/m. The receiving points are not distinguished but put together to show the relative errors varying with delay time |
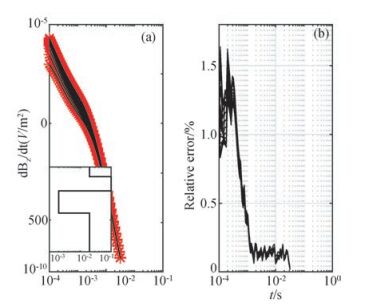
然后采用层状介质进行验证.由于层状介质不存在解析解,本文采用一维线性滤波正演与三维正演相互对比的方式进行验证.本次验证采用四层模型,每层上边界深度分别为0 m、90 m、225 m、434.6 m,对应的电导率分别为0.02 S/m, 0.1 S/m, 0.002 S/m, 0.02 S/m, 发射线圈、接收点以及采样时间点均与上一模型一致.结果对比如图 3所示.其中模型图嵌于图 3a左下角.从图 3a中可以看出一维正演和三维正演的数据吻合的非常好.图 3b给出了所有点所有时刻的相对误差.在最初阶段相对误差在1%附近波动,从10-3.8 s开始所有点的相对误差迅速衰减至1%以下.
|
图 3 四层模型的三维正演结果与一维正演结果对比其中(a)为具体的响应曲线,左下角嵌入层状介质模型图;(b)为三维正演结果相对于一维正演的相对误差. Figure 3 The comparison between the results of the 3D forward modeling results and the 1D forward modeling results of a four layered model (a) Shows the responses at all the receiving points, with the model imbedded in the southwest; (b) Shows the relative errors of the 3D results compared to the 1D results. |
两个模型的验证表明,研究所采用的一维正演与三维正演方法在本研究项目考虑的时间范围内均具有较高的精度,为接下来的研究提供了可靠保障.
2.2 一维LM反演验证针对图 3的四层模型三维正演数据,再对其进行一维LM反演,以验证反演的有效性.从原40个接收点中抽取三个典型的接收点P1[-292.5, 7.5] m、P2[-157.5, 7.5] m、P3[-7.5, 7.5] m分别进行反演,以验证大定源回线不同接收点反演的一致性.反演采用200层模型,最大深度设置为800 m,具体每一层上边界设置为
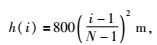
|
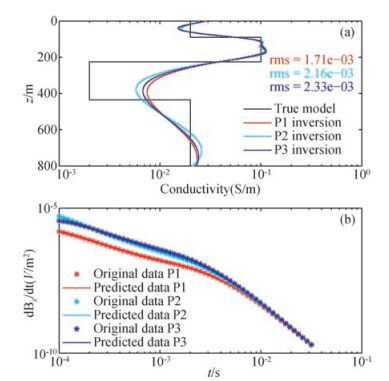
其中N为总层数,h(i)为第i层上边界.各个电性层初始电导率均为0.05 S/m.拟合残差达到最小值或迭代超过25次时停止迭代.反演结果如图 4所示.图 4a为分别利用这三个接收点的数据进行一维反演所得到的模型,其中黑色实线为真实地电模型, 红、蓝绿、蓝实线分别表示P1、P2、P3三处接收点反演的地下电导率模型, 拟合残差分别为1.71×10-3(P1)、2.16×10-3(P2)、2.33×10-4(P3).从图中可以看出三个点的反演结果非常一致,均较好地恢复了真实模型.其中第三层低导层位于第二层高导层之后,受到了一定程度的屏蔽,反演结果与真实电导率有一定的差距,但是模型总体的低-高-低-高变化趋势得到了很好的呈现,体现了反演方法的有效性.图 4b为三个接收点处原始数据与反演预测数据拟合情况,可以看出大回线原始数据与反演预测数据拟合非常好,验证了本文采用的反演方法的有效性.
|
图 4 四层模型P1[-292.5, 7.5]m、P2[-157.5, 7.5]m、P3[-7.5, 7.5] m三个点处数据分别反演的结果与真实模型(黑实线)的对比(a)以及相应的数据拟合程度(b) Figure 4 1D inversion results of the 4 layered model at P1[-292.5, 7.5] m, P2[-157.5, 7.5] m, and P3[-7.5, 7.5] m compared with the true model (black solid line) (a) and the corresponding data fit (b) |
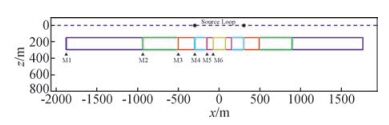
为详细研究一维反演对三维模型的适应性,首先设计了水平尺度不同而深度与厚度完全一致的6个三维高导异常体模型,如图 5所示.所有模型均关于x=0平面与y=0平面对称,因此仅给出y=0平面的x-z剖面图.图中模型1-6分别用M1-M6标记,并用黑色三角形分别标出各自异常体所对应的水平尺度.异常体垂直范围均统一为[150, 295] m.所有模型的背景电导率均为0.02 S/m,高导异常体电导率均设置为0.1 S/m.将M1-M6中异常体的电导率变为0.001 S/m,背景电导率维持不变,得到研究中需要的6个低导异常体模型,并分别标记为M7-M12.
|
图 5 六个水平尺度不同的高导异常体模型,并标记为M1~M6.所有模型均关于x=0和y=0平面对称.所有模型背景电导率为0.02 S/m, 异常体电导率为0.1 S/m.z=0处黑白两圆点分别为所采用的大定源的左右边框所在位置 Figure 5 Six models with different horizontal scale anomalous bodies, which labeled as M1 to M6. All the models are symmetric about x=0 and y=0. The conductivities of all the anomalous bodies are all 0.1 S/m, with all the background conductivities to be 0.02 S/m. Two small circles at z=0 are the positions of the left and right side of the source loop |
回线源以及相应的接收点如图 1所示.时间采样范围为[10-4, 10-1.5] s,60个采样点等对数分布于其中.
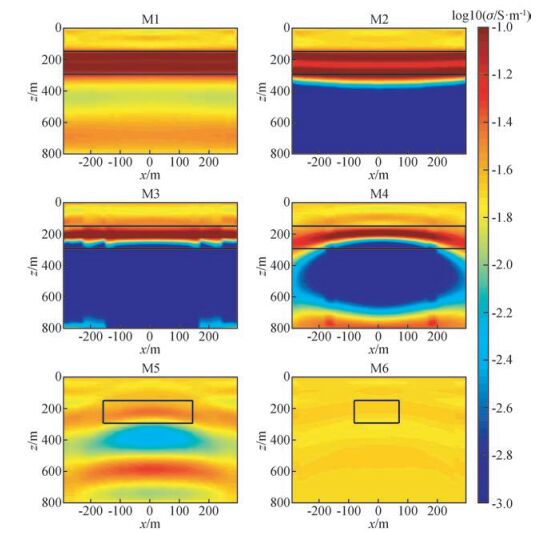
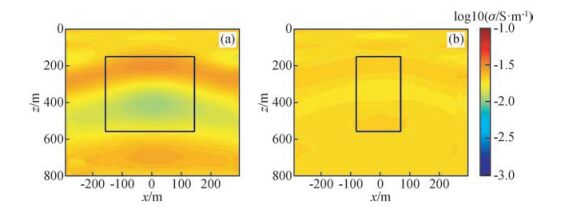
首先利用LM反演方法对6个异常体电导率为0.1 S/m的高导异常体模型M1~M6所有40个接收点数据逐一反演,然后拼接成二维图形,并进行光滑处理,结果如图 6所示.图中黑线圈出了模型或者模型一部分的真实位置.M1的异常体水平尺度达到了近4000 m,6倍于发射线框的尺寸,24倍于异常体埋深.从M1的反演结果可以看出,在测点范围内不管是异常体形态还是异常值的大小均得到了很好的恢复,而且没有出现明显虚假异常.可见M1在测点范围内能够很好地近似为一维模型.M2的水平尺度明显小于M1,但仍有3倍于发射线框尺寸,12倍于异常体埋深.M2的反演结果也基本恢复了测点范围内异常体的形态与异常值大小.但是在异常体下方很大范围内均出现了明显的反向电导率异常,异常体的三维效应体现了出来.M3的反演结果与M2类似,但是测点范围内异常体恢复情况开始变差,反向电导率出现的范围依然很大.M4异常体水平尺度已经与大定源回线尺度相当.从M4的反演结果可以看出,测点范围内异常体的恢复情况进一步变差,但是反向电导率出现的范围也明显缩小.随着异常体水平尺度的进一步缩小至大定源回线范围之内,从M5与M6的反演结果中可以看出,反演结果的异常值也有明显减小,不管是高导异常还是虚假的低导异常.尤其是M6的反演结果,电导率基本为在背景电导率附近的轻微波动,在实际测量中很可能淹没于噪声中.由此可见,异常体的水平尺度对反演结果影响明显.随着水平尺度的减小,反演所得到的异常体幅值会逐渐减小,对异常体形态的恢复也会逐渐变差.而由一维反演所引起的反向异常则会随着水平尺度的减小先增大,随后又逐渐减小.这期间对应着异常体三维效应先加强后减弱的过程.模型M5和M6由于水平尺度明显小于大定源尺度而导致异常响应比较弱,为进一步研究在水平尺度较小的情况下增加垂直尺度能否增加异常相应,将M5和M6异常体的垂直范围增加到[150, 525] m, 埋深不变,再次进行大定源反演,结果分别如图 7a与图 7b所示.对比图 6中M5和M6的反演结果,虽然异常体尺度在深度方面增加了近三倍,然后最终结果变化却不大.可见如果水平尺度过小,即使异常体垂直尺度较大,也很可能得不到更强的异常响应.
|
图 6 模型M1至M6的大定源一维LM反演结果.图中的黑色线框为异常体在显示范围内的真实位置 Figure 6 One dimensional fix loop data inversion results using LM method of model M1 to M6. The rectangle with black lines in each figure is the real position of the anomalous body within the range of the figure |
|
图 7 (a)和(b)分别为将模型M5和M6异常体垂直范围加大至[150, 525] m情况下的大定源一维LM反演结果,图中的黑色线框为异常体在显示范围内的真实位置 Figure 7 One dimensional inversion results using LM method of model M5 (a) and M6 (b) with the vertical scale of anomalous bodies changed to [150, 525] m. The rectangle with black lines in each figure is the real position of the anomalous body within the range of the figure |
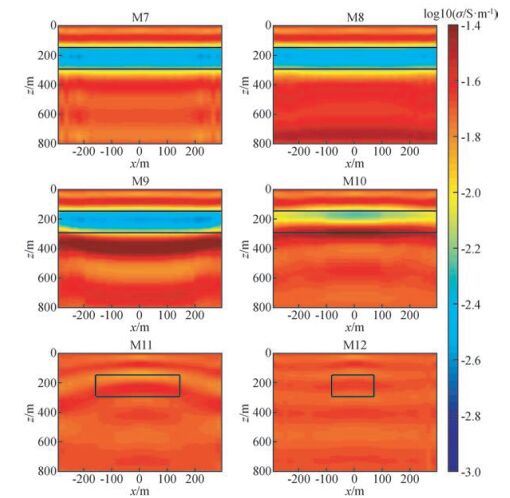
随后对6个与M1~M6具有同样几何结构的异常体电导率为0.001 S/m的低导异常体模型M7~M12所有40个接收点进行逐一反演并拼接成二维结果,如图 8所示.整体结果与高导异常体模型M1~M6类似.由于瞬变电磁法对低导异常体的敏感度相对较低,反演出的异常幅值均小于异常体的真实异常值,但是相应的虚假异常幅值与范围均较小.随着异常体水平尺度缩小至大定源范围之内,反演所得异常值变得更微弱,M11与M12的反演结果中基本已经看不到明显的低导异常体的存在.考虑到低导异常体模型与高导异常体模型在反演结果中的这种相似性,在接下来仅对高导异常体模型为目标做进一步研究.
|
图 8 模型M7至M12的大定源一维LM反演结果.图中的黑色线框为异常体在显示范围内的真实位置 Figure 8 One dimensional fix loop data inversion results using LM method of model M7 to M12. The rectangle with black lines in each figure is the real position of the anomalous body within the range of the figure |
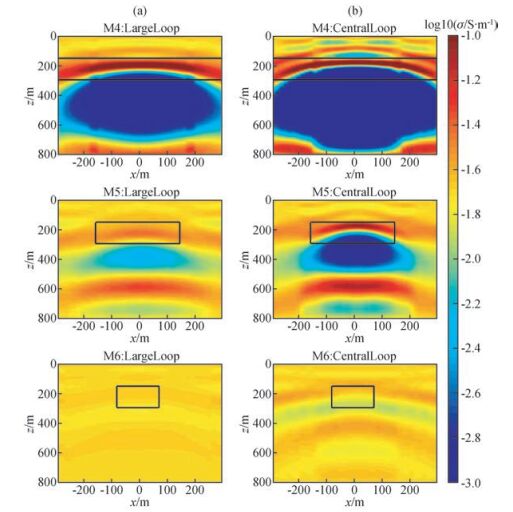
中心回线相比大定源每次测量均要移动发射线框和接收线圈,因此发射线框的尺寸一般比较小.本次研究中,中心回线测量线框尺寸设置为75 m×75 m,针对M4~M6三个模型对图 1所示的40个测点进行测量,并与相同模型大定源一维反演结果进行对比,结果如图 9所示,其中左侧为大定源一维反演结果,右侧为中心回线一维反演结果.从M4的对比结果中可以看出,虽然异常体的水平尺度已是中心回线线框尺度的8倍,但是中心回线的一维反演结果同样出现了大范围的反向异常,即使异常体正上方的测点也是如此.从M5的反演结果对比中可以看出中心回线测量得到了明显更强的异常相应,但是相应的反向异常也得到了明显加强.M6由中心回线测量得到的异常响应同样比较小,仅稍强于大定源回线.这很可能是由于M6异常体埋深大,而水平尺度较小造成的.在这种情况下不管使用大定源还是中心回线测量都较难得到理想的结果.此次的对比表明,使用更小线框的中心回线反演结果虽然可能获得比大定源反演结果获得更强的异常响应,但是异常体的三维效应并没有减弱,由异常体三维效应引起的反向异常反而得到了加强.
|
图 9 模型M4至M6大定源回线数据一维LM反演结果(a)与中心回线数据一维LM反演结果对比(b).图中的黑色线框为异常体在显示范围内的真实位置 Figure 9 One dimensional fix loop inversion results (a) of model M4 to M6 using LM method compared with one dimensional central loop inversion results (b) of model M4 to M6 using LM method. The rectangle with black lines in each figure is the real position of the anomalous body within the range of the figure |
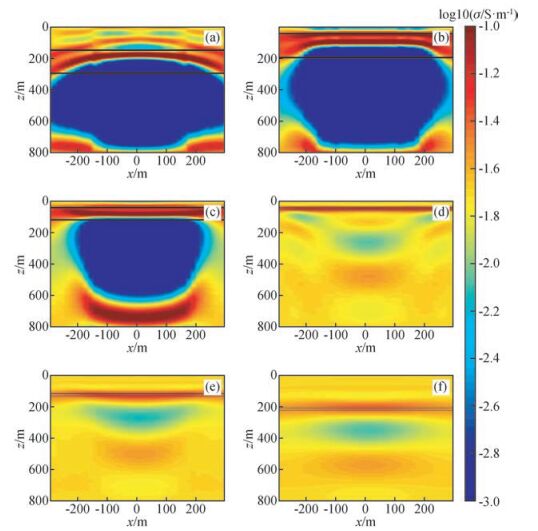
上文已提到M4的中心回线反演结果依然有很大范围的反向异常,即使在异常体正上方的测点也是如此,此情况下异常体水平尺度约为中心回线源尺度的8倍.而M1的异常体水平尺度为于大定源尺寸的6倍,却能很好的体现出一维性.为进一步研究该问题,将M4模型进行进一步修改,反演结果如图 10所示.首先将异常体埋深从150 m变浅至45 m,相应反演结果如图 10b所示.虽然异常区域恢复的更好,但是中心测点的虚假异常仍然很严重,异常体的三维效应仍然很明显.随后将异常体厚度减薄至75 m,相应的反演结果如图 10c所示.从图中可以看出,总体的结果的反向异常区域已经有所减小,但中心点的虚假异常依旧较明显.继续将异常体减薄至15 m,相应反演结果如图 10d所示.由于异常体过薄,为体现出其厚度,将数据采集时间提前至10-5 s.从图中可以看出,异常体的形态以及异常幅值都得到了很好的恢复,下方的虚假异常区域也基本消失.最后将此15 m厚度的薄异常体埋深分别下移至120 m与210 m处,相应反演结果分别如图 10e和图 10f所示.异常体的异常幅值随着埋深增加而减小,但是反向异常并没有减弱,这可能是随着异常体埋深的加深,异常体三维效应加强所导致.由此可见,使用LM方法进行一维反演可能要求异常体的水平尺度相对发射线圈、相对异常体埋深、相对异常体厚度均较大时,才能得到与异常体比较一致的结果.
|
图 10 模型M4的原始模型中心回线数据一维LM反演结果(a), 将埋深变浅至45 m后的中心回线数据一维LM反演结果(b),将埋深变浅至45 m后并将厚度分别减薄至75 m(c)和15 m(d)后的中心回线数据一维LM反演结果,以及将厚度减薄至15 m埋深分别变为120 m(e)和210 m(f)后的中心回线数据一维LM反演结果 Figure 10 One dimensional inversion results using LM method of model M4 (a), modified M4 with depth decreased to 45 m (b), modified M4 with depth decreased to 45 m and thickness decreased to 75 m (c) and 15 m (d) respectively, and modified M4 with thickness decreased to 15 m and depth changed to 120 m (e) and 210 m (f) respectively |
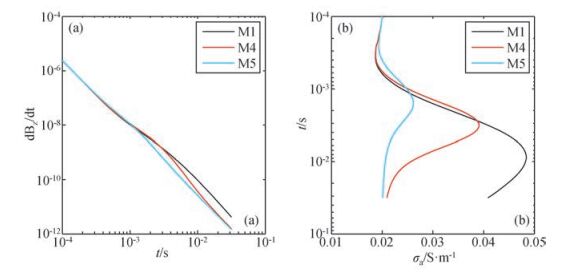
本文所讨论的多个模型的一维LM反演结果中相当一部分出现了明显的反向异常.整体来讲这些都可以归结为异常体三维效应的体现.此处将M1、M4与M5位于接收点[-7.5, 7.5] m处的中心回线数据进行比较,进一步分析三维效应的体现过程.中心回线数据与相应的全期视电阻率分别如图 11a和图 11b所示.从图 11a中可以看出,在10-3s之前,三者数据几乎一致,随后M5的数据曲线开始分离,这是因为M5的异常体比较小,其影响时间较短,幅值也较小.随着瞬变电磁场的进一步扩散,M4的异常体所产生的影响也慢慢消失,体现为M4与M1的数据发生分离,并朝着M5的数据曲线急剧下降.这种急速下降在一维模型中对应着具有非常小电导率层的存在,因此在一维LM反演中也体现出强烈的反向异常.从图 11b中也可以看出,M4的视电导率在达到峰值后迅速下降并靠近背景电导率,在一维模型中视电导率的这种现象也对应着具有非常小电导率层的存在.由此可见三维效应其实体现在瞬变场扩散初期,异常体所产生的影响与无限宽层状异常体产生的影响几乎一致,然而随着瞬变场的进一步扩散,三维异常体由于尺寸有限,其产生的影响可能迅速减小,导致响应曲线快速趋向于背景介质的响应曲线,而这种变化在一维层状介质模型中则体现为反向异常层的存在,进而导致一维LM反演结果呈现出反向异常.
|
图 11 模型M1、M4与M5在接收点[-7.5, 7.5] m处中心回线数据(a)与相应的全期视电导率(b) Figure 11 Central loop data of M1, M4, and M5 at the receiving point [-7.5, 7.5] m (a) and the corresponding all-time apparent conductivities (b) |
本文在充分验证了正演的准确性以及反演有效性的前提下,对多个三维模型的大定源数据与中心回线数据进行了一维LM反演分析,得出以下主要结论:
(1) 使用大定源测量时,随着异常体水平尺度的减小,利用一维LM反演所得异常体电导率幅值会逐渐减小,测点范围内异常体的结构恢复也越来越差,尤其当异常体水平尺度明显小于大定源尺度时,所得到的异常响应比较微弱,在实际测量中可能被噪声淹没.而由异常体三维效应引起的反向异常则随着水平尺度的不断缩小先增强,随后又逐渐减小.
(2) 中心回线数据相比大定源数据的一维LM反演结果可能得到更烈的异常响应,但是其相比大定源并不能削弱三维异常体引起的反向异常,甚至可能更强烈,容易给人带来虚假信息.因此在实际数据处理中可能需要结合多种方法进行解释,尽可能排除这些虚假信息.
(3) 使用LM方法进行一维反演,如要在测点范围内得到与异常体电导率与几何结构都相近而且反向异常不明显的结果,可能需要异常体的水平尺度明显大于异常体垂直尺度、异常体的埋深及发射线框的尺寸.
由于大定源测量对明显小于大定源发射线框尺寸的异常体不敏感,那么在实际测量中需要根据探测目标合理选择发射线框的尺寸,或者可以先使用大定源进行快速测量,然后利用中心回线对其中感兴趣的剖面进行更精细的测量,获取更强的异常响应.
致谢 感谢两位匿名审稿人对本文提出的宝贵意见,为本文文字表述的加强与逻辑水平的提升提供了强有力的帮助.| [] | Anderson W L. 1979. Numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering[J]. Geophysics, 44(7): 1287–1305. DOI:10.1190/1.1441007 |
| [] | Auken E. 1995. 1D time domain electromagnetic interpretations over 2D/3D structures[C].//Proceedings of the Symposium on the Application of Geophysics to Engineering and Environmental Problems. Orlando: Environment and Engineering Geophysical Society. |
| [] | Christensen N B. 2002. A generic 1-D imaging method for transient electromagnetic data[J]. Geophysics, 67(2): 438–447. DOI:10.1190/1.1468603 |
| [] | Constable S C, Parker R L, Constable C G. 1987. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 52(3): 289–300. DOI:10.1190/1.1442303 |
| [] | Farquharson C G, Oldenburg D W. 1993. Inversion of time-domain electromagnetic data for a horizontally layered Earth[J]. Geophysical Journal International, 114(3): 433–442. DOI:10.1111/gji.1993.114.issue-3 |
| [] | Fullagar P K, Reid J E. 2001. Emax conductivity-depth transformation of airborne TEM data[C].//15th Geophysical Conference. ASEG Extended Abstracts, 1-4. |
| [] | Goldman M, Tabarovsky L, Rabinovich M. 1994. On the influence of 3-D structures in the interpretation of transient electromagnetic sounding data[J]. Geophysics, 59(6): 889–901. DOI:10.1190/1.1443648 |
| [] | Guillemoteau J, Sailhac P, Behaegel M. 2012. Fast approximate 2D inversion of airborne TEM data: Born approximation and empirical approach[J]. Geophysics, 77(4): WB89–WB97. DOI:10.1190/geo2011-0372.1 |
| [] | Liang S. 2004. Application of central loop unit TEM in mine safety and engineering exploration[J]. Coal Technology (in Chinese), 23(1): 91–93. |
| [] | Liu J F, Deng J Z, CHEN H, et al. 2013. A method used for searching Lagrange multiplier in Occam inversion[J]. Chinese Journal of Engineering Geophysics (in Chinese), 10(3): 344–350. |
| [] | Liu Y, Liu S C, Yan S, et al. 2011. Research on detecting property of water-bearing in Coal Gob using large fixed TEM[J]. Chinese Journal of Engineering Geophysics (in Chinese), 8(1): 10–15. |
| [] | Nabighian M N. 1987. Electromagnetic Methods in Applied Geophysics: Volume 1, Theory[M]. Tulsa, Oklahoma: Society of Exploration Geophysicists. |
| [] | Newman G A, Hohmann G W, Anderson W L. 1986. Transient electromagnetic response of a three-dimensional body in a layered earth[J]. Geophysics, 51(8): 1608–1627. DOI:10.1190/1.1442212 |
| [] | Niu Z L. 2007. Theory of Time Domain Electromagnetic Method (in Chinese)[M]. Changsha: Central South University Press. |
| [] | Oldenburg D W, Haber E, Shekhtman R. 2013. Three dimensional inversion of multisource time domain electromagnetic data[J]. Geophysics, 78(1): E47–E57. DOI:10.1190/geo2012-0131.1 |
| [] | Piao H R. 1990. Theory of Electromagnetic Sounding (in Chinese)[M]. Beijing: Geological Publishing House. |
| [] | Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time[J]. Chinese Journal of Geophysics (in Chinese), 56(3): 1049–1064. DOI:10.6038/cjg20130333 |
| [] | Wang T, Hohmann G W. 1993. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling[J]. Geophysics, 58(6): 797–809. DOI:10.1190/1.1443465 |
| [] | Weng A H. 2007. Occam's inversion and its application to transient electromagnetic method[J]. Geology and Prospecting (in Chinese), 43(5): 74–76. |
| [] | Xue G Q, Li X, Di Q Y. 2008. Research progress in TEM forward modeling and inversion calculation[J]. Progress in Geophysics (in Chinese), 23(4): 1165–1172. |
| [] | Yang D K, Oldenburg D W. 2012. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit[J]. Geophysics, 77(2): B23–B34. DOI:10.1190/geo2011-0194.1 |
| [] | Zhdanov M S, Pavlov D A, Ellis R G. 2002. Localized S-inversion of time-domain electromagnetic data[J]. Geophysics, 67(4): 1115–1125. DOI:10.1190/1.1500372 |
| [] | Zhou J, Yuan W, Lian C L. 2014. Levenberg-Marquardt inversion method for CSAMT one-dimensional region data[J]. Science Technology and Engineering (in Chinese), 14(14): 129–134. |
| [] | 梁爽. 2004. 中心回线装置瞬变电磁法在矿山安全和工程勘察中的应用[J].煤炭技术, 23(1): 91–93. |
| [] | 刘俊峰, 邓居智, 陈辉, 等. 2013. 一种用于Occam反演中搜索拉格朗日乘子的方法[J].工程地球物理学报, 10(3): 344–350. |
| [] | 刘燚, 刘树才, 闫赛, 等. 2011. 大定源瞬变电磁法在探测煤矿采空区富水性中的研究[J].工程地球物理学报, 8(1): 10–15. |
| [] | 牛之琏. 2007. 时间域电磁法原理[M]. 长沙: 中南大学出版社. |
| [] | 朴化荣. 1990. 电磁测深法原理[M]. 北京: 地质出版社. |
| [] | 孙怀凤, 李貅, 李术才, 等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演[J].地球物理学报, 56(3): 1049–1064. DOI:10.6038/cjg20130333 |
| [] | 翁爱华. 2007. Occam反演及其在瞬变电磁测深中的应用[J].地质与勘探, 43(5): 74–76. |
| [] | 薛国强, 李貅, 底青云. 2008. 瞬变电磁法正反演问题研究进展[J].地球物理学进展, 23(4): 1165–1172. |
| [] | 周军, 袁伟, 连晨龙. 2014. 可控源音频大地电磁法(CSAMT)一维全区Levenberg-Marquardt反演方法[J].科学技术与工程, 14(14): 129–134. DOI:10.3969/j.issn.1671-1815.2014.14.024 |
 2017, Vol. 32
2017, Vol. 32


