2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
诸多岩体失稳致灾的演化方式是蠕变破坏或准蠕变破坏,即在长期缓慢的构造应力加载或环境因素作用下,岩体内微裂隙丛集导致宏观破裂的过程,大地震孕育过程是典型实例(杨百存等,2017).显然,预测大地震的前提是能测定沿断层面的深部滑移应变,但在目前技术条件下难以实现,故应寻求某种易测的替代物理量.
Benioff(1951)从岩石的蠕变特性出发,提出了根据地震释放的弹性应变能确定系统等效应变量(Benioff应变)的方法,在地震活动性分析等方面已得到广泛应用(Bowman et al., 1998; Scordilis et al., 2004; 蒋长胜等, 2010).Bufe和Varnes(1993)根据时间-破坏分析方法,研究了旧金山湾区地震活动性,认为计算参量选用Benioff应变优于地震矩和地震事件数.秦四清等(2010b)认为累积Benioff应变(CBS)可作为沿断层面深部滑移应变的测度,但未从力学上给出严格证明.鉴于此,本文基于孕震断层多锁固段脆性破裂理论和震例分析,论证了断层锁固段CBS与剪切应变的等效性.此外,还给出了详细的CBS值计算方法,以便于同行应用.
1 锁固段CBS与剪切应变的等效性地震源自于断层运动导致的岩石破裂,而断层运动模式及其相关地震活动性受断层面上一个或多个“锁固段”所控制.秦四清等(2010a,b)结合重正化群理论和损伤本构模型,构建了单锁固段体积膨胀点与峰值强度点之间的力学联系,即:
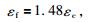
|
(1) |
式中,εc和εf分别为锁固段体积膨胀点和峰值强度点对应的沿断层面剪切应变值.
考虑到断层中可能存在多锁固段,基于式(1) 进而可建立多锁固段情况下体积膨胀点与峰值强度点之间的力学联系,即:
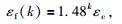
|
(2) |
式中,εc为第1个锁固段膨胀点对应的应变值,εf(k)为第k个锁固段峰值强度点对应的应变值.我们称锁固段在体积膨胀点和峰值强度点发生的显著地震为标志性地震事件.
式(2) 给出了锁固段加载过程中体积膨胀点与峰值强度点之间的量化应变关系.根据锁固段体积膨胀点对应的应变值,可提前给出其发生宏观破裂对应的临界应变值,结合实时监测信息可对标志性地震事件进行预测.
设某一锁固段沿断层的剪切应变在其内部均匀分布(Benioff,1951),则有:
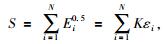
|
(3) |
式中,S为CBS值;Ei为第i次地震波辐射能量;εi为第i次地震发生时锁固段沿断层面的剪切应变;K=(0.5 μηiV)0.5,为比例系数;μ为剪切模量;ηi为第i次地震的地震效率;V为锁固段体积.
假设同一锁固段破裂发生的地震,其地震效率相同,易知K为常量,则式(3) 可写为
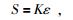
|
(4) |
式中,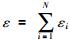
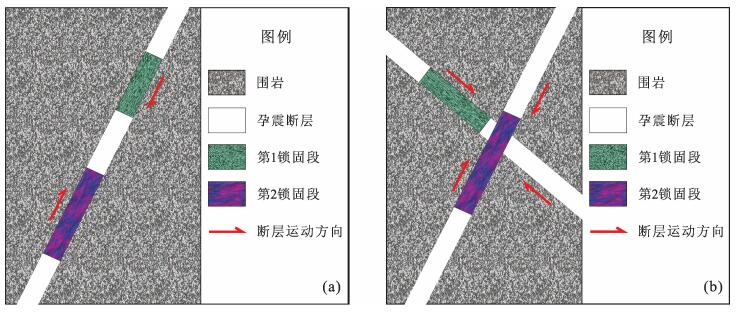
以某地震区两个断层锁固段为例(图 1),第1锁固段体积膨胀点和峰值强度点对应的应变可由式(4) 给出,即:
|
图 1 孕震断层锁固段概念模型 (a)一条断层有两个锁固段; (b)两条相交断层各有一个锁固段. Figure 1 A conceptual model of locked patches in seismogenic faults (a) Two locked patches in a seismogenic fault; (b) A locked patch in each of two cross seismogenic faults. |
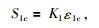
|
(5) |
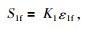
|
(6) |
式中,K1为第1锁固段比例系数,ε1c和S1c分别为第1锁固段体积膨胀点对应的剪切应变值和CBS值,ε1f和S1f分别为第1锁固段峰值强度点对应的剪切应变值和CBS值.
代式(5) 和(6) 入式(1) 得
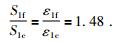
|
(7) |
同理,第2锁固段体积膨胀点和峰值强度点对应的应变可分别表达为:
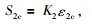
|
(8) |
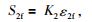
|
(9) |
式中,K2为第2锁固段比例系数,ε2c和S2c分别为第2锁固段体积膨胀点对应的剪切应变值和CBS值,ε2f和S2f分别为第2锁固段峰值强度点对应的剪切应变值和CBS值.
代式(8) 和(9) 入式(1) 得:
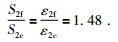
|
(10) |
显然,第2锁固段体积膨胀点对应的CBS值与第1锁固段峰值强度点对应的CBS值之间应满足如下关系,即:
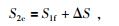
|
(11) |
式中,ΔS为第1锁固段宏观破裂后至第2锁固段被加载至体积膨胀点前的CBS增量,其是由第1锁固段发生宏观破裂后,应力向第2锁固段转移所致.
为减小CBS预测值与实际值之间的误差,有效提取锁固段本身破裂信息,秦四清等(2015)提出了最小有效性震级Mv确定方法.当数据处理考虑Mv时,ΔS约等于零,则式(11) 可近似表达为
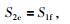
|
(12) |
结合式(7)、(10) 和(12) 得
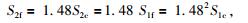
|
(13) |
以此类推,对于多锁固段情况,则式(13) 可进一步表达为
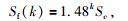
|
(14) |
式中,Sc为第1锁固段体积膨胀起点对应的CBS值,Sf(k)为第k个锁固段峰值强度点对应的CBS值.
对比式(2) 和(14) 知,在孕震断层多锁固段脆性破裂理论框架下,若假设锁固段沿断层的剪切应变在其内部均匀分布,且同一锁固段破裂发生地震的地震效率相同,则断层锁固段CBS与剪切应变等效.
2 CBS计算方法为计算特定地震区某孕育周期的CBS值,需按下述步骤对地震目录数据进行处理,即:
(1) 统一震级标度.地震目录常涉及到的震级标度包括地方震级(ML)、面波震级(MS)、矩震级(MW)、长周期体波震级(mB)、短周期体波震级(mb)、未知震级(Muk)、灾害信息确定的震级(MK)、断层面积震级(Mfa)和日本气象厅震级(Mj)等.秦四清等(2013, 2014a)认为,可采用以下经验公式进行不同震级标度之间的换算,即:
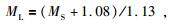
|
(15) |
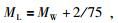
|
(16) |
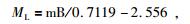
|
(17) |
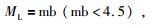
|
(18) |
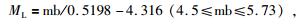
|
(19) |
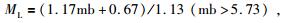
|
(20) |
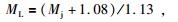
|
(21) |
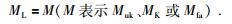
|
(22) |
(2) 根据秦四清等(2015)提出的最小有效性震级Mv确定方法,对统一标度后的地震目录进行筛选.
(3) 计算筛选后每次地震事件的地震矩M0、地震能量E和Benioff应变εBenioff,其公式分别为:
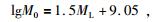
|
(23) |
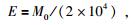
|
(24) |
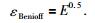
|
(25) |
(4) 计算CBS值,其公式为:
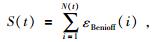
|
(26) |
式中,εBenioff(i)表示第i次地震的Benioff应变,N(t)表示在时间t已发生的地震事件数,S(t)表示第N(t)次地震发生后的CBS值.
3 实例分析 3.1 新源-阿拉木图地震区数据分析时,1963年12月31日前数据采用宋治平等(2011)提供的地震目录,之后采用国家地震科学数据共享中心(CEDC)地震目录(http://data.earthquake.cn/data,数据获取日期为2015年11月21日).具体计算步骤如下:
(1) 该区公元前250年至2015年11月21日之间共发生MS≥6.0级地震38次.其地震目录涉及的震级标度包括MS、MW、mb和Muk,利用式(15)、(16)、(20) 和(22),将震级标度统一为ML.
(2) 确定该区最优Mv值为ML 6.7,则数据处理时剔除ML < 6.7级地震事件.
(3) 利用式(23)~(25),依次计算地震事件的地震矩、地震能量和Benioff应变.
(4) 由式(26) 计算CBS值.
(5) 以地震序列中每次地震事件的发震时间为横坐标,对应的CBS值为纵坐标,绘制CBS时程曲线.
新源-阿拉木图地震区当前周期曾发生3次标志性地震事件(秦四清等,2016b),即1812年3月8日新疆尼勒克东MS 8.0级地震、阿拉木图1889年7月11日MS 8.4级地震与1911年1月3日MS 8.2级地震.从图 2看出,误差修正后标志性地震事件的孕育规律遵循式(14).根据秦四清等(2014b)提出的主震事件判识原则,判断该区当前孕育周期存在第3锁固段,当其被加载至峰值强度点时,应发生标志性地震事件.截止到2015年11月21日,该地震区CBS监测值约为1.78E+09J1/2,距临界值1.80E+09J1/2较近.
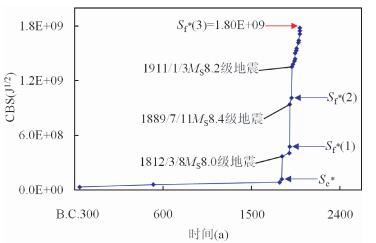
|
图 2 新源-阿拉木图地震区公元前250-2015.11.21之间CBS值与时间关系(据秦四清等(2016b)修改) (数据分析时选取ML≥6.7级地震事件;误差修正已被考虑) Figure 2 Temporal distribution of CBS in the period from B.C. 250 to 21 November 2015 for the Xinyuan-Almaty seismic zone (modified after Qin et al. (2016b)) (The earthquake events with ML≥6.7 are selected for data analysis. The error correction is also considered.) |
数据分析时,地震目录引自CEDC(数据获取日期为2015年11月21日).因具体计算步骤与新源-阿拉木图地震区相同,故不再详述.
小江地震区当前周期曾发生4次标志性地震事件(秦四清等,2016c),即1500年1月13日宜良MS 7.0级地震、1733年8月2日东川MS 7.5级地震、1833年9月6日嵩明MS 8.0级地震与1970年1月4日通海MS 7.8级地震.从图 3看出,误差修正后标志性地震事件的孕育规律遵循式(14).根据秦四清等(2014b)提出的主震事件判识原则,判断该区当前孕育周期存在第4锁固段,当其被加载至峰值强度点时,应发生标志性地震事件.截止到2015年11月21日,该地震区CBS监测值约为1.78E+09J1/2,远离临界值2.28E+09J1/2.
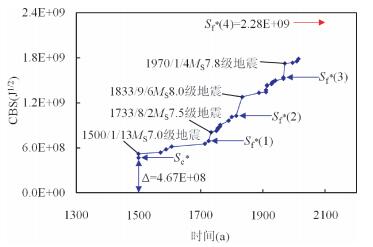
|
图 3 小江地震区1446.4.7-2015.11.21之间CBS值与时间关系(据秦四清等(2016c)修改) (数据分析时选取MS≥6.0级地震事件;误差修正已被考虑) Figure 3 Temporal distribution of CBS in the period from 7 April 1446 to 21 November 2015 for the Xiaojiang seismic zone (modified after Qin et al. (2016c)) (The earthquake events with MS≥6.0 are selected for data analysis. The error correction is also considered.) |
对新源-阿拉木图和小江地震区的实例分析表明,断层锁固段CBS与剪切应变等效,表明上述假设合理.此外,秦四清等(2016a,b,c)对全球其他60个地震区的震情分析亦表明确实存在这种等效性.这足以说明CBS可表征沿断层面深部滑移应变,且其是容易测定的物理量,能够用于大地震孕育过程分析.换句话说,分析地震区震情时,监测参量不管采用锁固段剪切应变还是替代物理量CBS,不会改变标志性地震事件孕育规律,故可利用CBS对标志性地震事件进行预测.
4 结论在孕震断层多锁固段脆性破裂理论框架下,断层锁固段CBS与剪切应变等效,且其是容易测定的物理量,可用于大地震孕育过程分析.
致谢 感谢国家自然科学基金资助项目(编号:41572311, 41302233) 对研究工作的资金支持.| [] | Benioff H. 1951. Earthquakes and rock creep[J]. B Seismol Soc Am, 41(1): 31–62. |
| [] | Bowman D D, Ouillon G, Sammis C G, et al. 1998. An observational test of the critical earthquake concept[J]. J Geophys Res, 103(B10): 24359–24372. DOI:10.1029/98JB00792 |
| [] | Bufe C G, Varnes D J. 1993. Predictive modeling of the seismic cycle of the Greater San Francisco Bay Region[J]. J Geophys Res, 98(B6): 9871–9883. DOI:10.1029/93JB00357 |
| [] | Jang C S, Zhao W Z, Wang X Z. 2010. Benioff strain release and periodic characteristics of strong earthquake activities in Asia[J]. Earthquake (in Chinese), 30(3): 72–80. |
| [] | Qin S Q, Li G L, Xue L, et al. 2013. Reanalysis of the future earthquake situation for some seismic zones in the Xinjiang region and its border areas[J]. Progress in Geophys (in Chinese), 28(5): 2376–2391. DOI:10.6038/pg20130519 |
| [] | Qin S Q, Li P, Xue L, et al. 2014b. The definition of seismogenic period of strong earthquakes for some seismic zones in southwest China[J]. Progress in Geophys (in Chinese), 29(4): 1526–1540. DOI:10.6038/pg20140407 |
| [] | Qin S Q, Li P, Yang B C, et al. 2016a. The identification of mainshock events for main seismic zones in seismic belts of the Circum-Pacific, ocean ridge and continental rift[J]. Progress in Geophys (in Chinese), 31(2): 574–588. DOI:10.6038/pg20160209 |
| [] | Qin S Q, Wang Y Y, Ma P. 2010a. Exponential laws of critical displacement evolution for landslides and avalanches[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 29(5): 873–880. |
| [] | Qin S Q, Xu X W, Hu P, et al. 2010b. Brittle failure mechanism of multiple locked patches in a seismogenic fault system and exploration on a new way for earthquake prediction[J]. Chinese J Geophys (in Chinese), 53(4): 1001–1014. DOI:10.3969/j.issn.0001-5733.2010.04.025 |
| [] | Qin S Q, Xue L, Li P, et al. 2014a. Analysis on the seismogenic processes of large or great earthquakes for some seismic zones aboard based on the brittle theory of multiple locked patches (Ⅰ)[J]. Progress in Geophys (in Chinese), 29(4): 1541–1554. DOI:10.6038/pg20140408 |
| [] | Qin S Q, Yang B C, Xue L, et al. 2015. Prospective prediction of major earthquakes for the Taiwan Strait seismic zone[J]. Progress in Geophys (in Chinese), 30(5): 2013–2019. DOI:10.6038/pg20150505 |
| [] | Qin S Q, Yang B C, Wu X W, et al. 2016b. The identification of mainshock events for some seismic zones in mainland China (Ⅱ)[J]. Progress in Geophys (in Chinese), 31(1): 115–142. DOI:10.6038/pg20160114 |
| [] | Qin S Q, Yang B C, Xue L, et al. 2016c. The identification of mainshock events for main seismic zones in the Eurasian seismic belt[J]. Progress in Geophys (in Chinese), 31(2): 559–573. DOI:10.6038/pg20160208 |
| [] | Scordilis E M, Papazachos C B, Karakaisis G F, et al. 2004. Accelerating seismic crustal deformation before strong mainshocks in Adriatic and its importance for earthquake prediction[J]. J Seismol, 8(1): 57–70. DOI:10.1023/B:JOSE.0000009504.69449.48 |
| [] | Song Z P, Zhang G M, Liu J, et al. 2011. Global Earthquake Catalog[M]. Beijing: Seismological Press. |
| [] | Yang B C, Qin S Q, Xue L, et al. 2017. A physical self-similarity law describing the accelerated failure behavior of rocks[J]. Chinese J Geophys (in Chinese), 60(5): 1746–1760. DOI:10.6038/cjg20170512 |
| [] | 蒋长胜, 赵祎喆, 王行舟. 2010. 亚洲地区Benioff应变释放和强震活动的周期性特征研究[J].地震, 30(3): 72–80. |
| [] | 秦四清, 李国梁, 薛雷, 等. 2013. 中国新疆及邻区某些地震区未来震情研判[J].地球物理学进展, 28(5): 2376–2391. DOI:10.6038/pg20130519 |
| [] | 秦四清, 李培, 薛雷, 等. 2014b. 中国西南地区某些地震区强震孕育周期界定[J].地球物理学进展, 29(4): 1526–1540. DOI:10.6038/pg20140407 |
| [] | 秦四清, 李培, 杨百存, 等. 2016a. 环太平洋、大洋海岭与大陆裂谷地震带主要地震区主震事件判识[J].地球物理学进展, 31(2): 574–588. DOI:10.6038/pg20160209 |
| [] | 秦四清, 王媛媛, 马平. 2010a. 崩滑灾害临界位移演化的指数律[J].岩石力学与工程学报, 29(5): 873–880. |
| [] | 秦四清, 徐锡伟, 胡平, 等. 2010b. 孕震断层的多锁固段脆性破裂机制与地震预测新方法的探索[J].地球物理学报, 53(4): 1001–1014. DOI:10.3969/j.issn.0001-5733.2010.04.025 |
| [] | 秦四清, 薛雷, 李培, 等. 2014a. 国外某些地震区大地震孕育过程分析(Ⅰ)[J].地球物理学进展, 29(4): 1541–1554. DOI:10.6038/pg20140408 |
| [] | 秦四清, 杨百存, 薛雷, 等. 2015. 台湾海峡地震区大震预测[J].地球物理学进展, 30(5): 2013–2019. DOI:10.6038/pg20150505 |
| [] | 秦四清, 杨百存, 吴晓娲, 等. 2016b. 中国大陆某些地震区主震事件判识(Ⅱ)[J].地球物理学进展, 31(1): 115–142. DOI:10.6038/pg20160114 |
| [] | 秦四清, 杨百存, 薛雷, 等. 2016c. 欧亚地震带主要地震区主震事件判识[J].地球物理学进展, 31(2): 559–573. DOI:10.6038/pg20160208 |
| [] | 宋治平, 张国民, 刘杰, 等. 2011. 全球地震目录[M]. 北京: 地震出版社. |
| [] | 杨百存, 秦四清, 薛雷, 等. 2016. 岩石加速破裂行为的物理自相似律[J].地球物理学报, 60(5): 1746–1760. DOI:10.6038/cjg20170512 |
 2017, Vol. 32
2017, Vol. 32


