随着卫星重力计划的逐步实施和完善以及大地测高等观测技术的飞速发展,地球重力场方面的研究取得了长足的进展.利用卫星重力资料并结合地面重力数据获得全球重力场模型的精度和分辨率在逐步提高(Sandwell and Smith, 2009;Pavlis et al., 2012;宁津生和王正涛, 2013).代表性的事件为美国国家地理空间局NGA与2008年发布的全球超高阶地球重力场模型EGM2008(Pavlis et al., 2008),该模型的完全阶次至2159(另外球谐系数的阶扩展至2190,次为2159),相当于模型的空间分辨率为5′(约9 km).其构建思路是用GRACE卫星数据建立的GGM02S地球重力模型的前60阶球谐系数,加上EGM96重力模型的61-360阶球谐系数,采用NGA的5′网格全球地面测量重力数据网,对该数据进行调和分析,构建2160阶次的重力场模型(郑伟等,2010;Pavlis et al., 2012;宁津生和王正涛, 2013;李新星,2013).但是在专利数据区或者无重力数据区则采用DTM地形数据合成的重力异常数据填充,即在前360阶后,再加上剩余地形重力模型的361-2160阶球谐系数计算得到的重力异常,合成5′的全球重力异常数据库.
显然,EGM2008模型的构建思路决定了它在重力专利区域的精度差于全球的平均精度10 mGal(10-5 ms-2),而中国大陆地区的重力数据保护使得模型数据在大陆地区精度较差.章传银等(2009)在中国大陆地区用模型值与5′平均空间异常对比,得到全国平均标准差为10.5 mGal,杨金玉等(2012)年的研究结果表明模型数据与实测数据在地形平坦的中国大陆地区差别较小,向西随着地形复杂程度的增加,两种数据之间的标准差从10 mGal增加到50多mGal.畸变点分析表明,精度极低的网络点均分布在地形起伏大的地区.付广裕等(2013)在四川盆地区域的研究中发现,模型值与实测重力异常的差值几乎是一个常数(10 mGal左右),其结果与之前研究结果基本一致.在全球范围内,美国、欧洲、澳大利亚等地区的测试发现,EGM2008模型极大提高了与实际数据的符合度,特别是在大型山脉地区(Pavlis et al., 2008;Claessens et al., 2010;Ellmann,2010).所以,如果有地面实测重力数据的支持,EGM2008重力模型将会有比较高的精度.
本研究将在EGM2008数据基础上,依据川西盆地及其西部四川高原区域的地面实测重力数据,利用基于‘消去-恢复’思路的最小二乘配置法(Hwang and Parsons, 1995;刘晓刚等,2012;刘晓刚等,2014)进行两种数据的融合,获得较高精度的川西区域重力异常场分布,然后按地形起伏特征区分研究区域进一步分析该数据融合方法的精度及适用性,并给出较合理的地面实测点布网密度参考.
1 基于‘消去-恢复’思路的最小二乘配置计算方法研究中我们使用了基于‘消去-恢复’思想的最小二乘配置计算方法(Hwang and Parsons, 1995;Olesen et al., 2002).我们将地面实测点自由空气重力异常(简称重力异常)与对应测点处EGM2008模型值的差值定义为模型的系统差.‘消去’既是用实测值消去对应模型值得到系统差的过程,进而利用最小二乘配置法推估所有待求点处的模型系统差,然后在所求得的系统误差基础上恢复对应点EGM2008重力场模型值,得到所求点处融合后重力异常值,这个过程即为‘恢复’.其计算公式(海斯卡涅和莫里斯,1979;Hwang and Parsons, 1995;管泽霖等,1997)为
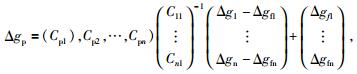
|
(1) |
其中, Cpi为未知点与已知点协方差; Δgp为待求点重力异常; Cij为已知点协方差;Δgi-Δgf为第i点处模型系统差; Δgf为EGM2008重力场模型重力异常值.最小二乘配置法关键问题在于如何确定合适的协方差函数.为此,首先对地面观测点上实测值与模型值的差值(模型系统差)进行协方差统计,获得测点距离和协方差之间的统计结果,选取相应的协方差函数, 并通过函数拟合获取相关系数.
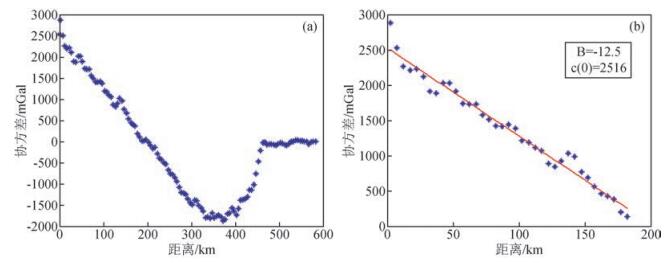
为了计算协方差函数及其对应的相关系数,在研究区域划分1551个6′×6′个间距的均匀网格点,通过实测数据和模型数据,我们获取测点距离和协方差值之间统计结果如图 1a所示,在测点距200 km内协方差符合良好的线性相关.因此在测点距0~200 km区间选择线形函数c(d)=B×d+c(0) 作为协方差函数,并对统计结果进行最小二乘拟合,得到协方差函数中待求的系数B=-12.5和c(0)=2516,如图 1b所示.通过获得的协方差函数,利用上述计算公式(1) 可对有地表重力观测资料的区域进行数据融合处理.
|
图 1 协方差计算值统计结果分布(a);一次协方差函数拟合结果(红线)(b) Figure 1 Covariance statistics results distribution(a); Linear covariance function fitting results(red line)(b) |
本研究中,我们利用的数据有四川盆地及其西部高原的地表实测重力异常数据和来自EGM2008地球重力场模型的重力异常数据(图 2).其中地表重力异常数据来自于付广裕等(2013)在四川盆地区域的流动重力/GPS联合观测.对联测结果进行平差后进行自由空气校正得到.自由空气校正公式为
|
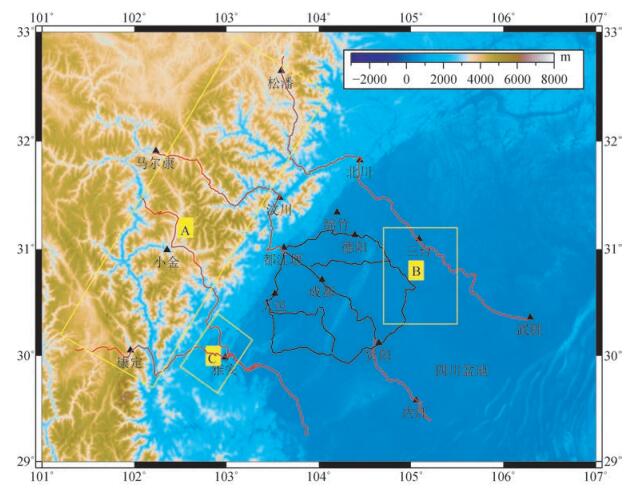
图 2 地表重力测量数据分布.黑线为实测数据,红线为数字化数据,黄色矩形框为具体分析的研究区域 Figure 2 The observation data distribution.Black lines are the measured data, red lines are the digital data, and the yellow rectangles are three concrete analysis of the study area |
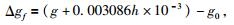
|
(2) |
h的单位为厘米; g为观测值; g0为理论值.还有一部分地表数据来自于数字化结果(Yang,2004;Zhang et al., 2014).EGM2008重力场模型重力异常数据从Satellite Geodesy网站(http://topex.ucsd.edu/)下载得到.随着地面观测数据的不断丰富,EGM2008模型也在不断更新,本文所用的重力场模型重力异常数据来自最新的全球重力场模型(V23.1 http://topex.ucsd.edu/cgi-bin/get_data.cgi).
为评估研究区重力模型数据的质量情况,我们将已知点位处的模型系统差进行了分析,其标准差为50.3 mGal,杨金玉等(2012)的研究结果在川西高原和青藏高原地区的模型标准差为52.1 mGal.由于本文所用地面测点包括川西盆地模型系统差较小区域,得到的标准差略小于杨金玉等人的结果,基本保持一致.
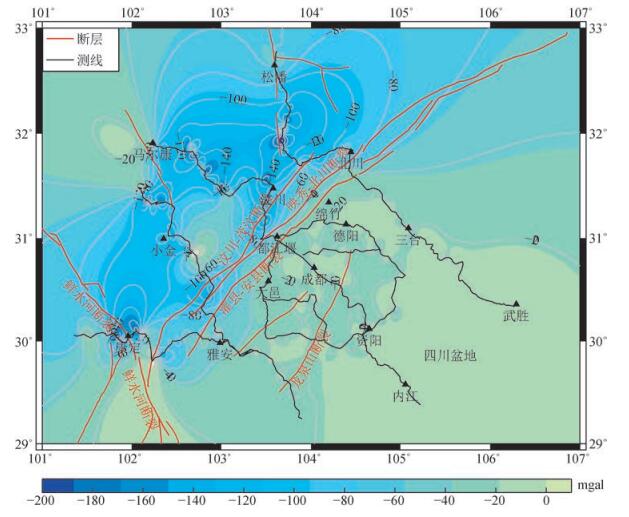
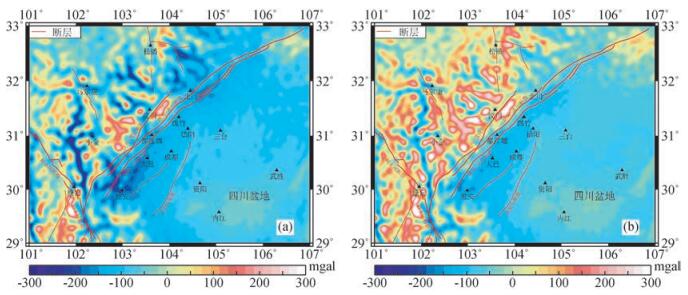
3 实测和模型数据融合计算结果与分析融合计算得到的研究区域模型系统差分布如图 3所示.从东部四川盆地到西部四川高原,模型系统差从-20 mGal左右到-150 mGal左右依次增加,在盆地和山地交界的龙门山附近有明显的梯度变化带,和该处的地形变化一致.该差异和杨金玉等人的研究结果基本一致.付广裕等(2013)年的研究结果显示,在川西盆地,模型值与实测值的差异几乎是个常数(-10 mGal左右),由于他的结果是归算到似大地水准面,反算到地表其差异正好是-20 mGal左右,和本文数据融合结果几乎一致.在盆地平坦区域,系统差在-20 mGal至-40 mGal之间浮动,并未出现明显高值区和低值区,和地形符合较好(图 3).明显的,在西部高原地区,实测线包围圈外部和距离实测线较远区域模型系统差等值线扩散现象显著,说明地面测点对远离测线和测线包围圈外部区域模型值控制相对较差,特别是在地形起伏剧烈区域尤为明显.利用模型系统差恢复模型重力异常,得到该区域融合后的重力异常分布(图 4a),图 4b为EGM2008模型重力异常分布.
|
图 3 融合计算得到的重力场模型系统差分布 Figure 3 System error of the gravity model distribution calculated by data fusion |
|
图 4 研究区域数据融合后重力异常分布图(a);EGM2008模型重力异常分布(b) Figure 4 The gravity anomaly distribution from data fusion(a); The gravity anomaly distribution from EGM2008 gravity model(b) |
计算结果显示,利用地面实测观测数据和卫星模型数据的融合,可以提供更精确的区域重力异常分布,同时实测数据密度对其融合结果有一些影响.为了验证地面测点密度对融合结果的影响,改变地面数据测点密度从2 km、4 km、8 km,融合计算得全部测点上的重力异常值,并将其与实测值进行比较,如图 5所示.计算结果与实测值差异较大的地方集中在地形起伏较大的山地区域.鉴于此,有必要根据不同地形特征分析地面测点密度对融合计算结果的影响.
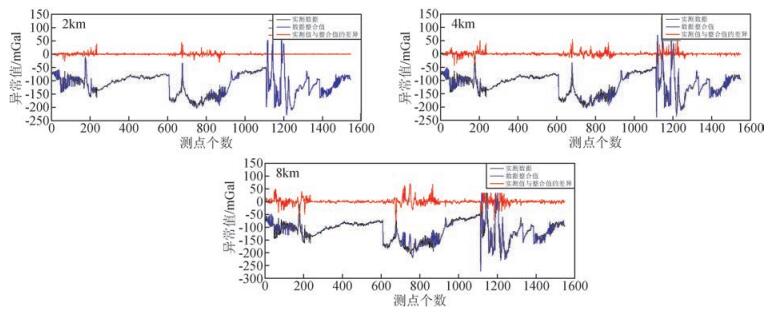
|
图 5 测点间距2 km、4 km、8 km时地面实测值和融合结果的差异 Figure 5 The difference between data fusion results which from different spacing measuring points and the ground observation(Each station 2 kilometers apart、Each station 4 kilometers apart、Each station 8 kilometers apart) |
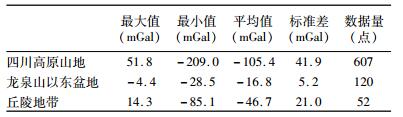
我们以地形特征为依据,将研究区域划分为A、B、C三个区域(图 1)进行详细分析.A区域为四川高原山地部分,B区域为龙泉山以东的盆地部分,C区域为盆地和山地交界的丘陵地带.三个区域的EGM2008模型重力异常与实测重力异常对比如表 1所示.不同地形特征区域模型和实测重力异常对比差异较大.四川高原的山地区域标准差达到41.9 mGal,平均值-105.4 mGal,而龙泉山以东的四川盆地区域,模型和实测值差异标准差为5.2 mGal,平均值-16.8 mGal.
|
|
表 1 EGM2008模型重力异常与实测重力异常差异 Table 1 The differences between EGM2008 model gravity anomaly value and the observed gravity anomaly value |
四川高原山地地形起伏异常剧烈,其海拔高度最高4391 m、最低681 m,标准差846 m.对该区域地面实测重力异常与EGM2008模型重力异常差异分布进行分析后,发现模型和实测值的差异绝大部分落在-50 mGal至150 mGal之间,平均值为-105.4 mGal,标准差41.9 mGal.在得到基本的地形特征背景后,分析验证在该地区不同测点密度分布对数据融合结果的影响.将地面实测点密度以2 km采样间隔加大(2 km、4 km、6 km…),与EGM2008模型数据进行融合计算,重新求得该区域所有测点的重力异常值.并将融合得到的新的重力异常值与该区域测点上的真实值进行对比.对此,选取2 km、4 km、8 km、16 km采样密度的融合结果,进行了统计(图 6).发现实测数据密度为2 km、4 km时候融合结果与真实值得差异符合标准正态分布,融合值与真实值差异基本在-20mGal至20 mGal之内.实测数据密度为大于16 km时,差异值分布开始出现离散,基本不再符合正态分布.
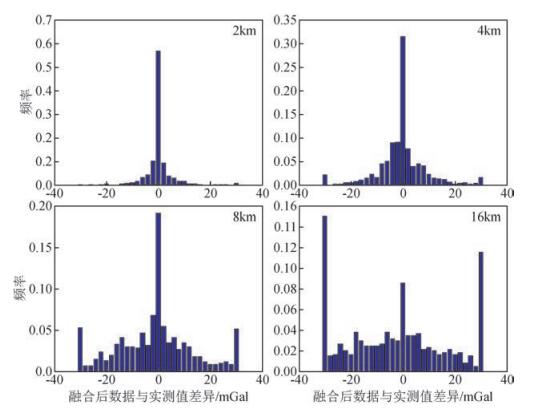
|
图 6 不同密度地面测点(2、4、8、16 km)得到的融合结果与观测值差异分布 Figure 6 Difference distribution between observed value and fusion results calculated by different density ground station (2、4、8、16 km) |
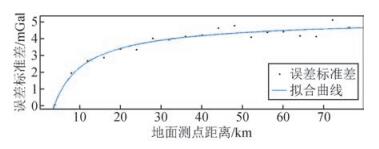
图 7给出了随着实测点密度与融合结果与实测值差异标准差的变化趋势,发现在地形起伏剧烈的四川高原山地,测点间距在16 km之后误差标准差变化趋于平缓,与16 km后模型与真实值差异分布离散一致.16 km测点密度以内,误差标准差趋势变化较快,因此,想将融合结果误差标准差控制在5 mGal以内,必须将地面测点密度控制在2 km以内,如果需要融合结果误差标准差10 mGal左右,地面实测点间距至少应该在5 km范围之内.
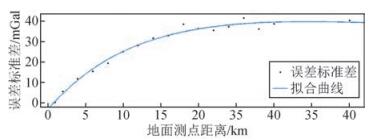
|
图 7 四川高原地区不同测点密度对应的融合结果误差标准差 Figure 7 Standard deviation of fusion results by different density ground station in the Sichuan plateau |
龙泉山以东的盆地地形平坦,其海拔高度最高513 m、最低328 m,标准差46 m,该区域地面实测重力异常与EGM2008模型重力异常差异分布进行分析后,实测值与模型值差异主要分布在在-15 mGal至-25 mGal之间,这与盆地区域平坦的地形背景相一致.将地面实测点密度以2 km采样间隔加大(4 km、8 km、12 km…),与EGM2008模型数据进行融合计算,重新求得该区域所有测点的重力异常值.并将融合得到的新的重力异常值与该区域测点上的真实值进行对比.由于龙泉山以东盆地地势平坦,模型与实测重力异常差异标准差较小,所以选取8 km、16 km、32 km、64 km密度的融合结果,进行了统计(图 8).不同于山地地区,在该平坦的区域,地面测点间隔即使到64 km,融合后的结果与真实值差异分布依然呈现良好的正态分布,90%的差异值依然能落在-5 mGal至5 mGal范围内.这与在山地8公里密度以后误差标准差就不再保持正态分布形成鲜明对比.这表明,在平坦地形地区,即使是64 km一个地面测点,用‘消去-恢复’思想的最小二乘配置方法依然能将模型与实测值差异从原来-15 mGal至25 mGal提高到-5 mGal至5 mGal的范围内.
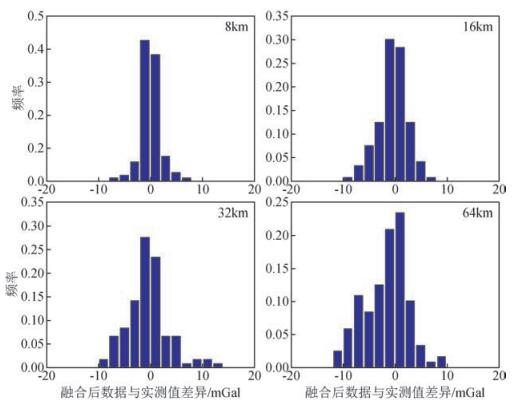
|
图 8 不同密度地面测点(8、16、32、64 km)得到的融合结果与观测值差异分布 Figure 8 Difference distribution between observed value and fusion results calculated by different density ground station (8、16、32、64 km) |
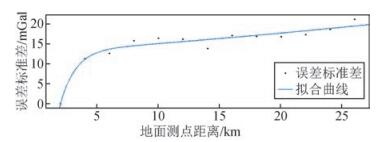
图 9给出了随着实测点密度与融合后结果与实测值差异标准差的变化趋势,发现在在龙泉山以东平坦的盆地,不同密度测点融合结果的误差标准差几乎都在5 mGal以内,这是由于该区域地形起伏较小,EGM2008的模型数据此区域起伏变化较为平缓,在平坦的盆地或平原地区,即使在60~70 km的测点间距的少量地面观测点也可以将EGM2008重力场模型的数据校正到比较高的精度.
|
图 9 龙泉山东部盆地不同测点密度对应的融合结果误差标准差 Figure 9 Standard deviation of fusion results by different density ground station in the Longquan mountain eastern basin |
川西盆地西南部盆地与山地交界的丘陵地带地形起伏介于盆地和山地之间,海拔最高1555 m、最低477 m、标准差231 m.此处的地面实测重力异常与EGM2008模型重力异常差异从-80~20 mGal,较为分散,没有集中高频分布现象.将地面实测点密度以2 km采样间隔加大(4 km、6 km、8 km…),与EGM2008模型数据进行融合计算,重新求得该区域所有测点的重力异常值.并将融合得到的新的重力异常值与该区域测点上的真实值进行对比.由于该处地面实测点较少,不可能将地面测点稀疏到太大间距,不失一般性的,我们选取4 km、8 km、16 km里间隔的测点融合结果与实测值进行对比(图 10).4 km、8 km间隔条件下差异分布呈现正态分布趋势,16 km间隔融合数据差异基本分布离散,这和四川高原山地地区情况较类似.8 km间隔的差异值分布主要在-20 mGal至20 mGal范围内,较融合前模型值与实测值差异,有明显提高.
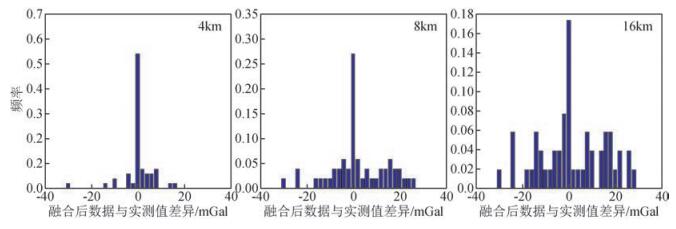
|
图 10 不同密度地面测点(4、8、16 km)得到的融合结果与观测值差异分布 Figure 10 Difference distribution between observed value and fusion results calculated by different density ground station (4、8、16 km) |
图 11给出了随着实测点密度与融合结围后误差标准差变化趋于平缓,大于5 km间隔后的误差标准差变化在15~20 mGal范围浮动.可以接受的误差精度出现在5 km以内,说明该地的起伏虽然没有山地那么剧烈,但是模型数据在此处依然会丢失很多细节,需要比较密集的地面测点来校正.将误差标准差控制在5 mGal之内,依然需要2 km以内的地面测点密度,而想要得到10 mGal左右的误差标准差,需要5 km以内的地面测点密度,该分布结果介于四川高原山地和龙泉山以东盆地的结果之间,说明模型值在区域内的细节信息精确度与地形起伏状况成负相关.
|
图 11 西盆地西南丘陵地带不同测点密度对应的融合结果误差标准差 Figure 11 Standard deviation of fusion results by different density ground station in the Sichuan southwestern foot hills |
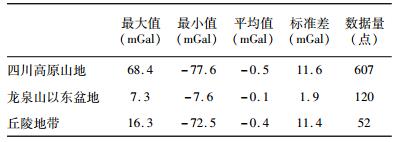
按地形起伏分区域对地面实测点密度分布对融合结果的影响验证分析后,我们在A区域山地以地面测点4 km间隔、B区域盆地以地面测点8 km间隔、C区域丘陵地带以地面测点4 km采样间隔融合EGM2008模型数据,重新得到不同区域重力异常值与地面测点真实值的差异,如表 2所示.较融合前精度(表 1)有大幅提高.
|
|
表 2 融合后重力异常与地面实测重力异常差异 Table 2 The differences between fusion gravity anomaly value and the measured surface gravity anomaly value |
我们将川西盆地及其西侧四川高原地区1549个地面实测点重力异常与EGM2008模型重力异常进行对比发现,EGM2008重力场模型数据对区域重力场变化趋势反映比较可靠,模型数据与实际观测值之间存在的系统差与距离之间存在良好的一次线性相关性,配合一定密度的地面实地观测,可以将模型数据校正到比较高的精度.
5.2按地形起伏特征分区域验证分析地面测点密度对融合结果的影响,在四川高原地区,地面测点间距4 km的情况下,可以将起伏剧烈的四川高原区域模型值标准差从41.9 mGal提高到11.6 mGal,平均差异从-105.4 mGal提高到-0.5 mGal.在龙泉山以东较为平坦的盆地地区,间隔8 km的地面实测点数据就可以将模型值标准差从5.2 mGal提高到1.9 mGal,平均差异从-16.8 mGal提高到-0.1 mGal(表 2).对不同地面测点密度对应的误差标准差分布进行分析,误差标准差梯度变化大的地区,融合后数据与实测值的差异符合良好正态分布,具有良好的统计性态.分区域验证分析的结果也为地面重力观测的测点布设提供了一种参考.在地形起伏剧烈的高原或山地区域,误差标准差要控制在10 mGal左右需要地面测点密度至少在5 km以内,要将误差标准差控制在5 mGal左右,地面测点密度至少要在2 km以内.而在平坦的盆地或者平原地区,60 km左右间隔的测点密度就能将模型数据的误差标准差校正到大约5 mGal.
5.3由于‘消去-恢复’思想的最小二乘配置法进行融合推估的是模型系统差,所以不同区域模型系统差的平稳度对数据融合计算结果精度有影响.EGM2008重力场模型数据虽然对区域重力数据的趋势变化刻画较为准确,但是对于小区域内地形起伏突变引起的重力变化反映较差,所以利用这些小区域地形起伏处的实测数据求得的模型数据系统差则可能会对融合计算结果造成一些影响.因此,在布置地面测点的时候如非必要,则尽量避开这种畸变位置.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Claessens S J, Featherstone W E, Anjasmara I M. 2010. Is Australian data really validating EGM2008, or is EGM2008 Just in/validating Australian data?[A].//Mertikas A P, ed. Gravity, Geoid and Earth Observation: International Association of Geodesy Symposia[M]. Berlin Heidelberg: Springer, 135: 473-479. |
| [] | Ellmann A. 2010. Validation of the new earth gravitational model EGM08 over the Baltic countries[A].//Mertikas A P, ed. Gravity, Geoid and Earth Observation: International Association of Geodesy Symposia[M]. Berlin Heidelberg: Springer, 135: 489-496. |
| [] | Fu G Y, Zhu Y Q, Gao S H, et al. 2013. Discrepancies between free air gravity anomalies from EGM2008 and the ones from dense gravity/GPS observations at west Sichuan Basin[J]. Chinese Journal of Geophysics (in Chinese), 56(11): 3761–3769. DOI:10.6038/cjg20131117 |
| [] | Guan Z L, Guan Z, Huang M T. 1997. Local Gravity Field Approximation Theory and Method (in Chinese)[M]. Beijing: Surveying and Mapping Press. |
| [] | Heiskanen W A, Moritz H. 1979. Physical Geology (in Chinese)[M]. Lu F K, Hu G L Trans. Beijing: Surveying and Mapping Press. |
| [] | Hwang C, Parsons B. 1995. Gravity anomalies derived from Seasat, Geosat, ERS-1 and TOPEX/POSEIDON altimetry and ship gravity: A case study over the Reykjanes Ridge[J]. Geophysical Journal International, 122(2): 551–568. DOI:10.1111/gji.1995.122.issue-2 |
| [] | Li S S, Wu X P, Zhang C D, et al. 2010. Calculation and analysis of the new statistical character parameters of gravity field in China[J]. Chinese Journal of Geophysics (in Chinese), 53(5): 1099–1108. DOI:10.3969/j.issn.0001-5733.2010.05.010 |
| [] | Liu M, Wang K, Deng K L, et al. 2013. Comparison of different local covariance functions in least-squares collocation[J]. Hydrographic Surveying and Charting (in Chinese), 33(2): 16–19. |
| [] | Liu X G, Wu X P, Wang K. 2012. Construction of the least squares collocation models for single component and composite components of disturbed gravity gradients[J]. Chinese Journal of Geophysics (in Chinese), 55(5): 1572–1580. DOI:10.6038/j.issn.0001-5733.2012.05.015 |
| [] | Liu X G, Yan Z C, Sun W, et al. 2014. Precision evaluation and analysis of least squares collocation method and spherical harmonic analysis method in the determination of the Earth's gravity field model[J]. Progress in Geophysics (in Chinese), 29(1): 46–50. DOI:10.6038/pg20140106 |
| [] | Ning J S, Wang Z T. 2013. Progress and present status of research on earth's gravitational field[J]. Journal of Geomatics (in Chinese), 38(1): 1–7. |
| [] | Olesen A V, Andersen O B, Tscherning C C. 2002. Merging of airborne gravity and gravity derived from satellite altimetry: Test cases along the coast of Greenland[J]. Studia Geophysica et Geodaetica, 46(3): 387–394. DOI:10.1023/A:1019577232253 |
| [] | Pavlis N, Kenyon S, Factor J, et al. 2008. Earth gravitational model 2008[C].//SEG Technical Program Expanded Abstracts, 761-763. |
| [] | Pavlis N K, Holmes S A, Kenyon S C, et al. 2012. The development and evaluation of the earth gravitational model 2008 (EGM2008)[J]. Journal of Geophysical Research, 117(B4): B04406. |
| [] | Sandwell D T, Smith W H F. 2009. Global marine gravity from retracked Geosat and ERS-1 altimetry: Ridge segmentation versus spreading rate[J]. Journal of Geophysical Research, 114(B1): B01411. |
| [] | Yang J Y, Zhang X H, Zhang F F, et al. 2012. On the accuracy of EGM2008 earth gravitational model in Chinese Mainland[J]. Progress in Geophysics (in Chinese), 27(4): 1298–1306. DOI:10.6038/j.issn.1004-2903.2012.04.003 |
| [] | Zhang C Y, Guo C X, Chen J Y, et al. 2009. EGM 2008 and its application analysis in Chinese mainland[J]. Acta Geodaetica et Cartographica Sinica (in Chinese), 38(4): 283–289. |
| [] | Zhang Y Q, Teng J W, Wang Q S, et al. 2014. Density structure and isostatic state of the crust in the Longmenshan and adjacent areas[J]. Tectonophysics, 619-620: 51–57. DOI:10.1016/j.tecto.2013.08.018 |
| [] | Zheng W, Xu H Z, Zhong M, et al. 2010. Progress and present status of research on earth's gravitational field models[J]. Journal of Geodesy and Geodynamics (in Chinese), 30(4): 83–91. |
| [] | 付广裕, 祝意青, 高尚华, 等. 2013. 川西地区实测自由空气重力异常与EGM2008模型结果的差异[J].地球物理学报, 56(11): 3761–3769. DOI:10.6038/cjg20131117 |
| [] | 管泽霖, 管铮, 黄谟涛, 等. 1997. 局部重力场逼近理论和方法[M]. 北京: 测绘出版社. |
| [] | 海斯卡涅, 莫里斯. 1979. 物理大地测量学[M]. 卢福康, 胡国理译. 北京: 测绘出版社. |
| [] | 李姗姗, 吴晓平, 张传定, 等. 2010. 我国重力场新的统计特征参数的计算分析[J].地球物理学报, 53(5): 1099–1108. DOI:10.3969/j.issn.0001-5733.2010.05.010 |
| [] | 刘敏, 王昆, 邓凯亮, 等. 2013. 最小二乘配置中两种局部协方差函数的比较[J].海洋测绘, 33(2): 16–19. |
| [] | 刘晓刚, 吴晓平, 王凯. 2012. 扰动重力梯度张量单分量和组合分量最小二乘配置法模型的建立[J].地球物理学报, 55(5): 1572–1580. DOI:10.6038/j.issn.0001-5733.2012.05.015 |
| [] | 刘晓刚, 闫志闯, 孙文, 等. 2014. 确定地球重力场模型的最小二乘配置法与调和分析法的精度评析[J].地球物理学进展, 29(1): 46–50. DOI:10.6038/pg20140106 |
| [] | 宁津生, 王正涛. 2013. 地球重力场研究现状与进展[J].测绘地理信息, 38(1): 1–7. |
| [] | 杨金玉, 张训华, 张菲菲, 等. 2012. EGM2008地球重力模型数据在中国大陆地区的精度分析[J].地球物理学进展, 27(4): 1298–1306. DOI:10.6038/j.issn.1004-2903.2012.04.003 |
| [] | 章传银, 郭春喜, 陈俊勇, 等. 2009. EGM 2008地球重力场模型在中国大陆适用性分析[J].测绘学报, 38(4): 283–289. |
| [] | 郑伟, 许厚泽, 钟敏, 等. 2010. 地球重力场模型研究进展和现状[J].大地测量与地球动力学, 30(4): 83–91. |
 2017, Vol. 32
2017, Vol. 32