由于全球导航卫星系统(GNSS)具有全天候、高精度、覆盖范围广等优势,有利于长期连续地监测电离层活动,获取不同时间和空间上的电离层信息,是目前研究电离层TEC的重要手段之一(Mannucci et al., 1998; Gao and Liu, 2002; 袁运斌, 2002; 耿长江, 2011).采用不同尺度覆盖的地基GNSS观测资料,能够反演高精度电离层TEC并建立区域或全球的精细化电离层TEC模型,对提高GNSS导航定位精度以及剖析电离层形态和空间结构具有重要意义,是近年来电离层的研究热点(Yuan and Ou, 2004; Jin et al., 2012; Wan et al., 2012; 章红平等, 2012; An et al., 2014).
电离层VTEC的全球建模通常采用低阶球谐函数,欧洲定轨中心(Center for Orbit Determination in Europe, CODE)基于全球200多个GPS/GLONASS观测站,采用15阶球谐函数建立全球电离层模型,并发布全球电离层图(Global Ionosphere Maps, GIM)(Schaer, 1999, 2014; Memarzadeh, 2009).由于VTEC球谐函数模型是基于地基GNSS观测数据建立的,数学上球谐函数要求全球均匀分布的GNSS观测站才能获得理想的效果,而由于实际客观环境导致全球GNSS观测站分布极不均匀,大部分集中在陆地,海洋和南极地区测站甚少,导致在这些区域的GNSS观测数据严重缺少甚至空白,因此球谐函数无法精确地表达这些区域的电离层VTEC,在某些地区甚至出现负值.该问题的处理方法通常有三种:第一类方法是通过对VTEC附加非负不等式约束条件来消除负值VTEC(Zhang et al., 2013),该类方法通常计算较为复杂,且仅从数值意义上保证了各地区的VTEC为正值,不具备明显的物理意义;第二类方法则是利用外部其他观测资料来弥补GNSS观测数据的不足,如采用GNSS电离层掩星数据(吴小成等, 2006; 周义炎等, 2012),但目前能够用于全球电离层建模的掩星资料非常有限,往往只能减弱而无法有效克服该问题;第三类方法则是采用经验物理电离层模型计算的VTEC值来填补观测空白区域,文献(王成等, 2014)采用国际参考电离层模型(International Reference Ionosphere, IRI)计算的VTEC值作为虚拟观测值对赤道周边和南半球区域进行约束,确保了全球各个地区的VTEC为正值,得到的全球VTEC结果与IGS结果的偏差精度约为3.7TECU.
针对GNSS观测数据稀少或空白区域的异常VTEC,CODE也采用了一系列算法进行平滑和约束,如卡尔曼滤波、序贯最小二乘、随机游走、分段线性以及不等式约束的高斯-马尔科夫模型等,使得全球VTEC变得更加精准.因此,本文以CODE发布的GIM产品为参考,评定全球VTEC建模精度.
显然,采用附加经验模型约束的全球电离层建模方法可直接对VTEC负值区域进行约束,计算简单,物理意义明确.目前常用的经验电离层模型主要有Klobuchar模型(Klobuchar, 1987; Memarzadeh, 2009)、IRI模型(Bilitza and Reinisch, 2008; Bilitza et al., 2011)和NeQuick模型(Nava et al., 2008; Radicella, 2009; Bidaine and Warnant, 2010),这三种经验模型在不同区域和不同时间的计算精度不同,因此,这些模型约束下的全球VTEC建模效果以及它们的差异值得研究.本文分别使用这三种经验模型对全球无电离层穿刺点覆盖的区域进行约束,即在这些区域添加虚拟穿刺点,并用经验模型计算虚拟穿刺点处的电离层VTEC作为虚拟观测值,一并参与全球球谐函数建模,旨在比较这三种经验模型对全球电离层建模精度的影响、对穿刺点空白区域的VTEC建模精度的改善效果、以及三种经验模型在全球不同地区的约束效果和适用性.
1 地基GNSS电离层球谐函数模型GNSS包含分米级精度的伪距和毫米级精度的相位两类基本观测量,它们都受到电离层的影响.由于相位观测值中包含了模糊度参数而无法直接求解绝对电离层延迟,通常采用载波相位平滑伪距观测值来反演电离层VTEC,对应的反演方程为
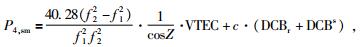
|
(1) |
式中,P4, sm为载波相位平滑后的伪距观测量,f1, f2为两个载波的频率,Z为穿刺点的卫星天顶角,VTEC为垂直总电子含量,c为光速,DCBr和DCBs分别为接收机和卫星的频间码偏差.
由于每个历元的VTEC均不相同,因此需要采用多个测站求解VTEC.与此同时,由于接收机和卫星的DCB参数是相关的,导致观测方程秩亏且秩亏数为1,因此需要引入至少1个基准约束方程.为了与CODE发布的DCB产品比较,本文采用与CODE相同的基准约束方程,即假设所有GPS卫星的DCB之和为0.
VTEC是随时间和空间变化的,若直接求解将需要引入大量参数,使得计算量增加且计算不稳定.因此将VTEC表达为随时间和空间变化的函数模型,通过求解函数模型的参数代替直接求解VTEC本身,从而有效减少参数个数,提高计算效率.Schaer提出采用球谐函数来描述全球电离层VTEC(Schaer, 1999),公式为
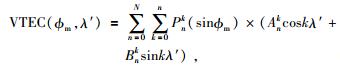
|
(2) |
式中,Ank,Bnk为球谐函数的参数,Pnk(sinφm)为缔合Legendre函数,N为模型阶数.λ′为过穿刺点的经线与过地心和太阳连线的经线构成的夹角,φM为地磁纬度,它们的表达式分别为
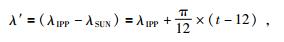
|
(3) |
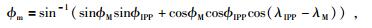
|
(4) |
其中,λIPP,φIPP分别为电离层穿刺点处的地理经纬度,t为观测历元的世界时;λM,φM分别为地磁北极的地理经纬度,本文计算取λM=79.3°N,φM=71.5°W.
将(2) 式代入(1) 式,得到利用球谐函数进行电离层建模的观测方程为
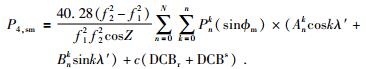
|
(5) |
由于电离层在一天内随时间变化极其复杂,仅用一组球谐函数系数无法精确地描述电离层在时间域的变化情况,因此,本文将一天划分为12个时段,每2个小时求解一组球谐函数系数,用来表达2小时时段内的全球VTEC.由于接收机和卫星的DCB在一天内是稳定的,因此DCB参数在一天内被视为一组常数求解.
在穿刺点空白区域添加虚拟穿刺点,每一历元用经验模型计算虚拟穿刺点处的VTEC作为虚拟观测值参与球谐函数建模.由于经验模型计算的VTEC精度较低,因此在采用经验模型约束时,必须要有合理的权比关系.本文计算中取相位平滑伪距P4, sm的权为单位权,根据实验计算分析,取虚拟观测值的权为0.01 m2/TECU2,虚拟观测方程为
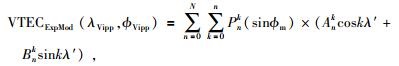
|
(6) |
式中,VTECBxpMod(λVippφVipp)为经验模型计算的虚拟穿刺点处的VTEC,方程右边为式(2) 中的VTEC球谐函数表达式.
2 三种经验电离层模型介绍Klobuchar模型是基于Bent电离层经验模型简化而来,是美国科学家Klobuchar于1987年提出的用于改正单频GPS接收机电离层延迟的经验模型,该模型计算简单、实用可靠,被广泛应用于GNSS导航领域.模型假设所有电子集中在高度为350km的薄层,采用余弦函数的形式反映电离层的周日变化特征,夜晚的电离层延迟被视为一个常量(Klobuchar, 1987),模型表达式为

|
(7) |
式中各参数的意义见文献(Memarzadeh, 2009).al和bl(l=0, …, 3) 为Klobuchar模型的8个参数,可从GPS广播星历文件中获得.
IRI模型是根据大量电离层探测数据得到的经验模型,可以计算海拔50~2000 km范围内的电子密度,2000km以上至GPS卫星轨道高度范围内的电子密度可通过外推得到.由IRI模型计算2000 km以下电子密度的方程式为
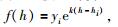
|
(8) |
式中,f(h)为高度h对应的电子密度,yi为高度hi对应的电子密度,k为待求系数.根据最小二乘解算系数k后可外推2000 km高度以上的电子密度,最后累加50 km至GPS卫星轨道高度范围内的电子密度,即可得到总电子含量(Bilitza and Reinisch, 2008; Bilitza et al., 2011; 王成等, 2014).目前IRI已发布了多种版本,本文使用IRI2012进行计算.
NeQuick模型是随时间变化的三维电离层电子密度经验模型,可以计算测站与卫星以及卫星与卫星之间任意给定时间、位置的电子密度及给定路径的电子含量,再沿高度进行数值积分得到传播路径上的电离层延迟.该模型主要由高度低于F2层峰值的底部公式和高度在F2层峰值以上的顶部公式组成(Radicella, 2009).模型基本形式为
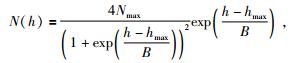
|
(9) |
式中各参数意义参见文献(Nava et al., 2008; Bidaine and Warnant, 2010).本文使用NeQuick 2版本计算.
3 实验分析选取2016年3月1日全球279个IGS站的GPS观测数据,用15阶球谐函数建立全球电离层模型.图 1为279个IGS站的位置分布,图 2为一天内所有测站对应的电离层穿刺点分布.显然,测站在北半球分布密集,在南半球特别是南极和海洋区域分布极少且不均匀,导致电离层穿刺点分布不均匀,甚至在南极和海洋的部分区域出现空白,如图 2,在A、B、C、D四个区域内没有穿刺点覆盖.

|
图 1 全球279个IGS站的位置分布 Figure 1 Distribution of global 279 IGS stations |

|
图 2 电离层穿刺点分布 Figure 2 Distribution of ionosphere pierce points |
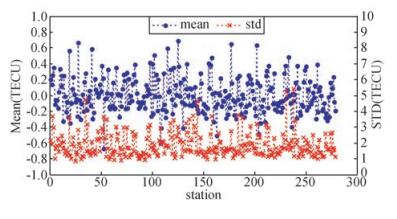
以CODE发布的GIM产品为参考,将球谐函数解算的全球电离层VTEC与CODE比较,评定建模精度.图 3给出了无约束的球谐函数模型解算的UT3、UT11和UT20三个时刻的全球VTEC与CODE的差值图.由于A、B、C、D四个区域无穿刺点覆盖,导致电离层建模时球谐函数无法精确表达这些区域的电离层VTEC,对应区域的VTEC与CODE相差较大.除四个穿刺点空白区域外,在其他地区,球谐函数均能较精确地表达电离层VTEC.模型VTEC与CODE差值的绝对值的平均值约为3.7TECU,其中65%小于3TECU、76%小于4TECU.图 4给出了所有测站一天内建模残差(即模型值与观测值之差)的均值与标准差,从图中可以看出,各站的残差均值基本在0附近波动,多部分在±0.5TECU以内,表明球谐函数能有效刻画TEC的变化,无明显的系统偏差;各站的残差标准差大部分在1~2TECU,最大不超过5TECU,表明球谐函数模型的解算精度可靠且比较稳定.

|
图 3 无约束的球谐函数模型解算的全球VTEC与CODE差值(从左往右依次为UT3、UT11、UT20时刻) Figure 3 Differences of global VTEC between unconstrained spheric harmonic function model and CODE (UT3, UT11 and UT20 from left to right) |
|
图 4 全球279个测站建模残差的均值和标准差 Figure 4 Means and STDs of modeling residuals above 279 stations |
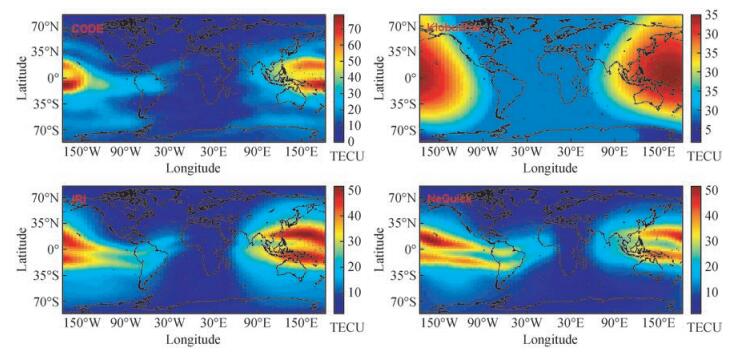
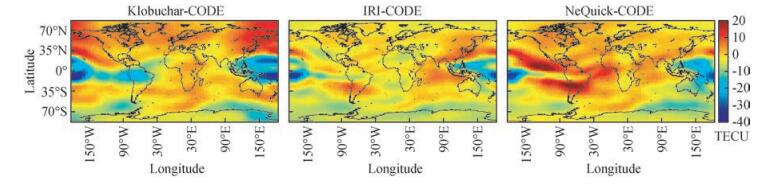
在研究附加经验模型约束的全球电离层球谐函数建模之前,对三种经验模型计算VTEC的效果进行简单分析.图 5给出了CODE及三种经验电离层模型计算的UT3时刻全球电离层VTEC图.以CODE为参考,可以看出夜间区域的电离层相对平静,白天赤道和低纬度区域的电离层活动剧烈.Klobuchar模型由于模型本身的特性,表达较为粗糙,无法细致地表达全球各地的电离层活动状态,如夜间区域的VTEC为一个常数,白天赤道周围特有的“双驼峰”结构“蔓延”到了中高纬度地区.IRI模型和NeQuick模型能更精细地表达出赤道及低纬度地区的电离层结构.将CODE全球电离层图作为标准,图 6给出了三种经验模型计算的全球电离层VTEC与CODE的差值.Klobuchar、IRI、NeQuick与CODE差值的RMS值分别为8.51、6.05和6.85TECU,差值绝对值的均值分别为6.05、4.59和4.85TECU.因此,IRI模型对全球电离层VTEC的总体表达效果最优,NeQuick模型次之,Klobuchar模型最差.IRI模型对赤道周围的电离层计算精度优于Klobuchar和NeQuick模型;IRI和NeQuick模型在细节上优于Klobuchar模型,这在夜间和赤道周围十分明显.然而,IRI和NeQuick模型的公式以及计算时效性均较Klobuchar模型复杂.
|
图 5 2016年3月1日UT3时刻CODE及三种经验电离层模型计算的全球电离层 Figure 5 Global ionosphere map calculated by CODE and three empirical models at UT3 on March 1, 2016 |
|
图 6 三种经验模型全球电离层图与CODE的差值 Figure 6 Differences of global ionosphere map between three empirical models and CODE |
分别使用上述三种经验模型对A、B、C、D四个穿刺点空白区域进行约束,即在这些区域添加虚拟穿刺点,并用经验模型计算虚拟穿刺点处的电离层VTEC作为虚拟观测值,参与全球球谐函数建模.四个穿刺点空白区域的范围分别为:A(15°N ~35°S,160°W~85°W),B(37.5°S ~72.5°S,160°W~85°W),C(75°S ~87.5°S,135°W~15°E),D(40°S~65°S,20°W~40°E).本文将不加约束的球谐函数建模方案记为“SH”,将附加三种经验模型约束后的建模方案分别记为“SH+Klob”、“SH+IRI”和“SH+NeQ”.
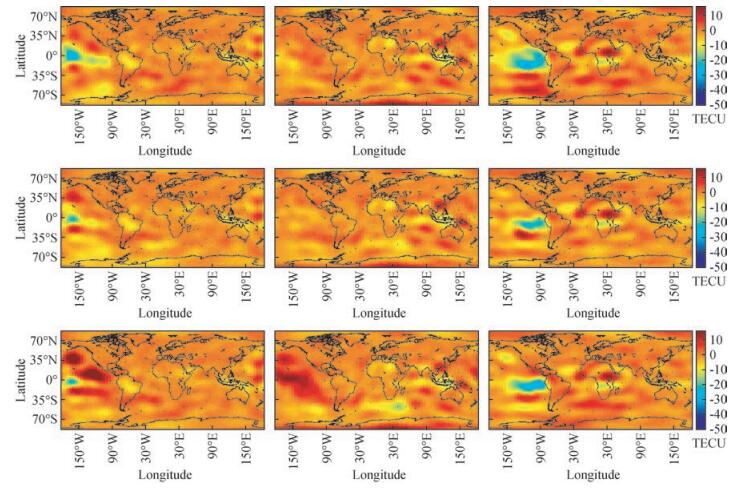
图 7(a, b, c)依次给出了附加三种经验模型约束后UT3、UT11和UT20三个时刻的全球电离层VTEC与CODE的差值.与图 3相比,附加三种经验模型约束后,四个穿刺点空白区域的电离层精度总体上得到了明显的提高,如UT3和UT11时刻的B区域,UT11时刻的C区域和UT20时刻的D区域.虽然,A区域的误差与其他区域相比较大,但较无约束结果仍有明显改善.结合图 3,仔细分析A区域在三个时刻的效果,三种约束解在UT11时刻都能明显提高A区域的拟合精度,这是由于当地时间正处于夜间,电离层活动平静,三种经验模型均较好地表达出了该地的电离层延迟.而在UT3和UT20时刻,A区域的当地时间分别为下午和正午,电离层活动比较活跃,具有赤道地区特有的异常结构,而经验模型表达赤道地区电离层异常结构的能力有限,因此A区域的拟合误差较其他区域仍偏大.
|
图 7 附加虚拟观测后的全球电离层VTEC图与CODE GIM之差 (从上到下依次对应:SH+Klob,SH+IRI和SH+NeQ;从左往右依次为UT3、UT11、UT20时刻) Figure 7 Differences of global VTEC map between models with virtual observations and CODE (SH+Klob, SH+IRIand SH+NeQ from top to bottom; UT3, UT11 and UT20 from left to right) |
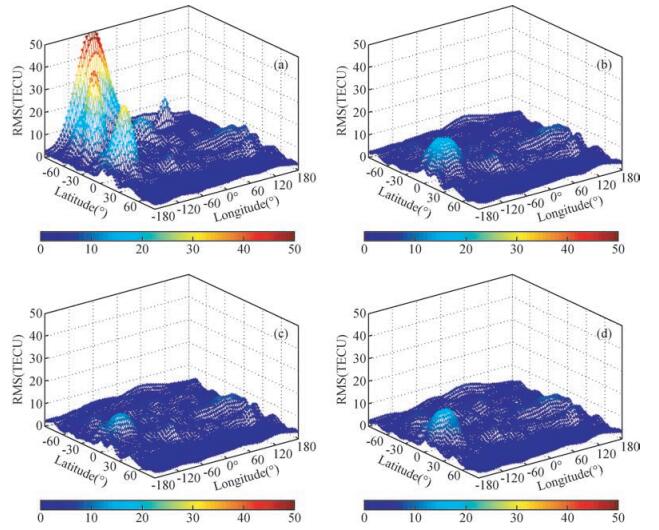
将全球划分为2.5°×5°的格网,并采用已建立的四种模型方案每小时分别计算所有格网点的VTEC与CODE差值,每个格网点一天共有24个差值,采用这24个差值计算每个格网点的RMS值作为该格网点处的VTEC精度.图 8(a~d)依次给出了四种建模方案的全球VTEC精度,从图中可以看出,“SH”方案在四个穿刺点空白区域的VTEC建模精度较差,尤其是A、B、C三个区域.附加三种经验模型约束后,四个空白区域的VTEC精度有了大幅度改善,特别是B、C、D三个区域,VTEC精度与周边其他区域一致.A区域的VTEC精度较其他区域仍然偏大,这是由赤道区域电离层活动激烈以及经验模型描述赤道周围电离层异常结构能力有限所共同造成.三种经验模型对全球电离层建模的约束效果相似.
|
图 8 四种方案的全球电离层VTEC建模精度 Figure 8 Accuracy of global VTEC modeling by four restraint methods (a) SH; (b) SH+Klob; (c) SH+IRI; (d) SH+NeQ. |
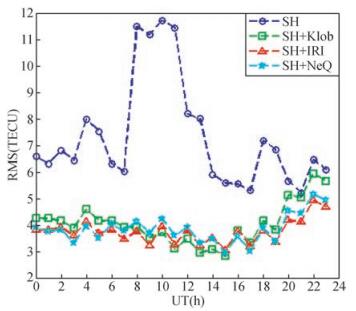
图 8在空间域上统计分析了电离层建模精度,下面分析在时间域上的电离层建模精度.计算每一时刻全球VTEC与CODE差值的RMS值,得到24个时刻的RMS值,如图 9所示.“SH”方案的全球建模精度较差,在UT8-11时段内RMS超过11TECU,精度最高时也超过了5TECU;附加三种经验模型约束的建模精度明显改善,在UT0~19时段内,RMS值均小于5TECU;UT20~23时段RMS值有所增大,这是由于该时段内A、B、C区域处在地方时正午前后,电离层活动比较激烈,导致经验模型本身的精度较差而导致约束效果欠佳.从一天24个时刻的RMS值来看,“SH+IRI”的效果略优.
|
图 9 四种方案一天24个时刻的全球VTEC精度 Figure 9 Global VTEC accuracy at 24 hours a day calculated by four methods |
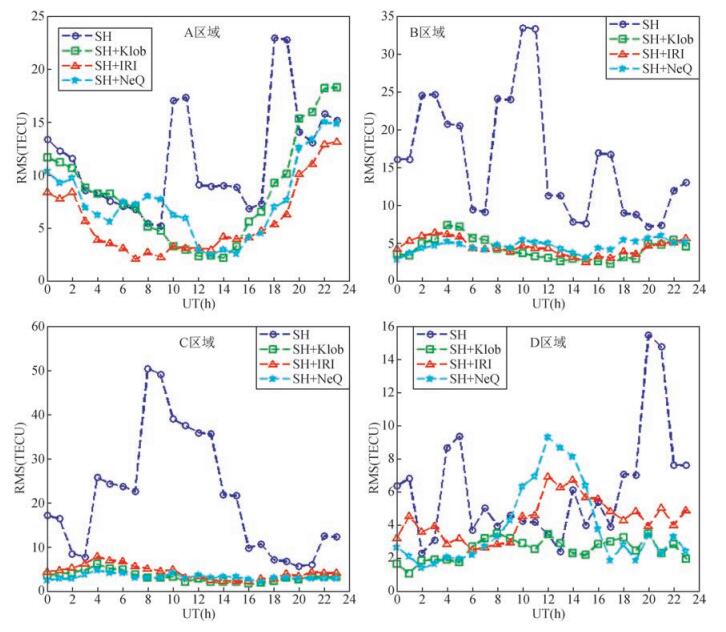
下面详细分析四个穿刺点空白区域在四种方案下电离层VTEC建模精度,图 10分别给出了这四个区域在24个时刻分别用四种方案的VTEC建模精度.
|
图 10 四个空白区域在一天24个时刻的VTEC精度 Figure 10 VTEC accuracy of four blank IPP areas at 24 hours a day |
对于A区域,在UT10~15和UT18~19时段内,三种约束模型能明显提高VTEC精度;而在其他时刻,VTEC精度提高不明显甚至变差,主要原因是A区域位于赤道周围,电离层活动强烈.然而,“SH+IRI”方案在24个时刻均提高了A区域的VTEC精度,表明IRI模型对于赤道区域的VTEC计算精度最高(如图 5),因此,对于赤道周围的穿刺点空白区域采用IRI模型约束效果最好.
对于B和C区域,即南半球中高纬度地区和南极地区,附加三种约束在一天24个时刻均提高了当地的VTEC精度;三种经验模型的约束效果相似,约束后的VTEC精度提高至5TECU左右且比较稳定,不受“SH”方案的VTEC精度较大波动的影响.
对于D区域,“SH”的效果要比A、B、C三个区域好,如在UT13时刻,“SH”方案在该区域的VTEC精度约为2TECU,这表明此时球谐函数已经能够精确地表达该地区的电离层VTEC,而附加经验模型约束后,只对VTEC精度较差的时段有所改善,其余时段改善不明显.换句话说,当“SH”不足以精确描述该区域的VTEC时,附加经验模型约束能改善VTEC的精度.此外,“SH+Klob”在整个时段总体表现优于“SH+IRI”和“SH+NeQ”方案,说明该区域采用Klobuchar模型约束更合理.
上述分析得出:A区域(赤道区域)采用IRI模型约束效果最优,D区域采用Klobuchar模型约束效果最优,B、C两个区域(南半球中高纬度和南极地区)采用三种经验模型的效果相似.
4 结论由于全球GPS测站分布极其不均匀,导致采用球谐函数建立全球电离层VTEC模型时,在电离层穿刺点空白区域的精度较差甚至出现负值,本文研究了采用经验电离层模型约束GNSS空白区域的全球电离层VTEC建模,比较分析了Klobuchar、IRI和NeQuick三种经验电离层模型在空间域和时间域上的约束效果.得出结论如下:
(1) 附加经验模型约束后,全球电离层建模的总体精度明显改善,三种模型约束效果相近.
(2) 穿刺点空白区域的VTEC精度显著提高;Klobuchar模型的约束效果在中纬度地区最显著,赤道地区采用IRI模型约束总体精度最高,南极和中高纬度地区采用三种经验模型约束的效果相似.
(3) 在穿刺点空白区域,特别是赤道和中低纬度地区,三种经验模型在不同时间的约束效果存在明显差异.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | An J C, Wang Z M, Ning X G. 2014. GPS-based regional ionospheric models and their suitability in Antarctica[J]. Advancesin Polar Science, 25(1): 32–37. |
| [] | Bidaine B, Warnant R. 2010. Assessment of the NeQuick model at mid-latitudes using GNSS TEC and ionosonde data[J]. Advancesin Space Research, 45(9): 1122–1128. DOI:10.1016/j.asr.2009.10.010 |
| [] | Bilitza D, Reinisch BW. 2008. International reference ionosphere 2007: Improvements and new parameters[J]. Advancesin Space Research, 42(4): 599–609. DOI:10.1016/j.asr.2007.07.048 |
| [] | Bilitza D, McKinnell LA, Reinisch B, et al. 2011. The international reference ionosphere today and in the future[J]. Journal of Geodesy, 85(12): 909–920. DOI:10.1007/s00190-010-0427-x |
| [] | Gao Y, Liu ZZ. 2002. Precise ionosphere modeling using regional GPS network data[J]. Journal of Global Positioning Systems, 1(1): 18–24. DOI:10.5081/jgps |
| [] | Geng C J. 2011. Theory and method on real time monitoring of ionospheric delay using ground based GNSS data (in Chinese)[Ph. D. thesis]. Wuhan:Wuhan University. |
| [] | Jin R, Jin S G, Feng G P. 2012. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases[J]. GPS Solutions, 16(4): 541–548. DOI:10.1007/s10291-012-0279-3 |
| [] | Klobuchar J A. 1987. Ionospheric time-delay algorithm for single-frequency GPS users[J]. IEEE Transactions on Aerospace and Electronic Systems, AES-23(3): 325–331. DOI:10.1109/TAES.1987.310829 |
| [] | Mannucci A J, Wilson BD, Yuan DN, et al. 1998. A global mapping technique for GPS-derived ionospheric total electron content measurements[J]. Radio Science, 33(3): 565–582. DOI:10.1029/97RS02707 |
| [] | Memarzadeh Y. 2009. Ionospheric modeling for precise GNSS applications[MSc. thesis]. Tehran, Iran: K. N. Toosi University of Technology. |
| [] | Nava B, Coïsson P, Radicella SM. 2008. A new version of the NeQuick ionosphere electron density model[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 70(15): 1856–1862. DOI:10.1016/j.jastp.2008.01.015 |
| [] | Radicella SM. 2009. The NeQuick model genesis, uses and evolution[J]. Annals of Geophysics, 52(3-4): 417–422. |
| [] | Schaer S. 1999. Mapping and predicting the earth's ionosphere using the global positioning system[Ph.D. thesis]. Bern, Switzerland: The University of Bern. |
| [] | Schaer S. 2014. GNSS ionosphere analysis at CODE[C].//2004 IGS Workshop.Berne, Switzerland. |
| [] | Wan W X, Ding F, Ren Z P, et al. 2012. Modeling the global ionospheric total electron content with empirical orthogonal function analysis[J]. Science China Technological Sciences, 55(5): 1161–1168. DOI:10.1007/s11431-012-4823-8 |
| [] | Wang C, Wang J X, Duan B B. 2014. Global ionospheric model with international reference ionosphere constraint[J]. Geomatics and Information Science of Wuhan University (in Chinese), 39(11): 1340–1346. |
| [] | Wu X C, Hu X, Zhang X X, et al. 2006. A calibrated TEC method for inversion of ionospheric GPS occultation data[J]. Chinese Journal of Geophysics (in Chinese), 49(2): 328–334. DOI:10.3321/j.issn:0001-5733.2006.02.004 |
| [] | Yuan Y B. 2002. Study on theories and methods of correcting ionospheric delay and monitoring ionosphere based on GPS (in Chinese)[Ph. D. thesis]. Wuhan:Institute of Geodesy and Geophysics Chinese Academy of Sciences. |
| [] | Yuan Y B, Ou J K. 2004. A generalized trigonometric series function model for determining ionospheric delay[J]. Progress in Natural Science, 14(11): 1010–1014. DOI:10.1080/10020070412331344711 |
| [] | Zhang H P, Han W H, Huang L, et al. 2012. Modeling global ionospheric delay with igs ground-based GNSS observations[J]. Geomaticsand Information Science of Wuhan University (in Chinese), 37(10): 1186–1189. |
| [] | Zhang H P, Xu P L, Han W H, et al. 2013. Eliminating negative VTEC in global ionosphere maps using inequality-constrained least squares[J]. Advancesin Space Research, 51(6): 988–1000. DOI:10.1016/j.asr.2012.06.026 |
| [] | Zhou Y Y, Shen W B, Wu Y, et al. 2012. Ground-based GPS VTEC constrained inversion method for ionospheric occultation[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1088–1094. DOI:10.6038/j.issn.0001-5733.2012.04.003 |
| [] | 耿长江. 2011. 利用地基GNSS数据实时监测电离层延迟理论与方法研究[博士论文]. 武汉: 武汉大学. |
| [] | 王成, 王解先, 段兵兵. 2014. 附有国际参考电离层约束的全球电离层模型[J].武汉大学学报·信息科学版, 39(11): 1340–1346. |
| [] | 吴小成, 胡雄, 张训械, 等. 2006. 电离层GPS掩星观测改正TEC反演方法[J].地球物理学报, 49(2): 328–334. DOI:10.3321/j.issn:0001-5733.2006.02.004 |
| [] | 袁运斌. 2002. 基于GPS的电离层监测及延迟改正理论与方法的研究[博士论文]. 武汉: 中国科学院测量与地球物理研究所. |
| [] | 章红平, 韩文慧, 黄玲, 等. 2012. 地基GNSS全球电离层延迟建模[J].武汉大学学报·信息科学版, 37(10): 1186–1189. |
| [] | 周义炎, 申文斌, 吴云, 等. 2012. 地基GPS VTEC约束的电离层掩星反演方法[J].地球物理学报, 55(4): 1088–1094. DOI:10.6038/j.issn.0001-5733.2012.04.003 |
 2017, Vol. 32
2017, Vol. 32

