基于岩石物理方法,分析青藏高原冻土区水合物地层,为水合物数值建模和地震正演模拟提供基础数据,并为地震方法研究水合物的响应特征、圈定水合物的分布区域以及后期的勘探开发提供岩石物理方面的支持及参考.本文主要根据青藏高原冻土区水合物勘探的数据资料,分析水合物地层的物性特征及水合物颗粒在岩石孔隙中的填充情况.
国外很早就开展了水合物地层的岩石物理研究,较早的有Lee等(1996)根据水合物地层三种主要成分的体积百分比含量,采用了三相时间平均公式计算水合物地层的速度,该公式是一定程度的近似计算,不考虑地层各成分的弹性模量.Helgerud等(1999)采用Gassmann公式计算干岩石的弹性模量并构建模型,采用此方法对美国东南海域Blake-Bahama Ridge区域的深海海底地层的水合物浓度做了估算,不过目前还没有采用这种方法对冻土区水合物地层进行相关分析.Dai等(2004)依据水合物颗粒与岩石骨架的微观结构,基于Blake Ridge地区的资料对含水合物岩层进行分类,其中岩层孔隙作为水合物填充及赋存空间的模式可以作为分析冻土区水合物模式的参考依据.Zhang等(2012)对墨西哥湾北部地区GC955测井项目的中子孔隙度测井数据和伽马测井数据做了统计分析,通过对比发现含水合物地层具有较高的纵波速度,这是区别于不含水合物地层的一个重要依据.Shankar等(2013)对印度东部海域的Krishna-Godavari盆地的水合物地层做了岩石物理分析,采用弹性介质理论对含水合物层段的水合物饱和度做了估算,采用的方法是通过不同饱和度的速度曲线与实际地层的速度数据进行对比,通过估算速度与实际速度的接近程度来实现对饱和度的预测.针对国内研究,赵省民等(2000)总结赋存水合物地层的地质和地球物理等识别标志,这为水合物的岩石物理分析指明了方向.宋海斌等(2002)和孙春岩等(2003)基于岩石物理方法计算水合物岩层的纵波与横波速度,没有与实际数据进行对比,因而缺乏对实际水合物的填充赋存模式及微观结构的实例分析.赵群等(2005)针对水合物的微观模式,制作了非固结微弱胶结高孔隙度三维物理模型,并指出随着温度的改变,胶结程度的改变会影响水合物地层的岩石物理性质.因此,对地震波在水合物地层中的传播速度进行研究,是水合物岩石物理分析的一个重要手段.地层的物性存在差异,速度也会发生改变,反之,通过研究水合物地层速度的变化,可以反映水合物地层的物性特征.另外,密度也是构建岩石物理模型的重要参数,通过联合速度和密度等物性参数能够更全面有效地反映水合物地层的特征.
对于青藏高原冻土区水合物,陈多福等(2005)和卢振权等(2008)分别从不同方面对其形成条件进行了分析.2008年我国首次在青藏高原祁连山冻土区发现水合物(祝有海等,2009),通过多个井的钻井取芯证实了水合物的存在,并借助测井数据获得了水合物地层的埋深、厚度、速度和密度等资料.卢振权等(2010)通过分析岩芯和测井数据发现水合物主要存在于砂岩、泥岩、油页岩等岩层的孔隙或裂缝中.祝有海等(2010)分析了水合物赋存于不同岩性地层中的方式及形态,以浸染状填充于砂岩孔隙中,以片状或团块状填充于泥岩和油页岩的裂缝中.郭星旺(2011)针对青藏高原水合物地层,对比了密度测井孔隙度数据和电阻率测井孔隙度数据,认为后者更接近实际水合物地层的原位孔隙度.庞守吉等(2013)认为碎屑沉积环境为地层中水合物提供了有利的存储空间,可见岩石孔隙是水合物填充及赋存的主要储集空间之一.为了在现有水合物勘探数据的基础上,对水合物地层的物性有深入的认识,主要从以下三个方面来探讨水合物地层的特征:(1) 针对不同岩性的水合物地层,分析地震波速度和密度的特征;(2) 随着孔隙度和饱和度的变化,分析水合物地层速度的变化情况;(3) 对于含水合物砂岩地层,分析水合物在地层孔隙中的填充及赋存方式,因此很有必要对含水合物地层进行岩石物理分析.
水合物地层的岩石物理分析,主要研究地层的岩性、孔隙度和饱和度等因素对地层的速度和密度的影响,并借助不同的岩石物理模型分析水合物颗粒在地层孔隙中的填充模式.首先,根据青藏高原木里地区钻孔的测井数据(郭星旺,2011),提取多个层段的速度和密度数据,并与同一井孔中相同岩性、不含水合物的地层进行对比,由此得出水合物地层速度与密度的特点.其次,采用时间平均方程(Lee et al., 1996;Dvorkin and Nur, 1998)提取水合物地层岩石骨架的物性参数,主要包括骨架的纵波速度、横波速度、密度、体积模量、剪切模量.最后,采用K-T方程(Zimmerman and King, 1986)的岩石物理模型和区分填充模式(Helgerud et al., 1999)的岩石物理模型,计算在一定孔隙度和饱和度条件下的水合物地层速度,并与实际数据进行对比,确定符合实际地层情况的水合物岩石物理模型.
1 水合物地层速度和密度的特征根据青藏高原冻土区钻探获得的岩芯资料(祝有海等,2009;卢振权等,2010),发现含水合物地层岩性以砂岩和泥岩为主,其中砂岩主要为细砂岩和粉砂岩.此次青藏高原水合物科学钻探工程,先后在多个井孔中发现含水合物地层.本文以青藏高原祁连山木里地区的三个井孔DK-1、DK-3和DK-4(郭星旺,2011)的测井数据及计算获得孔隙度和饱和度等相关数据为基础,制作速度密度交会图,测井数据包括采样点的深度数据、声波时差数据和密度数据.通过与相同岩性、不含水合物地层的速度和密度进行对比,获得含水合物地层速度与密度的特征.本次水合物勘探区域的三个井孔之间的水平距离均比较小,以DK1井为参照物,DK-3井孔位于DK-1孔南东东向约12 m处,DK-4井孔位于DK-1井孔北北东向约250 m处.
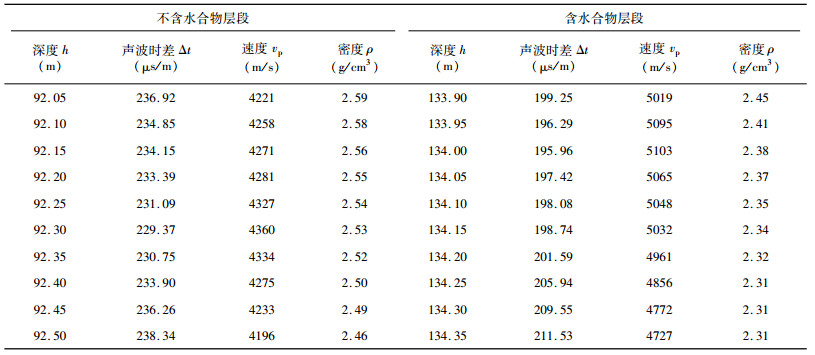
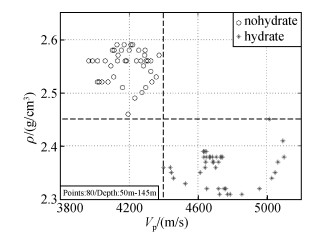
1.1 速度和密度的交会图对比含水合物地层与不含水合物地层的速度与密度,利用速度密度交会图来进行分析.表 1是DK-1井孔不同层段的深度(h)、声波时差(Δt)、纵波速度(vp)和密度(ρ)数据,其中纵波速度由声波时差计算得到.依据这些数据,制作DK-1井孔含水合物层与不含水合物层的速度密度交会图,在50~145 m深度范围取得80个数据样点,每个采样点对应一个速度值和一个密度值,见图 1,其中空心圆点表示不含水合物层的采样点,实心点表示含水合物层的采样点.通过比较发现交会图中不含水合物层采样点分布于图的左上部,具有速度小、密度大的特征;含水合物层采样点分布于图的右下部,具有速度大、密度小的特征.在速度密度交会图上,不含水合物和含水合物地层表现出不重叠、分区分布的特征.
|
|
表 1 DK-1井孔部分声波时差数据与密度数据 Table 1 Acoustic time dada and density data of DK-1 |
|
图 1 DK-1井孔含水合物细砂岩层与不含水合物细砂岩层的速度密度交会图 Figure 1 Velocity-density crossing plot of packsand for the hole of DK-1 |
DK-3井孔含水合物泥岩层与不含水合物泥岩层的速度密度交会图,见图 2,与前面DK-1井孔细砂岩相比,同样具有区域分布的特征.不含水合物层的速度小、密度大,采样点分布于图的左上部;含水合物层的速度大、密度小,采样点分布于右下部.

|
图 2 DK-3井含水合物泥岩层与不含水合物泥岩层的速度密度交会图 Figure 2 Velocity-density crossplot of mudstone for the hole of DK-3 |
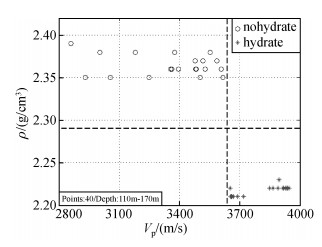
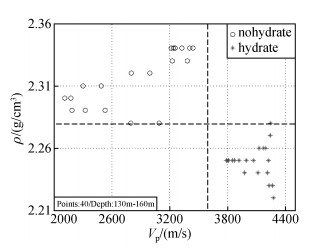
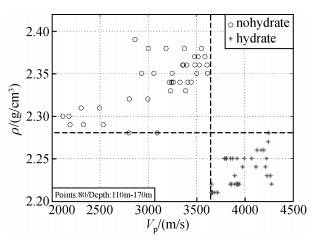
由于DK-4井孔包括粉砂岩地层与泥岩地层,因此分别针对两种岩性地层制作了交会图,见图 3和图 4,图 5包括两种岩性所用采样点速度的交会图.通过对比可知,在图中不含水合物层采样点与含水合物层采样点同样具有分区分布的特点.
|
图 3 DK-4井孔含水合物粉砂岩层与不含水合物粉砂岩层的速度密度交会图 Figure 3 Velocity-density crossplot of siltstone for the hole of DK-4 |
|
图 4 DK-4含水合物泥岩层与不含水合物泥岩层的速度密度交会图 Figure 4 Velocity-density crossplot of mudstone for the hole of DK-4 |
|
图 5 DK-4含水合物层与不含水合物层的速度密度交会图 Figure 5 Velocity-density crossplot for the hole of DK-4 |
分析每个井孔含水合物层段与不含水合物层段采样点的速度密度交会图,不难发现,不含水合物层段的采样点位于交会图的左上部,含水合物位于交会图的右下部,并且两者没有交叉重叠,呈现明显的“十字”分布特征.
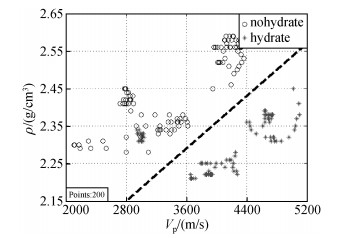
综合DK-1、DK-3和DK-4三个井孔的200个采样点的速度密度数据,两个参量的交会图见图 6,不含水合物层段采样点处于左上区,速度小、密度大,含水合物层段采样点处于右下区,速度大、密度小.不同于前面单井的情况,多井交会图中,不含水合物采样点与含水合物采样点分布于更大的区域,不过两者仍然具有较好的分区分布的特点,分别分布于对角线(图中虚线)的两侧.可以看出,含水合物层与不含水合物层的采样点在速度密度交会图上具有“对角线”分布的特征.
|
图 6 含水合物层与不含水合物层的速度密度交会图 Figure 6 Velocity-density crossplot for the hole of DK-1, DK-3 and DK-4 |
前面的多个速度密度交会图,反映了含水合物层与不含水合物层存在明显的差异,下面将通过定量计算进行说明.基于不同井孔的测井数据取得各层段的速度平均值和密度平均值,计算相同岩性的含水合物与不含水合物的速度密度的差值百分比,数据见表 2.
|
|
表 2 DK-1、DK-3和DK4三个井孔含水合物层段与不含水合物层段的速度和密度 Table 2 Velocities and densities of the hydrate segments and segments without hydrate in the holes of DK-1, DK-3 and DK-4 |
比较平均速度差值百分比(含水合物速度与不含水合物速度的差值)和平均密度差值百分比,可以看出,DK-1和DK-4井孔共三个砂岩层段的速度差值比为13.7%、12.1%和13%,密度差值比为-7.4%、-7.6%和-6.2%,而DK-3和DK-4井孔两个泥岩层段的速度差值分别为4.5%、44.3%,密度差值为-4.2%、-2.8%.显然砂岩层段的数值之间很接近,而泥岩相差较大.分析原因主是砂岩以孔隙作为水合物的储集空间,具有规律性,而泥岩以裂缝为储集空间,地层物性存在突变和不确定性.
因此,构建岩石物理模型选定水合物砂岩地层作为模拟的基础.本文确定DK-1和DK-4井孔含水合物粉砂岩层段的速度和密度数据进行岩石物理分析,提取骨架的物性参数,为冻土区水合物岩石物理模型提供基础数据.
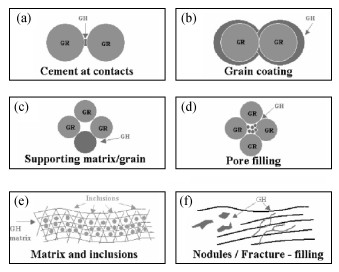
2 岩石物理参数提取水合物颗粒在地层孔隙和裂缝中以多种方式存在.综合Ecker(2001)、Dai等(2004)和张卫东等(2011)对水合物地层的分类,水合物地层微观结构模式主要有六种:接触结构、包裹结构、承载结构、流体悬浮结构、掺杂充填结构、结核及裂隙结构,见图 7.可以看出前五种微观结构主要是以孔隙为储集空间,相比第六种以裂缝为储集空间的微观结构,在物性上相对更均匀.青藏高原冻土区水合物处于勘探初期,目前还没有获得该地区详细的岩层微观结构资料,只是获知含水合物地层的岩性.如前面所述,含水合物地层主要有三种岩性:粉砂岩、细砂岩和泥岩.
|
图 7 水合物地层微观结构分类 (a)接触结构; (b)包裹结构; (c)承载结构; (d)流体悬浮结构; (e)掺杂充填结构; (f)结核及裂隙结构. (Ecker,2001;Dai et al., 2004;张卫东等,2011) Figure 7 Microstructure sketch of hydrate layers |
本文构建水合物岩石物理模型,以水合物充填于孔隙的砂岩地层(包括粉砂岩和细砂岩)为研究对象,即在理论上认为水合物均匀分布于砂岩孔隙中,对于30~100 Hz的地震子波,可以认为孔隙平均直径在厘米级以下的岩层为均匀地层介质.另外,假设水合物地层模型介质是各向同性的,暂不考虑岩石各向异性的问题.在这两个假设前提下,水合物地层的岩石物理模型介质的速度和密度都是均一的.
选定DK-1井孔143.40~144.20 m层段含水合物粉砂岩地层和DK-4井孔165.80~166.35 m层段含水合物粉砂岩地层,作为水合物岩石物理分析的基础,其中前者主要取得砂岩骨架的纵、横波速度速度比,为后者计算骨架的物性参数做准备.这两个井孔含水合物层段的物性数据,均源自于郭星旺(2011)的文献,其中孔隙度和饱和度均通过测井数据计算获得,与部分采样岩心的实测数据进行了对比并作了修正,因此本文所采用的数据符合实际情况.实际水合物砂岩地层中除了固态的水合物和液态的水,岩石骨架作为主要成分对整个地层物性的影响较大.因此对水合物地层的岩石物理分析,首先必须确定岩石骨架的物性参数,包括纵波速度(vp)、横波速度(vs)、密度(ρ)、体积模量(K)和剪切模量(G).
2.1 提取骨架物性参数的步骤DK-4井孔165.80~166.35 m层段含水合物粉砂岩地层,与DK-1井孔143.40~144.20 m层段含水合物粉砂岩地层相比,垂直方向上两个水合物地层埋深仅相差20 m左右,水平方向上DK-4井孔位于DK-1井孔北北东向约250 m处,属于同一个沉积体系(祝有海等,2009),可以认为DK-4和DK-1两井孔中含水合物地层的岩性是相同的或者很接近的.
对于DK-1井孔143.40~144.20 m层段含水合物粉砂岩,五个采样点的物性数据包括深度、孔隙度、水合物饱和度、密度、纵波速度和横波速度,见表 3.
|
|
表 3 DK-1井孔143.40~144.20 m层段含水合物粉砂岩的物性数据 Table 3 Physical data of hydrate siltstone in the segment 143.40~144.20 m of DK-1 |
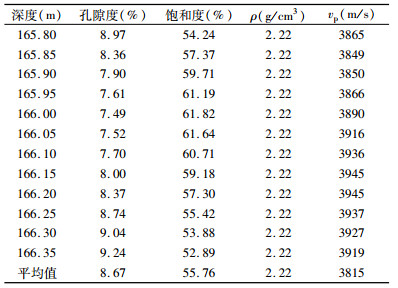
对于DK-4井孔165.80~166.35 m含水合物粉砂岩层段,十二个采样点的物性数据见表 4,包括深度、孔隙度、水合物饱和度、岩层密度和纵波速度,未获得横波速度数据.该层段的孔隙度接近10%,由于缺少横波速度,不能直接估算岩石的弹性模量.
|
|
表 4 DK-4井孔165.80~166.35 m含水合物粉砂岩层段的物性数据 Table 4 Physical data of hydrate siltstone in the segment 165.80~166.35 m of DK-4 |
由于这两个层段的粉砂岩属于同一个沉积体系,在没有其他相关资料的情况下,将前面DK-1井孔粉砂岩骨架的纵横波速度比r(vmp/vms),作为DK-4井孔的粉砂岩骨架的纵横波速度比,进而可以获得DK-4井孔骨架的横波速度,最终计算得到地层骨架的弹性模量.
水合物地层骨架的物性参数计算的步骤如下:
① 依据时间平均公式,计算DK-1井孔含水合物地层骨架的纵波速度和横波速度,并由此获得骨架的纵横波速度比,将此纵横波速度比作为DK-4井孔地层骨架的纵横波速度比.
② 再根据时间平均公式,计算DK-4井孔含水合物地层骨架的纵波速度和密度,已知前面① 中获得的纵横波速度比,可以得到DK-4井孔骨架的横波速度.
③ 利用弹性模量与岩石速度、密度的关系式,计算DK-4井孔骨架的体积模量和剪切模量.
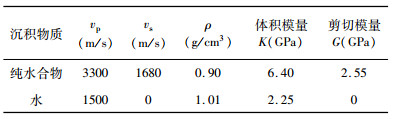
水合物地层岩石物理分析,还必须已知孔隙填充物——水合物和水的物性参数.本文参考Lee等(1996)关于水合物和水的物性数据,包括纵波速度(vp)、横波速度(vs)、密度(ρ)、体积模量(K)、剪切模量(G)共五项,见表 5.
|
|
表 5 沉积地层各成分的参数表(据Lee et al., 1996) Table 5 Properties of sediment constituents |
DK-1井孔143.40~144.20 m层段含水合物粉砂岩地层的主要成分为:粉砂岩、水合物和水,地层速度与孔隙度、饱和度、各组分的速度三者的关系,满足三相介质时间平均方程(Lee et al., 1996),其表达式如下:
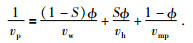
|
(1) |
由方程(1) 变换得出岩石骨架纵波速度vmp的表达式为
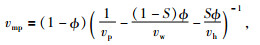
|
(2) |
(2) 式中vp为地层纵波速度,vw、vh、vmp分别表示水、水合物、砂岩骨架的纵波速度,Ф为孔隙度,S为饱和度.Ф、S、vp的取值分别为DK-1井孔水合物地层的孔隙度、饱和度、纵波速度的平均值(1.30%、73.5%、4688 m/s),见表 3.水的纵波速度vw、水合物的纵波速度vh分别取值为1500 m/s、3300 m/s,见表 5.
根据沉积地层中各组分的速度比、孔隙度和饱和度的关系式(Lee et al., 1996),计算DK-1井孔水合物地层骨架的横波速度vms,表达式为
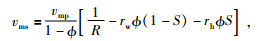
|
(3) |
(3) 式中R为DK-1井孔层段的纵横波速度比(取平均值1.991),见表 3.rw、rh分别是水和水合物的横、纵波速度比,由表 5中的数据计算得到.
利用(2) 式得到骨架纵波速度,再根据(3) 式获得横波速度,则可以计算得到DK-1井孔含水合物岩层骨架的纵横波速度比为1.980,将此速度比作为DK-4井孔地层骨架的纵横波速度比.
2.3 计算骨架的物性参数根据DK-4井孔165.80~166.35 m含水合物粉砂岩层段的物性参数,孔隙度、饱和度、密度和速度的平均值,见表 4,按照公式(2) 的方法可以计算得到该层段粉砂岩骨架的纵波速度是4198 m/s,DK-4井孔含水合物岩层骨架的纵横波速度比为1.980,得到横波速度2116 m/s.
计算DK-4井孔骨架的密度,通过岩石总体密度的公式见(4) 进行反推.ρ为岩层总体密度,ρw、ρh、ρm分别对应水、水合物、岩石骨架的密度,ρw、ρh的取值见表 5,Ф、S的取值见表 4中孔隙度和水合物饱和度的平均值.骨架密度ρm的表达式见(5),计算得到DK-4井孔含水合物岩层骨架密度为2.33 g/cm3.公式(4) 和(5) 为
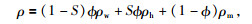
|
(4) |
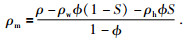
|
(5) |
根据纵、横波速度与弹性模量(体积模量和剪切模量)的关系式(邵才瑞等,2009),见公式(6) 和(7),计算骨架的体积模量Km和剪切模量Gm.根据前面的计算结果,DK-4井孔165.80~166.35 m含水合物地层骨架的纵波速度为4198 m/s、横波速度为2116 m/s、密度为2.33 g/cm3,由此得出体积模量Km和剪切模量Gm分别为27.2 GPa、10.5 GPa.公式(6) 和(7) 为
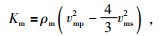
|
(6) |
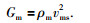
|
(7) |
综上推理和计算过程,得出DK-4井孔含水合物地层骨架的速度、密度和弹性模量等参数,见表 6.为后续分析含水合物岩层速度随孔隙度和饱和度的变化,提供了符合实际情况的基础数据,更为构建水合物岩石物理模型提供了基础数据.
|
|
表 6 DK-4井孔含水合物粉砂岩骨架的物性参数 Table 6 Properties of hydrate siltstone in the hole of DK-4 |
特别说明,水合物模型孔隙度Ф的范围是5%~20%,为了便于观察孔隙度变化对速度的影响,在DK-4井孔含水合物层段孔隙度(7.49%~9.24%)的基础上适当进行了扩大.
水合物模型饱和度Sh的范围确定为0~80%,在DK-4井孔含水合物层段水合物饱和度(52.89%~61.82%)的基础上,对上限和下限进行了适当地拓宽.
3 水合物地层岩石物理模型分析采用两种方法来构建水合物岩石物理模型,一种是基于K-T方程(Zimmerman R W et al., 1986)的岩石物理模型,这种模型假设地层各主要成分进行简单的混合,不考虑地层埋深、微观结构和水合物填充模式;另一种是区分水合物填充模式的岩石物理模型,将水合物填充于地层孔隙中分别以两类不同的模式进行处理.在一定的孔隙度(5%~20%)和饱和度(0~80%)的范围内,计算岩石物理模型的速度曲线,并与实际冻土区水合物地层(DK4井孔水合物层段)的速度进行对比,依据速度差异的大小判断岩石物理模型的优劣.
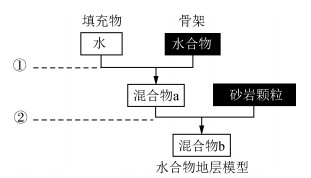
3.1 基于K-T方程的岩石物理模型K-T方程一般是对两相介质的地层进行速度估算,对于主要成分为水合物、水和岩石骨架的三相介质,通过两次叠加使用K-T方程,可以实现对三相介质岩石物理模型的计算.设置Ф是孔隙度,S是水合物饱和度.Kw、Kh、Km和Gw、Gh、Gm分别表示水、水合物、骨架的体积模量和剪切模量,各成分参数的具体数值见表 5和表 6.水合物地层模型三种组分逐步混合过程示意图见图 8,水合物模型的弹性模量和速度的计算步骤如下:
|
图 8 K-T方程法计算三相介质混合物的体积模量和剪切模量示意图(水合物与水为混合物a,混合物a与砂岩颗粒为混合物b) Figure 8 K-T equation sketch of calculating bulk modulus and shear modulus of three-phase mixture |
① 计算两相介质混合物(水合物和水)的体积模量K1和剪切模量G1.在混合物中将水合物看作骨架,水作为充填物,混合物中水合物与水的体积比为S/(1-S),计算混合物的弹性模量见公式(8).
② 计算三相介质混合物的体积模量K2和剪切模量G2.在步骤(1) 的混合物中再加入岩石骨架成分,将水合物和水作为三相介质混合物的充填物.三相介质混合物(水合物、水和骨架)的弹性模量计算公式见(9) 式.
③ 依据三相介质混合物的体积模量和剪切模量,参照公式(10) 计算地层的纵波和横波速度,模型的总体密度ρ依据前面公式(4) 计算得到.公式(8) 和(9) 为
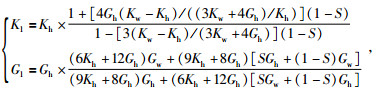
|
(8) |
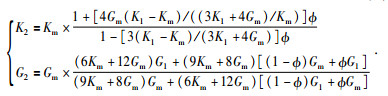
|
(9) |
取得含水合物岩层的体积模量K2和剪切模量G2,按照速度与弹性模量的关系式(10),可以计算得到水合物地层模型的纵波速度vp和横波速度vs,公式(10) 为
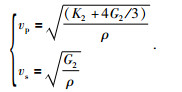
|
(10) |
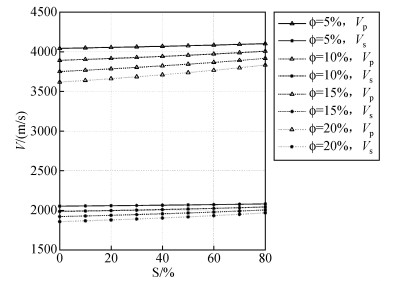
依照K-T方程的步骤,分别计算孔隙度为5%、10%、15%和20%的水合物地层随饱和度增加(变化范围是0~80%)的纵、横波速度,其中各主要成分的速度和密度见表 5和表 6,计算获得的速度曲线如图 9.对于vp,80%饱和度的速度相比0%饱和度的速度增大的程度,在孔隙度为5%、10%、15%和20%时分别是1.24%、2.47%、3.71%和4.97%,即孔隙度越大、速度增加的幅度越大,速度曲线越陡,K-T方程速度曲线整体上都比较平缓.
|
图 9 K-T equation计算纵、横波速度的曲线 四种线型从上到下分别对应的孔隙度为5%、10%、15%和20%,三角号线表示纵波速度,点号线表示横波速度,水合物饱和度的变化范围为0~80%. Figure 9 Curves of P-wave velocity and S-wave velocity by K-T equation |
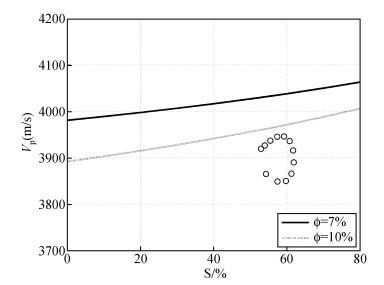
将基于K-T方程岩石物理模型的速度曲线与实际冻土区水合物地层的速度进行对比.K-T方程以孔隙度分别为7%和10%、饱和度范围为0~80%计算取得的速度曲线,见图 12,实线表示孔隙度为7%的速度曲线,虚线表示孔隙度为10%的速度曲线.图中实际水合物地层DK-4井孔十二个采样点数据以黑色空心点表示,其孔隙度范围是7.49%~9.24%,饱和度的范围是52.89%~61.82%.通过理论曲线与实际数据对比发现,K-T方程计算的理论值明显偏离实际数据,说明采用这种方法构建的水合物岩石物理模型,与实际水合物地层存在较大偏差.
|
图 10 K-T方程法理论计算速度与DK-4井孔165.80~ 166.35 m层段含水合物岩层速度对比.黑色点为DK-4井孔165.80~166.35 m层段采样点数据,实线表示孔隙度为7%的速度曲线、虚线表示孔隙度为10%的速度曲线 Figure 10 Comparison of theoretical velocity curves by K-T equation and actual data in the segment 165.80~166.35 m of DK-4 |
|
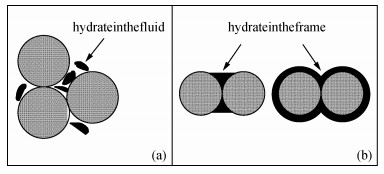
图 11 水合物模式Ⅰ和模式Ⅱ的示意图 阴影圆圈表示岩石骨架颗粒,黑色图案表示水合物,(a)水合物颗粒作为孔隙流体的一部分,(b)水合物作为岩石骨架的一部分:左小图,水合物胶结于岩石颗粒的接触点周围;右小图,水合物胶结于岩石颗粒表面(据Dvorkin et al., 1996). Figure 11 Filling-mode Ⅰ and filling-mode Ⅱ sketch of hydrate(Dvorkin and Nur, 1996) |
|
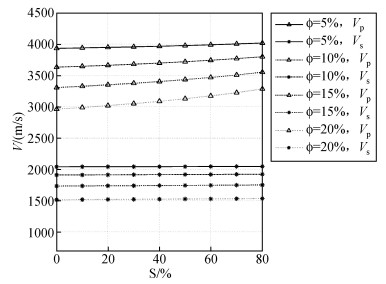
图 12 模式Ⅰ的纵、横波速度曲线 四种线型从上到下分别对应的孔隙度为5%、10%、15%和20%,三角号线表示纵波速度,点号线表示横波速度,水合物饱和度的变化范围为0~80%. Figure 12 Curves of P-wave velocity and S-wave velocity by filling-mode Ⅰ |
水合物在地层中以固体形式存在,将水合物地层的多种微观结构(Ecker,2001;Dai et al., 2004)分两类进行处理,即分别将水合物看作孔隙充填物和岩石骨架,由此定义水合物在岩石孔隙中的两种填充模式:(a)水合物颗粒悬浮于孔隙流体中,作为孔隙填充物的一部分,定义为模式Ⅰ;(b)水合物颗粒与岩石骨架颗粒接触紧密,甚至与岩石骨架颗粒胶结在一起,将水合物作为岩石骨架的一部分,定义为模式Ⅱ,图 11为模式Ⅰ与模式Ⅱ的示意图.在相同岩层孔隙度和水合物饱和度的条件下,水合物处于不同的微观结构模式,会使得水合物地层的物性存在明显差别.通过估算弹性模量并计算两种模式条件下水合物模型的速度来反映模式Ⅰ与模式Ⅱ的物性差别,最后再与实际数据进行对比.
针对两种不同模式填充的水合物岩石物理模型,采用弹性模量模型法(Helgerud et al., 1999)计算模型的弹性模量和速度,该方法考虑到地层深度的变化对弹性模量的影响,将沉积物(地层)可看成一个完整的颗粒系统,其地震波速度与孔隙度、有效压力、矿物组成、孔隙充填物的弹性性质、以及水、游离气与水合物的饱和度密切相关(Dvorkin et al., 2000).根据水合物在地层沉积物储集空间中的状态,分别将水合物作为填充物和骨架进行处理,并构建相应的岩石物理模型,计算模型的弹性模量和速度.
3.2.1 模式Ⅰ:将水合物看做孔隙中流体的一部分填充模式Ⅰ的水合物岩石物理模型中,水合物作为孔隙中流体的一部分,通过对填充混合物的弹性模量产生作用,进而影响水合物地层的弹性模量.由于弹性模量模型方法涉及到的公式、参数以及相关系数较多,这里采用递推的方法说明水合物模型速度的计算过程.
水合物模型纵波速度vp和横波速度vs的表达式为
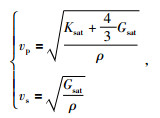
|
(11) |
Ksat和Gsat分别是模型介质的体积模量和剪切模量(含饱和充填物),岩层总体密度ρ的计算参照公式(4),各主要成分水合物、水和骨架的密度见表 5和表 6.
依据Gassman理论,通过公式(12)~(17) 获得水合物模型的体积模量Ksat和剪切模量Gsat,其中孔隙填充物(水合物和水)的体积模量为Kf,根据(14) 式计算.公式(12)~(17) 为
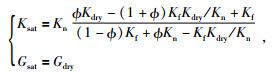
|
(12) |
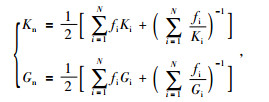
|
(13) |
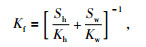
|
(14) |
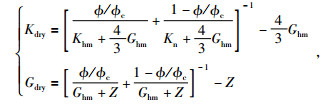
|
(15) |
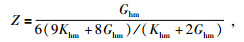
|
(16) |
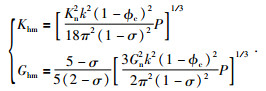
|
(17) |
各公式及相关参量的说明如下:
(12) 式中,Ф为孔隙度,Kn和Gn分别为骨架中n种岩性成分的体积模量和剪切模量,由(13) 式计算获取.Kf为孔隙填充物的体积模量,根据(14) 式计算.Kdry和Gdry分别为干岩石骨架的体积模量和剪切模量,计算公式见(15) 式.
(13) 式中N为不同岩性组分的数目,Ki为第i种组分的体积模量,Gi为第i种组分的剪切模量,fi为第i种组分所占的体积百分比.对于模式一的水合物地层,骨架为单一成分,因此N=1,则这里Ki和Gi对应的K1和G1分别表示岩石骨架的体积模量和剪切模量,具体弹性模量数值见表 6.
(14) 式中Kh和Kw分别是水合物和水的体积模量,Sh和Sw分别是水合物和水的饱和度,并且有Sw=1-Sh,水合物和水的体积模量数值见表 5.
(15) 式中Фc为临界孔隙度,其取值为0.4(Dvorkin and Nur, 1996;Helgerud et al., 1999).根据目前青藏高原水合物测井数据的分析结果,陆域水合物地层的孔隙度一般处于10%左右(郭星旺,2011),最多不超过30%,小于临界孔隙度Фc.另外,参数Z的表达式见(16) 式.
(16) 和(17) 式中,Khm和Ghm分别为岩石临界孔隙度的体积模量和剪切模量.σ为岩石骨架的泊松比,计算公式见(18) 式.P表示有效孔隙压力,根据(19) 式进行计算,其中ρm为骨架密度取值见表 6,水的密度ρw见表 5.h为深度,取值为165 m(DK-4井孔165.80~166.35 m含水合物粉砂岩层段的平均埋深),g为重力加速度,取值为9.8 m/s2.公式(18) 和(19) 为
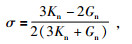
|
(18) |
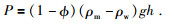
|
(19) |
特别说明,(17) 式中k表示骨架颗粒接触点的平均数目(Murphy,1982;Shankar et al., 2013),计算的表达式为
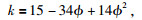
|
(20) |
k值的大小取决于地层的孔隙度Ф.对于青藏高原冻土区的水合物地层DK-4井孔含水合物层段的孔隙度Ф范围(7.49%~9.24%),依据经过调整的(20) 式(Helgerud et al., 1999)计算k值为11.7.
设定水合物岩石物理模型的孔隙度Ф分别为5%、10%、15%和20%,水合物饱和度Sh的范围为0~80%,采用弹性模量模型方法计算模式Ⅰ的的速度,其中水、水合物和岩石骨架的物性参数见表 5和表 6,获得的速度曲线见图 12.可以看出,对于相同饱和度S,随着孔隙度Ф的增加,vp(纵波速度)、vs(横波速度)明显减小;对于相同孔隙度Ф,随着水合物饱和度的增加,速度逐渐增加,说明水合物饱和度的增加使得水合物地层速度的增加,vp增加明显,vs略有增加,变化不是很明显.
3.2.2 模式Ⅱ:水合物看做岩石骨架的一部分将水合物作为岩石骨架的一部分,这种水合物填充于岩石孔隙中的模式定义为模式Ⅱ.因此,计算模式Ⅱ水合物模型速度,基于模式Ⅰ速度计算的思路并进行部分调整,将水合物从填充物的一部分划归为骨架的一部分,并且重新计算填充物和骨架的弹性模量.
对于填充物,模式Ⅱ水合物地层的填充物只有水这一种成分,此时体积模量Kf=Kw,填充流体的孔隙度调整为Ф′=Ф(1-Sh).
对于骨架,模式Ⅱ在原来单一岩石骨架的基础上增加了水合物成分,骨架由岩石和水合物两个固体组分构成,其中两个组分在整体骨架中所占的体积百分比,岩石为fs、水合物为fh,计算公式为

|
(21) |
在模式Ⅱ的条件下采用(13) 式计算弹性模量,N值调整为2,则Ki和Gi对应的K1、K2和G1、G2分别表示岩石骨架、水合物的体积模量和剪切模量,岩石骨架的弹性模量见表 6,水合物的弹性模量见表 5.
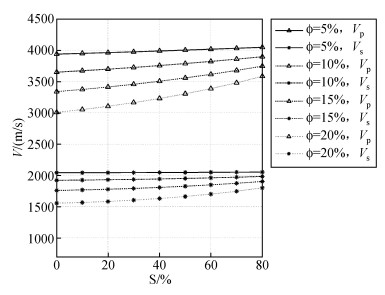
模式Ⅱ水合物岩石物理模型的速度计算,各组分的物性参数和其他参数的选择与模式Ⅰ完全相同,只是针对填充物、骨架的弹性模量的计算作了调整,取得的速度曲线见图 13.可以看出,曲线的走势类似于模式Ⅰ,不过模式Ⅱ的速度值要明显高于模式Ⅰ,说明将水合物作为岩石骨架的一部分,相对于模式Ⅰ的水合物颗粒在岩层孔隙中的悬浮状态,模式Ⅱ结构的岩层更紧凑一些,因此岩层的速度相对提高了.并且,图 13中20%孔隙度的横波速度vs曲线(蓝色虚线),与图 12中的20%孔隙度的横波速度vs曲线(蓝色虚线)相比,前者随着饱和度Sh的增加vs明显增大,后者随着饱和度的增加vs几乎没有显著变化,说明含水合物岩层处于不同的模式,其物性存在明显的差别,并且这种差别在横波速度上表现更为明显.
|
图 13 模式Ⅱ的纵、横波速度曲线 四种线型从上到下分别对应的孔隙度为5%、10%、15%和20%,三角号线表示纵波速度,点号线表示横波速度,水合物饱和度的变化范围为0~80%. Figure 13 Curves of P-wave velocity and S-wave velocity by filling-mode Ⅱ |
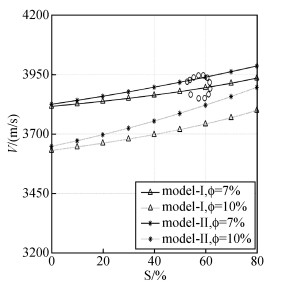
将区分填充模式的两种水合物模型的速度曲线,与实际冻土区水合物地层的速度进行对比.同样,将表 4的DK-4井孔采样点的速度数据(黑色空心点),与弹性模量模型的理论计算的速度曲线(两种孔隙度7%和10%,蓝线为模式Ⅰ,红线为模式Ⅱ)对比,见图 14,黑色空心点位于两条红色曲线(模式Ⅱ)之间,而与两条蓝色曲线(模式Ⅰ)只有部分区域交叉,说明DK-4井孔含水合物粉砂岩的微观结构模式,更符合模式Ⅱ,即水合物为骨架的一部分.从岩石物理分析的结果可以看出,DK-4井孔165.80~166.35 m层段中水合物不是悬浮于孔隙流体中,而是作为岩石骨架的一部分.当然,这一结论须要实际钻孔岩芯和其他相关数据资料的进一步验证,岩石物理模型的速度估算作为一种分析手段,在推断实际水合物地层物性的同时,能够作为冻土区水合物数值模型速度的设置方法,即在一定程度上可以反映实际情况.
|
图 14 弹性模量模型模式Ⅰ和模式Ⅱ理论计算速度与DK-4井孔165.80~166.35 m层段含水合物岩层速度对比.黑色空心点为DK-4井孔165.80~166.35 m层段12采样点数据,三角号线表示模式一速度曲线,点号线表示模式二速度曲线,其中实线表示孔隙度为7%、虚线表示孔隙度为10% Figure 14 Comparison of theoretical velocity curves by both filling-modes and actual data in the segment 165.80~166.35 m of DK-4 |
需要说明的是,由于青藏高原冻土区水合物处于勘探的初期,在没有获得充足的测井、钻井岩芯等资料前,不能确定该地区所有水合物地层都属于模式Ⅱ,仍然存在有模式Ⅰ水合物地层的可能性.青藏高原冻土区水合物勘探须要取得更多详实的钻测井和地震资料,才能进一步对水合物地层进行系统的岩石物理研究.
4 结论 4.1针对青藏高原冻土区DK-1、DK-3和DK-4三个井孔的含水合物地层和不含水合物地层的采样数据,制作了速度密度交会图,得出了水合物地层具有速度大、密度小的特征,并比较了不同岩性水合物地层的差异,砂岩水合物地层相比泥岩地层在速度和密度方面更具有规律性.并且,利用时间平均公式、弹性模量与速度密度的关系式,取得了骨架的纵波速度、横波速度、密度、体积模量和剪切模量,为建立岩石物理模型提供数据基础.
4.2基于目前获得的冻土区水合物地层的资料和数据,分别建立K-T方程岩石物理模型和区分填充模式的岩石物理模型,通过理论计算的速度曲线与实际水合物地层数据的对比,发现水合物填充模式Ⅱ的岩石物理模型更接近DK-4井孔165.80~166.35 m层段水合物地层,即水合物填充于地层孔隙中将其作为岩层骨架的一部分,更能反映实际水合物地层的物性.不过,由于陆域水合物处于勘探的初期,在没有获得充足的测井、钻井岩芯等资料前,不能确定该地区所有水合物层都属于模式Ⅱ,仍然存在有模式Ⅰ水合物层的可能性.
致谢 感谢中国地质科学院地球物理地球化学研究所的支持,感谢评审专家提出的宝贵意见和建议!| [] | Chen D F, Wang M C, Xia B. 2005. Formation condition and distribution prediction of gas hydrate in Qinghai-Tibet Plateau permafrost[J]. Chinese J. Geophys., 48(1): 165–172. DOI:10.3321/j.issn:0001-5733.2005.01.022 |
| [] | Dai J C, Xu H B, Snyder F, et al. 2004. Detection and estimation of gas hydrates using rock physics and seismic inversion: Examples from the northern deepwater Gulf of Mexico[J]. The Leading Edge, 23(1): 60–66. DOI:10.1190/1.1645456 |
| [] | Dvorkin J, Helgerud M B, Waite W F, et al. 2000. Introduction to physical properties and elasticity models[A].//Max M D ed. Natural Gas Hydrate: In Oceanic and Permafrost Environments[M]. Dordrednt: Kluwer Acad, 245-260. |
| [] | Dvorkin J, Nur A. 1996. Elasticity of high-porosity sandstones: Theory for two North Sea data sets[J]. Geophysics, 61(5): 1363–1370. DOI:10.1190/1.1444059 |
| [] | Dvorkin J, Nur A. 1998. Time-average equation revisited[J]. Geophysics, 63(2): 460–464. DOI:10.1190/1.1444347 |
| [] | Ecker C. 2001. Seismic characterization of methane hydrate structures[Ph. D. thesis]. Stanford, US: Standford University, 68-72. |
| [] | Guo X W. 2011. Well logging response characteristics and evaluation of gas hydrate in Qilian Mountain permafrost (in Chinese)[MSc thesis]. Beijing: Chinese Academy of Geological Sciences, 33-42. |
| [] | Helgerud M B, Dvorkin J, Nur A, et al. 1999. Elastic-wave velocity in marine sediments with gas hydrates: Effective medium modeling[J]. Geophys. Res., 26(13): 2021–2024. |
| [] | Lee M W, Hutchinson D R, Collett T S, et al. 1996. Seismic velocities for hydrate-bearing sediments using weighted equation[J]. J. Geophys. Res., 101(B9): 20347–20358. DOI:10.1029/96JB01886 |
| [] | Lu Z Q, Sultan N, Jin C S, et al. 2008. Semi-quantitative analysis of factors affecting gas hydrate formation conditions and its fractions[J]. Chinese J. Geophys., 51(1): 125–132. DOI:10.3321/j.issn:0001-5733.2008.01.016 |
| [] | Lu Z Q, Zhu Y H, Zhang Y Q, et al. 2010. Basic geological characteristics of gas hydrates in Qilian Mountain permafrost area, Qinghai Province[J]. Mineral Deposits, 29(1): 182–191. |
| [] | Murphy Ⅲ W F. 1982. Effects of microstructure and pore fluids on the acoustic properties of granular sedimentary materials[Ph. D. thesis]. San Francisco, CA: Stanford University, 144-147. |
| [] | Pang S J, Su X, He H, et al. 2013. Geological controlling factors of gas hydrate occurrence in Qilian Mountain permafrost, China[J]. Earth Science Frontiers, 20(1): 223–239. |
| [] | Shankar U, Gupta D K, Bhowmick D, et al. 2013. Gas hydrate and free gas saturations using rock physics modelling at site NGHP-01-05 and 07 in the Krishna-Godavari Basin, eastern Indian margin[J]. Journal of Petroleum Science and Engineering, 106: 62–70. DOI:10.1016/j.petrol.2013.04.004 |
| [] | Shao C R, Yin X Y, Zhang F M, et al. 2009. Shear wave velocity inversion with routine well logs based on rock physics and multi-mineral analysis[J]. Earth Science-Journal of China University of Geosciences, 34(4): 699–707. DOI:10.3799/dqkx.2009.077 |
| [] | Song H B, Matsubayashi O, Yang S X, et al. 2002. Physical Property Models of Gas Hydrate-bearing Sediments and AVA Character of Bottom Simulating Reflector[J]. Chinese J. Geophys., 45(4): 546–556. DOI:10.3321/j.issn:0001-5733.2002.04.012 |
| [] | Sun C Y, Zhang M Y, Niu B H, et al. 2003. Micromodels of gas hydrate and their velocity estimation methods[J]. Earth science Frontiers, 10(1): 191–198. |
| [] | Xu B X, Bai X B, Yu C Q. 2001. The information technology of seismic exploration-extraction, analysis and prediction[M]. Beijing: Geological Publishing House: 4-10. |
| [] | Zhang W D, Wang R H, Ren S R, et al. 2011. A study on physical models of gas hydrate reservoirs[J]. Acta Petrolei Sinica, 32(5): 866–871. |
| [] | Zhang Z J, McConnell D R, Han D H. 2012. Rock physics-based seismic trace analysis of unconsolidated sediments containing gas hydrate and free gas in Green Canyon 955, Northern Gulf of Mexico[J]. Marine and Petroleum Geology, 34(1): 119–133. DOI:10.1016/j.marpetgeo.2011.11.004 |
| [] | Zhao Q, Guo J, Hao S L, et al. 2005. Experiments of physical modeling for petrophysical properties of natural gas hydrate[J]. Chinese J. Geophys., 48(3): 649–655. DOI:10.3321/j.issn:0001-5733.2005.03.024 |
| [] | Zhao X M, Wu B H, Wang Y P, et al. 2000. Indirect indicators of gas hydrate occurrence within submarine sediments[J]. Earth Science-Journal of China University of Geosciences, 25(6): 624–628. |
| [] | Zhu Y H, Zhang Y Q, Wen H J, et al. 2009. Gas hydrates in the Qilian Mountain permafrost, Qinghai, Northwest China[J]. Acta Geologica Sinica, 83(11): 1762–1771. |
| [] | Zhu Y H, Zhang Y Q, Wen H J, et al. 2010. Gas hydrates in the Qilian Mountain permafrost and their basic characteristics[J]. Acta Geoscientia Sinica, 31(1): 7–16. |
| [] | Zimmerman R W, King M S. 1986. The effect of the extent of freezing on seismic velocities in unconsolidated permafrost[J]. Geophysics, 51(6): 1285–1290. DOI:10.1190/1.1442181 |
| [] | 陈多福, 王茂春, 夏斌. 2005. 青藏高原冻土带天然气水合物的形成条件与分布预测[J].地球物理学报, 48(1): 165–172. DOI:10.3321/j.issn:0001-5733.2005.01.022 |
| [] | 郭星旺. 2011. 祁连山冻土区天然气水合物测井响应特征及评价[硕士论文]. 北京: 中国地质科学院, 33-42. |
| [] | 卢振权, SultanN, 金春爽, 等. 2008. 天然气水合物形成条件与含量影响因素的半定量分析[J].地球物理学报, 51(1): 125–132. DOI:10.3321/j.issn:0001-5733.2008.01.016 |
| [] | 卢振权, 祝有海, 张永勤, 等. 2010. 青海省祁连山冻土区天然气水合物基本地质特征[J].矿床地质, 29(1): 182–191. |
| [] | 庞守吉, 苏新, 何浩, 等. 2013. 祁连山冻土区天然气水合物地质控制因素分析[J].地学前缘, 20(1): 223–239. |
| [] | 邵才瑞, 印兴耀, 张福明, 等. 2009. 利用常规测井资料基于岩石物理和多矿物分析反演横波速度[J].地球科学-中国地质大学学报, 34(4): 699–707. |
| [] | 宋海斌, MatsubayashiO, 杨胜雄, 等. 2002. 含天然气水合物沉积物的岩石物性模型与似海底反射层的AVA特征[J].地球物理学报, 45(4): 546–556. DOI:10.3321/j.issn:0001-5733.2002.04.012 |
| [] | 孙春岩, 章明昱, 牛滨华, 等. 2003. 天然气水合物微观模式及其速度参数估算方法研究[J].地学前缘, 10(1): 191–198. |
| [] | 徐伯勋, 白旭滨, 于常青. 2001. 地震勘探信息技术提取、分析和预测[M]. 北京: 地质出版社: 4-10. |
| [] | 张卫东, 王瑞和, 任韶然, 等. 2011. 天然气水合物储层物理模型[J].石油学报, 32(5): 866–871. DOI:10.7623/syxb201105020 |
| [] | 赵群, 郭建, 郝守玲, 等. 2005. 模拟天然气水合物的岩石物理特性模型实验[J].地球物理学报, 48(3): 649–655. DOI:10.3321/j.issn:0001-5733.2005.03.024 |
| [] | 赵省民, 吴必豪, 王亚平, 等. 2000. 海底天然气水合物赋存的间接识别标志[J].地球科学-中国地质大学学报, 25(6): 624–628. |
| [] | 祝有海, 张永勤, 文怀军, 等. 2009. 青海祁连山冻土区发现天然气水合物[J].地质学报, 83(11): 1762–1771. DOI:10.3321/j.issn:0001-5717.2009.11.018 |
| [] | 祝有海, 张永勤, 文怀军, 等. 2010. 祁连山冻土区天然气水合物及其基本特征[J].地球学报, 31(1): 7–16. |
 2017, Vol. 32
2017, Vol. 32