地球磁场是一个矢量场,作为地球本身的固有资源,可为移动机器人提供相对稳定的自主导航信息,是目前备受关注的导航方式(Goldenberg, 2006).地磁导航作为20世纪末新型的无源导航方法,具有隐蔽性强、抗干扰能力强、误差不会随时间产生累积等特点,它与惯性导航和卫星导航系统不同,是一种完全自主的导航定位系统.利用地磁信息对载体进行导航不仅可以克服水下载体通常的导航系统-惯导系统存在误差随时间累积的缺陷,而且可以弥补目前应用较广的卫星导航系统存在无线信号水中快速衰减的不足(Jiang and Ran, 2011),因此,地磁导航已成为目前的研究热点.
在水下环境中还没有一种导航方式能够与空中的全球定位系统(GPS)媲美,导航问题是发展自主水下航行器(Autonomous Underwater Vehicles,简称AUV)的关键所在(Stutters et al., 2008).水下导航常用惯性导航系统,但其存在定位误差随时间累积的缺陷,目前应用较广的卫星导航系统也存在无线信号水中快速衰减的不足(Kinsey et al., 2006).因此,利用地球物理场特征的导航理论和方法引起了国内外研究机构和学者的广泛关注,陆续展开了地磁导航、重力导航和地形导航等方面的研究.地磁导航由于具有无源隐蔽、全天候、全地域等特点,可以为水下航行器提供高精度的导航和定位信息,这是目前国内实现真正无源导航研究的热点.
目前,常用的磁场导航方法是基于磁图信息进行的匹配导航方法, 但是该方法对先验地磁图的完整度、精确度要求较高,需要有大量密集的测量数据和测点位置(Tyrén, 1982).地磁仿生导航是受自然界中生物利用地磁场进行导航行为的启发,研究在无先验地磁基准图条件下的自主导航方法.自然界中生物借助磁场进行导航现象普遍存在,如信鸽(Mora et al., 2004)、海龟(Benhamou et al., 2011)、鲑鱼(Putman et al., 2013)等.与传统的地磁匹配导航方法不同之处在于,地磁仿生导航方法不依靠任何事先存储的磁场数据或者磁图信息,仅通过实施测量当前位置的磁场信息,凭借磁趋势性敏感到达特定目标位置.
AUV通常在复杂多变的海洋环境中工作,洋流的存在对于AUV的作业有着非常重要的影响, 它能使水下机器人运动或转向的阻力增大, 并产生漂流运动, 使其偏离预定轨迹或者航向(Garau et al., 2005).因此,AUV在进行水下航行时应该考虑洋流的因素.近年来国内外研究者在地磁导航和洋流对AUV导航方法影响取得了大量的研究成果.但是在洋流影响下AUV地磁仿生导航方面的相关文献较少,主要侧重于洋流对AUV运动状态的影响.有关地磁仿生导航方面,Lohmann(2010)针对多种动物利用地磁导航的行为进行了相关的实验验证,研究表明:地磁场是动物长途运动中赖以信任的导航方式;Liu等(2013)从生物磁趋势性敏感角度出发,将地磁仿生导航看作是在多种磁场参量刺激下进行的搜索运动行为;刘明雍等(2014)研究地磁仿生导航问题,提出了一种基于时序进化策略的搜索方法.有关洋流影响下AUV导航方面,Baccou和Jouvencel(2003)研究“未知定常”特性的洋流干扰下多AUV的协同导航问题,并详细讨论了该情形下的洋流可观测;Gadre Aditya S(Gadre和Stilwell(2005))引入洋流影响,建立AUV运动学方程和距离量程方程,主要对导航系统的可观测性和洋流估计进行了深入的研究;刘明雍等(2014)研究基于运动矢径的AUV协同定位方法,该方法对未知定常洋流速度进行估计,以此对AUV进行实时补偿.
本文针对洋流干扰下的AUV运动轨迹发生漂移,造成导航算法失效的问题,建立了未知洋流影响下的AUV运动模型.通过定量描述洋流干扰下的AUV地磁导航方法,在刘明雍等人研究的基础上给出一种可以补偿洋流对AUV导航搜索干扰的方法,使得AUV能够在洋流影响下从指定位置到达目标位置.
1 问题描述二维平面内,考虑AUV具有如下的运动方程,公式为
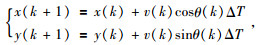
|
(1) |
式中,ΔT表示采样周期,k表示航行器运行的某一时刻(k可取0, 1, 2, …, K),v(k)表示运动速度,θ(k)表示航向角.假定航行器在ΔT内进行匀速运动,则v(k)可以用常量V表示,则(1) 式简化为
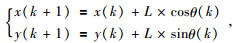
|
(2) |
式中,L=V×ΔT,L表示运动步长.
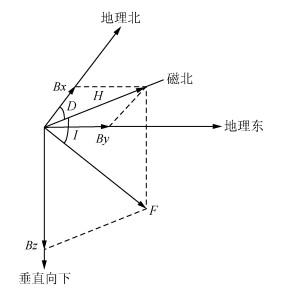
1.1 基于地磁分量的导航搜索地球磁场是一个包含多个分量的混合场,每个分量都有其自身的变化规律,图 1为地磁场七分量示意图(徐文耀,2009).
|
图 1 地磁场七分量(据徐文耀,2009) Figure 1 The seven components of geomagnetic field |
从仿生角度来讲,地磁导航过程表现为地磁场多个分量从起始位置到达各自目标收敛的过程(Liu et al., 2013).因此,一个具有n个地磁决策变量、m个目标函数的多目标搜索问题可表述为:参量分布规律未知情况下,地磁场分量向给定目标值收敛的过程,表达式为
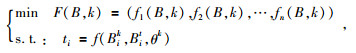
|
(3) |
式中:B=(B1, B2, …, Bn)为磁场的多个地磁分量;k表示为AUV运动的当前时刻;Bik为当前时刻位置处的地磁参量值;Bit为目标位置处的地磁参量值;F表示目标函数,可表示为
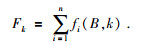
|
(4) |
目标函数Fk用来评价种群中个体好坏的标准,其值越小表明AUV运动方向趋向目标位置,个体所对应的解越好.在无先验基准地磁图的情况下,针对目标位置的磁趋势性,以目标位置与当前位置磁场分量的差值作为导航运动的刺激信息,即通过磁分量误差值表征对目标值的无限逼近,可表示为
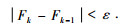
|
(5) |
洋流特征可表示为γ=(Vc, α),其中Vc为洋流速度,α为洋流方向,洋流干扰实际上影响AUV运动路径参量的执行效果,引起实际执行的运动路径参量θk随之发生改变,AUV运动轨迹产生漂移.
因此,考虑洋流干扰下的AUV平面运动学模型为
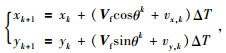
|
(6) |
其中:Vf和θk分别表示AUV在k时刻的速度和航向角,Vc=[vx, k, vy, k]T表示洋流作用的速度分量,未知洋流的幅度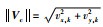
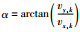
在γ的作用下,可看出洋流干扰引起了地磁参量与运动路径参量θk之间约束关系的变化,式(3) 中的约束方程变为
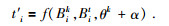
|
(7) |
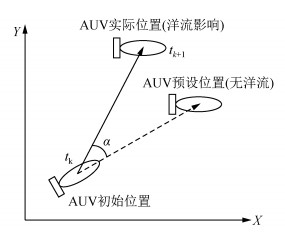
由于α的存在,在搜索空间中改变了预选的运动路径参量,使得AUV运动轨迹发生漂移,导致导航任务的失败,图 2简要说明了洋流引起AUV运动轨迹的变化.
|
图 2 洋流对AUV运动航向产生偏移示意图 Figure 2 The schematic diagram of the influence of the ocean currents for AUV |
因此,本文的研究目的主要针对洋流干扰下的AUV运动轨迹发生漂移,造成导航算法失效的问题,提出一种可以补偿洋流对AUV导航搜索干扰的方法,使得AUV能够在洋流影响下从起始位置到达目标位置.
2 洋流干扰下的AUV导航方法考虑水下未知定常洋流的影响,当AUV的运动方向与洋流的流向方向的夹角不为零时,AUV偏离航向,实际的航行方向表示为
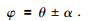
|
(8) |
由于AUV朝向目标点运动时,表现为
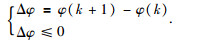
|
(9) |
进化算法(Evolutionary Algorithm,EA)是模拟自然界中生物进化过程的一种基于种群的启发式的搜索算法(李碧和郝志峰,2013).本文结合实际的导航运动,将导航搜索种群中的样本作为多目标搜索问题的行为解,在磁趋势性诱因的进化过程中,对部分或者全部样本进行操作,实现搜索过程真实解向目标解的收敛.
在进化搜索过程中,要求目标函数收敛至预设的最优值后稳定,不考虑洋流干扰时搜索向量θk必须收敛至最优向量θ*,从而使得F(θk, B)=(f1(B), f2(B), …, fn(B))中各元素也收敛至各自的最小值,即
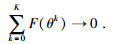
|
(10) |
由于海洋环境的复杂性,必须考虑洋流对AUV运动影响,故此,目标函数的收敛特性表达式为
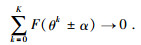
|
(11) |
针对目标位置的磁趋势特性,将目标位置处的地磁参量Bt与当前时刻所在位置处的地磁参量Bk之间的差值作为导航搜索的反馈激励,其中第i个地磁参量的目标搜索函数为
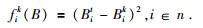
|
(12) |
若以地磁参量收敛状态作为样本性能的评价指标,且对其进行归一化处理,则多目标搜索函数F可表示为
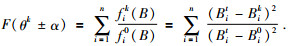
|
(13) |
考虑洋流影响下的地磁参量进化搜索的具体实现流程如下.
Step1:初始化
设置AUV起始位置和终止位置的地磁参量Bo和Bt、运动步长、终止范围及搜索算法相关参数.导航搜索中以航向角作为进化个体,个体集合为
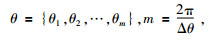
|
(14) |
式中,m为个体空间中的个数,Δθ为采样间隔.种群空间由个体集合中的个体组成,种群为Q={θj|j=1, 2, …, N},θj表示种群的第i个个体,θj=Δθ×i, i∈[1, m];N表示群体规模大小,如果取N=50,即种群规模为50,种群空间由个体空间中的个体组成,即
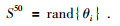
|
(15) |
Step2:随机选取航向角个体
从种群空间Q中任选选择一个个体θi(k)执行,由于一开始种群中个体的取向信息是未知的,所以选取各个体行为初始概率均相等,即:
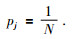
|
(16) |
选取各个体行为初始概率相等,意味着搜索初期,AUV不含有任何预定的方向决策.随着导航进程的进行,种群个体中具有较大概率值得个体行为被选中的频次越高,则k时刻,种群第i个样本θj被选中的概率为
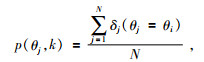
|
(17) |
其中,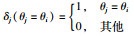
Step3:观测状态
依据磁传感器提供的环境信息,读取AUV当前的状态S(k)={Bik, φ},并计算其目标函数F(φk).从而得到未知定常洋流对AUV航向的偏移角α.
Step4:种群的更新
由于AUV当前位置是由前一时刻的位置和种群中的航向角个体共同决定的,搜索结果的优劣很大程度上取决于航向角的选取.种群的一个个体被选中,AUV进行行为操作,利用评价函数进行环境反馈,以实现对种群中个体航向角的更新.考虑到洋流影响的因素,种群中的样本更新可按照下述规则进行:
(1) 逼近目标值的解(即F(φk)≤F(φk-1))时,保留该个体,则
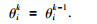
|
(18) |
(2) 远离目标值的解(即F(φk) > F(φk-1)时,对应一个个体的更新,则
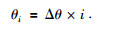
|
(19) |
Step5:种群个体选择概率更新
按照式(16),对种群中的样本个体进行选取,更新种群中个体的备选概率值p(θj).
Step6:航向角补偿
考虑到洋流对AUV产生的漂移运动,为此,对其进行补偿,即
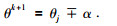
|
(20) |
Step7:到达目标点的判断
当前位置磁参量的误差平方和F(θk+1)较小,且在连续的搜索时间段内与上一时刻F(θk)比较,如满足公式(21):
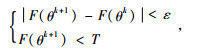
|
(21) |
则转向Step8;反之,重复Step4—Step7, 直到满足终止条件.
Step8:结束
4 仿真实验与结果分析为了验证算法的有效性,仿真环境为Windows 7系统,Intel Core2 Duo CPU E7500 2.93GHz、2G内存、2.94GHz主频的计算机上进行,软件环境为Matlab2012a.
通过Matlab2012a调用WMM2010函数,得到每一步迭代测量点的地磁参量数据.根据AUV的运动学模型,设定AUV的初始位置和目标位置,对算法进行仿真分析研究.在仿真中,AUV以5m/s速度航行,ΔT=100 s,vx, k=2m/s,vy, k=2m/s.选取磁场的三个分量(X方向分量,Y方向分量,磁场总强F)作为导航搜索的特征参量,起始位置的地磁参量值:Bxo=25069 nT, Byo=-1365 nT, BFo=49867 nT,目标位置的地磁参量值: Bxt=32438 nT, Byt=-3083 nT, BFt=50077 nT.算法的相关参数设置:种群规模N=50,Δθ=30°,ε=0.0007,T=0.003,K=1500.
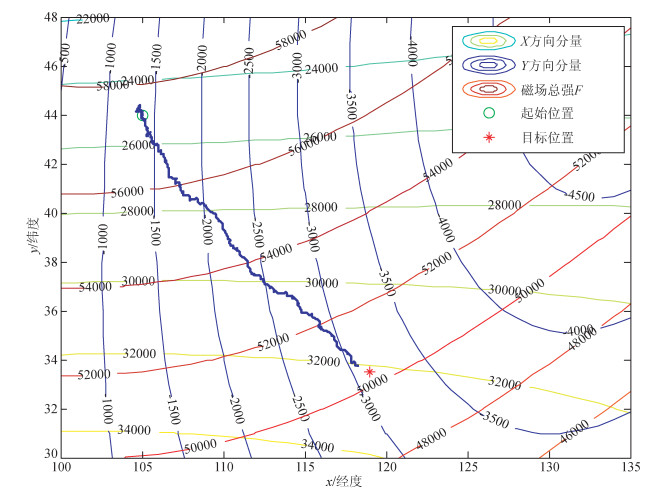
仿真环境中,“°”表示AUV的初始位置,“*”表示AUV的终止位置,粗线表示其运动轨迹.图 3给出了没有洋流影响下AUV根据目标位置磁趋势敏感进行目标搜索的仿真实例,该实验进行了590步迭代终止.从图 3中AUV的运动轨迹可以清楚地看到,在没有洋流影响下AUV导航进程的目标趋向性明确,收敛至目标位置处的速度快.
|
图 3 无洋流干扰下的磁趋势导航搜索路径 Figure 3 The navigational moving trajectory without the presence of unknown constant ocean current flow |
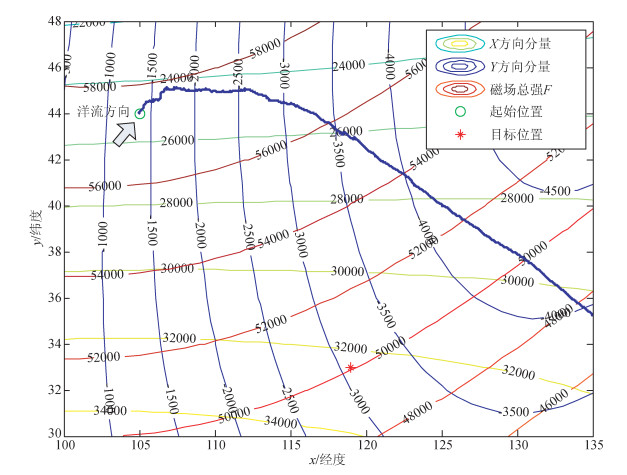
图 4给出了在洋流干扰下AUV导航搜索漂移路径的仿真实例.算法参数设置相同,在此只引入了未知定常洋流因素.从图 4给出的AUV导航轨迹可以清楚地看到,洋流干扰实际上影响AUV运动路径参量的执行效果,引起实际执行的运动路径参量θk随之发生改变,扰乱了AUV仅依靠磁趋势敏感进行目标搜索的机制,使得AUV运动轨迹产生漂移,使得AUV无法完成导航任务.
|
图 4 洋流干扰下的导航搜索漂移路径 Figure 4 The navigational moving drift in the presence of unknown constant ocean current flow |
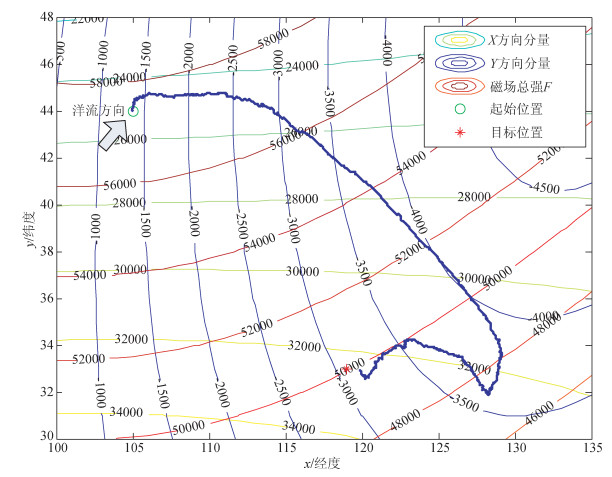
图 5给出了一个洋流影响下对其进行补偿的AUV导航搜索仿真实例.该实验进行了1300步迭代.同样的算法参数设置与洋流因素,对搜索算法引入航向角补偿操作.从图 5给出的AUV导航轨迹可以清楚地看到,洋流因素的存在使得AUV运动发生漂移,故此,在算法中引入洋流补偿操作以便克服其对AUV导航搜索产生的影响.本文所提出的进化搜索算法能够克服洋流干扰的影响,使得AUV最终到达目标位置.
|
图 5 洋流干扰下的磁趋势导航搜索路径 Figure 5 The navigational moving trajectory in the presence of constant unknown ocean current flow |
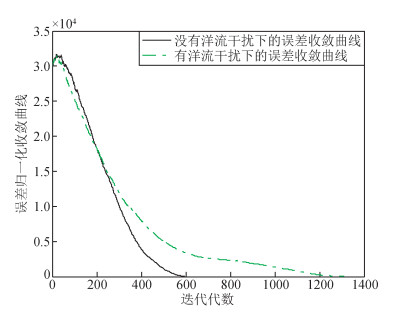
图 6给出了有和无洋流干扰下的两条AUV导航搜索收敛曲线仿真实例.从图 5给出的两条收敛曲线可以清楚地看到,无洋流干扰下导航收敛速度明显快于洋流干扰下的导航收敛速度.由于进化算法中个体更新方式对其收敛速度影响很大,新个体保留较优个体的信息越多,这在一定程度上提高了算法的收敛速度.由于洋流干扰的缘故,种群中多样性维持能力较差,种群提供方向性指导的能力减弱,因此,探索能力及收敛速度都急剧下降.综上所述,洋流影响下的AUV导航收敛速度减慢,且极易引起AUV运动轨迹发生飘移,本文所提出的洋流补偿方法能在一定程度上克服洋流对AUV的运动影响.
|
图 6 有和无洋流干扰下的导航搜索收敛曲线 Figure 6 Error convergence curve in two cases |
本文针对AUV地磁导航受水下洋流的影响,易造成AUV运动轨迹发生漂移的问题,提出一种具有洋流补偿的进化搜索导航方法.引入未知定常洋流,结合AUV运动学方程建立洋流影响下AUV地磁导航的运动方程.通过定量描述洋流实际上影响AUV运动路径参量的执行效果,引起实际执行的运动路径参量随之发生改变,因此,算法对洋流航向进行估计,以补偿洋流对AUV运动操作的影响.由仿真实验可知,该方法可以有效解决洋流环境下引起AUV运动轨迹发生漂移的问题.
致谢 感谢匿名审稿专家的支持和帮助.| [] | Baccou P, Jouvencel B. 2003. Simulation results, post-processing experimentations and comparisons results for navigation, homing and multiple vehicles operations with a new positioning method using on transponder[C].//Proceedings of 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems. Las Vegas, NV, USA: IEEE, 811-817. |
| [] | Benhamou S, Sudre J, Bourjea J, et al. 2011. The role of geomagnetic cues in green turtle open sea navigation[J]. PLoS One, 6(10): e26672. DOI:10.1371/journal.pone.0026672 |
| [] | Gadre A S, Stilwell D J. 2005. Underwater navigation in the presence of unknown currents based on range measurements from a single location[C].//Proceedings of the 2005 American Control Conference. Portland, OR, USA: IEEE, 656-661. |
| [] | Garau B, Alvarez A, Oliver G. 2005. Path planning of autonomous underwater vehicles in current fields with complex spatial variability: An A* approach[C].//Proceedings of the 2005 IEEE International Conference on Robotics and Automation. Barcelona, Spain: IEEE, 194-198. |
| [] | Goldenberg F. 2006. Geomagnetic navigation beyond the magnetic compass[C].//Proceedings of 2006 IEEE/ION Position, Location, and Navigation Symposium.Coronado, CA:IEEE, 684-694. |
| [] | Jiang L L, Ran L X. 2011. Pure geomagnetic homing navigation on earth surface[C].//Proceedings of the 2011 International Conference on Electronics, Communications and Control. Ningbo, China: IEEE, 971-974. |
| [] | Kinsey J C, Eustice R M, Whitcomb L L. 2006. A survey of underwater vehicle navigation: Recent advances and new challenges[C].//IFAC Conference of Manoeuvering and Control of Marine Craft. Lisbon, Portugal, 88: 1-12. |
| [] | Liu M Y, Liu K, Yang P P, et al. 2013. Bio-inspired navigation based on geomagnetic[C].//Proceedings of IEEE International Conference on Robotics and Biomimetics. Shenzhen, China: IEEE, 2339-2344. |
| [] | Lohmann K J. 2010. Animal behaviour: Magnetic-field perception[J]. Nature, 464(7292): 1140–1142. DOI:10.1038/4641140a |
| [] | Mora C V, Davison M, Wild J M, et al. 2004. Magnetoreception and its trigeminal mediation in the homing pigeon[J]. Nature, 432(7016): 508–511. DOI:10.1038/nature03077 |
| [] | Putman N F, Lohmann K J, Putman E M, et al. 2013. Evidence for geomagnetic imprinting as a homing mechanism in Pacific Salmon[J]. Current Biology, 23(4): 322–316. |
| [] | Stutters L, Liu H H, Tiltman C, et al. 2008. Navigation technologies for autonomous underwater vehicles[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 38(4): 581–589. DOI:10.1109/TSMCC.2008.919147 |
| [] | Tyrén C. 1982. Magnetic anomalies as a reference for ground-speed and map-matching navigation[J]. The Journal of Navigation, 35(2): 242–254. DOI:10.1017/S0373463300022025 |
| [] | 李碧, 郝志峰. 2013. 协同进化算法及其应用[M]. 北京: 科学出版社. |
| [] | 刘明雍, 张加全, 张立川. 2011. 洋流影响下基于运动矢径的AUV协同定位方法[J].控制与决策, 26(11): 1632–1636. |
| [] | 刘明雍, 刘坤, 李红, 等. 2014. 基于时序进化搜索策略的地磁仿生导航研究[J].西北工业大学学报, 32(6): 894–898. |
| [] | 徐文耀. 2009. 地球电磁现象物理学[M]. 合肥: 中国科学技术大学出版社: 18-29. |
 2017, Vol. 32
2017, Vol. 32

