随着电磁勘探和计算机技术的发展,电磁法多维正反演已基本成熟,正逐步推向实用化(赵国泽等,2007;Kelbert et al., 2008).然而,勘探精细化和三维探测急需发展,大规模和海量数据的电磁正反演计算成为当前难点和热点问题之一.正演是反演的基础,如何实现大规模网格的快速高精度电磁法正演模拟是问题的关键.电磁法正演通常利用有限差分法(FD)、有限单元(FE)、积分方程(IE)等方法对基本方程进行离散,结合边界条件形成大型稀疏线性方程组,然后利用迭代法或直接法进行求解,从而得到电磁场的解.电磁法正演的实质是大型稀疏线性方程组的存储和求解,随着剖分网格的增加,线性方程组的所需内存和计算时间成指数增加,因而对于大规模剖分问题的求解难于在PC机上实现.为提高多维电磁法正演效率,地球物理学者引入了大型稀疏线性方程组的多种快速求解算法,如预处理共轭梯度法(CG)(Smith,1996)、预处理双共轭梯度法(BICG)(Lin et al., 2011)、多重网格法(MG)(Mulder,2008;邓居智等,2011)、最小残差法(QMR)(Siripunvaraporn et al., 2002)等.这些算法虽然能够大大加快电磁法正演速度,但是所需内存空间并未减少甚至增加,因而仍难于实现大规模多维问题的计算.区域分解算法(DDM)通过将大规模问题分解为若干个小问题进行求解(Toselli and Widlund, 2005),缩小计算规模,极大节省内存空间,已成为多个科学工程领域解决大规模工程数值模拟的有力手段,如:电磁工程(厉天威等,2007;吕志清和安翔,2009;Shang and He, 2009;盛亦军等,2010;胡俊等,2011)、热传导(顾彩梅,2006;田敏和羊丹平,2008;修航,2014;金鑫禹,2015)和结构力学(刘佩和姚谦峰,2008;瞿叶高等, 2012, 2013;周忠双,2013)等领域.为此,引起地球物理学者极大兴趣,他们在多维正演模拟中引入区域分解算法.对于地球物理电磁正演问题,Zyserman等(1999)及Zyserman和Santos(2000)采用非重叠型区域分解算法分别实现电磁法2D和3D正演;Xiong(1999)采用自适应Schwarz重叠型区域分解算法实现可控源大地电磁法三维正演;Rung-Arunwan和Siripunvaraporn(2010)利用改进的分级区域分解算法实现二维MT的正演.
有鉴于此,本文以TM模式下大地电磁二维正演为例,将Schwarz重叠型区域分解算法与有限差分算法结合,实现基于Schwarz重叠型区域分解的大地电磁二维正演模拟,同时探讨子域数目、子域分解方式及子域重叠区域大小三个因素对计算效率的影响,为大规模问题的求解提供参考和依据.
1 理论基础 1.1 基于有限差分的MT二维正演理论在二维地电结构情况下,假设x轴为走向方向,y轴为与走向垂直的方向,z轴垂直向下.在准静态条件下,Rao和Babu(2006)给出磁场极化(TM模式)下大地电磁法二维正演模拟的控制方程和边界条件,可表示为
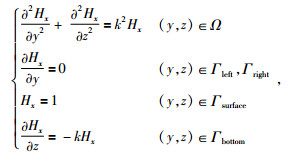
|
(1) |
其中,k2=-iσωμ,ω为角频率,σ为电导率, μ为磁导率,i为虚数单位.
首先,将求解区域采用规则网格剖分成若干个小的矩形网格;然后对于任意一个节点Hx采用5点有限差分格式对等式(1) 进行离散;结合给出的边界条件,能够合成待解的线性方程组,可表示为
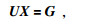
|
(2) |
其中,U是大型复稀疏对称矩阵.X表示待解的磁场Hx分量,G为右端项,与边界条件和场源相关.对于线性方程组(2) 通常采用直接分解法或Krylovz子空间迭代法进行求解得到磁场Hx分量的值,然后利用法拉第定律求得电场Ey分量,最后通过卡尼亚电阻率定义公式求得MT响应.
1.2 基于Schwarz重叠型区域分解算法的MT二维正演理论区域分解法分为重叠型(ODDM)和非重叠型(NDDM)两种(Toselli and Widlund, 2005).Schwarz交替法是重叠型区域分解算法(ODDM)中的一种,于1870年由德国学者H.A.Schwarz提出,经过长期推广和应用已成为重叠型区域分解法的经典理论.本文将Schwarz重叠区域分解算法与有限差分算法结合实现大地电磁二维正演模拟.
在Schwarz重叠区域分解算法中,将待求解区域Ω沿Z和Y方向分别分解N和M重叠子域,子域总数为N×M,子域用Ωi, j(i=1, …, N; j=1, …M)表示,子域边界记为 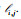
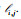
|
图 1 大地电磁二维正演3×3重叠区域分解示意图 (○:子域非重叠节点,●:子域重叠节点,实线框:重叠子域,阴影:子域重叠区域.) Figure 1 Schematic diagram about overlapping domain decomposition method of MT 2-D forward and subdivided into 3×3 (○: Non overlapping node,●: overlapping node,Solid line box: sub-domain,Shadow: Overlapping region of sub-domain.) |
在大地电磁二维正演模拟中,根据Schwarz交替法的思想,任意一个重叠子域Ωi, j满足的控制方程和边界条件可表示为
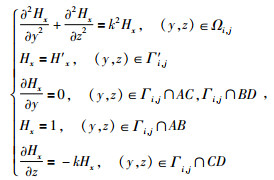
|
(3) |
其中,H′x为邻域内虚拟边界Γ′ i, j磁场Hx分量.对于控制方程(3) 可以采用与全域方程(1) 一样的离散方式,合成重叠子域待解线性方程为
|
(4) |
其中,Ui, j是重叠子域Ωi, j的复稀疏系数矩阵.Xi, j表示重叠子域Ωi, j内待解磁场Hx分量,Gi, j为右端项,与虚拟边界条件和邻域相关.对比式(4) 和式(2) 可以发现,全域待求解方程组能够转化为若干子域线性方程组进行求解,因而可缩小求解规模.
1.3 求解过程和算法流程图在大地电磁法二维正演求解过程中,本文利用Schwarz交替法通过子域重叠部分实现参数传递然后通过全域迭代实现求解.首先给定所有节点初值Hx0,这样所有子域控制方程(3) 的边界条件就可确定,按顺序独立求解每个重叠子域的线性方程组(4),把上一个子域的解作为下一个子域的新初值,然后再求解子域的定解问题式(4),如此反复迭代直到相邻两次解的误差达到某个精度δ,具体流程见图 2.公式为
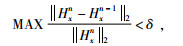
|
(5) |
|
图 2 MT二维正演的重叠型区域分解算法流程图 Figure 2 Flowchart based on overlapping domain |
在实际迭代求解中,只要地电模型和重叠区域分解确定后,对于每个子域的稀疏矩阵Ui, j保持不变,只需重新计算右端项Gi, j.由于重叠子域稀疏矩阵Ui, j相对全域系数矩阵U规模缩小很多,在迭代过程只需进行一次分解就能够通过回代实现快速迭代求解.因此本文重叠子域求解算法选用LU直接分解算法.
2 算法验证和数值模拟为了验证和对比本文提出的基于Schwarz重叠区域分解的大地电磁二维正演算法的可行性和有效性,本文算法结果和传统有限差分结果进行对比,同时研究重叠子域大小、子域数的影响规律.本文所有数值模拟均在笔记本电脑(内存4.0 GB, 处理器Intel(R)Core(TM)i5,主频1.70 GHz)上运行,开发环境为Intel Visual Fortran 2013和Visual Studio 2010.
2.1 算法验证为了验证本文算法的准确性,设计低阻异常模型.低阻异常体大小为26 km×11 km,电阻率为100 Ω·m,顶部埋深为4 km,围岩电阻率为500 Ω·m.整个求解区域大小为60 km×20 km采用等距剖分,剖分间隔500 m,剖分网格数为:120×40,计算频率为0.37 Hz.在重叠区域分解算法中,将求解区域剖分2×1个子域,重叠区域大小my=3,mz=0,子域求解算法采用LU直接求解法,全域迭代精度设为10E-8.图 3为低阻异常体模型大地电磁响应结果对比,(a)为视电阻率,(b)为阻抗相位.由图可知,采用重叠型区域分解算法的计算结果与传统有限差分法的计算结果基本重合,因此验证本文提出算法的准确性和可行性.
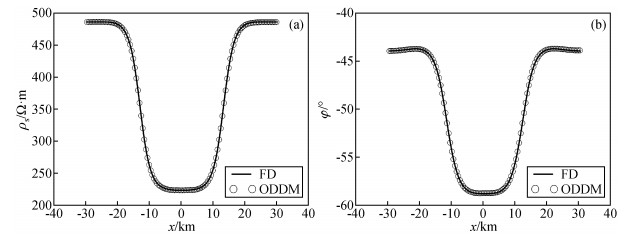
|
图 3 低阻异常体模型大地电磁响应结果对比和算法验证 (a)视电阻率;(b)相位. Figure 3 Comparison of electromagnetic response of low resistivity model and algorithm verification |
为了进一步分析Schwarz重叠区域分解算法的优势和计算效率,本文对子域数目、重叠区域大小和不同子域求解算法进行研究.
a)重叠子域分解方案
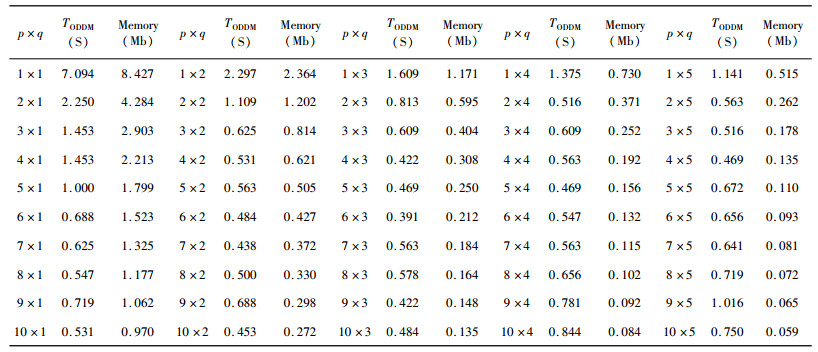
为了研究重叠子域数目和分解组合的影响规律,设计不同子域分解方案对低阻异常体模型进行数值模拟,模型参数和算法验证模型一致.模型求解区域剖分网格数为120×40,并分解成p×q个重叠子域.其中p和q分别为Y和Z方向重叠子域数,从1到10和1到5变化,子域重叠节点数均为3,子域求解选用LU直接求解法.对于传统有限差分LU直接求解法,剖分网格大小为My×Mz总内存近似计算公式为(My-1)(Mz-1)(3Mz-1)×16,16为双精度复数所占bites数(Tawat et al., 2010),所需内存约为8.4 Mbites,CPU运行时间T为7.094 s.由于本文采用不存储重叠子域分解矩阵,因此对于重叠型区域分解算法的内存计算公式可近似表示为:((my×(p-1)+My)/p-1)((mz×(q-1)+Mz)/q-1)(3×(mz×(q-1)+Mz)/q-1)×16.可以看出,重叠区域分解算法的内存使用量与子域组合、子域数目及子域重叠大小有关.表 1为不同重叠子域分解方案的CPU计算时间TODDM和内存使用量统计情况.为了清晰描述重叠区域分解算的优势,本文定义相对内存百分比(UODDM-UFD)/UFD×100%及相对时间百分比(TODDM-TFD)/TFD×100%,其中FD表示传统FD算法,ODDM表示重叠区域分解算法.图 4为重叠区域分解算法相对内存百分比和相对时间百分比等值线图,横轴为Y方向子域数目p,纵轴为Z方向子域数目q.由表 1和图 4可知,内存使用量随着子域数目增大而减小;CPU计算时间不随子域数目增大而严格减小,这是由于重叠子域缩小到一定规模后直接分解时间很小而全域迭代次数将增加引起的.在重叠子域分解为6×3时CPU计算时间最小为0.391 s,仅为传统FD算法CPU计算时间的5.5%,同时内存使用量也仅为2.5%.因此,在实际求解过程中应该选择合适的子域数目和剖分组合.
|
|
表 1 不同子域组合CPU计算时间TODDM及内存使用量 Table 1 CPU time of TODDM and memory usage of different sub-domain combination |
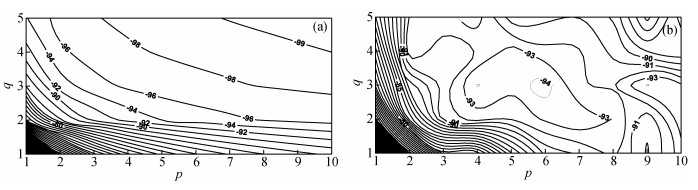
|
图 4 不同子域数目的大地电磁二维正演模拟效率和内存使用量对比 (a)内存使用量百分比;(b) 计算时间百分比. Figure 4 Contour map of the relative percent about CPU time and memory usage |
b)重叠区域大小
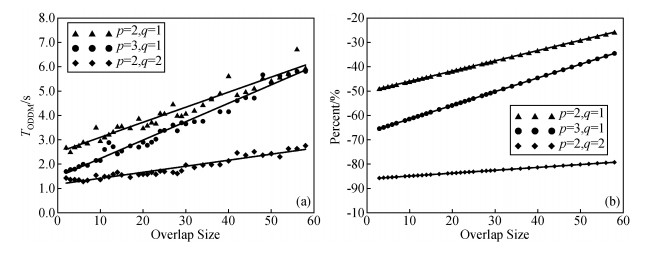
重叠型区域分解算法中,子域重叠规模大小是影响算法内存和计算时间的重要参数.为研究重叠区域大小对计算效率的影响,设计不同子域重叠规模大小对低阻模型进行数值模拟.模型参数与算法验证模型一致,求解区域大小和剖分网格数与上个模型一致.采用三种不同子域分解组合,分别为2×1,3×2,2×2,子域重叠规模大小从2到60变化.图6为不同子域重叠规模大小的CPU计算时间与内存使用量相对百分比.由图 5可知,不同子域组合的趋势基本一致,CPU计算时间随子域重叠规模大小呈线性增加;内存使用量相对量也随子域重叠规模大小呈线性增加.这是由于子域采用LU直接分解算法,对于子域间参数传递只有虚拟边界节点进行.因此,在实际求解过程中,子域重叠规模大小最佳选择为2.
|
图 5 不同子域重叠规模大小的内存和CPU计算时间变化规律 (a)CPU计算时间;(b)与全域求解法相比的内存使用量相对比值. Figure 5 Variation about CPU time and relative memory usage of sub-domain overlap size |
本文将大地电磁二维求解区域分解成若干重叠子域,通过Schwarz交替法构建子域虚拟边界,对于每个子域采用有限差分算法进行离散并采用LU直接分解算法进行独立求解,然后通过全域迭代实现大地电磁法二维正演模拟.通过典型低阻模型的数值模拟验证本文算法的准确性和可行性,并通过不同子域分解数目、子域分解组合及子域重叠规模的数值计算表明,重叠区域分解算法相对于传统有限差分算法,内存使用量和CPU计算时间都大大减少,在实际求解过程中子域重叠大小选择2为佳并选择合适子域数目和子域分解组合.因此,本文提出的重叠区域分解算法能够将大规模转化成若干小规模问题进行求解,为大规模大尺度电磁三维正演问题实现提供一种新的途径.本文程序设计存在不足,CPU计算时间结果仅供参考.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Deng J Z, Tan H D, Chen H, et al. 2011. CSAMT 3D modeling using staggered-grid finite difference method[J]. Progress in Geophysics, 26(6): 2026–2032. DOI:10.3969/j.issn.1004-2903.2011.06.017 |
| [] | Gu C M. 2006. Finite difference domain decomposition algorithm for numerical solution of the heat equation (in Chinese)[Ph. D. thesis]. Ji'nan: Shandong University. |
| [] | Hu J, Hong W, Zhou H X, et al. 2011. Overlapped domain decomposition method with congruent sub-domains for electromagnetic surface integral equations[J]. Journal of Applied Sciences, 29(4): 410–416. |
| [] | Jin X Y. 2015. The improvement of coupling software of CFD-DEM based on the domain decomposition method (in Chinese)[MSc thesis]. Changchun: Jilin University. |
| [] | Kelbert A, Egbert G D, Schultz A. 2008. Non-linear conjugate gradient inversion for global EM induction: Resolution studies[J]. Geophysical Journal International, 173(2): 365–381. DOI:10.1111/gji.2008.173.issue-2 |
| [] | Li T W, Ruan J J, Zhang Y, et al. 2007. Research of parallel computing electromagnetic field based on the domain decomposition method[J]. High Voltage Engineering, 33(5): 58–61, 93. |
| [] | Lin C H, Tan H D, Tong T. 2011. Three-dimensional conjugate gradient inversion of magnetotelluric impedance tensor data[J]. Journal of Earth Science, 22(3): 386–395. DOI:10.1007/s12583-011-0191-8 |
| [] | Liu P, Yao Q F. 2008. Domain decomposition method and importance sampling method for structural dynamic reliability calculation[J]. Journal of Vibration and Shock, 27(12): 52–55. |
| [] | Lü Z Q, An X. 2009. Auxiliary excitation algorithm of the domain decomposition method for 3-D large-scale electromagnetic problems[J]. Journal of Xidian University, 36(5): 851–856. |
| [] | Mulder W A. 2008. Geophysical modelling of 3D electromagnetic diffusion with multigrid[J]. Computing and Visualization in Science, 11(3): 129–138. DOI:10.1007/s00791-007-0064-y |
| [] | Qu Y G, Hua H X, Meng G, et al. 2012. A domain decomposition approach for vibration analysis of joined structures[J]. Journal of Shanghai Jiaotong University, 46(9): 1487–1492. |
| [] | Qu Y G, Chen Y, Long X H, et al. 2013. Vibration analysis of ring stiffened cylindrical-conical shell structures based on a domain decomposition method[J]. Chinese Journal of Computational Mechanics, 30(1): 166–172. |
| [] | Rao K P, Babu G A. 2006. EMOD2D—a program in C++ for finite difference modelling of magnetotelluric TM mode responses over 2D earth[J]. Computers & Geosciences, 32(9): 1499–1511. |
| [] | Rung-Arunwan T, Siripunvaraporn W. 2010. An efficient modified hierarchical domain decomposition for two-dimensional magnetotelluric forward modelling[J]. Geophysical Journal International, 183(2): 634–644. DOI:10.1111/j.1365-246X.2010.04768.x |
| [] | Shang Y Q, He Y N. 2009. Fourier analysis of Schwarz domain decomposition methods for the biharmonic equation[J]. Applied Mathematics and Mechanics, 30(9): 1177–1182. DOI:10.1007/s10483-009-0912-6 |
| [] | Sheng Y J, Jia H L, Chen R S. 2010. Analysis of electromagnetic scattering by non-conforming domain decomposition method[J]. Systems Engineering and Electronics, 32(10): 2111–2115. |
| [] | Siripunvaraporn W, Egbert G, Lenbury Y. 2002. Numerical accuracy of magnetotelluric modeling: A comparison of finite difference approximations[J]. Earth, Planets and Space, 54(6): 721–725. DOI:10.1186/BF03351724 |
| [] | Smith J T. 1996. Conservative modeling of 3-D electromagnetic fields, Part Ⅱ: Biconjugate gradient solution and an accelerator[J]. Geophysics, 61(5): 1319–1324. DOI:10.1190/1.1444055 |
| [] | Tian M, Yang D P. 2008. New overlapping domain decomposition parallel algorithm for the heat equation[J]. Numerical Mathematics A Journal of Chinese Universities, 30(1): 14–25. |
| [] | Toselli A, Widlund O B. 2005. Domain Decomposition Methods-Algorithms and Theory[M]. Berlin Heidelberg: Springer: 1-84. |
| [] | Xiong Z H. 1999. Domain decomposition for 3D electromagnetic modeling[J]. Earth, Planets and Space, 51(10): 1013–1018. DOI:10.1186/BF03351574 |
| [] | Xiu H. 2014. Investigation on domain decomposition preconditioner in heat conduction problem and research of cooling method in transition piece (in Chinese)[Ph. D. thesis]. Changchun: Jilin University. |
| [] | Zhao G Z, Chen X B, Tang J. 2007. Advanced geo-electromagnetic methods in China[J]. Progress in Geophysics, 22(4): 1171–1180. DOI:10.3969/j.issn.1004-2903.2007.04.024 |
| [] | Zhou Z S. 2013. Finite difference domain decomposition parallel implementation for elliptic equations based on MPI (in Chinese)[MSc thesis]. Ji'nan: Shandong University. |
| [] | Zyserman F I, Guarracino L, Santos J E. 1999. A hybridized mixed finite element domain decomposed method for two dimensional magnetotelluric modelling[J]. Earth, Planets and Space, 51(4): 297–306. DOI:10.1186/BF03352233 |
| [] | Zyserman F I, Santos J E. 2000. Parallel finite element algorithm with domain decomposition for three-dimensional magnetotelluric modelling[J]. Journal of Applied Geophysics, 44(4): 337–351. DOI:10.1016/S0926-9851(00)00012-4 |
| [] | 邓居智, 谭捍东, 陈辉, 等. 2011. CSAMT三维交错采样有限差分数值模拟[J].地球物理学进展, 26(6): 2026–2032. DOI:10.3969/j.issn.1004-2903.2011.06.017 |
| [] | 顾彩梅. 2006. 热传导方程的有限差分区域分解算法[博士论文]. 济南: 山东大学. |
| [] | 胡俊, 洪伟, 周后型, 等. 2011. 电磁场积分方程全等形子域的重叠型区域分解算法[J].应用科学学报, 29(4): 410–416. |
| [] | 金鑫禹. 2015. 基于区域分解法的CFD-DEM耦合软件改进[硕士论文]. 长春: 吉林大学. |
| [] | 厉天威, 阮江军, 张宇, 等. 2007. 基于区域分解法的电磁场并行计算研究[J].高电压技术, 33(5): 58–61, 93. |
| [] | 刘佩, 姚谦峰. 2008. 结构动力可靠度计算的区域分解法和重要抽样法[J].振动与冲击, 27(12): 52–55. DOI:10.3969/j.issn.1000-3835.2008.12.012 |
| [] | 吕志清, 安翔. 2009. 三维电大问题的辅助激励源区域分解算法[J].西安电子科技大学学报(自然科学版), 36(5): 851–856. |
| [] | 盛亦军, 贾会亮, 陈如山. 2010. 非共形区域分解法分析电磁散射问题[J].系统工程与电子技术, 32(10): 2111–2115. DOI:10.3969/j.issn.1001-506X.2010.10.20 |
| [] | 田敏, 羊丹平. 2008. 热传导方程的一类新型重叠型并行区域分解有限差分算法[J].高等学校计算数学学报, 30(1): 14–25. |
| [] | 修航. 2014. 热传导问题区域分解预处理器及过渡段结构冷却研究[博士论文]. 长春: 吉林大学. |
| [] | 赵国泽, 陈小斌, 汤吉. 2007. 中国地球电磁法新进展和发展趋势[J].地球物理学进展, 22(4): 1171–1180. DOI:10.3969/j.issn.1004-2903.2007.04.024 |
| [] | 周忠双. 2013. 基于MPI的一类椭圆型方程有限差分区域分解算法的并行实现[硕士论文]. 济南: 山东大学. |
| [] | 瞿叶高, 华宏星, 孟光, 等. 2012. 基于区域分解的组合结构振动分析方法[J].上海交通大学学报, 46(9): 1487–1492. |
| [] | 瞿叶高, 谌勇, 龙新华, 等. 2013. 基于区域分解的环肋圆柱壳-圆锥壳组合结构振动分析[J].计算力学学报, 30(1): 166–172. DOI:10.7511/jslx201301028 |
 2017, Vol. 32
2017, Vol. 32