2. 中海油深圳分公司开发部, 深圳 518067
3. 杭州迅美科技有限公司, 杭州 310012
4. 浙江大学, 杭州 310012
2. Development of CNOOC Shenzhen branch, Shenzhen 518067, China
3. Hangzhou Sumay Technologies, Hangzhou 310012, China
4. Zhejiang University, Hangzhou 310012, China
随钻电磁波测井仪器具有较深的探测深度,在层界面的预测以及地质导向中有着重要的作用.为了提供更完善的钻前预测,提供实时的地质导向信息,各大国外石油服务公司相继推出了具有方位探测能力的随钻方位电磁波测井仪器.但在实际应用中,因水平井和大斜度井的井眼环境复杂,测井响应受到很多因素的影响,各向异性地层电阻率测量数值与原状地层电阻率值有很大偏离;另一方面又因为仪器探测深度较深,指示边界作用的方向信号可能是多个层界面综合响应的叠加,因此需要进行反演获得地层真实电性参数和井眼剖面信息.
随着计算机及数值计算技术的发展,国内外已有不少二维的电场反演结果发表,对一、二维正反演问题研究的较系统和深入,其在实际应用中也简单易行 (Shima, 1990;Daily and Owen, 1991;张致付等,2004; 康俊佐等,2006).由于地下介质的复杂多样,地层多表现为三维电性结构,在三维空间中实现正反演更具有实际意义.目前国内外研究进展主要有基于Born近似的三维多边界反演 (Li and Oldenburg, 1992;王志刚等,2007;邢光龙等,2007;叶益信等,2015),Shima (1992)的层析成像反演,谭茂金等 (2007)和Zhang等 (1995)的Tarantola反演,吴小平和徐果明 (2000)的传统最小二乘反演等方法.近年来随着方位随钻电磁波仪器的成功应用,国外三大服务公司均开发了基于三维反演的边界探测技术,从生产应用效果来看,国外反演技术目前单边界反演较为成熟,双边界和多边界反演应用效果并不理想.究其原因国外反演技术方法主要是快速查库反演,没有考虑井眼、侵入、地层各向异性等因素影响,地层模型简化严重且适用范围受静态反演库影响.国内因仪器装备的落后,这方面数据处理技术研究还处于起步阶段,随着国内方位随钻仪器研发推进,对这方面的技术有着迫切的需要.本次研究提出将矢量有限元方法和马奎特方法结合的三维电阻率反演方法,为提高计算效率,在矢量有限元求解过程中对求解域添加完全匹配层条件,根据井眼环境对仪器方向信号测井响应影响特征考察对反演过程中模型做适当简化,同时三维空间剖分采用非等分的四面体网格以提高计算精度.
本文是在方位电阻率测井仪器正演仿真 (张中庆等,2011;刘庆龙和王瑞和,2014;刘乃震等,2015) 的基础上,进行三维多边界反演方法探索,通过对Gauss-Newton法的修正,避免三维反演因参数较多而产生的不收敛和多解性,在考察了井眼、泥浆、层界面、层厚、倾角等因素对仪器方向信号响应影响的基础上,为三维多边界反演提供初值选择、约束添加制定方案,有效的提高计算效率.同时,通过模型正演仿真结果再反演,对反演方法进行验证.最后针对南海油田某区水平井,根据多层界面三维电阻率反演结果,对比水平电阻率和探井 (直井) 测量的随钻电阻率,对比反演结果和实测测井信号,验证了计算方法和结果的可靠性,在该油田某区块生产实际应用20余次,效果显著.
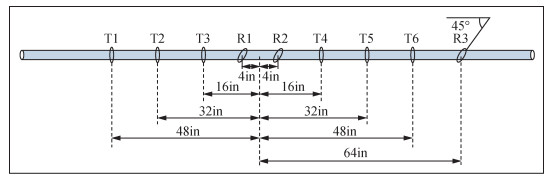
1 ADR仪器介绍哈里伯顿公司的方位深电阻率测量仪ADR基于多频率,多源距倾斜线圈概念,结合了补偿电阻率和方位测量的优点,能够同时进行地质导向和地层评价.该仪器包括了6个轴向发射线圈 (T1,T2,T3,T4,T5,T6) 和3个倾斜接收线圈 (R1,R2,R3),其中接收线圈相对于仪器轴向的倾斜角度为45°,采用旋转模式实现方位测量,当仪器穿过储层边界时,通过接收线圈上测量信号畸变形成的边界响应来识别地层边界 (图 1).本文根据方位电磁波仪器的这一响应特点,利用Marquardt方法对其响应进行反演计算,得到地层水平电阻率、地层垂直电阻率、各项异性系数、侵入深度、测量点到多个层界面的距离 (DTB) 等参数.
|
图 1 ADR仪器结构及工作模式示意图 Figure 1 ADR LWD Resistivity Logging Instrument Structure and working mode diagram |
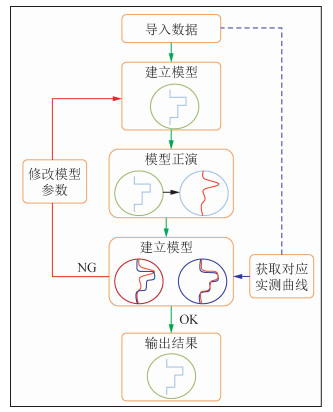
多层界面三维电阻率反演目的是利用大斜度井或水平井测井数据,通过反演获得准确的地层电性参数和地层结构参数.反演的过程为:通过测井曲线建立初始地层模型;调用正演仿真模块,计算测井工具的模型正演响应;对比正演响应与实际测量值,根据比较情况建立雅可比矩阵方程组,求解残差减小最快的模型修改量;根据模型修改量调整模型,重新调用正演计算模型响应和残差,直至残差足够小 (图 2).
|
图 2 多层界面三维电阻率反演过程 Figure 2 Multilayer 3D resistivity inversion flow chart |
反演原理是利用模拟信号与实测仪器响应构造非线性最小二乘方法目标函数,将三维电阻率反演归结为研究求解如下形式的非线性最小二乘问题,公式为
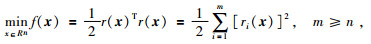
|
(1) |
其中r:Rn→Rm是x的非线性函数,n是未知量个数,m是曲线条数,x为待反演参数向量,r(x) 为模型正演响应与实测量之间的残差量,f(x) 为目标函数.非线性最小二乘问题可以看作为解方程组,公式为
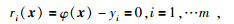
|
(2) |
其中x是待反演参数,φ(x) 是关于参量x的非线性函数 (对应于x的正演响应),yi是测井响应.设J(x) 是r(x) 的Jacobian矩阵,公式为
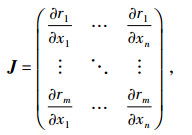
|
(3) |
则f(x) 的梯度为
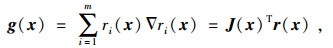
|
(4) |
f(x) 的Hesse矩阵为
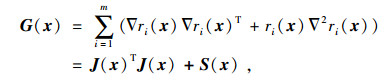
|
(5) |
其中: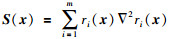
因此,目标函数f(x) 的二次模型为
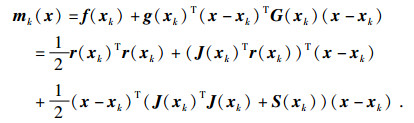
|
(6) |
从而,解问题 (1) 的Gauss-Newton法为
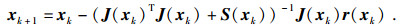
|
(7) |
目前Gauss-Newton解法存在三个方面的问题:一是Gauss-Newton法的成功完全依赖于所忽略的G(x) 中的二阶信息项S(x) 在G(x) 中的重要性,如果S(x*) 太大,则Gauss-Newton法可能不收敛;二是在Gauss-Newton法中,要求J(x *) 是满秩的,遗憾的是J(x *) 奇异的情形常常发生,使得算法常常收敛到一个非驻点,得到一个局部结果;三是在大斜度井和水平井测井中,因极化效应等因素影响常使部分测井曲线失真,三维多界面反演有较多未知量待求解,有效测井曲线较少时容易出现多解性.
为确保迭代过程收敛,避免多解性,并最大限度提高计算效率,本文采用线性搜索策略对Gauss-Newton进行修正,应用黄金分割法,保证目标函数每一步下降,公式为
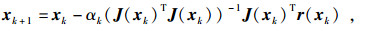
|
(9) |
其中αk是一维搜索因子.
另一方面,因为r(x) 是非线性函数,用线性化模型 (7) 代替r(x) 并不对所有x-xk都成立.本文考虑约束线性最小二乘问题,即考虑信赖域模型,公式为
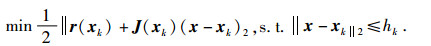
|
(10) |
可知,此模型的解可由方程组 (11) 表征,公式为
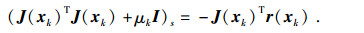
|
(11) |
从而
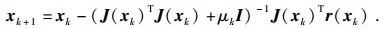
|
(12) |
如果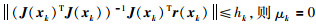
多层界面三维电阻率反演前,需建立初始地层模型,并对模型参数赋初值,初值的适合与否直接影响到反演计算收敛速度和收敛性,不适合的初值甚至会导致反演不收敛、多解性等.本文联合多种测井资料建立地层模型初始值,具体流程见图 3.通过探井 (或邻井) 视电阻率、自然伽马、密度曲线等划分层界面;根据方位密度 (或方位伽马) 确定井眼-地层界面相对倾角初始值;根据探井测量电阻率确定初始模型围岩电阻率赋初值;根据水平井视电阻率和方向信号响应,确定目的层电阻率和测量点到层界面距离赋初值.原则为选取更接近真实值模型参数作为初值,提高迭代过程收敛速度.
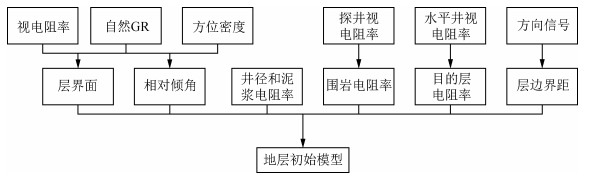
|
图 3 地层模型构建 Figure 3 The construction method of initial formation model |
ADR方位电磁波测量仪器采用轴向倾斜或横向线圈混合,当仪器的发射线圈和接收线圈存在夹角时,在地层介质中,接收线圈测得感应电动势的实部和虚部随着仪器旋转发生周期性变化,能够更好地提供有关地层方位的信息,指示地层的各向异性,识别地层边界,考察方向信号影响因素具有重要应用意义.
3.1 方向信号与层边界距关系假设地层模型为界面两侧电阻率分别是1 Ω·m和10 Ω·m,ADR仪器以接近水平姿态穿过层界面 (仪器轴线与地层法线夹角85°),分别模拟在2 MHz、500 kHz和125 kHz三种频率下模拟48 in (1 in=2.54 cm) 线圈距下仪器0°工具面角对应方向信号响应曲线.可以看到在该地层条件下,方位电磁波仪器的幅度方向信号曲线在2 MHz和500 kHz两种工作频率下,对层界面都有良好的指示和预测作用,仪器距离层界面越近,响应幅度信号越大,仪器远离层界面,响应幅度信号逐渐变小 (图 4).通过仪器方向信号这一响应特征,可以初步判定大斜度井和水平井中仪器穿过层界面位置,也可以定性判断层边界距离,为反演过程中约束边界距修正量.
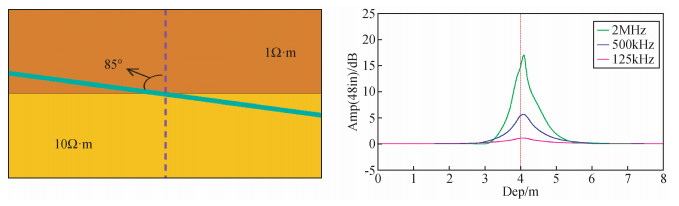
|
图 4 ADR仪器方向信号在层界面响应 Figure 4 Response characteristics of the directional signal of ADR logging while drilling in the layer interface |
1) 假设地层模型如图 5a所示三层模型,上下围岩电阻率均为1 Ω·m,中间层电阻率为10 Ω·m.仪器保持工具面角180°不变 (仪器不旋转),从上至下移动仪器位置以水平状态穿过地层界面 (仪器轴线与地层法线夹角90°).模拟仪器在一定频率下112in线圈距方向信号响应曲线,并通过改变中间层厚度,考察层厚对方向信号响应的影响.模拟结果可以看到在层界面处,仪器响应达到极值,从中间层中点 (位置B) 作为分界点,中间点以上仪器靠近上部低阻围岩,180°方向信号为负值,信号波峰指向高阻;当中间层为薄层时,方向信号幅值随层厚变小而变小,层厚较大时,方向信号幅值随层厚变化不明显;中间点 (位置B) 以下仪器比较靠近下面低阻围岩,180°方向信号为正值,信号波峰指向高阻侧.当仪器处于对称模型中点位置,方向信号对上下层界面响应相互抵消,信号值为0,如图 5b所示的位置B处.通过模拟结果可以看出,方向信号对层界面有良好的指示作用,通过方向信号峰值也可判断界面两侧电阻率相对大小.
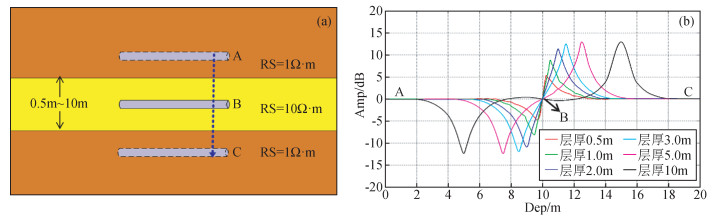
|
图 5 (a) 地层模型; (b) 不同层厚下的方向信号响应 Figure 5 (a) Formation model; (b) Directional signal logging response under different thickness |
2) 假设图 5a的三层模型,固定上围岩电阻率为10 Ω·m、中间层电阻率为20 Ω·m不变,下围岩电阻率在1~20 Ω·m范围变化,仪器以水平状态穿过地层界面 (仪器轴线与地层法线夹角90°).图 6a模拟在一定工作频率不同围岩对比度下0°工具面角对应方向信号响应.在上层界面1处,不同模型界面上下位置电阻率不变,方向信号响应幅度值大小也基本不变;在下层界面2处,不同模型改变下围岩电阻率,界面两侧电阻率对比度发生变化,方向信号响应幅度也发生变化.
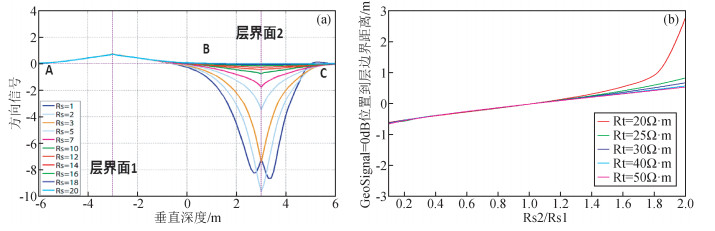
|
图 6 (a) 不同围岩对比度下方向信号响应; (b) 方向信号0点随围岩对比度变化 Figure 6 (a) Directional signal response of different surrounding rock contrast; (b) Zero point of the directional signal varies with the contrast of surrounding rock |
当电阻率对比度较大时 (20:1) 在界面处方向信号出现异常;在目的层靠近中点 (位置B) 的地方,方向信号由正差异变为负差异.上下围岩电阻率非对称地层,方向信号值为0的位置随上下围岩电阻率对比度不同而偏离中间点,偏离的方向和大小与背景电阻率和界面两侧电阻率对比度有关,如图 6b所示.进一步考察会发现,在非对称地层中,不同探测深度方向信号的0点位置是不同的,在靠近层中间位置,通过对比多种探测深度信号的组合,避免反演中的多解性,这也为多层界面三维电阻率反演可能性提供了理论依据.
3.3 方向信号与井筒条件关系1) 模拟有井眼影响情况下和无井眼影响情况下ADR仪器方向信号测井响应 (图 7),考察水平井测井响应受井眼影响程度.假设模型设置为三层模型,上下围岩电阻率分为1 Ω·m,中间层电阻率为10 Ω·m,仪器以水平状态穿过地层界面 (仪器轴线与地层法线夹角90°),模拟在一定工作频率下有井眼和无井眼两种环境下,112 in线圈距幅度方向信号在不同电阻率背景下的响应.由模拟结果可以看出,仪器从低阻进入高阻时 (入目的层),有无井眼影响方向信号幅度值基本不变,井眼影响可忽略;当仪器从高阻进入低阻时 (出目的层),低对比度电阻率情况下井眼对方向信号影响可忽略,高对比度电阻率情况下方向信号幅值变化明显.可见井眼对方向信号的影响与背景电阻率和界面两侧电阻率对比度有关.
|
图 7 有无井眼仪器响应对比 Figure 7 Comparison of the response of the borehole instruments |
2) 图 8是模拟不同井径和泥浆影响情况下仪器响应,考察水平井测井响应受井径大小和泥浆电阻率影响程度.模型上下围岩电阻率均为1 Ω·m,中间层电阻率为10 Ω·m,仪器以水平状态穿过地层界面 (仪器轴线与地层法线夹角90°),变化井径 (模型A) 和泥浆电阻率 (模型B),模拟仪器在一定工作频率下,112 in线圈距方向幅度信号在界面响应.由模拟结果 (A) 可以看出,在一定灵敏度下 (例如0.5 dB) 井眼直径对探测深度基本没有影响,只有在层界面处,方向信号的幅度值随井眼增大而轻微减小.由模拟结果 (B) 可以看出,泥浆电阻率对方向信号也基本没有影响,只有在层界面处,方向信号的幅度值随泥浆变化有轻微差异.
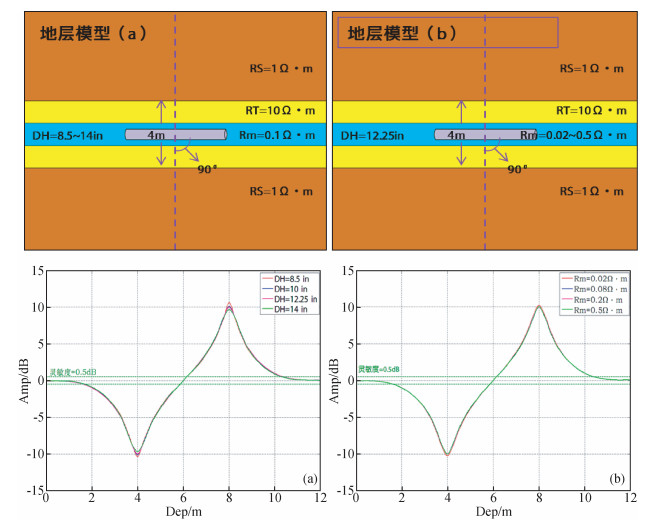
|
图 8 井径和泥浆对方向信号影响考察 Figure 8 Hole diameter and the mud on the direction of signal effect |
通过对井眼、泥浆对方向信号影响考察发现,井眼和泥浆的影响在一定程度上降低了方向信号响应幅度值,但是并不影响方向信号对边界的指示特性.在一定背景电阻率范围内,井眼、泥浆对方向信号影响有限,故在多层界面三维电阻率反演中,一定条件下可忽略井眼和泥浆的影响.据此在计算方向信号时可不考虑井眼、泥浆影响,简化三维地层模型,不损害反演精度条件下,有助于提高反演速度.
3.4 方向信号与倾角关系考察倾角对方向信号影响,假设两层地层模型,层界面两侧电阻率分别为2 Ω·m和20 Ω·m.固定其他参数不变,仪器以不同倾斜角度穿过地层界面,模拟仪器在一定工作频率下48 in线圈距方位幅度信号的界面响应 (图 9a).模拟结果如图 9b所示,倾角为0°(垂直井) 时方向信号为0,不能指示层界面;小斜度井 (倾角小于60°) 在层界面附近方向信号出现双峰,倾角越大双峰极值的绝对值差别越大;大斜度井 (井斜大于70°) 和水平井情况下,方向信号在层界面处单一极值,极值点随倾角变化与层界面位置有一定偏离.说明仪器与地层界面相对倾角对方向信号有很大影响.
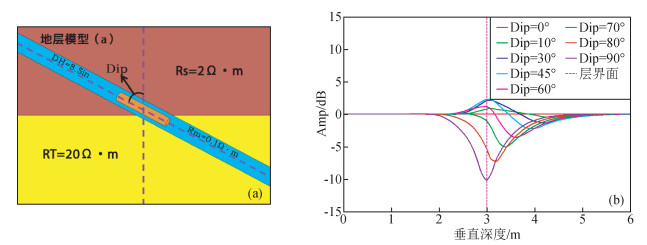
|
图 9 (a) 地层模型; (b) 不同倾角下的方向信号响应 Figure 9 (a) Formation model; (b) Direction response of the signal under different inclination |
通过倾角对方向信号影响考察可以看到,倾角不仅影响方向信号的幅度值大小,同时也影响其形态和幅度峰值位置,因此地层-井眼相对倾角是多层界面三维电阻率反演的关键参数之一,根据方向信号反演层界面位置和层边界距时,应充分考虑倾角的影响.
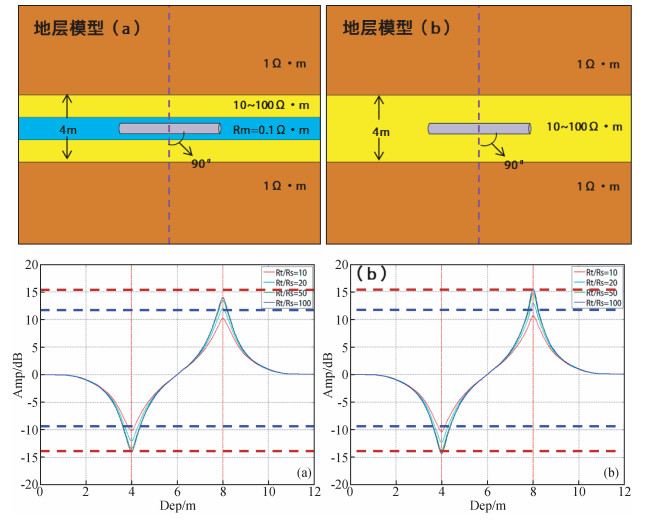
4 模型反演例证 4.1 模型一设定三维地层模型,目的层地层厚度为4 m,地层分界面为:0.0 m,4.0 m;井眼直径为Dh=8.5 in (即0.10795 m);泥浆电阻率为Rm=0.1 Ω·m;上围岩地层电阻率为Rs1=5.0~17.0 Ω·m;下围岩地层电阻率为Rs2=3.0~11.0 Ω·m;目的层无侵入,水平电阻率为Rh=20.0 Ω·m,垂直电阻率为Rv=20.0 Ω·m,无各向异性;大斜度井,目的层垂深跨度4 m,井眼轨迹水平位移152 m,层界面与水平面平行,ADR仪器以固定角度穿过目的层,井眼地层相对倾角约88°.模型反演测试输入参数为ADR仪器正演仿真得到的模拟信号,包含:2 MHz频率下相位差电阻率、幅度比电阻率;500 kHz频率下相位差电阻率、幅度比电阻率;500 kHz频率下相位方向信号、幅度方向信号;125 kHz频率下相位方向信号、幅度方向信号.自然GR和方位密度在反演中用于划分层界面、提取倾角和泥岩段约束,模型反演时第一个采样点层界面和倾角用已知值做初值,后面点反演用前一个点反演结果作为初值.从反演结果与正演模型对比来看 (图 10),真实值曲线和对应反演结果曲线重合,所有反演参数误差小于0.2%,反演精度高,152 m井段三维反演耗时3小时37分,反演计算速度可接受.
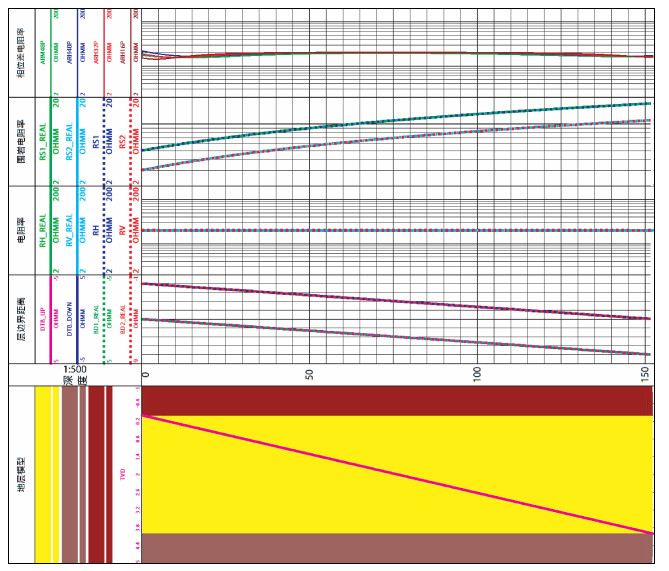
|
图 10 大斜度井三层模型反演结果验证 (注:从下向上第一道为地层模型;第二道为深度道;第三道为层边界距离与模型值对比 (虚线真实值,实线反演值);第四道为目的层电阻率反演结果与模型值对比 (虚线真实值,实线反演值);第五道为围岩电阻率与模型值对比 (虚线真实值,实线反演值);第六道为部分视电阻率道). Figure 10 Test of inversion results for three layer model of highly deviated wells |
设定三维地层模型为尖灭层模型,目的层地层最大厚度为4 m,地层开始分界面为:-2.0 m,2.0 m;井眼直径为Dh=8.5 in (即0.10795 m);泥浆电阻率为Rm=0.1 Ω·m;上围岩地层电阻率为Rs1=3.0 Ω·m;下围岩地层电阻率为Rs2=5.0 Ω·m;目的层无侵入,水平电阻率为Rh=20.0 Ω·m,垂直电阻率为Rv=20.0 Ω·m,无各向异性;水平井,井眼地层相对倾角90°,目的层厚度逐渐减小到0.0 m.
模型反演测试输入参数同模型一,从反演结果与正演模型对比来看 (图 11),真实值曲线和对应反演结果曲线重合,所有反演参数误差小于0.32%,反演精度高,152 m井段三维反演耗时3小时52分,计算速度可接受.反演结果如图 11(从下向上第一道为地层模型;第二道为深度道;第三道为层边界距离与模型值对比 (注:虚线真实值,实线反演值);第四道为目的层电阻率反演结果与模型值对比 (虚线真实值,实线反演值);第五道为围岩电阻率与模型值对比 (虚线真实值,实线反演值);第六道为视电阻率道).
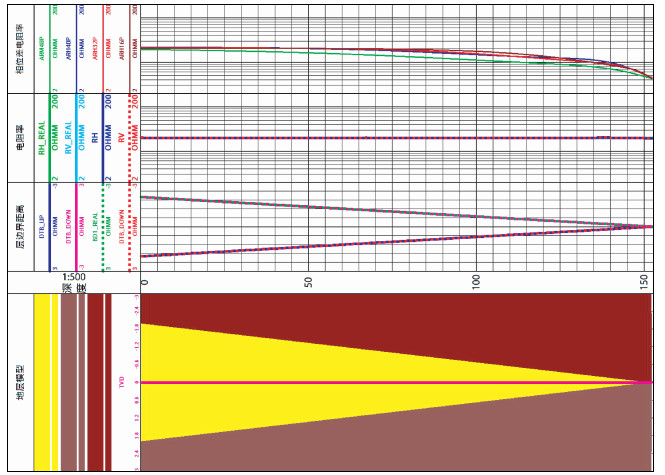
|
图 11 水平井尖灭模型反演结果验证 Figure 11 Test of inversion results for the Pinchout model |
模型反演结果分析表明:(1) 反演结果与正演模型对比,所有反演参数误差小于0.32%,反演精度高;(2) 三维反演涉及到待反演参数较多,反演过程中调用的三维正演程序计算量大,三维反演程序整体耗时较长,但对于资料后期处理来说,反演计算速度尚可接受.
5 实测资料处理与应用本应用在南海油田某区应用20井次以上,效果显著,该区目的层的沉积类型主要为一套辫状河三角洲沉积体系,自下而上由下三角洲平原向三角洲前缘、前三角洲逐渐演化,沉积微相类型主要为三角洲前缘的水下分流河道,从相邻井曲线对比可以看到,地层发育横向有一定连续性 (图 12).(注:GR为自然伽马曲线,RS为浅双侧向电阻率曲线,RD为深双侧向电阻率曲线,TNPL为中子孔隙度曲线,DEN为密度曲线).在该目的层的油层进行了密闭钻井取心,岩心分析孔隙度为11.0%~27.2%(平均孔隙度21.2%),空气渗透率24.6~2471.8 mD (平均渗透率569.1 mD),总体上属于中孔、中~高渗透率储集层.
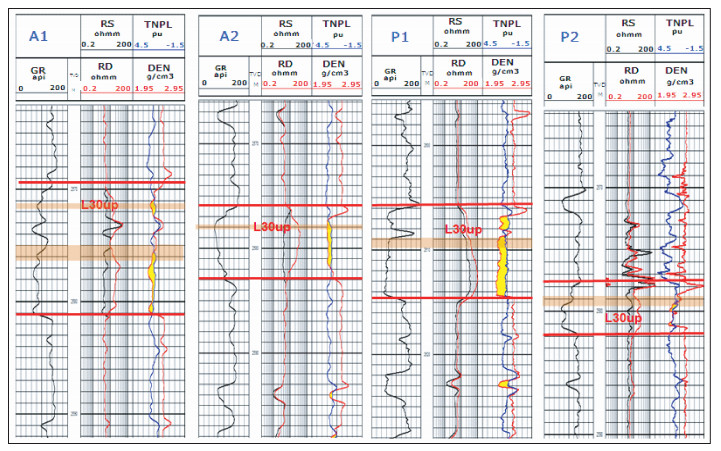
|
图 12 南海油田某区块油层邻井对比图 Figure 12 Comparison of adjacent wells in a block of the South China Sea oil field |
在探井 (直井) A1附近钻有水平井C井,水平段总进尺624 m,砂岩528 m,砂岩钻遇率84.6%,井斜角在81.74°~93.3°之间.A1井该油层视电阻率约9~38 Ω·m,而水平井C井对应该井段方位电阻率约20~100 Ω·m,最大甚至高达200 Ω·m,远高于邻近直井A1井电阻率范围.
从水平井C井进行多层界面三维电阻率反演结果分析 (图 13),C井水平电阻率值大部分集中在10 Ω·m到40 Ω·m之间,与邻近直井A1井电阻率范围接近,说明反演结果合理.储层各向异性系数大部分在1~2.5之间,少数层大于2.5,地层具有一定的各向异性,水平电阻率与ARH48PC比值大部分小于1,垂直电阻率与ARH48PT比值主要集中在1.0倍到2.5倍之间.储层侵入半径大部分在0.4 m以下,部分储层侵入较深,侵入半径大于0.6 m (图 14),利用三维反演后结果更能准确评价地层客观特性.
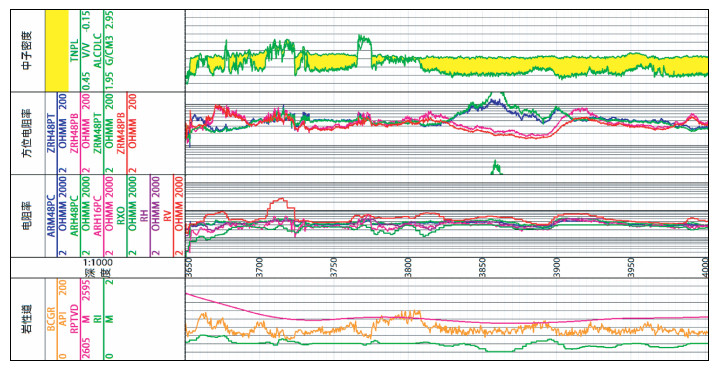
|
图 13 南海油田某区块水平井C井随钻测井多层界面三维电阻率反演结果 (注:图 13中第一道BCGR为自然GR曲线,RPTVD为垂直深度曲线,RI为反演结果得到的侵入带半径;第二道为深度道;第三道ARM48PC为500 kHz频率,48 in源距下经井眼校正后方位平均相位差电阻率;ARH48PC为2 MHz频率,48 in源距下经井眼校正后方位平均相位差电阻率;ARH16PC为2 MHz频率,16 in源距下经井眼校正后方位平均相位差电阻率;RXO为反演得到侵入带电阻率;RH为反演得到原状地层水平电阻率;RV为反演得到的原状地层垂直电阻率;第四道ZRH48PT为2 MHz频率,48 in源距0°方位相位差电阻率;ZRH48PB为2 MHz频率,48 in源距180°方位相位差电阻率;ZRM48PT为500 kHz频率,48 in源距0°方位相位差电阻率;ZRM48PB为500 kHz频率,48 in源距180°方位相位差电阻率;第五道TNPL为中子孔隙度曲线,ALCDLC为密度曲线). Figure 13 Three dimensional resistivity inversion results of C well logging in horizontal well in the South China Sea oil field |
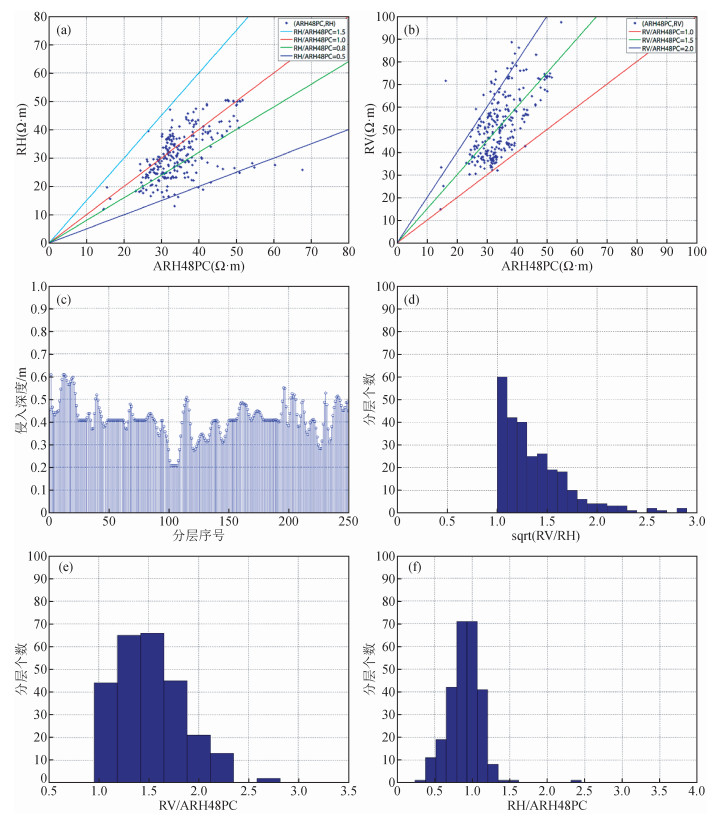
|
图 14 南海油田某区水平井C井三维电阻率反演结果分析 (a) 水平电阻率与ARH48PC交汇图; (b) 垂直电阻率与ARH48PC交汇图; (c) 侵入半径分层统计; (d) 各向异性系数分布情况 (e) Rv与ARH48PC比值分层统计; (f) Rh与ARH48PC比值分层统计. Figure 14 Three dimensional resistivity inversion results of C well in a horizontal well in the South China Sea oil field (a) Horizontal resistivity and ARH48PC intersection graph; (b) Vertical resistivity and ARH48PC intersection graph; (c) Stratified statistics of invasion radius; (d) Anisotropic coefficient distribution statistics; (e) Vertical resistivity and ARH48PC ratio stratified statistics. (f) Horizontal resistivity and ARH48PC ratio Stratified statistics. |
图 15为多边界反演结果的井眼轨迹-地层关系图,可以看到井眼轨迹在地层位置与测量方位信号指示一致;反演结果得到的多层模型各层电阻率与方位电阻率和平均电阻率指示一致,说明多边界反演结果准确可靠,在实际地质导向中具有广阔的应用前景.

|
图 15 南海油田某区块水平井C井多边界反演结果绘制井眼轨迹-地层关系图 Figure 15 Multi boundary inversion results of C well in the horizontal well in the South China Sea oil field |
(注:从下向上第一道为多边界反演结果显示的井眼轨迹-地层位置关系对应地层模型;第二道是深度道 (水平位移);第三道是方位自然伽马道;第四道是方位电阻率道;第五道是平均视电阻率道;第六道是密度和中子孔隙度道).
6 结论 6.1本次研究根据水平井和大斜度井复杂环境中多层界面地层,提出将矢量有限元方法和马奎特方法结合的三维电阻率反演方法,通过对Gauss-Newton法的修正,避免三维反演因参数较多而产生的不收敛和多解性;根据井眼环境对仪器方向信号测井响应影响特征考察对反演过程中模型做适当简化,同时三维空间剖分采用非等分的四面体网格,提高了计算精度和运算效率.
6.2模拟考察了大斜度井和水平井环境下,地层界面、地层厚度、界面两侧电阻率对比度、井眼半径、泥浆电阻率等参数对方向信号测井响应关系.
6.3通过对模型反演进行精度验证,模型计算结果显示误差小于0.32%,反演计算精度较高;通过生产井反演得到水平电阻率与探井电阻率对比,统计结果显示二者处于同一范围,结果合理可靠.
6.4本文研究的基于三维地层模型的多界面反演方法,准确获得了测量点到上下层界面距离、井眼轨迹-地层界面相对倾角等地层结构参数,同时得到水平电阻率、垂直电阻率、侵入带电阻率等地层电性参数,方法适合直井、斜井、大斜度井和水平井各种井况.结合随钻方位电阻率仪器具有的方位识别能力、探测深度较深特征,在远离层界面地方也可以反演得到准确地层方位信息,在实际生产中效果显著,打破了外方公司技术垄断.
致谢 感谢杭州迅美科技有限公司在论文完成过程中给予的有益指导和宝贵意见.| [] | Daily W, Owen E. 1991. Cross-borehole resistivity tomography[J]. Geophysics, 56(8): 1228–1235. DOI:10.1190/1.1443142 |
| [] | Kang J Z, Xing G L, Yang S D. 2006. A study on the two-dimensional full-parameter inversion method of the electromagnetic propagation resistivity logging[J]. Chinese Journal of Geophysics (in Chinese), 49(1): 275–283. DOI:10.3321/j.issn:0001-5733.2006.01.035 |
| [] | Li Y G, Oldenburg D W. 1992. Approximate inverse mappings in DC resistivity problems[J]. Geophys. J. Int., 109(2): 343–362. DOI:10.1111/gji.1992.109.issue-2 |
| [] | Liu N Z, Wang Z, Liu C. 2015. The simulations of formation resistivity imaging by applying directional resistivity tool with a joint-coil antenna while drilling[J]. Progress in Geophysics (in Chinese), 30(6): 2897–2905. DOI:10.6038/pg20150659 |
| [] | Liu Q L, Wang R H. 2014. Boundary effects and factor analysis on azimuthal resistivity tool measurement while drilling[J]. Well Logging Technology (in Chinese), 38(4): 411–415. |
| [] | Shima H. 1990. Two-dimensional automatic resistivity inversion technique using alpha centers[J]. Geophysics, 55(6): 682–694. DOI:10.1190/1.1442880 |
| [] | Shima H. 1992. 2-D and 3-D resistivity image reconstruction using crosshole data[J]. Geophysics, 57(10): 1270–1281. DOI:10.1190/1.1443195 |
| [] | Tan M J, Zhang G J, Zhang H Y, et al. 2007. 3-D numerical mode-matching (NMM) method for resistivity logging responses in nonsymmetric conditions[J]. Chinese Journal of Geophysics (in Chinese), 50(3): 939–945. DOI:10.3321/j.issn:0001-5733.2007.03.037 |
| [] | Wang Z G, He Z X, Wei W B. 2007. Fast 3D inversion of borehole ground electrical method data based on born approximation[J]. Progress in Geophysics (in Chinese), 22(2): 508–513. DOI:10.3969/j.issn.1004-2903.2007.02.024 |
| [] | Wu X P, Xu G M. 2000. Study on 3-D resistivity inversion using conjugate gradient method[J]. Chinese Journal of Geophysics (in Chinese), 43(3): 420–427. DOI:10.3321/j.issn:0001-5733.2000.03.016 |
| [] | Xing G L, Yang S D, Li S G. 2007. Cenozoic post-rift unconformity and the accelerated subsidence events of the Jiyang Depression, Bohai Bay Basin and preliminary analyses on their original mechanism[J]. Chinese Journal of Geophysics (in Chinese), 50(2): 642–650. DOI:10.3321/j.issn:0001-5733.2007.02.040 |
| [] | Ye Y X, Zhang Z Y, Wu X M, et al. 2015. Three-D regularized focusing inversion of resistivity data based on minimum support functional[J]. Progress in Geophysics (in Chinese), 30(5): 2399–2403. DOI:10.6038/pg20150557 |
| [] | Zhang J, Mackie R L, Madden T R. 1995. 3-D resistivity forward modeling and inversion using conjugate gradients[J]. Geophysics, 60(5): 1313–1325. DOI:10.1190/1.1443868 |
| [] | Zhang Z F, Cheng Z P, Ruan B Y, et al. 2004. Approximate inversion on three-dimensional resistivity sounding data[J]. Progress in Geophysics (in Chinese), 19(1): 131–136. |
| [] | Zhang Z Q, Mu L X, Zhang X, et al. 2011. Application of vector finite element method to simulate logging-while-drilling resistivity tools[J]. Journal of China University of Petroleum (in Chinese), 35(4): 64–71. |
| [] | 康俊佐, 邢光龙, 杨善德. 2006. 电磁传播电阻率测井的二维全参数反演方法研究[J]. 地球物理学报, 49(1): 275–283. DOI:10.3321/j.issn:0001-5733.2006.01.035 |
| [] | 刘乃震, 王忠, 刘策. 2015. 基于交联线圈的随钻方位电阻率仪的地层电阻率成像仿真[J]. 地球物理学进展, 30(6): 2897–2905. DOI:10.6038/pg20150659 |
| [] | 刘庆龙, 王瑞和. 2014. 随钻方位电阻率边界探测影响因素分析[J]. 测井技术, 38(4): 411–415. |
| [] | 谭茂金, 张庚骥, 运华云, 等. 2007. 非轴对称条件下用三维模式匹配法计算电阻率测井响应[J]. 地球物理学报, 50(3): 939–945. DOI:10.3321/j.issn:0001-5733.2007.03.037 |
| [] | 王志刚, 何展翔, 魏文博. 2007. Born近似快速三维反演井地电法数据[J]. 地球物理学进展, 22(2): 508–513. DOI:10.3969/j.issn.1004-2903.2007.02.024 |
| [] | 吴小平, 徐果明. 2000. 利用共轭梯度法的电阻率三维反演研究[J]. 地球物理学报, 43(3): 420–427. DOI:10.3321/j.issn:0001-5733.2000.03.016 |
| [] | 邢光龙, 杨善德, 李曙光. 2007. 电磁波测井资料反演中Jacobi矩阵的快速算法及其特性分析[J]. 地球物理学报, 50(2): 642–650. DOI:10.3321/j.issn:0001-5733.2007.02.040 |
| [] | 叶益信, 张志勇, 吴信民, 等. 2015. 基于最小支撑泛函模型约束的电阻率法三维聚焦反演[J]. 地球物理学进展, 30(5): 2399–2403. DOI:10.6038/pg20150557 |
| [] | 张致付, 程志平, 阮百尧, 等. 2004. 三维电阻率测深数据Zohdy近似反演方法[J]. 地球物理学进展, 19(1): 131–136. |
| [] | 张中庆, 穆林雪, 张雪, 等. 2011. 矢量有限元素法在随钻电阻率测井模拟中的应用[J]. 中国石油大学学报 (自然科学版), 35(4): 64–71. |
 2017, Vol. 32
2017, Vol. 32

