2. 中国石油大学 (华东) 地球科学与技术学院, 青岛 266580
3. 同济大学海洋与地球科学学院海洋地质国家重点实验室, 上海 200092
2. School of Geosciences, China University of Petroleum, Qingdao 266580, China
3. School of Ocean and Earth Science, Tongji University, Shanghai 200092, China
在地表条件复杂的区域,如黄土塬、山前带等地区,静校正问题十分突出,精确地近地表速度模型对解决静校正问题尤为重要,对速度分析及偏移成像的质量也起着非常重要的影响.近地表速度建模的方法 (崔栋等,2014) 有很多,包括层析法,小折射法,面波法等,其中小折射法 (文雪康等,2012) 仅适用于地表相对平坦、速度界面相对稳定的地区.微测井法虽然可以求取各层速度,但是只能反映井段资料在黄土塬等覆盖层厚的地区施工成本很大.雷达测深法是将声纳技术引入地震勘探测定低降速带的一种方法,但当黄土厚度大时,该方法的精度很低.
旅行时层析法是目前速度建模的一种准确高效的方法,其基于射线理论,利用地震波旅行时信息来反演地下速度,因其不受地表及近地表结构变化的约束,目前已得到国内外广泛的研究应用 (井西利等,2002).本文就是利用了初至旅行时层析进行近地表建模,并在起伏异常体模型上进行了近地表建模,考虑到山前带等地区的近地表非常复杂,本文将真地表经过不同程度平滑后校正到平滑地表上,进行了高程校正.根据射线理论,本文推导出了射线下行穿透深度与偏移距之间存在规律,在起伏异常体模型上进行了炮检点时间校正,模型测试说明了本文中方法在山前带等复杂近地表地区进行静校正等的有效性.
1 初至走时层析反演基本理论 1.1 最短路径射线追踪正演理论最短路径射线追踪技术是基于地震波传播的Fermat原理和网络理论中最短路径算法来实现的.Moser (1991)把射线追踪问题转化为求网络中最短路径问题,首先对地下复杂介质进行离散化处理,把介质划分成若干小矩形单元,单元边界或角点上的节点以及彼此相邻节点的连线就构成了一个网络,只不过节点和节点之间的连线的权变为波从一个节点传播到另一个节点的走时.Fermat原理指出,地震波沿着旅行时最小的路径传播.所以可以将用图论和网络理论中的最短路径算法得到的震源节点与接收节点的最短路径点路径看做近似的为射线路径.这种方法是无条件稳定的,对模型的维数和复杂性没有任何限制,在射线阴影区仍可得到绕射波的最小走时,并可以比较准确地模拟复杂结构的地震射线分布.这里对该方法的算法实现步骤不做详细介绍.
1.2 层析反演理论在高频近似理论下,地震波可以认为是沿着射线路径在慢度场内进行传播,地震记录的反射旅行时则是地震波沿射线路径的传播时间,在各向同性条件下,旅行时可以表示为沿着射线路径的Radon变换 (将x,y域变为s,r激发接收点域),公式为
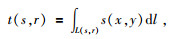
|
(1) |
其中,s和r分别是激发点和接收点,L(s, r) 是从激发点s到接收点r的射线路径,s(x, y) 是慢度 (速度的倒数),在离散情况下上式变为
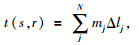
|
(2) |
其中Δlj表示当前射线在j网格内的长度,mj为j网格内的慢度,每条射线都对应一个层析方程,所有射线的方程便组成了一个庞大的稀疏线性方程组,公式为
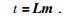
|
(3) |
首先要建立一个假设的初始速度模型.此模型越接近真实速度模型越好.在这个初始速度模型中进行射线追踪得到矩阵L和旅行时t,将此时间即为tcal,实际观测到的走时为tobs将这两个时间相减得到
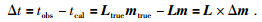
|
(4) |
通过旅行时残差和L矩阵的逆就可以得到慢度扰动来更新速度场.通过对初始速度场进行修正得到新的模型,再射线追踪求取矩阵L,求逆得到新的修正值,这样的过程反复迭代多次,直到达到人们事先给定的精度为止.
2 实现步骤 2.1 偏移距选取本文中方法理论上适合所有偏移距范围,但是考虑到在近偏移距处计算的旅行时,受折射波穿透深度的影响,将其加入反演有可能会造成模型反演的不确定性.韩晓丽等 (2008)也认为近偏移距对于低、降速带不太厚,地形起伏不太大的地区,用于反演的偏移距范围为400~3500 m.本文对不同偏移距范围段对模型反演的影响在起伏异常体模型上进行了测试,因测试模型最大偏移距为2000 m,因此本文选择只去掉小于100 m的近偏移距数据.
2.2 平滑半径选取对西部近地表复杂、地表起伏变化剧烈的地区,高程起伏剧烈,抖动严重.因为起伏地表的影响,一般不能在真地表上进行数据反演,需要将起伏地表高程先进行平滑,校正到平滑地表上.韩晓丽等 (2008)认为可以通过横向平滑减小静校正高频分量的误差,一般可选择反演最大偏移距的1/4.本文选择了平滑半径分别为20 m、50 m和100 m时,基于这三种不同的平滑半径对高程校正及炮检点时差校正进行了分析.
2.3 高频分量计算高频分量的计算也就是短波长静校正量的计算,是由实际的初至旅行时与经层析建模的模型计算出的初至旅行时的时差,经过层析反演进行的.
2.4 低频分量计算低频分量即长波长静校正量的计算,需要通过因此真地表高程与平滑地表高程之间存在高程差,高程校正就是将这部分高程对反演的影响进行校正.真地表高程校正到平滑地表高程引起的高程差对反演结果的影响,除了需要进行高程校正外,这部分高程差引起的初至波的旅行时差也需要校正,根据折射波传播的规律,一般炮检点时差校正都为垂直校正,公式为
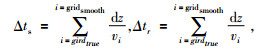
|
(5) |
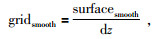
|
(6) |
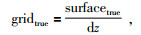
|
(7) |
其中surfacetrue为真地表高程,surfacesmooth为平滑地表高程,dz为纵向采样间隔.但是其实真实的射线路径并不是垂直传播的,因此以上公式存在误差,本文中根据射线传播深度与偏移距之间的关系进行校正,其中炮点时差校正为
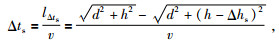
|
(8) |
其中d=offset/2,h为射线穿透深度,Δhs为炮点处真地表与平滑地表高程差.将以上公式简化为

|
(9) |
其中h=ratio×d
同样的,检波点处时差校正公式为
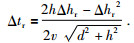
|
(10) |
真实的初至旅行时为

|
(11) |
因此最后利用公式 (9)、(10) 和 (11) 实现对炮点和检波点处低频分量的校正.
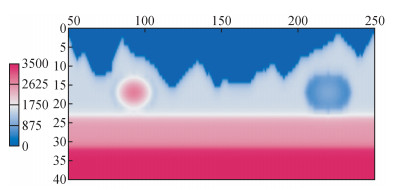
3 模型试算速度模型采样点为201×41,采样间距都为10 m,三层速度分别为:1500 m/s,2500 m/s,3500 m/s.起伏面下位置网格点位置 (43, 17) 加入一高速异常体,速度3000 m/s;网格点位置 (170, 17) 加入一低速异常体,速度值为1000 m/s,如图 1所示.观测系统为地面激发地面接收:第一炮位置 (0, 0),炮间隔10 m,共201炮,每炮201道接收,第一道位置 (0, 0),道间隔10 m.以梯度模型作为初始模型.
|
图 1 真实速度场 Figure 1 True velocity |
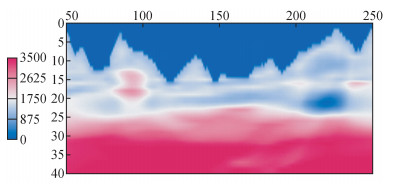
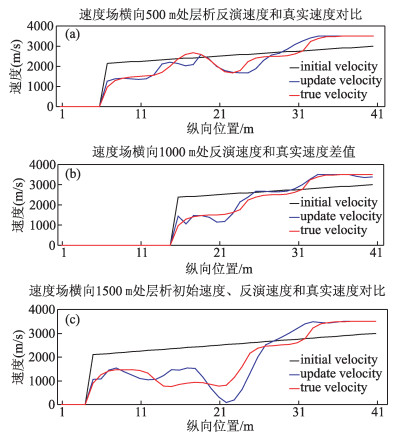
图 2是层析建模速度场,可以发现层析反演速度场的层析位置和真实速度场非常接近,并且高速异常体和低速异常体的位置反演准确.通过对速度场横向500 m、1000 m、1500 m的反演速度与真实速度对比发现,如图 3所示,可以发现反演速度场的走向趋势和真速度场吻合,尤其是在高速和低速异常体位置区域,反演速度和真实速度的趋势是一致的.
|
图 2 层析建模速度场 Figure 2 Velocity model by tomography |
|
图 3 初始速度、反演速度与真实速度对比 Figure 3 (a) initial velocity (black)、update velocity (blue) and true velocity (red) from 100 m; (b) initial velocity (black)、update velocity (blue) and true velocity (red) from 1000 m; (c) initial velocity (black)、update velocity (blue) and true velocity (red) from 1500 m |
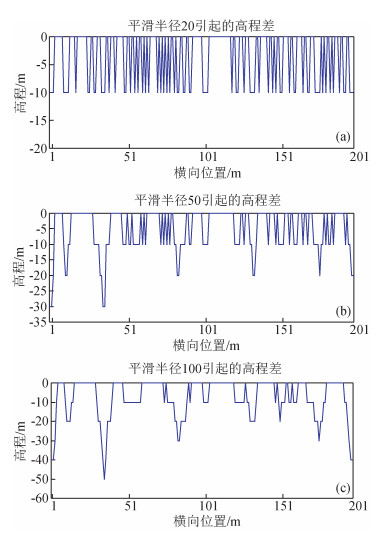
以上是我们在真地表高程进行了初至层析反演,下面我们需要先对真地表高程进行平滑,图 4是真地表高程平滑后引起的高程差,(a) 为平滑半径20 m,(b) 平滑半径为50 m,(c) 平滑半径为100 m,来测试一下不同平滑半径对近地表速度修正的影响.
|
图 4 真地表高程平滑后引起的高程差,平滑半径分别为 (a)20 m, (b) 50 m, (c)100 m Figure 4 Elevation difference by surface smoothing (a) smoothing radius 20 m (b) smoothing radius 50 m (c) smoothing radius 100 m |
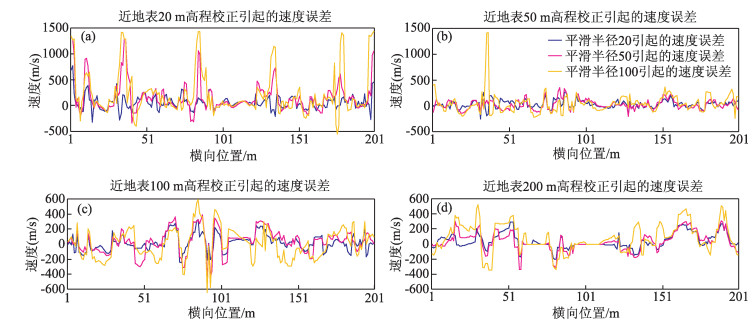
图 5分别是近地表 20 m (a)、50 m (b)、100 m (c)、200 m (d) 不同平滑半径下的高程校正量,发现对近地表 20 m和50 m来说,高程校正的影响要大于100 m和200 m.平滑半径100 m的高程校正量最大,50 m次之,20 m最小.可以发现,对从真地表到平滑地表的地表变化最剧烈的横向位置处,可以清楚看到高程校正对近地表建模的影响.越是在这些地表变化最剧烈的位置,高程校正对它们的影响也就越大;同时对其他的横向位置,可以看到经过高程校正后的近地表速度更加接近真实速度.
|
图 5 近地表高程校正后速度修正,分别为 (a)20 m, (b) 50 m, (c)100 m, (d)200 m Figure 5 Velocity difference by elevation correction (a) smooth radius 20 m (b) smooth radius 50 m (c) smooth radius 100 m |
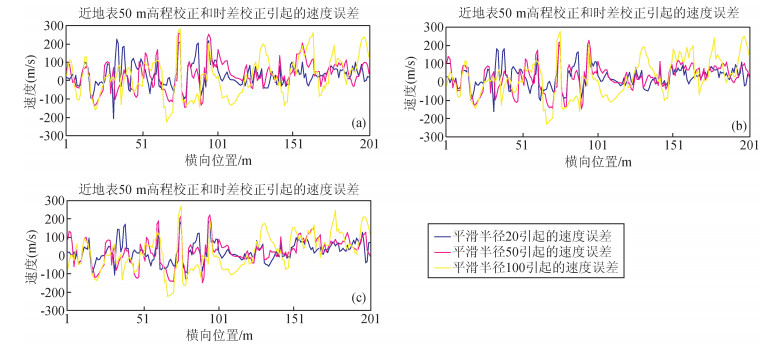
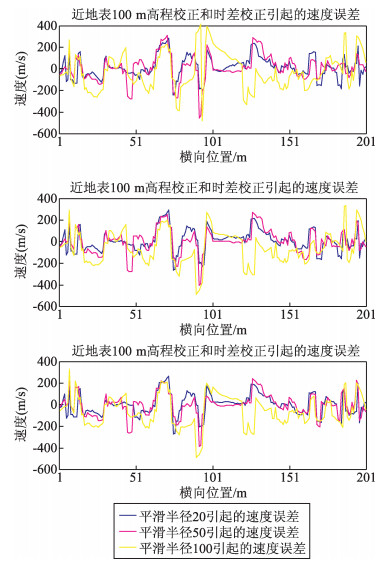
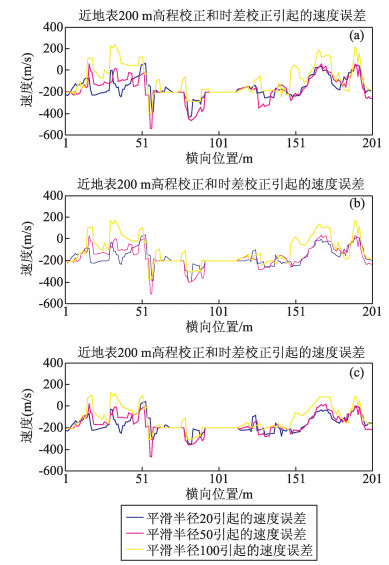
图 6分别是近地表 20 m处不同穿透深度与偏移距关系的炮检点时差校正,(a) 为h=0.1×offset, (b) 为h=0.2×offset, (c) 为h=0.3×offset.图 7分别是近地表 50 m处不同穿透深度与偏移距关系的炮检点时差校正,(a) 为h=0.1×offset, (b) 为h=0.2×offset,(c) 为h=0.3×offset.图 8分别是近地表 100 m处不同穿透深度与偏移距关系的炮检点时差校正,(a) 为h=0.1×offset, (b) 为h=0.2×offset, (c) 为h=0.3×offset.图 9分别是近地表 200 m处不同穿透深度与偏移距关系的炮检点时差校正,(a) 为h=0.1×offset, (b) 为h=0.2×offset (c) 为h=0.3×offset.

|
图 6 近地表 20 m炮检点校正后速度修正,分别为 (a)h=0.1×offset, (b)h=0.2×offset, (c) h=0.3×offset Figure 6 Velocity difference by shot and recerver correction at 20m near surface (a)h=0.1×offset, (b)h=0.2×offset, (c) h=0.3×offset |
|
图 7 近地表 50 m炮检点校正后速度修正,分别为 (a)h=0.1×offset, (b)h=0.2×offset, (c) h=0.3×offset Figure 7 Velocity difference by shot and recerver correction at 50 m near surface (a)h=0.1×offset, (b)h=0.2×offset, (c) h=0.3×offset |
|
图 8 近地表 100 m炮检点校正后速度修正,分别为 (a)h=0.1×offset, (b)h=0.2×offset, (c) h=0.3×offset Figure 8 Velocity difference by shot and recerver correction at 100m near surface (a)h=0.1×offset, (b)h=0.2×offset, (c) h=0.3×offset |
|
图 9 近地表 200 m炮检点校正后速度修正,分别为 (a)h=0.1×offset, (b)h=0.2×offset, (c) h=0.3×offset Figure 9 Velocity difference by shot and recerver correction at 200m near surface (a)h=0.1×offset, (b)h=0.2×offset, (c) h=0.3×offset |
综合图 6、7、8和9,平滑半径的大小影响趋势和上述是一样的,在实际资料处理中,综合考虑到浅层速度的大小及速度修正量的大小选择适合的平滑半径.当偏移距同深度关系系数对浅层的影响比深层的影响要大,对同一近地表高程来说,不同的偏移距同深度关系系数的变化起到了对浅层速度进行微调的效果,在保证整体速度场构造大致不变的前提下,对速度场的低频分量进行了校正,实现了近地表模型构造细节上的修正,这也正是我们期望看到的结果.
4 结论本文实现了一种近地表初至层析建模静校正技术,考虑到山前带等地区的近地表特点,本文在起伏异常体模型上进行了测试,高程校正的结果说明了本文中方法可以实现复杂地表的近地表建模.随后本文根据初至波的传播特点,推导出了初至波穿透深度与偏移距之间的关系公式,并根据该公式进行了炮检点时间校正,提出了一种新的静校正量的评价思路.测试结果说明了本文中方法在近地表建模中的适用性及有效性.因本文中方法是基于二维的,将其推广应用到三维将会起到非常重要的工作价值.
致谢 本研究得到了中国石油化工股份有限公司石油物探技术研究院地震成像技术研究所以及中国石油大学 (华东) 郭立鹏硕士的热情帮助和支持,在此表示衷心的感谢.| [] | CHEN Qi-Yuan, WANG Yan-Chun, DUAN Yun-Qing, et al. 2001. A study on the methods of static correction in complicated mountain area[J]. Geophysical Prospecting for Petroleum (in Chinese), 40(1): 73–81. |
| [] | CUI Dong, ZHANG Yan, HU Ying, et al. 2014. The review of near surface velocity modeling[J]. Progress in Geophysics (in Chinese), 29(6): 2635–2641. DOI:10.6038/pg20140625 |
| [] | Dijkstra E W. 1959. A note on two problems in connexion with graphs[J]. Numerische Mathematik, 1(1): 269–271. DOI:10.1007/BF01386390 |
| [] | HAN Xiao-Li, YANG Chang-Chun, MA San-Huai, et al. 2008. Static of tomographic inversion by first breaks in complex areas[J]. Progress in Geophysics (in Chinese), 23(2): 475–483. |
| [] | JING Xi-Li, YANG Chang-Chun, LI You-Ming. 2002. Study of tomographic inversion in the construction of velocity model[J]. Geophysical Prospecting for Petroleum (in Chinese), 41(1): 72–75. |
| [] | LI Lu-Ming, LUO Xing-Xian, ZHAO Bo. 2000. Tomographic inversion of first break in surface model[J]. Oil Geophysical Prospecting (in Chinese), 35(5): 559–564. |
| [] | LI Man-Shu, FANG Wu-Bao, ZHOU Teng, et al. 2004. Inversion of near-surface velocity through first-arrival traveltime in complex region[J]. Geophysical Prospecting for Petroleum (in Chinese), 43(1): 72–75. |
| [] | LIN Bo-Xiang, SUN Jing-Mei, LIU Qing-Lin. 2002. Tomography for LVZ velocity inversion and statics[J]. Geophysical Prospecting for Petroleum (in Chinese), 41(2): 136–140. |
| [] | LIN Bo-Xiang, SUN Jing-Mei, XU Ying. 2013. Static correction comparison workflow and stacking velocity modification method[J]. Geophysical Prospecting for Petroleum (in Chinese), 52(1): 30–34, 78. |
| [] | Moser T J. 1991. Shortest path calculation of seismic rays[J]. Geophysics, 56(1): 59–67. DOI:10.1190/1.1442958 |
| [] | Nakanishi I, Yamaguchi K. 1986. A numerical experiment on nonlinear image reconstruction from first-arrival times for two-dimensional island arc structure[J]. Journal of Physics of the Earth, 34(2): 195–201. DOI:10.4294/jpe1952.34.195 |
| [] | PAN Yan-Mei, DONG Liang-Guo, LIU Yu-Zhu, et al. 2006. Review of tomographic inversion for near-surface velocity structure[J]. Progress in Exploration Geophysics (in Chinese), 29(4): 229–234. |
| [] | QIN Zi-Geng, LI Zi-Xuan, TUO Xian-Guo, et al. 2015. Application of chromatography modeling techniques in the Kuqa depression statics exploration area east Akiyama[J]. Progress in Geophysics (in Chinese), 30(2): 769–775. DOI:10.6038/pg20150239 |
| [] | Vidale J. 1988. Finite-difference calculation of travel times[J]. Bulletin of the Seismological Society of America, 78(6): 2062–2076. |
| [] | WEN Xue-Kang, LIU Sheng, LI Shi-Qiong, et al. 2012. The application of chromatography technology to near-surface structure investigation of the loess area[J]. Geophysical and Geochemical Exploration (in Chinese), 36(5): 766–771. |
| [] | XU Kun, WU Lu, WANG Miao-Yue. 1998. Improved Moser ray trace[J]. Progress in Geophysics (in Chinese), 13(4): 60–66. |
| [] | YU Hao. 2012. Applicability analysis of refraction static correction and tomographic inversion static correction[J]. Progress in Geophysics (in Chinese), 27(6): 2577–2584. DOI:10.6038/j.issn.1004-2903.2012.06.035 |
| [] | ZHANG Ji-Guo, LIU Lian-Sheng. 2006. Static corrections by first breaks tomographic inversion in complex area[J]. Oil Geophysical Prospecting (in Chinese), 41(4): 383–385, 395. |
| [] | ZHANG Jian-Zhong, CHEN Shi-Jun, XU Chu-Wei. 2004. A method of shortest path raytracing with dynamic networks[J]. Chinese Journal of Geophysics (in Chinese), 47(5): 899–904. DOI:10.3321/j.issn:0001-5733.2004.05.023 |
| [] | ZHANG Jian-Zhong, CHEN Shi-Jun, YU Da-Xiang. 2003. Improvement of shortest path ray tracing method[J]. Progress in Geophysics (in Chinese), 18(1): 146–150. DOI:10.3969/j.issn.1004-2903.2003.01.025 |
| [] | ZHAO Hou-Yue, ZHANG Mei-Gen. 2014. Tracing seismic shortest path rays in anisotropic medium with rolling surface[J]. Chinese Journal of Geophysics (in Chinese), 57(9): 2910–2917. DOI:10.6038/cjg20140916 |
| [] | 陈启元, 王彦春, 段云卿, 等. 2001. 复杂山区的静校正方法探讨[J]. 石油物探, 40(1): 73–81. |
| [] | 崔栋, 张妍, 胡英, 等. 2014. 近地表速度建模方法综述[J]. 地球物理学进展, 29(6): 2635–2641. DOI:10.6038/pg20140625 |
| [] | 韩晓丽, 杨长春, 麻三怀, 等. 2008. 复杂山区初至波层析反演静校正[J]. 地球物理学进展, 23(2): 475–483. |
| [] | 井西利, 杨长春, 李幼铭. 2002. 建立速度模型的层析成像方法研究[J]. 石油物探, 41(1): 72–75. |
| [] | 李录明, 罗省贤, 赵波. 2000. 初至波表层模型层析反演[J]. 石油地球物理勘探, 35(5): 559–564. |
| [] | 李满树, 方伍宝, 周腾, 等. 2004. 初至波走时信息在复杂地区近地表速度反演中的应用[J]. 石油物探, 43(1): 72–75. |
| [] | 林伯香, 孙晶梅, 刘清林. 2002. 层析成像低速带速度反演和静校正方法[J]. 石油物探, 41(2): 136–140. |
| [] | 林伯香, 孙晶梅, 徐颖. 2013. 静校正对比流程与叠加速度修正方法[J]. 石油物探, 52(1): 30–34, 78. |
| [] | 潘艳梅, 董良国, 刘玉柱, 等. 2006. 近地表速度结构层析反演方法综述[J]. 勘探地球物理进展, 29(4): 229–234. |
| [] | 秦自耕, 李子轩, 庹先国, 等. 2015. 层析建模技术在库车坳陷东秋山地区静校正应用探索[J]. 地球物理学进展, 30(2): 769–775. DOI:10.6038/pg20150239 |
| [] | 文雪康, 刘胜, 李世琼, 等. 2012. 层析法在黄土塬区近地表结构调查中的应用[J]. 物探与化探, 36(5): 766–771. DOI:10.11720/wtyht.2012.5.12 |
| [] | 许琨, 吴律, 王妙月. 1998. 改进Moser法射线追踪[J]. 地球物理学进展, 13(4): 60–66. |
| [] | 于豪. 2012. 折射波静校正与层析静校正技术适用性分析[J]. 地球物理学进展, 27(6): 2577–2584. DOI:10.6038/j.issn.1004-2903.2012.06.035 |
| [] | 张继国, 刘连升. 2006. 复杂区初至层析反演静校正[J]. 石油地球物理勘探, 41(4): 383–385, 395. |
| [] | 张建中, 陈世军, 徐初伟. 2004. 动态网络最短路径射线追踪[J]. 地球物理学报, 47(5): 899–904. DOI:10.3321/j.issn:0001-5733.2004.05.023 |
| [] | 张建中, 陈世军, 余大祥. 2013. 最短路径射线追踪方法及其改进[J]. 地球物理学进展, 18(1): 146–150. DOI:10.3969/j.issn.1004-2903.2003.01.025 |
| [] | 赵后越, 张美根. 2014. 起伏地表条件下各向异性地震波最短路径射线追踪[J]. 地球物理学报, 57(9): 2910–2917. DOI:10.6038/cjg20140916 |
 2017, Vol. 32
2017, Vol. 32

