2. 大地测量与地球动力学国家重点实验室, 武汉 430077
3. 中国石油集团公司东方地球物理公司物探技术研究中心, 涿州 072751
2. State Key Laboratory of Geodesy and Earth's Dynamics, Wuhan 430077, China
3. Research & Development Center, BGP, CNPC, Zhuozhou 072751, China
地震勘探是一个通过地表数据采集预测地下目标体结构和属性的系统工程.我们从地表获取包含地下目标体信息的走时和振幅等数据,通过地震偏移方法重建地下构造的精确形态,借助反演策略估计反射面的物理属性.半个世纪以来,常规地震勘探方法已经有了巨大的发展,方法日趋成熟和完善.对于大尺度缓倾角横向均匀介质构造,反射地震勘探取得良好的效果,承担着工业界进行油气开发的主要勘探任务.随着油气勘探程度的不断加深,单纯的大尺度构造型油气藏已经越来越少,勘探目的层系越来越深,地质和地表条件越来越复杂,常规的地震勘探在面临复杂地质结构条件时遇到新的挑战.
随着振幅分析技术 (AVO) 在工业界的推广应用,保幅偏移成像技术对于AVO-AVA分析和参数反演具有重要意义 (李振春,2014;Gray,2014),人们在提供精确地质构造图像的同时开始关心振幅保真度.传统反射波地震勘探认为地下一次反射波是主要能量,将其他不相干地震信号 (面波,绕射波,多次波) 视为干扰,这种线性观点忽视了地震信号中有用的成分,是客观非线性地球物理问题的粗略表达,难以保证精确成像和振幅保真.不相干信号往往由地震波在地下介质中的小规模不均匀体间相互传播产生的 (Coates and Charrette, 1993),常规地震勘探很显然对这类特征波长小于或与地震波主波长相当的小尺度构造难以精确成像,甚至会造成误差和错误,这明显偏离精细勘探的宗旨.散射波作为地震波传播的最基本的形式,在处理复杂非均匀介质时,探测尺度可大大小于入射波主波长,因此其理论分辨率可远高于地震学的常规方法 (贾豫葛等,2005;尹军杰等,2005).近些年非均匀体的地震散射波特征研究逐渐成为热点,针对非均匀介质的地震波散射波模拟和逆散射成像开始引起地震勘探学者的关注.
散射理论将地球介质视为背景介质和扰动介质的叠加,描述介质扰动与其引起的地震波场之间的关系.散射波的传播遵循惠更斯原理,震源激发的地震波在背景介质中传播形成背景波场,遇到扰动介质,背景波场与扰动介质发生一次散射形成新的震源,新的震源形成新的波前子震源继续传播与其他扰动介质发生多次散射作用,形成更高阶散射波,这些不同阶次的散射波最终在地表观测点上相互叠加形成非线性地震波场,它包含了地下介质的所有信息.理论上正散射序列可以完整表达这一过程,逆散射则是求取介质扰动的逆过程.我们从两个方面阐述:(1) 正散射将背景介质和扰动作为输入,输出实际波场或者散射波场;(2) 逆散射是给定背景介质以及地表观测波场,来逆向求取地下介质的扰动 (Weglein et al., 2003).地表观测的波场数据与地下介质参数之间存在非线性关系,而逆散射就是通过求解这个非线性方程从而获得地下介质扰动的估计,当然目前这一非线性关系还难以找到确切的解.
地震反演方法种类有很多,基本可以归结为两种:直接反演和迭代反演.其中基于散射理论的反演方法属于直接反演中的近似反演方法,包含两大类.第一类是基于一阶Born近似 (单散射) 的线性反演方法,其基本思路是将相应的地震反演问题线性化并显示地给出线性反演问题解的解析表达式.Cohen和Bleistein (1977, 1979) 对常背景和变背景速度下的波速扰动反演进行了系统的研究,建立起了以小扰动理论和Born近似为理论基础的速度反演理论,并将他们所提出的方法应用到二维声波速度模型中.Raz (1981a, b) 在层状双参数声波介质模型中考虑了常数背景下速度和密度直接线性反演方法.Clayton和Stolt (1981)利用Green函数的WKBJ近似将Cohen和Bleistein、Raz的结果推广到三维变背景声波介质情形,在频率波数域中推导出速度和密度线性解.从应用的观点出发,勘探物理学家希望知道物性参数发生突变或者间断的位置,及其梯度变化的大小 (真振幅成像和反演).Miller提出了线性真振幅成像和反演的最初轮廓 (Miller et al., 1984, 1987)——求解广义Radon变换的反投影算子,使绕射叠加几何方法 (French,1974;Gardner et al., 1974) 更趋完善,而且更适合于处理复杂地质构造及震源和检波器任意排列的情况.Beylkin (1984, 1985) 利用小扰动技术和Born近似将反问题线性化,引入了一种Fourier积分算子并忽略其所有光滑项 (只保留奇性项),有效解决了具有震荡积分核的第一类Fredholm积分方程的求解问题,奠定了奇性反演 (即间断面反演) 的理论基础.Beylkin和Burridge (1990)将GRT方法推广到各向同性弹性介质中,提出了与单散射夹角有关的多参数反演方法.基于单散射的逆散射反演算法在某种程度上比较完美,线性化下的理论在数学上也可以获得比较准确的解.Born近似在这一阶段地震数据处理中起到了重要作用,成为非线性方程进行线性化处理的重要手段.
Born近似的适用性依赖于背景格林函数算子模拟两点之间的直达波的准确度,如果背景格林算子描述直达波不够准确,这种情况Born近似值得怀疑 (Clayton et al., 1981).另外,Born近似省略了序列中的高阶项,忽略了非线性多散射效应对成像的作用,这种近似处理使得线性化偏移在面对复杂介质反演振幅时难以保真.只有将散射序列中的高阶项用于反演框架中,才能从本质上克服线性小扰动假设的不足.20世纪80年代开始,学者为了使逆散射理论适用于大扰动的情形,开始关注逆散射序列中的高阶项.Clayton (1981)表明通过利用散射序列里的高次项可以获得高阶近似.勘探地球物理学家开始从散射级数角度出发研究非线性逆散射偏移反演技术 (Inverse scattering series,ISS).Weglein (1999; Weglein et al., 1997),Matson (1996)和Ikelle (1999; Ikelle et al., 2002) 开始研究逆散射序列,利用逆散射理论去除地震数据中的多次波.Weglein等在一维声波单参数介质中对主波场分别利用逆散射成像子级数和逆散射反演子级数进行成像和反演任务 (Weglein et al., 2002, 2003;Shaw et al., 2004).Liu等 (2005)将ISS成像方法推广到二维声波单参数介质中.Zhang和Weglein (2009a, b) 分别在一维多参数声波介质和一维各向同性弹性介质中考虑了直接ISS反演方法.从ISS成像技术的最新进展可以看出该方法的数值试验都是在二维简单声波模型中进行,没有用复杂模型检测其有效性,并且假定所有多次波都已消除.Weglein等研究的散射序列反演方法比较吸引人的地方在于无需详细的先验信息,利用散射序列构建了地震波场与介质物性参数之间较为完整的非线性关系.散射序列是一种无穷序列,如何选取其中的子序列应用于实践,还有待进一步研究.另外高维复杂介质数值计算的稳定性以及计算成本还有待于探讨.
为了克服一阶Born近似线性反演仅对弱散射介质有效的局限性,避开逆散射级数的复杂性和计算量,Mao等 (2013)在Beylkin (1985)GRT线性反演方法的基础上提出一种基于二阶Born近似的非线性反演新思路.Ouyang等 (2015)将Mao的方法推广到任意观测系统.本文分别从正演和反演角度验证这一方法,并应用相关模型进行测试.首先给出一阶Born近似积分方程和二阶Born近似积分方程,从正向散射的角度分析对比二阶Born近似和一阶Born近似对地震波场模拟的准确度.为了研究基于二阶Born近似下的非线性反演框架,我们提出一个有意义的假设,仅在一个局部范围内考虑二次散射的影响,去逼近实际二次散射.通过测试验证了这一假设的合理性并推导了局部区域的二次散射积分项,这个二次散射项作为实际二次散射的近似,能够将二次散射作用作为一个关于扰动的非线性项加入到GRT线性保幅偏移框架中去,在完成GRT线性偏移后解一个非线性方程就能获得在二阶Born近似下散射场的扰动解.在实现非线性保幅反演的同时,并不需要增加额外的计算量.数值算例表明,二阶Born近似对散射场的模拟比线性单散射近似更为准确,二次散射作用主要收敛在一个特定半径的局部圆域内,超过这一区域,二次散射强度趋于稳定.单界面层状介质和复杂SEG/EAGE盐丘模型数值算例表明,基于二阶Born近似的GRT非线性反演相比线性反演,更适应强扰动介质,能实现更为精确的真振幅偏移成像.
1 二阶Born近似从点源常密度声波波动方程出发,公式为
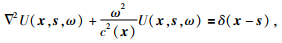
|
(1) |
其中▽2是Laplace微分算子,U是声压场,c是声速,ω是角频率,δ是震源脉冲函数.
类比Lippman-Schwinger方程,U可以表示为
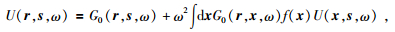
|
(2) |
其中G0是背景格林函数 (背景介质的声速为c0),r和s分别表示接收器和震源的位置,x表示散射点的位置,f是散射位势,它是表征扰动介质相对背景介质的散射强度,其定义为
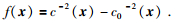
|
(3) |
用L和L0表示地震波在实际和背景介质中的传播算子,公式为
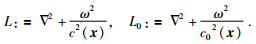
|
(4) |
并定义相应的扰动算子V:=L0-L, 通过不断迭代 (2) 式右端积分项,可以得到无穷序列为
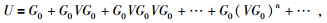
|
(5) |
或者
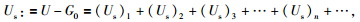
|
(6) |
其中Us表示散射场,(Us)n:=G0(VG0)n表示相应的n次散射积分项 (n≥1).
(6) 式是散射场的完整表达式,如果只保留散射场的首阶项 (Us)1,则得到散射场的一阶Born近似为
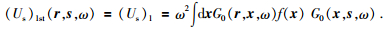
|
(7) |
一阶Born近似符合传统地震反射勘探的一次波假设,基于一阶Born近似 (单散射) 与偏移之间存在特定的数学关系,地震勘探学者提出并论证了直接线性反演框架 (Cohen and Bleistein, 1977,1979;Gray et al.,1979;Raz, 1981a, b;Miller,1983;Beylkin, 1984, 1985),解决了地震反演中的一些经典问题.但值得注意的是一阶Born近似实际上是将总波场近似为背景介质的入射场,忽略了扰动引起的多次散射,该方法仅适用于小扰动情况 (Weglein and Gray, 1983, Bleistein,1987;符力耘等,1998; 符力耘,2010).总结前人的研究,可以得到一般化的结论是,散射波相对入射波振幅很弱的情况下,一阶Born近似方法可以比较准确地近似散射波场,因为在弱散射情形下,散射波之间的相互干涉很弱,多次散射影响可以忽略.
然而,在复杂非均匀介质中,多次散射效应对散射场能量的贡献往往不能忽略.我们尝试考虑散射序列高阶项来弥补单散射的不足,主要探讨散射场序列的前两项 (n=2),即二阶Born近似, 公式为
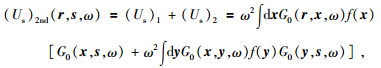
|
(8) |
其中二次散射项为
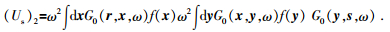
|
(9) |
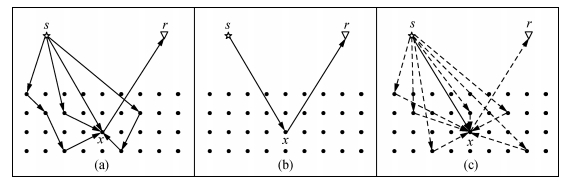
图 1简要给出了以扰动点x为主散射点的Born序列示意图,s为炮点位置,r为接收器位置.图 1a为高阶Born近似散射路径图示,地震波分别与其他散射点经过不同阶次的散射后与主散射点x相互作用传播到r;图 1b为一阶Born近似散射路径图示,地震波从s出发,直接传播到x发生一次散射作用再传播到r,也称为单散射;图 1c是二阶Born近似散射路径示意图,包括单散射 (黑粗) 和二次散射 (虚线),其中二次散射是地震波与所有散射点发生一次散射作用,再经主散射点x散射一次,最后传播到r的过程.
|
图 1 散射序列示意图 (以x为主散射点) (a) 高阶Born近似散射;(b) 一阶Born近似散射;(c) 二阶Born近似散射. Figure 1 Schematics of scattering series (a) Schematics of High order Born scattering; (b) Schematics of first order (single) scattering; (c) Schematics of second order scattering. |
20世纪60年代以来,很多学者研究过单散射一阶Born近似积分方法的适用性.其中一类属于解析方法,直接分析近似项的相对量级.还有一类采用数值模拟方法,对于已知的经典模型解析解,比较数值模拟的近似解准确度 (Coates and Charrette, 1993).本文从水平层状单界面模型的解析解出发,计算散射场一阶、二阶Born近似的数值模拟数据,比较这两种近似积分方法的准确度.
对于常密度简单层状介质,可以获取解析数据 (Zhang和Weglein,2009),公式为
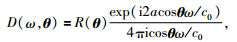
|
(10) |
其中θ为入射角,a是界面深度,R(θ) 为反射系数.当θ小于临界角时,反射系数可以表示为 (Keys,1989):
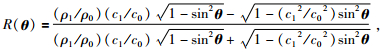
|
(11) |
其中c1为下层速度,c0为上层速度,ρ1为下层密度,ρ0为上层密度.
二维常波速介质的格林函数有高频近似解 (Miller, 1987;Bleistein et al., 2001),公式为
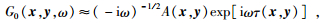
|
(12) |
其中ω是角频率,x和y为两个散射点的位置坐标,A为传播振幅,τ为射线从x传播到y的走时.这里A和τ可以具体表示为
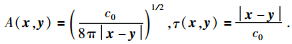
|
(13) |
将 (12) 式代入 (7) 式,我们可以将一阶Born近似进一步展开为
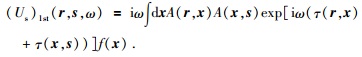
|
(14) |
类似的,将 (12) 式代入 (8) 式,对应的二阶Born近似可以展开为
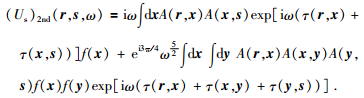
|
(15) |
二阶Born近似实际是在一阶Born近似基础上考虑了二次散射项 (Us)2作用,相应计算量也主要集中在二次散射积分的计算上.它描述了地震波传播到扰动点y,再传播到扰动点x,分别产生作用形成散射波场,再经背景场传播到接收器r的过程.算法设计上我们在时间域中计算积分部分,再利用快速FFT转换到频率域,考虑频率因子后再转换到时间域,采用多核并行计算.
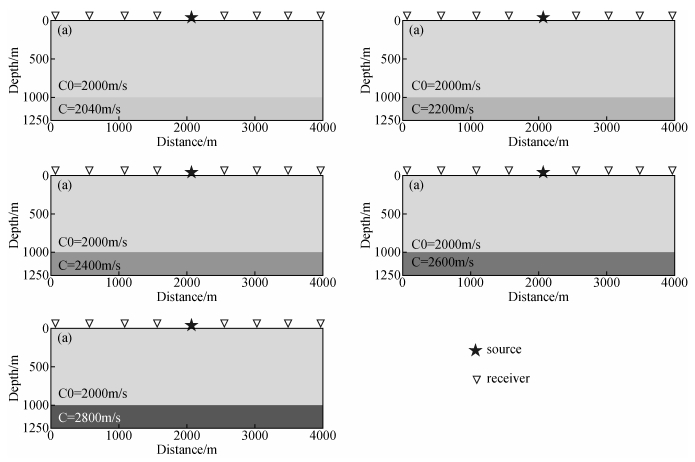
理论上常规一阶Born数据能够在一阶精度上近似散射波场.二阶Born数据考虑了二次散射的作用,能给出散射场更高阶精度的模拟.为了验证这一结论,本文设置5个不同速度扰动的单界面层状模型,如图 2,通过计算对应扰动模型的一阶Born数据和二阶Born数据,并与解析数据对比,分析一阶、二阶Born模拟散射波场的准确程度.图 2为5个单界面层状模型,每个模型横向网格节点数401,横向网格间距10 m,长4000 m,纵向网格节点数251,纵向网格间距5 m,深1250 m,速度扰动界面深度位置1000 m.采用中间单炮激发,两侧接收,震源函数选择主频20 Hz的Ricker子波,采样时间4 s,采样间隔4 ms.在5个单界面模型中,界面以上均为常数背景速度c0=2000 m/s,按照背景速度扰动δc依次为2%,10%,20%,30%,40%分别设置5个模型界面以下扰动速度分别为c=2040 m/s,2200 m/s,2400 m/s,2600 m/s,2800 m/s.
|
图 2 5个水平单界面层状模型示意图,上层背景速度为2000 m/s (a~e) 依次按相对扰动δc 2%,10%,20%,30%,40%变化 Figure 2 Five two layered models with horizontal interface, the top velocity is 2000 m/s, the bottom velocity from a to e is with the relative perturbation δc of 2%, 10%, 20%, 30% and 40% of the top velocity, respectively |
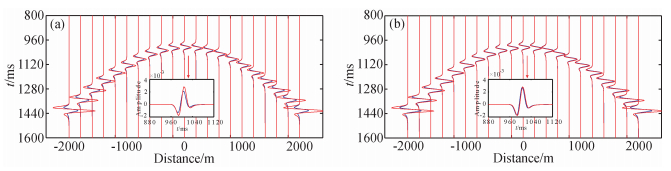
我们分别计算这5个模型的一阶Born数据,二阶Born数据以及解析数据.图 3是以其中速度扰动40%(c=2800 m/s,δc=40%) 的模型为例,显示了一阶、二阶Born数据与解析数据随偏移距变化特征.其中图 3a是一阶Born数据 (蓝色实线) 与解析数据 (红色实线) 振幅对比图;图 3b为二阶Born数据 (蓝色实线) 与解析数据 (红色实线) 振幅对比图.从合成数据剖面上看,一阶、二阶Born数据的走时同相轴位置准确,振幅随偏移距变化特征与解析数据基本一致.一阶、二阶Born数据振幅随偏移距变化都有不同程度大小的误差,其中一阶Born数据更为明显.
|
图 3 40%扰动层状模型一阶Born和二阶Born数据分别与解析解合成记录对比图 (a) 一阶Born近似与解析数据合成记录对比图;(b) 二阶Born近似与解析数据合成记录对比图. Figure 3 Comparison of Born approximate data and analytical data from 40% perturbation model (a) First order Born approximation; (b) Second order Born approximation. |
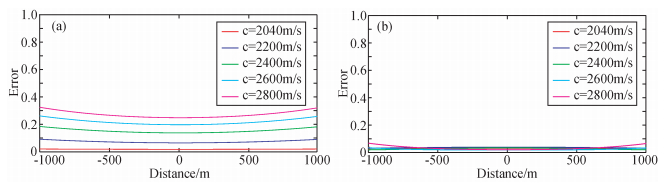
为了进一步分析一阶、二阶Born数据在振幅上的差异,以及随不同扰动大小的变化,我们以解析数据为标准,分别计算5种不同扰动模型的一阶、二阶Born数据振幅的相对误差 (图 4).图 4a为不同扰动模型的一阶Born数据与解析数据近偏移距道集振幅误差分布曲线图,图 4b为不同扰动模型的二阶Born数据与解析数据近偏移距道集振幅误差分布曲线图.从图 4a可见,一阶Born数据随着速度扰动由2%增大到40%,误差也逐渐变大.注意到在小速度扰动2%(红色实线) 时,误差曲线比较平缓,共炮点各道集振幅误差都很小.由图 4b易见,不同速度扰动大小模型的二阶Born数据振幅误差都比较小,基本控制在5%以内,不同速度扰动模型共炮点数据所有道集均比较保幅.由图 4可得到结论,一阶Born近似合成数据在小扰动情形是比较准确的,但随速度扰动变大,误差快速增大.二阶Born近似数据准确度明显得到提高,尤其在近偏移距道集,不同速度扰动的数据都非常接近解析解.
|
图 4 不同扰动下一阶Born近似和二阶Born近似误差随偏移距分布曲线 (a) 一阶Born近似误差;(b) 二阶Born近似误差. Figure 4 Error distribution curves as offset changes from Born data of different perturbation (a) First order Born approximate data error; (b) Second order Born approximate data error. |
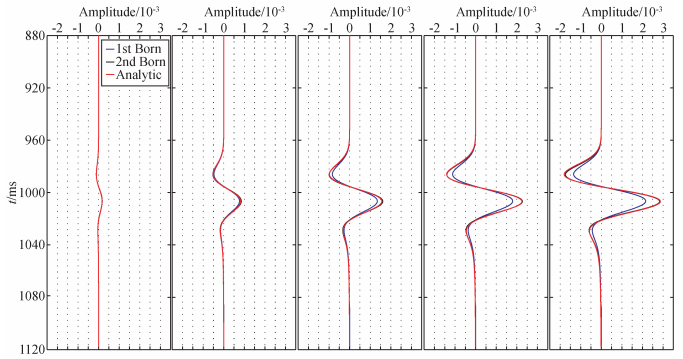
图 5从左到右是按速度扰动2%,10%,20%,30%,40%变化的5个单界面模型三种方法计算的合成数据中间道集的振幅对比图.其中红色实线为解析数据,蓝色实线为一阶Born数据,黑色为二阶Born数据.可以看出在小扰动的情形,一阶Born (蓝色实线) 振幅比较准确,而随着扰动增大,误差逐渐增大;二阶Born数据 (黑色实线) 则基本与解析数据 (红色实线) 保持重合,随扰动增大仍然保持高准确度.
|
图 5 三种方法计算的合成数据中间道集振幅对比图 Figure 5 Comparison diagram of amplitude from middle trace of synthetic data by three methods |
前文通过单界面层状模型,从正演的角度验证了二阶Born近似比传统单散射一阶Born近似能更加准确地模拟散射波场,尤其在大扰动情形.很自然地可以联想到能否建立基于二阶Born近似的偏移反演方法.与基于单散射一阶Born近似的线性偏移反演方法相比,求解基于二阶Born近似的积分方程反问题的难点在于如何有效的处理二次散射项.到目前为止,还很难从 (8) 式中直接求取散射位势f的准确解.
散射场二阶Born近似是单次散射和二次散射的叠加.我们这里专注分析二次散射项 (Us)2,二次散射的过程是地震波从震源s点处激发,遇到散射点y相互作用后形成新的震源传播到主散射点x,产生二次散射作用后传播到接收器r,形成观测到的散射场.基于二阶Born近似积分方程求解的考虑以及散射波叠加干涉特征,我们提出一种局部二次散射假设,认为二次散射效应主要集中在局部圆域内,尝试性研究局部二次散射与实际二次散射的等效性.
如图 6,假设二次散射作用仅在主散射点x周围的圆域范围.考虑散射点x周围一定半径的圆形区域内的所有散射点y对它的二次散射作用,将 (9) 式二次散射项 (Us)2做进一步近似为
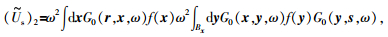
|
(16) |
|
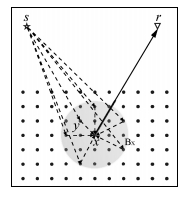
图 6 局部二次散射示意图 Figure 6 Schematics of second order scattering within a local area |
前文 (9) 式二次散射项 (Us)2中的散射点x和y都是在整个扰动区域内积分,称为实际二次散射项.(16) 式则是对该二次散射项的积分区域做了一个假设,散射点x仍然是整个扰动域内的积分,而散射点y的积分区域则是以散射x点为圆心的圆域Bx,其半径为ε=2πl(x)c0(x)/ω.这里l(x) 为散射点x处的局部二次散射系数因子.我们称 (Ũs)2为局部二次散射项.
为了验证 (16) 式局部二次散射项 (Us)2与 (9) 式实际二次散射项 (Ũs)2的等效性,我们通过模型试算比较两种二次散射的数值模拟结果.局部二次散射项的计算与实际二次散射项类似,只需要限制y的积分范围在以x为圆心的圆域Bx内,利用快速FFT变换和高性能并行计算.我们沿用上节5个单界面速度模型,分别计算5个扰动模型的实际二次散射数据,以及在不同系数因子l下的局部二次散射数据,并进行振幅分析.
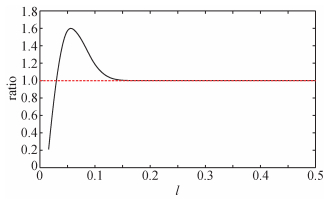
图 7是以40%扰动模型为例,局部二次散射 (Ũs)2与实际二次散射 (Ũs)2振幅的比值随系数因子l变化的曲线图.这里振幅是指两种方法计算的二次散射数据中间道的振幅峰值.事实上,比较其他扰动模型的局部二次散射数据和实际二次散射数据,均能得到类似的结果.l从0到0.05左右,振幅比值单调递增并超过红色虚线1(红色虚线),在0.05左右比值达到峰值;l从0.05开始,比值开始逐渐减小,一直到l在0.15左右比值接近红色虚线1并保持稳定.可以看到,在l超过0.15以后局部二次散射振幅与实际二次散射基本相当.若考虑背景主波长λ=c0(x)/ω0(ω0为主频率),根据局部圆域半径表达式,合理的局部二次散射效应的最小圆域半径 (ε=2πlλ) 接近一个主波长.图 7的结果揭示了常速度背景单界面层状介质二次散射作用的特征,在约半个波长的半径范围圆域内,其他散射点对主散射点的二次散射作用逐渐干涉叠加积累,二次散射强度迅速增强,超过半个波长左右二次散射作用相互干涉相消减弱,在一个主波长以外范围的其他散射点对该散射点的二次散射作用则可以忽略,这证实了我们对于二次散射的局部圆形区域假设是合理的,基于局部二次散射的二阶Born近似可以等价于实际的二阶Born近似.
|
图 7 实际二次散射与局部二次散射振幅的比值随波长系数l变化的曲线图 Figure 7 Amplitude ratio of true and local 2nd order scattering as l value changes |
对于经典声波广义Radon变换问题,其反演解已有学者研究 (Beylkin, 1984, 1985;Miller et al.,1987).根据Beylkin (1985),考虑广义Radon变换 (GRT) 算子ℜ为
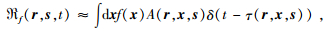
|
(17) |
相应的逆算子ℜ*为
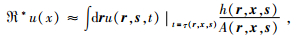
|
(18) |
其中δ为震源脉冲函数,h为Beylkin行列式 (见Beylkin,1985).
通过 (17) 式,可以直接建立散射场一阶Born近似 (Us)1st式与算子ℜ的联系,公式为
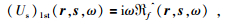
|
(19) |
其中ℜf(r, s, ω) 是ℜf(r, s, t) 对t做傅里叶变换.如果将 (18) 式中u取为
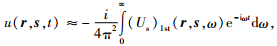
|
(20) |
则可以得到散射场一阶Born近似下的GRT线性反演公式为
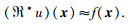
|
(21) |
上节中通过单界面水平层状模型测试研究了二次散射作用范围,验证了局部二次散射作用区域的合理性.利用二次散射的局部作用特征,类比散射场一阶Born近似的反演框架,我们尝试求解基于局部二阶Born近似下的非线性反问题.
利用一阶泰勒近似,可以将圆形邻域Bx内的散射点y (见图 6) 的散射位势表示为
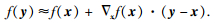
|
(22) |
此时,方程 (8) 二阶Born近似 (Us)2nd可以合理地近似表示成:
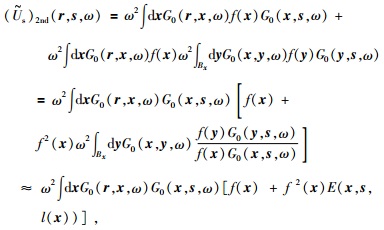
|
(23) |
其中:
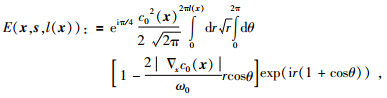
|
(24) |
这里E只与背景模型速度以及局部二次散射系数因子l有关.
(23) 式是基于局部二次散射的二阶Born近似表达式,这个表达式类似于一阶Born近似 (单散射) 表达式.推导出这个表达式的目的是将二阶Born近似表达成类似声波GRT的结构,进一步可以通过逆GRT偏移反演出关于散射位势f的组合二次项,实现非线性反演.其中的传导因子E则可以看成是二次扰动的加权项,是局部二次散射假设的核心所在,具体推导过程见 (Ouyang et al., 2015).
对方程 (23) 采用前面GRT线性反演思路,可以得到在局部二阶Born近似下的扰动量f的二次方程式为
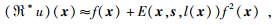
|
(25) |
此处x是成像点,ℜ*是逆GRT算子,u取为
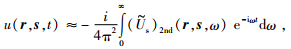
|
(26) |
通过求解方程 (25) 可以得到基于二阶Born近似的逆散射问题的渐近解f(x).
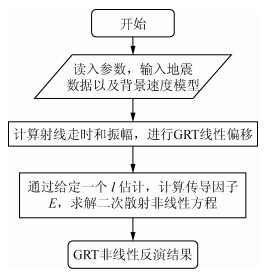
根据上面建立的基于二阶Born近似GRT非线性反演框架,给出流程图如下.
|
图 8 GRT非线性反演方法流程图 Figure 8 Flow chart of GRT nonlinear inversion method |
这里的地震数据通常是非线性的,背景速度可以为常数也可以是变化的.相比传统线性偏移反演,我们仅仅增加了计算传导因子E和求解非线性方程的过程.整个反演框架是直接进行的,不需要任何迭代步骤.只在计算传导因子的阶段需要给出对参数l的一个估计.
首先我们沿用上节的5个不同扰动的层状模型,分别对这些模型的二阶Born合成数据,进行GRT非线性偏移反演,验证我们的非线性反演框架的可行性.为了分析线性和非线性方法对界面振幅反演的准确度和保幅情况,我们抽取各偏移反演剖面中界面对应位置的振幅,归一化后进行对比.
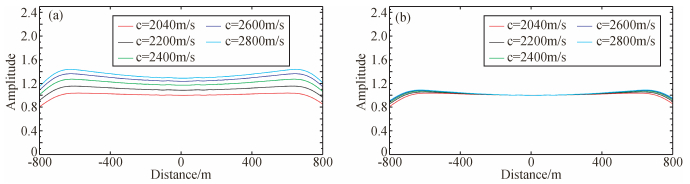
如图 9,图 9a是5个不同速度扰动模型的GRT线性反演剖面的界面振幅归一化曲线图.图中可以看到,随着扰动量逐渐增大,GRT线性反演结果逐渐偏离真实值1(红色实线).这表明基于一阶Born近似线性反演理论只适用于小扰动变化的介质模型.图 9b则是不同扰动模型的二阶Born数据GRT非线性反演的扰动界面振幅归一化曲线图.可以看到,对不同扰动大小的二阶Born数据进行GRT非线性反演,都能获得比较准确的振幅.我们统计非线性反演中参数l值的大小来分析l的变化规律.小扰动 (c=2040 m/s) 情形下,线性反演结果基本准确,以该准确结果为标准,对不同速度扰动模型进行非线性反演.上节局部二次散射效应分析可知,二次散射强度基本在l > 0.15后保持稳定.由表 1可以看到,l值分布从0.190到0.265,随扰动速度增大逐渐变小.二阶Born近似数据的非线性反演结果验证了上节讨论的局部二次散射特征,表明了我们的反演框架是比较合理的.
|
图 9 不同扰动模型二阶Born数据GRT线性反演和非线性反演界面振幅规一化曲线图 (a) GRT线性反演;(b) GRT非线性反演. Figure 9 Comparison of normalized inverted amplitudes from GRT linear and nonlinear inversion with 2nd order Born data from different perturbation models (a) GRT linear inversion; (b) GRT nonlinear inversion. |
|
|
表 1 不同程度扰动模型二阶Born数据非线性反演值l表 Table 1 The l value of nonlinear inversion with 2nd Born data from different perturbation models |
本文前面推导了散射波场一阶、二阶Born近似表达式,并通过单界面层状模型测试从正演模拟的角度验证了二阶Born近似的准确度.通过论证二次散射合理区域,建立了基于二阶Born近似的非线性反演框架,并用简单模型的二阶Born近似数据验证了反演框架与正演过程能保持吻合.本节利用单界面层状模型和复杂SEG/EAGE盐丘模型的合成数据测试非线性反演方法的适用性.首先我们沿用上节中的5个不同速度扰动层状模型的解析合成数据,分别进行线性和非线性反演.
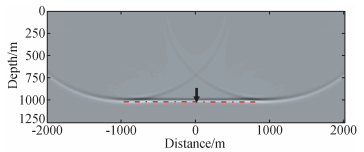
图 10是以40%速度扰动为例的层状模型解析数据GRT线性偏移成像剖面图,界面的成像比较准确.注意到在单炮有限孔径下,最大偏移距椭圆等时面不能完全叠加,界面成像两端椭圆画弧现象很明显.5个不同扰动模型的数据经过GRT线性偏移反演都能得到类似的偏移成像剖面图.分别抽取这些偏移剖面的中间道集在界面处 (黑色箭头) 反演振幅,分析不同速度扰动线性反演结果随扰动变化的规律.GRT线性偏移反演得到的散射位势估计与实际模型的散射位势是存在系统误差的,我们选择小扰动模型线性反演结果对大扰动模型进行标定,归一化后可以给出各扰动模型线性反演的误差.抽取不同扰动模型线性偏移反演剖面中间道集在界面处的振幅F与真实散射位势f,定义GRT线性误差因子fac=abs (F/f),比较可得表 2.
|
图 10 40%扰动模型反射数据GRT线性偏移成像剖面图 Figure 10 GRT linear migration imaging section with analytical reflection data from 40% perturbation model |
|
|
表 2 不同程度扰动模型GRT线性反演振幅误差表 Table 2 GRT Linear inversion amplitude error with different perturbation models |
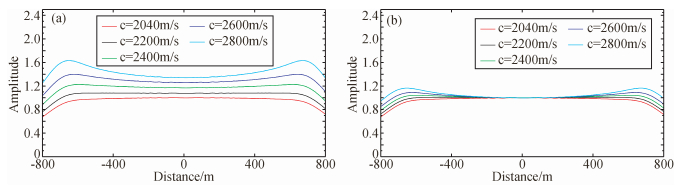
由表 2可以看到,随着速度扰动量δc变大,散射位势真值f增强,线性反演误差因子fac逐渐增大,这说明线性反演结果随着扰动变大偏离真实值.从Born近似线性单散射适合小扰动的经典假设出发,我们认为2%扰动模型的结果是比较准确的,将其对应的误差因子视为系统误差并以此为标准进行归一化,得到不同扰动下GRT线性反演误差因子的归一化值,可以看出,随着扰动增大,误差因子逐渐偏离‘1’,说明了在大扰动情形下,线性反演误差增大,反演值并不可靠.为了分析GRT线性和非线性方法对界面振幅反演的准确度和保幅情况,我们抽取各扰动模型的线性偏移反演剖面中界面对应位置 (图 10红色虚线) 的振幅曲线进行对比.图 11是不同扰动模型解析合成数据线性及非线性反演剖面的界面振幅归一化曲线.
|
图 11 不同扰动模型解析合成数据GRT线性反演和非线性反演界面振幅归一化曲线图 (a) GRT线性反演;(b) GRT非线性反演. Figure 11 Comparison of normalized inverted amplitudes from GRT linear and nonlinear inversion with analytical synthetic data from different perturbation models (a) GRT linear inversion; (b) GRT nonlinear inversion. |
图 11a可以看到,与二阶Born数据类似,随着扰动量逐渐增大,GRT线性反演结果逐渐远离真实值.图 11b则是GRT非线性反演的扰动界面振幅规则化曲线图.可以看出,对不同扰动大小的解析合成数据进行GRT非线性反演,都能获得比较准确的振幅.表 3给出了不同速度扰动的单界面模型解析合成数据在二次非线性反演中的l值参数.表中显示,l值变化与上节二阶Born数据非线性反演l值的变化基本相似,但数值上还是有所差异,这是因为理论合成的二阶Born数据只包括一次散射和二次散射作用,与实际的解析数据相比仍旧是有误差的,可以看到l值随扰动速度增大而变小.
|
|
表 3 不同程度扰动模型解析合成数据非线性反演l值表 Table 3 l value of nonlinear inversion with analytical reflection data from different perturbation models |
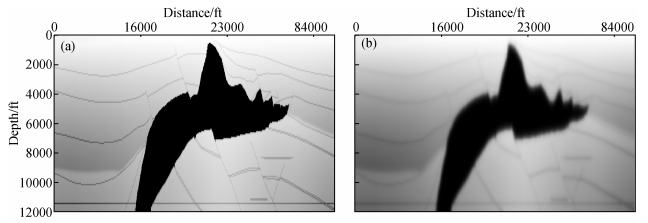
为了验证GRT非线性反演对于复杂模型的适用性,我们用SEG/EAGE盐丘模型测试了该算法.图 12a是盐丘的真实速度模型,图 12b则是光滑背景速度模型.模型横向网格节点数649,横向网格间距80 ft,长51920 ft,纵向网格节点数300,纵向网格间距40 ft,深12000 ft.该模型中部含有高速盐丘,且有三套大断层和若干微幅构造,盐下成像难度较大.本文采用共计326炮激发,固定左侧排列接收,震源函数选择最大频率45 Hz的雷克子波,采样时间4 s,采样间隔4 ms.利用该模型的FD有限差分数据检测本文GRT非线性反演算法的应用效果.
|
图 12 SEG/EAGE盐丘模型 (a) 实际模型;(b) 光滑模型. Figure 12 Velocity profile of SEG/EAGE salt model (a) True model; (b) Smoothed model. |
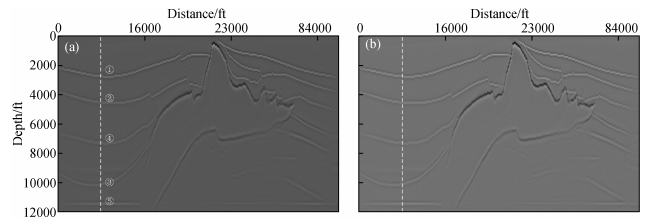
图 13是对盐丘模型FD (Finite Deference) 合成数据分别进行GRT线性和非线性反演的散射位势剖面.图 13a为GRT线性偏移反演剖面,图 13b是基于一个平均估计的l值 (l=0.215) 的非线性反演剖面.可以看到,线性和非线性保幅反演对模型主要的结构成像都是比较准确的,仅在高速盐丘体下方,断层界面成像效果不理想.我们选择第100道 (图中白色虚线位置) 分析比较两种方法对振幅估计的准确度.该道对应背景速度随深度层位编号①②③④⑤依次增大,在界面处速度有局部突跳,局部速度扰动都在15%左右,真实散射位势 (图 14红色实线) 变化则有所区别,浅层第①层和第②层界面散射位势较强,深部三个界面则相对较弱,反演结果见图 14.
|
图 13 SEG/EAGE盐丘模型线性和非线性散射位势反演剖面 (a) 线性反演剖面;(b) 非线性反演剖面. Figure 13 Inverted scattering potential section from linear and nonlinear approaches for SEG/EAGE salt model (a) Linear inversion; (b) Nonlinear inversion. |
|
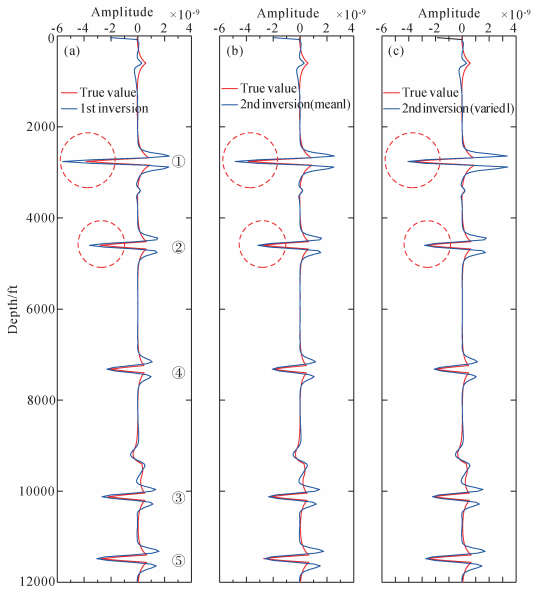
图 14 SEG/EAGE盐丘模型线性和非线性散射位势反演剖面单道振幅曲线对比图 (a) 线性反演振幅与真实振幅曲线对比图;(b) 非线性反演振幅与真实振幅曲线对比图 (一个平均估计l);(c) 非线性反演振幅与真实振幅曲线对比图 (变化l). Figure 14 Comparison of inverted scattering potential traces from linear and nonlinear approaches at location of the red line in Fig. 13 (a) True amplitude and linear inversion amplitude; (b) True amplitude and nonlinear inversion amplitude with an average estimation of l; (c) True amplitude and nonlinear inversion amplitude with different estimations of l. |
图 14a为GRT线性反演剖面第100道振幅曲线 (蓝色实线) 与实际模型散射位势真值 (红色实线) 对比图,注意到红色虚线圈内,可以看到浅层第①、②层界面线性反演误差较大,深层三个界面误差则比较小.图 14b是基于二阶Born近似的GRT非线性反演界面振幅曲线 (蓝色实线) 与实际模型散射位势 (红色实线) 对比图,在非线性反演中我们选择了一个平均估计下的常数l值 (l=0.215),可以看到各界面反演值的准确度都有明显提高.图 14c图则是我们考虑不同散射位势强度给定相应的l值参数 (见表 4) 进行非线性反演与真实散射位势值曲线的对照图,可以看到反演振幅曲线基本与真实曲线重合,各界面都能得到准确反演.在表 4中,δc是对应层位速度扰动百分比,c是对应层位的实际扰动速度.从l值分布可以看到,在复杂盐丘模型试验中,非线性反演l值基本扰动速度增大而变小,这与简单常背景层状模型结果保持一致. SEG/EAGE盐丘模型试验结果说明本文的GRT非线性反演对于变化背景的复杂模型仍然适用,在获得良好的结构成像的同时可以得到更为准确的反演估计,值得一提的是,我们的非线性反演是在线性反演基础之上求解一个传导因子积分和二次方程,并没有明显增加额外的计算量.
|
|
表 4 SEG/EAGE盐丘模型参数及非线性反演l值表 Table 4 Model parameters and l value of nonlinear inversion with SEG/EAGE salt model |
为了克服线性反演弱扰动的限制条件,本文讨论的二阶Born近似利用了散射场Born级数中的前两项,考虑了强扰动下散射波的二次散射效应,比传统单散射Born近似更为准确,适应速度强扰动模型.基于二阶Born近似积分方程及二次散射作用局部收敛的认识,本文基于局部二次散射下的二阶Born近似,推导了GRT非线性反演方法,通过单界面层状模型和SEG/EAGE盐丘模型得出了一些结论:
(1) 单界面层状模型正演模拟测试表明,在弱扰动情况下,单散射一阶Born近似可以较为准确地模拟散射波场,但随着速度扰动超过10%,波场振幅误差逐渐增大.在考虑二次散射作用下,二阶Born近似在速度扰动40%内都能准确地模拟散射场.
(2) 单界面层状模型的二次散射分析表明,常背景速度下,二次散射作用区域基本在主散射点为中心的圆域内,其半径为一个主波长左右,超过这一区域,二次散射强度保持稳定不变,即二次散射影响可忽略.
(3) 单界面层状模型和复杂盐丘SEG/EAGE模型的反演结果表明,随着扰动增强,GRT线性反演振幅误差越大,而应用本文的GRT非线性反演,对强扰动模型仍然可以获得比较准确的振幅.
(4) 在GRT非线性反演中,根据参数l的分布特征,本文的结论是,在进行非线性反演时,我们选取了一个背景介质,这个背景对应存在一个参考二次散射区域,区域半径ε由背景速度和参考l值决定.在层状常背景速度模型试验中,背景速度一定,二次散射区域即确定,在对不同程度扰动的模型进行非线性反演时,散射点扰动速度越大,l值越小,l值与散射点速度成反关系.复杂SEG/EAGE中的结果也验证了这个结论.在进行非线性反演中,我们要分析模型速度大小选择合适的l值.
5.2本文是在常密度声波条件下推导出的非线性反演方法,在模型试算中取得一定的效果,尚未应用到弹性, 黏弹性,各向异性,多参数等复杂介质情况,这些是我们下一步待研究的问题.
致谢 感谢审稿专家提出的修改意见和编辑部的支持!| [] | Beylkin G. 1984. The inversion problem and applications of the generalized Radon transform[J]. Communications on Pure and Applied Mathematics, 37(5): 579–599. DOI:10.1002/(ISSN)1097-0312 |
| [] | Beylkin G. 1985. Imaging of discontinuities in the inverse scattering problem by inversion of a causal generalized Radon transform[J]. Journal of Mathematical Physics, 26(1): 99–108. DOI:10.1063/1.526755 |
| [] | Beylkin G, Burridge R. 1990. Linearized inverse scattering problems in acoustics and elasticity[J]. Wave Motion, 12(1): 15–52. DOI:10.1016/0165-2125(90)90017-X |
| [] | Bleistein N. 1987. On the imaging of reflectors in the earth[J]. Geophysics, 52(7): 931–942. DOI:10.1190/1.1442363 |
| [] | Bleistein N, Cohen J K, Stockwell J W Jr. 2001. Mathematics of Multidimensional Seismic Imaging, Migration, and Inversion[M]. New York: Springer. |
| [] | Clayton R W, Stolt R H. 1981. A born-WKBJ inversion method for acoustic reflection data[J]. Geophysics, 46(11): 1559–1567. DOI:10.1190/1.1441162 |
| [] | Coates R T, Charrette E E. 1993. A comparison of single scattering and finite difference synthetic seismograms in realizations of 2-D elastic random media[J]. Geophys. J. Int., 113(2): 463–482. DOI:10.1111/gji.1993.113.issue-2 |
| [] | Cohen J K, Bleistein N. 1977. An inverse method for determining small variations in propagation speed[J]. SIAM Journal on Applied Mathematics, 32(4): 784–799. DOI:10.1137/0132066 |
| [] | Cohen J K, Bleistein N. 1979. Velocity inversion procedure for acoustic waves[J]. Geophysics, 44(6): 1077–1087. DOI:10.1190/1.1440996 |
| [] | French W S. 1974. Two-dimensional and three-dimensional migration of model-experiment reflection profiles[J]. Geophysics, 39(3): 265–277. DOI:10.1190/1.1440426 |
| [] | Fu L G, Yang H Z, Mu Y G. 1998. Volume integral equation method for scattering problems of inhomogeneous media[J]. Acta Mechanica Sinica (in Chinese), 30(4): 488–494. |
| [] | Fu L Y. 2010. Born-series dispersion equations and Born-Kirchhoff propagators[J]. Chinese Journal of Geophysics (in Chinese), 53(2): 370–384. DOI:10.3969/j.issn.0001-5733.2010.02.015 |
| [] | Gardner G H F, French W S, Matzuk T. 1974. Elements of migration and velocity analysis[J]. Geophysics, 39(6): 811–825. DOI:10.1190/1.1440468 |
| [] | Gray S H. 2014. Seismic imaging and inversion:What are we doing, how are we doing, and where are we going?[C].//84th Annual International Meeting, SEG. Expanded Abstracts, 4416-4420. |
| [] | Ikelle L T. 1999. Using even terms of the scattering series for deghosting and multiple attenuation of ocean-bottom cable data[J]. Geophysics, 64(2): 579–592. DOI:10.1190/1.1444565 |
| [] | Ikelle L T, Amundsen L, Yoo S. 2002. An optimization of the inverse scattering multiple attenuation method for OBS and VC data[J]. Geophysics, 67(4): 1293–1303. DOI:10.1190/1.1500392 |
| [] | Jia Y G, Li X F, Zhang M G, et al. 2005. Some important progress in research upon seismic wave scattering[J]. Progress in Geophysics (in Chinese), 20(4): 939–944. DOI:10.3969/j.issn.1004-2903.2005.04.009 |
| [] | Keys R G. 1989. Polarity reversals in reflections from layered media[J]. Geophysics, 54(7): 900–905. DOI:10.1190/1.1442718 |
| [] | Li Z C. 2014. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting (in Chinese), 49(1): 1–21. |
| [] | Liu F, Weglein A B, Innanen K A, et al. 2005. Extension of the non-linear depth imaging capability of the inverse scattering series to multidimensional media:Strategies and numerical results[C].//9th International Congress of the Brazilian Geophysical Society & EXPOGEF. Salvador, Bahia, Brazil, 2257-2261. |
| [] | Mao W J, Ouyang W, Li X L. 2013. Nonlinear migration inversion with second-order Born approximation[C].//75th EAGE Conference & Exhibition incorporating SPE EUROPEC 2013. Extended Abstracts. |
| [] | Matson K, Weglein A B. 1996. Removal of elastic interface multiples from land and ocean bottom data using inverse scattering[C].//Annual Meeting Abstracts, Society of Exploration Geophysicists. Extended Abstracts, 1526-1530. |
| [] | Matson K H. 1996. The relationship between scattering theory and the primaries and multiples of reflection seismic data[J]. Journal of Seismic Exploration, 5: 63–78. |
| [] | Miller D, Oristaglio M, Beylkin G. 1984. A new formalism and an old heuristic for seismic migration[C].//54th Annual International Meeting, SEG. Expanded Abstracts, 704-707. |
| [] | Miller D, Oristaglio M, Beylkin G. 1987. A new slant on seismic imaging:Migration and integral geometry[J]. Geophysics, 52(7): 943–964. DOI:10.1190/1.1442364 |
| [] | Ouyang W, Mao W J, Li X L. 2015. Approximate solution of nonlinear double-scattering inversion for true amplitude imaging[J]. Geophysics, 80(1): R43–R55. DOI:10.1190/geo2014-0123.1 |
| [] | Raz S. 1981a. Direct reconstruction of velocity and density profiles from scattered field data[J]. Geophysics, 46(6): 832–836. DOI:10.1190/1.1441220 |
| [] | Raz S. 1981b. Three-dimensional velocity profile inversion from finite-offset scattering data[J]. Geophysics, 46(6): 837–842. DOI:10.1190/1.1441221 |
| [] | Shaw S A, Weglein A B, Foster D J, et al. 2004. Isolation of a leading order depth imaging series and analysis of its convergence properties for a 1D acoustic medium[J]. Journal of Seismic Exploration, 13(2): 99–120. |
| [] | Weglein A B. 1999. How can the inverse-scattering method really predict and subtract all multiples from a multidimensional earth with absolutely no subsurface information?[J]. The Leading Edge, 18(1): 132–136. DOI:10.1190/1.1438142 |
| [] | Weglein A B. 2009. A new, clear and meaningful definition of linear inversion:Implications for seismic inversion of primaries and removing multiples[C].//79th Annual International Meeting, SEG. Expanded Abstracts, 3059-3063. |
| [] | Weglein A B, Araújo F V, Carvalho P M, et al. 2003. Inverse scattering series and seismic exploration[J]. Inverse Problems, 19(6): R27. DOI:10.1088/0266-5611/19/6/R01 |
| [] | Weglein A B, Gray S H. 1983. The sensitivity of Born inversion to the choice of reference velocity:A simple example[J]. Geophysics, 48(1): 36–38. DOI:10.1190/1.1441404 |
| [] | Weglein A B, Gasparotto F A, Carvalho P M, et al. 1997. An inverse-scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 62(6): 1975–1989. DOI:10.1190/1.1444298 |
| [] | Weglein A B, Foster D J, Matson K H, et al. 2002. Predicting the correct spatial location of reflectors without knowing or determining the precise medium and wave velocity:Initial concept, algorithm and analytic and numerical example[J]. Journal of Seismic Exploration, 10(4): 367–382. |
| [] | Yin J J, Liu X W, Li W H. 2005. The view of seismic wave scattering theory and its applications[J]. Progress in Geophysics (in Chinese), 20(1): 123–134. DOI:10.3969/j.issn.1004-2903.2005.01.024 |
| [] | Zhang H Y, Weglein A B. 2009a. Direct nonlinear inversion of 1D acoustic media using inverse scattering subseries[J]. Geophysics, 74(6): WCD29–WCD39. DOI:10.1190/1.3256283 |
| [] | Zhang H Y, Weglein A B. 2009b. Direct nonlinear inversion of multiparameter 1D elastic media using the inverse scattering series[J]. Geophysics, 74(6): WCD15–WCD27. DOI:10.1190/1.3251271 |
| [] | 符力耘, 杨慧珠, 牟永光. 1998. 非均匀介质散射问题的体积分方程数值解法[J]. 力学学报, 30(4): 488–494. |
| [] | 符力耘. 2010. Born序列频散方程和Born-Kirchhoff传播算子[J]. 地球物理学报, 53(2): 370–384. DOI:10.3969/j.issn.0001-5733.2010.02.015 |
| [] | 贾豫葛, 李小凡, 张美根, 等. 2005. 地震波散射研究的若干重要进展[J]. 地球物理学进展, 20(4): 939–944. DOI:10.3969/j.issn.1004-2903.2005.04.009 |
| [] | 李振春. 2014. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 49(1): 1–21. |
| [] | 尹军杰, 刘学伟, 李文慧. 2005. 地震波散射理论及应用研究综述[J]. 地球物理学进展, 20(1): 123–134. DOI:10.3969/j.issn.1004-2903.2005.01.024 |
 2017, Vol. 32
2017, Vol. 32


