信息预测理论是翁文波院士于20世纪80年代所创立,他认为预测大致上可分为两类:一类是以体系中各元素共性为依据的统计预测;另一类是以体系中各元素的特性为依据的信息预测 (翁文波等,1996).同时,他又把客观存在的事件划分为常态子集和异态子集两类,前者中的事件是一般、经常性等有代表性的事件,以数学期望、方差、均值等要素为统计量,应用概率统计原理和方法进行预测,但是,这类事件通常需要大量样本的支持,因此对于重大天灾等 (诸如地震) 小概率事件的预测往往难于进行.而后者中的事件是异常、例外等事件,它们的主要要素是信息,因此需要应用信息论原理和方法取得信息并进行预测.
可公度法作为信息预测方法中的一种,由翁文波院士首先将其应用到了预测科学中,并曾利用可公度性信息系对1976年的唐山7.8级大地震和1982年的华北干旱等现象做过成功的预测 (翁文波,1984),为重大自然灾害预测开辟了一条崭新的道路,之后陆续被国内外学者在自然灾害预测中广泛使用 (门可佩和王元兴,1999; 杨丽萍和王小平,2001;龙小霞等,2006;门可佩, 2009;蔡金凤等,2009;白晶等,2010;李双双和延军平,2012;吴梦初和延军平,2013;石玥和曹广超,2013;Hu et al., 2013; 刘铮瑶等,2014;陈爱娟等,2014;马兰等,2014;唐宝琪等,2015;Su and Hui, 2015).自1998年张北6.2级地震后,华北地区6级地震平静时间长达18年之久,统计分析显示华北地区随时有发生6级地震的危险.鉴于此,本文应用华北地区1900年以来的MS≥6.0级地震资料,基于可公度分析的基础上,探讨了该区地震活动的发展趋势和可能的发震地点,研究结果可为华北地区地震大形势研究和中长期预测预警工作提供参考.
1 资料与方法 1.1 资料与来源通常,华北地区大体上是指贺兰山以东,燕山、阴山以南,秦岭—大别山以北以及黄海以西的地区,构造上属于华北板块.而在地震资料的分析上有时也采用“大华北”的概念,即向西包括了鄂尔多斯地台以及银川—河套断陷盆地;向东扩展到黄海、渤海等区域.山西地震带、河北平原地震带及郯庐地震带构成了大华北地区三条北北东向地震活动带 (尹相好等,2011).本文研究对象为大华北地区 (34°~42°N, 110°~126°E)1900年以来的MS≥6.0级地震 (表 1),数据主要来源于中国地震台网中心的地震数据管理与服务系统(http://www.csndmc.ac.cn/newweb/index.jsp)以及中国历史地震目录库CHINA5.
|
|
表 1 1900年以来华北地区MS≥6.0地震目录 Table 1 The catalogue of MS≥6.0 earthquakes in north China from 1900 |
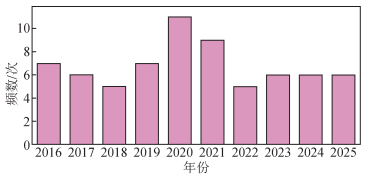
可公度性 (commensurability) 源于天文学,是自然界中客观存在的现象,表示自然界事物之间的一种秩序,是自然现象周期性的一种客观的外在反映,是周期性的扩张 (翁文波, 1981, 1984).可公度的计算方法包括三元、四元、五元可公度法.在可公度趋势判断的过程中,优选三元法,其次参考四元、五元可公度法.在预测结果中首选临近年份中频数最多的或是几个元计算结果中均有计算结果的年份为最终结果,最后综合得出比较合理的结论.为便于计算,将统计时间内发生的地震编为一组,并以组内最后一次地震计算时间.在计算过程中如果在同一年发生两次或多次地震通常按一次计算.可公度信度可以用概率等方法加以估算,如果实测数列的可公度数平均值为m,预测序列的可公度数mP,则发布预测一般选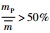
在时间对称性方面,本文利用三元、四元和五元可公度法进行计算,得出预测年份;再利用蝴蝶结构图和可公度结构系对预测年份进行验证,算出预测年份的随机概率.在空间对称性方面,主要根据地震事件的经纬度坐标信息寻找其空间结构和迁移规律,进而确定其空间对称的走向趋势,初步预测下次地震的大致方位.
2 时间对称性及趋势分析 2.1 可公度性分析常用的可公度计算方法包括三元、四元和五元可公度法,其对应的公式为 (翁文波,1981):
三元:N=A+(B-C).
四元:N=A+B+(C-D),亦可写作:ΔX=A+B-C-D,(则N=最后年份+ΔX).
五元:N=A+(B-D)+(C-E).
公式中A、B、C、D、E为表 1中的历史地震年份,N为预测年份.
2.1.1 三元可公度预测由表 1,1900年以来华北地区发生MS≥6.0级地震的年份有1910、1917、1922、1929、1932、1937、1944、1945、1948、1966、1967、1969、1975、1976、1977、1989和1998年.则可构建可公度集X={1910,1917,1922,1929,1932,1937,1944,1945,1948,1966,1967,1969,1975,1976,1977,1989,1998},即χ1=1910,χ2=1917,…,χ17=1998.因此,利用三元可公度计算公式可以得到各个样本的三元可公度值,由表 3最后一列可见,每个历史地震年份都能写出两组以上三元可公度式子,即满足m>1,说明样本具有可公度信息,可以据此进行预测.为了进一步验证方法的可行性,首先使用1989年前 (包括1989年) 的地震年份资料对随后可能发生的地震进行预测,结果如表 2所示.
|
|
表 2 1990-1999年地震频数预测 Table 2 Prediction of earthquake frequency from 1990 to 1999 |
从表 2中发现,在1989年之后的未来十年预测结果中,可公度频数较大的三个年份分别为1996、1997和1998.也就是说,从三元可公度的结果看,1996、1997和1998这三年中发生6级以上地震的可能性较大.事实上1998年的确发生了预期中的6级地震 (1998年1月10日张北6.2地震),如表 1.那么1996年和1997年频数也相对较高,却没有6级地震对应,是否为虚报呢?由中国历史地震目录库CHINA5可知,1996年5月3日内蒙包头发生6.4级地震,震中位于北纬40.7度,东经109.6度,与表 1中研究所用地震目录的统计范围 (34°~42°N, 110°~126°E) 相距不到50km.1997年频数高或许也对应了1998年1月10日的张北6.2级地震,因为本文侧重讨论的是中长期地震趋势预测,故在构建公度集时忽略了地震发生月份和日期的影响,由此导致误差范围为±1年.
对历史地震年份的检验结果表明,华北地区M≥6.0级地震年份不仅具有较好的可公度性,而且在地震年份的外推预测上也具有一定的可信度,因此可以据此进行后续地震的预测.图 1为华北地区未来10年的三元可公度预测结果,从中可以看出,2020年和2021年的可公度值较大,分别为11和9.而由表 3可知,1900年以来华北地区历史年份的平均公度值m为14,因此2020年mP/m =78.6% > 50%,2021年mP/m =64.3% > 50%,均满足发布预测的条件.其余8年的预测结果,其公度值依次为7、6、5、7、5、6、6、6(图 1),显然它们的公度值与历年公度均值14相比均不大于50%,因此不满足发布预测的条件.
|
|
表 3 三元可公度信息计算结果表 Table 3 The ternary commensurability value of the samples |
|
图 1 三元可公度外推频数 Figure 1 The extrapolate frequency of ternary commensurability |
根据上文的四元可公度式 (ΔX=A+B-C-D,N=最后年份+ΔX),可公度集X={1910,1917, 1922, 1929, 1932, 1937, 1944, 1945, 1948, 1966, 1967, 1969, 1975, 1976, 1977, 1989,1998}的四元预测结果显示,未来10年同样有2个年份的公度值较高,分别为2020和2021年,其公度值分别为88和74,如表 4.
|
|
表 4 四元可公度计算结果 Table 4 The quarternary commensurability value of the samples |
此外,五元可公度预测的结果显示未来10年2019个2020年的公度值相对较高,分别为2112和2232,具体结果略.
综上所述,华北地区6级地震三元可公度预测结果显示频数较高的年份为2020和2021年,四元可公度频数较高的年份同样为2020和2021年,五元可公度预测结果频数较高的年份为2019和2020.因此综合分析认为,2020和2021年华北地区发生MS≥6.0级地震的趋势明显.
2.2 蝴蝶结构图分析蝴蝶结构是对可公度方法的推广,是自然灾害时间对称性结构的体现,即时间序列中存在等时间间隔的特点 (Cristo et al., 2011; Arlt, 2009).其可公度特征是不同长度的周期叠加后表现出的混合规律,所以它反映的是多变量间的一种周期性共振变化,其主要解决可公度计算中两年份信号都较强时如何抉择的问题.图 2为华北地区MS≥6.0级地震蝴蝶结构图,右侧标注的数字 (1a、7a、8a、12a、22a、23a、31a、32a) 为间隔年数,即出现4次或以上的主周期.从中发现,能够与2020年衍生的“蝴蝶结构”套合的主周期有22a和31a两种,与2021年有关的周期只有32a一种.可见2020年华北地区发生MS≥6.0级地震的信号比2021年强.

|
图 2 1900年以来华北地区MS≥6.0级地震时间序列蝴蝶结构图 Figure 2 The butterfly structural drawing of MS≥6.0 earthquakes in North China since 1900 |
蝴蝶结构的随机性概率定义为T=M/N,不漏报的置信水平为 (1-a)=M/(N+1),其中T为灾害事件时间序列中预测年份发生的可能概率,N为总灾害事件的次数,M为参与实际预测的灾害次数,即和主周期关联的年份统计 (唐宝琪等,2015;延军平等, 2010, 2011).对于上述时间序列{X}有N=17,M2020=14,M2021=8.因此,计算得出,2020和2021年华北地区发生MS≥6.0级地震的随机性概率为82.4%和47.1%,不漏报的置信水平为77.8%和44.4%.因此,依据蝴蝶结构图判断2020华北地区有发生MS≥6.0级地震的可能,不漏报置信水平为77.8%.
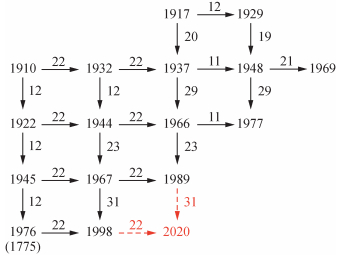
2.3 可公度结构系图分析可公度结构系是自然灾害时间对称性结构的另一种体现,主要表达灾害事件的相互次序以及时间的韵律特征 (翁文波,1984).具有极工整规范的网络特征与韵律结构,是依据时间对称周期特点绘制出的自然灾害事件向量图.图 3为1900年以来华北地区MS≥6.0地震的可公度结构系图.如图 3所示,可公度结构系也是验证可公度法的有效途径之一,它能更清楚直观地展现华北地区MS≥6.0级地震的发生在时间上具有显著的对称性,其中最显著的对称周期为22和23年,这一结果刚好与宋治平等 (2013)研究发现的中国大陆及邻区强震存在显著23年尺度的特有周期相吻合.同时也可以得出与上文同样的预测结果,即2020年华北地区存在发生MS≥6.0级地震的可能.
|
图 3 华北地区MS≥6.0级地震可公度结构图 (箭头附近数字代表间隔年数) Figure 3 The commensurability structural system of MS≥6.0 earthquakes in North China since 1900 (The figures near the arrows represent the interval time) |
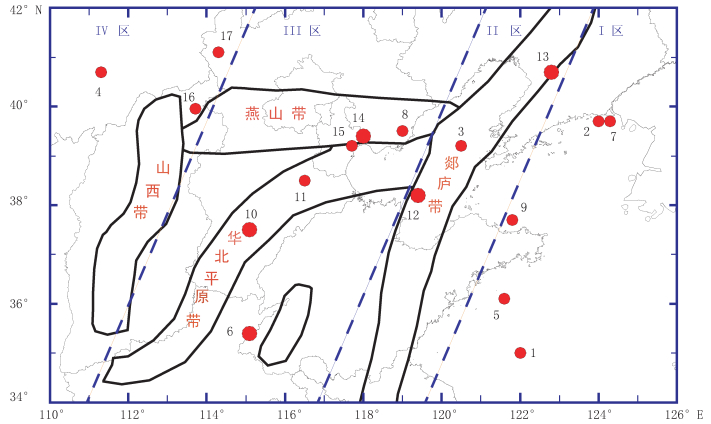
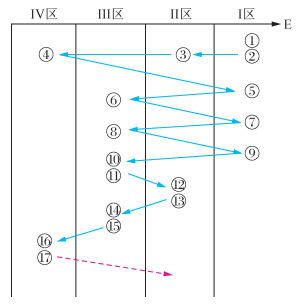
依据华北地区地质构造和主要地震带 (尹相好等,2011),再结合表 1中华北地区1900年以来历次6.0级地震的震中分布图,可将华北地区由东至西依次分成4个小的区域:黄海和渤海海域、郯庐带及其附近地区、华北平原地区和晋冀蒙交界地区,即图 4中的Ⅰ区、Ⅱ区、Ⅲ区和Ⅳ区.为了更直观的展示上述地震的空间对称性,特绘制了简化后的四个分区的示意图 (图 5).由图 5可以看出,①~⑨ 号地震基本上以Ⅱ区为中心轴左右对称,即1900~1950年期间,华北地区的MS≥6.0级地震主要以郯庐带为中心轴东西对跳.也就是说,大部分6.0级以上地震首先发生在郯庐带以东的黄海和海域,之后跳迁到郯庐带以西的华北平原地区 (③、④ 号地震例外).但1966年邢台7.2级地震 (图中⑩ 号) 开始,华北地区6.0级地震的主要活动地区迁移到郯庐带及其以西地区,且有在各区成对发生的现象.如Ⅲ区的⑩ 和B11、B14和B15号地震,即1966年邢台7.2级和1967年河北河间6.3级地震为一对,1976年唐山7.8级和1977年天津宁河6.2级地震为一对,B12和B13、B16和B17号地震分别为Ⅱ区和Ⅳ区的成对地震.由上述四组成对地震的发生规律来看,成对地震发生之后通常由东至西或由西至东顺次在Ⅱ区、Ⅲ区和Ⅳ区迁移.最后一组成对地震 (1989年大同6.1和1998年张北6.2) 位于晋冀蒙交界地区 (Ⅳ区),因此,后续华北地区MS≥6.0级地震向东迁移的可能性较大,即迁移到Ⅲ区或Ⅱ区.同时,由华北地区6.0级地震的空间分布 (图 4) 可进一步推测,未来华北地区6.0级地震发生在Ⅲ区和Ⅱ区交界区域的可能性更大,即图 4所示的郯庐带和华北平原带交汇地区及其附近——环渤海地区.
|
图 4 华北地区主要地震带与表 1中MS≥6.0级地震空间分布图 (震中附近数字为表 1中地震序号) Figure 4 The main earthquake belts in north China and MS≥6.0 earthquake spatial distribution in table 1 (The figures near the epicenter represent the seismic serial number in table 1) |
|
图 5 华北地区简化分区及6.0级地震空间对称示意图 (图中带圈数字为表 1中地震序号) Figure 5 The schematic diagram of the partition and space symmetry of MS6.0 earthquakes in north China (The figures represent the seismic serial number in table 1) |
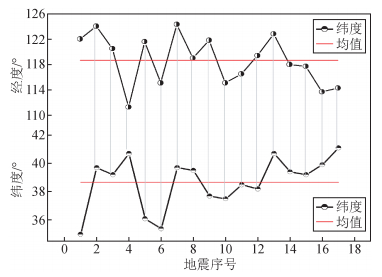
此外,从1900年以来华北地区MS≥6.0级地震经纬向迁移图可看出,华北地区6.0级地震主要以东经118.7度,北纬38.7度为对称轴,除个别年份外,震中经向迁移和纬向迁移具有较好的同步性,即当震中向西迁移时,纬度上则向北迁移;当震中向东迁移时,纬度上则向南迁移,即大体上由西北→东南→西北→东南往复迁移 (图 6).由目前图像,推断下次地震往118.7°E和38.7°N附近迁移的可能性较大,即渤海海峡及其附近地区,和图 4中的预测结果一致.
|
图 6 华北地区MS≥6.0级地震经纬向迁移图 Figure 6 The drawing of longitudinal and latitudinal migration of MS≥6.0 earthquakes in the North China |
本文基于1900年来华北地区MS≥6.0地震资料,利用“可公度法”、“蝴蝶结构图”和“可公度结构系图”对未来华北地区6.0级地震进行了趋势判断,同时分析了6.0级地震的空间分布及迁移规律,基本结论如下:
(1) 1900年以来华北地区MS≥6.0级地震具有较好的“可公度”特征.三元、四元、五元可公度计算显示,2020年和2021年发震信号较强,其中2020年发震的可能性大于2021年.
(2) 华北地区MS≥6.0地震震中空间迁移经纬向呈现明显的同步性和对称性.其中纬向迁移对称轴在38.7°N左右,经向迁移对称轴在118.7°E左右.1900~1950年期间,震中主要以郯庐带为中心轴东西对跳迁移;1966年邢台7.2级地震开始,华北地区6.0级地震的主要活动地区迁移到郯庐带及其以西地区,且有在各区成对发生之后顺次在各区间迁移的现象.由此推测,未来华北地区6.0级地震向郯庐带和河北平原带交汇地区及其附近迁移的可能性较大,即渤海海峡及其附近地区,这一结果与曹凤娟等 (2015)关于南北带与华北块体间的迁移规律得到的研究结果相一致.
4.2将“可公度法”和“蝴蝶结构图”相结合,可提高地震预测的准确性和未来趋势判断的可靠性.尽管如此,数学预测方法应用的毕竟是表象模式,更需要物理机制和方法的配合,因此,只有将可公度方法研究出的规律与物理预测相结合,才能更好地为防震减灾工作服务.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Arlt R. 2009. The butterfly diagram in the eighteenth century[J]. Solar Physics, 255(1): 143–153. DOI:10.1007/s11207-008-9306-5 |
| [] | Bai J, Yan J P, Su K H. 2010. The time-space symmetry and the tendency judgment of future MS ≥ 7 earthquake in Xinjiang[J]. Inland Earthquake, 24(4): 323–329. |
| [] | Cai J F, Shi G N, Wang Y. 2009. Commensurability's application on the forecast of the drought and flood[J]. Journal of Harbin University of Science and Technology, 14(S1): 131–133, 136. |
| [] | Cao F J, Wang L, Li J, et al. 2015. Relevant migration characteristics of strong earthquakes between the North-South Seismic Belt and North China block[J]. Acta Seismologica Sinica, 37(4): 554–564. DOI:10.11939/jass.2015.04.003 |
| [] | Chen A J, Yin S Y, Yan J P. 2014. Space-time symmetry of MS ≥ 5.1 earthquake disasters in Qilian-Liupan mountain seismic belts[J]. China Earthquake Engineering Journal, 36(4): 1126–1130. |
| [] | Cristo A, Vaquero J M, Sánchez-Bajo F. 2011. HSUNSPOTS:A tool for the analysis of historical sunspot drawings[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 73(2-3): 187–190. DOI:10.1016/j.jastp.2009.12.010 |
| [] | Hu H, Han Y B, Su Y J, et al. 2013. Commensurability of earthquake occurrence[J]. Journal of Asian Earth Sciences, 70-71: 27–34. DOI:10.1016/j.jseaes.2013.02.027 |
| [] | Li S S, Yan J P. 2012. Space-time symmetry of MS ≥ 8 earthquake in north-western pacific plate subduction[J]. Progress in Geophysics, 27(3): 960–966. DOI:10.6038/j.issn.1004-2903.2012.03.017 |
| [] | Liu Z Y, Yan J P, Dong Z B. 2014. Earthquake tendency in Iran region based on commensurability[J]. Progress in Geophysics, 29(2): 523–528. DOI:10.6038/pg20140208 |
| [] | Long X X, Yan J P, Sun H, et al. 2006. Study on earthquake tendency in Sichuan-Yunnan region based on commensurability[J]. Journal of Catastrophology, 21(3): 81–84. |
| [] | Ma L, Cao G C, Cao S K. 2014. Spatio-temporal characteristics of strong earthquakes in Turkey since the year 1971[J]. Acta Seismologica Sinica, 36(2): 244–251. |
| [] | Men K P. 2009. Research on earthquake chains and its orderly network structure in Jiangsu-South Yellow Sea region[J]. Chinese Journal of Geophysics, 52(10): 2573–2579. DOI:10.3969/j.issn.0001-5733.2009.10.016 |
| [] | Men K P, Wang Y X. 1999. Esearch on commensurability of medium-strong earthquakes in Jiangsu-South yellow sea region and its prediction[J]. Plateau Earthquake Research, 11(1): 25–31. |
| [] | Shi Y, Cao G C. 2013. he tendency judgment of future MS ≥ 6.0 earthquake in Qinghai:A commensurability-based research[J]. Science Technology and Engineering, 13(35): 10579–10581, 10594. |
| [] | Song Z P, Yin J Y, Xue Y, et al. 2013. The global and sub-zone period characteristics for large earthquakes[J]. Chinese Journal of Geophysics, 56(6): 1868–1876. DOI:10.6038/cjg20130609 |
| [] | Su Y J, Hu H. 2015. Application of commensurability in earthquake prediction[J]. International Journal of Geosciences, 6(6): 619–624. DOI:10.4236/ijg.2015.66049 |
| [] | Wang F Q, Xu S G. 2008. Commensurability for flood over Yangtze river basin with applications to prediction[J]. Journal of Yangtze River Scientific Research Institute, 25(6): 23–27. |
| [] | Weng W B. 1981. Commensurability[J]. Acta Geophysica Sinica, 24(2): 151–154. |
| [] | Weng W B. 1984. Prediction Theory Basis[M]. Beijing: Petroleum Industry Press. |
| [] | Weng W B, Lü N D, Zhang Q. 1996. Prognostics[M]. Beijing: Petroleum Industry Press. |
| [] | Wu M C, Yan J P. 2013. The space-time symmetry of the earthquake disasters (MS ≥ 6.8) in western Yunnan and Myanmar[J]. Plateau Earthquake Research, 25(4): 10–16. |
| [] | Yan J P, Bai J, Su K H, et al. 2011. Research on symmetry and tendency of several major natural disasters[J]. Geographical Research, 30(7): 1159–1168. |
| [] | Yan J P, Yan J H, Bai J, et al. 2010. Discussion on trends of major natural disasters in Shaanxi province and its vicinities based on commensurable method[J]. Journal of Catastrophology, 25(2): 18–20. |
| [] | Yang L P, Wang X P. 2001. Preliminarily discussion on the commensurability of strong earthquakes in Qinghai province and its neighboring areas[J]. Plateau Earthquake Research, 13(2): 14–19. |
| [] | Yin X H, Tian F D, Zhao Q H, et al. 2011. Relative analysis on the active periods of the seismic belts of North China[J]. Earthquake Research in Sichuan(3): 32–36. |
| [] | 白晶, 延军平, 苏坤慧. 2010. 新疆MS ≥ 7地震时空对称性及未来趋势判断[J]. 内陆地震, 24(4): 323–329. |
| [] | 蔡金凤, 石冠男, 王勇. 2009. 可公度方法在旱涝灾害中的应用[J]. 哈尔滨理工大学学报, 14(S1): 131–133, 136. |
| [] | 曹凤娟, 王亮, 李君, 等. 2015. 南北地震带与华北地块强震间的相关迁移[J]. 地震学报, 37(4): 554–564. DOI:10.11939/jass.2015.04.003 |
| [] | 陈爱娟, 殷淑燕, 延军平. 2014. 祁连山-六盘山地震带MS ≥ 5.1地震时空对称性研究[J]. 地震工程学报, 36(4): 1126–1130. |
| [] | 李双双, 延军平. 2012. 西太平洋俯冲带北部地区MS ≥ 8强震时空对称特征[J]. 地球物理学进展, 27(3): 960–966. DOI:10.6038/j.issn.1004-2903.2012.03.017 |
| [] | 刘铮瑶, 延军平, 董治宝. 2014. 基于可公度方法的伊朗地区地震活动趋势判断[J]. 地球物理学进展, 29(2): 523–528. DOI:10.6038/pg20140208 |
| [] | 龙小霞, 延军平, 孙虎, 等. 2006. 基于可公度方法的川滇地区地震趋势研究[J]. 灾害学, 21(3): 81–84. |
| [] | 马兰, 曹广超, 曹生奎. 2014. 1971年以来土耳其强震时空特征研究[J]. 地震学报, 36(2): 244–251. |
| [] | 门可佩. 2009. 江苏-南黄海地区地震链及其有序网络结构研究[J]. 地球物理学报, 52(10): 2573–2579. DOI:10.3969/j.issn.0001-5733.2009.10.016 |
| [] | 门可佩, 王元兴. 1999. 江苏-南黄海地区中强地震的可公度性及其预测研究[J]. 高原地震, 11(1): 25–31. |
| [] | 石玥, 曹广超. 2013. 青海MS ≥ 6.0地震未来趋势判断——基于可公度方法的研究[J]. 科学技术与工程, 13(35): 10579–10581, 10594. |
| [] | 宋治平, 尹继尧, 薛艳, 等. 2013. 全球及各地震区带强震活动周期特征[J]. 地球物理学报, 56(6): 1868–1876. DOI:10.6038/cjg20130609 |
| [] | 王富强, 许士国. 2008. 长江流域洪水的可公度性及其预测研究[J]. 长江科学院院报, 25(6): 23–27. |
| [] | 翁文波. 1981. 可公度性[J]. 地球物理学报, 24(2): 151–154. |
| [] | 翁文波. 1984. 预测论基础[M]. 北京: 石油工业出版社. |
| [] | 翁文波, 吕牛顿, 张清. 1996. 预测学[M]. 北京: 石油工业出版社. |
| [] | 吴梦初, 延军平. 2013. 滇西及缅甸MS ≥ 6.8级地震时空对称性研究[J]. 高原地震, 25(4): 10–16. |
| [] | 延军平, 白晶, 苏坤慧, 等. 2011. 对称性与部分重大自然灾害趋势研究[J]. 地理研究, 30(7): 1159–1168. |
| [] | 延军平, 闫军辉, 白晶, 等. 2010. 基于可公度方法的陕西及邻近地区重大自然灾害发生趋势探讨[J]. 灾害学, 25(2): 18–20. |
| [] | 杨丽萍, 王小平. 2001. 初探青海及邻区强震的可公度性[J]. 高原地震, 13(2): 14–19. |
| [] | 尹相好, 田凤东, 赵庆红, 等. 2011. 华北地区地震带活跃时段相关性分析[J]. 四川地震(3): 32–36. |
 2017, Vol. 32
2017, Vol. 32

