2. 中国地震局兰州地震研究所, 兰州 730000
3. 中国地震台网中心, 北京 100045
2. Lanzhou Institute of Seismology, China Earthquake Administration, Lanzhou 730000, China
3. China Earthquake Networks Center, Beijing 100045, China
由于全球大陆板块的不断漂移和地震事件的频繁发生,地球内部的构造状态在不断地调整,岩石的破裂会引起波速变化,故强震前后地壳内部的波速会有一定的改变.通过对地壳内部波速变化的实时监测,了解地壳内部应力及流体的变化,进一步实现地震预测.传统成像方法是通过天然地震事件或人为创造震源,但这两种成像结果的分辨率都不高.通过布设更加均匀密集的台站可以提高面波成像的分辨率,但全球的天然地震震源大多数分布在板块边缘区域或断裂带附近,这对研究造成了非常大的限制,想要提高成像结果的分辨率很难,故许多学者希望可以在地震背景噪声中提取出一些有用信息.
背景噪声也称地脉动,是指在无地震事件发生的情况下,地震仪器上所记录到的随机波动信号,是一种在地球内部传播的波.这种随机波动的源 (倪四道等,2013) 包括:大气与陆地的相互作用、海洋与陆地的相互作用、人类与地面的相互作用、地球内部之间的相互作用、火山活动等,其中人为因素包括日常交通、工地施工等人类各种活动,因此,背景噪声是一种连续稳定的自然源.背景噪声作为一种杂乱无章的信号,它的产生是平稳随机的过程,其中包含丰富的地下介质信息,这一思路起源于著名的地震学家Aki在1957年提出的通过背景噪声信息来探索地球内部构造的大胆想法,其想法是对两两台站记录到的长时间连续的噪声信号进行互相关计算来获得台站间的格林函数,并成功地通过噪声信息获得了地表的一些传播特质.
通过背景噪声计算互相关进而提取台站间的格林函数首先在超声学中展开研究,Weaver和Lobkis (2001)通过声学实验发现,计算热噪声互相关获得的波形可以近似为两点间的格林函数,这一具有开创性意义的结果随即被应用于地震学中,并且地震学家们找到了与热噪声波具有相似特征的地震尾波.
2003年,Campillo和Paul (2003)利用远震事件的地震尾波进行互相关计算,经过叠加处理后成功得到了台站间的面波格林函数,在地震学中证实了该假想.同年,Campill和Paul (2003)对台站记录到的101个远震同时间段的尾波信息进行互相关运算,再通过“one-bit”时域归一化,使计算结果的信噪比进一步提高,结果显示:该波形具有Rayleigh面波和Love面波的群速度特征.2004年,Shapiro和Campillo (2004)对两个相隔较远台站39天的噪声记录作互相关计算得到了面波格林函数,进而获得地球内部结构的速度信息.
2005年,Shapiro等 (2005)利用加利福尼亚州62个台站,对30天的连续噪声进行互相关计算,得到的波形与台站间的格林函数仅有幅度上的差异,并由此得到该地区高分辨率的短周期面波群速度分布图,其水平分辨率为60-100km,这项研究开启了背景噪声方法在地震研究中的先河,成为了地震背景噪声探索研究的奠基石.同年,Shapiro等 (2005)通过对背景噪声的互相关计算,得到Rayleigh波的格林函数并得到了5-150s的频散曲线,自此无源成像开始被应用于地震等多方面研究.通过对强震前后格林函数的对比,即可获知地震前后地下介质的变化信息.同时学者们研究发现,通过无源成像获得的格林函数不仅包含直达波的相关信息,还包含尾波的相关信息.因此,将尾波干涉方法用于无源成像所得到的格林函数中能够得到介质更为精细的变化,即可实现面向目标介质的连续动态监测.
一定条件下,台站间的互相关函数可以近似为台站间的格林函数 (Campillo and Paul, 2003;Wapenaar et al., 2004;Shapiro and Campillo, 2004;Shapiro et al., 2005).通过噪声互相关函数来获得格林函数,进一步得到地球内部的速度结构,是当下快速发展起来的一种崭新的成像方法 (齐诚等,2007;孙进和高原,2011).背景噪声层析成像 (Ambient Noise Tomography,ANT),只需要连续的波形资料,不依赖于地震事件的发生,是一种无源成像.与天然地震相比,它避免了地震定位不精确和不可重复性等问题;与人工地震相比,它利用了传统上被认为无用的信息,变废为宝,节省了实验花费,并可以实现较长时间和距离上的波速变化.作为一个崭新的成像方法,已经被普遍应用于地壳成像、沉积盆地结构、监测火山喷发和地震的实时监测等多个研究领域.
随着噪声层析成像技术的应用,在研究区域和频带范围方面都有扩展,在国外取得了一些较为可信的研究结果,大大提高了对地壳浅层结构的分辨能力.在国内,越来越多的学者将背景噪声方法应用于不同区域,也取得了一些成果,对中国大陆的地壳、上地幔浅部地质构造和地震预测领域都有推进作用.但是,目前噪声成像方法仍然不太成熟,还存在一些问题,比如怎样使成像结果的精度更高,怎样探测更深的地下结构,怎样精确得到“地下云图”,怎样改进数据预处理中的时间域归一化等问题,这些都有待更加深入的探索.
本文通过对噪声成像的发展背景、方法原理及研究现状等几个方面的综述,分析其优缺点,并介绍其在地震预测研究中的应用与结果的可靠性,并在此基础上探讨了其未来的发展方向与需要解决的问题.
1 噪声成像的原理方法背景噪声是经过地下各层介质散射后被地震仪所记录到的地球内部的一种特殊波,其产生源比较复杂,是一种非震源产生的波 (庞广华等,2014;李玲利等,2014).噪声成像方法是对台站对连续噪声信息进行互相关运算得到格林函数,再通过时频分析获得频散曲线,得到各个周期的群速度或相速度,然后通过反演计算得到每一点的群速度或相速度,最后得到地球内部的速度成像图.噪声成像过程主要有五个部分:单台数据预处理、提取格林函数、频散曲线测量、质量控制、面波层析成像.
1.1 单台数据预处理单台数据预处理是整个过程中最基础最重要的一个环节,Bensen (2007)提出的单台数据预处理基本方法包括以下三步:
(1) 首先对不符合格式要求的台站数据进行数据的格式转换,然后进行去趋势和去均值、截取和重采样、去除仪器响应、带通滤波等处理.
(2) 时域归一化,可以抑制噪声中的天然地震事件,去除地震仪器故障等造成的异常信号.
(3) 频域归一化,这项处理是为了压制单频信号的影响.
单台数据预处理是为了去掉天然地震的影响和仪器自带的异常信号,最后得到背景噪声数据 (刘志坤和黄金莉,2010).时域归一化是数据预处理中最重要的一个步骤,滑动绝对窗法和“one-bit”正则化法是效果最好的两种方法,最常用的是利用“one-bit”正则化法.一般情况下,采用频域滑动绝对值归一化方法来进行谱白噪化分析,有效地抑制了台站周围场地效应的干扰,不仅可以拓宽频带,而且提高了长时间格林函数的信噪比.
1.2 格林函数的提取计算两个时间序列的互相关会获得两个方向相反的正负分支,波形中一般包含各个频率的信号,提取到的格林函数则是不同频率信号谐波的叠加结果 (杨文等,2011).频散是地震面波的主要特征,面波的传播速度随着深度的增加而增加,不同的面波成分携带了从浅到深地球内部各层介质的速度和衰减特性信息,故通过面波便可获得地下的一些有用信息.无地震事件发生时,仪器记录到的噪声中包含大量有关地球内部构造的信息,找到格林函数和互相关函数之间的相互关系,拓展了人们对地下构造的了解.利用背景噪声互相关提取格林函数基于时间反演不变性和弥散场假设,噪声成像是不依靠天然地震事件的一种创新性方法 (潘纪顺等,2011).时间反演不变性是:一个物理系统随时间的演化过程可逆,即称时间反演不变性;弥散场假设是指:Weaver的声学实验是基于模式均分的解释和两条基本假设,一是弥散场的简正模式互不相关,二是弥散场的模态在时间域是随机分布,并且振幅互不相关 (Weaver and Lobkis, 2003).
根据Weaver等 (2005)提出的利用地震背景噪声的互相关函数提取台站间格林函数,其物理原理显示出:在各向同性的散射波场中,一条射线到达一个接收点后,再到达另一个接收点,震相不发生改变.即使是噪声信号,却是相关的,其互相关函数与格林函数只有幅度差异.因此,背景噪声没有固定的相谱,是地面的一种稳定的非重复性随机波动.
因为频带越宽的噪声其对应的带宽越小,故时域内互相关函数和它导数的到时结构相似,因此,可以用互相关函数来近似其格林函数 (Claerbout,1968).为了提高信噪比,格林函数可以近似为互相关函数反序叠加后的均值结果.提取格林函数主要有三个步骤:
(1) 计算所有台站对的互相关函数;
(2) 互相关系数反序叠加;
(3) 互相关系数叠加后的平均结果近似面波格林函数.
1.3 频散曲线的测量由经验格林函数 (EGF)(Sabra et al., 2005) 或噪声互相关函数 (NCF)(Shapiro and Campillo, 2004;Shapiro et al., 2005) 可以得到群 (相) 速度的频散曲线.采用时频分析对其进行测量,而时频分析基于快速傅里叶变换与数字滤波技术,可以提取出地震数据中的频散信息.目前,主要有移动窗分析法和多重滤波法,大多数应用多重滤波法对群 (相) 速度进行频散曲线测量.
1.4 质量控制质量控制是非常必要的一步,因为频散曲线的质量直接影响层析成像结果的可靠性,故需要对频散曲线的质量进行严格控制和筛选.一般情况下,距离较近的台站对,其互相关函数的正负分支会互相干扰,这会严重影响频散曲线的测量,因此测量频散需选择台站距大于三倍波长以上的数据.还有选择射线路径相似的台站对进行可靠性分析,舍去一些不正常的频散曲线.检验频散曲线测量结果的稳定性可以采用信噪比 (SNR) 测量,满足SNR大于10的结果认为是相对稳定的 (李佳鹏等,2015).
1.5 面波层析成像地震面波是沿着介质分界面传播的波,频散是面波最主要的特征,长周期的面波波长更长,穿透深度也更深.层析成像是利用观测走时与通过初始速度模型计算得到的理论走时两者之间的走时残差进行反演计算.首先,建立参考模型和研究区域地壳模型参数化,主要应用的是模型离散化方法,然后进行射线追踪,最后进行反演计算并分析解的可靠性,反演方法主要有阻尼最小二乘法和LSQR法.
具体算法是:首先对研究区域进行网格划分,获得速度的二维分布图像,然后计算得到所有网格节点的路径频散曲线,再根据线性或非线性方法来反演所有网格的频散曲线,最后获得所有网格S波速度的垂向分布 (Bensen et al., 2007;王琼和高原,2012).一般利用数值模拟方法对解的可靠性进行评判,主要有检测板实验和还原分辨率实验,若反演得到的解没有进行可靠性评价,那么其结果无法被肯定.
2 噪声成像方法在地震预测研究中的应用当前,地震预测问题仍然是一个世界性的科学难题,如何才能较为准确地判断出地震预测三要素:时间、地点和震级,是现在地震研究需要继续探索的一个方向.利用背景噪声方法探索地球内部构造和一些变量在震前震后的变化特征,寻找可以有效判断震前参数变化的方法,是一个具有重大探索意义的的研究方向.随着“十五数字化改造”等项目的实施,地震台网建设不断拓展,可以得到高质量的波形资料,利用动态成像技术研究强震前后震源区的速度变化可实现性越来越高.近些年,随着利用噪声成像方法反演地下速度结构技术的快速发展,许多国内外学者应用中国地震台网数据计算得到面波经验格林函数,并反演得到了中国各个区域的成像图,结果显示了中国大陆各区域迥异的速度结构和地壳厚度.通过噪声互相关计算来提取台站间的经验格林函数,最后得到地震前后的速度结构图像来对比分析震前震后速度结构动态变化,以此来分析震前地下介质状态的变化,以期用于地震预测研究.
利用噪声互相关研究地下介质的速度结构变化是目前地震学的研究热点之一,姚华健等 (2006)通过噪声互相关方法分析了西藏东南地区的Rayleigh面波相速度层析成像,并且所得到的地壳及上地幔速度结构和易桂喜等 (2008)通过两两台站间互相关方法获得的速度结构研究结果一致,其研究结果说明我们不仅仅可以获得群速度,也可以得到对应的相速度成像.基于此研究,Lin等 (2008)利用地震背景噪声分别研究了美国西部地区的Rayleigh面波和Love面波的相速度成像.付媛媛和高原 (2016)研究了东北地区背景噪声的Rayleigh和Love波相速度层析成像.
随后,应用背景噪声进行面波成像得到了广泛应用.Zheng等 (2010)第一次利用CNSN台网的47个台站和中国大陆周边IRIS台网的12个台站18天的连续波形数据进行互相关计算,提取了8~60 s的Rayleigh波群速度频散曲线,并获得了对应周期的群速度成像图.其结果的短周期 (10~20 s) 群速度分布勾勒出主要盆地的形态,同时频散曲线在时间和空间上稳定,说明了利用背景噪声可以提取到可靠的面波信号.
房立华等 (2009)通过噪声数据垂直分量得到了华北地区Rayleigh面波群速度成像图,并结合地下结构与地质构造分析发现6级以上强震多发生于高群速度和低群速度的过渡地带.房立华等 (2013)又通过噪声成像获得了华北地区4~30 s的Rayleigh面波群速度分布图 (如图 1),并且大部分区域可以达到0.25×0.25的横向分辨率.其结果表明地壳越厚反映出来是低速现象,地壳越薄反映出来是高速现象.其研究结果使得人们对于华北地区地下不同深度的构造有了进一步的认识与了解,并且对于将噪声成像方法应用于地震预测研究具有很大的参考价值.
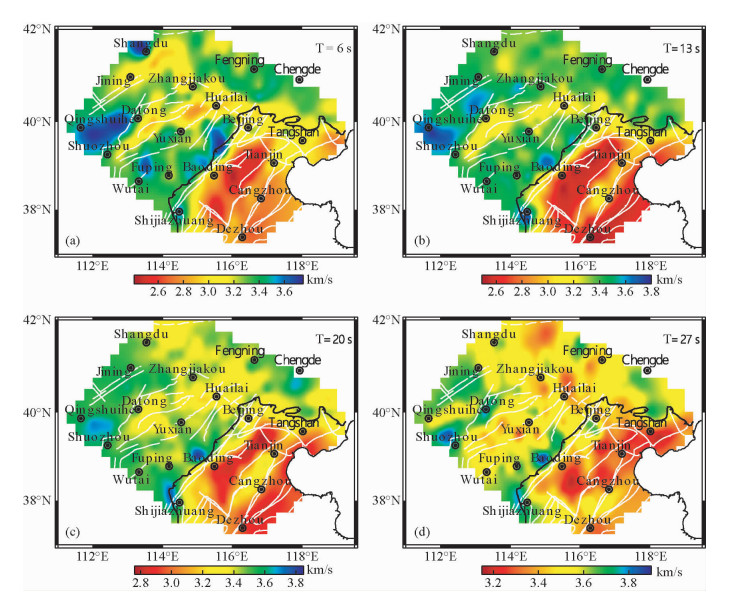
|
图 1 不同周期的勒夫波群速度分布图像 (a)(b)(c)(d)(T=6 s,13 s,20 s,27 s)(来源于 (房立华等,2013)) Figure 1 Love wave group velocity distribution images in different period (T=6 s, 13 s, 20 s, 27 s) |
李昱等 (2010)通过噪声成像方法反演获得川西地区2~35 s周期的Rayleigh面波相速度分布图,其相速度分布显示出了明显的南北分区现象.此结果与易桂喜等 (2008)得到的南北地震带始终处于相对低速,成为划分东、西两大不同速度特征区的天然分界的结果一致.其研究结果使得人们对于川西地区地下构造有了进一步的认识.
刘志坤和黄金莉 (2010)利用2007-2009年四川数字地震台网的宽频带连续波形资料计算得到了2008年汶川8.0级地震震源及其周边区域波速的空间变化.结果得到,汶川地震造成了震源及起附近区域地壳介质速度急剧下降,横跨余震带或离余震带较近的台站对地震波速降低较为明显,最大降幅达0.4%.发震断层附近的龙门山地区和四川盆地出现明显的同震波速降低,作者认为地震导致波速变化的主要原因是断层区内部结构破坏和周边介质应力状态改变.因此,噪声方法为人们探测地下构造状态变化提供了一种新思路,也为地震的预测研究提供了一个新方向,对于将噪声成像方法应用于地震预测研究具有很大的参考价值,争取通过这种新方法沿着这个新方向突破地震预测难关,或取得更大的进步.
随着数据资料的进一步完善,越来越多的学者分析研究震前速度结构出现的异常现象,李军等 (2009)采用福建省地震台网25个宽频台资料通过噪声成像方法得到Rayleigh面波群速度在福建地区的分布,并得到该地区Rayleigh面波时空相对变化的图像.杨润海等 (2011)利用2007年11月至2010年5月云南测震台网46个台站共31个月的连续测震记录,用滑动窗方法得到云南地区的相速度动态扰动图像,将不同时段的速度扰动图像与云南中强地震作对比研究,发现在该区域中强地震发生前,川滇菱形块体中段Rayleigh面波波速表现出的高速异常现象.以上学者都得到了较为可靠的速度成像结果,为以后的研究进展提供了参考价值.
仅仅得到速度结构的对比差异,不足以说明波速变化,而杨文和刘杰 (2013)通过噪声成像方法反演得到了2012年4月11日苏门答腊8.6级地震前后川滇地区速度变化.文章还分析了震前震后川滇地区地震活动 (Benioff应变比) 的变化特征,其结果表明:波速变化与地震活动性变化具有明显的相关性,震后波速增强的区域地震活动也增强,波速降低的区域地震活动也降低.将成像结果与区域地震活动性进行对比分析结果表明研究得到的波速变化结果 (图 2和图 3),综合分析波速的变化趋势,其结果有一定的可信度,故噪声成像方法的应用为地震预测方面提供了一种崭新的可能的途径.
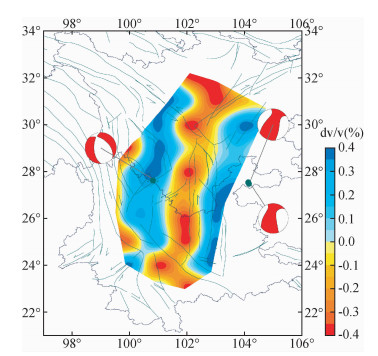
|
图 2 2012年苏门答腊地震8.6级地震前后的波速变化 (来源于 (杨文和刘杰,2013)) Figure 2 The wave velocity changes of before and after the 2012 Sumatran earthquake of 8.6 magnitude |
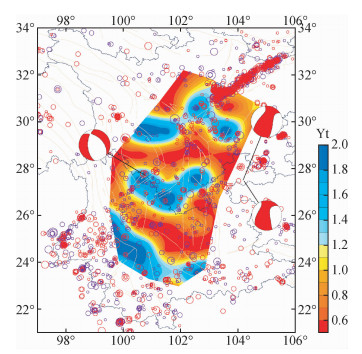
|
图 3 苏门答腊地震前后应变能释放响应比 (来源于 (杨文和刘杰,2013)) Figure 3 Before and after the Sumatra earthquake response than the strain energy release |
噪声成像技术可以用来进行地壳结构动态变化研究.Xu和Song (2009)研究了印尼苏门答腊的三次大地震,他们发现,面波速度时移的发生来自地震后介质速度的变化,这种现象可以解释为地震前后应力的变化和随后的应力松弛.Obermann等 (2013)研究了关于火山喷发的预测和地下介质状态变化的问题,他们利用背景噪声方法来研究火山喷发前后速度结构的差异,并根据这差异分析地下介质状态的变化.其结果表明:火山喷发的预测地点与实际位置吻合,并且得到的该地区的速度结构与其已知的地质构造特点是一致的,这很好地说明了基于背景噪声方法得到火山喷发前后速度结构的差异来进行地点和时间的预测结果是可信的.因此,类似可应用于地震预测的时间和地点预测,为应用此方法进行地震预测增加了信心.但是,想要将此方法应用于地震预测研究,最重要的是能否在震前发现这种波速异常,若震前的变化可以被观测或计算到,将会推进地震预测的研究更上一个台阶.
3 结果的可靠性分析一般情况下,台站所记录到的噪声信号在一段时间内并不是长时间连续的 (其间可能由于天然地震事件、设备故障和人为因素等干扰而间断),况且大多数地震发生在板块边缘地带,台站分布不均匀,故背景噪声不是完全均匀的.台站对射线的有效覆盖区域和各方向路径的均匀分布对于反演的精度有很大的影响,台站对射线覆盖区域越均匀,噪声成像结果的分辨率越高.为了提高互相关函数的信噪比,就必须去掉一些射线,然而这样会影响结果的分辨率和可靠性.故不必舍去那些覆盖不均匀的射线,而采取叠加长时间的互相关函数来提高信噪比 (马小军等,2014).利用分段最大相位相关函数 (PMCC) 的方法来求解信号的瞬时相位,相同的时间分辨率的前提下,它比其他类似的结果更加接近真实的相位曲线.相位加权叠加方法是一种非线性叠加方法,能够有效地压制相关性不好的噪声信号,增强相关性较好的噪声信号 (Schimmel and Paulssen, 1997).陆一锋等 (2011)利用相位加权叠加方法对地震台站的各径向接收函数进行叠加,与线性叠加结果相比发现:不相关的噪声信号很明显被压制或去除掉了,得到的莫霍转换波的Ps震相较于其他方法更加清晰.用广义S变换对地震背景噪声数据进行去噪处理,解决了标准S变换中基本小波形态固定的缺陷,在分析非平稳信号时能更好地刻画其时频特性,数据信噪比大大提高,可以为数据反演提供更精确的数据 (李红光等,2015).
实际上,噪声源的分布是非均匀的 (Yao et al., 2006; Pedersen and Krüger,2007),不同周期的噪声源空间分布差异很大,时间分布上也表现出一定的季节性和方向性变化,受大陆结构、海浪冲击海岸和人类活动等多种因素影响.由于提取格林函数的基本要求是噪声源随机均匀分布,而实际情况中噪声源的非均匀分布严重影响了提取格林函数和频散曲线结果的可靠性与稳定性 (Karplus等,2013).同时,弥散场假设和时间反演不变性也不能一直满足.则正负分支上的噪声信号强度和信噪比不是对称相等的,正负分支 (正分支为因果信号,负分支为非因果信号) 的信号强度差异比较明显.同时,噪声成像结果在时间上的分辨率比较低,故数据叠加一般是长时间的,短时间叠加得到的结果不可靠;空间上的分辨能力也比较复杂,通常不同时间段、不同周期得到的速度分布图像差异明显.由于背景噪声信号具有较强的季节性变化特征,一般采用长时间段的噪声信号进行叠加计算可以有效地避免随机干扰,尽量使噪声源处于均匀状态,来提高成像结果的分辨率.噪声成像在地震预测中的研究受到噪声源的分布、成像时间分辨率、空间分辨率以及噪声源的季节变化等多种因素的影响,还需要进行更多的探索研究.因此,分析噪声源的性质和时空分布特征,来降低由于噪声源的不均匀分布和季节性变化引起的在研究地下速度结构和波速变化时所带来的误差 (Bensen,2006),影响因素的研究对于整个过程的结果具有重要意义.
在地震学研究中,地震尾波和背景噪声均可以形成随机波场,而相比于地震尾波,背景噪声不依赖于地震事件的发生并可重复利用,对于地震较少地区的研究更加方便实用,能够满足更多研究者的需求.地震背景噪声层析成像原理的关键是噪声互相关函数 (NCF) 中的有效信号,而NCF提取的信号包括短周期面波、长周期面波、地壳体波、深部间断面体波反射信号等 (朱良保和王清东,2011;倪四道等,2013;徐义贤和罗银河,2015;赵盼盼等,2015),这一过程是噪声成像的基础,若此过程得到的结果有误,则测量得到的频散曲线不可靠,故而最后的成像结果也是不可靠的.目前,许多研究者的应用结果都得到了可靠地结果并给出了可信的判据.根据其计算过程,可以从以下几个方面来判定成像结果可靠性:计算台站间互相关结果的信噪比;将成像结果与实际资料 (例如已知的地下结构特点) 进行对比,比较其一致性.基于以上多方面讨论研究可以得到较高分辨率并且与实际情况吻合的某一时间段的速度结构图,利用噪声成像得到的成像图较根据天然地震和人工地震得到的成像图更加精细,这说明根据背景噪声计算互相关,进而提取格林函数,然后进行频散曲线测量和层析成像,最后将结果应用于地震预测研究这一方法得到的结果是可信的.
综上所述,背景噪声方法是对传统成像方法很好的拓展,作为一种具有可挖掘性、创新性的成像方法,经过多年的成功应用已被证实可以得到较为可靠的成像结果,给人们创造了一个可以更加详细了解地球内部构造的机会.而且背景噪声不依靠地震事件的发生,只与台站布设密度有关,故该方法更适合做动态成像研究,可用于监测地壳介质的速度变化,可用于对中强震的地点进行预测研究.背景噪声提取格林函数方法在地震学领域中的应用开始于地震尾波,基于噪声互相关函数和尾波干涉理论,测量不同时间段的噪声互相关函数 (NCF) 与参考NCF的差异,来测量波速变化,这一结果的可靠性已经被普遍认可.2015年,肖卓和高原 (2015)等详细阐述了地震尾波干涉方法在研究震源位置变化和监测散射体运移状态的相关应用与发展,还探讨了利用噪声互相关函数 (NCF) 监测地下介质波速变化的尾波干涉方法的优缺点及发展方向.目前,想利用不同时间段的频散曲线反演得到的速度分布图的差异来研究变化,试图利用介质波速变化探索发现地震预测的新方法.但是,所得到的结果在国内缺乏较为系统性的严谨研究,是否可靠,将其应用于地震预测研究有待进一步探讨,可以将结果与GPS、应力分析、地磁地电等多方面分析的结果进行对比分析讨论.
4 讨论与展望 4.1目前为止,已有的地震预测方法很多,孕震区介质波速变化是目前较有希望的一个研究方向,希望对地壳内部的波速变化进行监测,分析地壳内部区域应力状态的变化,争取在地震预测方面有所突破.
4.2噪声成像方法的应用拓展了传统成像方法,不依赖震源位置和天然地震的发生是其独有的特点.可以得到短周期面波,提高了对浅层地壳的研究和垂直分辨率,水平分辨率主要受台站分布和射线密度的影响,因此只要区域射线分布均匀,射线密度足够大,就可以得到分辨率较高的面波层析成像结果.对传统的构造带进行噪声互相关计算提取格林函数,进而分析其地下结构,有助于对该区域地震活动性进行研究.
4.3通过不同时间段的频散曲线反演得到的速度分布图的差异来研究变化,这是一种实现预测地震的新方法,目前已经有多位学者进行相关工作与研究,实现一个动态监测平台,进一步实现对震源区进行实时监控,但是,其结果的可靠性还需要进一步的讨论.试图利用地震背景噪声层析成像方法实现地震预测已被众多学者关注,期待可以找到一个预测地震的突破口.随着这项新技术的大范围应用,在背景噪声中将可以发现更多未知的地下信息,可以继续利用噪声成像方法对国内外中强地震进行多方面的研究,分析总结其震前的波速变化,进一步认识了解震前应力状态的变化,并时刻关注其发展动态,期待此方法可以使地震预测向前跨出一大步.
4.4另一个方向是利用背景噪声方法监测危险断裂带的相对波速变化.我们已经知道,尾波干涉方法利用多次散射波路径长和采样充分的优势提取震源及介质的细微变化,这些变化对地震和火山的孕育、形成及发展有着重要的参考意义,因此其有着广泛的应用前景 (Shohei et al., 2011).利用尾波干涉理论计算得到介质的动态波速变化是介质在时间和空间上的平均变化,将尾波干涉方法应用于无源成像所得到的格林函数中能够得到介质更为精细的变化,可实现断层附近介质的连续动态监测,进而可能会实现监测危险断裂带的目标.
4.5噪声成像方法的应用,为认识地下构造提供了新的技术,为了解地震孕育规律带来了新的启示,为监测地球内部波速动态变化带来了可能,为地震预测研究带来了崭新的想法.随着当前地震台站研究的不断深入,观测仪器的数字化,观测质量的提高,计算方法的改进等,将会增强对背景噪声的记录能力,将会得到更加精细的地下速度结构图,从而促进对地震孕育规律和地震预测的探索研究.相信在不久的未来,科学家们会解决目前存在的一些弊端,并在地震预测方面取得较为可信的结果,最终地震预报将会向天气预报一样被人们所依靠信赖!
致谢 衷心感谢审稿专家提出的宝贵修改意见和编辑部老师的帮助!| [] | Aki K. 1957. Space and time spectra of stationary stochastic waves, with special reference to microtremors[J]. Bulletin of the Earthquake Research Institute, 35(3): 415–456. |
| [] | Bensen G D, Ritzwoller M H, Barmin M P, et al. 2007. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements[J]. Geophys. J. Int., 169(3): 1239–1260. DOI:10.1111/gji.2007.169.issue-3 |
| [] | Campillo M, Paul A. 2003. Long-range correlations in the diffuse seismic coda[J]. Science, 299(5606): 547–549. DOI:10.1126/science.1078551 |
| [] | Claerbout J F. 1968. Synthesis of a layered medium from its acoustic transmission response[J]. Geophysics, 33(2): 264–269. DOI:10.1190/1.1439927 |
| [] | Fang L H, Wu J P, Lü Z Y. 2009. Rayleigh wave group velocity tomography from ambient seismic noise in North China[J]. Chinese Journal of Geophysics, 52(3): 663–671. DOI:10.1002/cjg2.v52.3 |
| [] | Fang L H, Wu J P, Wang W L, et al. 2013. Love wave tomography from ambient seismic noise in North-China[J]. Chinese Journal of Geophysics, 56(7): 2268–2279. DOI:10.6038/cjg20130714 |
| [] | Fu Y Y, Gao Y. 2016. Phase velocity tomography of Rayleigh and Love waves using ambient noise in Northeast China[J]. Chinese Journal of Geophysics, 59(2): 494–503. DOI:10.6038/cjg20160209 |
| [] | Karplus M S, Klemperer S L, Lawrence J F, et al. 2013. Ambient-noise tomography of north Tibet limits geological terrane signature to upper-middle crust[J]. Geophysical Research Letters, 40(5): 808–813. DOI:10.1002/grl.50202 |
| [] | Li H G, Sun G, Xing Y L. 2015. Application of generalized S-transform in ambient seismic noise data processing[J]. China Earthquake Engineering Journal, 37(3): 867–872. |
| [] | Li J, Jin X, Zhou Z R, et al. 2009. Near real-time monitoring the change of group velocity of short-period surface wave via seismic noise analysis[J]. Acta Seismologica Sinica, 31(6): 629–640. |
| [] | Li J P, Zhong W X, Li H Y, et al. 2015. Application research on velocity structure of subsurface medium and its changes in the Chinese mainland using ambient noise[J]. China Earthquake Engineering Journal, 37(1): 235–241. |
| [] | Li L L, Wang W T, Zhu B L, et al. 2014. Processing seismic ambient noise data to obtain reliable surface wave dispersion measurements[J]. Earthquake, 34(3): 235–241. |
| [] | Li Y, Tao H J, Liu Q Y, et al. 2010. Phase velocity array tomography of Rayleigh waves in western Sichuan from ambient seismic noise[J]. Chinese Journal of Geophysics, 53(4): 842–852. DOI:10.3969/j.issn.0001-5733.2010.04.009 |
| [] | Lin F C, Moschetti M P, Ritzwoller M H. 2008. Surface wave tomography of the western United States from ambient seismic noise:Rayleigh and Love wave phase velocity maps[J]. Geophys. J. Int., 173(1): 281–298. DOI:10.1111/gji.2008.173.issue-1 |
| [] | Liu Z K, Huang J L. 2010. Temporal changes of seismic velocity around the Wenchuan earthquake fault zone from ambient seismic noise correlation[J]. Chinese Journal of Geophysics, 53(4): 853–863. DOI:10.3969/j.issn.0001-5733.2010.04.010 |
| [] | Lobkis O I, Weaver R L. 2001. On the emergence of the Green's function in the correlations of a diffuse field[J]. J. Acoust. Soc. Am., 110(6): 3011–3017. DOI:10.1121/1.1417528 |
| [] | Obermann A, Planès T, Larose E, et al. 2013. Imaging preeruptive and coeruptive structural and mechanical changes of a volcano with ambient seismic noise[J]. J. Geophys. Res., 118(12): 6285–6294. DOI:10.1002/2013JB010399 |
| [] | Pang G H, Zhang L H, Liu T T, et al. 2014. An overview of development of ambient noise's application on crust and upper mantle's structure[J]. Progress in Geophysics, 29(4): 1518–1525. DOI:10.6038/pg20140406 |
| [] | Pedersen H A, Krüger F. 2007. Influence of the seismic noise characteristics on noise correlations in the Baltic shield[J]. Geophys. J. Int., 168(1): 197–210. DOI:10.1111/j.1365-246X.2006.03177.x |
| [] | Qi C, Chen Q F, Chen Y. 2007. A new method for seismic imaging from ambient seismic noise[J]. Progress in Geophysics, 22(3): 771–777. DOI:10.3969/j.issn.1004-2903.2007.03.017 |
| [] | Rickett J, Claerbout J. 1999. Acoustic daylight imaging via spectral factorization:Helioseismology and reservoir monitoring[J]. The Leading Edge, 18(8): 957–960. DOI:10.1190/1.1438420 |
| [] | Sabra K G, Gerstoft P, Roux P, et al. 2005. Surface wave tomography from microseisms in Southern California[J]. Geophysical Research Letters, 32(14): L14311. |
| [] | Schimmel M, Paulssen H. 1997. Noise reduction and detection of weak, coherent signals through phase-weighted stacks[J]. Geophys. J. Int., 130(2): 497–505. DOI:10.1111/gji.1997.130.issue-2 |
| [] | Shapiro N M, Campillo M. 2004. Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise[J]. Geophysical Research Letters, 31(7): L07614. DOI:10.1029/2004GL019491 |
| [] | Shapiro N M, Campillo M, Stehly L, et al. 2005. High-resolution surface-wave tomography from ambient seismic noise[J]. Science, 307(5715): 1615–1618. DOI:10.1126/science.1108339 |
| [] | Shohei M, keshi T, Shiro O, et al. 2012. Monitoring seismic velocity change caused by the 2011 Tohoku-Okay earthquake using ambient noise records. Geophysical Research Letters, VOL.39, L09309, Doi:10.1029/2012GL051405. |
| [] | Wapenaar K, Thorbecke J, Dragoon D, et al. 2004. Relations between reflection and transmission responses of three-dimensional inhomogeneous media[J]. Geophysical Journal International, 156(3): 179–194. |
| [] | Weaver R L, Lobkis O I. 2001. Ultrasonics without a source:Thermal fluctuation correlations at MHz frequencies[J]. Physical Review Letters, 87(13): 134301. DOI:10.1103/PhysRevLett.87.134301 |
| [] | Weaver R L, Lobkis O I. 2003. Elastic wave thermal fluctuations, ultrasonic waveforms by correlation of thermal phonons[J]. J. Acoust. Soc. Am., 113(5): 2611–2621. DOI:10.1121/1.1564017 |
| [] | Xu Y X, Luo Y H. 2015. Methods of ambient noise-based seismology and their applications[J]. Chinese Journal of Geophysics, 58(8): 2618–2636. DOI:10.6038/cjg20150803 |
| [] | Xu Z J, Song X D. 2009. Temporal changes of surface wave velocity associated with major Sumatra earthquakes from ambient noise correlation[J]. Proceedings of the National Academy of Sciences of the United States of America, 106(34): 14207–14212. DOI:10.1073/pnas.0901164106 |
| [] | Yao H J, van der Hilst R D, de Hoop M V. 2006. Surface-wave array tomography in SE Tibet from ambient seismic noise and two-station analysis-I[J]. Phase velocity maps[J]. Geophys. J. Int., 166(2): 732–744. |
| [] | Yi G X, Yao H J, Zhu J S, et al. 2008. Rayleigh-wave phase velocity distribution in China continent and its adjacent regions[J]. Chinese Journal of Geophysics, 51(2): 402–411. DOI:10.3321/j.issn:0001-5733.2008.02.013 |
| [] | Zhao P P, Chen J H, Liu Q Y, et al. 2015. Fine structure of middle and upper crust of the Longmenshan Fault zone from short period seismic ambient noise[J]. Chinese Journal of Geophysics, 58(11): 4018–4030. DOI:10.6038/cjg20151111 |
| [] | Zheng Y, Yang Y J, Ritzwoller M H, et al. 2010. Crustal structure of the northeastern Tibetan plateau, the Ordos block and the Sichuan basin from ambient noise tomography[J]. Earthquake Science, 23(5): 465–476. DOI:10.1007/s11589-010-0745-3 |
| [] | Zhou L Q, Ji P. 2012. Ambient noise Rayleigh wave tomography across Taiwan[J]. Progress in Geophysics, 27(4): 1350–1358. DOI:10.6038/j.issn.1004-2903.2012.04.008 |
| [] | Zhu L B, Wang Q D. 2011. An expression of the cross-correlation of ambient seismic noise:A derivation based on the surface-wave theory[J]. Chinese Journal of Geophysics, 54(7): 1835–1841. DOI:10.3969/j.issn.0001-5733.2011.07.017 |
| [] | 房立华, 吴建平, 吕作勇. 2009. 华北地区基于噪声的瑞利面波群速度层析成像[J]. 地球物理学报, 52(3): 663–671. |
| [] | 房立华, 吴建平, 王未来, 等. 2013. 华北地区勒夫波噪声层析成像研究[J]. 地球物理学报, 56(7): 2268–2279. DOI:10.6038/cjg20130714 |
| [] | 付媛媛, 高原. 2016. 东北地区背景噪声的Rayleigh和Love波相速度层析成像[J]. 地球物理学报, 59(2): 494–503. DOI:10.6038/cjg20160209 |
| [] | 李红光, 孙刚, 邢艺兰. 2015. 广义S变换在背景噪声数据处理中的应用[J]. 地震工程学报, 37(3): 867–872. |
| [] | 李军, 金星, 周峥嵘, 等. 2009. 利用地震噪声准实时监测短周期面波波速变化[J]. 地震学报, 31(6): 629–640. |
| [] | 李佳鹏, 钟卫星, 李红谊, 等. 2015. 利用噪声研究地下介质速度结构及其变化在中国大陆的应用[J]. 地震工程学报, 37(1): 235–241. |
| [] | 李玲利, 王伟涛, 朱良保, 等. 2014. 从背景噪声提取瑞利面波频散曲线——方法与应用实例[J]. 地震, 34(3): 108–116. |
| [] | 李昱, 姚华建, 刘启元, 等. 2010. 川西地区台阵环境噪声瑞利波相速度层析成像[J]. 地球物理学报, 53(4): 842–852. DOI:10.3969/j.issn.0001-5733.2010.04.009 |
| [] | 刘志坤, 黄金莉. 2010. 利用背景噪声互相关研究汶川地震震源区地震波速度变化[J]. 地球物理学报, 53(4): 853–863. DOI:10.3969/j.issn.0001-5733.2010.04.010 |
| [] | 陆一锋, 徐鸣洁, 王良书, 等. 2011. 相位加权叠加方法在探测鄂尔多斯东南缘地壳结构中的应用[J]. 高校地质学报, 17(4): 562–568. |
| [] | 马小军, 马禾青, 李军, 等. 2014. 青藏高原东北缘背景噪声特征分析[J]. 地震研究, 37(4): 607–613. |
| [] | 倪四道, 曾祥方, 王伟涛, 等. 2013.地震背景噪声源研究进展[A].//中国地球物理2013——第十四分会场论文集[C].北京:中国地球物理学会, 445. |
| [] | 潘纪顺, 谷芳莹, 李自立, 等. 2011. 地震背景噪声成像技术进展[J]. 华北水利水电学院学报, 32(1): 87–90. |
| [] | 庞广华, 张林行, 刘婷婷, 等. 2014. 利用背景噪声研究壳幔结构发展综述[J]. 地球物理学进展, 29(4): 1518–1525. DOI:10.6038/pg20140406 |
| [] | 齐诚, 陈棋福, 陈颙. 2007. 利用背景噪声进行地震成像的新方法[J]. 地球物理学进展, 22(3): 771–777. DOI:10.3969/j.issn.1004-2903.2007.03.017 |
| [] | 孙进, 高原. 2011. 中国大陆背景噪声成像研究及应用前景[J]. 国际地震动态(3): 12–17. |
| [] | 王琼, 高原. 2012. 噪声层析成像在壳幔结构研究中的现状与展望[J]. 地震, 32(1): 70–81. |
| [] | 肖卓, 高原. 2015. 尾波干涉原理及其应用研究进展综述[J]. 地震学报, 37(3): 516–526. |
| [] | 徐义贤, 罗银河. 2015. 噪声地震学方法及其应用[J]. 地球物理学报, 58(8): 2618–2636. DOI:10.6038/cjg20150803 |
| [] | 杨润海, 王彬, 郑定昌, 等. 2011. 云南地区波速变化与强震孕育[J]. 地震研究, 34(4): 420–427. |
| [] | 杨文, 刘杰, 史海霞, 等. 2011. 用噪声成像方法研究云南地区强震前地震面波速度变化[J]. 地震, 31(3): 103–111. |
| [] | 杨文, 刘杰. 2013. 2012年4月11日苏门答腊8[J]. 6级地震前后川滇地区波速变化研究[J].地震, 33(4): 248–256. |
| [] | 易桂喜, 姚华建, 朱介寿, 等. 2008. 中国大陆及邻区Rayleigh面波相速度分布特征[J]. 地球物理学报, 51(2): 402–411. DOI:10.3321/j.issn:0001-5733.2008.02.013 |
| [] | 赵盼盼. 2011.汶川地震区地壳速度相对变化的地震环境噪声自相关研究[硕士论文].北京:中国地震局地质研究所, 1-50. |
| [] | 赵盼盼, 陈九辉, 刘启元, 等. 2015. 龙门山断裂带中上地壳速度结构的短周期环境噪声成像[J]. 地球物理学报, 58(11): 4018–4030. DOI:10.6038/cjg20151111 |
| [] | 郑定昌, 盖增喜, 杨润海, 等. 2014. 云南地区背景噪声层析成像[J]. 地震学报, 36(4): 602–614. |
| [] | 郑现, 赵翠萍, 周连庆, 等. 2013. 利用背景噪声数据提取地震台站间面波的可靠性分析[J]. 地震学报, 35(2): 218–228. |
| [] | 周龙泉, 吉平. 2012. 台湾地区的随机噪音瑞利波层析成像研究[J]. 地球物理学进展, 27(4): 1350–1358. DOI:10.6038/j.issn.1004-2903.2012.04.008 |
| [] | 朱良保, 王清东. 2011. 地震背景噪声互相关函数的面波理论表达形式[J]. 地球物理学报, 54(7): 1835–1841. DOI:10.3969/j.issn.0001-5733.2011.07.017 |
 2017, Vol. 32
2017, Vol. 32

