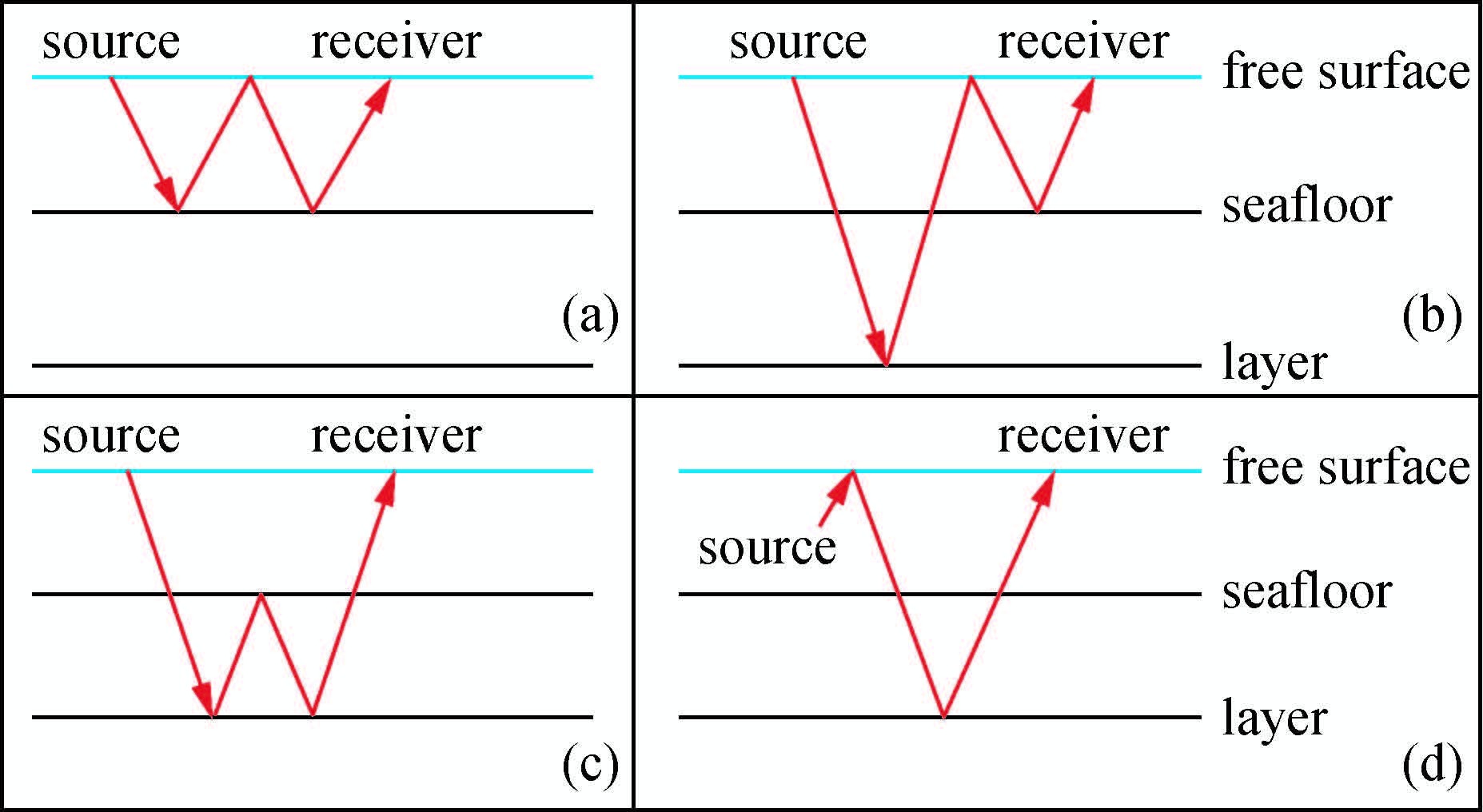
当今海洋资源的开发与应用已经成为关乎人类未来发展与可持续性的重要问题,因此对于海洋地震资料的处理与解释就显得尤为重要.在海洋地震勘探中,由于海底界面和海平面等强反射面的存在,多次波相比陆地上发育更为显著.当前资料处理中的共中心点道集(CMP)叠加技术和偏移成像都是基于一次反射波,而多次波的存在会严重干扰对于一次波的识别,降低地震资料的信噪比,为地震成像与反演带来困难,因此如何有效地进行多次波的衰减就成为了海洋地震资料处理中必须首先面对的问题.由于多次波在不同界面会发生多次反射,其路径特征和振幅特征较一次波相比都更为复杂,为研究方便,根据多次波反射界面和反射路径的不同可以将其分为全程多次波、表层多次波、层间多次波和鬼波四种基本类型,如图 1所示(陆基孟,2009).
|
图 1 多次波类型 (a)全程多次波;(b)表层多次波;(c)层间多次波;(d)鬼波. Figure 1 The types of multiples (a)Entire multiples;(b)Surface multiples;(c)Peg-leg multiples;(d)Ghost. |
由于不同类型的多次波的反射特征和传播特点各不相同,如何在保护一次波的前提下有效地识别并衰减多次波一直是国内外海洋地震资料处理中的一个难点.国内外对于多次波衰减问题的研究由来已久,直至今日对于多次波衰减已发展了多种有效的方法,这些方法根据出发点和原理的不同可以分为两大类:滤波法和波动理论法(Weglein,1999).滤波法主要依据多次波和一次波的差异性进行多次波和一次波的分离,而波动理论法则是从波动理论出发,建立多次波模型实现对多次波的预测,并通过自适应相减去除预测的多次波,所以波动理论法方法也称为预测减去法.滤波法的原理较为简单,计算效率高,在多次波和一次波差异明显的情况下可以达到较好的衰减效果,因此被广泛应用于工业中.波动理论法虽然计算较为复杂,但适用性更为广泛,因此具有更大的研究意义和价值.
多次波衰减是当前海洋地震资料处理过程中必须首先解决的问题,特别是我国南海海域多次波发育情况十分显著(刘伊克等,2015),能否有效衰减海洋地震资料中的多次波关系到我国海洋资源的开发与应用.滤波法和波动理论法作为多次波衰减的经典方法,具有很强的实用价值和较为完整的理论体系,但两种方法本身也存在一定的局限性,难以满足复杂勘探目的层的要求.基于这一点,本文首先选取了滤波法和波动理论法中各自具有代表性的经典方法,对其中不同多次波衰减方法的思路和本质进行了分析和对比,从不同方法的基本原理和数学方法出发,指出了它们各自的适用性和优缺点;其次,在总结经典多次波衰减方法的同时,对近些年来国内外多次波衰减新技术的发展进行了归纳和概括;最后,在论述当今国内外多次波衰减问题研究进展的基础上,总结了该领域研究当前取得的进展和存在的不足,并对未来多次波衰减技术的研究重点和发展方向做出了展望.
1 滤波法在当前的海洋地震资料处理过程中,滤波法是应用较为广泛的一类多次波衰减方法,该类方法的基本思想是利用多次波和一次反射波之间的差异性来预测和压制多次波(Weglein et al.,2011).多次波和一次波的差异性主要表现在两个方面,一是多次波和一次波的剩余时差差异,由于地震波在地下介质中的传播速度大体呈现出随深度而增加的趋势,而多次波的射线路径大多位于浅层,因此多次波与一次波相比具有更小的动校正速度,利用这一速度差异可以将多次波和一次波在动校正后转换到不同域进行分离,从而达到去除多次波的目的,常见的方法有Radon变换(Foster and Mosher,1992; Hargreaves et al.,2001; 刘喜武等,2004)、F-K滤波(Sengbush,1983; 吴战培,1995)和聚束滤波(胡天跃和王润秋,2000;胡天跃等,2002)等;二是多次波的周期性特征,在海洋地震勘探中,多次波在水平层状介质和零偏移距的理想情况下周期性特征较为明显,利用这一特征可以对多次波进行预测进而达到衰减多次波的目的,但是实际情况下多次波的周期性会随着偏移距的增大逐渐减弱,所以这种衰减方法会随着偏移距的增大而效果降低,典型的如预测反褶积法(Peacock and Treitel,1969; Morley and Claerbout,1983; 杨积凯和徐伯勋,1992)等.虽然不同滤波方法的思路和适应性各有不同,但是其出发点都是利用多次波和一次波的差异性,表 1列出了不同滤波法在衰减多次波时需转换到的不同域和所依据的多次波和一次波的差异特性,本文将对这些方法的基本原理进行简单阐述,并指出这些方法各自存在的优缺点和适用范围.
|
|
表 1 多次波衰减滤波法 Table 1 Filtering method in multiple wave attenuation |
Radon变换法是当前海洋勘探工业中应用较为广泛的一种多次波衰减方法.该方法的基本原理是利用多次波和一次波的剩余时差差异(动校速度差异),将一次波速度作为动校正速度对CMP道集进行动校正,使得多次波动校不足,同相轴向下弯曲近似于抛物线形态,然后利用Radon变换将地震数据转换到τ-p域,在τ-p域中多次波与一次波的分离特征较为明显,从而得到一次波和多次波各自对应的能量团,然后进行滤波处理切除多次波,最后再反变换到x-t域,得到衰减多次波后的地震记录.在进行Radon变换时,根据不同的积分路径可以分为三种变换形式,分别是线性Radon变换、双曲Radon变换和抛物Radon变换,当前工业中所采用的主要为抛物Radon变换.
抛物Radon变换由Hampson(1986)最早提出,在该变换中利用最小二乘反演可将Radon域的一个点转换为x-t域内的一条抛物线,转换公式为
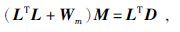
|
(1) |
(1)式中,L和LT为离散化后的Radon变换算子,D和M分别为地震原始数据和Radon域数据,Wm为权系数矩阵.此后,Sacchi和Ulrych(1995)使用稀疏先验法对同相轴的曲率方向进行约束,大大提高了Radon域成像的分辨率,但是该方法基于时间域的计算效率很低.之后,Sacchi和Porsani(1999)又利用循环矩阵和共轭梯度算法反演Hermitian算子,提高了高分辨率Radon变换的计算效率,为高分辨率 Radon变换的发展奠定了理论基础.熊登等(2009)提出了一种混合域Radon变换方法,基本思路是在时间域添加时变稀疏权算子,通过迭代计算Radon变换,然后利用抛物变换在频率域解耦的特征转换到频率域进行计算,一定程度上兼顾了高分辨率和计算效率.王保丽等(2014)提出了基于保幅Radon变换的多次波衰减方法,该方法将Radon变换后的地震数据分成两部分,一部分用于模拟零偏移距处的反射波能量,另一部分用于模拟反射波振幅的AVO特性,从而保护了一次波的AVO特征.
总的来说,Radon变换法是一种成本较低、实用性强且效果较为理想的多次波衰减方法,因而在工业中被广泛应用.但是,Radon变换法要达到较好的分离效果,要求多次波与一次波具有明显的速度差,而且地层的垂直速度变化不大,否则一次波的能量会泄漏到切除域,导致切除时一次波信号损伤,但在实际情况下一次波和多次波的剩余时差在切除域往往不大,从而导致Radon变换的衰减效果不好甚至损伤一次波,这一点也是当前整个滤波法所具有的通病.其次,由于Radon变换的计算是在离散条件下进行的,也容易产生空间假频问题从而使地震信号受到干扰.
1.2 聚束滤波法聚束滤波法的基本原理与Radon变换法相似,通过建立数据模型将地震信号中的一次波和相关噪声联系起来,然后利用聚束滤波器响应将一次波和相关噪声进行分离,从而达到去除多次波的目的.Shumway和Dean(1968)最早给出了MVU(最小方差、无偏)聚束滤波法的数学理论基础,利用噪声能量最小和地震信号不发生畸变这两个条件求取聚束滤波器响应.White(1988)将MVU聚束滤波法应用于地震勘探资料的处理并成功从地震叠前道集中提取了一次波信号.胡天跃和王润秋(2000)在此基础上提出了自适应聚束滤波法,能够对地震信号的振幅、相位和时间延迟以及未知信号进行估计,分析一次波和噪声随偏移距变化的信号特征.此后,胡天跃等(2002)将聚束滤波法应用于南海深海地震资料进行多次波的去除,在多次波十分突出的情况下通过多次聚束滤波在近道和远道都取得了很好的衰减效果.洪菲等(2004)提出了优化聚束滤波法,有效解决了低覆盖低信噪比的地震资料多次波难以去除的问题.洪菲等(2005)通过将地震资料按方位角分区后引入动态平衡面元,将聚束滤波方法的应用拓展到三维地震资料的处理.
总的来说,聚束滤波法的核心思想就是在噪声能量最小的情况下,从地震信号中提取无偏的一次波信号.与Radon变换法相比,聚束滤波法从数据模型出发,不会出现Radon变换中存在的空间假频问题,且能够从数据模型中分析一次波和噪声信号的振幅和相位随偏移距的变化特征(AVO和PVO),有利于避免信号的畸变,更好地保护一次波.在实际处理海洋地震资料时,特别是在多次波十分突出的情况下,聚束滤波法衰减多次波的效果相比Radon变换更好.由于聚束滤波法本质上与Radon变换法原理相同,都是根据多次波和一次波的时差进行多次波衰减,该方法并不能解决多次波和一次波时差不大时Radon变换存在的种种问题,但是该方法的提出和发展具有十分重要的意义,为多次波衰减提供了一种相比Radon变换更加优化的选择,在保护一次波信号特征和和去除多次波两方面找到了更好的平衡点.
1.3 预测反褶积法预测反褶积法是基于多次波的周期性特征来衰减多次波的方法,由Peacock和Treitel(1969)最早提出.该方法从多次波的周期性特征出发,通过设计最佳维纳滤波器f(t)来消除地震数据中的多次波.由于该方法要求多次波保持有良好的周期性,但实际资料中多次波的周期性会随着偏移距的增加越来越弱,针对这一问题Taner(1980)根据多次波在τ-p域周期性较好的特性提出了τ-p域的预测反褶积法.此后Morley和Claerbout(1983)对预测反褶积法进行了相应的改进,使得该方法的假设限制大大降低,适用性明显提高.
预测反褶积法的理论基础是基于地震记录的褶积模型,即地震道记录x(t)为震源子波w(t)和地层脉冲相应e(t)的褶积,表示为
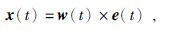
|
(2) |
该方法的关键是求取最佳维纳滤波器f(t),该滤波器与x(t)褶积得到的实际输出yt和预测值dt之间的最小平方误差要保证最小.具体表达式为
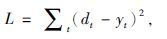
|
(3) |
yt=f(t)×x(t)=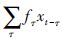
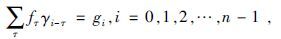
|
(4) |
其中γi-τ=∑txt-τxt-i为地震记录的自相关,可以通过地震记录x(t)直接求取,gi=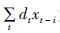
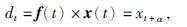
|
(5) |
(5)式代入互相关函数gi可得
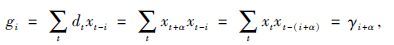
|
(6) |
将(6)式代入(4)式中可以得到
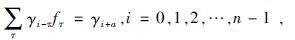
|
(7) |
(7)式写成矩阵形式为
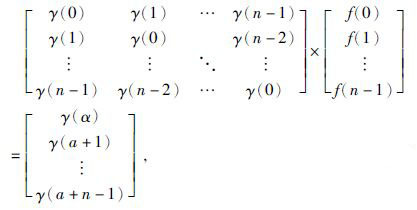
|
(8) |
(7)式中,γi-τ为地震记录的自相关函数,通过上述方程即可以计算出预测因子f,然后代入(5)式可以得到未来某个时刻t+α时的预测值xt+a,将这一预测值从实际未来值中减去即可得到去除了多次波的地震记录.
预测反褶积法作为滤波法的一种,虽然不要求多次波和一次波的具有明显的视速度差异,但是需要多次波的周期性保持较好.在水平层状介质近偏移距时,多次波具有良好的周期性,预测反褶积的效果十分理想,但是在地下构造起伏和地层横向变化的情况下,多次波的周期性遭到破坏,该方法不再适用,因此预测反褶积方法衰减多次波主要取决于实际地下构造.此外,预测反褶积法存在两个先验假设:(1)地层脉冲响应e(t)是随机的互不相关的白噪声序列;(2)假设地震子波为最小相位子波.前者保证了利用地震记录自相关γx代替地震子波自相关γw的准确性,而后者则是预测滤波器算子f(t)与输入地震道记录x(t)的进行褶积运算的前提.这些假设在处理海洋实际地震资料时往往很难满足,特别是在实际资料中地震子波往往是混合相位,难以满足最小相位子波的先验条件.不规则的层间反射和噪声干扰的存在也会使预测因子长度和预测步长的大小难以确定.这些都给该方法的发展带来了困难,但是预测反褶积对于短周期多次波和交混回响的衰减作用是不可忽视的,因此对于该方法的研究和改进一直是多次波衰减领域的一大热点.在此基础上,近年来又发展了基于自适应线性滤波技术的自适应反褶积(杨积凯和徐伯勋,1992; 朱四新和秦鸿飞,2013),该方法采用自适应算法对每个采样点进行设计,可以有效地滤掉层间反射和噪声干扰.张军华等(2009)从模型研究出发,探讨了预测反褶积时预测步长的选取和算子长度等问题.赵昌垒等(2013)将线性Radon预测反褶积应用于南海海洋资料的多次波衰减处理,在消除海底多次波时取得了良好的效果.
2 波动理论法由于滤波法的出发点是基于多次波和一次波的差异性来实现多次波和一次波的分离,进而达到衰减多次波的目的,因此当多次波与一次波的差异性不大时,该方法的衰减效果就会受到很大的限制.为解决这一问题发展了基于弹性波动理论预测多次波的波动理论法,该方法从波动方程出发,根据地震波的传播特点建立多次波模型,或者寻找多次波和一次波在某一界面传播的数值关系进行多次波的预测,然后从原始数据中将预测的多次波自适应减去得到衰减后的地震数据.当前波动理论法发展较为成熟的方法有波场外推法、反馈迭代法和逆散射级数法三种,三种方法的基本特征可见表 2.
|
|
表 2 多次波衰减波动理论法 Table 2 Wave equation-based method in multiple wave attenuation |
波场外推法是较早出现的利用波动方程衰减多次波的方法,该方法的基本思想是利用波动方程的解建立地震波场的外推方程,将检波器得到的地震数据向下或上延拓建立多次波模型,然后把得到的多次波模型从原始数据中减去,从而得到多次波衰减后的地震记录.波场外推方程可以表示为
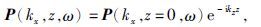
|
(9) |
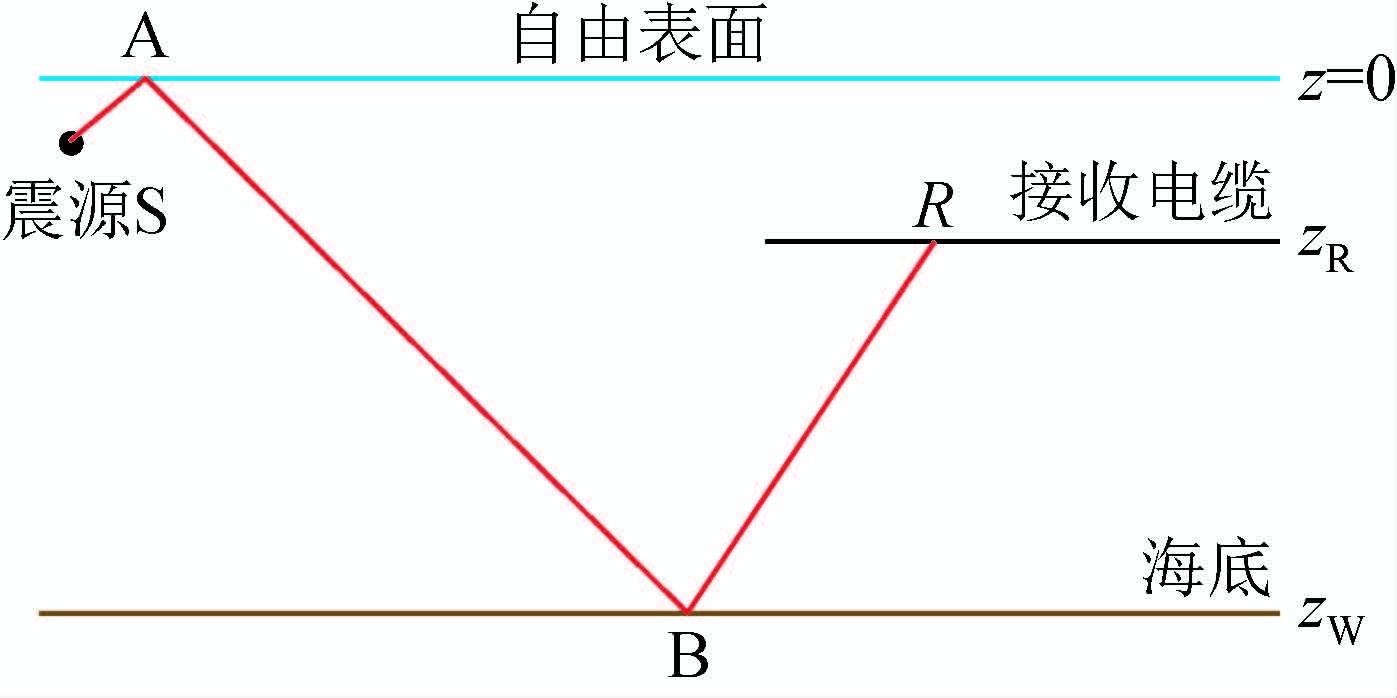
(9)式中,kx为水平波数,ω表示圆频率,kz为垂直波数,P(kx,z,ω)为深度z的波场,利用该式可以将某一深度的地震波场(通常为检波器处记录的波场)进行外推得到另一深度的波场数据(通常为海底波场).Loewenthal等(1974)、Riley和Claerbout(1976)、Morley和Claerbout(1983)和Berryhill和Kim(1986)先后对这一方法进行了完善和发展.随后,Wiggins(1988)在前人的工作基础上提出了能够适应复杂海底的波场外推法,如图 2所示.将zR处的地震波场通过外推方程正反向延拓至海底,得到海底处的下行波场D(h,zw,ω)和上行波场U(h,zw,ω),具体表达式为
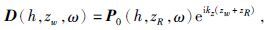
|
(10) |
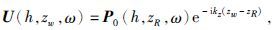
|
(11) |
(10)式和(11)式中h为偏移距,zR为检波器深度,zw为海水深度,P0(h,zR,ω)为检波器深度zR处记录到的波场,通过(8)式和(9)式中可以得到海底处不含多次波的地震波场Pp(h,zw,ω),具体表示为
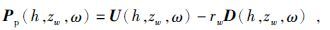
|
(12) |
(12)式中rw为海底反射系数.最后将Pp(h,zw,ω)延拓至检波器深度即可得到不含多次波的检波器波场Pp(h,zR,ω).此后,Jiao等(2002)等针对波场外推法存在空间假频的问题,利用LMO(线性时差方法)先消除空间假频,然后再进行多次波的预测和衰减,取得了很好的效果.
波场外推法利用波动方程实现地震波场的外推,建立海底界面的多次波模型,在海平面较为平坦的情况下可以很好地预测海底多次波.但是,由于该方法对海底模型的准确性具有很高的要求,即必须精确估计海底反射系数,当海底界面较为复杂时往往难以满足这一要求.实际证明,当海底介质情况不是很复杂,多次波反射特征较为清楚的情况下,该方法能够有效衰减多次波;但当海底介质复杂,层数较多时,该方法的压制效果较差.除此之外,波场延拓过程还会引入一定的相关噪声,影响自适应匹配的结果.总而言之,由于不能解决海底复杂介质对多次波波场的影响,这一方法的应用受到了一定的限制,但是该方法提供了一种利用波动方程衰减多次波的重要思路,为整个波动理论法的发展奠定了基础.
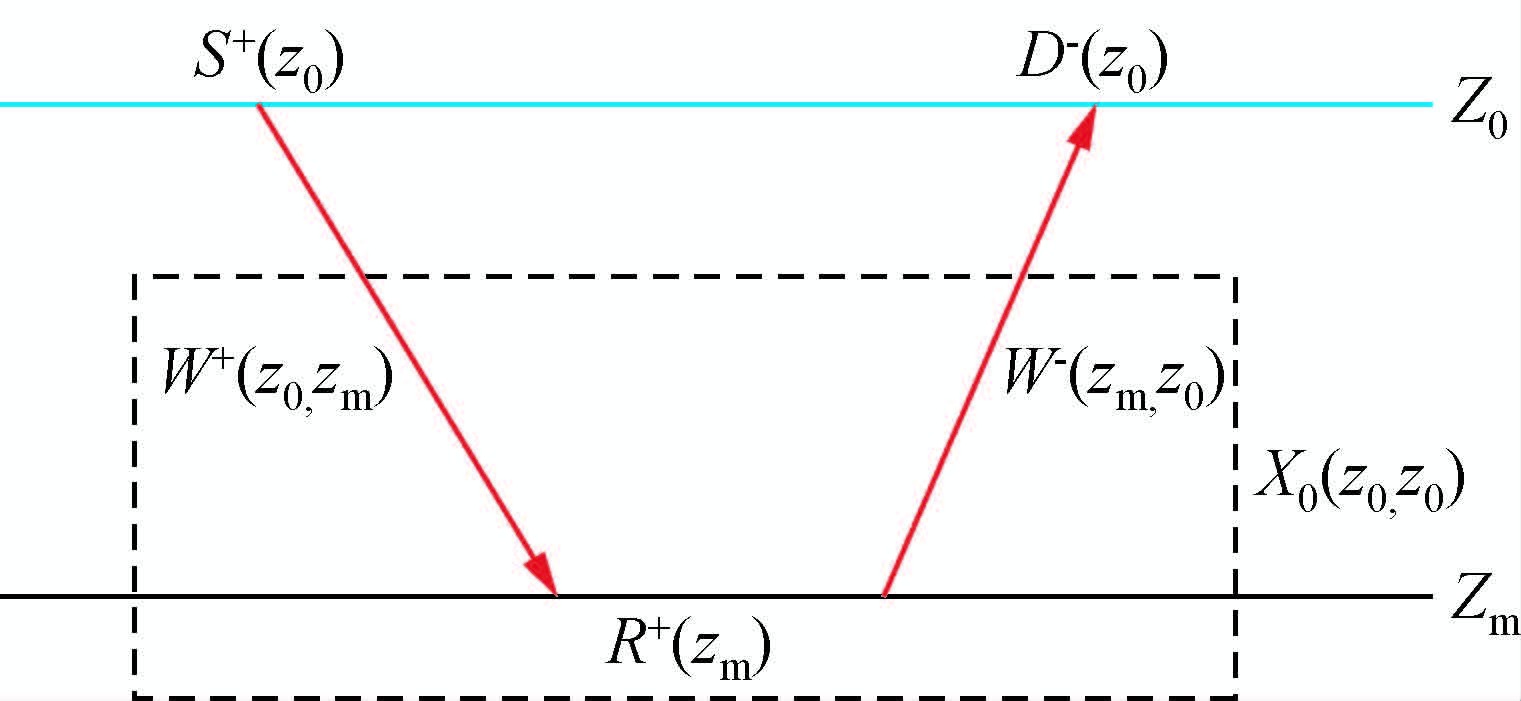
2.2 反馈迭代法反馈迭代法是当前基于波动理论的多次波衰减方法中研究较为广泛的核心方法之一.该方法不同于波场外推法着眼于对整个波场传播过程的描述,而是利用波动理论建立相应的多次波数据模型,然后根据地震波场在特定界面的传播路径特点寻找多次波和一次波之间的数值关系,利用一次波预测多次波从而达到去除多次波的目的,这里的特定界面包括自由界面和层界面两种不同的情况.Kennett(1979)最早提出了一维空间自由界面多次波的模拟方法,为反馈迭代法理论框架的建立打下了基础.此后荷兰Delft大学的Berkhout(1985)提出了用于消除自由界面多次波的算法,在已知震源子波的情况下可以预测多次波,该方法考虑了震源和检波器的特性且适用于复杂的地下结构,能够很好地衰减自由表面多次波.随后同属于Delft大学的Verschuur等(1992)发展了这种方法,根据衰减多次波后剩余波场能量最小的准则,利用最小二乘法进行计算达到衰减自由表面多次波的目的,并成功估算出了震源子波.此后Berkout和Verschuur提出了SRME(Surface Related Multiple Elimination)方法,即自由表面多次波压制方法(Berkout and Verschuur,1997;Berkhout,1981,2006).该方法基于波动理论建立反馈迭代模型(WRW,如图 3所示)正演模拟有效波场和多次波场在自由表面的关系,图 3中S+(z0)和D-(z0)分别表示震源处的下行波场和检波器算子,W+(z0,zm)和W-(zm,z0)分别表示下行传播矩阵和上行传播矩阵,R+(zm)表示zm处下行反射的反射算子,从而可以将地下介质不包含自由界面反射的脉冲响应X0(z0,z0)表示为
|
图 2 波场外推法原理图 Figure 2 The priociple diagram of wave tield extrapolation method |
|
图 3 WRW波场正演模型(不包括自由界面的反射) Figure 3 WRW wave field forward mode(retlections from free surface were not included) |
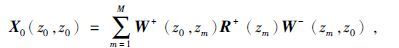
|
(13) |
利用(13)式可以将自由表面处的有效波场和多次波场分别表示出来,然后将地震波场中的多次波作级数展开,利用反复迭代方法确定震源子波,在每次迭代中通过最小二乘匹配多次波模型和原始数据,迭代公式为
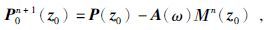
|
(14) |
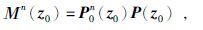
|
(15) |
(14)、(15)式中P0n+1为n+1次迭代后的多次波压制结果,Mn为预测出的多次波波场即多次波模型,A为界面的自适应算子,用来表征震源、检波器和界面的反射性质,在自由表面情况下A仅与频率ω有关.通过(13)、(14)两式可知每次迭代的输出将作为下次迭代的输入,如果给出多次波压制后的估计数据P00,通过迭代可以求得更为精确的多次波压制结果Pn+10.在实际操作中,理想的情况是使得P00=P0,即迭代初始值即为有效波场,但这一点是不可能做到的,因为P0正是我们最终所要求解的,因此常用原始记录P近似代替P0作为初值带入迭代式,或者将滤波法得到的有效波场作为初始值带入.
SRME方法能有效解决自由表面多次波的衰减问题,随后Verschuur和Berkout(2005,2012)又将这一方法推广到了层间多次波的预测和衰减,具体包括两种思路:第一种是基于层界面的算法,利用CFP(共聚焦点)道集将震源和检波器延拓到产生层间多次波的界面,然后再利用SRME方法预测层间多次波;第二种是基于边界面的算法,该方法不需要指定产生层间多次波的相关界面,只需在该界面下某一深度建立相应的等效基准面,然后利用CFP道集将层间多次波分成三段进行褶积计算.这两种方法都可以看成是SRME方法在层间多次波衰减中的推广.
反馈迭代法的产生与发展对于多次波衰减的理论研究具有十分重要的意义.首先,该方法相比一般的滤波法并不需要多次波和一次波之间存在较大的速度差异;其次,由于该方法并不需要建立多次波的全波场方程,只需在特定界面利用一次波和多次波的关系预测多次波,并将其从一次波中分离,因此该方法理论上不需要任何地下介质层的信息.当然该方法也存在一定的局限性.首先,反馈迭代法不需要地下介质层信息是在震源子波已知的前提下,而在实际资料处理过程中,震源子波往往难以精确估算;其次,反馈迭代法的实现过程需要从零偏移距到最大偏移距的所有数据,但实际采集中近偏移距数据常常会出现缺失,因此需要进行相应的外推或内插以保证获得全波场信息.除此之外,在反馈迭代法的应用过程中存在级数展开和迭代两种计算方式,石颖等(2012)通过对比分析反馈迭代法过程中涉及的级数展开法和迭代法两种处理,指出级数展开法需要多个预测项求和,与迭代法相比虽然计算量小,但在多次波压制过程中会出现误差.
2.3 逆散射级数法逆散射级数法是一种基于散射理论的多次波衰减方法,该理论的实质是通过扰动分析将介质中的地震波场用已知的参考波场的扰动来表示,因此逆散射级数法的核心就是通过测量的地震波场数据求取扰动波场的级数解,进而实现多次波的预测.Moses(1956)和Prosser(1969)最早提出了逆散射级数法,之后Stolt和Dan(1980)将逆散射级数法用于多次波衰减方面的研究,基本思路是应用散射级数推导出逆散射级数,利用该级数中的高阶项压制多次波.Weglein等(1997)利用逆散射原理,根据自由表面和点散射模型,进行多维直接反演,求取扰动算子实现对多次波的预测逆散射级数法就是从散射波场出发,这里的扰动算子表征了已知的参考波场和实际介质产生的波场差异,具体可表示为
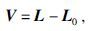
|
(16) |
(16)式中,V表示扰动算子,L和L0分别表示实际波场和参考波场的微分形式.
根据Lippmann-Schwinger方程,可以将散射场、参考波场和扰动算子联系起来,具体可以写为
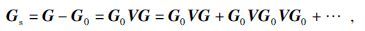
|
(17) |
(17)式中Gs表示散射场的格林函数,G表示实际波场的格林函数,G0表示参考波场的格林函数.如果用D表示散射场Gs在散射体外表面上记录的数据,并将扰动算子V作级数展开,则可以由(16)得到
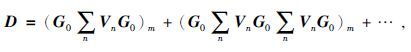
|
(18) |
(18)式中(·)m表示对震源和接收点所在的平面进行积分.利用等式两边各阶项对应相等,便可以利用散射数据D得到V1,再由V1得到V2,最终迭代可以求得扰动算子为
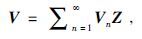
|
(19) |
由此可见,逆散射级数法的实质就是将扰动算子V(参考介质和实际介质的差别)和散射波场(参考波场和实际波场的差别)联系起来,求取逆散射级数并利用其中的子序列来去除海洋地震数据中的自由表面多次波和层间多次波.
由于逆散射级数法从实际测量的地震波场数据出发,利用散射理论确定扰动算子预测多次波,不需要地下介质的任何信息,所以适用于地下构造比较复杂的情况,适用性较其他的多次波衰减方法有了明显的提高.但是,在实际海洋地震资料处理过程中,逆散射级数法从数据出发的特点也会带来一些问题,比如震源子波估计的准确性和近偏移距的数据缺失会严重影响该方法的衰减效果.其次,当地下介质构造复杂时,仅仅从数据出发预测多次波的准确性就存在着问题,实测数据往往难以解释地下复杂构造产生的复杂反射特征.最后,逆散射级数法由于计算量大,计算过程复杂,因此限制了该方法在海洋勘探工业中的应用和发展.
国内对于逆散射级数法的研究起步较晚,近年来的研究主要集中于提高逆散射级数法的计算效率和解决原始数据的数据缺失问题.刘洪等(2007)对地震逆散射波场和扰动算子进行了相应的研究,给出了横向非均匀介质中地震反射数据的逆散射广义谱分解方程;金德刚等(2008)改进了Weglein提出的一维预测公式,优化了逆散射级数层间多次波的算法,大大提高了计算效率;李翔和胡天跃(2009)采用能量最低法则和带限抛物Radon变换法补偿原始地震资料中的缺失信息,使得逆散射级数法衰减过程中一次波保存.陈小宏和刘华锋(2012)将多次波衰减的逆散射级数法和SRME法进行了比较,将二维逆散射级数法进行了降维简化,从而比较了二维逆散射级数法、1.5维逆散射级数法和二维SRME方法的衰减效果和优缺点.刘伊克等(2014)针对南海北部陆坡区的构造特征,提出了多区域、多尺度的多次波压制方法,一定程度上解决了逆散射级数法需要预先知道多次波类型这一前提,且针对我国南海北部海域提出了一套可行的多次波压制的系统策略.
3 多次波衰减新技术的发展滤波法和波动理论法作为海洋多次波衰减的经典方法,其各自的理论体系均已发展得较为成熟,并被广泛应用到当前的地震资料处理过程中.但是,随着海洋地震勘探的发展,地下介质的复杂程度愈来愈高,现有的多次波衰减方法因其自身的局限性往往难以满足海洋地震勘探的要求.滤波法计算简单,效率高,但需要满足多次波和一次波差异性较大的假设,当多次波和一次波差异性不大时该方法便不再适用.波动理论法不需要对地震波场作先验假设,不存在滤波法适用条件的问题,但是方法本身计算量大,并且建立多次波数据模型要求得到全波场的数据和已知震源子波,而实际勘探中往往会出现近偏移距缺失、震源子波难以精确估计等问题.因此,发展多次波衰减新技术以适应海洋地震勘探的要求就显得尤为重要.当前对于多次波衰减新技术的发展主要存在两种思路:一是通过将滤波法和波动理论法两种方法结合对多次波进行衰减,弥补每种方法各自存在的局限性,以使多次波衰减的先验假设得到更好的符合;二是通过寻找一种新的多次波衰减方法打破已有的先验假设的束缚,使得海洋地震资料多次波衰减达到更好的效果.
3.1 综合法无论是滤波法还是波动理论法,在多次波衰减处理过程中都存在一定的局限性.在多次波衰减过程中如果能将两种方法综合运用就能一定程度上提高多次波衰减的准确性和彻底性.因此,当前多次波衰减研究的一个重要发展方向就是将滤波法和波动理论法结合,使多次波衰减达到更好的效果,对复杂构造地区的适应性更强.Kabir和Verschuur(1995)提出了利用抛物Radon变换恢复缺失的近偏移距数据,从而解决了SRME方法在实际勘探中近偏移距缺失的问题,为两类方法的结合提供了理论支持.Zhou和Greenhalgh(1996)提出了将滤波法中的抛物Radon变换和波动理论法中预测多次波的方法相结合,利用波动方程预测海底表层多次波,再利用抛物Radon变换进行拟合衰减,虽然该方法对衰减多次波的类型有严格的要求,但为后来的研究提供了一种新的思路与方法.
近些年来国内也有部分学者对两种方法的结合进行了相应的研究,并且取得了良好的多次波衰减效果.针对波动理论法中近偏移距数据缺失的问题,王维红和刘洪(2005)利用最小平方抛物Radon变换和Levinson递推算法,对近偏移距地震波场进行叠前重建和外推从而得到全波场数据,用于波动理论法对多次波的预测;王建立等(2009)提出了一种海上多次波的联合衰减法,即利用波场外推法建立海底多次波模型,预测并减去全程多次波,然后利用预测反褶积和Radon变换进一步分离层间多次波和剩余的全程多次波;黄兆林(2012)针对深水资料模型将3D-SRME方法与高分辨率Radon方法结合进行多次波的衰减;李贺等(2014)针对中、深层海洋地震资料的长周期和短周期多次波,将SRME方法、tau-p域内预测反褶积和高精度Radon变换结合起来进行衰减.
综合法一定程度上综合了两类方法各自的特点,改善了单一方法衰减多次波过程中存在的问题.但是,随着海洋地震勘探地下介质的复杂性越来越高,目前并没有找到一种通用的结合手段,只能根据不同的海洋勘探资料提出不同的结合方法进行多次波的衰减.将滤波法和波动理论法结合是当前多次波衰减一个重要的发展方向,这种方法同时兼顾了多次波衰减过程中的计算效率和适用性两大问题,但是如何在这两类方法之间寻找一个最佳的结合点是当前该技术必须面对和解决的一大难题.
3.2 稀疏反演法稀疏反演法(EPSI,Estimation of Primaries by Sparse Inversion)是近些年发展起来的新兴的多次波衰减方法,该方法的实质是基于最速下降法(梯度法)的最优化反演.最速下降法的核心思想是通过建立目标函数ψ(m),若ψ(m)在m=a处可微且有定义,则函数ψ(m)在a点处沿负梯度-Δψ(a)下降最快,从而得到:
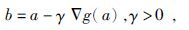
|
(20) |
(20)式中g(a)=-Δψ(a)为目标函数梯度,若上式在γ足够小时成立,则可以得到迭代关系为
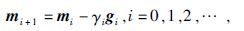
|
(21) |
(21)式中mi为第i次迭代的解向量,gi为目标函数在解mi处的梯度向量,其负方向为目标函数的下降方向,γi为当前迭代的修正步长,一般通过插值线搜索进行求取(Moré and Toraldo,1989).
van Groenestijn和Verschuur(2009a,b)最早将该方法引入到自由表面多次波的衰减过程中,并利用反馈迭代模型建立了一次波及其相关的自由表面多次波与上行波场数据的关系,具体表示为
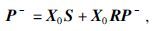
|
(22) |
(22)式中P- 表示海面上接收到的上行波场,X0为地下脉冲响应,S表示震源子波,R为反射系数,一般取为-1.从而目标函数J可以表示为
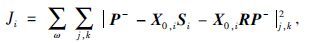
|
(23) |
(23)式中,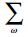
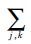
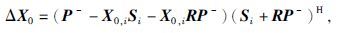
|
(24) |
(24)式中,(·)H表示共轭矩阵,从而根据(19)式可以得到X0 的迭代公式为
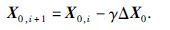
|
(25) |
在迭代过程中通过设计时窗拾取时间域的脉冲响应X0,得到炮集的稀疏脉冲响应,在每次迭代过程中通过增大时窗下边界以保证收敛性,避免局部极值对目标函数的影响.对于Si 可以利用同样的过程进行迭代求解,从而实现了对于脉冲响应和震源子波的稀疏反演过程,再根据这两个参数就可以得到衰减多次波后的一次波数据.Lin和Herrmann(2013)在此基础上对EPSI方法进行了修改,提出了稳健稀疏反演法(Robust EPSI),利用基追踪方法(Basis Pursuit)通过最小化1-范数将信号稀疏表示为约束极值问题,进而将自由表面多次波衰减问题转化为凸优化问题,提高了稀疏反演的计算效率和对大数据集的适应性和稳定性.刘国昌等(2013)将拖缆数据与OBS(Ocean Bottom Seismometer)数据联合,利用EPSI方法压制多次波,解决了OBS检波点稀疏的问题,并通过实际算例比较了SRME方法和EPSI方法衰减多次波的结果,进一步证明了EPSI方法的优越性.王维红和井洪亮(2015)将稀疏反演方法拓展到三维自由表面多次波的压制,应用高分辨率Radon变换稀疏反演解决了三维地震数据中横测线稀疏的问题,有效压制了三维自由表面多次波.
与传统的波动理论法中的SRME方法相比,EPSI方法不需要将多次波的预测和自适应相减分成两个独立的过程,避免了在自适应减去过程中损伤有效信号,而且该方法的运用有助于近偏移距数据的重建(van Groenestijn and Verschuur,2009a),一定程度上解决了在实际勘探时近偏移距数据缺失的问题,因而具有广阔的研究前景和应用价值.利用反演的方法进行多次波的去除是未来多次波衰减技术一个重要的发展方向,反演能够使海洋地震勘探提供的地震数据得到最大程度的利用,且反演过程本身不需要任何先验假设,对复杂勘探地区的适用性更强,但是该方法目前也存在计算量大,对计算机运行速度要求高的问题.稀疏反演法是利用反演解决多次波衰减问题的一次重要尝试,随着反演理论在地震勘探中的应用越来越广泛,利用反演的方法去除多次波必将成为海洋多次波衰减技术的核心手段.
3.3 多次波成像由于当前的地震资料处理和解释都是基于一次波的CMP叠加和偏移成像,所以多次波在数据处理时往往作为噪声采取相应的手段进行衰减,但是多次波相比一次波对于地下储层的照亮范围更广并且携带有更丰富的地下信息,因此当前多次波研究的另一个重要思路是直接利用多次波进行成像,而不是仅仅将其作为噪声进行去除.当前利用多次波成像主要有两种思路,一是将多次波转化为一次波,然后利用一次波偏移方法进行成像,Berkhout和Verschuur(2006)在SRME方法的基础上,通过利用反馈模型建立的自由表面多次波和一次波的关系,将原来利用一次波预测多次波的加权褶积过程转换为加权互相关过程,从而将多次波数据转化为伪一次波数据,然后利用一次波的偏移方法进行成像.另一种是直接对多次波进行偏移成像,无需将多次波转化伪一次波,目前研究较为成熟的方法有最小二乘逆时偏移(LSRTM,Least-squares Reverse Time Migration),该方法的实质为线性波形反演(Tang,2009;Dai et al.,2011; Zhang and Schuster,2014).Liu等(2011)改进了传统的一次波逆时偏移方法,将震源和接收点的多次波场沿时间延拓到不同深度层,利用同一深度的多次波记录自相关进行成像,将LSRTM方法拓展到双程波动方程.Wong等(2011)利用LSRTM对多次波和自由表面多次波进行联合成像,通过增加叠前滤波算子提高了该方法的收敛性和稳健性,并给出了三维多次波成像的实际算例.Tan和Huang(2014)利用波场分离成像条件对LSRTM方法进行了改进,提高了陡倾断层区的成像分辨率并且减少了成像假象.
多次波成像是近些年来多次波研究领域发展起来的新的思路,多次波不再被看作是一种噪声,而是一种有效信号,实际中利用多次波成像可以提高地下储层的成像分辨率,得到比一次波更多的信息.利用多次波直接成像是未来多次波研究领域的重要内容,随着对海洋多次波的认识越来越深刻,单纯的多次波衰减已经难以适应复杂勘探地区的要求,多次波成像作为一项新技术突破了原有的理论体系,为多次波问题的研究开辟了新的思路和方法.当然,该方法的研究目前还处在探索阶段,存在串扰假象(Crosstalk)的问题,今后对于如何去除多次波成像过程中产生的串扰假象将成为该方法研究的重点和难点.
4 小 结 4.1滤波法从几何地震学出发,利用多次波和一次波的差异性以及在变换域中的可分离性进行多次波的衰减,这里的差异性包括视速度和周期性的差异.该方法在地质构造较为简单的地区且两种波差异较大时是比较有效的,且计算量小,易于操作,因此这种方法在当前的海洋勘探工业上应用比较普遍.但是,随着海洋勘探对地下介质层的复杂性要求越来越高,当多次波和一次波差异性不大时,使用该方法容易使一次波信号受到损伤,因而该方法不再适用.波动理论法从弹性波动理论出发,利用波动方程建立相应的多次波数据模型,通过数据反演预测多次波,然后自适应相减衰减多次波.该方法通过数据输入直接反演介质属性,因此不需要任何地下界面的信息,相比滤波法能够适用于地下复杂介质的情况.但是,该方法从数据出发这一点也会带来很多的问题,比如震源子波估计的准确性、实际数据近偏移距缺失、自适应相减损伤有效信号等.此外波动理论法的计算量很大,这一点限制了该方法在实际勘探中的应用,如何在保证衰减多次波效果的前提下简化该方法在预测多次波模型计算时的复杂过程,是该方法当前继续发展所必须面对的问题.
4.2当前发展的多次波衰减新方法可以归为综合法、稀疏反演法和多次波成像法三类.综合法通过分析两种方法各自的优缺点,根据实际需要采用两种方法结合的手段进行多次波衰减,一定程度上解决了两种方法各自存在的问题,能够得到较好的多次波衰减效果,但是考虑到海底地形复杂和多次波的种类的多样性等因素的干扰,综合法目前并没有找到一个完善的衰减过程来得到最好的衰减效果,今后对于如何更好地将两种方法结合以求获得最佳的衰减效果,将成为一个研究的重点与难点,如果这一问题得到解决,多次波衰减技术的发展将会进入一个崭新的阶段.其次,利用稀疏反演的方法衰减多次波,是将最优化反演的手段运用到多次波衰减问题的一次重要尝试,但由于多次波自身存在类型多样和路径的复杂性,其反演过程本身就存在很大的挑战性,目前的反演手段只能得到某一特定类型的多次波,因此有待于进一步的研究和发展.多次波成像改变了传统的将多次波作为噪声去除的理念,在多次波问题的研究中是一次很大的突破,当前的多次波成像方法基于多次波预测实现一种走时上的匹配,但解决不了振幅和相位的匹配的一致性,因此在多次波偏移过程中会产生串扰假象,这也是未来该方法需要改进和重点研究的问题.4.3 总的来说,海洋地震资料多次波衰减技术的发展经历了一个从滤波法到波动理论法,又到两种方法结合的过程,但是随着海洋勘探进一步发展,地下介质的复杂程度越来越高,这两类方法的适用性和衰减精度都受到了挑战.特别是在海洋中,除了存在自由表面和海底两个强反射界面外,往往还会出现高速屏蔽层现象影响地震资料的成像,单纯从数据出发难以解释这些特殊界面所产生的反射效果.滤波法和波动理论法这两种方法的成立需要满足的假设太多,包括一次波和多次波必须存在周期性或速度上的差异、地下介质模型横向速度无变化、衰减理论能够适用于各阶多次波以及不同偏移距的等效性等等,但是在实际勘探中往往很难满足这些假设,而且两种方法都忽视了倾斜界面倾角对多次波周期性的破坏性.除此之外,当前的海洋多次波理论框架都是基于纯P波场,并没有考虑转换波场的影响,这种近似处理肯定会带来不可忽视的误差.因此今后多次波衰减的研究方向应是在传统方法的研究基础上,寻找新的方法能摆脱目前所需要的种种假设,且能够考虑到海底高速层和转换波的影响,使海洋地震资料多次波衰减技术具有更强的适应性,从而能够满足复杂介质情况下对海洋地震勘探的要求,而当前所发展的稀疏反演法和多次波成像法均是对于新的多次波衰减理论体系的重要探索,虽然目前还存在各种问题和不足,但为我们指明了多次波研究未来的发展方向.
致谢 感谢于光明老师和蔡明刚老师在本文写作过程中提出的意见和建议,感谢司洁戈博士对本人工作的帮助和支持.| [] | Berkhout A J .1981. Wave field extrapolation techniques in seismic migration, a tutorial[J]. Geophysics, 46 (12) : 1638–1656. DOI:10.1190/1.1441172 |
| [] | Berkhout A J. 1985. Seismic Migration:Imaging of Acoustic Energy by Wave Field Extrapolation[M]. Amsterdam:Elsevier. |
| [] | Berkhout A J .2006. Seismic processing in the inverse data space[J]. Geophysics, 71 (4) : A29–A33. DOI:10.1190/1.2217727 |
| [] | Berkhout A J, Verschuur D J .1997. Estimation of multiple scattering by iterative inversion, Part I:Theoretical considerations[J]. Geophysics, 62 (5) : 1586–1595. DOI:10.1190/1.1444261 |
| [] | Berkhout A, Verschuur D .2006. Imaging of multiple reflections[J]. Geophysics, 71 (4) : SI209–SI220. DOI:10.1190/1.2215359 |
| [] | Berryhill J R, Kim Y C .1986. Deep-water peg legs and multiples:Emulation and suppression[J]. Geophysics, 51 (12) : 2177–2184. DOI:10.1190/1.1442070 |
| [] | Chen X H, Liu H F .2012. Comparison between inverse scattering series method and SRME method in free surface related multiple prediction[J]. Progress in Geophysics (in Chinese), 27 (3) : 1040–1050. DOI:10.6038/j.issn.1004-2903.2012.03.026 |
| [] | Dai W, Wang X, Schuster G T .2011. Least-squares migration of multisource data with a deblurring filter[J]. Geophysics, 76 (5) : R135–R146. DOI:10.1190/geo2010-0159.1 |
| [] | Foster D J, Mosher C C .1992. Suppression of multiple reflections using the Radon transform[J]. Geophysics, 57 (3) : 386–395. DOI:10.1190/1.1443253 |
| [] | Hampson D. 1986. Inverse velocity stacking for multiple elimination[C].//56th Annual International Meeting. SEG Expanded Abstracts, 422-424. |
| [] | Hargreaves N, Cooper N, Whiting P. 2001. High-resolution Radon demultiple[C].//15th Geophysical Conference. ASEG Extended Abstracts, 1-4. |
| [] | Hong F, Hu T Y, Zhang W P, et al .2004. Attenuating multiples for low signal-to-noise ratio seismic data using optimal beamforming[J]. Chinese Journal of Geophysics (in Chinese), 47 (6) : 1106–1110. DOI:10.3321/j.issn:0001-5733.2004.06.025 |
| [] | Hu T Y, Wang R Q .2000. Beamforming in seismic data progressing[J]. Chinese Journal of Geophysics (in Chinese), 43 (1) : 105–115. DOI:10.3321/j.issn:0001-5733.2000.01.013 |
| [] | Hu T Y, Wang R Q, Wen S L .2002. Multiple attenuation of seismic data from south China sea by using beam-forming filtering method[J]. Oil Geophysical Prospecting (in Chinese), 37 (1) : 18–23. |
| [] | Huang Z L .2012. Multiple attenuation in deep water seismic exploration with combined application of SRME and Radon filtering[J]. Chinese Journal of Engineering Geophysics (in Chinese), 8 (6) : 659–665. |
| [] | Jiao J W, Leger P, Stevens J. 2002. Enhancements to wave-equation multiple attenuation[C].//2002 SEG Annual Meeting. SEG Expanded Abstracts, 2098-2101. |
| [] | Jin D G, Chang X, Liu Y K .2008. Algorithm improvement and strategy of internal multiples prediction based on inverse scattering series method[J]. Chinese Journal of Geophysics (in Chinese), 51 (4) : 1209–1217. |
| [] | Kabir M M N, Verschuur D J .1995. Restoration of missing offsets by parabolic radon transform[J]. Geophysical Prospecting, 43 (3) : 347–368. DOI:10.1111/gpr.1995.43.issue-3 |
| [] | Kennett B L N .1979. The suppression of surface multiples on seismic records[J]. Geophysical Prospecting, 27 (3) : 584–600. DOI:10.1111/gpr.1979.27.issue-3 |
| [] | Li H, Zhou D S, Zhou Q, et al .2014. A modular method for the attenuation of multiple waves in seismic data[J]. Value Engineering (in Chinese), 33 (7) : 323–324. |
| [] | Li P, Liu Y K, Chang X, et al .2006. Progress on the multiple problems[J]. Progress in Geophysics (in Chinese), 21 (3) : 888–897. DOI:10.3969/j.issn.1004-2903.2006.03.029 |
| [] | Li X, Hu T Y .2009. Surface-related multiple removal with inverse scattering series method[J]. Chinese Journal of Geophysics (in Chinese), 52 (6) : 1633–1640. DOI:10.3969/j.issn.0001-5733.2009.06.026 |
| [] | Lin T T Y, Herrmann F J .2013. Robust estimation of primaries by sparse inversion via one-norm minimization[J]. Geophysics, 78 (3) : R133–R150. DOI:10.1190/geo2012-0097.1 |
| [] | Liu G C, Chen X H, Song J W .2013. Estimation of primaries and multiples by sparse inversion for OBS data with integration of streamer data[J]. Chinese Journal of Geophysics (in Chinese), 56 (12) : 4288–4296. DOI:10.6038/cjg20131231 |
| [] | Liu H, Yuan J H, Gou Y F, et al .2007. Spectral factorization of wavefield and operator in seismic inverse scattering[J]. Chinese Journal of Geophysics (in Chinese), 50 (1) : 240–247. DOI:10.3321/j.issn:0001-5733.2007.01.030 |
| [] | Liu X W, Liu H, Li Y M .2004. High resolution Radon transform and its application in seismic signal processing[J]. Progress in Geophysics (in Chinese), 19 (1) : 8–15. DOI:10.3969/j.issn.1004-2903.2004.01.002 |
| [] | Liu Y K, Chang X, Wang H, et al .2008. Internal multiple removal and its application by wavepath migration[J]. Chinese Journal of Geophysics (in Chinese), 51 (2) : 589–595. DOI:10.3321/j.issn:0001-5733.2008.02.032 |
| [] | Liu Y K, Chang X, Jin D G, et al .2011. Reverse time migration of multiples for subsalt imaging[J]. Geophysics, 76 (5) : WB209–WB216. DOI:10.1190/geo2010-0312.1 |
| [] | Liu Y K, Zhu W L, Mi L J, et al .2014. Characteristics of multiples in the slope of the northern South China Seaand the suppressing method[J]. Chinese Journal of Geophysics (in Chinese), 57 (10) : 3354–3362. DOI:10.6038/cjg20141022 |
| [] | Loewenthal D, Lu L, Roberson R, et al. 1974. The wave equation applied to migration and water bottom multiples[C].//44th Annual SEG Meeting. Expanded Abstracts. |
| [] | Lu J M .2009. Principle of Seismic Exploration (in Chinese)[M]. 3rd ed. Dongying: China University of Petroleum Press . |
| [] | Moré J J, Toraldo G .1989. Algorithms for bound constrained quadratic programming problems[J]. Numerische Mathematik, 55 (4) : 377–400. DOI:10.1007/BF01396045 |
| [] | Morley L, Claerbout J .1983. Predictive deconvolution in shot-receiver space[J]. Geophysics, 48 (5) : 515–531. DOI:10.1190/1.1441483 |
| [] | Moses H E .1956. Calculation of the scattering potential from reflection coefficients[J]. Physical Review, 102 (2) : 559–567. DOI:10.1103/PhysRev.102.559 |
| [] | Peacock K L, Treitel S .1969. Predictive deconvolution:Theory and practice[J]. Geophysics, 34 (2) : 155–169. DOI:10.1190/1.1440003 |
| [] | Prosser R T .1969. Formal solutions of inverse scattering problems[J]. Journal of Mathematical Physics, 10 (10) : 1819–1822. DOI:10.1063/1.1664766 |
| [] | Riley D C, Claerbout J F .1976. 2-D multiple reflections[J]. Geophysics, 41 (4) : 592–620. DOI:10.1190/1.1440638 |
| [] | Sacchi M D, Porsani M. 1999. Fast high resolution parabolic Radon transform[C].//69th Annual International Meeting. SEG Technical Program Expanded Abstracts, 1477-1480. |
| [] | Sacchi M D, Ulrych T J .1995. High-resolution velocity gathers and offset space reconstruction[J]. Geophysics, 60 (4) : 1169–1177. DOI:10.1190/1.1443845 |
| [] | Sengbush R L. 1983. Seismic wave propagation[A].//Sengbush R L ed. Seismic Exploration Methods[M]. Netherlands:Springer, 13-30. |
| [] | Shi Y, Jing H L, Li Y .2012. Surface-related multiple suppression effect analysis by feedback iteration approach[J]. Progress in Geophysics (in Chinese), 27 (4) : 1493–1500. DOI:10.6038/j.issn.1004-2903.2012.04.024 |
| [] | Shumway R H, Dean W C .1968. Best linear unbiased estimation for multivariate stationary processes[J]. Technometrics, 10 (3) : 523–534. DOI:10.1080/00401706.1968.10490599 |
| [] | Stolt R H, Jacobs B. 1980. Inversion of seismic data in a laterally heterogeneous medium[R]. SEP Report, 135-152. |
| [] | Tan J, Wang X T .2012. Multiple attenuation based on event tracing[J]. Periodical of Ocean University of China (in Chinese), 42 (6) : 99–106. |
| [] | Tan S R, Huang L J .2014. Least-squares reverse-time migration with a wavefield-separation imaging condition and updated source wavefields[J]. Geophysics, 79 (5) : S195–S205. DOI:10.1190/geo2014-0020.1 |
| [] | Taner M T .1980. Long Period sea-floor multiples and their suppression[J]. Geophysical Prospecting, 28 (1) : 30–48. DOI:10.1111/gpr.1980.28.issue-1 |
| [] | Tang Y X .2009. Target-oriented wave-equation least-squares migration/inversion with phase-encoded Hessian[J]. Geophysics, 74 (6) : WCA95–WCA107. DOI:10.1190/1.3204768 |
| [] | van Groenestijn G J, Verschuur D J .2009a. Estimating primaries by sparse inversion and application to near-offset data reconstruction[J]. Geophysics, 74 (3) : A23–A28. DOI:10.1190/1.3111115 |
| [] | van Groenestijn G J, Verschuur D J .2009b. Estimation of primaries and near-offset reconstruction by sparse inversion:Marine data applications[J]. Geophysics, 74 (6) : R119–R128. DOI:10.1190/1.3213532 |
| [] | Verschuur D J, Berkhout A J .2005. Removal of internal multiples with the common-focus-point (CFP) approach:Part 2-Application strategies and data examples[J]. Geophysics, 70 (3) : V61–V72. DOI:10.1190/1.1925754 |
| [] | Verschuur D J, Berkhout A J, Wapenaar C P A .1992. Adaptive surface-related multiple elimination[J]. Geophysics, 57 (9) : 1166–1177. DOI:10.1190/1.1443330 |
| [] | Verschuur D J, Berkhout A J .2012. Estimation of multiple scattering by iterative inversion, Part Ⅱ:Practical aspects and examples[J]. Geophysics, 62 (5) : 1596–1611. |
| [] | Wang B L, Sacchi M D, Yin X Y, et al .2014. Multiple attenuation based on amplitude preserving Radon transform[J]. Chinese Journal of Geophysics (in Chinese), 57 (6) : 1924–1933. DOI:10.6038/cjg20140623 |
| [] | Wang J L, Wang Z L, Zhang H Z, et al .2009. A joint technique of mMultiple attenuation for offshore seismic data processings[J]. Progress in Geophysics (in Chinese), 24 (6) : 2070–2078. DOI:10.3969/j.issn.1004-2903.2009.06.020 |
| [] | Wang W H, Cui B W, Liu H .2007. Research progress in surface-related multiple attenuation[J]. Progress in Geophysics (in Chinese), 22 (1) : 156–164. DOI:10.3969/j.issn.1004-2903.2007.01.022 |
| [] | Wang W H, Jing H L .2015. 3D surface-related multiple elimination based on sparse inversion[J]. Chinese Journal of Geophysics (in Chinese), 58 (7) : 2496–2507. DOI:10.6038/cjg20150725 |
| [] | Wang W H, Liu H .2005. Near offset wavefield extrapolation based on parabolic Radon transform[J]. Progress in Geophysics (in Chinese), 20 (2) : 289–293. DOI:10.3969/j.issn.1004-2903.2005.02.004 |
| [] | Weglein A B .1999. Multiple attenuation:An overview of recent advances and the road ahead (1999)[J]. The Leading Edge, 18 (1) : 40–44. DOI:10.1190/1.1438150 |
| [] | Weglein A B, Gasparotto F A, Carvalho P M, et al .1997. An inverse-scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 62 (6) : 1975–1989. DOI:10.1190/1.1444298 |
| [] | Weglein A B, Hsu S Y, Terenghi P, et al .2011. Multiple attenuation:Recent advances and the road ahead (2011)[J]. The Leading Edge, 30 (8) : 864–875. DOI:10.1190/1.3626494 |
| [] | Weglein A B, Gray S H .1983. The sensitivity of Born inversion to the choice of reference velocity:A simple example[J]. Geophysics, 48 (1) : 36–38. DOI:10.1190/1.1441404 |
| [] | White R E. 1988. A multichannel method of multiple attenuation based on hyperbolic moveout curves[C].//50th EAEG Meeting. The Hague, Extended Abstracts, 1-22. |
| [] | Wiggins J W .1988. Attenuation of complex water-bottom multiples by wave-equation-based prediction and subtraction[J]. Geophysics, 53 (12) : 1527–1539. DOI:10.1190/1.1442434 |
| [] | Wong M, Ronen S, Biondi B. 2011. Least-squares reverse time migration/inversion for ocean bottom data:A case study[C].//2011 SEG Annual Meeting. SEG Technical Program Expanded Abstracts, 2369-2373. |
| [] | Wu Z P .1995. F-K filtering method after nmo correction in shot domain[J]. Oil Geophysical Prospecting (in Chinese), 30 (3) : 422–423. |
| [] | Xie S L, Liu Y K, Wang Y B, et al .2013. Study of diffracted multiple elimination on steep slope zone in deep water[J]. Chinese Journal of Geophysics (in Chinese), 56 (9) : 3118–3123. DOI:10.6038/cjg20130924 |
| [] | Xiong D, Zhao W, Zhang J F .2009. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple[J]. Chinese Journal of Geophysics (in Chinese), 52 (4) : 1068–1077. DOI:10.3969/j.issn.0001-5733.2009.04.024 |
| [] | Yang J K, Xu B X .1992. Adaptive predictive deconvolution[J]. Geophysical Prospecting for Petroleum (in Chinese), 31 (4) : 59–69. |
| [] | Yin J J, Wang W, Wang Y, et al .2007. Multiple wave attenuation based on scattering imaging[J]. Geophysical Prospecting for Petroleum (in Chinese), 46 (4) : 319–323. |
| [] | Zhang D L, Schuster G T .2014. Least-squares reverse time migration of multiples[J]. Geophysics, 79 (1) : S11–S21. DOI:10.1190/geo2013-0156.1 |
| [] | Zhao C L, Ye Y M, Yao G S, et al .2013. Prediction deconvolution in linear radon domain on the application of ocean multiples attenuation[J]. Progress in Geophysics (in Chinese), 28 (2) : 1026–1032. DOI:10.6038/pg20130256 |
| [] | Zhou B Z, Greenhalgh S .1996. Multiple suppression by 2D filtering in the parabolic τ-p domain:A wave-equation-based method[J]. Geophysical Prospecting (in Chinese), 44 (3) : 375–401. DOI:10.1111/gpr.1996.44.issue-3 |
| [] | Zhu S X, Qin H F .2013. Application of adaptive predictive deconvolution multiple attenuation in marine seismic data processing[J]. Science Technology and Engineering, 13 (36) : 10780–10786. |
| [] | 陈小宏, 刘华锋.2012. 预测多次波的逆散射级数方法与SRME方法及比较[J]. 地球物理学进展, 27 (3) : 1040–1050. DOI:10.6038/j.issn.1004-2903.2012.03.026 |
| [] | 洪菲, 胡天跃, 张文坡, 等.2004. 用优化聚束滤波方法消除低信噪比地震资料中的多次波[J]. 地球物理学报, 47 (6) : 1106–1110. DOI:10.3321/j.issn:0001-5733.2004.06.025 |
| [] | 洪菲, 胡天跃, 王润秋.2005. 利用三维聚束滤波方法消除相关噪声[J]. 石油地球物理勘探, 40 (1) : 42–47. |
| [] | 胡天跃, 王润秋.2000. 地震资料处理中的聚束滤波方法[J]. 地球物理学报, 43 (1) : 105–115. DOI:10.3321/j.issn:0001-5733.2000.01.013 |
| [] | 胡天跃, 王润秋, 温书亮.2002. 聚束滤波法消除海上地震资料的多次波[J]. 石油地球物理勘探, 37 (1) : 18–23. |
| [] | 黄兆林.2012. SRME与Radon滤波方法组合衰减深水多次波[J]. 工程地球物理学报, 8 (6) : 659–665. |
| [] | 金德刚, 常旭, 刘伊克.2008. 逆散射级数法预测层间多次波的算法改进及其策略[J]. 地球物理学报, 51 (4) : 1209–1217. |
| [] | 李贺, 周大森, 周卿, 等.2014. 一种组合式衰减地震资料中多次波的方法[J]. 价值工程, 33 (7) : 323–324. |
| [] | 李鹏, 刘伊克, 常旭, 等.2006. 多次波问题的研究进展[J]. 地球物理学进展, 21 (3) : 888–897. DOI:10.3969/j.issn.1004-2903.2006.03.029 |
| [] | 李翔, 胡天跃.2009. 逆散射级数法去除自由表面多次波[J]. 地球物理学报, 52 (6) : 1633–1640. DOI:10.3969/j.issn.0001-5733.2009.06.026 |
| [] | 刘国昌, 陈小宏, 宋家文.2013. 基于稀疏反演的OBS数据多次波压制方法[J]. 地球物理学报, 56 (12) : 4288–4296. DOI:10.6038/cjg20131231 |
| [] | 刘洪, 袁江华, 勾永峰, 等.2007. 地震逆散射波场和算子的谱分解[J]. 地球物理学报, 50 (1) : 240–247. DOI:10.3321/j.issn:0001-5733.2007.01.030 |
| [] | 刘喜武, 刘洪, 李幼铭.2004. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 19 (1) : 8–15. DOI:10.3969/j.issn.1004-2903.2004.01.002 |
| [] | 刘伊克, 常旭, 王辉, 等.2008. 波路径偏移压制层间多次波的理论与应用[J]. 地球物理学报, 51 (2) : 589–595. DOI:10.3321/j.issn:0001-5733.2008.02.032 |
| [] | 刘伊克, 朱伟林, 米立军, 等.2014. 南海北部陆坡区多次波发育特征及压制策略分析[J]. 地球物理学报, 57 (10) : 3354–3362. DOI:10.6038/cjg20141022 |
| [] | 刘伊克, 朱伟林, 米立军, 等.2015. 南海深水多次波成像[J]. 中国科学:地球科学, 45 (2) : 152–160. |
| [] | 陆基孟.2009. 地震勘探原理[M]. 3版. 东营: 中国石油大学出版社 . |
| [] | 石颖, 井洪亮, 李莹.2012. 反馈迭代法压制表面多次波效果分析[J]. 地球物理学进展, 27 (4) : 1493–1500. DOI:10.6038/j.issn.1004-2903.2012.04.024 |
| [] | 谭军, 王修田.2012. 基于同相轴追踪的多次波衰减[J]. 中国海洋大学学报, 42 (6) : 99–106. |
| [] | 王保丽, SacchiM D, 印兴耀, 等.2014. 基于保幅拉东变换的多次波衰减[J]. 地球物理学报, 57 (6) : 1924–1933. DOI:10.6038/cjg20140623 |
| [] | 王建立, 王真理, 张洪宙, 等.2009. 海上多次波的联合衰减法[J]. 地球物理学进展, 24 (6) : 2070–2078. DOI:10.3969/j.issn.1004-2903.2009.06.020 |
| [] | 王维红, 刘洪.2005. 抛物Radon变换法近偏移距波场外推[J]. 地球物理学进展, 20 (2) : 289–293. DOI:10.3969/j.issn.1004-2903.2005.02.004 |
| [] | 王维红, 崔宝文, 刘洪.2007. 表面多次波衰减的研究现状与进展[J]. 地球物理学进展, 22 (1) : 156–164. DOI:10.3969/j.issn.1004-2903.2007.01.022 |
| [] | 王维红, 井洪亮.2015. 基于稀疏反演三维表面多次波压制方法[J]. 地球物理学报, 58 (7) : 2496–2507. DOI:10.6038/cjg20150725 |
| [] | 吴战培.1995. 炮点域动校正后FK滤波[J]. 石油地球物理勘探, 30 (3) : 422–423. |
| [] | 谢宋雷, 刘伊克, 王一博, 等.2013. 深水陡坡带绕射多次波压制方法研究[J]. 地球物理学报, 56 (9) : 3118–3123. DOI:10.6038/cjg20130924 |
| [] | 熊登, 赵伟, 张剑锋.2009. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J]. 地球物理学报, 52 (4) : 1068–1077. DOI:10.3969/j.issn.0001-5733.2009.04.024 |
| [] | 杨积凯, 徐伯勋.1992. 自适应预测反褶积[J]. 石油物探, 31 (4) : 59–69. |
| [] | 尹军杰, 王伟, 王赟, 等.2007. 基于散射成像的多次波衰减[J]. 石油物探, 46 (4) : 319–323. |
| [] | 张军华, 缪彦舒, 郑旭刚, 等.2009. 预测反褶积去多次波几个理论问题探讨[J]. 物探化探计算技术, 31 (1) : 6–10. |
| [] | 赵昌垒, 叶月明, 姚根顺, 等.2013. 线性拉东域预测反褶积在海洋多次波去除中的应用[J]. 地球物理学进展, 28 (2) : 1026–1032. DOI:10.6038/pg20130256 |
| [] | 朱四新, 秦鸿飞.2013. 自适应预测反褶积多次波衰减技术在海上地震资料处理中的应用[J]. 科学技术与工程, 13 (36) : 10780–10786. |
 2016, Vol. 31
2016, Vol. 31


