2. 中国石油集团测井有限公司油气评价中心, 西安 710077
3. 中国石油吐哈油田分公司开发部, 吐鲁番 838202
2. Oil and Gas Evaluation Center, CNPC Logging Co. Ltd., Xi'an 710077, China
3. Development Department of Tuha Oilfield Company, Tulufan 838202, China
随着油气勘探开发的不断深入,常规中高孔渗储集层的测井评价方法已趋于成熟,评价的重点转为非常规储层,其中低孔低渗透的泥质砂岩储层占很大比例(杨雪,2008;张丽华等,2010).测井定量评价储层流体饱和度最常用的方法是建立电阻率—饱和度模型,而低孔渗泥质砂岩储层由于泥质含量多、微孔隙发育、束缚水饱和度高,岩石的导电机理复杂且容易形成低阻油气层,使储层电阻率与含水饱和度的对应关系不明显,流体性质确定及定量评价困难(葛新民等,2011;宋延杰等,2014).正是由于这种导电机理的复杂性,以及不同储层岩性和孔隙结构的地区差异,目前针对泥质砂岩储层的导电模型种类多样,其中应用最广的是Waxman-Smits模型(以下简称W-S模型)和双水模型,而它们的应用效果也随着泥质含量的多少和分布形式的变化而有所限制(石玉江等,2008;李霞等,2012),作者针对这种情况,通过理论分析与实验数据验证,对这两种模型进行对比并提出改进方法,旨在通过细化它们的最佳适用条件从而使饱和度评价的精度得以提高.
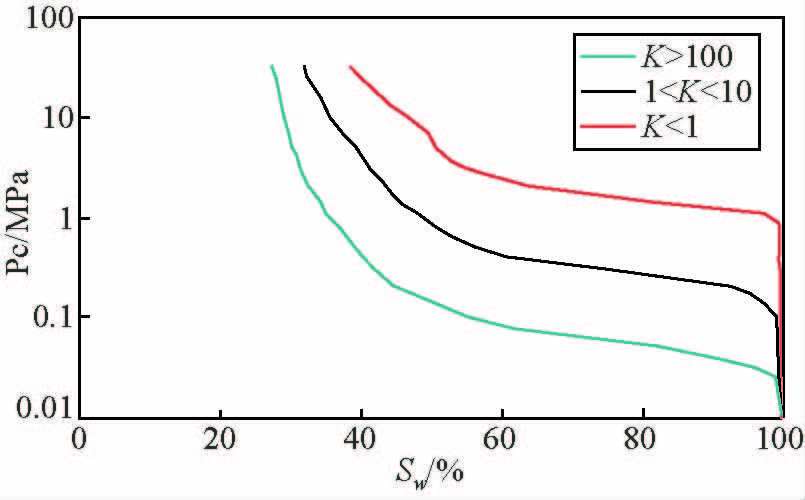
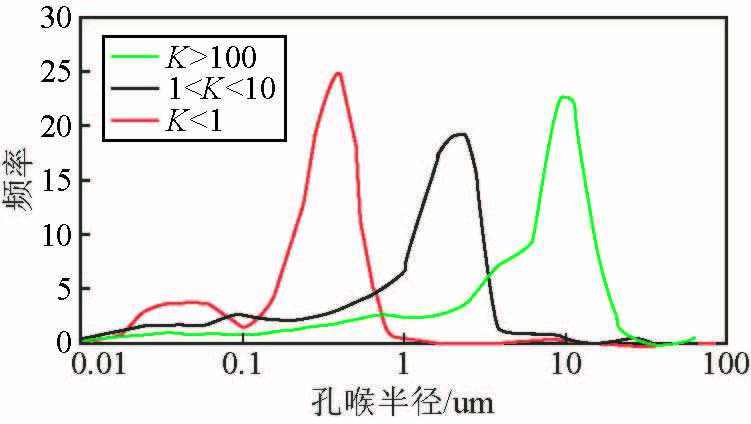
1 低孔渗泥质砂岩储层的物性和岩电特征低渗透储层一般矿物成熟度低,岩石中不稳定组分和粘土含量高,这种低成熟度的矿物在成岩过程中容易形成复杂的孔隙结构.同时这类储层更容易形成微孔隙和溶蚀孔隙,孔隙半径小且连通性差(曾大乾和李淑贞,1994).图 1和图 2分别为研究区不同渗透率范围内岩样的毛管曲线和孔喉半径分布图,可以看出渗透率K<1 mD的岩样毛管力明显增加且束缚水饱和度非常高,小孔径的孔隙占总孔隙体积的比例非常大.
|
图 1 不同渗透率范围的岩样毛管压力曲线 Figure 1 Capillary pressure curves for cores with different permeability |
|
图 2 不同渗透率范围的岩样孔喉分布曲线 Figure 2 Pore throat distribution for cores with different permeability |
低孔渗泥质砂岩储层的上述物性和孔隙结构特征,容易导致以下电性特征:①小孔径孔隙体积比例高、束缚水饱和度高使岩石整体导电性增强,使油水层之间的电阻率差别不明显,即形成低阻油气层.②复杂的孔隙结构与较高的泥质含量使岩石的导电机理复杂,电导率与含水饱和度的关系不符合常规阿尔奇公式,饱和度模型建立困难.③储集层的低孔低渗特性导致测井响应复杂多解.储层的物性差,含油饱和度低,岩性、孔隙结构等非流体因素对测井响应的影响增大,使油水层定量评价困难(张海涛,2010;孔强夫等,2015).
2 W-S模型及应用效果分析泥质砂岩储层的饱和度模型普遍认为岩石整体的导电性是其各个组成部分并联导电的结果.且岩石中颗粒较粗、分选性好、孔隙较大的部分,对其导电机理的认识比较一致,即自由流体的离子导电,并满足阿尔奇公式.而对于低孔渗泥质砂岩微孔隙内的流体导电或是泥质中的粘土导电,则不同的模型采用不同的计算方法.
2.1 W-S模型电导率公式W-S模型假设泥质砂岩的导电性是自由地层水和粘土的阳离子交换并联导电的结果,且交换阳离子传导的电流和自由地层水中离子传导的电流是沿着同样的路径传输的,即并联电导率公式中二者的权系数相同,通过计算得到系数为泥质砂岩地层因数的倒数,由此得到W-S模型的电导率公式为(雍世和和张超谟,2002):
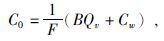
|
(1) |
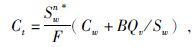
|
(2) |
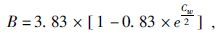
|
(3) |
其中,C0、Ct、Cw分别为完全含水泥质砂岩、含油气泥质砂岩和地层水的电导率;F为泥质砂岩的地层因数;Qv为泥质砂岩的阳离子交换容量;B为交换阳离子的当量电导率;Sw为含油气泥质砂岩的总含水饱和度.
W-S模型在泥质砂岩储层的评价中应用较为广泛,但仍然存在一些实际困难:①Qv的准确求取存在一定的困难;②泥质砂岩真实地层因数或者说是岩电参数由于泥质附加导电影响偏小,需要经过Qv校正后得到.
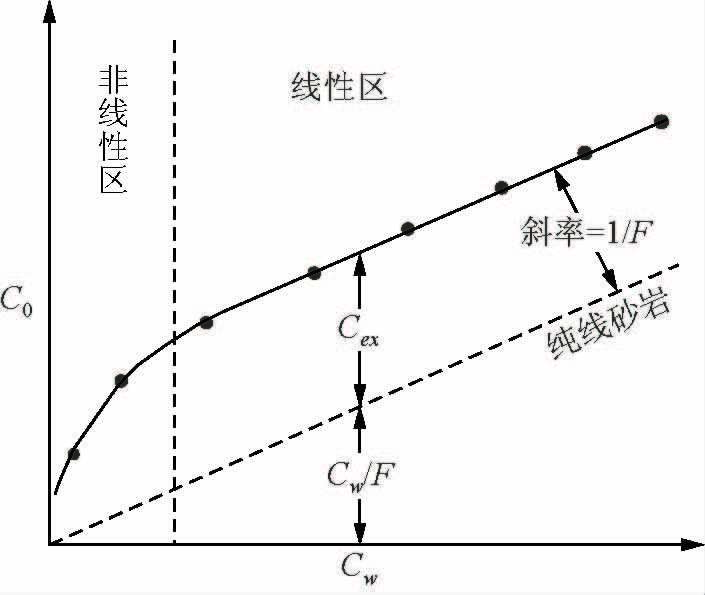
2.2 W-S模型应用效果分析由于认为泥质砂岩的导电性是自由地层水和粘土的阳离子交换并联导电的结果,所以含水泥质砂岩的电导率与孔隙度和泥质砂岩总孔隙度相等的纯砂岩相比要高一些,其岩石电导率与地层水电导率在对数坐标下的关系如图 3,泥质砂岩线总是在纯砂岩线的上方.在Cw较小时,C0增加的速度大于Cw,此后Cw再进一步增加时C0呈线性增加,其中直线部分的斜率与孔隙度和泥质砂岩总孔隙度相等的纯砂岩线斜率相同,等于公式(1)中的1/F.仿纯砂岩阿尔奇公式,设泥质砂岩的视地层因数为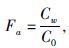
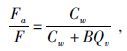
|
(4) |
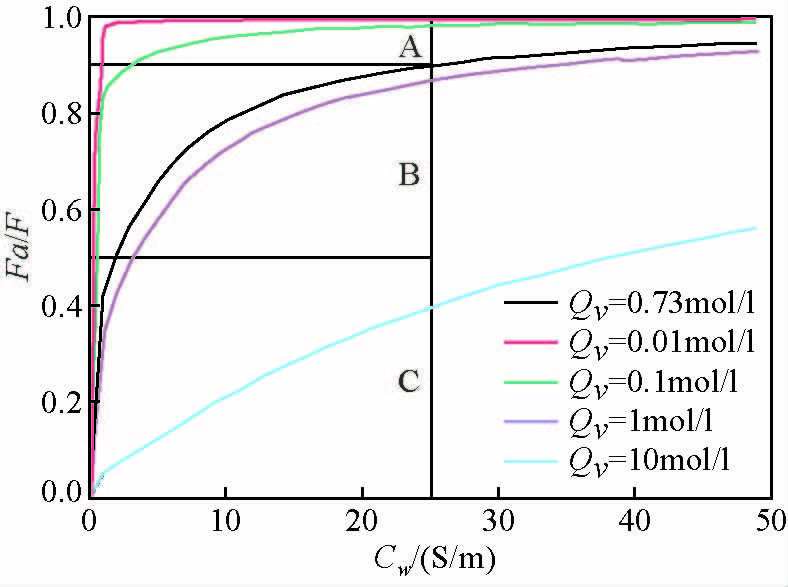
Fa/F表示泥质砂岩偏离阿尔奇特性的程度.当BQv=0,Fa/F=1,为纯砂岩导电,即满足阿尔奇公式;泥质砂岩中BQv>0,Fa/F<1,呈现出非阿尔奇性的特点.图 4中横坐标为地层水电导率Cw,纵坐标为泥质砂岩偏离阿尔奇公式的量度Fa/F,不同的曲线代表泥质含量即Qv的大小不同.根据Fa/F的大小可将图上的区域分为三部分:A区(Fa/F >0.9)为阿尔奇砂岩区,B区(0.5 <Fa/F<0.9)为一般泥质砂岩区,C区(Fa/F<0.5)为重泥质砂岩区.从图上不同曲线的分布位置可以看出,泥质砂岩导电规律是否符合阿尔奇公式,主要是由Qv也就是泥质含量决定的,Qv越大,曲线越偏离阿尔奇区(Worthington,2004,2007).其中Qv=0.73的曲线正好通过Cw=25 s/m(此电导率是室温下NaCl溶液在实验室中能达到的最大值)与Fa/F=0.9的交点,说明Qv<0.73的岩石可以通过增大饱和溶液电导率Cw的方法来使岩样点沿着特定曲线进入A区,即可以通过泥质校正得到岩样的真实地层因数,而Qv>0.73的岩石,从曲线上可以看出饱和溶液的电导率达到最大值25 s/m时也无法进入A区,即Qv引起的偏离阿尔奇的程度无法得到完全校正,也就是说,W-S模型中泥质砂岩的真实地层因数F无法准确确定,所以W-S模型在Qv较大的泥质砂岩中应用效果较差(单沙沙,2011).
3 双水模型分析及改进 3.1 双水模型电导率公式作为对W-S模型的改进,双水模型认为粘土孔隙中的水性质与大孔隙中的自由水不同,它由于粘土颗粒表面的排盐作用,矿化度比自由水要低且具有阳离子交换导电作用,但二者的导电路径相同,可以看作并联导电,混合后溶液的电导率为(雍世和和张超谟,2002):
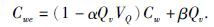
|
(5) |
而岩石的导电性是这两种溶液共同导电的结果,仿阿尔奇公式,可得完全含水泥质砂岩的电导率方程为
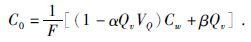
|
(6) |
含油气泥质砂岩的电导率方程为
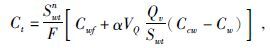
|
(7) |
其中,α为Na+扩散层的扩散因子;β为粘土水中补偿离子Na+的等效电导率(S/m),β=0.0857T(℃)-0.143;VQ为Qv=1 mmol/cm3时粘土水占据的孔隙体积,VQ=1/[2.853+0.019T(℃)];Ccw为粘土水的电导率,Ccw=β/αVQ,Cwf为自由水的电导率(S/m).
双水模型与W-S模型相比,考虑了粘土表面的排盐作用和离子双电层中的不可动水膜对于岩石导电性的影响.但是双水模型所需要的基本参数包括φt、Cw、Ccw、α、VQ和Qv,需要确定的参数较多,且仍然需要准确确定Qv的值来得到真实的地层因数.
|
图 3 W-S模型中岩石电导率与地层水电导率的关系 Figure 3 The relationship between rock conductivity and formation water conductivity of W-S model |
|
图 4 W-S模型中Fa/F随地层水电导率的变化 Figure 4 The Fa/F changes with formation water conductivity of W-S model |
鉴于双水模型中Qv难以确定的困难提出改进思路,即避开Qv而通过其他方法计算真实的地层因数.实验发现双水模型中C0与Cw的关系与W-S模型中泥质砂岩线永远在纯砂岩线之上不同,而是两条曲线在Cw达到一定值时相交,如图 5,即在此地层水矿化度下泥质砂岩与等效纯砂岩的电导率相同,将此时的Cw=Cwn称为“中和点”,则:
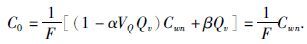
|
(8) |
|
图 5 双水模型岩石电导率随地层水电导率的变化 Figure 5 The rock conductivity changes with formation water conductivity of Dual-water model |
将式(8)与双水模型中的电导率方程及参数计算公式联立可求出Cwn=7.0 S/m.即泥质砂岩的导电性与具有相同孔隙度和曲折度,孔隙中被电导率为Cwn的单一均匀溶液所饱和的纯砂岩一样,于是泥质砂岩真实地层因数F就等于Cw=Cwn时所观察到的视地层因数,而不需要经过Qv校正,减少了由于Qv测量不准确而导致的误差.
3.3 改进模型的应用效果分析仿照对于W-S模型的分析,双水模型中岩石视地层因数与真实地层因数的比值为:

|
(9) |
其关系曲线如图 6所示,双水模型的Fa/F值与W-S模型中恒小于1不同,在双水模型中视地层因数可能大于也可能小于真实地层因数,这与地层水的矿化度有关.图中无论砂岩岩样点落在哪个区域,在室温所能达到的饱和溶液电导率范围内都找到一个电导率值Cw,使得岩样点能够进入阿尔奇区域即能得到该岩样的真实地层因数.并且对于具有不同Qv的泥质砂岩的Fa/F-Cw曲线都交于Cw=7.0 S/m点,在此点处Fa/F=1.也就是说无论Qv的值如何,Cw=7.0 S/m点的视地层因数恒为岩样的真实地层因数.也就是说岩样的真实地层因数可直接由Cw=7.0时的饱含水岩样的电导率与溶液电导率的比值得出,与Qv无关不用再去进行泥质校正.

|
图 6 双水模型中Fa/F随地层水电导率的变化 Figure 6 The Fa/F changes with formation water conductivity of Dual-water model |
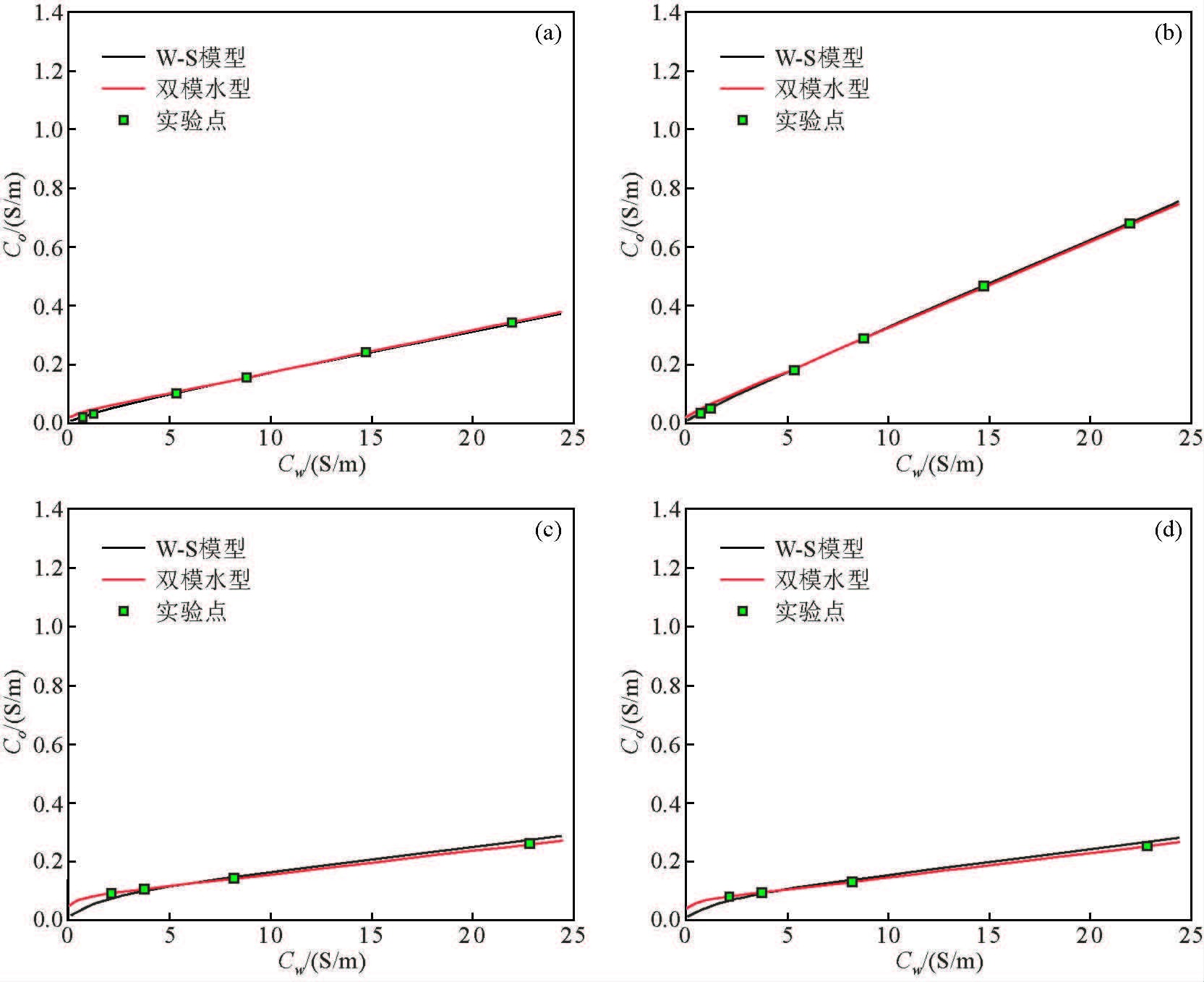
对某地区低孔低渗的岩样进行岩电实验,对其中4块进行编号,其中1、2号岩样Qv较小,而3、4号岩样Qv较大,泥质含量多.图 7为这四块岩样的岩石电导率与饱和水电导率的关系图,从图中可以看出,泥质含量少的岩石,W-S模型和改进的双水模型的模拟曲线都符合实验结果(图 7a、图 7b),而泥质含量重的岩石,W-S模型的计算结果在Cw较大时与实验结果相吻合,在Cw较小时符合率较差,改进的双水模型计算的结果基本与实验数据完全吻合(图 7c、图 7d).
|
图 7 W-S模型和双水模型计算结果与实验数据对比图 (a)岩样1:por=0.095,K=0.2,Qv=0.578;(b)岩样2:por=0.165,K=0.9,Qv=0.232;(c)岩样3:por=0.119,K=0.35,Qv=2.057;(d)岩样4:por=0.122,K=0.83,Qv=1.669. Figure 7 The comparison of calculation results and experimental data of W-S model and Dual-water model |
W-S模型中:①Qv的确定至关重要,直接影响到饱和度模型的计算结果;②地层水矿化度低时W-S模型的C0-Cw曲线为非直线,地层因数难以确定,地层水矿化度较高时地层因数接近等效纯砂岩的地层因数;③泥质含量少的泥质砂岩可以通过Qv校正得到真实的地层因数,而泥质含量重的泥质砂岩无法得到真实的地层因数.
4.2双水模型在W-S模型的基础上进行了改进,考虑了粘土水与自由水导电性的不同;泥质砂岩的真实地层因数可以通过Qv校正得到,也可以通过改变岩石饱和溶液的电导率直接进行测量得到;双水模型在泥质含量较重的岩石中的应用效果比W-S模型要好.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Ge X M, Fan Y R, Yang D G, et al .2011. Study on the influential factors of saturation exponent based on the equivalent rock element theory[J]. Oil Geophysical Prospecting (in Chinese), 46 (3) : 477–481. |
| [] | Kong Q F, Zhou C C, Zhang Y, et al .2015. Numerical simulation methods of rock electrical properties based on digital cores:A review[J]. Progress in Geophysics (in Chinese), 30 (2) : 718–724. DOI:10.6038/pg20150232 |
| [] | Li X, Zhao W Z, Zhou C C, et al .2012. Dual-porosity saturation model of low-porosity and low-permeability clastic reservoirs[J]. Petroleum Exploration and Development (in Chinese), 39 (1) : 82–91. DOI:10.1016/S1876-3804(12)60018-4 |
| [] | Shan S S. 2011. Research on the conductive mechanism of low-permeability Shaly Sand (in Chinese)[MSc. thesis]. Qingdao:China University of Petroleum. |
| [] | Shi Y J, Li G R, Zhou J Y .2008. Study on Litho-electric character and saturation model of argillaceous low-permeability sandstone reservoir[J]. Well Logging Technology (in Chinese), 32 (3) : 203–206. |
| [] | Song Y J, Zhang X, Song Y, et al .2014. On effective medium conductivity model based on non-efficient electrical pore for tight sandy conglomerate reservoirs[J]. Progress in Geophysics (in Chinese), 29 (1) : 209–216. DOI:10.6038/pg20140129 |
| [] | Worthington P F .2004. Characterization of the intrinsic porosity exponent through dual-salinity measurements of electrical conductivity[J]. Petrophysics, 45 (6) : 499–516. |
| [] | Worthington P F .2007. Petrophysical type curves for identifying the electrical character of petroleum reservoirs[J]. SPE Reservoir Evaluation & Engineering, 10 (6) : 711–729. |
| [] | Yang X. 2008. Determination of water saturation model on low porosity and low permeability reservoir and its application in SongNan area (in Chinese)[MSc. thesis]. Changchun:Jinlin University. |
| [] | Yong S H, Zhang C M .2002. Logging data processing and comprehensive interpretation (in Chinese)[M]. Dongying: China University of Petroleum Press . |
| [] | Zeng D Q, Li S Z .1994. Types and Characteristics of low permeability sandstone reservoirs in China[J]. Acta Petrolei Sinica (in Chinese), 15 (1) : 38–46. |
| [] | Zhang H T. 2010. Well logging identification method of gas reservoir in Sulige field (in Chinese)[Ph. D. thesis]. Xi'an:Northwest University. |
| [] | Zhang L H, Pan B Z, Li Z B, et al .2010. New three-water conduction model and its application in evaluation of low porosity and low permeability reservoir[J]. Oil Geophysical Prospecting (in Chinese), 45 (3) : 431–435. |
| [] | 葛新民, 范宜仁, 杨东根, 等.2011. 基于等效岩石组分理论的饱和度指数影响因素[J]. 石油地球物理勘探, 46 (3) : 477–481. |
| [] | 孔强夫, 周灿灿, 张艳, 等.2015. 基于数字岩心岩石电性数值模拟方法综述[J]. 地球物理学进展, 30 (2) : 718–724. DOI:10.6038/pg20150232 |
| [] | 李霞, 赵文智, 周灿灿, 等.2012. 低孔低渗碎屑岩储集层双孔隙饱和度模型[J]. 石油勘探与开发, 39 (1) : 82–91. |
| [] | 单沙沙. 2011. 低渗透泥质砂岩导电模型研究[硕士论文]. 青岛:中国石油大学. http://cn.bing.com/academic/profile?id=4f71c6c2ff4b683b02d23198378a751b&encoded=0&v=paper_preview&mkt=zh-cn |
| [] | 石玉江, 李高仁, 周金昱.2008. 泥质型低渗砂岩储层岩电性质研究及饱和度模型的建立[J]. 测井技术, 32 (3) : 203–206. |
| [] | 宋延杰, 张啸, 宋杨, 等.2014. 基于无效导电孔隙概念的致密砂砾岩有效介质导电模型[J]. 地球物理学进展, 29 (1) : 209–216. DOI:10.6038/pg20140129 |
| [] | 杨雪. 2008. 低孔低渗储层含水饱和度模型的确定及在松南地区的应用[硕士论文]. 长春:吉林大学. http://cn.bing.com/academic/profile?id=31d0b0b89363a5873eb4a9a938a4e67e&encoded=0&v=paper_preview&mkt=zh-cn |
| [] | 雍世和, 张超谟.2002. 测井数据处理与综合解释[M]. 东营: 中国石油大学出版社 . |
| [] | 曾大乾, 李淑贞.1994. 中国低渗透砂岩储层类型及地质特征[J]. 石油学报, 15 (1) : 38–46. |
| [] | 张海涛. 2010. 苏里格地区有效储层测井识别方法研究[博士论文]. 西安:西北大学. |
| [] | 张丽华, 潘保芝, 李舟波, 等.2010. 新三水导电模型及其在低孔低渗储层评价中的应用[J]. 石油地球物理勘探, 45 (3) : 431–435. |
 2016, Vol. 31
2016, Vol. 31

