近年来,不断增加的油气需求迫使向更为复杂的油气藏类型勘探,带来对油气储集体的判识难度也随之加大,因此对流体敏感参数的识别能力提出更高的要求.为了从地震资料中获取更多反映储层流体的有效信息,充分利用纵、横波反射信息,国内外学者相继提出了基于弹性理论、孔隙介质理论和各向异性理论的多种“定量”流体因子来提高储层流体判识的能力,并取得了较好的应用效果(Zong et al.,2013; 印兴耀等,2013; Russell,2014; 陈怀震等,2014; 张震等,2014; 谢春辉等,2015).
基于地震资料的储层流体描述是一项综合性强、与实际资料联系紧密且需长期研究的课题(印兴耀等,2014).Smith和Gidlow(1987)率先提出基于权差方法的储层含油气性预测方法.Russell等人(2006)结合Gassmann孔隙流体理论,研究了基于Gassmann流体项f的流体识别方法.Zhang等人(2010)等研究了Gassmann流体项的适用范围,指出在孔隙度变化剧烈的区域,f对油气检测的准确度会降低.郑静静等(2011)通过对流体因子关系的分析,构建了一种新的流体因子.宗兆云等(2012)基于叠前弹性阻抗反演理论,构建了基于纵横波模量的弹性阻抗方程,发展了基于纵横波模量的流体检测方法.李红梅(2013)研究了泊松比参数直接反演方法,并发展了基于泊松比参数的储层油气识别方法.余振等(2014)针对薄层流体的精细预测问题,将带岩性遮挡的地质统计学反演和叠前AVA同步反演相结合,提出一种高分辨率流体预测方法.
结合Han和Batzle(2004)岩石物理实验结果,在Russell等人(2006)提出的多孔饱和流体弹性介质的反射特征方程基础上,推导出包含流体等效体积模量的固液解耦流体弹性波阻抗方程,并利用该反演方法实现了胜利油田埕岛地区东斜坡下第三系不整合圈闭碎屑岩储层流体识别,研究表明,通过流体等效体积模量对下第三系油气层分布有了进一步的认识,取得了不错的应用效果.
1 固液解耦纵波反射系数基于多孔弹性介质岩石物理和AVO理论的深入研究,Russell等人(2006)在2006年提出了包含Gassmann流体项f的反射系数近似公式为

|
(1) |
Han和Batzle(2004)通过对碎屑岩进行岩石物理统计,提出了突出流体等效体积模量的Gassmann流体项的经验公式为
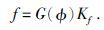
|
(2) |
将公式(2)代入到公式(1)中,并将μ替换为干岩石剪切模量μdry变换可得:
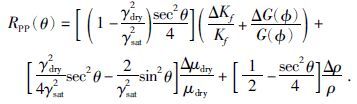
|
(3) |
接下来,利用临界孔隙度模型构建增益函数G(ø)与干岩石剪切模量μdry之间的联系.Nur等人(1998)通过大量研究表明,对于小于临界孔隙度的岩石,可以用与临界孔隙度øc有关的线性函数来表示其干岩石的体积模量和剪切模量,公式为
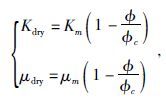
|
(4) |
其中,øc表示临界孔隙度,Kdry、Km分别代表干岩石、矿物颗粒的体积模量,μdry、μm分别代表干岩石、矿物颗粒的剪切模量.
通常情况下的储层,特别是碎屑岩储层,一般都属于小于临界孔隙度的承载域,利用临界孔隙度模型可以较好的表征其干岩石体积模量和剪切模量随孔隙度的变化规律.以Nur等人(1998)模型为纽带对公式(3)进一步解耦可得:
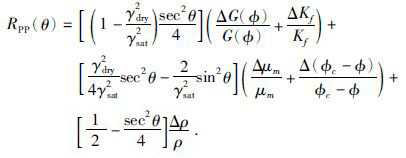
|
(5) |
将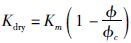
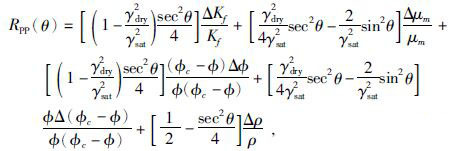
|
(6) |
化简得到:
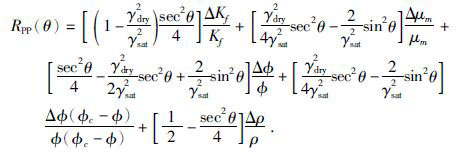
|
(7) |
假设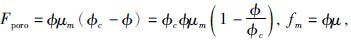
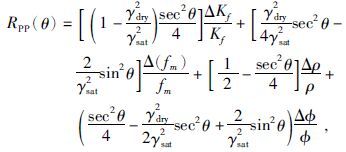
|
(8) |
其中,fm=øμ,称为为固体刚性参数.
2 精度分析为了验证上式的精度,结合某碎屑岩工区的实际数据,利用流体替代的方法设计了三种两层砂岩模型进行测试.模型参数如表 1所示,其中临界孔隙度均为27%.模型一为上层含气砂岩,下层含水砂岩,两层孔隙度相同;模型二的两层均为含水砂岩,但孔隙度存在差异,上层孔隙度为25%,下层孔隙度为15%;模型三的两层砂岩所含流体与孔隙度均不同,上层含气砂岩,孔隙度为15%,下层含水砂岩,孔隙度为25%,分别采用精确的Zoeppritz方程、Aki-Richard近似公式以及固液两相解耦AVO近似公式计算三种模型界面的反射系数,计算结果分别如图 1~3所示,并对误差结果进行分析.
|
|
表 1 三种砂岩模型参数 Table 1 Three parameters of sandstone model |
|
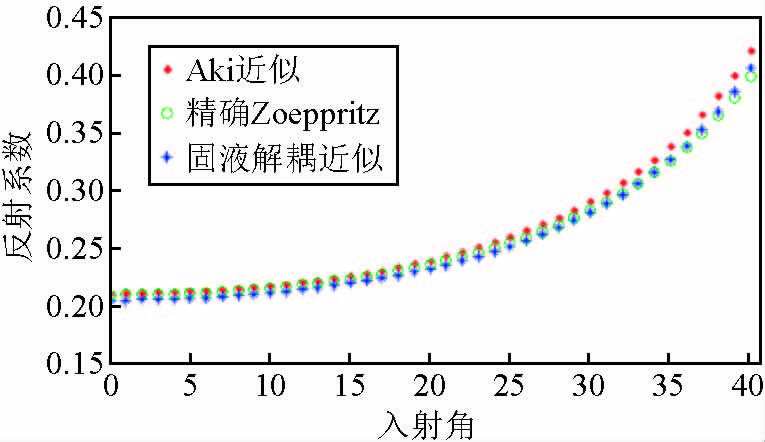
图 1 模型一的反射系数结果 Figure 1 The reflection coefficient of model 1 |
|
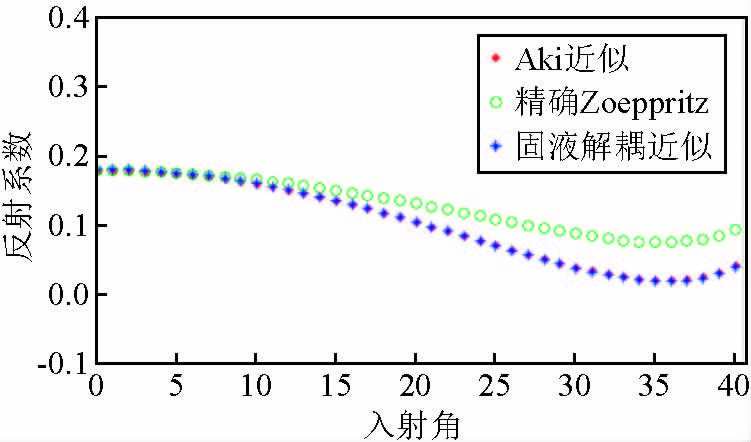
图 2 模型二的反射系数结果 Figure 2 The reflection coefficient of model 2 |
|
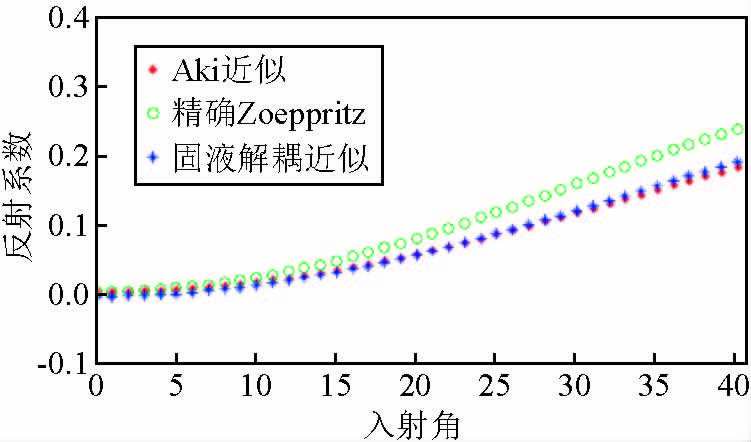
图 3 模型三的反射系数结果 Figure 3 The reflection coefficient of model 3 |
从图 1可知,当界面两侧介质仅存在孔隙流体不同时,固液解耦的AVO近似公式精度与Aki-Richard近似吻合较好,且均能够与Zoeppritz精确结果有较好的匹配;从图 2可知,当界面两侧介质孔隙流体相同,孔隙度发生变化时,随着入射角的增大,固液解耦的AVO近似仍与Aki-Richard近似吻合较好,但是两者的计算数值均逐渐偏离精确Zoeppritz结果,但是在入射角度小于40度的范围内,两者的相对误差并不大;从图 3可知,当界面两侧介质的孔隙度和孔隙流体均存在差异时,固液解耦AVO近似与Aki-Richard近似仍然一致,但两者同样随着入射角度的增加偏离精确Zoeppritz方程计算结果.分析其原因得出,固液解耦的AVO近似是基于Aki-Richard近似公式推导而来的,因此两者的近似精度的能够保持一致.此外,两者在孔隙度变化时产生较大误差,究其原因是因为AVO线性近似公式的建立在界面两侧具有微小弹性扰动的假设条件下的,而孔隙度的变化会对岩石模量信息造成较大影响,进而引起了大角度入射情况下的较大误差.但是,从宏观的角度来看,固液解耦的AVO近似公式在小角度入射情况下满足反射系数的近似精度,而实际应用中使用的角道集一般也不会超过30°,因此,固液解耦的AVO近似公式在误差允许的范围内能够满足反射系数精度要求.
3 弹性阻抗标准化方程借鉴Connolly(1999)、Whitcombe(2002)及印兴耀等(2010)推导的弹性阻抗思想,将反射系数表达为弹性阻抗的函数,即:
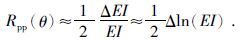
|
(9) |
将(8)式代入上式,得到:
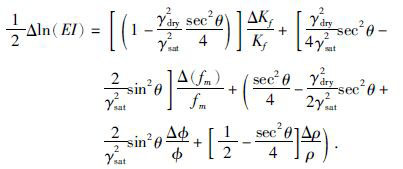
|
(10) |
将弹性参数的相对变化量表示为对数形式,可以得到:
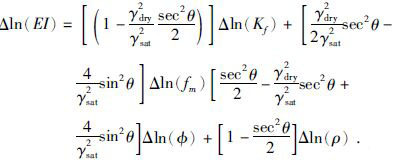
|
(11) |
再次变形,可得:
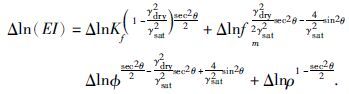
|
(12) |
将公式(12)作积分和指数化变形,可得:
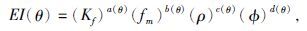
|
(13) |
其中,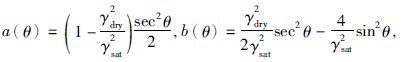
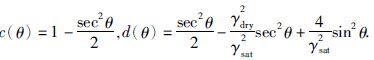
由于公式(13)中的弹性阻抗量纲随角度变化较大不利用不同角度的比较,在此引入EI0,f0,μ0和ρ0四个常数,对其作标准化处理,可得:
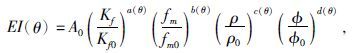
|
(14) |
Kf0,fm0,ρ0以及ø0分别定义为Kf,fm,ρ以及ø的平均值.A0为标准化因子,具体表达式为
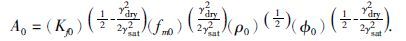
|
(15) |
利用方程(14)从EI(θ)中提取各项参数,但是此方程式是非线性的,若直接求解势必带来不少的麻烦,为此可将方程进行变换,采用印兴耀等(2010)给出的方法,使之成为线性形式并进行方程组的求解,就可以得到井旁道任意一个采样点处的Kf、fm、ρ、ø值.在提取了流体等效体积模量参数后,基于岩石物理分析标准即可直接用于流体识别.
4 实际资料应用 4.1 工区概况埕岛地区位于济阳坳陷、渤中坳陷和郯庐断裂带三大构造体系交汇处,受多期运动叠加的影响,形成了以潜山披覆构造含油为主的油气分布特点,在下第三系地层发育有多级不整合地层圈闭.目前,该区块东营组已探明储量可观,油气成藏具有平面上区块分散,主体及周边均有探明.含油面积小,但单井产能高的特点.在构造、岩性、古地貌等控制下,形成多种油藏类型,在东部斜坡带地层位于潜山披覆构造上,沙河街组部分缺失,东营组各段向潜山斜坡层层披覆,形成各类岩性、地层隐蔽油藏.研究重点为东部斜坡带不整合圈闭储层含油气分布预测.
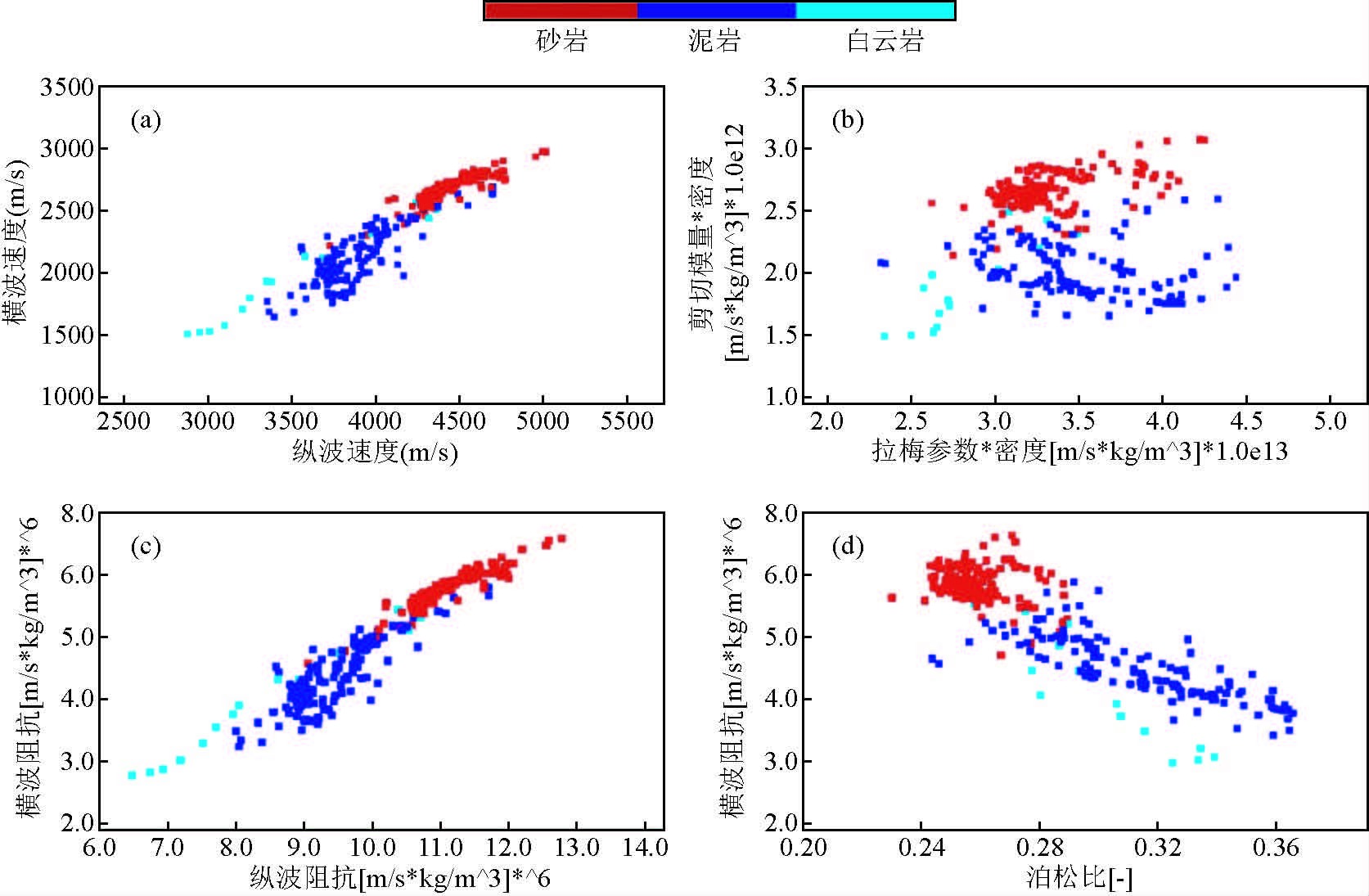
4.2 岩石物理分析结合工区录井资料,利用SP、GR和电阻率等测井曲线分析单井相特征,并分析22口井的储层岩性,从而明确储层沉积类型为滨浅湖滩坝,岩性为砂岩、灰质砂岩、生物灰岩、白云岩,厚度从1.5 m到17 m,平均5 m.选择对储层类型反映敏感的岩石物性参数,对储层预测和流体识别意义重大,选定合适的参数可以减小地震储层解释的不确定性和多解性.通过已有井资料对工区内多种岩石弹性参数进行岩石物理交会分析,发现利用常规多种弹性参数均可区分砂泥岩(图 4).
|
图 4 sh8井弹性参数交会分析结果 Figure 4 Analysis results of the elastic parameters of sh8 well |
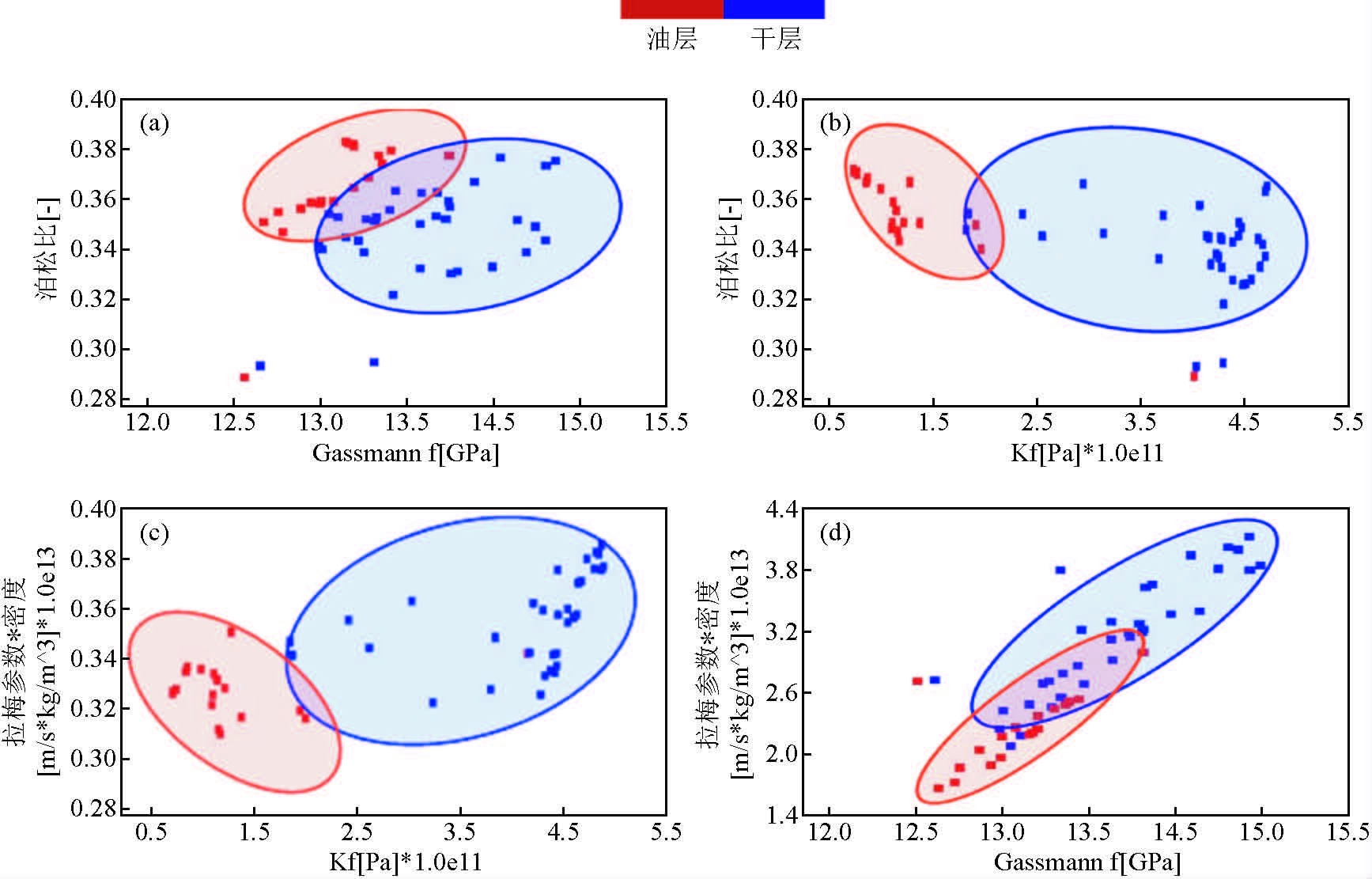
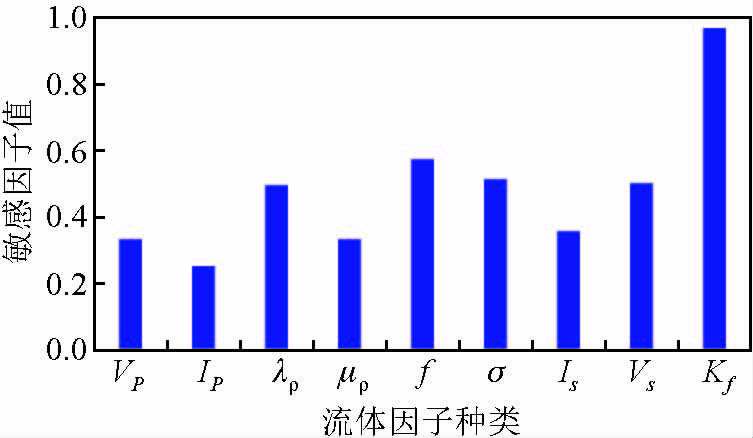
为了找到较好的敏感流体因子,统计出不同弹性参数对流体的敏感系数(图 5),最终发现流体等效体积模量Kf对流体的敏感性最高,能够较好地区分岩石孔隙所含流体类型.通过对胜海801井进行流体交会分析,发现流体等效体积模量比Gassmann流体项对流体的判识效果更好,验证了利用基于固液解耦的流体因子叠前地震直接反演方法对不整合圈闭储层进行含油气预测的可行性.
|
图 5 不同弹性参数流体敏感性评价图 Figure 5 Evaluation of fluid sensitivity with different elastic parameters |
|
图 6 sh801井流体交会分析结果 Figure 6 Analysis of fluid intersection in sh801 well |
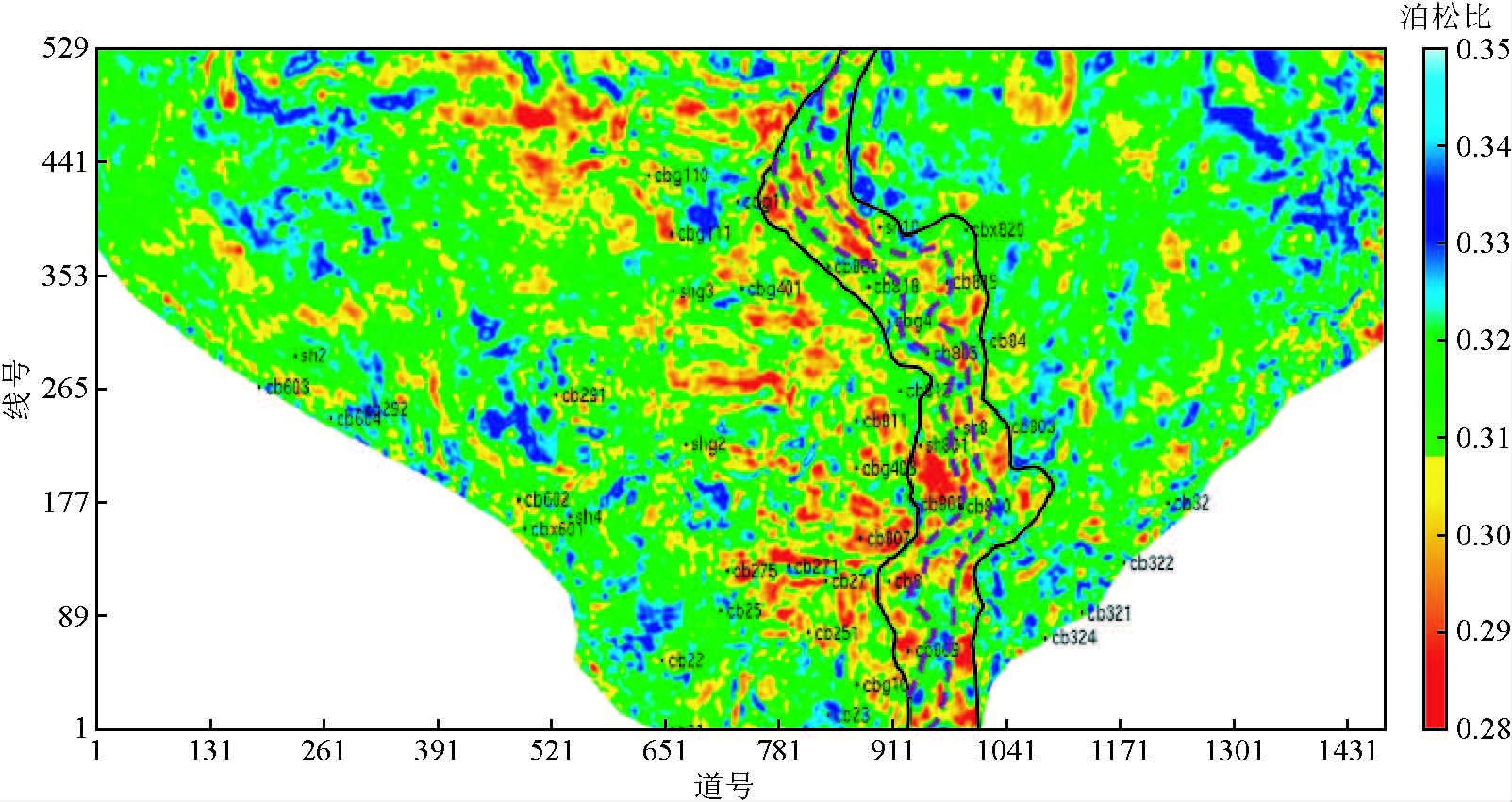
首先,基于岩石物理理论和实际测井资料进行了不同弹性参数的岩性交会,对比交会结果确定利用泊松比参数识别东斜坡带的砂质滩坝储层.利用叠前地震反演技术反演得到工区内的泊松比数据体,完成研究区内下第三系砂质滩坝储层的预测.图 7为由反演得到的泊松比数据体获取的目的层段泊松比切片图,图中黑色曲线圈定区域代表埕岛东斜坡湖相沉积带,里面的泊松比红黄色低值区域可以反映着沿岸不均匀发育窄条带滩坝相砂岩储层分布情况,图中虚线刻画出湖相沉积沿岸分布的特征,预测结果与钻井结果吻合率达82%.因此,泊松比参数可有效识别砂质滩坝储层.
|
图 7 不整合圈闭泊松比切片 Figure 7 Poisson's ratio section of unconformity traps |
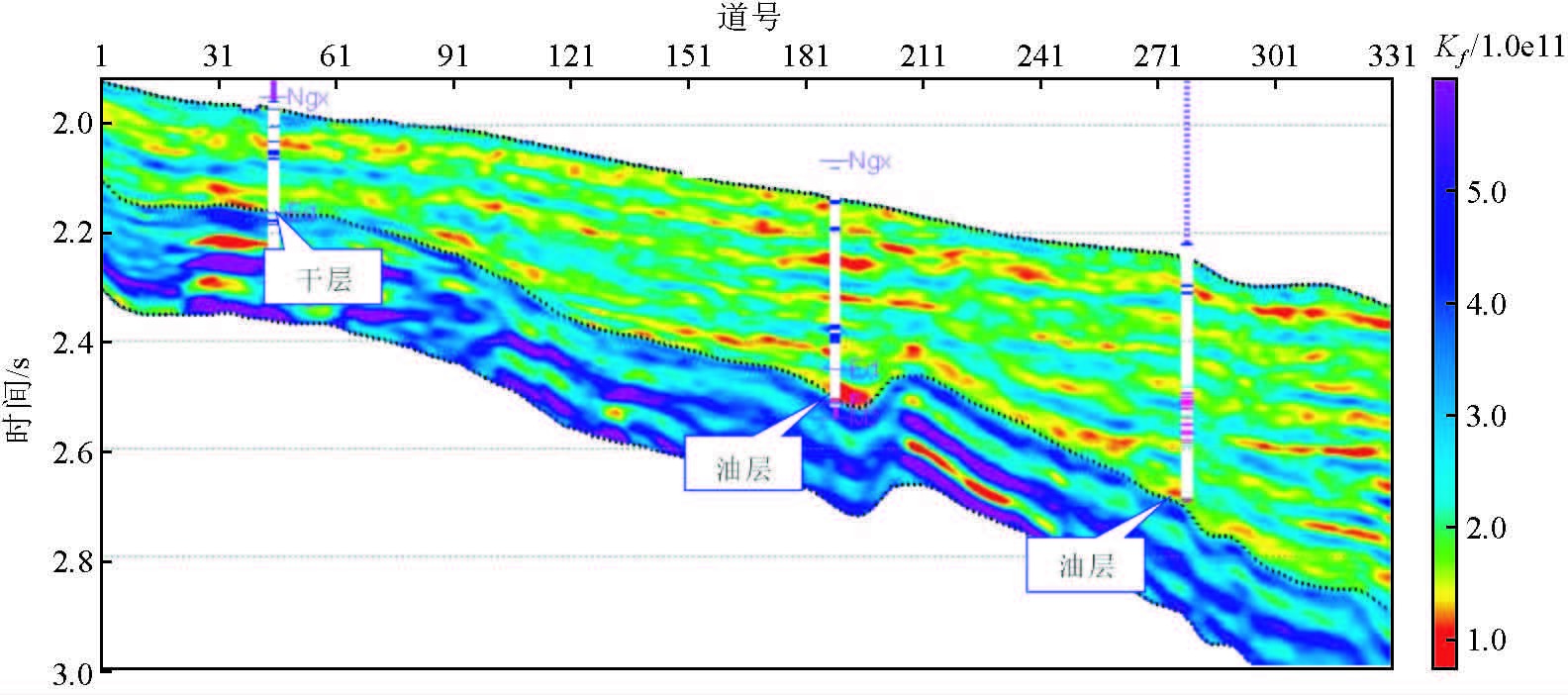
其次,利用流体等效体积模量参数开展流体检测.通过不同弹性参数的地震岩石物理交会结果分析可知,流体等效体积模量参数比其他弹性参数对储层含油气性的检测更为敏感.利用流体弹性波阻抗反演技术,获得研究区内流体等效体积模量参数数据体.图 8为研究区内过埕北古401-埕北818-埕北819连井线的流体等效体积模量剖面图,红色区域代表油气分布情况,与已钻井的油层解释结果吻合.
|
图 8 过cbg401-cb818-cb819连井剖面 Figure 8 Cross cbg401-cb818-cb819 well profile |
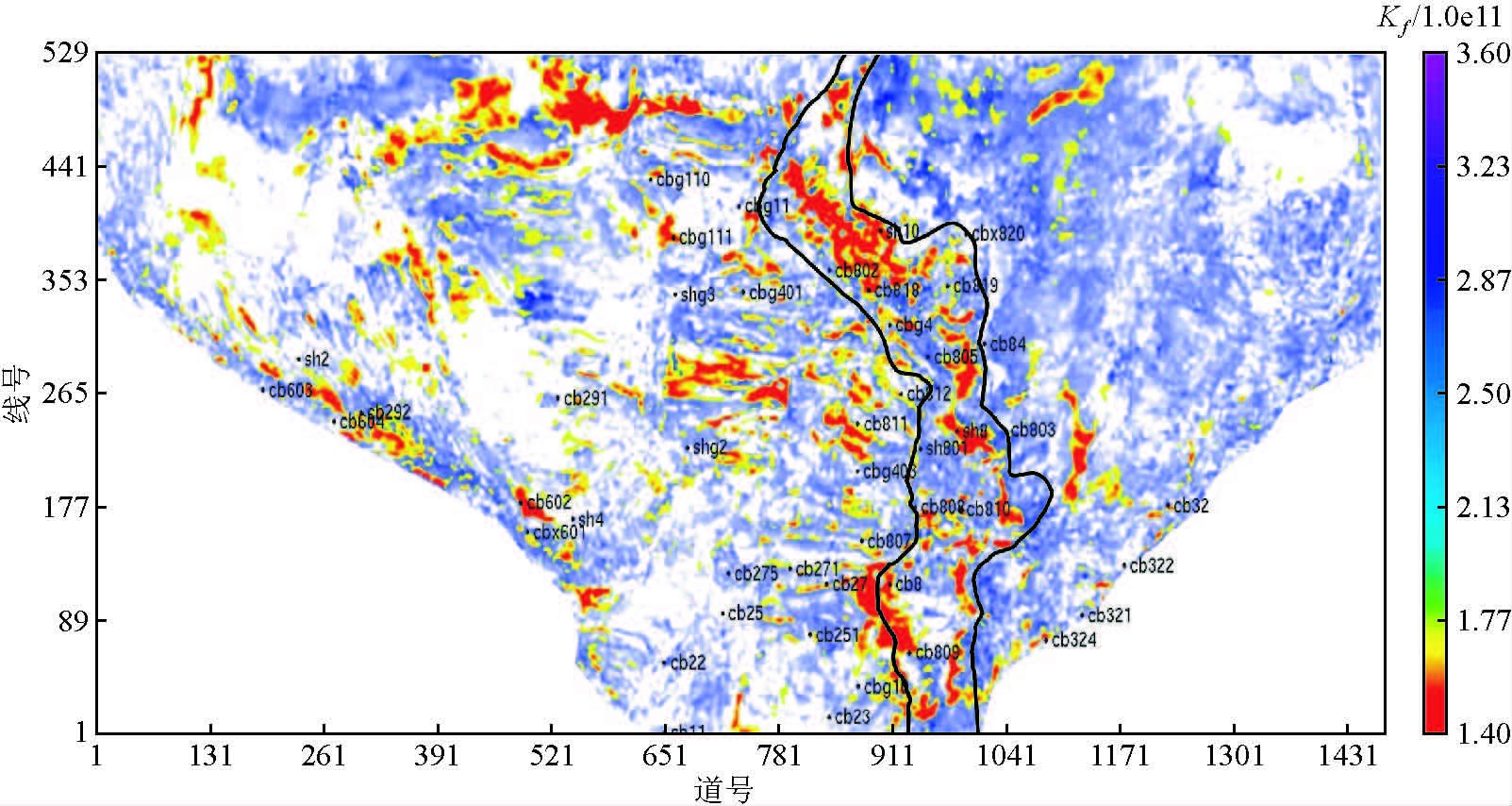
最后,利用流体等效体积模量进行含油气砂体的平面分布描述.图 9为目的层流体等效体积模量镂空与均方根振幅叠合切片图,红黄色区域表示油气分布范围,对比东斜坡带砂质滩坝内的井,预测结果与钻井油层吻合率达到75%.因此,流体等效体积模量能有效检测油气.
|
图 9 不整合圈闭等效流体模量切片图(红色圆圈标注的井为该目的层含油井) Figure 9 Equivalent fluid model slice of unconformity trap(the well marked by the red circle is an oil well) |
基于双相介质理论和岩石物理实验构建的孔隙流体等效体积模量能够降低岩石固液耦合效应产生的流体识别假象,对于固结成熟的碎屑岩储层,该流体因子能够比Gassmann流体项更好的区分孔隙流体类型,并具有较高的流体指示敏感性.通过固液解耦的流体弹性波反演方法直接提取流体等效体积模量参数,实现了埕岛东斜坡下第三系不整合圈闭储层流体识别,预测出含油气储层的分布,为油气的勘探和开发提供依据.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Chen H Z, Yin X Y, Gao C G, et al .2014. AVAZ inversion for fluid factor based on fracture anisotropic rock physics theory[J]. Chinese Journal of Geophysics (in Chinese), 57 (3) : 968–978. DOI:10.6038/cjg20140326 |
| [] | Connolly P .1999. Elastic impedance[J]. The Leading Edge, 18 (4) : 438–452. DOI:10.1190/1.1438307 |
| [] | Han D H, Batzle M L .2004. Gassmann's equation and fluid-saturation effects on seismic velocities[J]. Geophysics, 69 (2) : 398–405. DOI:10.1190/1.1707059 |
| [] | Li H M .2013. Application of Poisson's ratio direct inversion to reservoir hydrocarbon detection[J]. Progress in Geophysics (in Chinese), 28 (6) : 3049–3055. DOI:10.6038/pg20130628 |
| [] | Nur A, Mavko G, Dvorkin J, et al .1998. Critical porosity:A key to relating physical properties to porosity in rocks[J]. The Leading Edge, 17 (3) : 357–362. DOI:10.1190/1.1437977 |
| [] | Russell B H .2014. Prestack seismic amplitude analysis:An integrated overview[J]. Interpretation, 2 (2) : SC19–SC36. DOI:10.1190/INT-2013-0122.1 |
| [] | Russell B H, Gray D, Hampson D P, et al. 2006. Linearized AVO and poroelasticity[R]. CREWES Research Report. http://cn.bing.com/academic/profile?id=c1ccab73cd75628fb8f21e1e755381e4&encoded=0&v=paper_preview&mkt=zh-cn |
| [] | Smith G C, Gidlow P M .1987. Weighted stacking for rock property estimation and detection of gas[J]. Geophysical Prospecting, 35 (9) : 993–1014. DOI:10.1111/gpr.1987.35.issue-9 |
| [] | Whitcombe D N .2002. Elastic impedance normalization[J]. Geophysics, 67 (1) : 60–62. DOI:10.1190/1.1451331 |
| [] | Xie C H, Yong X S, Yang W Y, et al .2015. The method for identification of fluid in fractured reservoirs[J]. Chinese Journal of Geophysics (in Chinese), 58 (5) : 1776–1784. DOI:10.6038/cjg20150527 |
| [] | Yin X Y, Cao D P, Wang B L, et al .2014. Research progress of fluid discrimination with pre-stack seismic inversion[J]. Oil Geophysical Prospecting (in Chinese), 49 (1) : 22–34. |
| [] | Yin X Y, Zhang S X, Zhang F C, et al .2010. Utilizing Russell approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting (in Chinese), 45 (3) : 373–380. |
| [] | Yin X Y, Zhang S X, Zhang F .2013. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification[J]. Chinese Journal of Geophysics (in Chinese), 56 (7) : 2378–2390. DOI:10.6038/cjg20130724 |
| [] | Yu Z, Wang Y C, He Y, et al .2014. A high resolution approach for fluid prediction based on prestack AVA simultaneous inversion and geostatistical inversion[J]. Oil Geophysical Prospecting (in Chinese), 49 (3) : 551–560. |
| [] | Zhang S X, Yin X Y, Zhang F C, et al. 2010. Quasi fluid modulus for delicate lithology and fluid discrimination[C].//80th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 404-408. |
| [] | Zhang Z, Yin X Y, Hao Q Y .2014. Frequency-dependent fluid identification method based on AVO inversion[J]. Chinese Journal of Geophysics (in Chinese), 57 (12) : 4171–4184. DOI:10.6038/cjg20141228 |
| [] | Zheng J J, Yin X Y, Zhang G Y .2011. Fluid factor analysis and the construction of the new fluid factor[J]. Progress in Geophysics (in Chinese), 26 (2) : 579–587. DOI:10.3969/j.issn.1004-2903.2011.02.024 |
| [] | Zong Z Y, Yin X Y, Wu G C .2012. Fluid identification method based on compressional and shear modulus direct inversion[J]. Chinese Journal of Geophysics (in Chinese), 55 (1) : 284–292. DOI:10.6038/j.issn.0001-5733.2012.01.028 |
| [] | Zong Z Y, Yin X Y, Wu G C .2013. Direct inversion for a fluid factor and its application in heterogeneous reservoirs[J]. Geophysical Prospecting, 61 (5) : 998–1005. DOI:10.1111/gpr.2013.61.issue-5 |
| [] | 陈怀震, 印兴耀, 高成国, 等.2014. 基于各向异性岩石物理的缝隙流体因子AVAZ反演[J]. 地球物理学报, 57 (3) : 968–978. DOI:10.6038/cjg20140326 |
| [] | 李红梅.2013. 泊松比参数直接反演方法在储层油气检测中的应用[J]. 地球物理学进展, 28 (6) : 3049–3055. DOI:10.6038/pg20130628 |
| [] | 谢春辉, 雍学善, 杨午阳, 等.2015. 裂缝型储层流体识别方法[J]. 地球物理学报, 58 (5) : 1776–1784. DOI:10.6038/cjg20150527 |
| [] | 印兴耀, 曹丹平, 王保丽, 等.2014. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 49 (1) : 22–34. |
| [] | 印兴耀, 张世鑫, 张繁昌, 等.2010. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 45 (3) : 373–380. |
| [] | 印兴耀, 张世鑫, 张峰.2013. 针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究[J]. 地球物理学报, 56 (7) : 2378–2390. DOI:10.6038/cjg20130724 |
| [] | 余振, 王彦春, 何静, 等.2014. 基于叠前AVA同步反演和地质统计学反演的高分辨率流体预测方法[J]. 石油地球物理勘探, 49 (3) : 551–560. |
| [] | 张震, 印兴耀, 郝前勇.2014. 基于AVO反演的频变流体识别方法[J]. 地球物理学报, 57 (12) : 4171–4184. DOI:10.6038/cjg20141228 |
| [] | 郑静静, 印兴耀, 张广智.2011. 流体因子关系分析以及新流体因子的构建[J]. 地球物理学进展, 26 (2) : 579–587. DOI:10.3969/j.issn.1004-2903.2011.02.024 |
| [] | 宗兆云, 印兴耀, 吴国忱.2012. 基于叠前地震纵横波模量直接反演的流体检测方法[J]. 地球物理学报, 55 (1) : 284–292. DOI:10.6038/j.issn.0001-5733.2012.01.028 |
 2016, Vol. 31
2016, Vol. 31

