2. 吉林省有色金属地质勘查局六○七队, 吉林 132105
3. 中国冶金总局中南地质勘探查院, 武汉 430062
4. 中国地质大学, 地球物理与信息技术学院, 北京 100083
2. Jilin Nonferrous Metal Geological Exploration Bureau 607 team, Jilin 132105, China
3. Introduction to Central South Geo-exploration Institute, Wuhan 430062, China
4. China university of geosciences, School of Geophysics and information Technology, Beijing 100083, China
小波分析是包括函数空间、广义函数、傅里叶级数和积分、奇异积分算子与拟微分算子等领域半个世纪以来的研究结晶,也是信号与图像分析和工程技术在数学方法上的重大突破.它克服了付里叶分析不能获得信号局部特性,因而不能应用于局部分析的缺欠.随着该方法的深入发展,其优越性越来越得以显现.近年来,小波变换被越来越广泛地应用于地球物理各个领域.其中,将位场进行小波多尺度分解,给重磁异常的处理解释提供了非常有利的数学工具.重磁异常是处于不同深度和不同尺度地质体所产生的位场叠加,通过对位场进行适当的分解,可以定量地反演计算场源的物性和几何参数.
对于复杂的重磁异常,由于区域异常和局部异常的谱部分重叠,付立叶分析方法对异常的分离效果不尽人意.异常谱重叠越多,分离就越困难,要求的先验信息也越多.利用小波变换的多分辨原理,可得到复杂重磁异常在不同分辨率下的逼近和细节信息.同时,由于可合理地确定分解层数,根据异常的识别结果进行位变重构,从而使复杂异常得到分层次的最佳分离,解决了重磁资料解释中对复杂异常难以正确解释的难题(侯遵泽和杨文采,1997,2001;杨文采等,2004).
多年来,应用小波多尺度分析分解重磁位场时,确定各阶小波细节所反映的深度一直是应用频谱分析的方法.该方法的缺陷是人为因素较强,很难得到确切的小波细节所反映的深度.本文应用正演模拟计算方法,通过试验和分析,找到小波多尺度变换细节所反映的深度与该细节分解尺度之间的关系,为小波多尺度分析在重磁数据处理中的应用打下基础.我们还将该方法应用到吉林省磐石县红旗岭铜镍矿实测数据处理说明本文方法的有效性.
1 小波多尺度分析理论基础函数f(x)的小波变换定义为
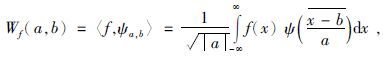
|
(1) |
其中ψ(x)∈L2(R)称为小波函数.
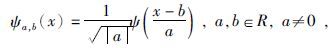
|
(2) |
相应的小波逆变换为
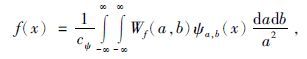
|
(3) |
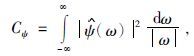
|
(4) |
$\tilde{\psi }$(ω)是ψ(x)的付氏变换.取a=a0m,b=nb0a0m,a0>1,b0∈R,则函数f的离散小波变换为
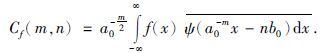
|
(5) |
从(5)式可以看出,小波变换对不同的频率成分(a0-m)在空间域上的取样步长(b0a0m)是具有调节作用的.高频(即小m值)取样步长小,低频(即大m值)取样步长大.小波变换能将信号或图像等分解成交织在一起的多种尺度成分,并对于大小不同的尺度成分采用相应的空间域取样步长,从而能够不断地聚焦到对象的任意微小细节.由此可以看出,小波变换在空间域和频率域同时具有良好的局部化性质.正因如此,小波变换被誉为数学显微镜.
小波分析具有多尺度分解功能,典型的算法是Mallat塔式分解算法.简述如下.
设{VJ}是L2(R)空间中一个给定的多分辨分析,φ和ψ分别是相应的尺度函数和小波函数,我们对一个函数f进行如下分解,公式为
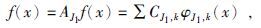
|
(6) |
由于
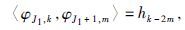
|
(7) |
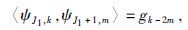
|
(8) |
我们有
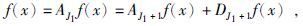
|
(9) |
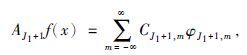
|
(10) |
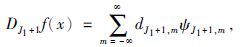
|
(11) |
上式中的C和d是与尺度函数和小波函数相关的分解系数,可由如下公式计算(Hou,1997,1998),公式为
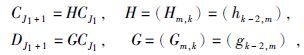
|
(12) |
如此递推,我们得到
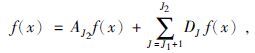
|
(13) |
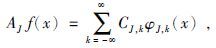
|
(14) |
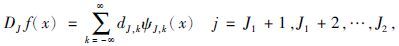
|
(15) |
而
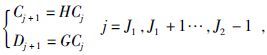
|
(16) |
(16)式便是Mallat的塔式分解算法. 我们称AJf为f在2J分辨率下的连续逼近,DJf为f在2J分辨率下的连续细节.(13)~(16)式表明,按Mallat的塔式分解算法,将函数f分解成不同频率通道成分,并将每一频道成分按相位进行了分解—频率越高者,相位划分越细,反之则越疏.
2 小波多尺度分析在重磁异常分解中的应用原则在重磁勘探中,地表的观测值实际上是地下地质体特征在地表的某种近似反映.一般来说,对于大比例尺详查工作,采样密度越大,获得的地下地质信息越丰富.反之,对于小比例尺勘查,采样密度较小,采样点间隔较大,采集数据所携带的信息量小,分辨率也低.对于给定的采样值,其中既含有浅部的细节信息,又包含有深部的构造信息及噪声.如何将它们区分开来,即将异常分解成不同的频段成分,从而识别不同大小、不同埋深的地质体,是勘探地球物理的目标之一.小波多尺度分析理论为我们提供了理论基础,Mallat的快速算法给我们提供了一条解决问题的途径.
Mallat 塔式算法,从原理分析到实际计算都体现出小波多尺度分析的一个准则,称为低阶细节不变准则,它反映了离散小波分解的优越性.
设位场数据矩阵为D,经 n 阶(整数n≥2)离散小波变换后产生小波细节D1,D2,…,Dn-1,Dn和n阶逼近Da,其中小波细节 D1,D2,…,Dn-1不随n的增大而改变.这个准则的优点在于,不管怎样选择 n,小波变换出来的低阶小波细节都是一样的,不同的只是小波细节的个数和n 阶逼近.例如,如果想要将重力异常分解为区域场和局部异常,则可以利用上述准则进行.首先假设 n=3,小波分析后取得小波细节 D1,D2,D3和三阶逼近 Da(n=3),如果 Da 显示出平滑的区域场特征,则 Da 为区域场,,DL=D1+D2+D3 为局部场;如果 Da 仍然包含小尺度的异常信息,则进行4阶小波变换(n=4),显示 Da(n=4),如此类推,直到n使得Da满足区域场的要求,则 DL+Dn为局部场,Da为区域场.
离散小波变换的小波细节,其尺度是随2m而增大的.假设数据取样网格间距为Δ,记一阶小波细节的尺度为 L(一般为4Δ到 8Δ),则2阶小波细节的尺度为 2L,3 阶细节为 4L,4 阶细节为8L,5阶细节为16L,对应高阶逼近的尺度远大于16L(Hou,2011).
3 高精度重力小波多尺度分析模型实验 3.1 重力模型设置根据Mallat 塔式算法,离散小波变换的小波细节尺度是随2m增大的,要寻找小波细节与分解尺度之间的关系,需将目标体放置于小波细节分解尺度的深度来考察所表现的重力异常特点.
基于这样的思想,本实验按不同剖分网格设置三个模型,如图 1所示.将大小不等的立方体勘探目标按小波细节的分解尺度放置于不同深度,即一阶小波细节的尺度为 L=4Δ(网格长度),2阶小波细节的尺度为 2L,3阶细节为4L,四阶小波细节为8L,五阶小波细节为16L,六阶小波细节为32L.由此,可得表 1中模型1~3的目标体中心埋深.模型3的目标体则不是按上述规律设置的,主要用于与上述三个模型的对比,考察其不同之处.为了方便对比,四个模型取同样的剩余密度.
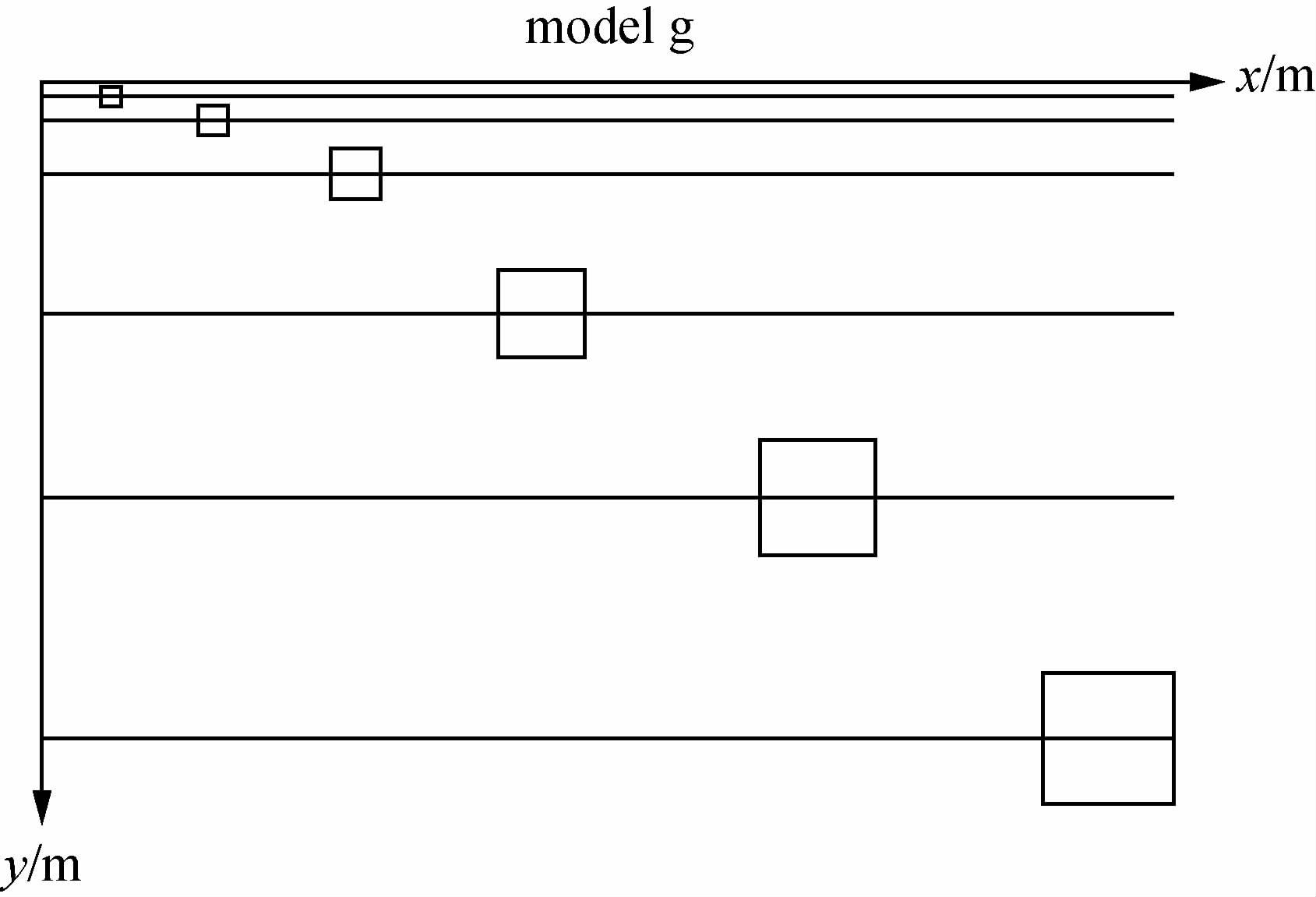
|
图 1 重力小波分析模型示意图 Figure 1 The model for gravity wavelet analysis |
|
|
表 1 重力小波分析模型参数设置 Table 1 Parameters for gravity wavelet analysis |
在对以上模型的重力场进行正演得到综合重力场值后,再进行小波细节分析,得到一系列小波细节图.
模型1的剖分网格为10 m×10 m,正演计算得到综合重力场值为g-1,经小波分析后得到六阶细节.我们用g-1d1、g-1d2、g-1d3、g-1d4、g-1d5、g-1d6表示一阶至六阶小波细节,g-1a6为区域场六阶逼近(图 2);模型2的剖分网格是25 m×25 m,正演计算得到综合重力场为g-2,经小波分析后得到五阶小波细节,依次为g-2d1、g-2d2、g-2d3、g-2d4、g-2d5,五阶小波逼近为g-2a5(图 3);模型3的剖分网格是50 m×50 m,正演计算得到综合重力场为g-3,经小波分析后得到四阶小波细节,依次为g-3d1、g-3d2、g-3d3、g-3d4,四阶小波逼近为g-3a4(图 4).
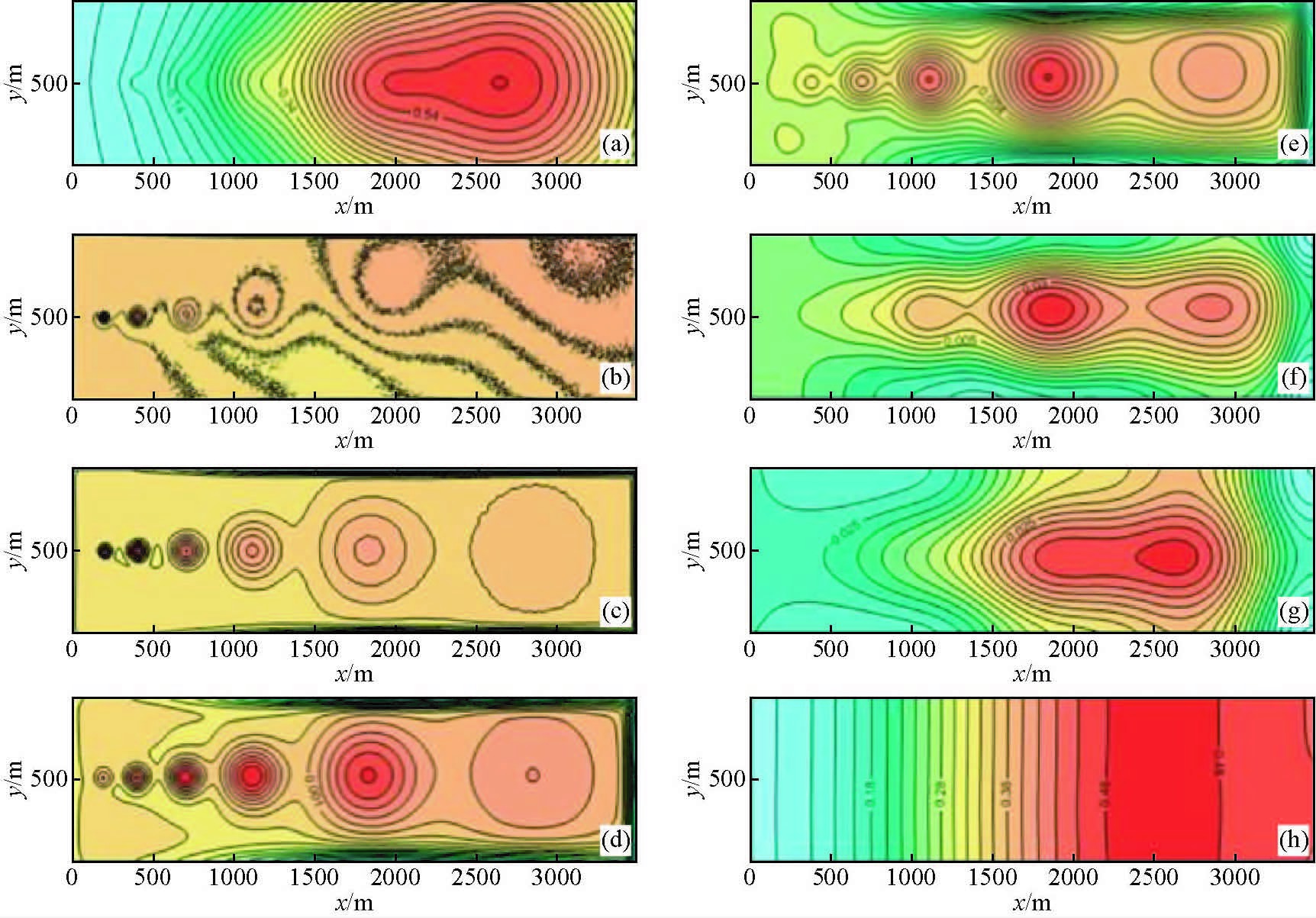
|
图 2 模型g-1小波分析细节重力平面等值线图(单位:μgal) (a)g-1,综合重力场值;(b)g-1d1,一阶小波细节;(c)g-1d2,二阶小波细节;(d)g-1d3,三阶小波细节;(e)g-1d4,四阶小波细节;(f)g-1d5,五阶小波细节;(g)g-1d6,六阶小波细节;(h)g-1a6,六阶小波逼近. Figure 2 Contour map of wavelet analysis details for model g-1(Unit: μgal) (a)g-1,comprehensive gravity field;(b)g-1d1,first scale of wavelet detail;(c)g-1d2,second scale of wavelet detail;(d)g-1d3,third scale of wavelet detail;(e)g-1d4,fourth scale of wavelet detail;(f)g-1d5,fifth scale of wavelet detail;(g)g-1d6,sixth scale of wavelet detail;(h)g-1a6,sixth scale of wavelet approximation. |
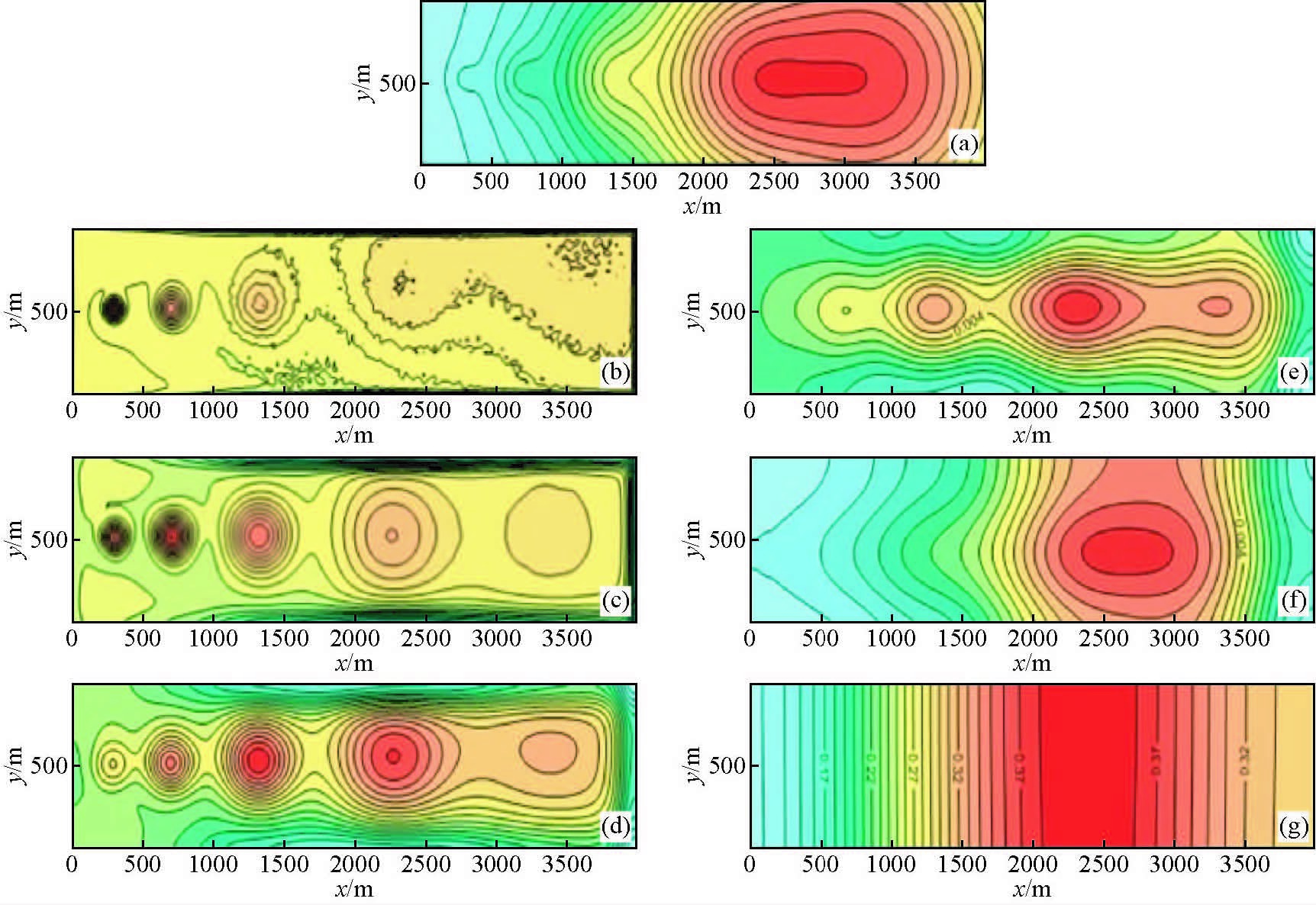
|
图 3 模型g-2小波分析细节平面等值线图(单位:μgal) (a)g-2,综合重力场值;(b)g-2d1,一阶小波细节;(c)g-2d2,二阶小波细节;(d)g-2d3,三阶小波细节;(e)g-2d4,四阶小波细节;(f)g-2d5,五阶小波细节;(g)g-2a5,五阶小波逼近. Figure 3 Contour map of wavelet analysis details for model g-2(Unit:μgal) (a)g-2,comprehensive gravity field;(b)g-2d1,first scale of wavelet detail;(c)g-2d2,second scale of wavelet detail;(d)g-2d3,third scale of wavelet detail;(e)g-2d4,fourth scale of wavelet detail;(f)g-2d5,fifth scale of wavelet detail;(g)g-2a5,fifth scale of wavelet approximation. |
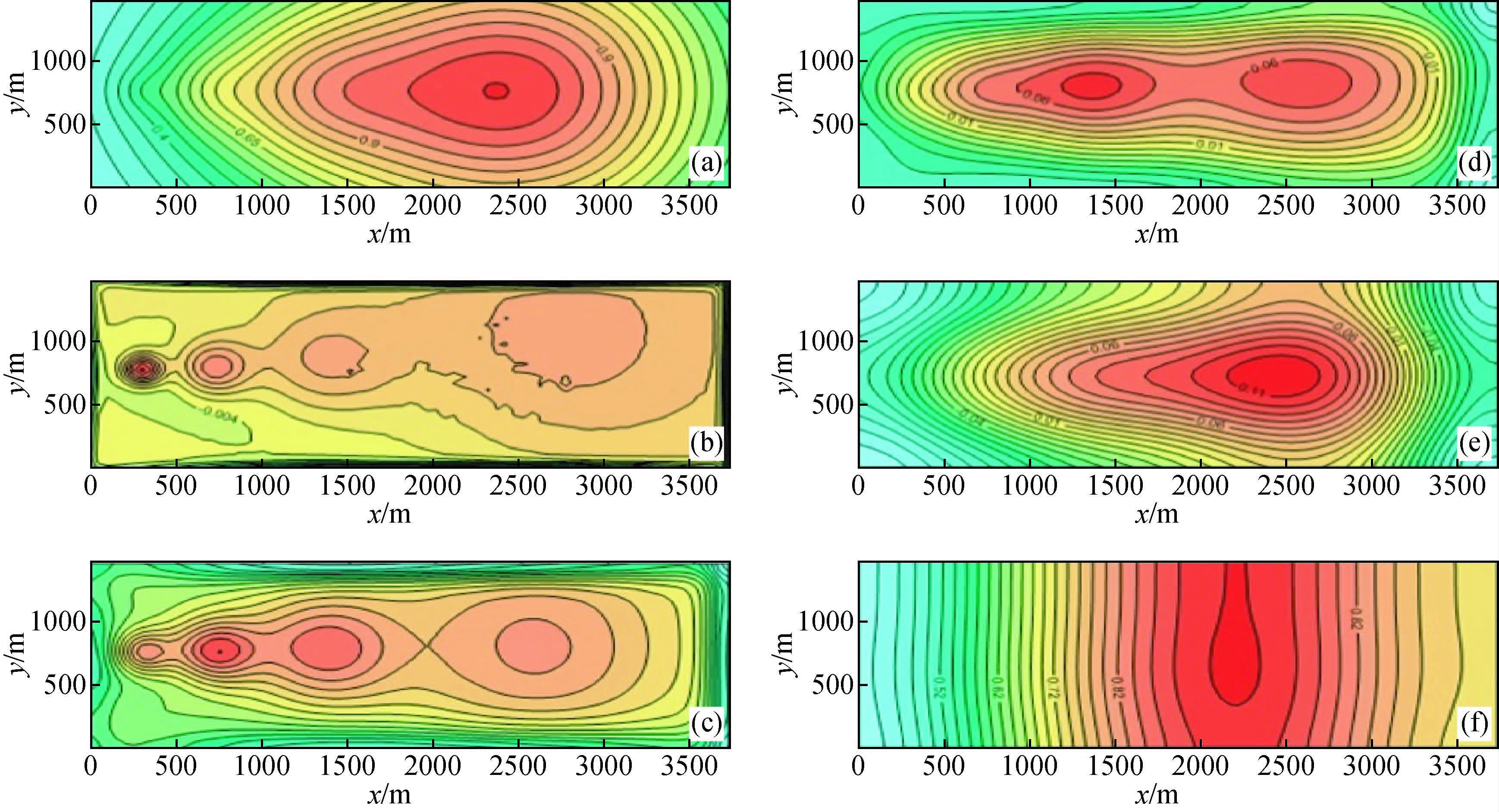
|
图 4 模型g-3小波分析细节平面等值线图(单位:μgal) (a)g-3,综合重力场值;(b)g-3d1,一阶小波细节;(c)g-3d2,二阶小波细节;(d)g-3d3,三阶小波细节;(e)g-3d4,四阶小波细节;(f)g-3a4,四阶小波逼近. Figure 4 Contour map of wavelet analysis details for model g-3(Unit: μgal) (a)g-3,comprehensive gravity field;(b)g-3d1,first scale of wavelet detail;(c)g-3d2,second scale of wavelet detail;(d)g-3d3,third scale of wavelet detail;(e)g-3d4,fourth scale of wavelet detail;(f)g-3a4,fourth scale of wavelet approximation. |
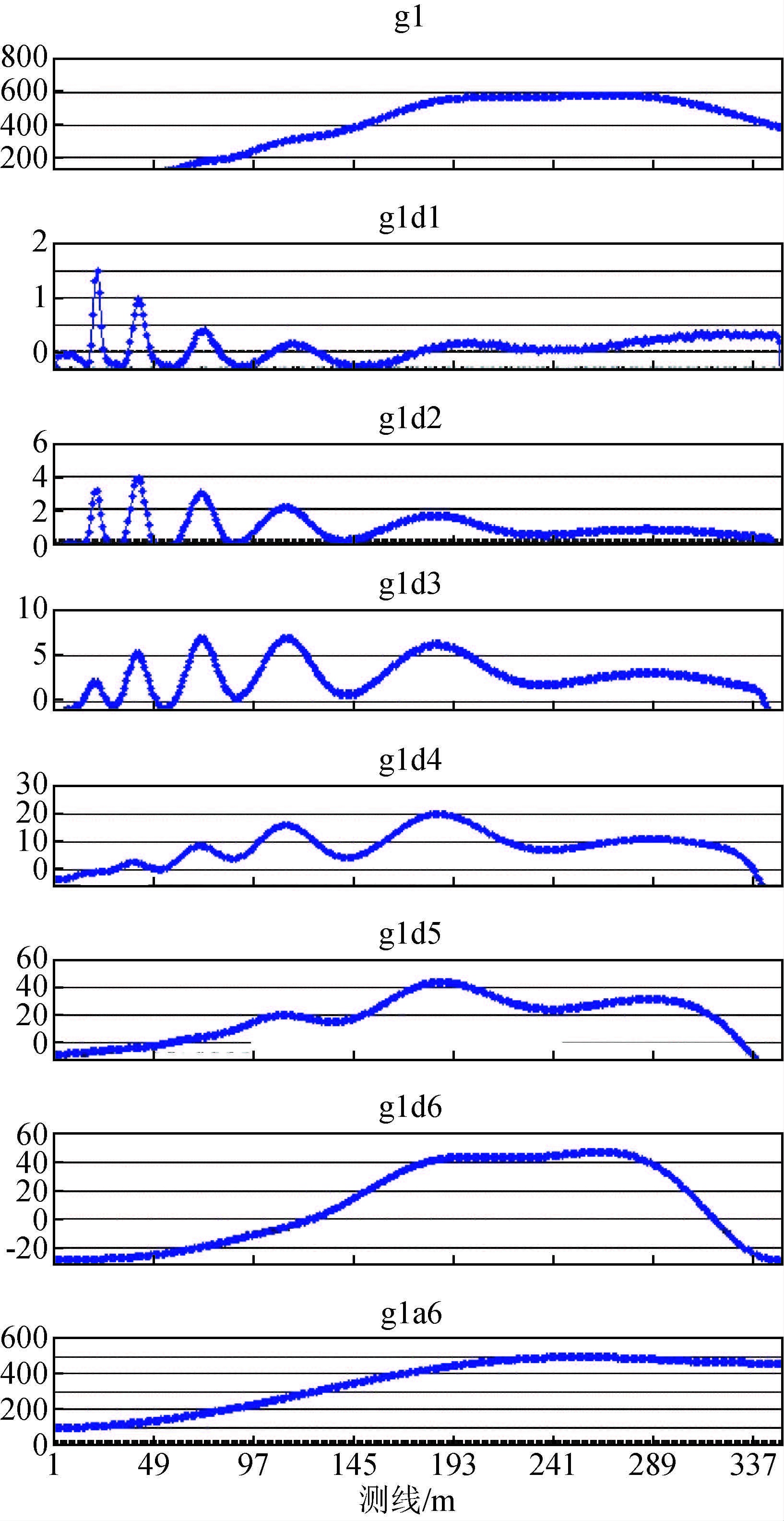
从图中给出的实验结果不难看出,三个模型通过小波分解后得到一个共同的规律,即每阶细节图中,中心埋深位于该阶分解尺度上的目标体,重力异常值最明显.以网格度为10×10的模型1为例,一阶细节的分解深度是40 m,主要反映浅层的第一个目标体的重力值,后面临近深度的几个目标体也有异常反映,但只有处于一阶分解尺度上、埋深为40 m的第一个目标体的重力值最高;二阶细节分解尺度是80 m,细节图主要反映浅层第二个目标体的重力值.虽然临近深度的第一个和第三个目标体也有反映,但只有埋深处于80 m的目标体异常反映最明显.无论平面还是剖面图上,均可看出第二个目标体的异常是最大的;三阶细节上第二、第三、第四个目标体的异常都很明显,但异常值最大的仍然是第三个目标体,即处于三阶分解尺度埋深的目标体异常幅值最大.依次类推,按小波分析原则,在六阶细节上,小波分解尺度是26×10=1280 m,重力异常最大值在第六个目标体的位置上.六阶逼近反映的是大于1280 m深度的区域场,即为这个深度上重力场的区域反映.
模型4是用于对比的模型,其埋深并不是按小波分解尺度设置,虽然经过小波分析后,综合重力场也得到了分解,但并没有得到上述三个模型得到的明显规律性(图 5).

|
图 5 模型g-4小波分析细节平面等值线图(单位:μgal) (a)g-4,综合重力场值;(b)g-4d1,一阶小波细节;(c)g-4d2,二阶小波细节;(d)g-4d3,三阶小波细节;(e)g-4d4,四阶小波细节;(f)g-4d5,五阶小波细节;(g)g-4d6,六阶小波细节;(h)g-4a6,六阶小波逼近. Figure 5 Contour map of wavelet analysis details for model g-4(Unit: μgal) (a)g-4,comprehensive gravitational field;(b)g-4d1,first scale of wavelet detail;(c)g-4d2,second scale of wavelet detail;(d)g-4d3,the third scale wavelet detail;(e)g-4d4,the fourth scale wavelet detail;(f)g-4d5,the fifth scale wavelet detail;(g)g-4d6,the sixth scale wavelet detail;(h)g-4a6,the sixth scale wavelet approximation. |
为直观起见,将模型1的小波细节最大值剖面截图排列在一起进行比较(图 6),上述规律更加明显.其他三个模型的剖面效果与模型1相似,为节省篇幅没有列出.
|
图 6 模型g-1小波分析细节最大值处截取剖面图横座标:测点距离(m);纵座标:重力值(μgal). (a)g-1,综合重力场值;(b)g-1d1,一阶小波细节;(c)g-1d2,二阶小波细节;(d)g-1d3,三阶小波细节;(e)g-1d4,四阶小波细节;(f)g-1d5,五阶小波细节;(g)g-1d6,六阶小波细节;(h)g-1a6,六阶小波逼近. Figure 6 Profile at the maximal value of wavelet analysis details for model g-1(Unit: μgal)The horizontal axis denotes the survey station in meters,while the vertical axis denotes gravity field. (a)g-1,comprehensive gravity field;(b)g-1d1,first scale of wavelet detail;(c)g-1d2,second scale of wavelet detail;(d)g-1d3,third scale of wavelet detail;(e)g-1d4,fourth scale ofwavelet detail;(f)g-1d5,fifth scale of wavelet detail;(g)g-1d6,sixth scale of wavelet detail;(h)g-1a6,sixth scale of wavelet approximation. |
从理论上讲,小波分析细节所反映的深度是依据功率谱分析得到的,但是实际应用中,用谱分析的方法确定深度含有较多人为因素,且有时分层不明显,存在很大的不确定性.本文通过实验找到了一条可以确定小波细节深度的便捷途径.
模型1-3都是按着小波分析应用原则中的各阶细节分解尺度设计的目标体中心埋深,目的是通过模型实验得到的各阶小波细节的异常表现,说明分解尺度与该尺度对应的细节所反映的深度之间的关系.三个网格剖分的模型实验结果表明,无论如何进行网格剖分,中心埋深处于细节分解尺度上的目标体都是该细节中反映最好的,也是这个目标体在所有细节中的最大重力值体现.换句话说,小波分析不但能够将重力场中处于不同尺度的重力异常分解开来,而且分解出来的每阶细节反映最好的异常就是以分解尺度为埋深的目标体.因此,小波细节反映的深度就是该阶细节的分解尺度.
然而,在相邻的细节上也可能存在旁侧影响.比如模型1中,二阶细节上第一个和第三个目标体的异常也很明显,在判断时要综合分析后再做进行取舍.
模型4的目标体中心埋深没有严格按照分解尺度设计,分解出来的小波细节就没有最大化地体现目标体的重力异常值,也没有其他三个模型出现的明显对应规律.这从反面支持了上述论点.
4 红旗岭3号矿体应用实例本节将以上实验结论应用于吉林省红旗岭铜镍矿3号岩体的研究,以验证小波分析结果与钻探揭露该岩体的赋矿深度及丰度之间的吻合程度,并说明该实验结论的可靠性.
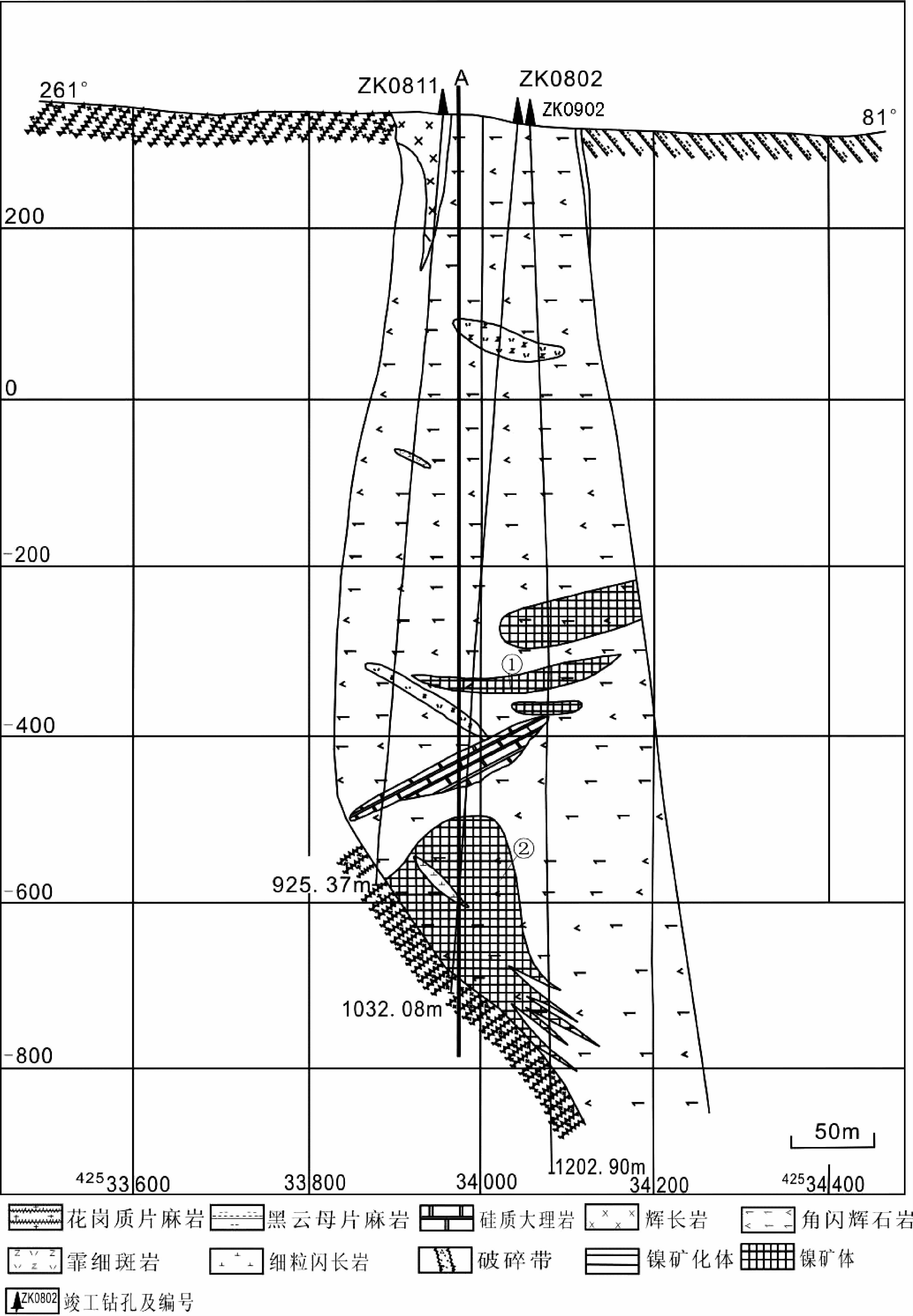
4.1 红旗岭3号岩体的地质概况该岩体在地表有露头,矿体产在杯状岩体的底部,岩矿体延伸至一千米以下.由于勘探深度的限制,多年来对其底部的矿体一直缺乏深入了解.近年的危机矿山接替资源项目在3号岩体勘查区先期进行瞬变电磁法测量.根据瞬变电磁法异常,设计施工了ZK0802孔.该孔见矿很好,自孔深724 m处见矿,直到1068 m断续有矿显,终孔深度为1120 m,这是红旗岭矿区深部找矿的重大突破.后期相继开展了高精度重力、可控源音频大地电磁法、高精度磁法等物探工作,同样发现了电法、重力、磁法综合异常,并设计了ZK0811和ZK0902,也都见矿.图 7是根据该钻孔和ZK0811、ZK0902钻孔揭露的岩体情况绘制的3号岩体地质剖面图.
|
图 7 红旗岭3号岩体5号勘探线地质剖面图(吉林省有色金属地质勘查局六○七队提供资料) Figure 7 Geological section of survey line 5 over rock mass No.3 in Hongqiling |
我们对红旗岭3号岩体及周边地区高精度重力布格异常数据进行小波多尺度分析.该区重力测量精度为110000,网格度100 m×40 m,测点数1505个,我们对经过各项改正后的布格重力异常进行小波多尺度分析.根据分解原则,取一阶小波细节分析尺度为400 m,由此二阶细节分析尺度为800 m,三阶细节为1600 m,三节逼近为更深的区域场,得到分析结果如图 8(ori、d1、d2、d3、s3)所示.从图可以看到,一个完整的布格重力异常圈通过小波分解后,在一阶、二阶、和三阶细节图上,被分解为若干个清晰程度不等的小异常圈.其中一阶细节图上异常分布比较零散,除了位于图幅中部较为清楚的3号岩体及其南端的一个异常圈之外,没有其他明显异常圈.由于3号岩体出露地表,在反映浅部的一阶细节图上,3号岩体的重力异常最为明显,这也与一阶细节反映400 m深度相吻合.紧邻3号岩体南端的一个与3号岩体走向相同的小异常体,看似一个独立的岩体,与地质图核对后发现是蝌蚪状3号岩体的尾部,在布格异常图上显示的是等值线走向上的拐点,而在分解出来的一阶细节图上则是一个明显的异常圈.3号岩体尾部因出露面积不大,一直未引起勘探工作者的重视.通过小波多尺度分析,在一至三阶细节图上均呈现为一个独立的闭合圈,提示了这个位于3号岩体南东部的异常有很大的找矿潜力.从异常的独立性看,该异常可能是由含矿小岩体引起.该含矿小岩体可能是与3号岩体分开的小岩体或是3号岩体在深部的另一膨大部分.

|
图 8 红旗岭3号岩体高精度重力布格异常及小波分析d1、d2、d3、a3重力等值线平面图(单位:μgal) Figure 8 Contour map of high-precision gravity anomaly and wavelet analysis details of d1,d2,d3 and a3 for No.3 rock mass in Hongqiling |
在二阶细节平面图上,新3号岩体异常变得清晰,且异常走向由一阶细节图上呈现的与3号岩体平行,转成与3号岩体成近似90度角,这一变化揭示了新3号岩体的真实走向和产状.另外,在图幅西北部呈现的异常体是2号岩体的一部分,从异常形态上看,其规律及异常大小与3号岩体相仿.
三阶细节图上新3号岩体的异常和3号岩体的异常合在一起,表明两个岩体在这个深度归于同根(这一结论与钻孔验证一致).但3号岩体尾部的异常仍然独立,且能看出走向上略有错位,表明3号岩体的尾部与主体的确不是整体,其间有一定的接触关系,但在地质图上这个位置并没有断层的标志,其构造性质还需要进一步勘查.3号岩体向西南方向伸出的低缓异常揭示了3号岩体并不是如地表出露的那样为北西走向的蝌蚪状,它在深部是向西南方向延伸的,这在二阶细节图上已有迹象.然而,从异常值来看,西南向的延伸显然属于枝节性延伸,因为在反映区域规律的三阶逼近图上,这部分伸出的枝节不复存在.据此判断整块岩体的根部在出露的3号岩体下方偏西北的位置.
4.3 红旗岭3号岩体高精度重力小波多尺度剖面分析为了进一步说明小波分析细节与深度的关系,便于与钻孔资料进行对比,在小波细节平面图上截取了钻孔所在的5剖面的一阶、二阶、三阶细节和三阶逼近重力值剖面图(图 9).从图可以清楚地看到,在一阶细节剖面图上,异常位置与地表出露的岩体相对应,重力异常反映的是岩体重心位置,这与一阶细节所反映的400 m深度相吻合.峰值靠左是因为3号岩体在该部位由辉长岩和角闪辉石岩两种岩性组成.两种岩性的密度值存在差异,辉长岩的平均密度是3.09 t/m3,角闪辉岩的平均密度是2.96 t/m3,含矿角闪辉石岩的平密度是2.98 t/m3.由于辉长岩在岩体的西侧覆盖在角闪辉石岩之上,矿体产在角闪辉石岩体底部,所以反映岩体浅部的一阶细节图重力异常峰值偏左.

|
图 9 3号岩体小波细节分析最大值处截取剖面图横座标:测点距离(m);纵座标:重力值(μgal). (a)line3,综合重力场值;(b)line3d1,一阶小波细节;(c)line3d2,二阶小波细节;(d)line3d3,三阶小波细节;(e)line3d4,四阶小波细节. Figure 9 Profile at the maximal wavelet details for model g-1(Unit: μgal) The horizontal axis denotes the survey station in meters,while the vertical axis denotes gravity field. (a)line3,comprehensive gravity field;(b)line3d1,first scale of wavelet detail;(c)line3d2,second scale of wavelet detail;(d)line3d3,third scale of wavelet detail;(e)line3d4,fourth scale of wavelet detail. |
二阶细节剖面上的异常峰值相对于一阶细节向右位移150 m,三个见矿钻孔恰好打在二阶细节的峰值上,且矿显最好的ZK0802孔在最大峰值处.由于3号矿体主要赋存在800 m左右的深度,正是二节细节的峰值位置.
三阶细节的重力异常峰值较二阶细节向右偏50~100 m,说明3号岩体的根部有向北东方向移动的趋势,也就是说该岩体的根部可能呈岩墙状向北东倾斜,这与3号岩体东边界断层的倾向及推覆断层性质相吻合.
4.4 红旗岭3号岩体验证区通过小波分析,推测在3号岩体深部还存在另一处小异常体,该异常体处在紧邻3号岩体南端且与3号岩体走向基本平行的部位(17号勘探线附近).从异常形态可以看出,岩体走向有明显变化,自南向北由北西(NW)变为北北西(NNW),说明该处岩体恰处在构造变化有利成矿部位,深部可能存在膨大的高密度地质体.
5 结 论本文通过正演模拟试验找到了小波变换细节所反映的深度与该细节分解尺度之间的关系,即小波各阶细节的分解尺度可以反映异常体源的深度.这一结论可以替代以往应用频谱分析近似确定深度的方法,为重磁反演提供了定量的深度依据,使小波变换理论在重磁勘探数据处理中的应用更加准确可靠.红旗岭3号岩体重力异常小波分析的实例有力论证了本文小波分解方法在深部找矿应用中的有效性.
致谢 感谢候遵泽教授在本文的模型试验和数据处理中给予的指导和帮助.感谢审稿人和编辑对本文提出忠恳的修改意见和建议.| [] | Hou Z Z, Yang W C .1995. Applied research on wavelet analysis[J]. Computing techniques for geophysical and geochemical exploration, 17 (3) : 1–9. |
| [] | Gao D Z, Hou Z Z, Tang J .2000. Multi-scale analysis of gravity anomalies on East China Sea and adjacent regions[J]. Chinese Journal of Geophysics, 43 (6) : 842–849. |
| [] | Hou Z Z, Yang W C .1997. Wavelet transform and multi-scale analysis on gravity anomalies of China[J]. Acta Geophys Sin, 40 (1) : 85–95. |
| [] | Hou Z Z, Yang W C, Liu J Q .1998. Multiscale inversion of the elensity Contrast within the crust of China[J]. Acta Geophys Sin, 41 (5) : 641–651. |
| [] | Hou Z Z .1998. Applied research on wavelet analysis for geophysics exploration[J]. Geophysical and Geochemical Exploration, 22 (1) : 71–75. |
| [] | Hou Z Z, Yang W C .2001. The program of two-dimensional wavelet analysis(Ⅰ)-method and programming[J]. Computing techniques for geophysical and geochemical exploration, 23 (1) : 74–76. |
| [] | Hou Z Z, Yang W C .2001. The program of two-dimensional wavelet analysis(Ⅱ)-setup and application[J]. Computing techniques for geophysical and geochemical exploration, 23 (2) : 155–159. |
| [] | Hou Z Z, Fang S M .2001. Multi-scale analysis of Bouguer gravity anomalies in the area of North China[J]. The annual Chinese Geophysical Society, 17 (1) : 299–299. |
| [] | Hou Z Z, Yang W C .2002. Applied research on wavelet analysis[J]. Computing techniques for geophysical and geochemical exploration, Supplementary issue (1) : 49–52. |
| [] | Hou Z Z .2009. Study on gravity method for detecting subsurface mass[J]. Computing techniques for geophysical and geochemical exploration, 31 (5) : 413–416. |
| [] | HOU Z Z, YANG W C .2011. Multi-scale inversion of density structure from gravity anomalies in Tarim Basin[J]. Science China Earth Sciences, 54 (3) : 399–409. DOI:10.1007/s11430-011-4169-2 |
| [] | Liu T Y, Liu D W, ZHAN Y L, et al .2006. The application of new magnetic data processing methods to the potentiality exploration in crisis mines[J]. Geophysical and Geochemical Exploration, 30 (5) : 377–381. |
| [] | Liu T Y .2007. A new method field exploration data processing[M]. . |
| [] | Liu T Y, Wu Z C, Zhan Y L .2007. Wavelet Multi-Scale Decomposition of Magnetic Anomaly and Its Application in Searching for Deep-Buried Minerals in Crisis Mines:A Case Study from Daye Iron Mines[J]. Earth Science-Journal of China University of Geosciences, 32 (1) : 135–140. |
| [] | Yang W C, Shi Z Q, Hou Z Z, et al .2001. Discrete wavelet transform for multiple decomposition of gravity[J]. Chinese Journal of Geophysics, 44 (4) : 534–541. |
| [] | Yang W C, Xu J R, Cheng Z Y, Hou Z .2005. Geophysics of crust mantle interaction in SuLu-Dabie orogenic belt[M]. Beijing: Geological Publishing House . |
| [] | Yang X L. Research of Geophysical Methods on Deep Cu-Ni SulfideDeposit Exploration-Case Studies on Hongqiling Cu-Ni Sulfide Deposit[D]. Beijing:China university of geosciences, 2012. |
| [] | Zhang H L, Liu T Y .2009. The magnetic field data processing and interpretation methods based on wavelet analysis[J]. Geophysical and Geochemical Exploration, 33 (6) : 686–690. |
| [] | 侯遵泽, 杨文采.1995. 小波分析应用研究[J]. 物探化探计算技术, 17 (3) : 1–9. |
| [] | 高德章, 侯遵泽, 唐建.2000. 东海及邻区重力异常多尺度分解[J]. 地球物理学报, 43 (6) : 842–849. |
| [] | 侯遵泽, 杨文采.1997. 中国重力异常的小波变换与多尺度分析[J]. 地球物理学报, 40 (1) : 85–95. |
| [] | 候遵泽, 杨文采, 刘家琦.1998. 中国大陆地壳密度差异多尺度反演[J]. 地球物理学报, 41 (5) : 642–651. |
| [] | 侯遵泽.1998. 小波分析及其在勘查地球物理中的应用[J]. 物探与化探, 22 (1) : 71–75. |
| [] | 侯遵泽, 杨文采.2001. 二维小波分析程序Ⅰ——方法与设计[J]. 物探化探计算技术, 23 (1) : 74–76. |
| [] | 侯遵泽, 杨文采, 高德章.2001. 二维小波分析程序Ⅱ——安装与使用[J]. 物探化探计算技术, 23 (2) : 155–159. |
| [] | 侯遵泽, 方盛明.2001. 华北地区大陆布格重力异常多尺度分析[J]. 中国地球物理学会年刊, 17 (1) : 299–299. |
| [] | 侯遵泽, 杨文采.2002. 小波方法重力场多尺度分解及其应用[J]. 物探化探计算技术 (1) : 49–52. |
| [] | 侯遵泽.2009. 探测地下目的物的重力方法技术研究[J]. 物探化探计算技术, 31 (5) : 413–416. |
| [] | 侯遵泽, 杨文采.2011. 塔里木盆地多尺度重力场反演与密度结构[J]. 中国科学:地球科学, 41 (1) : 29–39. |
| [] | 刘天佑, 刘大为, 詹应林, 等.2006. 磁测资料处理新方法及在危机矿山挖潜中的应用[J]. 物探与化探, 30 (5) : 377–381. |
| [] | 刘天佑.2007. 位场勘探数据处理新方法[M]. 北京: 科学出版社 . |
| [] | 刘天佑, 吴招才, 詹应林.2007. 磁异常小波多尺度分解及危机矿山的深部找矿:以大冶矿为例[J]. 地球科学——中国地质大学学报, 32 (1) : 135–140. |
| [] | 杨文采, 施志群, 侯遵泽, 程振炎.2001. 离散小波变换与重力异常多重分解[J]. 地球物理学报, 44 (4) : 534–541. |
| [] | 杨文采, 徐纪人, 程振炎, 侯遵泽.2005. 苏鲁大别造山带地球物理与壳幔作用[M]. 北京: 地质出版社 . |
| [] | 杨学立.铜镍硫化物矿床深部找矿地球物理方法综合研究[D].北京:中国地质大学(北京),2012. http://cn.bing.com/academic/profile?id=edb001576644939b33a0926938eba236&encoded=0&v=paper_preview&mkt=zh-cn |
| [] | 张恒磊, 刘天佑.2009. 基于小波分析的磁测数据处理流程及解释方法[J]. 物探与化探, 33 (6) : 686–690. |
 2016, Vol. 31
2016, Vol. 31

