2. 吉林大学地球探测科学与技术学院, 长春 130026
2. Collage of Exploration Science and Technology, Jilin University, Changchun 130026, China
1948年夏,第一套航空电磁系统在加拿大成功试飞,被视为航空电磁探测的开始(Fountain,1998).经过六十多年的发展,航空电磁法已逐渐成为一门相对成熟的地球物理探测方法.国外航空电磁法应用广泛,对常用的系统进行了正演和反演研究(Annetts et al.,2000; Sattel,2002).正演模拟多为三维,反演则以一维为主(Sengpiel and Siemon,1998),由于电磁场的复杂性,二维正反演研究较少.在一维反演中,有基于均匀半空间和层状介质的优化反演方法,以及视电阻率的直接转换方法.其中包括基于均匀半空间的电导率转化方法、电导率深度转换方法、Zohdy反演方法和采用横向电导率约束的反演方法(Huang and Fraser,2001; Fraser,1978).在这些方法中,虽然最优化的方法能够得到相对较准确的地下岩石电阻率分布,但计算时间长,而且计算的结果只有电导率.国内的航空电磁测量起步于20世纪50年代末,投入生产飞行也有三十多年的勘查史,取得了很好的地质效果.但由于方法的特殊性,我国航空电磁法的数据处理和解释方法研究却相对滞后,在矿产资源普查方面,还停留在定性解释为主的阶段(尹大伟等,2013;王卫平等,2015).国内航空电磁法正反演研究也不多,钱立新(1990)和雍蔚华(1993)尝试过侧重于求解非线性方程组方法和技巧的二层反演,孟庆敏(2005)和刘云鹤、殷长春(2013)做过三维正演研究,磁性条件下频率域航空电磁法反演及其应用方面所做的工作和讨论就更少了(王卫平等,2013).
其实,航空电磁法的解释方法与地面电磁法并没有本质的区别.但由于航空电磁法以飞机为运载工具并实现连续自动测量,获得的数据量大而质量相对较差,而且,从实用的角度出发,频率域航空电磁法主要用于普查,获得电阻率分布的大致估计,快速圈定远景区,故不应追求绝对的“精确”,而应追求效率,因此,快速实用的反演方法就成为了研究重点.常用的频率域航空电磁法反演方法是视电阻率转换法,相位矢量图法就是其中的一种.传统相位矢量图模型是基于均匀半空间,假设航空电磁异常不受地下介质磁性参数的影响,只有电阻率和飞行高度两个参数.在实际应用中,若地下岩石的磁性较强,导致计算电阻率值偏小,从而影响对地下目标体的解释效果.
本文首先系统研究了磁性条件下层状介质模型的频率域航空电磁法正演算法,实现了对常用频率域航空电磁响应积分方程核函数的求解;然后针对强磁性区域频率域航空电磁法反演问题,在传统相位矢量图的基础上考虑了磁导率因素,对其进行了改进应用,从而提高了磁性条件下电阻率反演精度.
1 频率域航空电磁数值计算方法 1.1 正演计算方法为了使公式推导的适用范围更广,本文采用圆形回线源进行频率域航空电磁响应计算.只要回线的线圈半径足够小,就可以等同于小线圈的垂直磁偶极源;当线圈半径r<<s收发距时,线圈内产生的磁场等价于垂直或水平磁偶极子发射场.而且本文应用的收发线圈可以在空中或者在地面,从而不仅适用于航空电磁法,同样适用于地面地磁法.
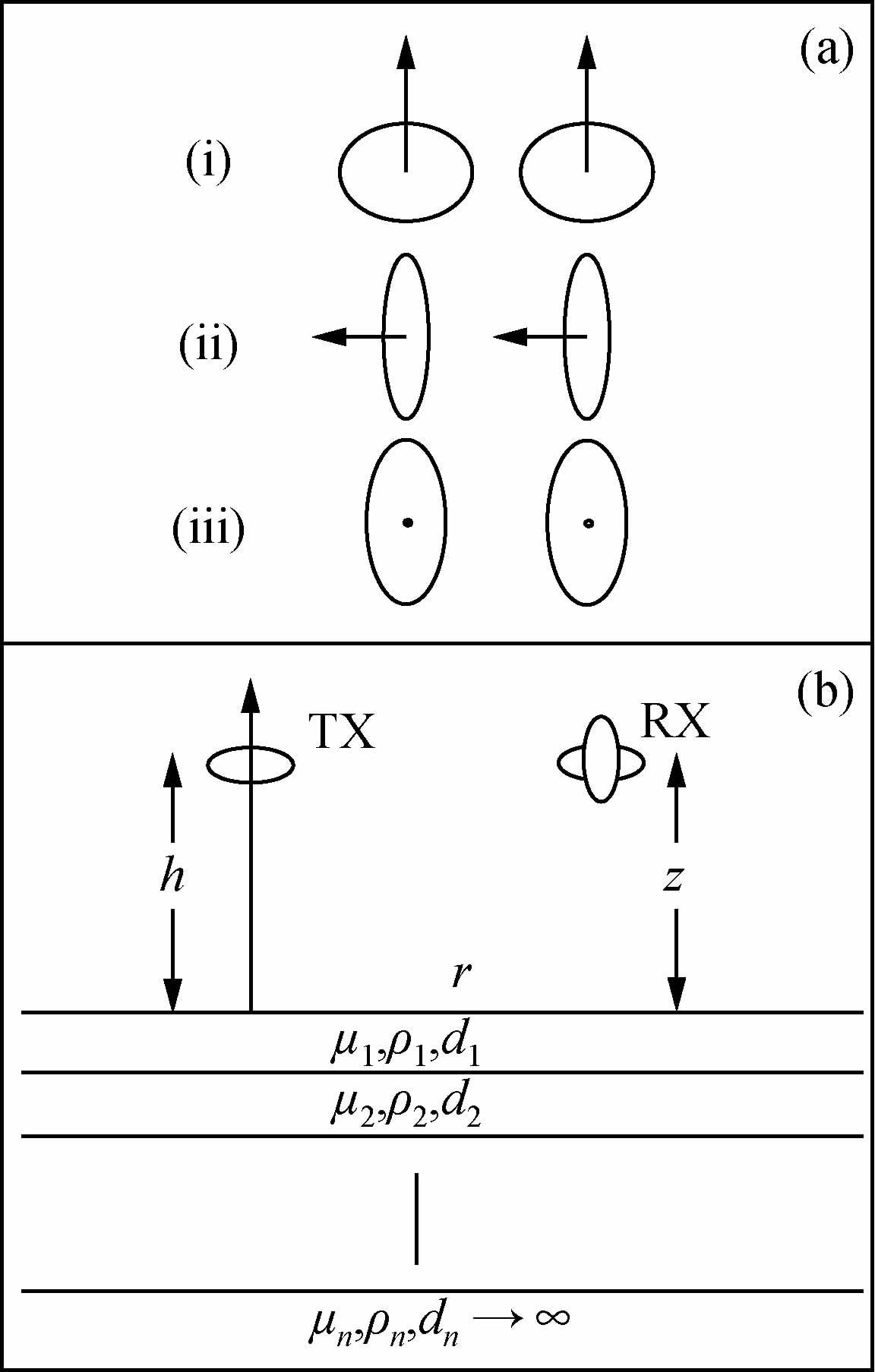
频率域航空电磁法发射-接收线圈有不同的装置类型(习建军,2010)(图 1).水平层状介质频率域航空电磁法的一维正演,要求计算垂直磁偶源在其断开后,在空中垂直线圈内生成的感应电动势随频率衰变的过程.
|
图 1 频率域航空电磁法装置类型及层状介质模型 (a)水平共面、垂直同轴和垂直共面装置示意图;(b)层状介质模型图. Figure 1 The device type of AEM in frequency domain and its model of layered medium |
假设大地为n层水平层,各层磁导率,电阻率和厚度分别为μ1,ρ1,d1;μ2,ρ2,d2……;μn,ρn,dn,→∞.发射线圈TX位于地面上空,高度为h;接收线圈RX的高度为z,与TX的水平距离为r.设圆柱坐标系原点0位于TX正下方地面上,z轴垂直地面向上.当激发源在-h上,接收装置置于均匀大地表面上z(z在-h与0之间)时,可获得以下2种装置的电磁相应计算公式(Huang and Fraser,2001):
(1) 垂直共面装置(以Hz为例,收发距离大于5倍的线圈半径):

|
(1) |
(2) 水平共面装置(以HX为例):
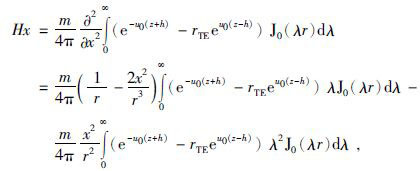
|
(2) |
其中:
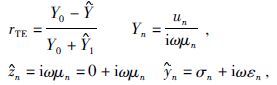
|
(3) |

|
(4) |
rTE是TE极化的反射系数,Yn是本征阻抗,Yn是面波阻抗,z是接收线圈离地面的高度,h是发射线圈离地面的高度(h>0表示地面以上),r是收发距,a是发射线圈的半径,I(ω)是激发电流,ω是角频率.将上述两种装置的基本计算公式归纳为一次场与二次场的分离形式(5).其中,积分内括号中第一项为一次场,第二项为二次场(郑圣谈等,2007).公式为

|
(5) |
以上的层状介质电磁响应计算采用Anderson(1992)的算法,但为了保证计算精度,同时考虑计算效率,我们采用高密度方法(郑圣谈,2007)进行计算,下面讨论其计算方法.
综合(1)(2)两式,无论哪种装置模式,其基本的计算问题都是一次场与二次场的分离,公式为

|
(6) |
其中,m=πa2,r>5a or r >5ds.
在正演计算算法中的关键问题包括以下两点:①(3)式中含磁导率的反射系数计算 ;②对于多层介质结构,解决(4)式计算溢出的问题.
1.2 核函数中反射系数rTE的计算在(4)、(5)式中,TE极化反射系数rTE是核函数计算中重要的一项(习建军,2010),它的特性影响着核函数是收敛还是发散,下面讨论一下它随频率变化的衰减性.
以两层模型为例,反射系数计算公式中n=2;计算模型如图 2所示.线圈半径为0.3 m,发射接收线圈到地面的距离为30 m,第一层厚度为500 m,电阻率为10 Ω·m,相对磁导率为1,介电常数为1;第二层电阻率为20 Ω·m,相对磁导率为1,介电常数为1.
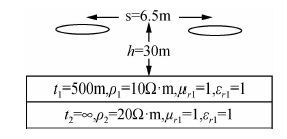
|
图 2 两层介质频率域航空电磁法地电模型 Figure 2 The two layer media geoelectric model diagram |
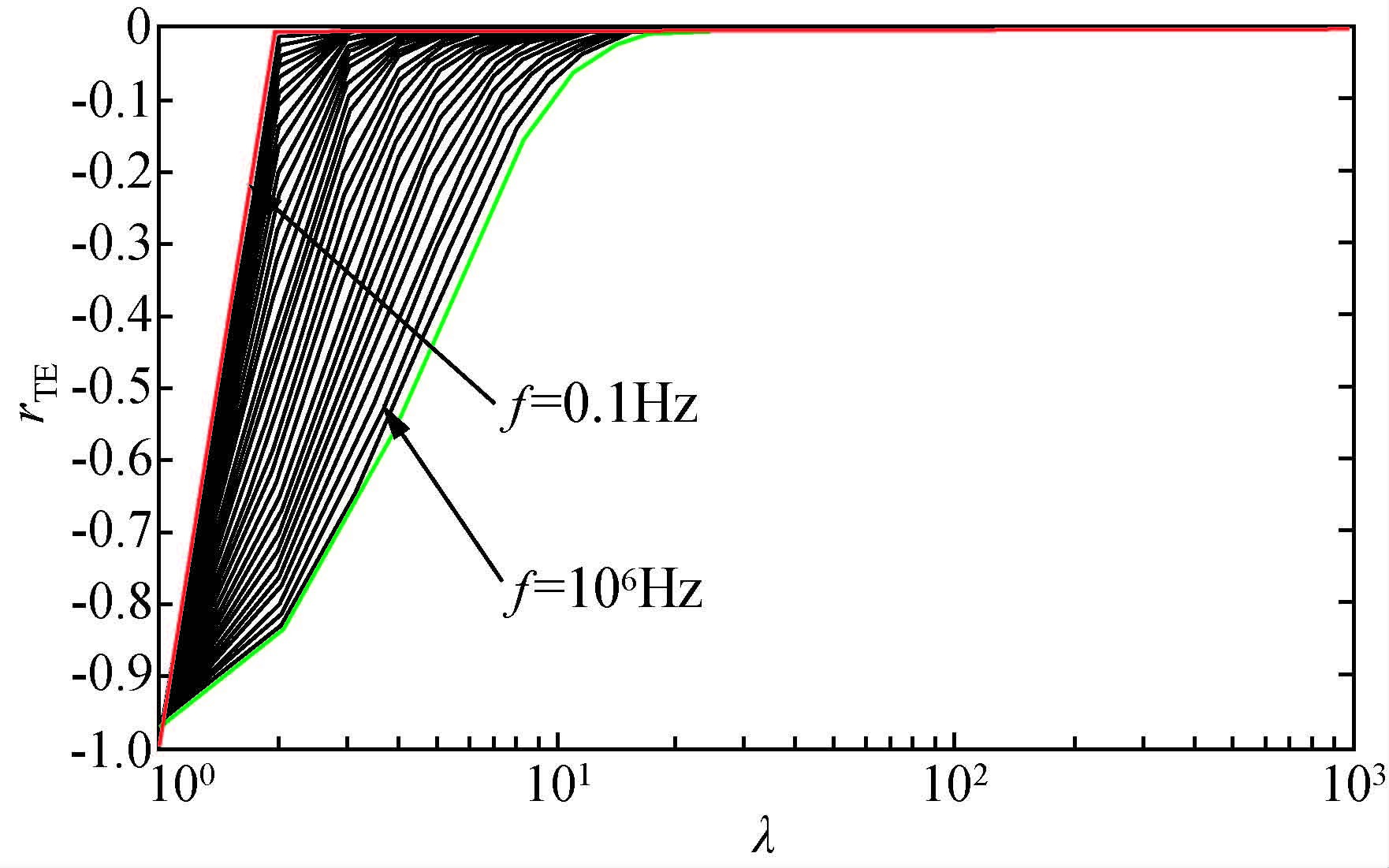
当频率从10-1Hz~106 Hz变化时,反射系数与被积变量λ的关系图如图 3所示.
|
图 3 两层介质的反射系数rTEvs被积变量λ的衰减曲线 Figure 3 The attenuation curve of two layer media reflection coefficient rTE vs product variable λ |
由图 3可知,当频率很低时,反射系数衰减很快;频率越高,反射系数衰减越慢;但是,只要频率小于106 Hz,当被积变量λ大于10时,反射系数基本上衰减为零.所以,低频条件下反射系数是收敛的.
1.3 直接数值积分法和线性滤波算法磁场响应计算的比较针对正演计算中的贝塞尔函数积分,分别用直接数值积分法和线性滤波算法计算半空间模型下地表大回线源垂直磁场实、虚分量的第一项,对比二者的计算效果.
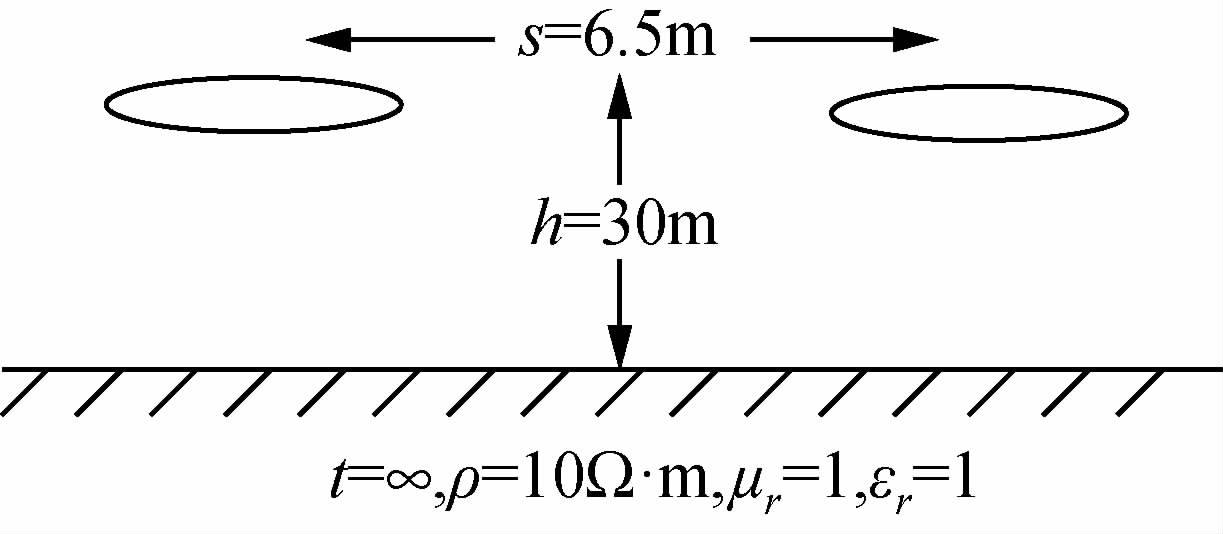
均匀半空间模型如图 4所示.线圈半径为0.3 m,收发距6.5 m,发射接收线圈到地面的距离30 m,大地电阻率为10 Ω·m,相对磁导率为1,介电常数为1.
|
图 4 均匀半空间地电模型图 Figure 4 AEM homogeneous half-space geoelectric model of frequency domain |
为了更好地对比两种算法计算效果,本文只提取(5)式中的第一项进行讨论,公式为
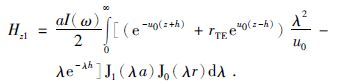
|
(7) |
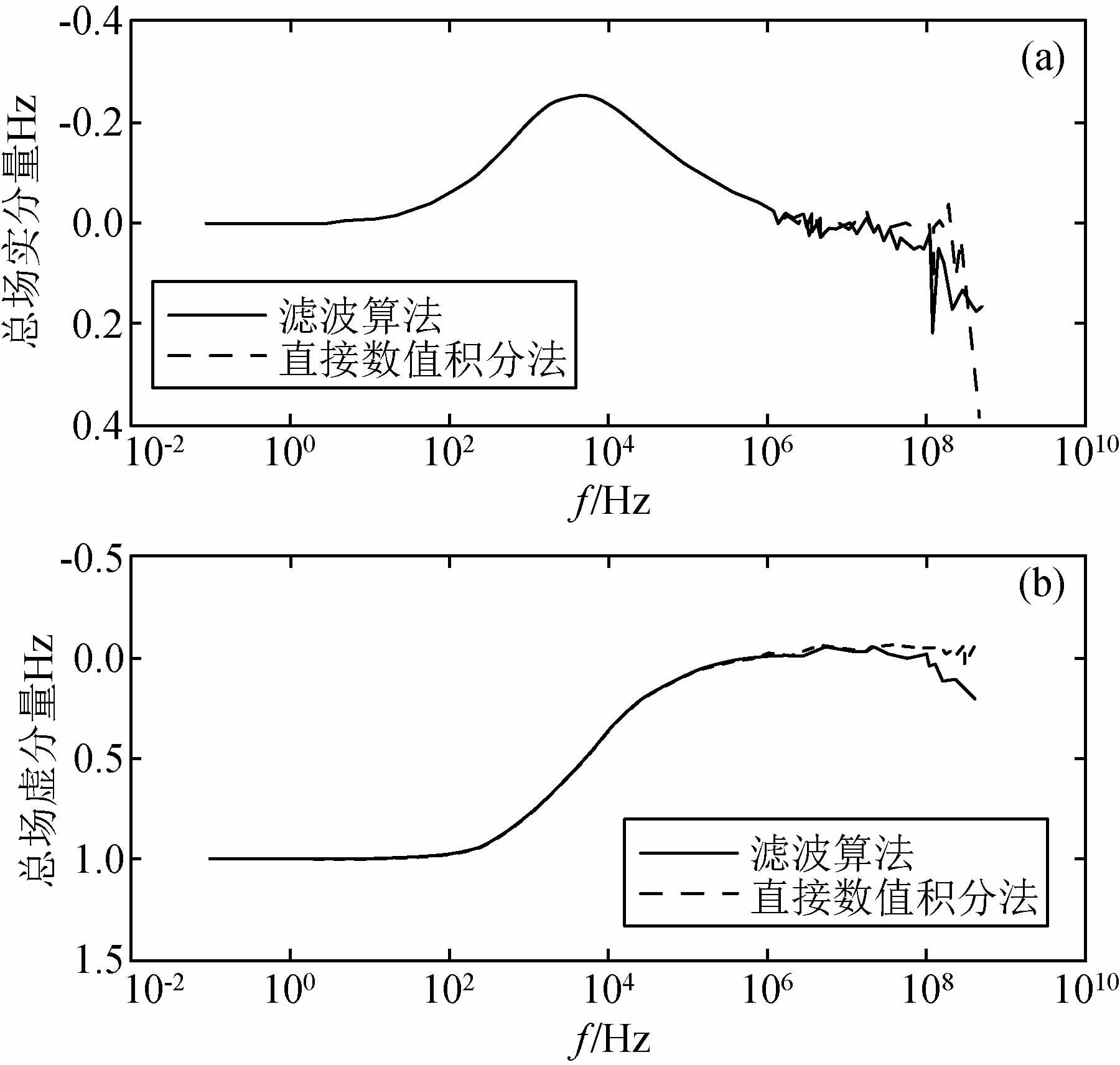
图 5a、b分别为采用直接数值积分法和120点线性滤波算法计算(7)式中垂直磁场总场第一项实、虚分量成果对比图.从图中可以看出,当频率小于106赫兹时,采用直接数值积分法计算结果与滤波算法计算结果吻合很好(见图 5);当频率大于106赫兹时,两种算法计算的磁场响应都会发生震荡,但直接数值积分法相对更加稳定,它的计算精度更高.120点滤波算法计算结果与直接积分法在航空电磁法的有效频段内几乎没有差别,但是,它的计算速度很快,所以更加适合于大量数据的航空电磁法数据处理.
|
图 5 两种积分方法精度对比 (a)实分量计算;(b)虚分量计算. Figure 5 Accuracy comparison of two methods |
因此,为了提高计算速度,实现实用化反演,可以在正演计算中采用数字滤波算法,并把正演计算式简化为:小线圈、准静态、收发线圈同高度、半空间模型,并直接计算互耦值.图 6为基本正演计算程序流程图.
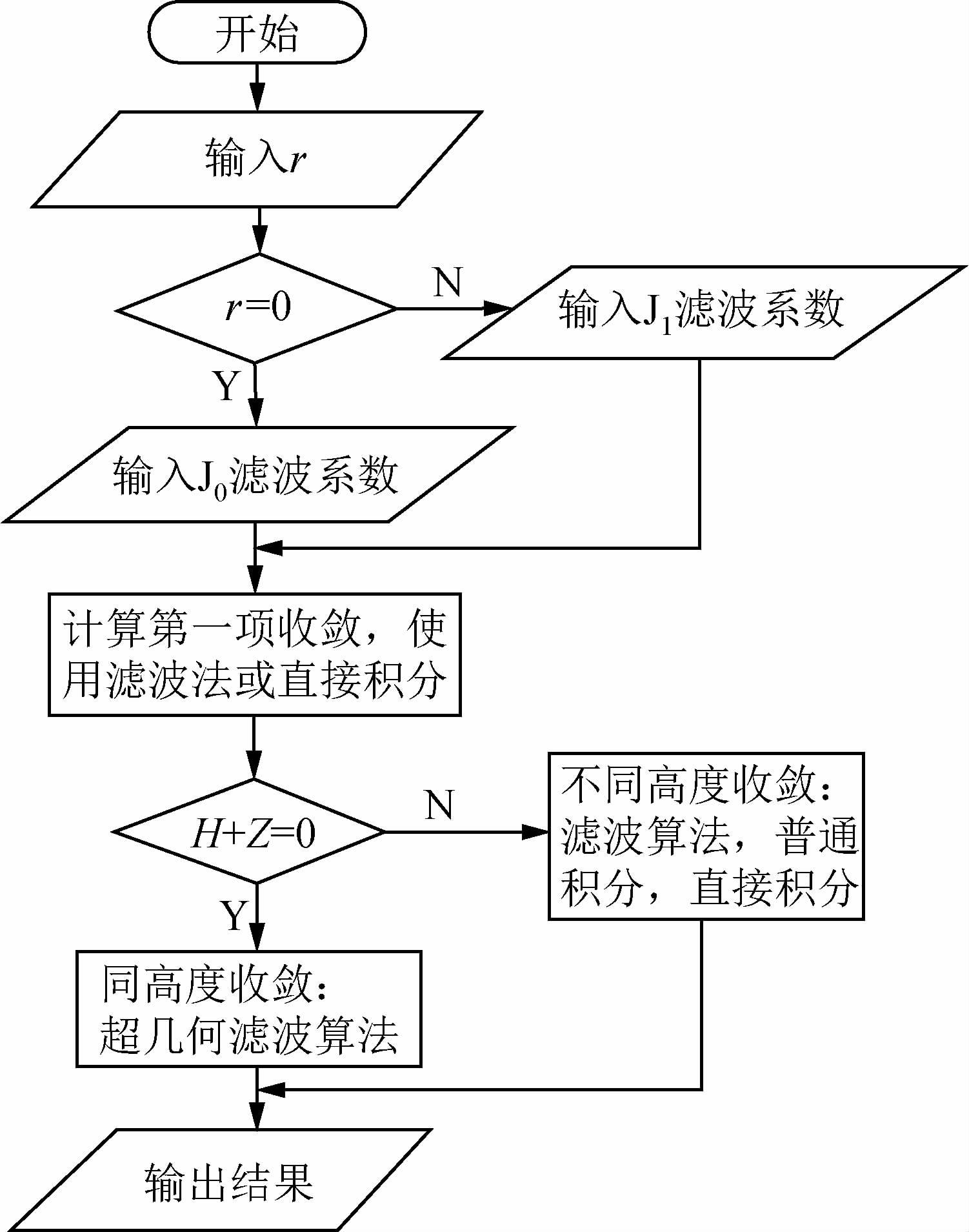
|
图 6 层状介质正演程序流程图 Figure 6 The structure of layered medium forward program |
在频率域航空电磁法中,层状介质模型(见图 1)是航空电磁法中常用的地球物理模型,当大地只有一层介质时,整个空间可以看作是被一个水平面分割成上、下半空间两层波数不同的介质,这就是均匀半空间模型.
以水平共面线圈为例,当发射线圈电流为1安培,线圈半径为0.3 m,收发距6.5 m,飞行高度为90 m,大地电阻率为10 Ω·m,频率从10-2~107 Hz变化时,可以得到在给定飞行高度和线圈收发距,以及不同磁导率μr与不同感应数θ条件下的均匀半空间归一化的二次场实、虚分量磁响应曲线,如图 7所示.图中为水平共面线圈在均匀半空间条件下的磁场响应,μr为均匀大地的相对磁导率,大地电阻率为10 Ω·m,频率从10-2~107 Hz.
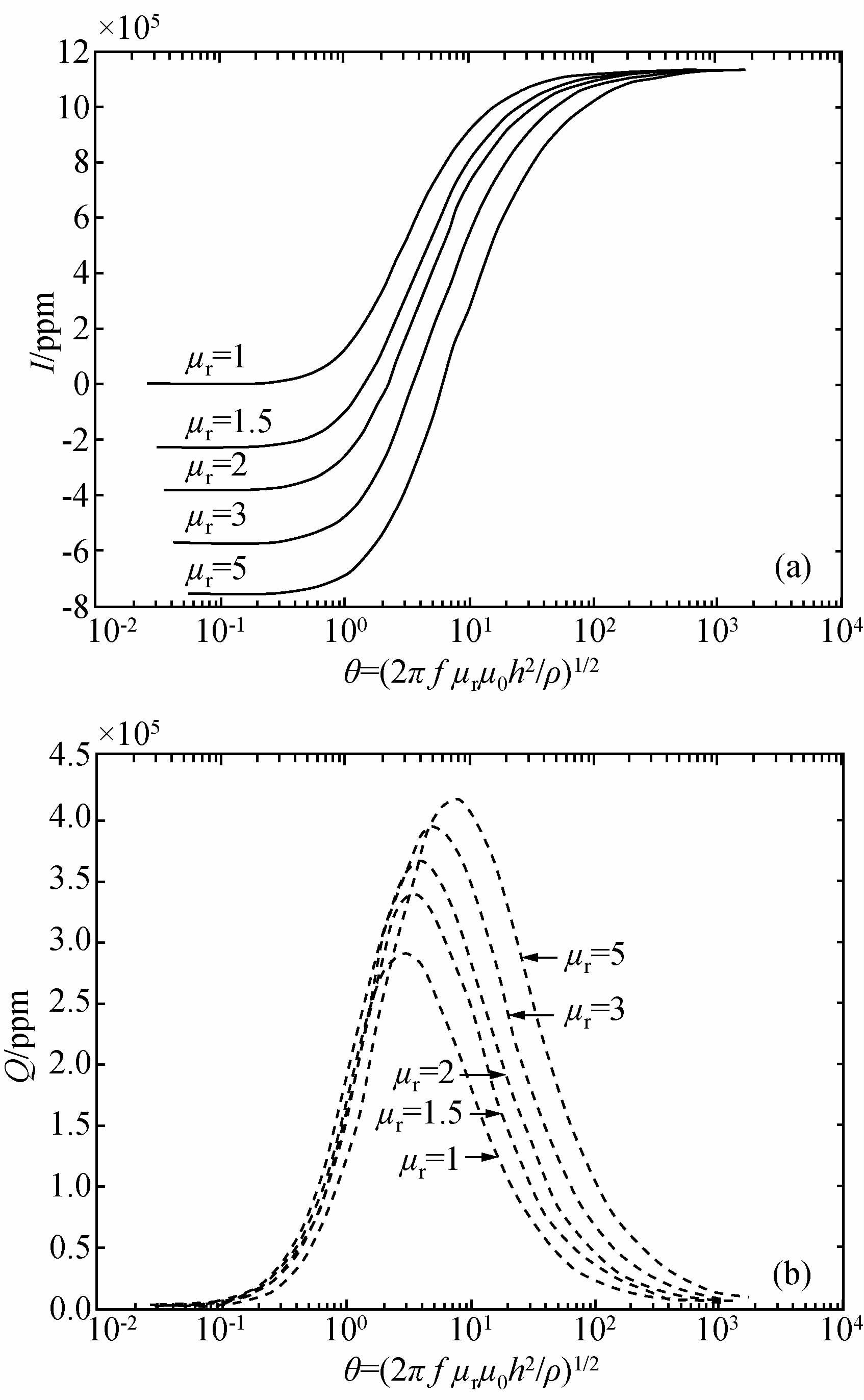
|
图 7 不同相对磁导率条件下的电磁响应随感应数变化的曲线图 (a)实分量I;(b)虚分量Q. Figure 7 The curves of electromagnetic response change with induction number in different relative permeability |
从图 7可以看出,归一化二次场的实分量(I)和虚分量(Q)是感应数θ的函数,且对应着不同的μr值.磁导率μ >μ0的作用是两方面的,首先,磁导率增加了感应数θ的值;其次,当感应数θ很小时,响应函数I+iQ主要受磁化强度影响.
2 磁性条件下的相位矢量图法传统的频率域航空电磁反演是根据野外实测的实、虚分量的场值(电磁图)进行定性的解释.由于航空电磁法所获得的数据量很大,这就要求我们快速可靠地反演实际地下介质的电性情况,所以选择合适的航空电磁法反演方法非常重要.相位矢量图(Argand diagram)是根据理论计算或模型实验的方法获得的数据绘制成的,表示虚、实分量异常和不同参数变化关系的列线图.可以用它来进行定性或定量解释一部分航空电磁法实测的异常资料.
在非磁性区域,不用考虑介质磁导率的变化.传统上,人们用横坐标表示归一化二次场实分量,纵坐标表示归一化二次场虚分量,然后在均匀半空间模型上取不同电阻率值和不同飞行高度的数值计算求得二次响应的实、虚分量值,然后以飞行高度和电阻率为参数分别连成曲线,做成相位矢量图.这样,在相位矢量图中进行插值求解视电阻率的同时,还能够插值得到视飞行高度.然而在强磁性区域,因为磁极化电流叠加到传导电流,会使得计算电阻率的值变大,从而,传统忽略磁导率的相位矢量图法并不适用于高磁性区域的视电阻率转换.所以,有必要讨论磁性条件下的相位矢量图.
本文在传统的二维相位矢量图的基础上,对传统的相位矢量图法进行了改进,添加了磁导率参量的计算.用横坐标表示归一化二次场实分量,纵坐标表示归一化二次场虚分量,然后在均匀半空间模型上取不同电阻率、不同相对磁导率和不同飞行高度的数值计算得到归一化二次场响应的实、虚分量值,然后再以飞行高度和电阻率、以及相对磁导率为参数分别连成曲线,形成三维立体图,然后对这个三维相位矢量图按飞机飞行高度取切片,就可以得到某个固定高度上以电阻率和磁导率为参量的二维相位矢量图.
为了分析飞行高度、电阻率、以及相对磁导率三个参量相互变化时的磁场响应,需要分别变化每个参量,具体变化规律是:(1)飞行高度h离散取值,相对磁导率μr离散取值,大地电阻率ρ连续变化;(2)飞行高度h离散取值,大地电阻率ρ离散取值,相对磁导率μr连续变化;(3)相对磁导率μr离散取值,大地电阻率ρ离散取值,飞行高度h连续变化.通过这样的规律变化取值,就可以得到飞机飞行高度h、大地电阻率ρ、相对磁导率μr三个参量对应的归一化二次场响应的实、虚分量值的三维相位矢量图.以下分别就这三种情况结合具体数值进行讨论:
本文以均匀半空间为计算模型(见图 8).当发射线圈电流为1安培,线圈半径为0.3 m,收发距6.5 m,频率固定为104赫兹,飞机飞行高度分别为:10、20、30、40、50、60、70、80、90、100、110、120、130、140、150、160、200、300 m,然后,对应每一个飞行高度,相对磁导率分别依次取1~10等数值、大地电阻率从10-2~107 Ω·m变化,这样就可以得到在固定高度、收发距和频率情况下,不同磁导率分别对应大地电阻率变化的电磁响应曲线.当飞行高度取h=90 m时,得到不同相对磁导率和变化电阻率情况下的归一化二次场响应的实、虚分量曲线,具体见图 9中纵测线所示.
|
图 8 AEM均匀半空间地电模型 Figure 8 AEM homogeneous half-space geoelectric model |
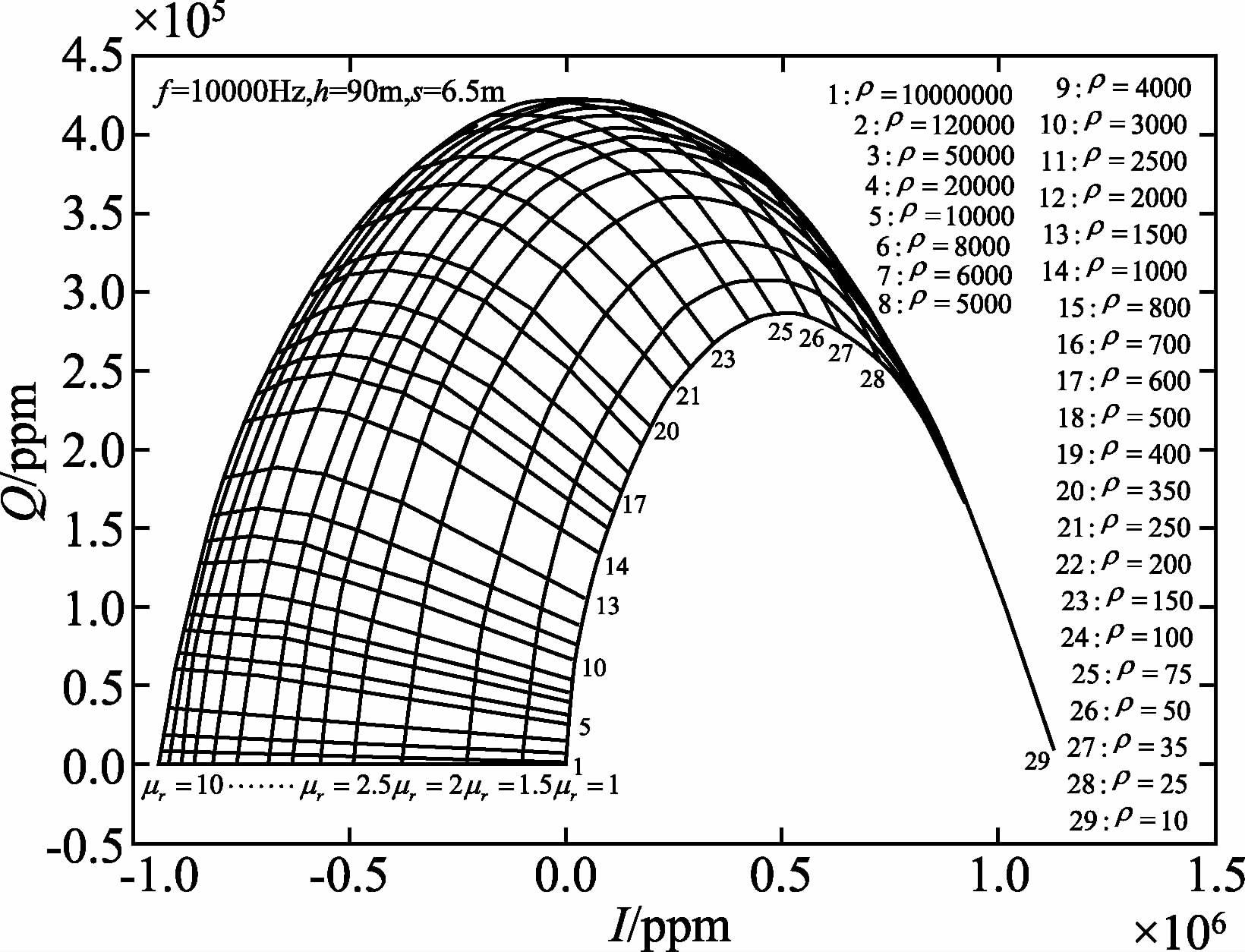
|
图 9 以磁导率、电阻率和飞行高度为参量的三维相位矢量图切片 Figure 9 3D phase vector graphics section with magnetic permeability,resistivity and flight altitude |
(2) 当发射线圈电流为1安培,线圈半径为0.3 m,收发距6.5 m,频率固定为104赫兹,飞行高度分别从10~300 m变化,然后,对应每一个飞行高度,大地电阻率分别依次取107、1.2×105、5×104、2×104、104、8×103、6×103、5×103、4×103、3×103、2.5×103、2×103、1.5×103、103、800、700、600、500、400、350、250、200、150、100、75、50、35、25、10 Ω·m、相对磁导率从1~10连续变化时,就可以得到在固定高度、收发距和固定频率的情况下,不同大地电阻率ρ分别对应相对磁导率μr变化的电磁响应曲线.如果飞机飞行高度取h=90 m时,得到电阻率和相对磁导率情况下的归一化二次场响应的实、虚分量曲线,具体见图 9中横测线所示.
(3) 当发射线圈电流为1安培,线圈半径为0.3 m,收发距6.5 m,频率固定为104赫兹,相对磁导率分别取1、1.2、1.5、2、2.5、3、3.5、4、5、6、7、8、9、10等数值,对应每一个相对磁导率值,大地电阻率分别依次取107~10 Ω·m、飞行高度从10~300 m连续变化,这样就可以得到在固定相对磁导率、收发距和频率情况下,不同大地电阻率分别对应飞行高度变化的电磁响应曲线.
通过以上计算,最后得到了一个以飞机飞行高度h、大地电阻率ρ、相对磁导率μr三个参量所对应的归一化二次场响应的实、虚分量值的三维立体图,这里,我们取飞机飞行高度h=90 m,得到三维线性图中的一个切片图,见图 9所示.这个图就是以磁导率、电阻率为参量的在高度h=90 m时相位矢量图.
另外,在上面的计算中频率都固定为104赫兹一个值,在实际应用中,可以根据计算需要更改为10-2~107赫兹的任意一个频率值,例如IMPULSE吊舱式直升机航空电磁测量系统每种装置可以发射三个频率,每个频率都可以得到一个对应的三维相位矢量图.
从图 9可以得出以下结论:
(1) 在三维相位矢量图中,用实测的归一化二次场实、虚分量在图中进行插值,可以在求解视电阻率ρs的同时,还能够插值得到该坐标点对应大地的相对磁导率μr和被称为ha的视飞行高度.当飞行高度h固定时,则可以从相对磁导率和电阻率对应的相位矢量图中插值得到μr和ρs的值.
(2) 从图中可以看到,当电阻率较大,相对磁导率较小时,相位矢量图中网格清晰明了,在这些网格中可以有效地进行插值.
因此,相位矢量图插值法用于简单的一维模型,反演速度快,计算效率高.但是,当考虑磁导率参量的时候,相位矢量图的数据变成了关于μr、ρs、h的归一化二次场实、虚分量的三维数据.
为了进一步评价这种成像方法的有效性,下面分别对以上模型中每组参数反演得到的视相对磁导率和视电阻率进行误差分析,得出其相对误差情况,见表 1所示.
|
|
表 1 三维相位矢量图法计算参数的相对误差表 Table 1 Relative error of calculation parameters for 3-D phase vector graphics |
从表 1中可以看到,使用本文的近似反演方法计算得出的数据与真实模型相对误差(Er<5%)较小,这就验证了本文的三维相位矢量图法的有效性.这种算法因为不需要迭代,速度快,而且精度也能满足要求,通过加密图 9中磁导率、电阻率、飞行高度的曲线,可以进一步提高计算精度.
3 结 论 3.1讨论了垂直磁场响应表达式中核函数的收敛性,采用了先从积分核中减去磁场表达式中的某部分核函数,再在计算结果中加上这部分函数的解析解的方法来保证核函数收敛;通过分析反射系数的性质,得出了低频时,反射系数衰减很快,频率越高,反射系数衰减越慢的结论;然后分析了线性滤波算法和直接数值积分法的原理,对比二者计算结果表明:在频率域电磁法频段范围内二者计算精度相当,但线性滤波算法法计算速度快.因为航空电磁法处理的数据量庞大,本文采用120点线性滤波算法来求解汉克尔变换以提高计算效率.
3.2针对强磁性区域问题,讨论了经典的视电阻率转换方法—相位矢量图法的不足,在传统的二维相位矢量图的基础上,添加了磁导率参量的计算,绘制成不同电阻率、不同相对磁导率和不同飞行高度的三维相位矢量图,然后对这个三维图形按飞机飞行高度取切片,就可以得到某个高度上以电阻率和磁导率为参量的二维相位矢量图,从而可以通过双变量插值获取实测磁场实、虚分量对应的视电阻率和视相对磁导率的值.对于强磁性区域可以很好的提高视电阻率反演的准确率,并有利于对地下地质体物性的分析.
3.3三维相位矢量图法既保持了传统相位矢量图方法快速的特点,同时又能够较精确地获得电导率、磁导率和视高度等多种参数,为实测资料的处理解释提供了很好的基础支持.但是,当磁导率较大或者电阻率较小时,相位矢量图中的网格会发生重叠,数据可区分性降低,使得进行插值困难,因此,在这些情况下,应该调整网格大小,提高插值精度.
3.4在将来的研究中应注重程序的多线程并行化处理,在处理较大的实测数据比较耗时,这一方面是因为实测航空电磁数据量庞大,另一方面是因为在我们的反演过程中,每一点的数据迭代都需要带入相应位置的飞行高度进行循环差值,这样做的好处是可以精确的刻画每一个点反演时的带入参数,提高反演精度,但在部分飞行高度变化不大区域,我们完全可以设定一个具体的飞行高度值进行计算,这样可以很好的节省计算量.另外,对于程序的并行化处理,例如基于GPU,MPI等方法的并行化处理也是重要的研究方向.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Annetts D, Sugeng F, Macnae J, et al .2000. Modelling the airborne electromagnetic response of a vertical contact[J]. Exploration Geophysics, 31 (2) : 115–125. DOI:10.1071/EG00115 |
| [] | Fountain D .1998. Airborne electromagnetic systems-50 years of development[J]. Exploration Geophysics, 29 (2) : 1–11. DOI:10.1071/EG998001 |
| [] | Fraser D C .1978. Resistivity mapping with an airborne multi-coil electromagnetic system[J]. Geophysics, 43 (1) : 144–172. DOI:10.1190/1.1440817 |
| [] | Huang H P, Fraser D C .2001. Mapping of the resistivity, susceptibility, and permittivity of the earth using a helicopter-borne electromagnetic system[J]. Geophysics, 66 (1) : 148–157. DOI:10.1190/1.1444889 |
| [] | Liu Y H, Yin C C .2013. 3D inversion of frequency-domain HEM data[J]. Chinese Journal of Geophysics (in Chinese), 56 (12) : 4278–4287. DOI:10.6038/cjg20131230 |
| [] | Meng Q M. 2005. Inversion and application of frequency-domain AEM data from a layered earth (in Chinese)[Ph. D. thesis]. Beijing:China University of Geosciences (Beijing). |
| [] | Qian L X. 1990. 1-D inversion in frequency-domain airborne electromagnetic method and application in airborne resistivity mapping(in Chinese)[MSc thesis]. Langfang:Research Institute of Physical and Chemical. |
| [] | Sattel D. 2002. Modelling AEM data with Zohdy's method[C]//64th Ann. Internat. Mtg., Soc. Expi. Geophys. Expanded Abstracts, 30-33. |
| [] | Sengpiel K P, Siemon B .1998. Examples of 1-D inversion of multifrequency HEM data from 3-D resistivity distributions[J]. Exploration Geophysics, 29 (3) : 133–141. |
| [] | Wang W P, Zeng Z F, Li J, et al .2015. Topographic effects and correction for frequency airborne electromagnetic method[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 45 (3) : 941–951. |
| [] | Wang W P, Zeng Z F, Wu C P, et al .2013. Frequency Dotmain airborne electromagnetic dual-frequency inversion method based on magnetic permeability[J]. Geological Science and Technology Information (in Chinese), 32 (2) : 181–186. |
| [] | Xi J J. 2010. A study of forward and inversion for frequency-domain airborne electromagnetic method in terms of permeability and resistivity (in Chinese)[MSc thesis]. Changchun:Jilin University. |
| [] | Yin D W, Lin J, Zhu K G, et al .2013. Simulation research on coil motion noise removal for time domain airborne electromagnetic data[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 43 (5) : 1639–1645. |
| [] | Yong Y H. 1993. Research on the inversion interpretation method and its application of the frequency domain airborne electromagnetic method(in Chinese)[MSc thesis]. Beijing:China University of Geosciences (Beijing). |
| [] | Zheng S T, Zeng Z F, Zhang D G, et al .2007. Calculation about high-frequency electromagnetic response and cases analyzing[J]. Progress in Geophysics (in Chinese), 22 (6) : 1772–1776. |
| [] | 刘云鹤, 殷长春.2013. 三维频率域航空电磁反演研究[J]. 地球物理学报, 56 (12) : 4278–4287. DOI:10.6038/cjg20131230 |
| [] | 孟庆敏. 2005. 频率域航空电磁法层状反演及应用研究[博士论文]. 北京:中国地质大学(北京). http://cn.bing.com/academic/profile?id=18c80eb5881cd61a8142dfcfd0269cd0&encoded=0&v=paper_preview&mkt=zh-cn |
| [] | 钱立新. 1990. 频率域航空电磁法的一维反演及在航空电阻率填图中的应用[硕士论文]. 廊坊:地质矿产部地球物理地球化学勘查研究所. |
| [] | 王卫平, 曾昭发, 李静, 等.2015. 频率域航空电磁法地形影响和校正方法[J]. 吉林大学学报(地球科学版), 45 (3) : 941–951. |
| [] | 王卫平, 曾昭发, 吴成平, 等.2013. 基于磁导率的频率域航空电磁法双频反演方法[J]. 地质科技情报, 32 (2) : 181–186. |
| [] | 习建军. 2010. 基于磁导率和电阻率的频率域航空电磁法正反演研究[硕士论文]. 长春:吉林大学. http://cn.bing.com/academic/profile?id=8d6e22aecaa918ee204c90d561477c9d&encoded=0&v=paper_preview&mkt=zh-cn |
| [] | 尹大伟, 林君, 朱凯光, 等.2013. 时间域航空电磁数据线圈运动噪声去除方法仿真研究[J]. 吉林大学学报(地球科学版), 43 (5) : 1639–1645. |
| [] | 雍蔚华. 1993. 频率域航空电磁法资料的反演解释方法及其应用研究[硕士论文]. 北京:中国地质大学(北京). |
| [] | 郑圣谈, 曾昭发, 张代国, 等.2007. 层状介质高频电磁场计算方法及结果分析[J]. 地球物理学进展, 22 (6) : 1772–1776. |
 2016, Vol. 31
2016, Vol. 31

