随着石油勘探开发的不断发展,勘探目标由构造油藏转移到小砂体、薄互层、微裂缝等隐藏型油气藏,勘探的目标地层也越来越深.目标储层埋藏深、规模小,地表震源激发的地震波在介质中经过较长时间的传播与散射以及介质非弹性效应造成的地震反射信号的衰减,使得地表检波器接收到的反射信号能量相对较弱,经常被淹没在背景噪声中,波形也常发生畸变.地震资料解释储层时多以振幅能量特征为依据,弱信号或者空间弱变化信号难以有效检测,弱信号拾取难度大,难以确定小地质体的边界.因此如何从地表接收到的信号中检测、提取并重建淹没在背景噪声中的有效地震弱信号是目前地震信号处理需要解决的问题.目前常用的地震弱信号的检测与提取方法包括基于随机共振的弱信号检测(Benzi et al.,1981;段江海等,2003),混沌振子系统的弱信号检测(李继永,2010),独立分量分析的方法(ICA)(李宏等,2010;高伟,2011),基于小波变换的弱信号提取,卡尔曼滤波方法(Baziw et al.,2002;宋维琪和吕世超,2009)等.
本文的主要研究工作把独立变量分析与卡尔曼两种方法有机结合起来,发挥它们的优势,实现弱地震反射系数的提取.卡尔曼滤波算法是根据信号状态变量和状态空间变化特征,通过已知资料得到有用信号和噪声的初始估计,利用递归方法进行有用信号的最佳估计.ICA算法基本思路是将随机噪声作为源信号,近似取相邻两道的记录的两次观测结果为混合信号,再用ICA算法进行分离,就可得到分离后的信号和噪声.卡尔曼估计方法的好处是,不但考虑初始输入,更注重过程.独立变量分析对初始变量可以进行独立分析,得到相对准确的初始变量的估计.研究方法,通过理论模型资料和实际资料验证,效果明显,证明方法在弱信号提取方法是可行的.
1 独立变量分析理论方法独立分量分析(即ICA)是伴随盲信号分量(Blind Signal Separation,BSS)问题发展起来的,BSS是指仅从观测的混合信号中恢复独立的源信号,这里的“盲”是指:(1)源信号是不可观测的;(2)混合系统是事先未知的.如果混合系统是已知的,则以上问题就退化成简单的求混合矩阵的逆矩阵.但是在更多的情况下,人们无法获取有关混合系统的先验知识,这就要求人们从观测信号来推断这个混合矩阵,实现盲源分离.
ICA的最简形式:n个观测信号xi∈{x1,x2,…,xn},设其是si∈{s1,s2,…,sn}的线性组合,si是未知且统计独立的源信号:
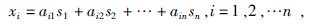
|
(1) |
其中aij是混合系数,表示第i个观测信号中第j个源信号的权重.一般假设观测信号xi和源信号si都零均值.将式(1)改成向量形式为

|
(2) |
式(2)中X={xi},S={si},A={aij}是混合矩阵,i=1,2,…,n;j=1,2,…,n.式(2)为ICA混合模型.由于ICA假设混合矩阵A和独立分量S都是未知,只有观测信号X已知,则由观测信号估计出混合矩阵A和独立分量S是一个盲信号分离(BSS)问题.假设A可逆,则有分离矩阵B=A-1,使S=BX,从而恢复源信号.但是A是未知的,B=A-1需要通过估计得到,而后利用分离矩阵得到信号为
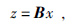
|
(3) |
式(3)表明ICA方法需要优化分离矩阵B来分离得到信号z来逼近实际源信号s.
2 基于卡尔曼最优估计理论的独立变量分解方法 2.1 独立变量分析提取弱地震信号的可行性一般来说,反射系数和地震子波均是未知的,仅从已知的地震记录x(t)中重构出未知的反射系数r(t)与地震子波b(t),符合盲信号分离(BSS)问题的基本要求.重写分解方程,Z=BX,X为观测的地震信号,B为分离矩阵,Z为被分离的分量,在这里,Z=[r,b,n1,n2]T,由反射系数、子波及噪声分量组成.独立变量分解就是通过一定的算法设计,构造最佳的分离矩阵,实现各个分量的最优分离,即对地震信号进行最优分解,获得反射系数.
2.2 地震信号独立变量分析的卡尔曼最优估计 2.2.1 估计基本方程卡尔曼估计是观测向量空间中对状态空间变量在最小方差下的最优估计,描述该过程方程分别是差分方程和线性方程,即
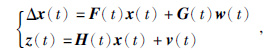
|
(4) |
其中x(t)为状态变量,Δx(t)为x(t)的差分;F(t)为状态转移矩阵,w(t)为输入的影响状态变量均值为零的白噪声,z(t)为观测值,H(t)为观测矩阵,G(t)为输入函数;v(t)是影响观测结果的均值为零的白噪声.式(4)离散形式为
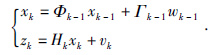
|
(5) |
卡尔曼估计不同独立变量分析,卡尔曼估计在进行递推估计时,要求提供估计分量的先验信息,然后再通过状态分量的预测与估计获得后验信息.一般情况下,采用原始样本数据求取状态变量、噪声分量及观测记录的统计特征参数如方差参数等.实际上我们只知道地震记录数据,建立的状态方程和观测方程中的各变量是通过递推估计后获得的,这样给出的先验信息具有极大的不确定性.如果把观测的地震记录进行独立变量分解,就可以得到初步的分解变量,尽管可能各分量顺序不确定,但是至少提供了有用信号和噪声信号各分量信息.这时再求各分解分量的先验信息,就更接近真实估计.因此,把独立分量分解和卡尔曼最优估计结合起来,会取得更好的效果.
地震记录是子波和反射系数的褶积,对于薄层反射记录,包含了相邻层的相互干涉效应.对地震数据进行独立变量分解,得到初始分解分量,对各分量和地震记录建立卡尔曼估计状态方程,根据建立的方程,利用递推寻优过程进行分量的最佳估计.考虑到实际薄层地震记录,建立如下的状态方程和观测方程:
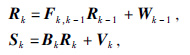
|
(6) |
其中Rk=[rk,-m,rk,-m+1,...,rk,m]T为邻近地层干涉反射系数分量,对于薄层是情况更具代表性.Wk=[wk,-m,wk,-m+1,...,wk,m]T,Vk=[vk,-m,vk,-m+1,…,vk,m]T分别是与反射系数和观测数据有关的噪声分量,这些分量的初始分量通过独立变量分解得到,其方差分别是向量Qk,Ck.
为了对上述离散方程便于算法实现,给出具体的实现过程:
状态递推估计:
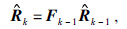
|
(7) |
误差协方差递推为
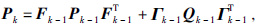
|
(8) |
其中Γk-1Qk-1Γk-1T为输入误差协方差;Fk-1为状态转移矩阵;Qk-1为随机游散过程的方差矩阵,Pk为误差协方差阵.
状态估计更新为
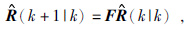
|
(9) |
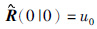
误差协方差阵更新:
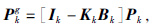
|
(10) |
上述式中Ik为单位矩阵,Kk为卡尔曼增益矩阵,其表达式为
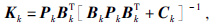
|
(11) |
状态分量的更新估计为
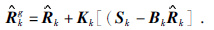
|
(12) |
上式说明反射系数向量下一步的估计,是上一步估计结果与新息量和观测数据预测误差乘积的综合结果.在以上估计中,涉及到初始方差值的选取问题,即如何确定反射系数初始方差和地震观测值的初始方差.这里利用独立变量分解的噪声分量来计算地震记录噪声的初始方差.反射系数的初始方差,由反射系数确定.
2.2.3 最优逼近估计目前独立变量分析逼近估计是通过个分解分量的迭代逼近计算,使各分量满足相互独立的条件作为终止迭代的条件.由于源数、混合矩阵的维数难以准确确定,尽管输出的各分量虽然相互独立了,但是各分量不能够完全包含了源真实信号的信息.卡尔曼估计中是把参量初始状态和递归过程联系在一起,估计过程的具有较强的无偏性和稳定性.独立分量分析采用卡尔曼估计逼近,分量逼近结果不至于偏离太大.为了实施进一步约束,考虑到地震记录的横向相关信息.相邻道组成一个状态方程组和观测记录方程组.建立多道方程进行研究,可以在寻优逼近迭代过程中,增加有用信号横向相关信息约束.
2.2.4 冗余性分析和冗余分量的删除独立变量分析的分解条件是,源信号分量独立,分解分量独立.不满足此条件时,得不到正确的分解结果.要满足以上条件,首先进行源信号分量的独立性分析.
地震记录是各种因素的叠加结果,进行独立分量分析时,需对其结果进行处理,尽量使各输入量相对独立,即不相关.对实际数据如何处理才能得到相对独立的输入变量呢?可以对单道进行处理,也可以对多道进行处理.本文采用单道处理办法,具体:以计算点为中心,对一个大约子波长度的时窗,分成若干相同长度的小时窗,
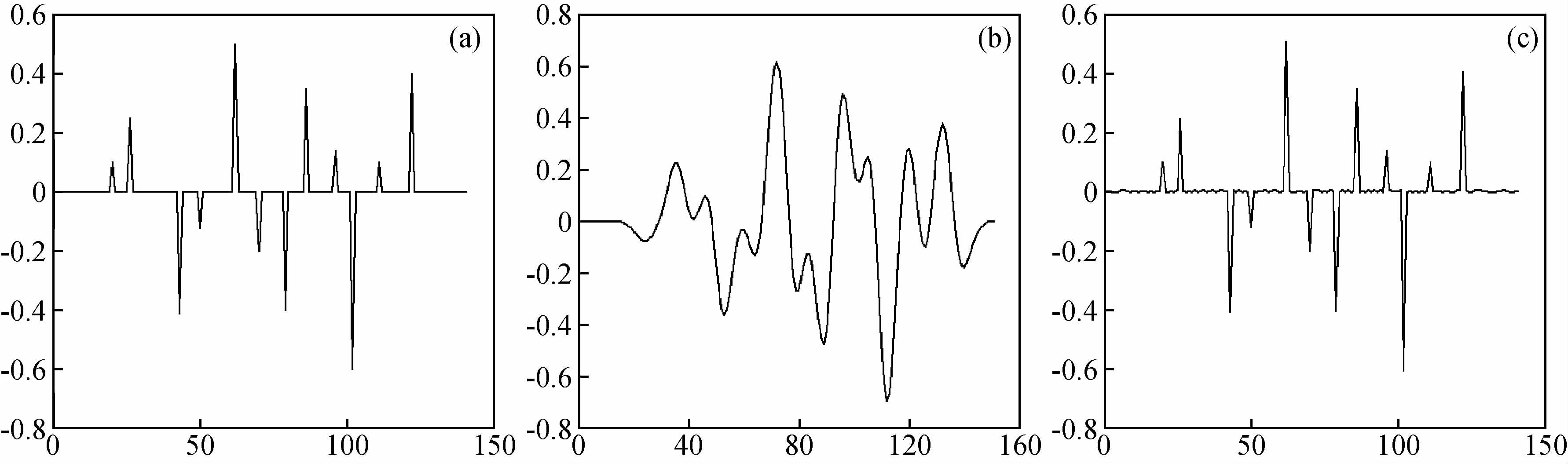
为了验证方法,首先应用理论模型进行试验分析,如图 1,图 1(a)为反射系数,图 1(b)为合成地震记录,图 1(c)为研究方法提取的结果,从图中分析模型结果可以看出处理后的结果中被强反射系数掩盖的弱反射系数得到呈现.
|
图 1 理论模型结果 (a)反射系数;(b)合成记录;(c)提取结果. Figure 1 The result of theoretical model (a)Reflection coefficients;(b)Synthetic seismogram;(c)The extracting result. |
为了进一步验证方法,利用加噪模型进行试验分析,如图 2,图 2(a)为反射系数,图 2(b)为加噪后的合成地震记录,图 2(c)为研究方法提取结果,结果表明存在噪声的情况下,研究方法也能够很好的提取弱反射系数,弱反射系数相对于强反射系数的位置正确,但由于受到噪声的影响,弱反射系数相对大小受到一定的影响.

|
图 2 加噪理论模型结果 (a)反射系数;(b)加噪后的合成记录;(c)提取结果. Figure 2 The result of theoretical model with noise (a)Reflection coefficients;(b)Synthetic seismogram added with noise;(c)The extracting result. |
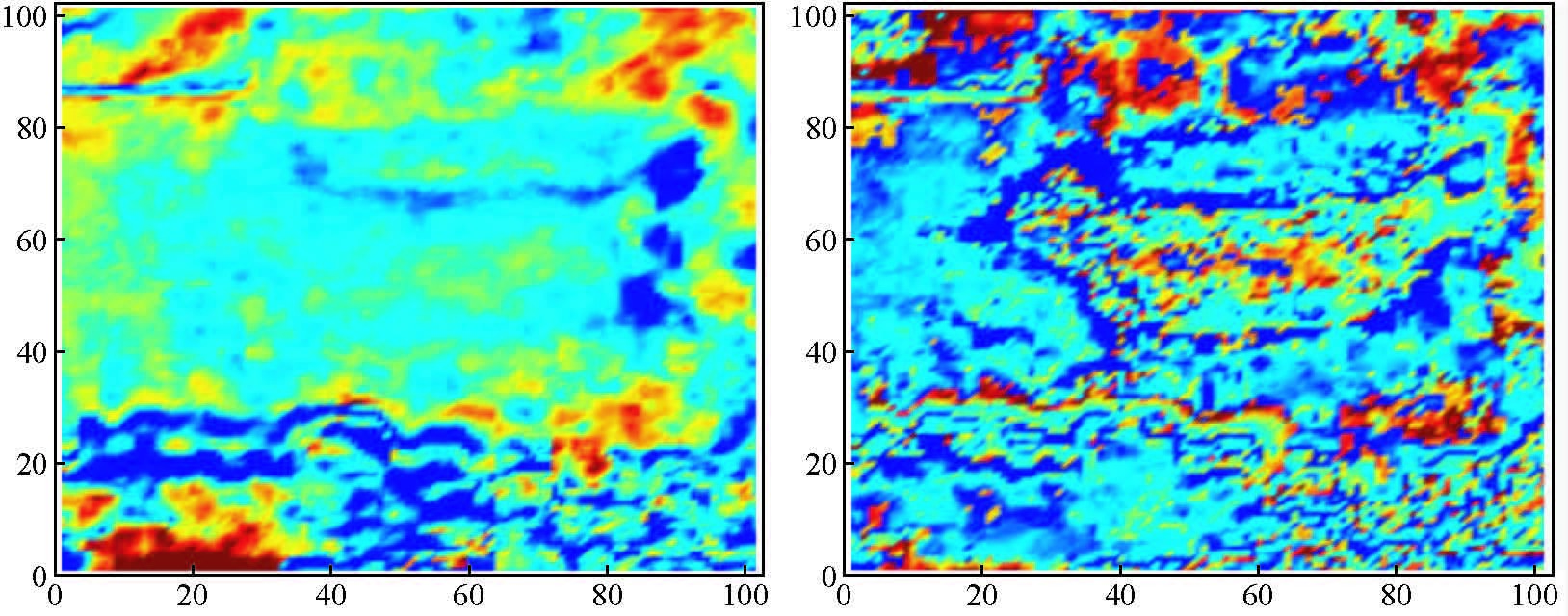
为了进一步验证方法的应用效果,对过商61井地震剖面利用上述研究的方法进行处理,如图 3.对比商61井声波测井曲线,处理后结果剖面中原来较弱的在原始地震剖面上看不到的信息,得到清楚的显示.对工区的三维地震数据进行了处理,图 4为不同测线的处理结果,对比处理前后结果,地震剖面的分辨率提高,弱信号成分得到显现.同时对层切片处理前后进行比较(如图 5),从图 5中可以看到经过处理后较小规模的地质体和地质体的边缘得到清楚地揭示.

|
图 3 实际资料处理结果比较 (a)地震剖面;(b)处理后结果 ;(c)声波测井曲线. Figure 3 The processing result of actual data (a)Seismic section;(b)The result after processing;(c)Acoustic logging trace. |

|
图 4 不同剖面的处理结果 (a)第126线处理前后结果比较;(b)第233线处理前后经过比较. Figure 4 The processing result of different seismic sections (a)Comparison of pre- and post-processing profile in the 126th line;(b)Comparison of pre- and post-processing profile in the 233th line. |
|
图 5 处理前后层切片结果比较 Figure 5 Comparison of pre-and post-processing section in strata slice |
地震反射系数和地震子波是独立的,满足独立变量分析基本条件.观测的地震记录是各种结果分量的叠加量,包含有用信号和噪声信号的先验信息模糊.通过独立变量分析方法,把地震记录进行分解成为多个分解分量,呈现出有用信号和噪声信号的先验信息.利用卡尔曼最优估计理论中先验信息估计特点,再进行独立分量的更新迭代逼近估计,使得逼近估计结果更加准确可靠.
5.2由于源数、混合矩阵的维数难以准确确定,尽独立变量分析输出的各分量虽然相互独立了,但是各分量不能够完全包含了源真实信号的信息.为了尽量减小这种源信息的不确定性,在寻优逼近过程中增加相邻道横向相关信息约束,可以减小了逼近结果失真程度.通过理论模型和实际资料论证了方法的正确可靠性,实际应用效果显著.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Baziw E, Weir-Jones I .2002. Application of Kalman Filtering Techniques for Microseismic Event Detection[J]. Pureand Applied Geophysics, 159 (1-3) : 449–471. |
| [] | Benzi R, Sutera A, Vulpiani A .1981. The mechanism of stochastic resonance[J]. Journal of Physics A:Mathematical and General, 14 (11) : :L453–L457. |
| [] | Li H, Dai X C, Ge C K, et al .2007. Seismic signal detection and first arrival pickup based on mutual information[J]. Chinese Journal of Geophysics (in Chinese), 50 (4) : 1190–1197. DOI:10.3321/j.issn:0001-5733.2007.04.028 |
| [] | Liu X W, Ga o W, Zhang N, et al .2007. ICA with banded mixing matrix based seismic blind deconvolution[J]. Progressin Geophysics (in Chinese), 22 (4) : 1153–1163. DOI:10.3969/j.issn.1004-2903.2007.04.022 |
| [] | Liu X W, Liu H .2003. Survey on seismic blind deconvolution[J]. Progressin Geophysics (in Chinese), 18 (2) : 203–209. DOI:10.3969/j.issn.1004-2903.2003.02.005 |
| [] | Robinson E A, Treitel S .1980. Geophysical signal analysis[M]. New Jersey: Prentice-Hall . |
| [] | Saruwatari H, Kawamura T, Nishikawa T, et al .2006. Blind source separation based on a fast-convergence algorithm combining ICA and beamforming[J]. IEEE Transactionson Audio, Speech, and Language Processing, 14 (2) : 666–678. |
| [] | 曹思远, 陈香朋, 李美.2003. 基于极大后验估计的卡尔曼滤波反褶积[J]. 勘探地球物理进展, 26 (4) : 273–276. |
| [] | 邓自立.2005. 最优估计理论及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社 . |
| [] | 段江海, 宋爱国, 王一清.2003. 随机共振理论在微弱信号检测中的应用研究[J]. 信号处理, 19 (6) : 569–572. |
| [] | 李辉, 戴旭初, 葛洪魁, 等.2007. 基于互信息量的地震信号检测和初至提取方法[J]. 地球物理学报, 50 (4) : 1190–1197. DOI:10.3321/j.issn:0001-5733.2007.04.028 |
| [] | 理华, 侯朝焕, 马晓川, 等.2009. 一种适用于微弱信号提取的盲源分离算法[J]. 应用声学, 28 (4) : 249–253. |
| [] | 李宏, 林义刚, 张冬生, 等.2010. ICA在地震信号处理中的应用研究[J]. 科学技术与工程, 10 (9) : 2057–2060. |
| [] | 李继永. 2010. 基于混沌振子的微弱信号检测技术研究[硕士论文]. 成都:电子科技大学. |
| [] | 刘喜武, 刘洪.2003. 地震盲反褶积综述[J]. 地球物理学进展, 18 (2) : 203–209. DOI:10.3969/j.issn.1004-2903.2003.02.005 |
| [] | 刘喜武, 高伟, 张宁, 等.2007. 基于带状混合矩阵ICA实现地震盲反褶积[J]. 地球物理学进展, 22 (4) : 1153–1163. DOI:10.3969/j.issn.1004-2903.2007.04.022 |
| [] | 宋维琪, 吕世超.2009. 基于卡尔曼最优估计理论的地震反褶积方法[J]. 石油物探, 48 (4) : 342–346. |
| [] | 王亮. 2005. 基于独立成分分析的盲信号分离算法研究[硕士论文]. 西安:西北工业大学. |
| [] | 袁野. 2006. 基于混沌理论的微弱信号检测与勘探地震学中同相轴的恢复[硕士论文]. 长春:吉林大学. |
 2016, Vol. 31
2016, Vol. 31

