全波形反演(Full waveform inversion,FWI)自从Lailly和Tarantola等人(Lailly,1983; Tarantola,1984,1986,1988)在20世纪80年代提出以来,已经从理论上被证明是反演高精度地下岩石物理参数有效手段.全波形反演是以波动方程为基础,通过正演模拟技术得到模拟地震数据,利用模拟数据与实际数据中的振幅和相位信息进行匹配,得到匹配后的残差,然后利用数据残差中的运动学和动力学信息进行速度反演,与传统的速度反演方法相比,它具有理论框架完备、反演精度高的特点.时间域全波形反演算法在实现过程中主要包括2个过程:以地震子波为震源的正演过程和以残差波形为震源的波场反传过程.通过正演波场和反传波场在时间上零延迟互相关可产生模型弹性参数更新量(梯度),从而迭代更新初始弹性参数模型.
近年来,很多研究者对理论模型反演做了大量的研究工作,而且反演结果精度非常高,然而在实际数据应用的实例却非常少,其最主要的原因是实际数据中低频的缺失(Shin and Cha,2008).在实际数据全波形反演中,目前通过速度分析手段得到的速度场精度非常低,为了反演速度模型的低波数成分,需要利用观测记录的低频成分和长偏移距的信息.然而由于采集技术的限制,实际数据中的低频成分和偏移距长度都无法满足全波形反演的要求.Gauthier等(Gauthier et al.,1986)证明当初始速度模型与真实模型有10%的误差时,反演会陷入局部极值出现周波跳跃现象,全波形反演就会失败.为了提高全波形反演对初始速度的稳健性,一些学者提出了多尺度全波形反演方法,通过将问题分解为不同尺度(频率)求解以保证反演过程稳定收敛(Bunks et al.,1995;张文生等,2015).最近一些学者也针对此问题提出了一些新的解决办法,例如频率外推(Xie,2013)、利用地震数据振幅包络进行反演(Chi et al.,2014),但是这些技术在实际数据应用中仍然存在很多困难.
我们在前人的基础上进一步指出了全波形反演梯度角度域多尺度性,即相同主频数据得到的不同反射角范围的梯度具有不同频率的特征.因此,可以在频率不变的情况下,可以把梯度进一步分解得到不同频率的梯度,在反演初始阶段利用梯度中的低频信息.此外,全波形反演梯度在浅层存在频率很低的成分,尤其是构造复杂、地层倾角较大情况下,噪声会干扰实际梯度算子求取,影响反演结果.
全波形反演梯度角度域分解借鉴地震叠前深度偏移角度域分解思想,利用地下速度、地震数据及炮检关系求得地下散射点处的局部反射角,进而把成像数据映射到相应的角度.地震叠前数据角度域分解或者说角度域道集提取根据偏移方法的不同可以分为基于波动方程(de Bruin et al.,1990; Prucha et al.,1999; Rickett and Sava,2002; Xie and Wu,2002; Stolk and Symes,2004; Biondi and Tisserant,2004)和射线(Operto et al.,2000; Xu et al.,2001)两大类,角度域道集分解最早源于1990年de Bruin等(de Bruin et al.,1990)提出利用波动方程叠前偏移技术获得地下共成像点反射系数随入射角度的变化.角度域道集分解都是利用炮点、检波点及速度场所包含的地下局部反射角信息,然后在偏移成像过程中把相应的数据映射到对应的共成像点道集.这个过程可以在成像前进行也可以在成像后进行,Sava等(Sava and Vlad,2011)明确区分了成像前提取角度域共成像点道集方法和成像后提取角度域共成像点道集方法区别:即只有在成像后将局部偏移距域共成像点道集通过倾斜叠加转化为角度域共成像点道集的方法才属于成像后提取方法.基于波动方程的角度域道集分解主要有两类:(1)利用扩展成像条件生成共偏移距道集,然后利用倾斜叠加变换出角度域道集(Sava and Vlad,2011);(2)利用Yoon和Marfurt等人基于Poynting矢量确定波的传播方向的理论(Yoon and Marfurt,2006),根据波的传播方向求得地下反射界面的局部反射角信息,然后在成像条件中引入反射角得到角度域道集,文中即是采用此方法.
针对全波形反演中的低频问题,采用由低频到高频进行多尺度反演策略.由于不同地下反射角对应的梯度具有频率的多尺度性,借鉴Yoon和Marfurt等人逆时偏移成像角度域分解的思想(Yoon and Marfurt,2006),在每个主频反演过程中,将全波形反演的梯度也进行角度域分解,分解为不同角度范围的角度域梯度.对比不同频率不同角度范围的梯度,结果表明梯度的波数在不同频率不同角度具有一致性,即高频大角度梯度与低频小角度梯度在垂向上波数范围一致.先后应用大角度到小角度进行反演,在数据主频不变的情况下,进一步实现角度域多尺度反演.同时,反演过程中去掉浅层大角度(>80°)的梯度,有利于浅层速度细节刻画,而深层梯度局部反射角相对较小,因此不会对深层速度反演产生影响.
1 全波形反演理论简介 1.1 波动方程本文采用时间域声波一阶应力—速度方程,其二维表达式为
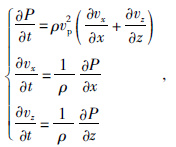
|
(1) |
上面方程组中,ρ为地下岩石的密度,vp为地下岩石纵波速度,P为地下质点的应力,vx、vz分别为地下质点水平与垂直方向的振动速度.
1.2 梯度计算全波形反演的过程是利用波动方程模拟数据umod匹配实际观测数据uobs,通过数据残差Δu=umod-uobs计算得到梯度不断修正地下介质的物性参数m来实现模拟数据与实际数据一致,也就是残差最小.目标函数的表达式为
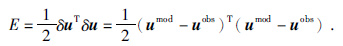
|
(2) |
角度域全波形反演的基本流程为:
(1) 通过给定的初始模型和给定的地震子波进行全波场的波动方程正演模拟,以获得地震记录和正演全波场;
(2) 将正演波场和实际野外地震记录进行波场匹配,求取波场残差,根据反演的目标函数求取目标函数值;
(3) 以波场残差为震源,进行残差波场反传,获得反传的全波场;
(4) 根据梯度公式,利用正演全波场和残差反传全波场求取Poynting矢量,进一步求取地下局部反射角,利用正演全波场、残差反传波场及反射角信息求取角度域梯度;
(5) 利用二次抛物及Wolfe-Powell收敛准则(Nocedal and Wright,2006)搜索求取合适步长;
(7) 利用求取的梯度、步长更新初始模型,对新的模型求取新的目标函数值;
(8) 进行迭代收敛判断,是否满足条件.满足条件,迭代终止,输出反演模型,不满足条件,重新进行正演求取波场残差,进行迭代循环.
2 梯度角度域分解 2.1 利用Poynting矢量求取地下局部反射角Poynting矢量也称为能流密度,它是由Poynting在1884年首先提出来,用来表征单位时间内穿过垂直于此矢量方向的单位表面的电磁场能量.Yoon和Marfur(Yoon and Marfurt,2006)将Poynting矢量引入到地震波场中表示地下地震波场波的传播方向,地震波场中的Poynting矢量表达式为
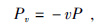
|
(3) |
其中v=(vx,vz)表示地下介质振动的速度分量,P表示波场的应力分量.通过炮点正传波场及检波点逆推波场求得正传波场和反传波场的Poynting矢量Pvf及Pvb,然后根据余弦定理可以求得两个向量之间的夹角,公式为
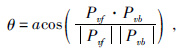
|
(4) |
纵波地下介质局部反射角等于两个向量夹角的一半,即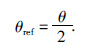
在利用正传波场和检波点逆推波场求得地下每个点的局部反射角以后,就可以利用所求的反射角对梯度进行角度域分解,得到不同反射角范围的梯度.梯度角度域分解是在不同角度范围应用Hanning窗,这样就限定了得到梯度的反射角范围.具体计算公式为
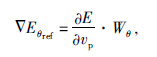
|
(5) |
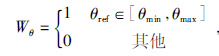
|
(6) |
其中Wθ代表窗函数,仅仅保留θref∈[θmin,θmax]范围内的梯度.
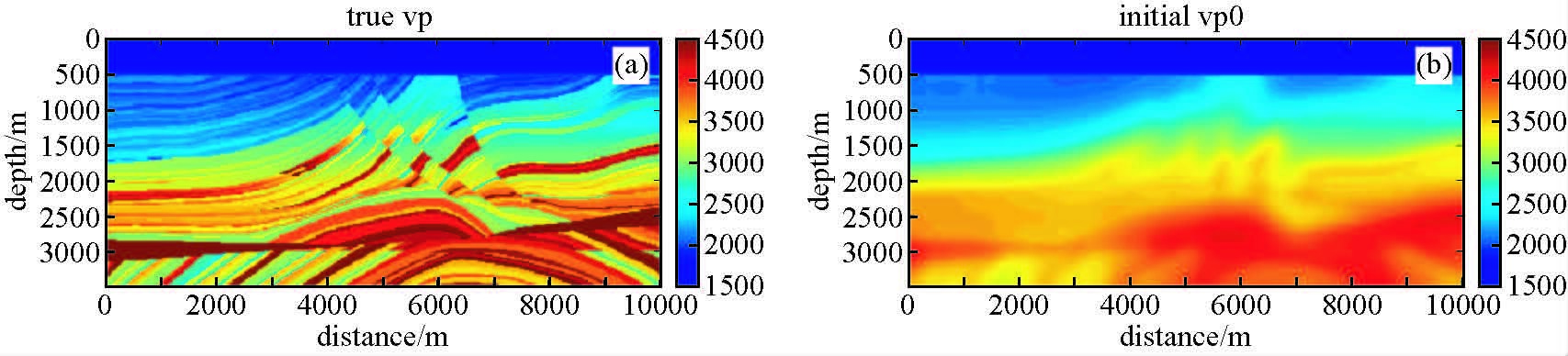
3 数值试验为了测试梯度角度域分解及全波形反演效果,采用Marmoussi Ⅱ纵波速度模型,模型总的大小为3.48 km×10 km,表层包含厚度440 m水层,离散化模型的网格点数为175×501,模型空间计算步长dx=20 m、dz=20 m,总计算炮数为63炮,炮间距为160 m,检波点位于水面,检波点数为501个,覆盖整个模型,地震记录的时间长度为4 s.初始速度模型为真实模型高斯平滑结果,平滑算子的相关长度为200 m,速度模型如图 1所示.
|
图 1 Marmoussi Ⅱ速度模型(a)及平滑后的初始速度模型(b) Figure 1 Marmoussi II velocity model(a)and smoothed velocity(b)as initial velocity |
采用3 Hz主频Ricker子波分别利用真实模型和初始平滑模型进行正演计算,然后利用正演数据残差计算梯度,图 2为第16炮单炮全角度梯度及不同角度范围分解后的梯度.
|
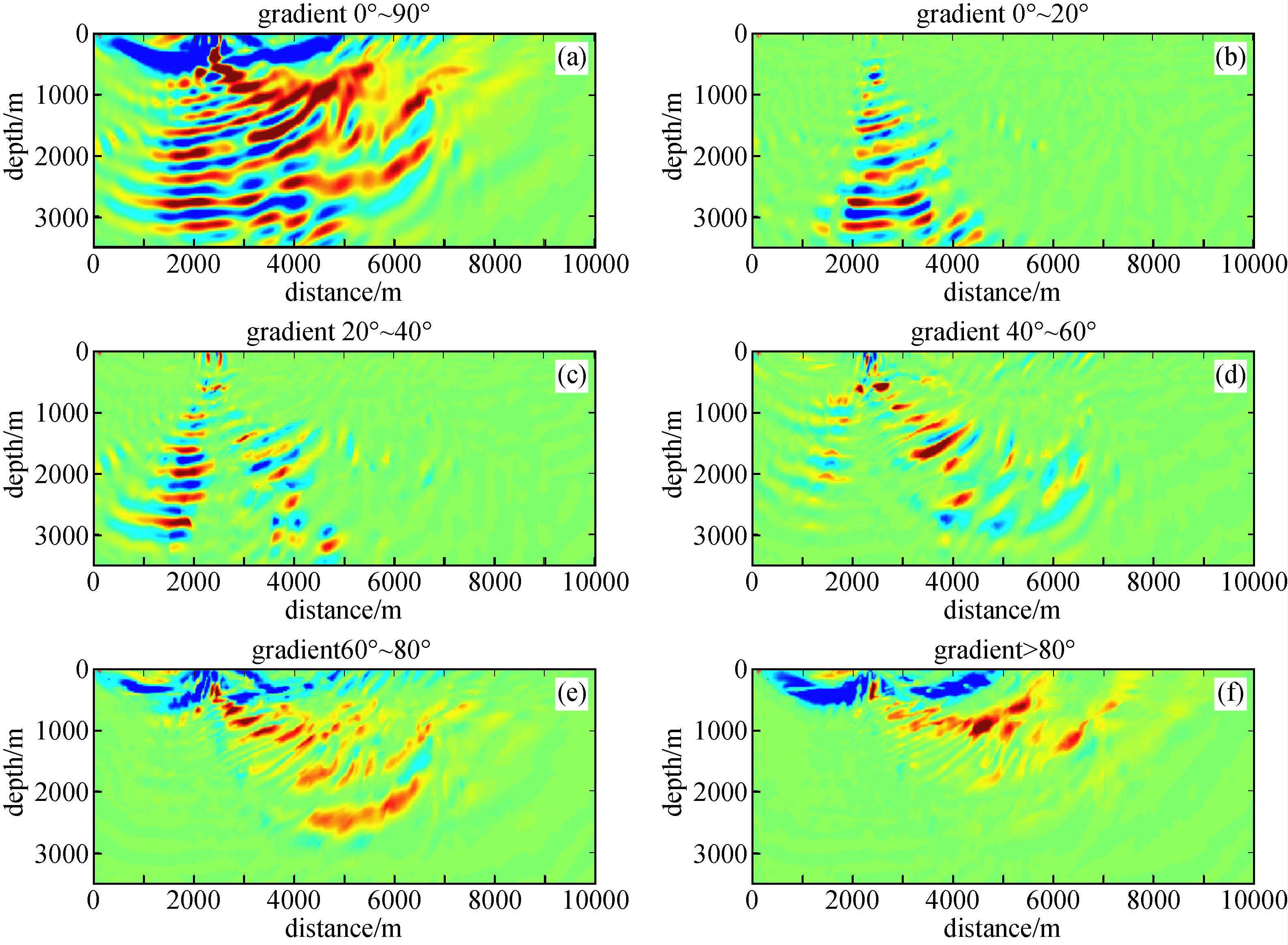
图 2 单炮梯度不同地下反射角范围分解 (a)全角度梯度;(b)0°~20°梯度;(c)20°~40°梯度;(d)40°~60°梯度;(e)60°~80°梯度;(f)>80°梯度. Figure 2 gradient decomposition in angle domain of single shot (a)full angle;(b)0~20 degrees;(c)20~40 degrees;(d)40~60 degrees;(e)60~80 degrees;(f)>80 degrees. |
从图 2a全角度梯度可以看到,全角度梯度中既包含小角度高波数的分量,也包含大角度低波数分量,高波数分量与低波数分量混合在一起,浅层梯度振幅强的主要是低波数成份,而深层梯度振幅强的主要是中低波数成份.而按照地下局部反射角分解后的角度域梯度则将低波数和高波数分量基本上分开,如图 2b~f所示.倾斜地层的角度域梯度不随炮点成对称分布,也就是说不随偏移距成对称分布,而是以地下地层法线为对称轴对称分布.小角度的梯度由浅到深分布范围逐渐变大,成一个扇形分布,这主要是因为浅层地层深度小,相同偏移距接收到信号的反射角大,相反,深层反射信号的反射角较小.
多炮叠加后的梯度如图 3所示,从图中可以看到,随着角度的增加,梯度垂向波数逐渐变小,这间接说明了长偏移距对全波形反演低频反演的重要性,因为偏移距增加,对应的反射角也在变大,得到的梯度垂向波数越小,而低波数对全波形反演至关重要,直接决定了反演结果的好坏甚至是反演的成功与失败.
|
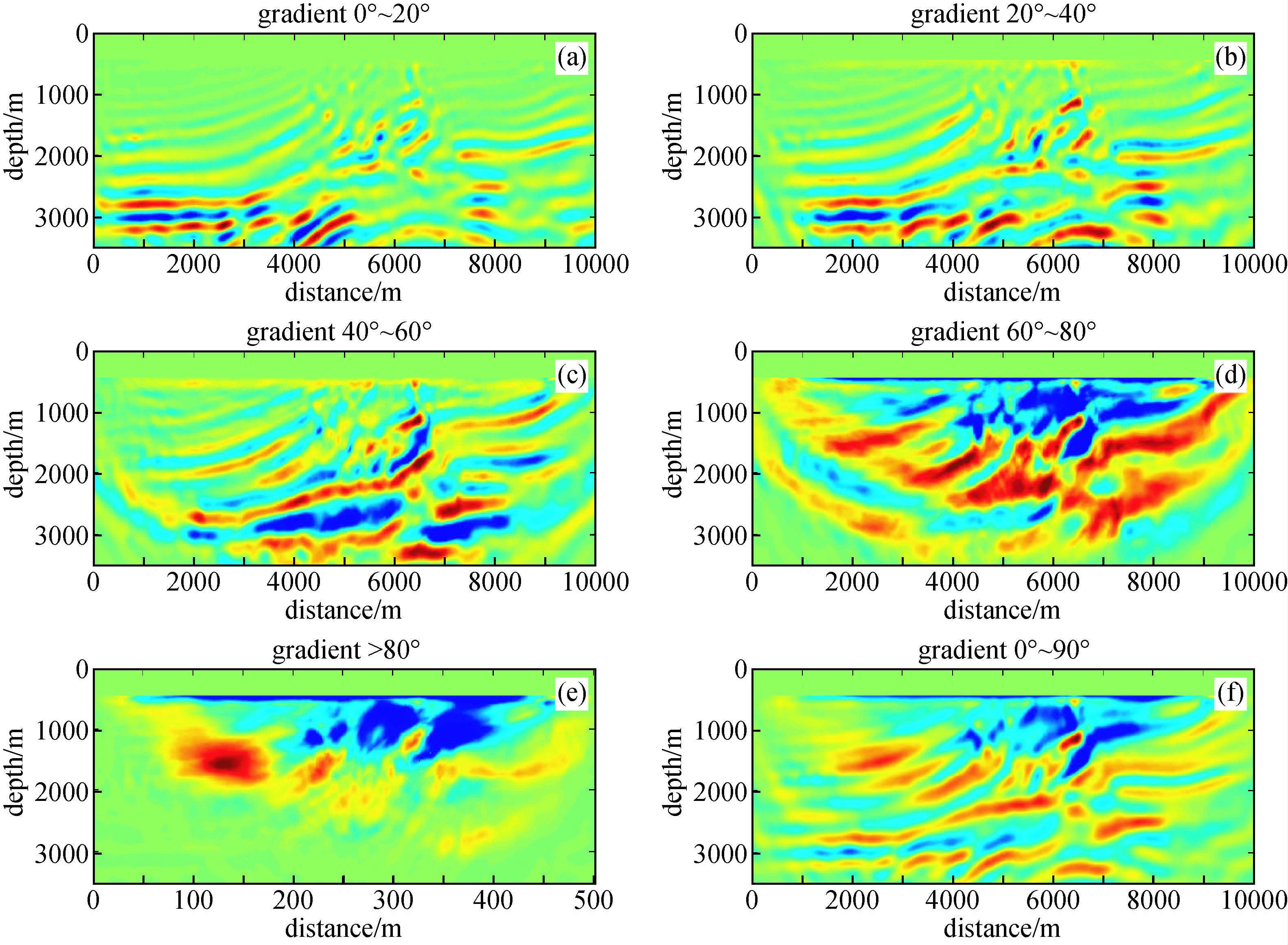
图 3 不同地下反射角范围梯度多炮叠加结果 (a)0°~20°梯度;(b)20°~40°梯度;(c)40°~60°梯度;(d)60°~80°梯度;(e)>80°梯度;(f)全角度梯度. Figure 3 stacked gradient in angle domain (a)0~20 degrees;(b)20~40 degrees;(c)40~60 degrees;(d)60~80 degrees;(e)>80 degrees;(f)full angle. |
多炮叠加后的梯度显示,中小角度范围(<40°)梯度振幅由浅到深,明显逐渐减弱,引起这种现象的主要原因是,对于相同反射角范围,浅层地层检波器接收到的道数明显要小于深层地层被接收到的 该反射角范围道数;相比而言,浅层大角度的梯度能量较强,而深层大角度的能量较弱.总的来说,对于有限长的观测系统而言,检波器接收到的反射能量,浅层地下局部反射角较大,而深层局部反射角较小.
从叠加梯度上还可以看到,同一主频数据计算的中小角度范围梯度(<40°)浅层和深层的频率基本一致,因此可以一起进行反演;而40°~60°与60°~80°两个角度范围的梯度深层频率基本一致,但是浅层梯度频率差异较大,因此分为两个阶段分别反演;大于80°的梯度主要是浅层的大角度折射和反射能量残差,频率很低,而浅层速度误差的频率相对较高,因此在本研究反演过程中,不使用该角度范围的梯度.
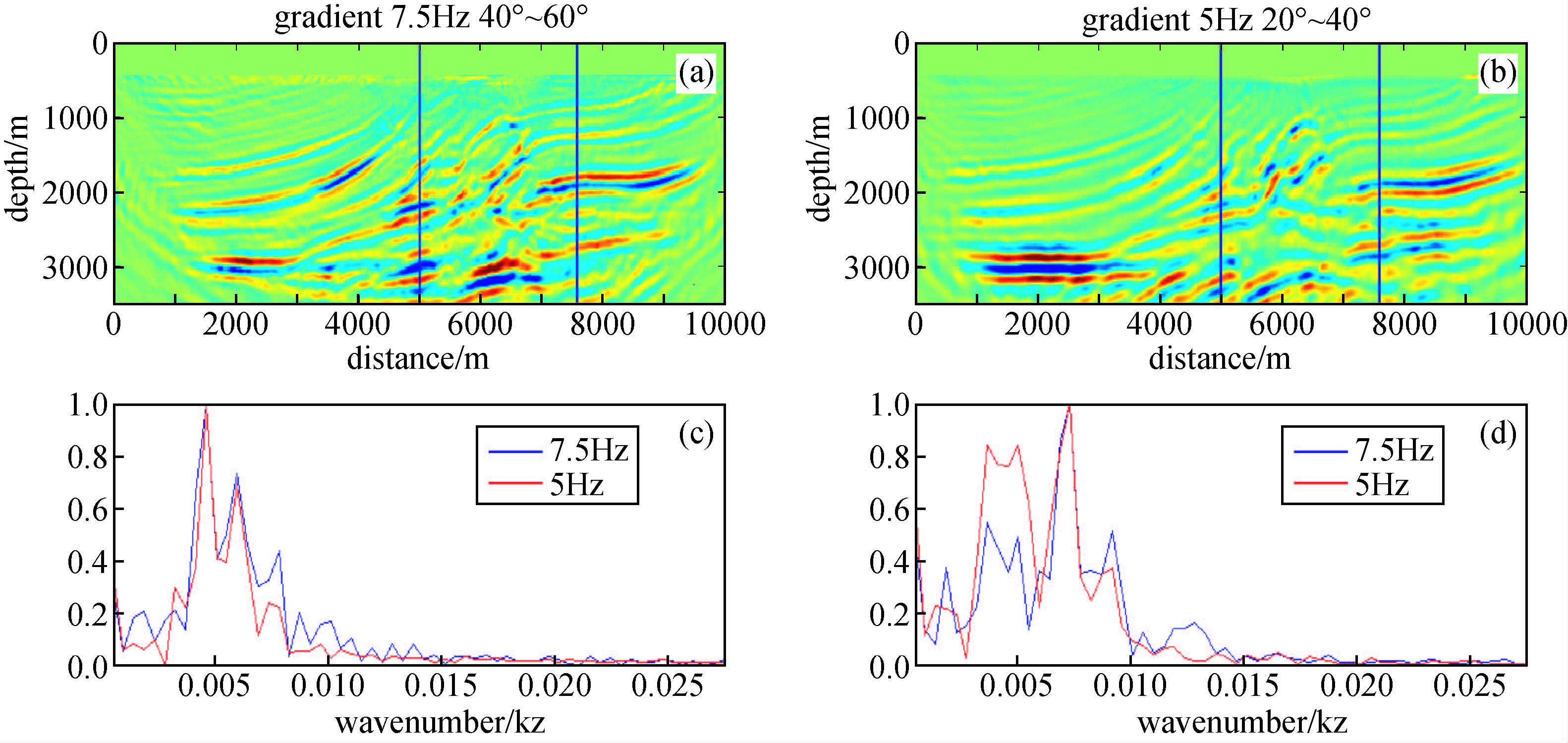
利用初始速度,分别用5 Hz主频和7.5 Hz主频数据进行梯度计算,对比5 Hz主频数据20°~40°角度范围梯度及7.5 Hz主频数据40°~60°角度范围梯度(如图 4所示),可以看到二者梯度在垂直方向的波数是基本一致的,说明了不同频率不同角度范围梯度垂向波数具有一致性,也进一步说明了同一主频数据不同角度范围梯度的多尺度性.
|
图 4 7.5 Hz 40°~60°梯度(a)与5 Hz 20°~40°梯度(b)对比,5000 m处梯度波数谱(c),7800 m处梯度波数谱(d) Figure 4 (a)gradient with angle range 40~60 degrees(7.5 Hz dominant frequency);(b)gradient with angle range 20~40 degrees (5 Hz dominant frequency);(c)wavenumber spectrum at position x=5000 m;(d)wavenumber spectrum at position x=7800 m |
根据不同地下反射角范围的梯度的频率域多尺度特性,在反演主频不变的情况下,依次进行3 Hz、5 Hz及7.5 Hz反演,每个频带范围又分为三个梯度范围(①60°~80°、②40°~60°、③0°~40°)进行依次反演.每个阶段反演都在前一阶段反演的结果基础上进行,迭代至误差下降率(当前误差/上一次误差)大于0.8自动进入下一阶段反演.
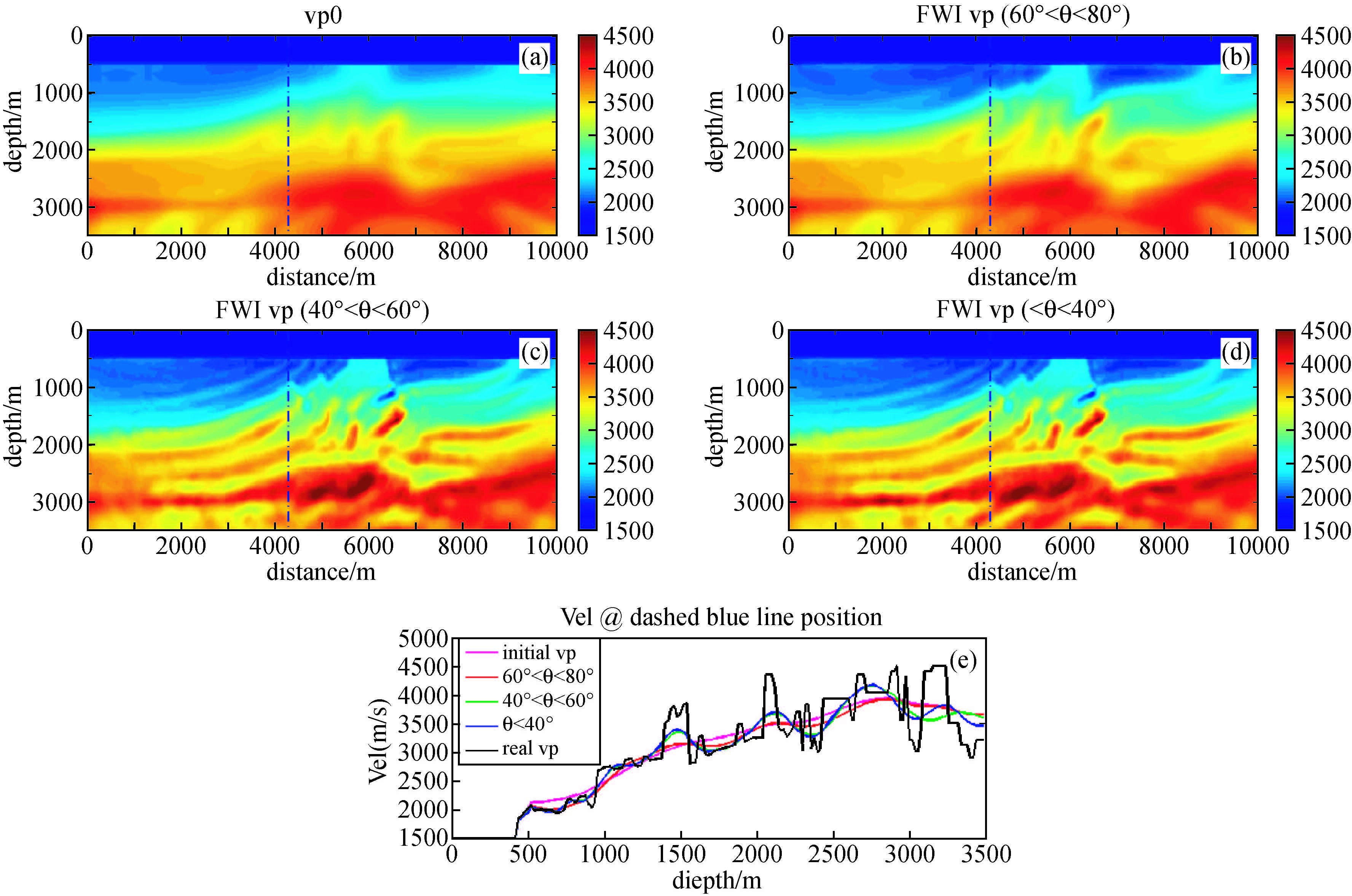
3 Hz Ricker子波三个不同角度范围反演结果如图 5所示,从反演结果可以看到,60°~80°角度范围的反演结果主要更新了大尺度的速度趋势,尤其是浅层大的速度趋势误差得到了明显的修正(500~1000 m),反演速度与初始速度差异不太大;经过角度40°~60°范围反演后,中深层(>1300 m)的大的速度趋势得到了进一步的更新,基本上与真实速度的趋势相吻合;而经过角度0°~40°范围反演,速度更新步长很小,速度更新量很小,除了深层以外,速度基本上没太大变化;在早期的反演过程中,由于需要更新的速度主要是低频部分,反演过程中的梯度主要是中大角度范围(40°~80°)的梯度起主要作用.
|
图 5 3 Hz主频角度域反演结果 (a)初始速度;(b)60°~80°梯度反演结果;(c)40°~60°梯度反演结果;(d)0°~40°梯度反演结果;(e)4100 m处各角度范围梯度反演结果速度曲线. Figure 5 Inverted velocity with 3 Hz dominant frequency (a)initial velocity;(b)using gradient with angle range 60~80 degrees;(c)using gradient with angle range 40~60 degrees; (d)using gradient with angle range 0~40 degrees;(e)velocity curves comparison of(a),(b),(c),(d)at position x=4100 m(dashed blue line). |
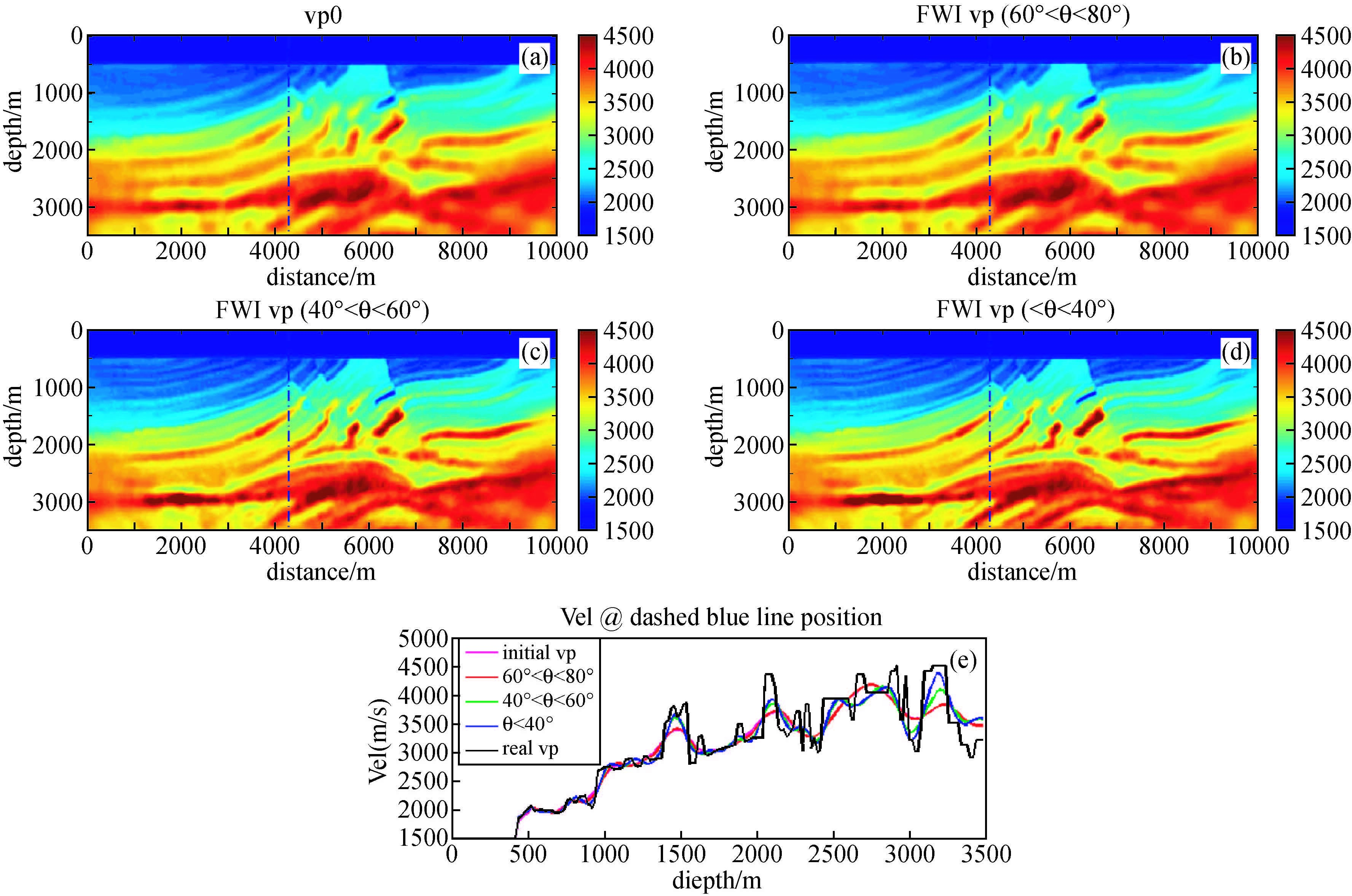
在3 Hz 主频Ricker子波反演结果基础上,5 Hz 主频Ricker子波三个不同范围的反演结果如图 6所示,从反演结果可以看到,与3 Hz Ricker子波反演结果明显不同的是,大角度范围60°~80°的梯度对速度更新量很小,对速度更新的贡献主要来自于40°~60°角度范围的梯度;同样,小角度0°~40°范围梯度对速度更新贡献也是比较小的,除了深层以外,中浅层速度基本没有太大更新量.
|
图 6 5 Hz主频角度域反演结果 (a)初始速度(3 Hz反演结果);(b)60°~80°梯度反演结果;(c)40°~60°梯度反演结果;(d)0°~40°梯度反演结果;(e)4100 m处各角度范围梯度反演结果速度曲线. Figure 6 Inverted velocity with 5 Hz dominant frequency (a)initial velocity(final velocity using 3Hz dominant frequency);(b)using gradient with angle range 60~80 degrees; (c)using gradient with angle range 40~60 degrees;(d)using gradient with angle range 0~40 degrees; (e)velocity curves comparison of(a),(b),(c),(d)at position x=4100m(dashed blue line). |
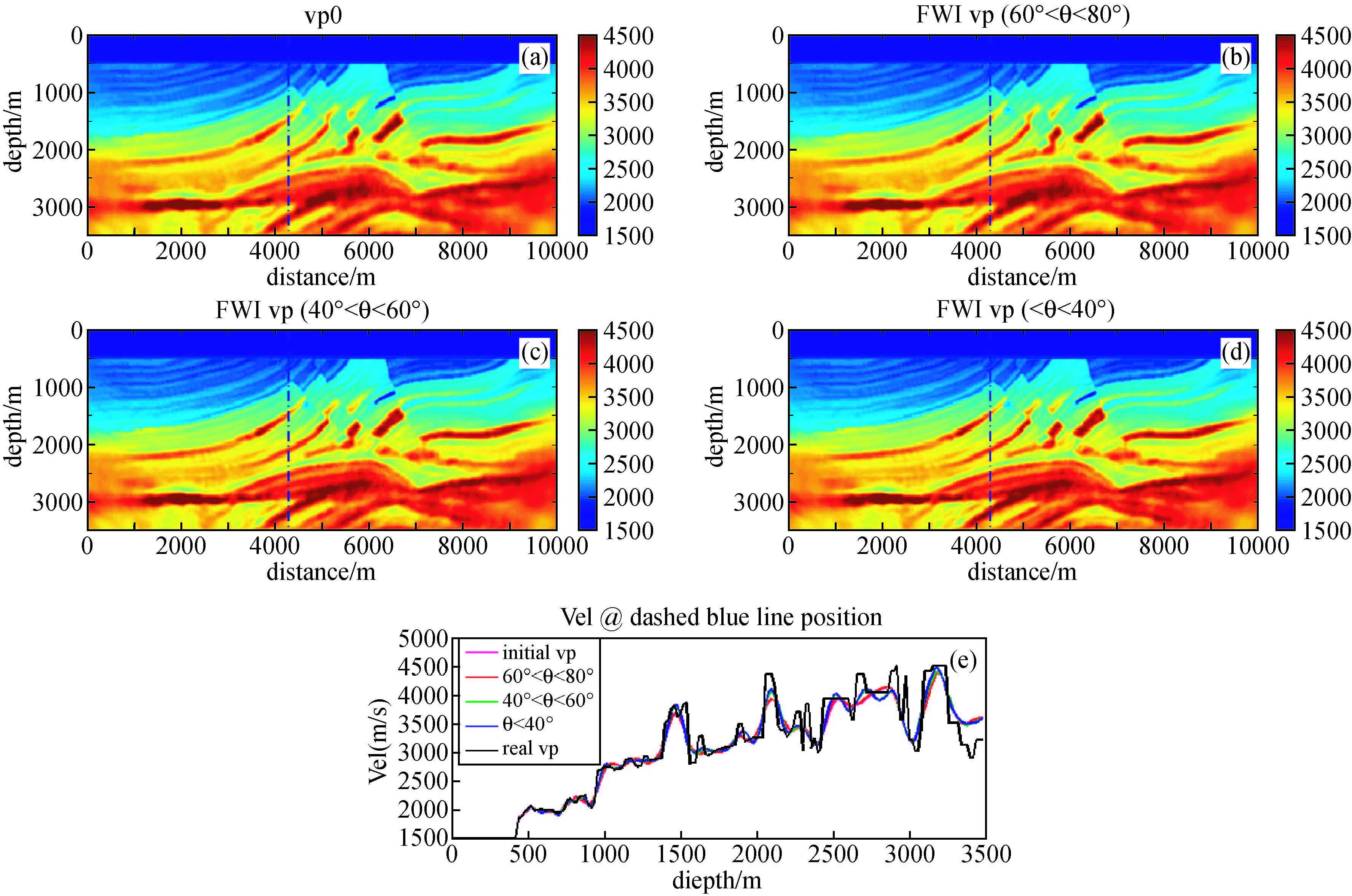
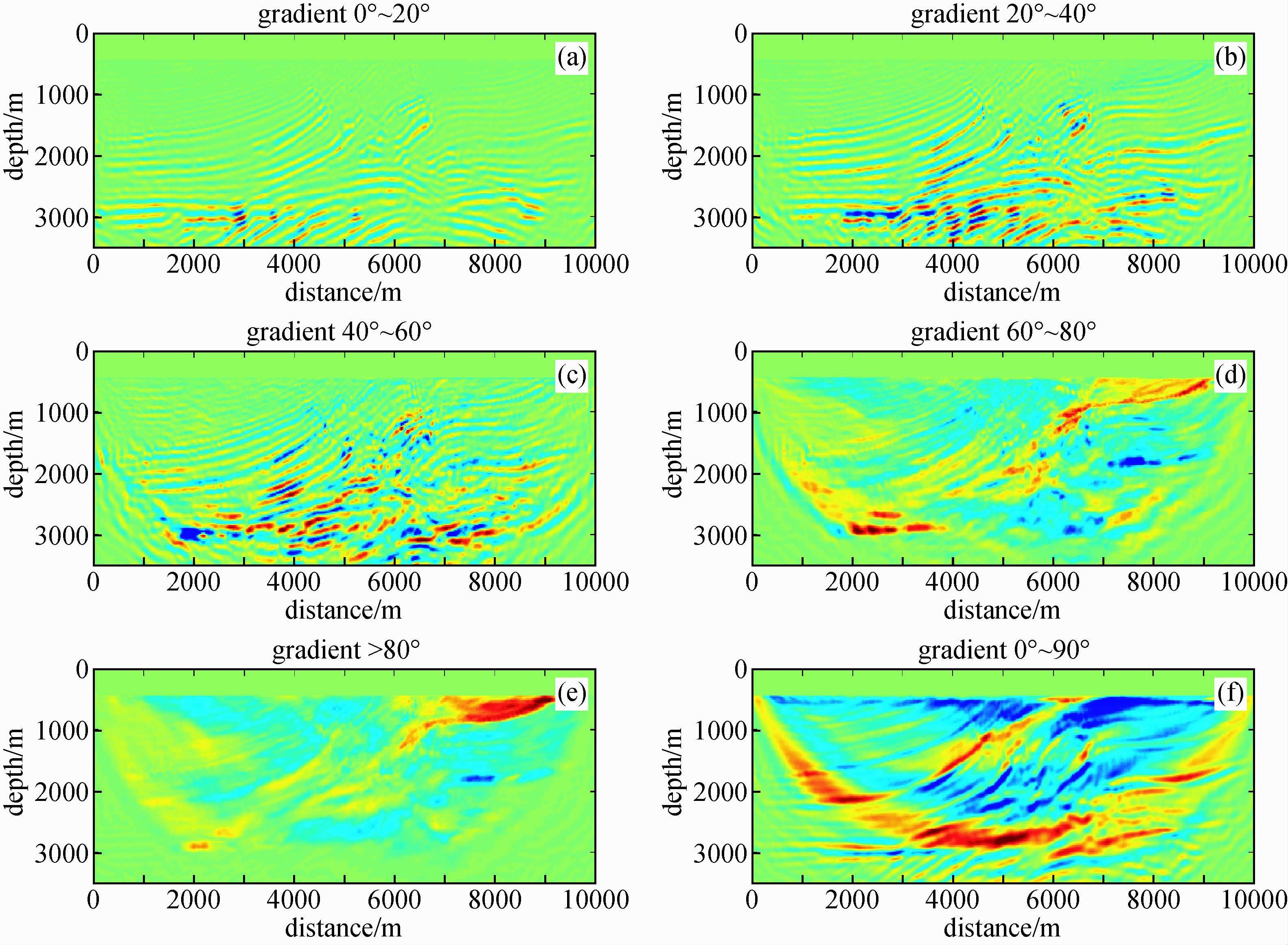
在5 Hz 主频Ricker子波反演结果基础上,7.5 Hz 主频Ricker子波三个不同范围的反演结果如图 7所示,从反演结果可以看到,除了局部细节以外,不同角度范围梯度反演结果基本上对模型更新量不大,这一点从7.5 Hz主频不同角度范围的梯度(如图 8所示)也可以看出,除了60°~80°角度范围的梯度依然频率很低以外,其他角度范围的梯度频率随着频率的提高,梯度垂向波数差异正在变小.而在5 Hz反演结果的基础上,大角度(60°~80°)梯度无法对模型进行较大的修正,因此主要是中小角度范围的梯度对模型修正起了主要作用,从最后的反演结果曲线可以看到,反演速度大的趋势基本保持不变.
|
图 7 7.5 Hz主频角度域反演结果 (a)初始速度(5 Hz反演结果);(b)60°~80°梯度反演结果;(c)40°~60°梯度反演结果;(d)0°~40°梯度反演结果;(e)4100 m处各角度范围梯度反演结果速度曲线. Figure 7 Inverted velocity with 7.5 Hz dominant frequency (a)initial velocity(final velocity using 5Hz dominant frequency);(b)using gradient with angle range 60~80 degrees; (c)using gradient with angle range 40~60 degrees;(d)using gradient with angle range 0~40 degrees; (e)velocity curves comparison of(a),(b),(c),(d)at position x=4100 m(dashed blue line). |
|
图 8 7.5 Hz主频第6次迭代多炮梯度不同地下反射角范围分解 (a)0°~20°梯度;(b)20°~40°梯度;(c)40°~60°梯度;(d)60°~80°梯度;(e)>80°梯度;(f)全角度梯度. Figure 8 Angle domain decomposed gradient at 6th iteration with 7.5 Hz dominant frequency(a)0~20 degrees;(b)20~40 degrees;(c)40~60 degrees;(d)60~80 degrees;(e)>80 degrees;(f)full angle. |
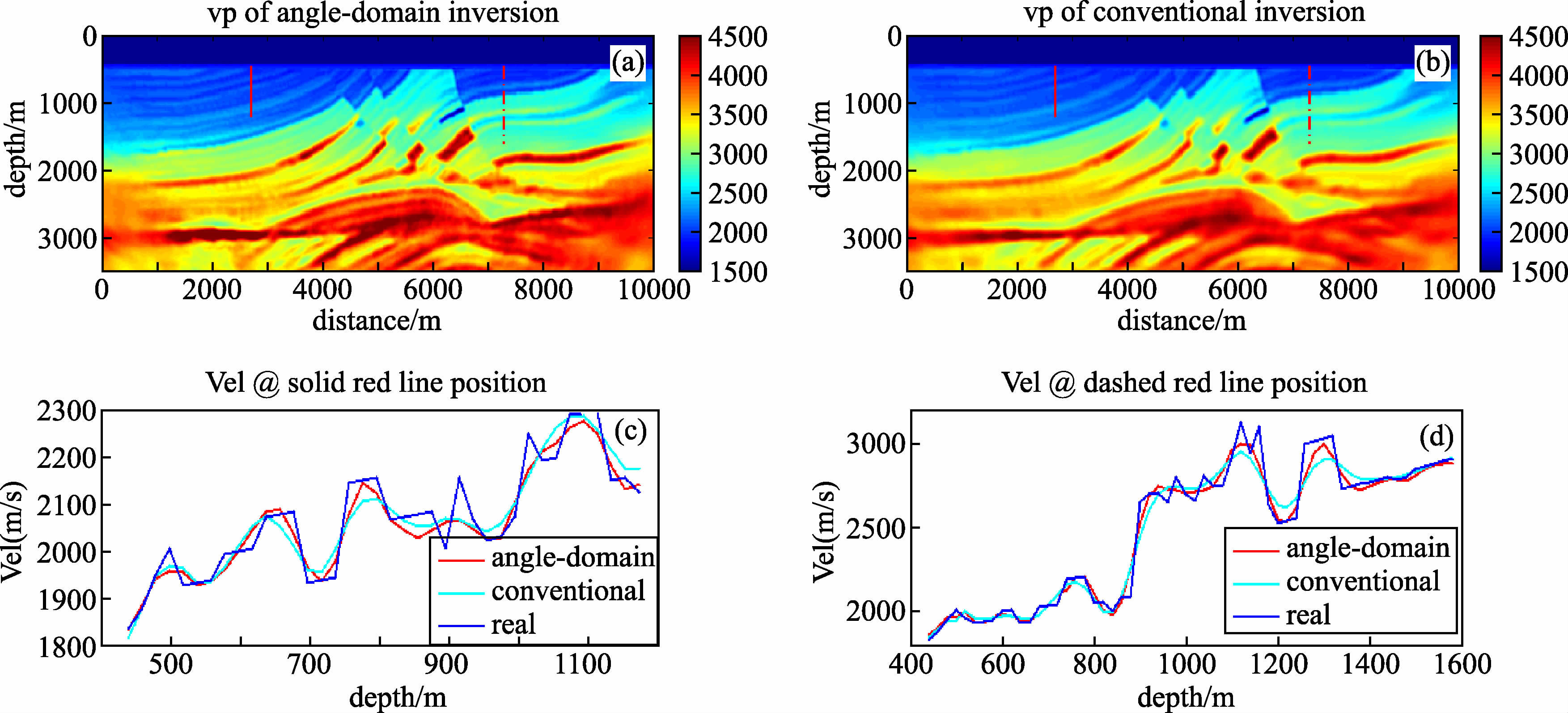
角度域全波形反演不仅仅表现出了梯度垂向波数的多尺度性,由于传统全波形反演是所有角度梯度都参与速度更新,而超大角度(>80°)的梯度主要是以干扰信息为主,尤其是高频数据对高波数速度细节的反演过程中,这种低波数的梯度分量不适合参与速度更新.对比7.5 Hz传统全波形反演及角度域全波形最终反演结果(如图 9所示),可以看到反演数据主频相同情况下,角度域全波形反演对浅层高波数速度细节反演更好,这正是由于合适的角度域梯度使反演收敛更好.
|
图 9 7.5 Hz主频角度域全波形反演 (a)与传统全波形反演结果(b)对比;(a)与(b)红色实线位置速度曲线对比(c);(a)与(b)红色虚线位置速度曲线对比(d). Figure 9 Comparison of finally inverted velocity between conventional and angle domain method(7.5 Hz dominant frequency) (a)using angle domain method;(b)using conventional method;(c)velocity curves comparison at solid red line position; (d)velocity curves comparison at dashed red line position. |
本文将全波形反演梯度求取与地下波场角度域分解结合起来,在使用相同主频数据的情况下,将梯度进行角度域分解得到不同角度范围的梯度,进一步实现了角度域多尺度全波形反演,把相同主频的梯度分为低波数分量和高波数分量分阶段进行反演.研究结果表明不同频率反演模型更新量最大的梯度角度范围是不一样的,低频大角度梯度对速度更新大,高频中小角度的梯度对速度更新大.同时,反演过程中,尤其是高频反演,去掉浅层超大角度(>80°)的梯度,有利于浅层速度细节刻画,而深层梯度局部反射角较小,因此不会对深层反演产生影响.对梯度进行角度域分解得到不同角度范围的梯度,合理选择合适角度范围的梯度进行反演,不仅仅可以在同一频率范围进一步实现多尺度反演,还能去掉梯度中无效的干扰信号,使反演收敛更好.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Biondi B, Tisserant T .2004. 3D angle-domain common-image gathers for migration velocity analysis[J]. Geophysical Prospecting, 52 (6) : 575–591. DOI:10.1111/gpr.2004.52.issue-6 |
| [] | Bunks C, Saleck F M, Zaleski S, et al .1995. Multiscale seismic waveform inversion[J]. Geophysics, 60 (5) : 1457–1473. DOI:10.1190/1.1443880 |
| [] | Chi B X, Dong L G, Liu Y Z .2014. Full waveform inversion method using envelope objective function without low frequency data[J]. Journal of Applied Geophysics, 109 : 36–46. DOI:10.1016/j.jappgeo.2014.07.010 |
| [] | de Bruin C G M, Wapenaar C P A, Berkhout A J .1990. Angle-dependent reflectivity by means of prestack migration[J]. Geophysics, 55 (9) : 1223–1234. DOI:10.1190/1.1442938 |
| [] | Gauthier O, Virieux J, Tarantola A .1986. Two-dimensional nonlinear inversion of seismic waveforms:Numerical results[J]. Geophysics, 51 (7) : 1387–1403. DOI:10.1190/1.1442188 |
| [] | Lailly P. 1983.The seismic inverse problem as a sequence of before stack migrations[A].//Bednar J B ed. Conference on Inverse Scattering:Theory and Application[M]. Philadelphia, PA:Society for Industrial and Applied Mathematics. |
| [] | Nocedal J, Wright S J .2006. Numerical Optimization[M]. New York: Springer . |
| [] | Operto M S, Xu S, Lambaré G .2000. Can we quantitatively image complex structures with rays?[J]. Geophysics, 65 (4) : 1223–1238. DOI:10.1190/1.1444814 |
| [] | Prucha M L, Biondi B L,Symes W W. 1999. Angle-domain common image gathers by wave-equation migration[C].//69th Ann. Internat Mtg., Soc. Expi.Geophys.Houston, USA:Expanded Abstracts, 824-827. |
| [] | Rickett J E, Sava P C .2002. Offset and angle-domain common image-point gathers for shot-profile migration[J]. Geophysics, 67 (3) : 883–889. DOI:10.1190/1.1484531 |
| [] | Sava P, Vlad I .2011. Wide-azimuth angle gathers for wave-equation migration[J]. Geophysics, 76 (3) : S131–S141. DOI:10.1190/1.3560519 |
| [] | Shin C, Cha Y H .2008. Waveform inversion in the Laplace domain[J]. Geophysical Journal International, 173 (3) : 922–931. DOI:10.1111/gji.2008.173.issue-3 |
| [] | Stolk C, Symes W .2004. Kinematic artifacts in prestack depth migration[J]. Geophysics, 69 (2) : 562–575. DOI:10.1190/1.1707076 |
| [] | Tarantola A .1984. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 49 (8) : 1259–1266. DOI:10.1190/1.1441754 |
| [] | Tarantola A .1984. Linearized inversion of seismic reflection data[J]. Geophysical Prospecting, 32 (6) : 998–1015. DOI:10.1111/gpr.1984.32.issue-6 |
| [] | Tarantola A .1986. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 51 (10) : 1893–1903. DOI:10.1190/1.1442046 |
| [] | Tarantola A .1988. Theoretical background for the inversion of seismic waveforms including elasticity and attenuation[J]. Pure and Applied Geophysics, 128 (1-2) : 365–399. DOI:10.1007/BF01772605 |
| [] | Xie X B. 2013. Recover certain low-frequency information for full waveform inversion[C].//83rd Ann.Internat.Mtg, Soc. Exp. Geophys.Expanded Abstracts, 1053-1057. |
| [] | Xie X B,Wu R S. 2002. Extracting angle domain information from migrated wavefield[C].//72nd Ann. Internat.Mtg., Soc. Exp. Geophys.Salt Lake City, USA:Expanded Abstracts, 1360-1363. |
| [] | Zhang Wensheng, Luo Jia, Teng Jiwen .2015. Frequencymultiscale full-waveform velocity inversion[J]. Chinese Journal of Geophysics (in Chinese), 58 (1) : 216–228. |
| [] | Xu S, Chauris H, Lambaré G, Noble M .2001. Common-angle migration:a strategy for imaging complex media[J]. Geophysics, 66 (6) : 1877–1894. DOI:10.1190/1.1487131 |
| [] | Yoon K, Marfurt K J .2006. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 37 (1) : 102–107. DOI:10.1071/EG06102 |
| [] | 张文生, 罗嘉, 滕吉文.2015. 频率多尺度全波形速度反演[J]. 地球物理学报, 58 (1) : 216–228. |
 2016, Vol. 31
2016, Vol. 31

