2. 地下信息探测技术与仪器教育部重点实验室和地质过程与矿产资源国家重点实验室, 北京 100083
3. 武警黄金第六支队, 西宁 810021
2. Key Laboratory of Geo-detection(China University of Geosciences, Beijing), Ministry of Education;State Key Laboratory of Geological Processes and Mineral Resources(China University of Geosciences, Beijing), Beijing 100083, China
3. No.6 Gold Geological Party of CAPF, Xining 810021, China
大地电磁作为地下深部结构探测的一种重要手段(石应骏等,1985),已被广泛应用于地壳和上地幔的电性结构探测工作(谭捍东等,2004;魏文博等,2006;金胜等,2009,2010;谢成良等,2012).自2008年我国SinoProbe专项启动以来,已获得了大量的覆盖华北、青藏高原地区的大地电磁测深阵列数据(魏文博等,2010;董树文等,2012).如何利用这些宝贵的数据构建出可靠的地下电性结构模型,成为资料解释工作中的重点.地下介质导电性结构常具有三维性特征,实际资料解释宜采用三维反演方法(Jones,2011).然而,三维反演计算需要耗费大量的计算时间和计算内存(李焱等,2012;胡祥云等,2012),使其模型的数据密度以及网格密度受限,导致模型分辨率不高.因此,大地电磁二维反演仍是目前应用最为广泛的反演方法(董浩等,2012).
大地电磁测深二维反演原理要求,地电模型为严格的二维构造,并且观测剖面与异常体的走向垂直.但是,在实际工作中,同一地区的不同地质体往往具有不同的走向,尤其是在大区域的MT阵列观测工作中,截取的MT长剖面往往跨越多个地质构造单元,很难保证剖面与所有的地质体走向垂直.尽管,维性分析结果仍指示地下结构接近二维性,但已经不满足严格的二维反演条件,这里将这类情况称为“准二维”.在“准二维”条件下,是否适合进行二维反演?如果进行二维反演,剖面方向和电性主轴旋转角度如何选择?它们对二维反演结果有何影响?
关于二维反演求解复杂电性结构的问题,前人已经开展过一些工作,并获得了一定的认识(胡祖志等,2005;陈小斌等,2008;蔡军涛和陈小斌,2010;董浩等,2012).但前人研究中,设计的理论模型多数只包含一个异常体,即使有多个异常体,各异常体的走向也比较接近.为了对“准二维”条件下的二维反演问题有一个更透彻的认识,本文构建了三个不同的理论电性模型,每个理论模型均包含多个异常体,除模型1外,模型2和模型3中,各异常体的走向相差较大.利用大地电磁三维正演和二维反演技术对各模型进行了响应计算和数据分析,对不同的反演模式和数据旋转策略对二维反演结果的影响进行了分析,对MT二维反演在解释“准二维”结构问题中的适用性进行了深入探讨.
1 大地电磁测深理论与方法大地电磁测深法是通过观测电磁波在地下介质中传播时,地表电磁场分布情况来反推地下介质电性分布情况的一种地球物理手段(石应骏等,1985).其中,电磁波的场源是高空中的天然电磁场,在地表处可以近似为平面波,并假设它是垂直射入地下介质的.在一般的地下二维介质中,电磁场沿介质的电性主轴方向传播时可分解为两组互不相关的线性偏振波,即电场水平分量平行构造走向、磁场水平分量垂直构造走向的横电模式(TE)和电场水平分量垂直构造走向、磁场水平分量平行构造走向的横磁模式(TM).当x轴方向为地质体构造走向,y轴方向为地质体的倾向方向,z轴垂直向下时,两种极化模式的波阻抗分别为
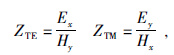
|
(1) |
其中ZTE和ZTM分别为TE和TM模式波阻抗,Ex和Ey分别为x方向和y方向电场分量,Hx和Hy分别为x方向和y方向的磁场分量,ω为角频率,μ为介质中的磁导率,ρTE和ρTM分别为TE和TM模式下的视电阻率.相应的可得到两种极化模式下的视电阻率,公式为
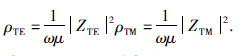
|
(2) |
由于ZTE≠ZTM,因而ρTE≠ρTM,表明在二维介质情况下将会得到两条不同的视电阻率曲线.此外,由于在二维条件下磁场的垂向分量HZ≠0,故又将水平磁场与垂直磁场之间的比值定义为倾子TP,公式为
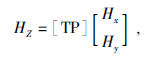
|
(3) |
其中HZ为磁场垂直分量,TP为倾子.
本文研究中,采用Siripunvaraporn等(2005)开发的WSINV3DMT程序的三维正演模块计算各理论模型的大地电磁响应,该正演模块是基于交错采样有限差分法(S-GFD)(Mackie et al.,1993)开发的.二维反演则是采用WinGLink反演软件.WinGlink是GEOSYSTEM公司开发的综合解释平台,其MT数据的二维反演算法采用非线性共轭梯度算法(NLCG)(Rodi and Mackie,2011).
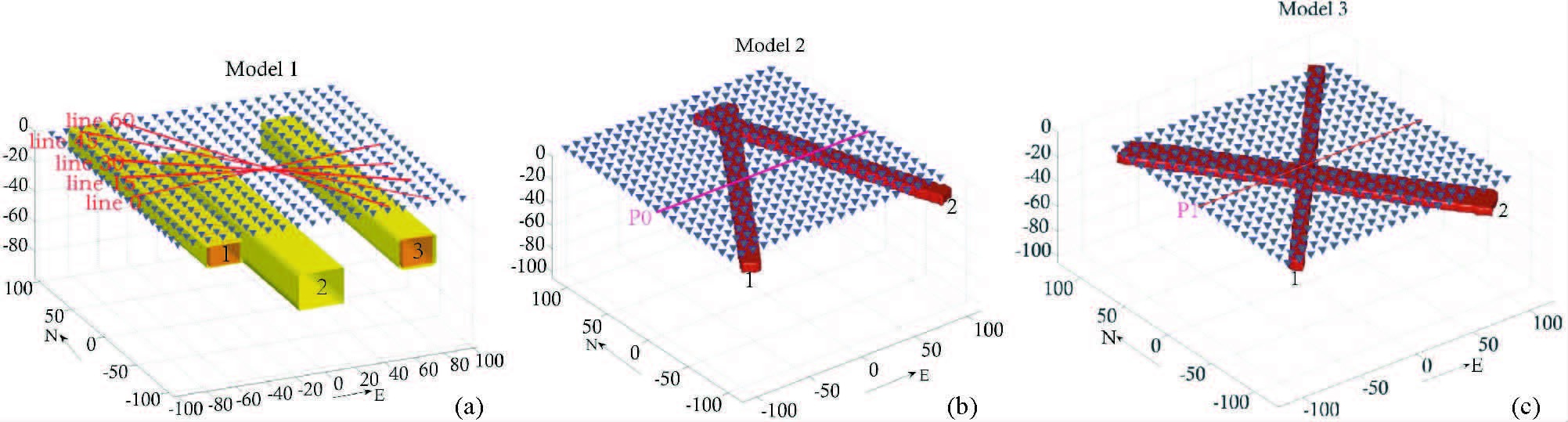
2 模型设计与正演计算对实际可能存在的复杂地质构造进行简化,设计三个理想的二维地电模型开展研究.图 1a为均匀半空间中赋存有三个南北方向无限延伸的低阻体模型,称为模型1.其中,均匀半空间电阻率值为100 Ω·m;由西向东,第一个低阻体的电阻率为3 Ω·m,其顶面埋深为10 km,横截面为10 km×10 km的矩形.第二个低阻体的电阻率为10 Ω·m,其顶面埋深为30 km,横截面为30 km×30 km的矩形;第三个低阻体的电阻率为3 Ω·m,其顶面埋深为20 km,横截面为20 km×20 km的矩形.三个低阻体水平间距为20 km.
|
图 1 理论地电模型示意图 (a)模型1;(b)模型2;(c)模型3. Figure 1 Sketch of the synthetic model (a)Model1;(b)Model2;(c)Model3. |
图 1b所示模型中,两个有限延伸低阻体赋存于电阻率为100 Ω·m的均匀半空间中,称为模型2.图中,两个低阻体横截面为矩形,大小为10 km×10 km,顶面埋深均为10 km,电阻率值为3 Ω·m.两个低阻体的走向不同,夹角近50度,并在北端相交.
图 1c为均匀半空间赋存有两个有限延伸的低阻体模型,称为模型3.均匀半空间的电阻率值为100 Ω·m;低阻体的电阻率值均为3 Ω·m,低阻体1横截面为10 km×10 km的矩形,低阻体2横截面为30 km×10 km的矩形;两个低阻体的空间展布如图所示,二者之间的夹角为90度,埋深不同,低阻体1的顶界面为6 km,低阻体2的顶界面为16 km.
设置如图 1所示的大地电磁地面测网进行模拟观测.模型1中,测站在南北和东西方向上的间距均为10 km,共布设了400个测站;模型2和模型3中,测站间距与模型1相同,各布设了420个测站.正演计算中,选取的频带范围为0.0003~100 Hz,按照各频点在对数域均匀分布的原则,共设计34个计算频点,每个数量级大约6个频点.
3 阻抗数据分析采用相位张量(Caldwell et al.,2004)对模拟测站的数据进行维性分析.图 2中给出了上述三个模型的阻抗响应在10 s、100 s、1000 s和2000 s四个频点下的相位张量分析结果.图 2a的分析结果表明,模型1所有测站阻抗相位张量椭圆的偏离度角β均小于2°,在异常体分布的区域,椭圆的极化率略高,地电结构具有二维性特征,异常体分布之外的区域相位张量退化为圆,表现为一维性.图 2b为模型2在这四个频点下的分析结果,绝大部分测站的偏离度角β小于2°显示一维或二维特性,且二维性分布区域与异常体的分布区域对应.模型2中的异常体在走向方向延伸有限,导致局部区域出现偏离度角较大的测站,这些测站主要分布在异常体的边界.图 2c为模型3在这四个频点下的分析结果,分析结果与模型2的结果相似.相位张量分析表明,地下地质构造具一维或二维性特征,适于进行二维反演研究.

|
图 2 各模型模拟测站相位张量分析结果图 (a)模型1在四个频点下分析结果;(b)模型2在四个频点下分析结果;(c)模型3在四个频点下分析结果. Figure 2 Phase tensor map for each synthetic model (a)Model1 results at four different frequencies;(b)Model2 results at four different frequencies; (c)Model3 results at four different frequencies. |
经过对比,选取表 1所示的反演参数,对TE、TM、TE+TM以及TM+TP四种模式的大地电磁理论数据进行二维反演,研究剖面方向、电性主轴旋转角度、反演模式对反演结果的影响.
|
|
表 1 二维反演参数设置 Table 1 Two dimensional inversion parameter setting |
在模型1中,共布设了5条不同方向的测线.如图 1a所示,Line0测线与异常体走向方向垂直;Line15测线与Line0测线夹角为15°;Line30与Line0测线夹角为30°;Line45与Line0测线夹角为45°;Line60与Line0测线夹角为60°.
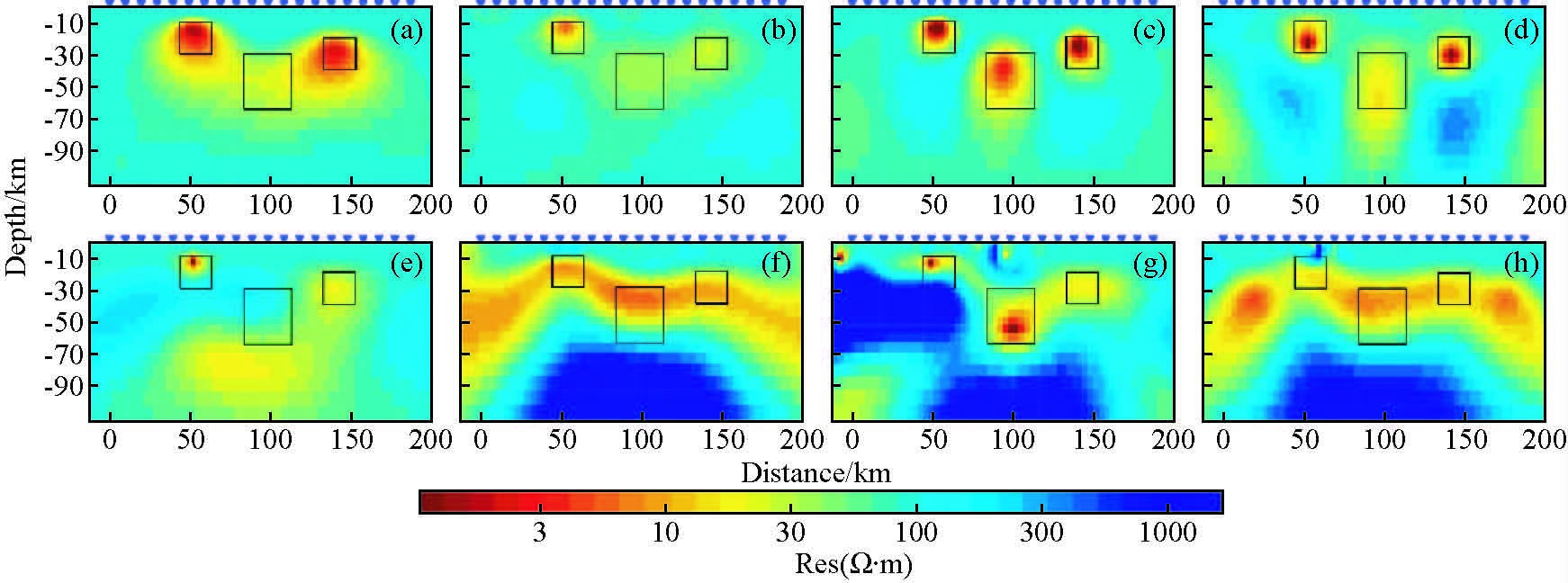
图 3为Line0测线四种模式二维反演的电性模型.其中,图 3a~d为阻抗数据电性主轴旋转至低阻体走向方向的反演结果;图 3e~h为阻抗数据电性主轴旋转至测线方向的反演结果.由图可知,电性主轴旋转至测线方向时,反演结果与真实模型相差较大,反演效果不好.电性主轴旋转至低阻体走向方向时,TE+TM联合模式的反演效果较好,反演结果比较准确地指示了三个低阻体的位置、形态和电阻率值,且高阻假异常不明显;TM模式反演的效果稍差,反演结果能够指示三个低阻体的位置和形态,但电阻率值与真实值相差较大,且高阻假异常不明显;TE模式反演结果对浅层低阻体的反映较好,但对低阻体2的反映不明显;TM+TP模式反演结果对浅部低阻体1和3反映较好,但低阻体2却出现了强烈的纵向拉伸变形,同时,在两个浅部低阻体的下方还出现了规模较大的高阻假异常.综上,阻抗数据电性主轴旋转至不同方向时,反演结果相差较大.其中,电性主轴旋转至低阻体走向方向时,TE+TM联合模式和TM模式的反演结果,明显优于其他反演结果.
|
图 3 Line0线二维反演结果,a~d依次为电性主轴旋转至低阻体走向方向TE、TM、TE+TM和TM+TP模式反演结果,e~h分别为电性主轴旋转至测线方向四个模式反演结果,图中黑框标示了低阻体的原始位置 Figure 3 2D inversion results of Line0,a to d:results in TE,TM,TE+TM and TM+TP mode with electrical strike paralleling to the direction of abnormal body;e to h:results in four modes with electrical strike paralleling to the direction of the line. Black boxes indicate the location of the anomalies in the forward models |
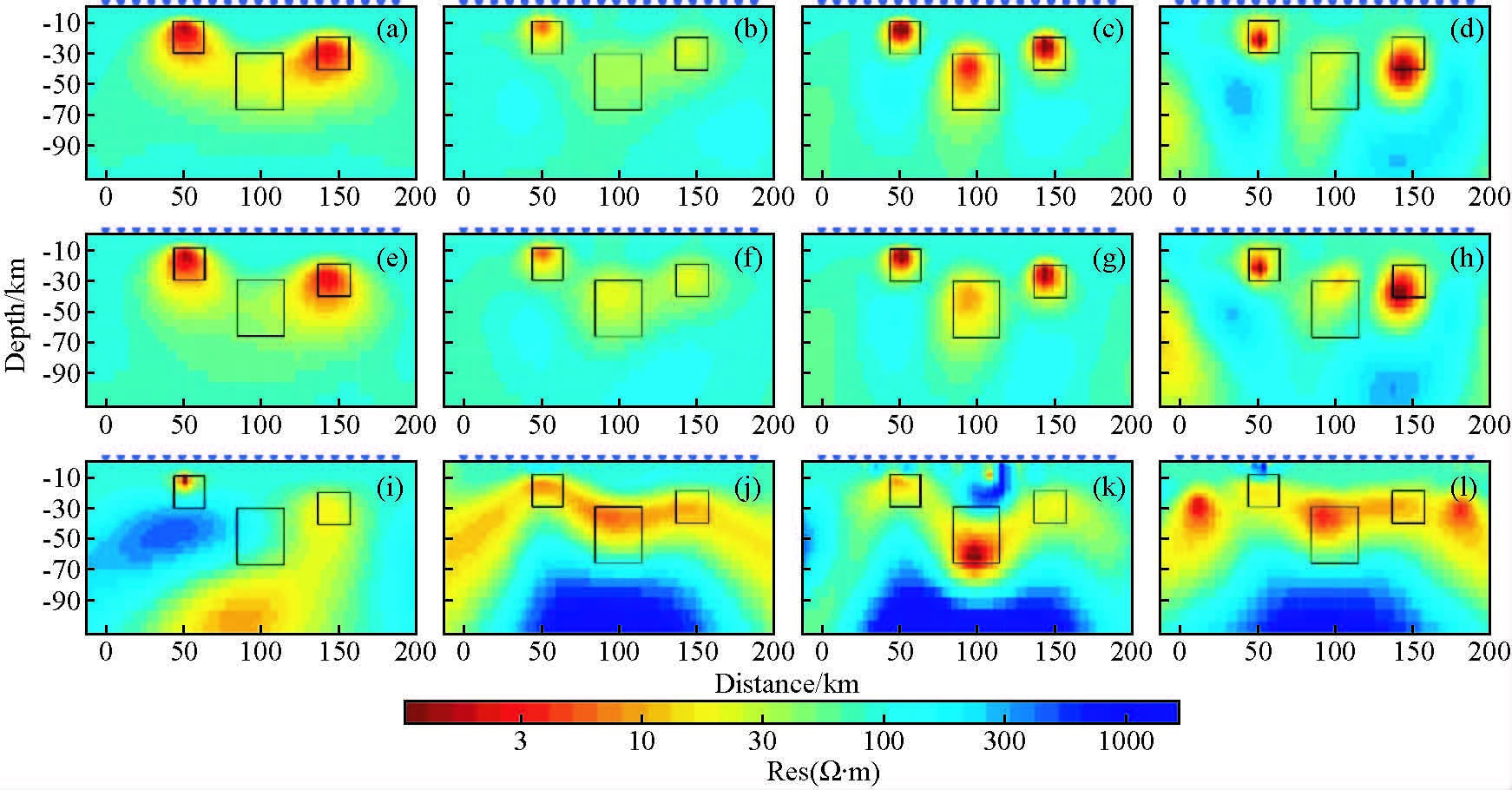
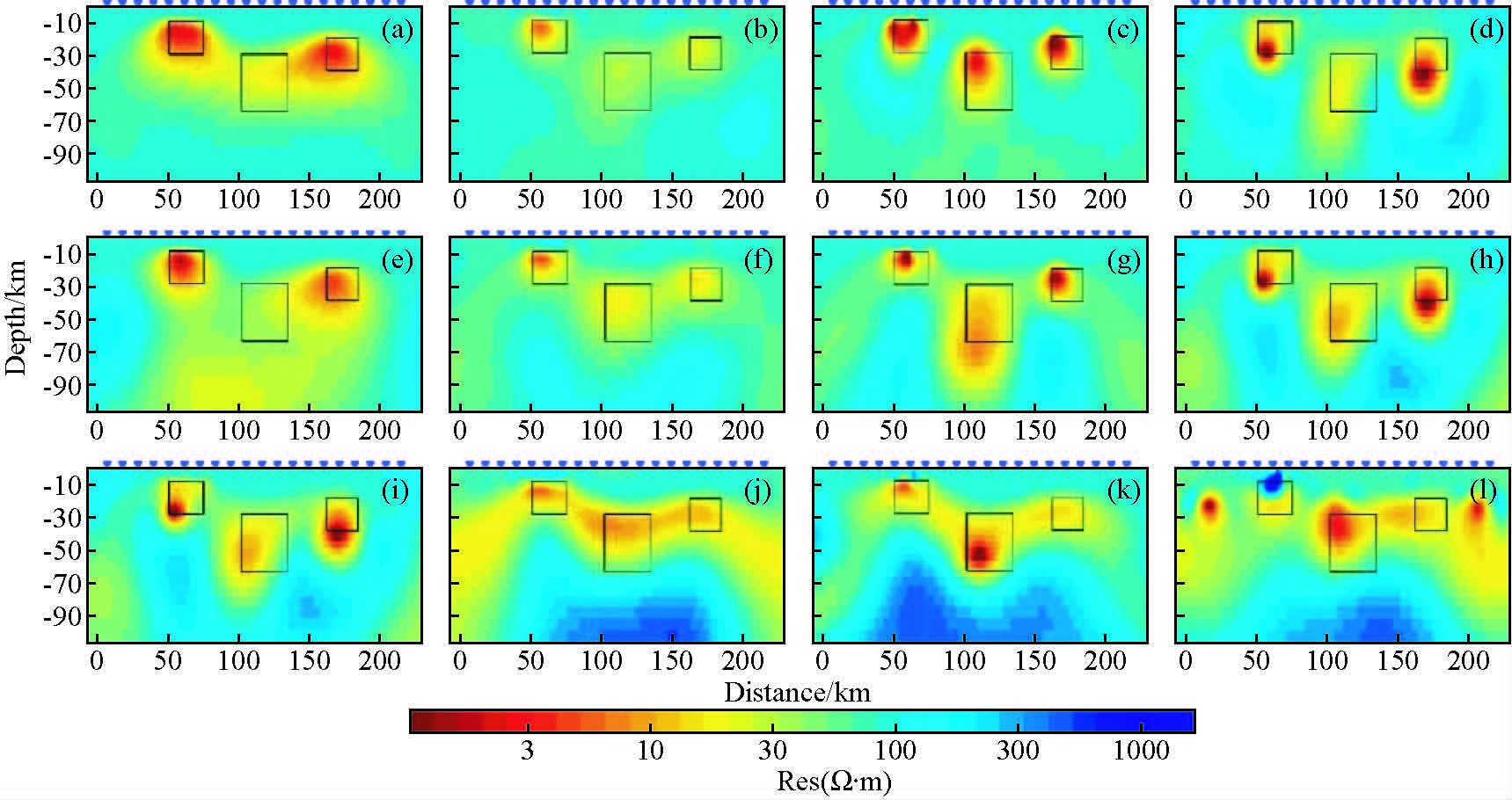
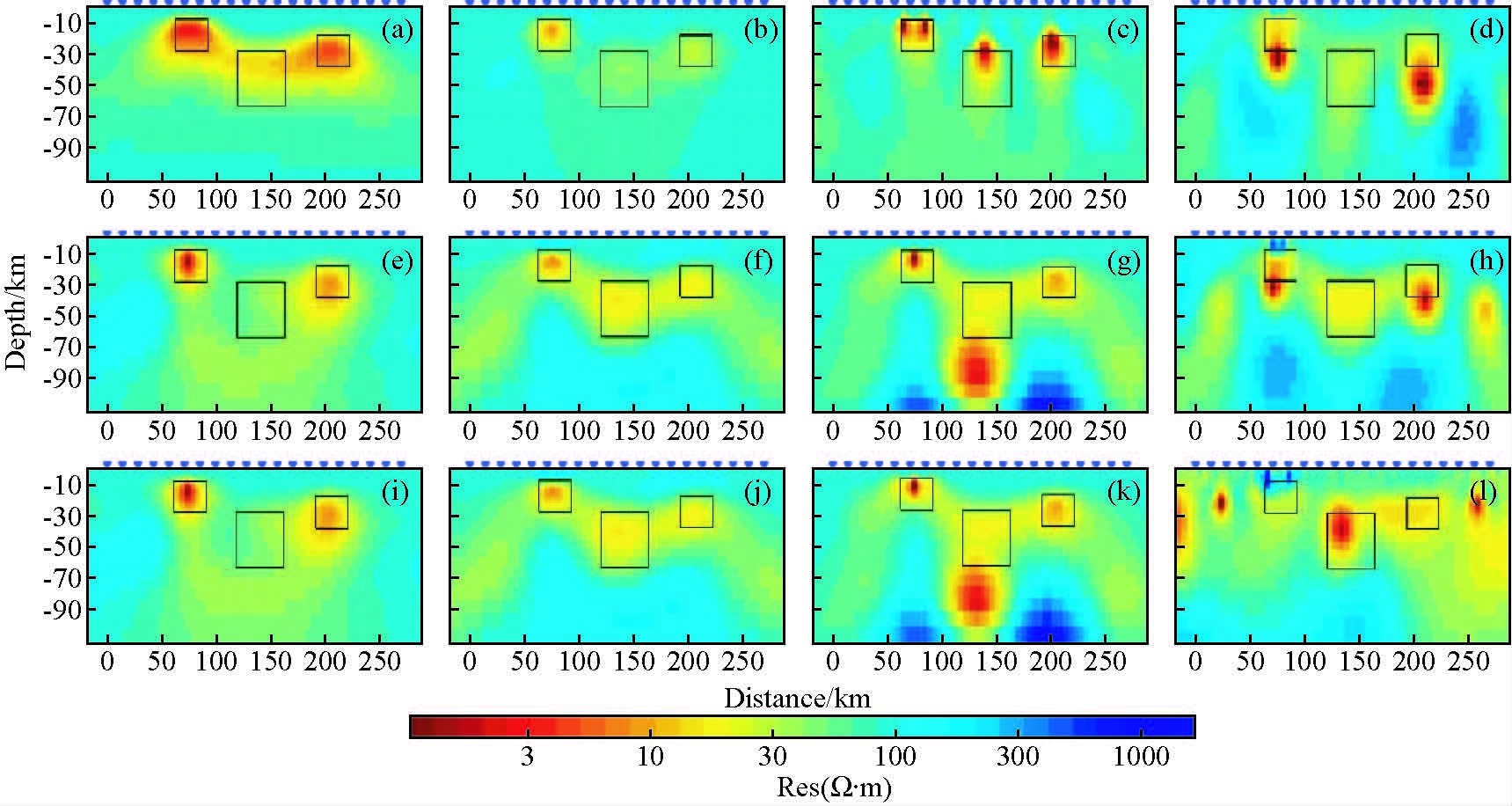
图 4为Line15测线四种模式二维反演的电性模型.其中,图 4a~d为阻抗数据电性主轴旋转至低阻体走向方向时的反演结果;图 4e~h为阻抗数据电性主轴旋转至测线垂向方向时的反演结果;图 4i~l为阻抗数据电性主轴旋转至测线方向时的反演结果(图 5、6、7各小图的编号与此相同).由图可知,电性主轴旋转至低阻体走向方向和电性主轴旋转至测线垂向方向时,TE+TM联合模式和单独TM模式反演效果较好,其他模式反演效果较差.电性主轴旋转至测线方向时,无论采用何种模式反演,所得结果均比较差.图 5~7分别为Line30、Line45、Line60的反演结果.由图中各条测线的反演模型可以看出,电性主轴旋转至低阻体走向方向的反演结果优于其他两种旋转角度的结果.模式选择上,TE+TM和TM模式的反演结果普遍较好.对比上述五条测线的反演结果,发现,测线与低阻异常体走向夹角大于45°时,反演结果受测线方向的影响较小;夹角小于45°之后,反演结果与真实模型相差较大,并且开始出现明显的假异常.
|
图 4 Line15线二维反演结果,a~d依次为电性主轴旋转至低阻体走向方向TE、TM、TE+TM和TM+TP模式反演结果,e~h分别为电性主轴旋转至测线垂向方向四个模式反演结果,i~l分别为电性主轴旋转至测线方向四个模式反演结果,图中黑框标示了低阻体的原始位置 Figure 4 2D inversion results of Line15,a to d:results in TE,TM,TE+TM and TM+TP mode with electrical strike paralleling to the direction of abnormal body;e to h:results in four modes with electrical strike perpendicularto the direction of the line;i to l:results in four modes with electrical strike paralleling to the direction of the line. Black boxes indicate the location of the anomalies in the forward models |
|
图 5 Line30线二维反演结果,a~d依次为电性主轴旋转至低阻体走向方向TE、TM、TE+TM和TM+TP模式反演结果,e~h分别为电性主轴旋转至测线垂向方向四个模式反演结果,i~l分别为电性主轴旋转至测线方向四个模式反演结果,图中黑框标示了低阻体的原始位置 Figure 5 2D inversion results of Line30,a to d: results in TE,TM,TE+TM and TM+TP mode with electrical strike paralleling to the direction of abnormal body;e to h:results in four modes with electrical strike perpendicular to the direction of the line;i to l:results in four modes with electrical strike paralleling to the direction of the line.Black boxes indicate the location of the anomalies in the forward models |
|
图 6 Line45线二维反演结果,a~d依次为电性主轴旋转至低阻体走向方向TE、TM、TE+TM和TM+TP模式反演结果,e~h分别为电性主轴旋转至测线垂向方向四个模式反演结果,i~l分别为电性主轴旋转至测线方向四个模式反演结果,图中黑框标示了低阻体的原始位置 Figure 6 2D inversion results of Line45,a to d:results in TE,TM,TE+TM and TM+TP mode with electrical strike paralleling to the direction of abnormal body;e to h:results in four modes with electrical strike perpendicular to the direction of the line;i to l:results in four modes with electrical strike paralleling to the direction of the line. Black boxes indicate the location of the anomalies in the forward models |
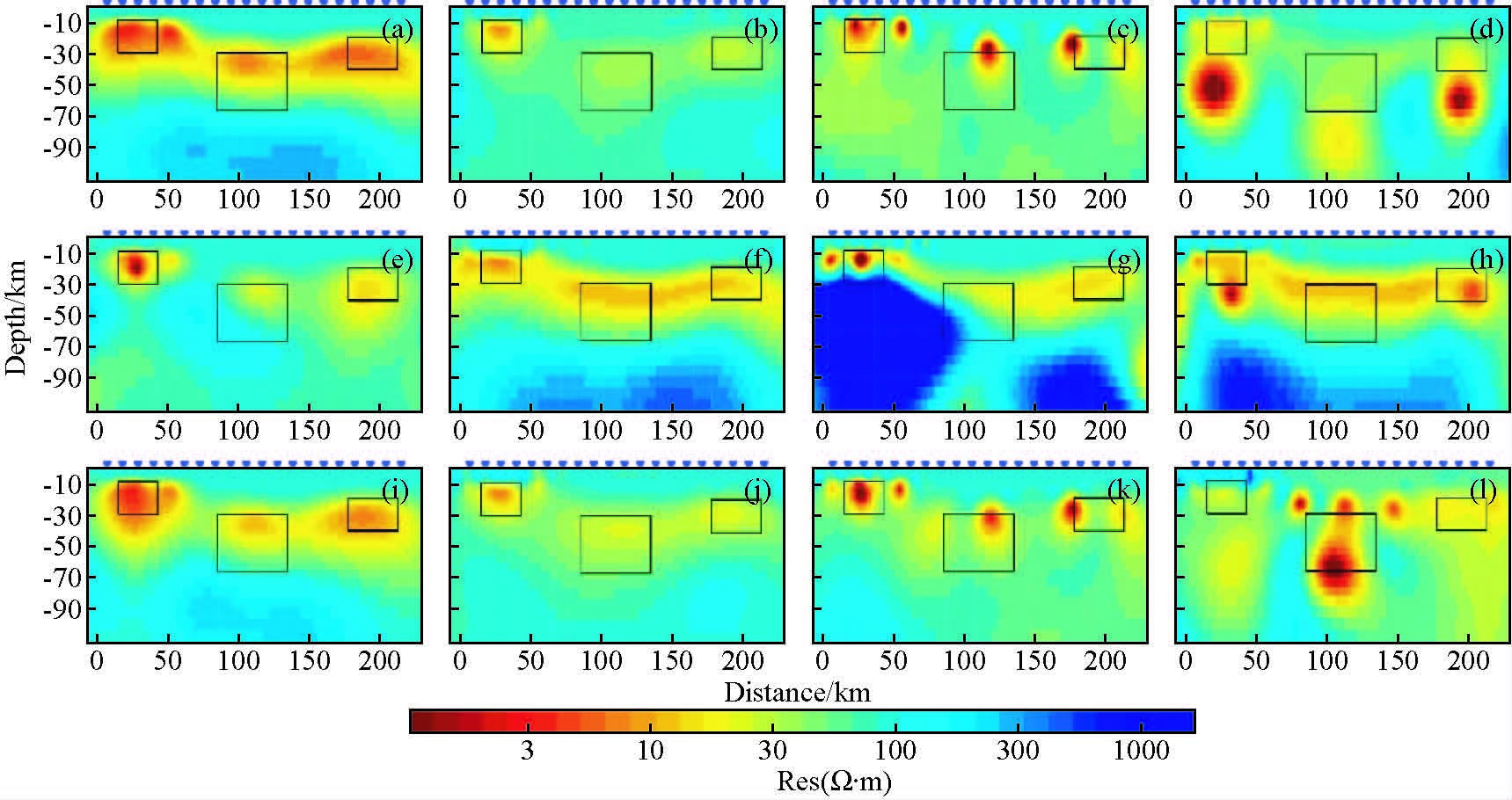
|
图 7 Line60线二维反演结果,a~d依次为电性主轴旋转至低阻体走向方向TE、TM、TE+TM和TM+TP模式反演结果,e~h分别为电性主轴旋转至测线垂向方向四个模式反演结果,i~l分别为电性主轴旋转至测线方向四个模式反演结果,图中黑框标示了低阻体的原始位置 Figure 7 2D inversion results of Line60,a to d:results in TE,TM,TE+TM and TM+TP mode with electrical strike paralleling to the direction of abnormal body;e to h:results in four modes with electrical strike perpendicular to the direction of the line;i to l:results in four modes with electrical strike paralleling to the direction of the line.Black boxes indicate the location of the anomalies in the forward models |
通过上述对模型1反演结果的分析,可以得到以下认识:(1)阻抗数据旋转角度对反演结果的影响较大,其中将阻抗数据旋转至电性主轴方向时,反演结果与真实模型最接近;(2)测线方向对二维反演结果影响相对较小,只有当测线方向与异常体走向夹角较小(小于45°)时,测线方向对反演结果的影响才开始明显;(3)相对而言,TE+TM和TM模式的反演结果较其他模式的效果好.
4.2 模型2反演结果对比实际观测中,一条MT测线常常跨越多个地质体单元,各地质单元内的构造走向往往不一致,相互之间存在一定夹角.这种情况下,如何进行MT数据的二维反演才能获得一个可靠的电性结构模型?下面就这个问题展开讨论.依据模型1的结论,这里只讨论阻抗数据旋转方向对反演结果的影响.
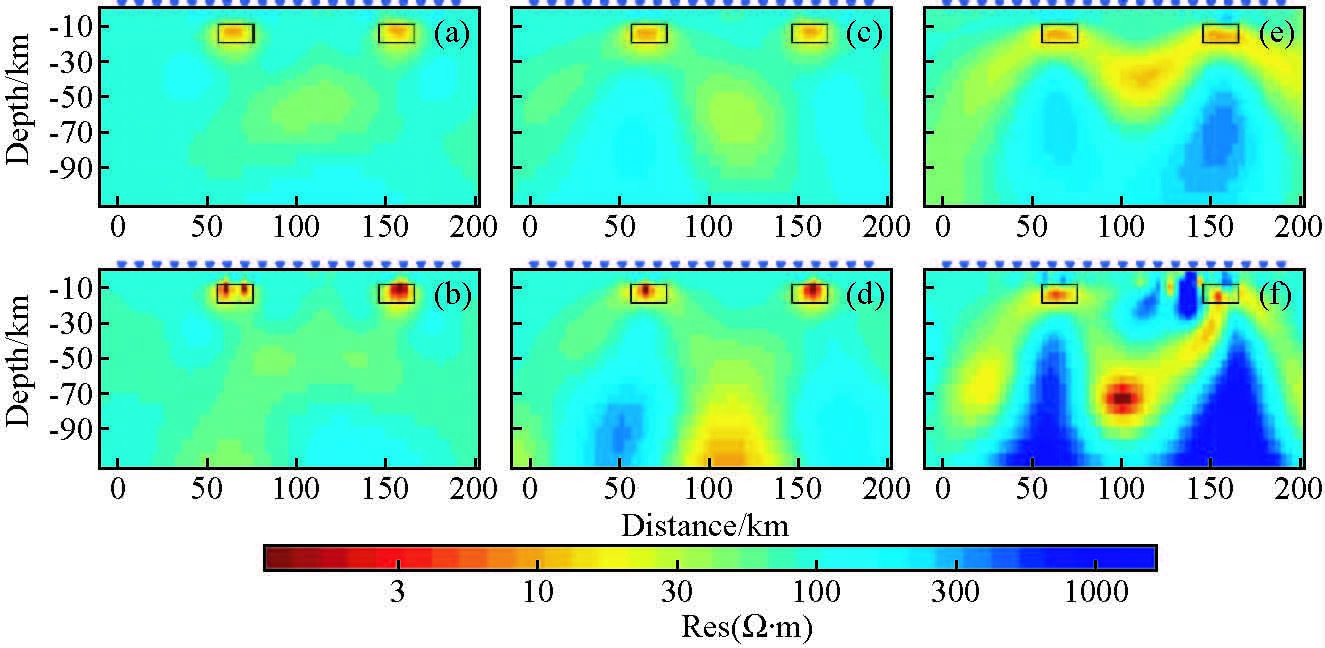
在图 1b所示地电模型2上布设一条东西向测线P0,提取测线上各测站的MT阻抗数据.对整条剖面的阻抗数据采用两种旋转策略进行反演研究:1.电性主轴旋转相同角度;2.分段旋转不同角度.统一旋转时,分别将整条剖面数据旋转至测线垂向方向和测线方向;分段旋转则是先根据相位张量分析的结果确定一个分段点,以这个分段点为界将整条剖面分为两段,每段分别旋转至各自的电性主轴方向.对旋转后的MT阻抗数据分别进TM和TE+TM模式的二维反演,见图 8.图 8a~b为分段旋转至各自地下异常体电性主轴方向的结果,图 8c~d为整条剖面统一旋转至测线垂向方向的反演结果,图 8e~f为统一旋转至测线方向的反演结果.对比图 8中不同旋转情况的反演结果,可以看出分段旋转的效果较好,反演结果比较准确地指示了两个低阻体的位置、形态和电阻率值,且高阻假异常不明显;数据统一旋转至测线垂向方向的反演效果稍差,TE+TM和TM模式较好的指示出了设计的两个低阻异常体,但在低阻体的下方出现了一定规模的高阻假异常;统一旋转至剖面方向的反演效果整体较差,不论TM还是TE+TM模式的反演结果,恢复出来的低阻异常体横向连为一体,变形严重,且在其下方出现规模较大的高阻假异常,与设计的模型相差甚远.
|
图 8 Model2二维反演结果,a~b分别为分段旋转后TM和TE+TM模式反演结果,c~d分别为统一旋转至测线垂向方向TM和TE+TM模式反演结果,e~f分别为统一旋转至测线方向TM和TE+TM模式反演结果 Figure 8 2D inversion results of Model2,a to b:results in TM and TE+TM mode with deferent electrical strike section by section along the line;c to d:results in TM and TE+TM mode with same electrical strike perpendicular to the direction of the line;e to f:results in TM and TE+TM mode with same electrical strike paralleling to the direction of the line. Black boxes indicate the location of the anomalies in the forward models |
通过模型2的反演研究,得到如下认识:当一条测线下方存在走向不同的多个异常体时,应当根据电性主轴分析结果,将阻抗数据分段旋转至各自的电性主轴方向,此时,二维反演所得的地电模型比较可靠.
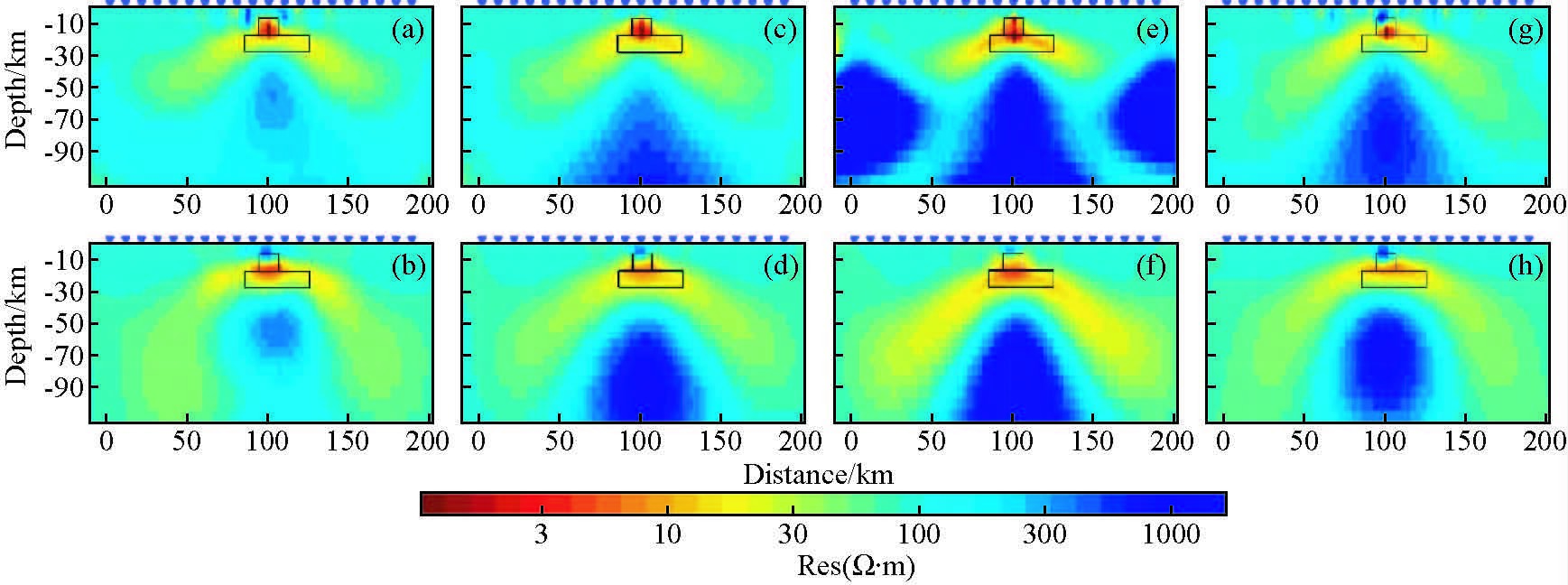
4.3 模型3反演结果对比实际工作中常遇到另一种更为复杂的地电模型,即,研究区地质构造走向随深度发生较大变化,常见的有“立交桥”模型(程顺有等,2003).此次研究中,将其简化为地电模型3.模型3中布设一条东西方向的测线P1,如图 1c所示,对整条测线阻抗数据进行四种策略电性主轴旋转,然后分别进行二维反演,见图 9.其中,a~b为分频段电性主轴旋转的结果.根据相位张量分析的结果,以100 s为分界频点,100 s以上的频点的阻抗数据电性主轴旋转至浅部低阻体1的走向方向(45°),100 S以下的频点电性主轴旋转至深部异常体2的走向方向(135°);c~d为电性主轴统一旋转至测线垂向方向的反演结果;e~f为电性主轴统一旋转至浅部异常体走向方向的反演结果.g~h为电性主轴统一旋转至深部异常体走向方向的反演结果.
|
图 9 Model3二维反演结果,a、b分别为分频段旋转TE+TM和TM模式反演结果,c、d分别为统一旋转至测线垂向方向TE+TM和TM模式反演结果,e、f分别为统一旋转至浅部低阻异常体走向方向TE+TM和TM模式反演结果,g、h分别为统一旋转至深部低阻异常体走向方向TE+TM和TM模式反演结果 Figure 9 2D inversion results of Model3,a to b:results in TM and TE+TM mode with deferent electrical strike by frequency-band division;c to d:results in TM and TE+TM mode with same electrical strike perpendicular to the direction of the line;e to f:results in TM and TE+TM mode with same electrical strike paralleling to the direction of shallow abnormal body;g to h:results in TM and TE+TM mode with same electrical strike paralleling to the direction of deep abnormal body. Black boxes indicate the location of the anomalies in the forward models |
对比反演结果,发现,各模型都能指示出低阻异常体的存在,但各反演结果之间存在很大差别.总体上,分频段旋转电性主轴的反演模型,高阻假异常规模相对较小,反演效果优于其他旋转角度的反演结果;对同一旋转策略而言,TE+TM模式对浅部低阻体恢复好于TM模式,而TM模式对深部低阻体的反演效果好于TE+TM模式.
分析模型3的反演结果,笔者认为对于“立交桥”模式的“准二维”情况进行二维反演时,应分频段将阻抗数据的电性主轴旋转至对应的构造走向方向后,再进行反演;反演模式的选择上,应进行TE+TM联合模式和单独TM模式两种反演,二者相互补充,才能构建出较为合理地下电性结构模型.
5 结论 5.1本文结合实际工作,设计了三种类型的理论地电模型,通过模型的正反演试算,对“准二维”地质构造进行了MT二维反演研究,获得以下认识:
(1) 相对于测线方向而言,阻抗数据旋转角度对反演结果的影响较大,其中将阻抗数据旋转到电性主轴方向时,反演结果与真实模型最接近;测线方向对二维反演结果影响相对较小,只有当测线方向与异常体走向夹角较小(小于45°)时,测线方向对反演结果的影响才开始明显.
(2) 在本文的模型反演中,TE+TM模式和TM模式的反演结果较其他模式的效果好.
(3) 当一条测线下方在横向与纵向上存在走向不同的多个异常体时,应该根据电性主轴分析结果,将整条剖面分测点、分频段进行阻抗数据的电性主轴旋转,这样才能通过二维反演得到较为合理的地电模型.
5.2本文研究结论是在三个简化地电模型反演研究的基础上得出的,对于更为复杂的地电模型,该结论是否有效,还需要开展更深入的研究与分析.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Cai J T, Chen X B .2010. Refined techniques for data processing and two-dimensional inversion in magnetotelluric Ⅱ:Which data polarization mode should be used in 2D inversion[J]. Chinese Journal of Geophysics(in Chinese), 53 (11) : 2703–2714. DOI:10.3969/j.issn.0001-5733.2010.11.018 |
| [] | Caldwell T G, Bibby H M, Brown C .2004. The magnetotelluric phase tensor[J]. Geophys.J.Int., 158 (2) : 457–469. DOI:10.1111/gji.2004.158.issue-2 |
| [] | Chen X B, Zhao G Z, Ma X .2008. Preliminary discussion on selecting rotation direction in 2-D MT inversion[J]. Oil Geophysical Prospecting(in Chinese), 43 (1) : 113–118. |
| [] | Cheng S Y, Zhang G W, Li L .2003. Lithospheric electrical structure of the Qinling orogen and its geodynamic implication[J]. Chinese Journal of Geophysics(in Chinese), 46 (3) : 390–397. DOI:10.3321/j.issn:0001-5733.2003.03.017 |
| [] | Dong H, Wei W B, Ye G F, et al .2012. Study of two dimensional magnetotelluric inversions of complex three dimensional structures[J]. Chinese Journal of Geophysics(in Chinese), 55 (12) : 4003–4014. DOI:10.6038/j.issn.0001-5733.2012.12.012 |
| [] | Dong S W, Li T D, Chen X H, et al .2012. Progress of deep exploration in mainland China:A review[J]. Chinese Journal of Geophysics(in Chinese), 55 (12) : 3884–3901. DOI:10.6038/j.issn.0001-5733.2012.12.002 |
| [] | Hu X Y, Li Y, Yang W C, et al .2012. Three-dimensional magnetotelluic parallel inversion algorithm using data space method[J]. Chinese Journal of Geophysics (in Chinese), 55 (12) : 3969–3978. DOI:10.6038/j.issn.0001-5733.2012.12.009 |
| [] | Hu Z Z, He X Y, He Z X .2005. Using 2-D inversion for interpretation of 3-D MT data[J]. Oil Geophysical Prospecting(in Chinese), 40 (3) : 353–359. |
| [] | Jin S, Wei W B, Ye G F, et al .2009. The electrical structure of Bangong-Nujiang suture:Results from magnetotelluric sounding detection[J]. Chinese Journal of Geophysics (in Chinese), 52 (10) : 2666–2675. DOI:10.3969/j.issn.0001-5733.2009.10.027 |
| [] | Jin S, Wei W B, Wang S, et al .2010. Discussion of the formation and dynamic signification of the high conductive layer in Tibetan crust[J]. Chinese Journal of Geophysics (in Chinese), 53 (10) : 2376–2385. DOI:10.3969/j.issn.0001-5733.2010.10.011 |
| [] | Jones A G .2011. Three-dimensional galvanic distortion of three-dimensional regional conductivity structures:Comment on "Three-dimensional joint inversion for magnetotelluric resistivity and static shift distributions in complex media"by Yutaka Sasaki and Max A[J]. Meju[J]. Journal of Geophysical Research, 116 (B12) . |
| [] | Li Y, Hu X Y, Yang W C, et al .2012. A study on parallel computation for 3D magnetotelluric modeling using the staggered-grid finite difference method[J]. Chinese Journal of Geophysics (in Chinese), 55 (12) : 4036–4043. DOI:10.6038/j.issn.0001-5733.2012.12.015 |
| [] | Mackie R L, Madden T R, Wannamaker P E .1993. Three-dimensional magnetotelluric modeling using difference equations-theory and comparisons to integral-equations solutions[J]. Geophysics, 58 (2) : 215–226. DOI:10.1190/1.1443407 |
| [] | Rodi W, Mackie R L .2001. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 66 (1) : 174–187. DOI:10.1190/1.1444893 |
| [] | Shi Y J, Liu G D, Wu G Y, et al .1985. Magnetotellurics (in Chinese)[M]. Beijing: Seismological Press . |
| [] | Siripunvaraporn W, Egbert G, Lenbury Y, et al .2005. Three-dimensional magnetotelluric inversion:Data-space method[J]. Physics of the Earth and Planetary Interiors, 150 (1-3) : 3–14. DOI:10.1016/j.pepi.2004.08.023 |
| [] | Tan H D, Wei W B, Unsworth M, et al .2004. Crustal electrical conductivity structure beneath the Yarlung Zangbo Jiang suture in the southern Xizang plateau[J]. Chinese Journal of Geophysics (in Chinese), 47 (4) : 685–690. DOI:10.3321/j.issn:0001-5733.2004.04.020 |
| [] | Wei W B, Jin S, Ye G F, et al .2006. Conductivity structure of crust and upper mantle beneath the northern Tibetan plateau:Results of super-wide band magnetotelluric sounding[J]. Chinese Journal of Geophysics (in Chinese), 49 (4) : 1215–1225. DOI:10.3321/j.issn:0001-5733.2006.04.038 |
| [] | Wei W B, Jin S, Ye G F, et al .2010. On the conductive structure of Chinese continental lithosphere-experiment on "standard monitoring network"of continental EM parameters(SinoProbe-01)[J]. Acta Geologica Sinica (in Chinese), 84 (6) : 788–800. |
| [] | Xie C L, Ye G F, Wei W B, et al .2012. Electrical features of the main faults beneath Northern Tibetan Plateau[J]. Chinese Journal of Geophysics (in Chinese), 55 (12) : 3991–4002. DOI:10.6038/j.issn.0001-5733.2012.12.011 |
| [] | 蔡军涛, 陈小斌.2010. 大地电磁资料精细处理和二维反演解释技术研究(二)-反演数据极化模式选择[J]. 地球物理学报, 53 (11) : 2703–2714. DOI:10.3969/j.issn.0001-5733.2010.11.018 |
| [] | 陈小斌, 赵国泽, 马霄.2008. 关于MT二维反演中数据旋转方向的选择问题初探[J]. 石油地球物理勘探, 43 (1) : 113–118. |
| [] | 程顺有, 张国伟, 李立.2003. 秦岭造山带岩石圈电性结构及其地球动力学意义[J]. 地球物理学报, 46 (3) : 390–397. DOI:10.3321/j.issn:0001-5733.2003.03.017 |
| [] | 董浩, 魏文博, 叶高峰, 等.2012. 大地电磁测深二维反演方法求解复杂电性结构问题的适应性研究[J]. 地球物理学报, 55 (12) : 4003–4014. DOI:10.6038/j.issn.0001-5733.2012.12.012 |
| [] | 董树文, 李廷栋, 陈宣化, 等.2012. 我国深部探测技术与实验研究进展综述[J]. 地球物理学报, 55 (12) : 3884–3901. DOI:10.6038/j.issn.0001-5733.2012.12.002 |
| [] | 胡祥云, 李焱, 杨文采, 等.2012. 大地电磁三维数据空间反演并行算法研究[J]. 地球物理学报, 55 (12) : 3969–3978. DOI:10.6038/j.issn.0001-5733.2012.12.009 |
| [] | 胡祖志, 胡祥云, 何展翔.2005. 三维大地电磁数据的二维反演解释[J]. 石油地球物理勘探, 40 (3) : 353–359. |
| [] | 金胜, 魏文博, 叶高峰, 等.2009. 班公-怒江构造带的电性结构特征-大地电磁探测结果[J]. 地球物理学报, 52 (10) : 2666–2675. DOI:10.3969/j.issn.0001-5733.2009.10.027 |
| [] | 金胜, 魏文博, 汪硕, 等.2010. 青藏高原地壳高导层的成因及动力学意义探讨-大地电磁探测提供的证据[J]. 地球物理学报, 53 (10) : 2376–2385. DOI:10.3969/j.issn.0001-5733.2010.10.011 |
| [] | 李焱, 胡祥云, 杨文采, 等.2012. 大地电磁三维交错网格有限差分数值模拟的并行计算研究[J]. 地球物理学报, 55 (12) : 4036–4043. DOI:10.6038/j.issn.0001-5733.2012.12.015 |
| [] | 石应骏, 刘国栋, 吴广耀, 等.1985. 大地电磁测深法教程[M]. 北京: 地震出版社 . |
| [] | 谭捍东, 魏文博, UnsworthM, 等.2004. 西藏高原南部雅鲁藏布江缝合带地区地壳电性结构研究[J]. 地球物理学报, 47 (4) : 685–690. DOI:10.3321/j.issn:0001-5733.2004.04.020 |
| [] | 魏文博, 金胜, 叶高峰, 等.2006. 藏北高原地壳及上地幔导电性结构-超宽频带大地电磁测深研究结果[J]. 地球物理学报, 49 (4) : 1215–1225. DOI:10.3321/j.issn:0001-5733.2006.04.038 |
| [] | 魏文博, 金胜, 叶高峰, 等.2010. 中国大陆岩石圈导电性结构研究-大陆电磁参数"标准网"实验(SinoProbe-01)[J]. 地质学报, 84 (6) : 788–800. |
| [] | 谢成良, 叶高峰, 魏文博, 等.2012. 藏北高原主要断裂带电性结构特征[J]. 地球物理学报, 55 (12) : 3991–4002. DOI:10.6038/j.issn.0001-5733.2012.12.011 |
 2016, Vol. 31
2016, Vol. 31


