2. 东方地球物理公司国际事业部, 涿州 072751
3. 胜利油田物探研究院, 东营 257022
2. Eastern Geophysical Company International Business Department, Zhuozhou 072751, China
3. Geophysical Research Institute of Shengli Oilfield, Dongying 257002, China
常规采集的单炮数据是一种时间上无重叠但空间上有重叠的炮记录.随着勘探目标的日益复杂,以及对成像精度越来越高的要求,传统的采集很难对地下复杂区域进行有效照明,从而无法获得高质量的成像剖面.为了解决这一问题,研究人员提出了混叠数据的采集方式,它得到的是一种在时间和空间上都有重叠的炮记录.这种方式解决了传统采集方式照明不足的问题,也大大提高了野外原始数据的采集效率.但是对这种数据进行处理的时候,由于不相关炮的波场进行互相关,会产生串扰噪声,严重影响成像质量.为了减少串扰噪声,消除偏移假象,许多学者提出了一系列解决方法.早期消除串扰噪声项的方法主要是Rietveld和Berkhout(1994)提出的相移法,这种方法使波场在复杂区域有很好的照明.Tieman(1997)引入了平面波偏移方法,Morton和Ober(1998)使用随机相位编码的方法对偏移进行加速.Whitmore等(1995)和Liu等(2006)使用平面波方式来压制交叉项.Soubaras(2006)采用Modulated编码方式来压制交叉项.这几种方法的共同特点都是对交叉项引入差异的时移量,通过交叉项的非同相叠加消除串扰噪声.一些正则化算子也被用于串扰噪声的消除,并取得了较好的应用效果(王彦飞,2013;沈雄君和刘能超,2012).编码的方式也是一种重要的压制串扰噪声的策略,近年来逐渐成为研究的热点(王西文等,2013),不同的编码策略也被应用在最小二乘偏移(LSM)和全波形反演(FWI)(黄建平等,2013a,2014a;周华敏等,2014).Jing等(2000)和Krebs等(2009)提出了一种极性编码算子,该方法随机地给各炮乘以+1或-1的极性.此外,Jing针对相位编码的多炮数据偏移经验性的总结出当6炮编码在一起时串扰噪声相得到适当的压制,Krebs则经验性的发现在FWI中使用这种编码方法能够在计算量减少一个数量级的前提下得到与传统单炮FWI结果相近的速度场.Godwin和Sava(2010)引入振幅编码的方式压制交叉项,并通过奇异值分布控制编码次数.Godwin和Sava(2011)系统地比较了包括Modulated,Hartley basis,平面波等几种编码方式.Huang和Schuster(2012)在最小二乘偏移中使用一种分频的编码方法,具体做法是寻求一个合适的编码矩阵,尽量使串扰噪声矩阵接近单位矩阵,从而达到消除串扰噪声项的目的.
编码方法的选择对偏移结果有重要影响,编码策略的差异也严重影响成像效果.Morton和Ober(1998)提出一种动态地决定偏移次数和信噪比的方法.Romero等(2000)比较了两种编码策略,一种是将部分炮编码在一起,对每炮只使用一次;另一种是将所有炮编码在一起,多次使用.Schuster等(2011)使用了迭代叠加和最小二乘偏移两种策略,并给出了信噪比与超道集个数、迭代次数等之间的关系式.Huang和Schuster(2012)在分频编码的最小二乘偏移中引入动态编码方式,模型试算成像效果保幅性及噪声压制效果较好.黄建平等(2013b,2014b,c;2015)实现了基于不同方程的编码最小二乘偏移算法,并进行了初步应用及不同算法的对比分析.
在前人研究的基础上,本文首先介绍混叠数据偏移的原理,在模型试算中使用分频编码方式,利用最小二乘裂步法对多炮数据进行偏移,在迭代过程中使用不同编码策略:动态、静态和混合编码,测试数据和模型的收敛情况,总结编码方式对计算效率和偏移结果的影响.
1 方法原理传统的波动方程偏移通常由两步组成,对震源波场和接收波场进行重建,对波场运用成像条件进行成像,这样就能够得到如下的成像结果R为
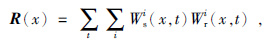
|
(1) |
公式(1)中Wsi(x,t),Wri(x,t)分别代表重建的震源波场和接收波场.所有的波场可以用一个单炮波场组成的矢量来表示,公式为
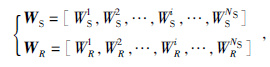
|
(2) |
其中,NS表示总的炮数.传统的地震成像相当于这两个矢量的內积:R=WSWRH,H表示复共轭转置.
为了说明多炮数据的偏移,本文引入编码矩阵E,它是一个Ns×Ne的矩阵,Ns是炮的数目,Ne是编码的次数.由于Ne$ \ll $Ns,混叠数据偏移通过减少传统方法的偏移次数成倍的提高计算效率.编码矩阵的元素可以表示为
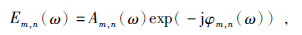
|
(3) |
其中Am,n代表第n次编码中第m个炮集的振幅权重(振幅编码),φm,n代表第n次编码中第m个炮集的相移(相位编码).同样的编码方法可以是频率相关的,也可以是频率无关的.
本文使用的分频编码方式可以表示为

|
(4) |
编码后多炮的波场可以表示为
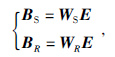
|
(5) |
而成像结果可以表示为
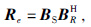
|
(6) |
由于在对震源波场和接收波场运用成像条件的时候,震源波场与其不相关的接收波场互相关就形成了串扰噪声,它严重影响混叠数据的成像质量.将上式展开,即:
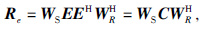
|
(7) |
其中矩阵C称为串扰噪声矩阵,维数为Ns×Ns,我们将上式写成两部分,公式为
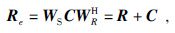
|
(8) |
R表示正确的成像结果,它可以表示为R=WSIWRH,I是单位矩阵,X代表串扰噪声项.为此,可以将R和C写成如下形式:
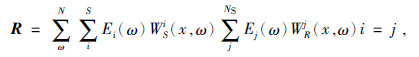
|
(9) |
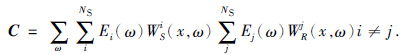
|
(10) |
在编程实现方法的基础上,本文采用SEG/SALT模型进行不同编码策略下成像结果的测试.之所以选择盐丘模型进行成像算法优劣的测试,主要是因为:SALT模型中既包含有典型的高速岩体,也含有高陡断层,且速度模型横向变化较为明显,能较好地用于测试成像方法对高陡构造及盐下成像能力.
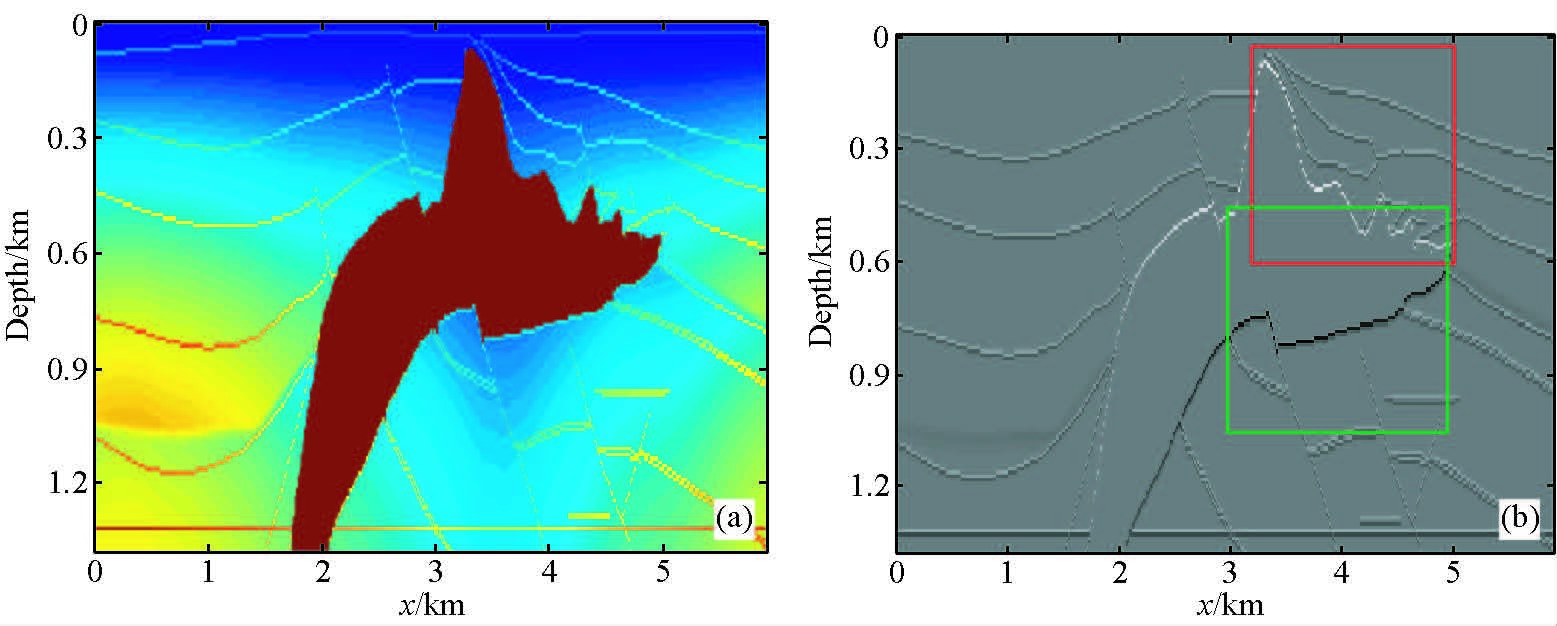
主要模型参数为:深度方向150个采样点,水平方向645个采样点,速度范围从1524 m/s到4481 m/s,模型如图 1a所示;计算参数为:震源为主频30 Hz的雷克子波.观测系统的设计:本文计算过程中模拟放炮的总炮数为320炮,炮间隔18.46 m,645道检波器,道间隔9.23 m,采用双边接收方式.记录分为2个超道集,每个超道集160炮.计算过程中的反射系数模型通过速度模型和常密度假设得到,如图 1b所示.模型中反射系数界面非常清晰,盐丘形态明显,盐丘下部断层也很清楚.图 1b中红色方框和绿色方框部分,分别代表模型中的高陡复杂构造变化剧烈区域和盐下成像的目标区域,在下文不同编码策略的成像结果对比中,将对这些区域进行突出显示,以展示不同编码策略下成像方法对高陡构造和盐下成像能力的差异.
|
图 1 速度模型和反射系数模型 (a)速度模型;(b)反射系数模型. Figure 1 Velocity model and reflection coefficient model (a)Velocity model;(b)Reflection coefficient model. |
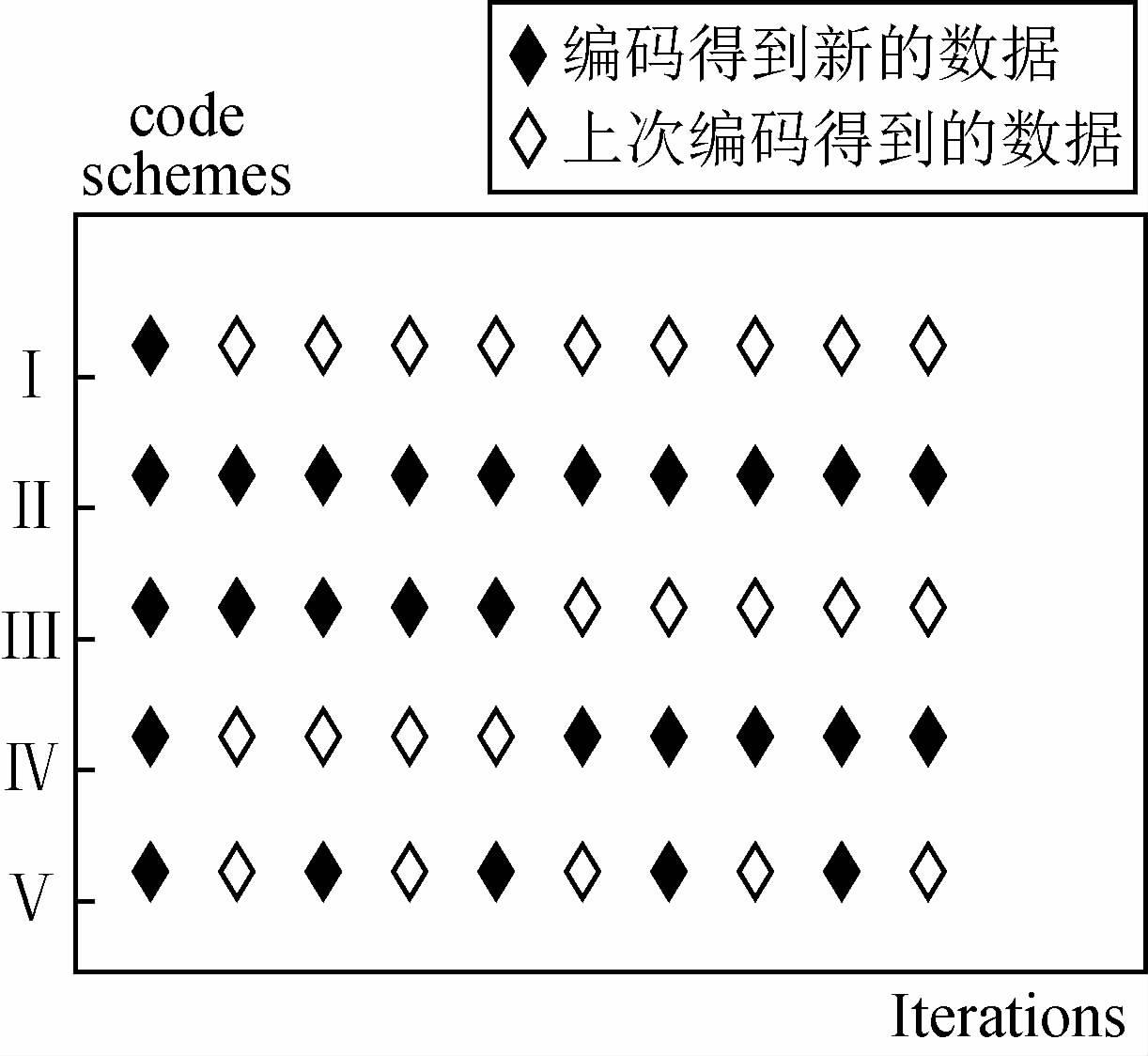
本文尝试设计不同的编码策略,采用分频编码的方式,基于最小二乘裂步法偏移对不同编码策略进行成像测试.对于每种方法,计算过程中迭代次数均为50次.主要用到的编码策略包括:在编码过程中采用静态编码、动态编码以及混合编码;在编码实施上采用多样化的编码顺序.其中,静态编码是指,在迭代过程中使用的数据是上一次编码得到数据;而动态编码的实现过程为:每一次迭代都重新编码得到新的数据.本文设计的几种编码策略的示意图如图 2所示.
|
图 2 不同编码方式示意图 Figure 2 Schematic diagram for different encoding |
图 2中纵坐标代表五种不同的编码策略和编码方式:Ⅰ完全静态编码表示最小二乘的全部迭代过程只进行一次编码,Ⅱ完全动态编码表示每一次迭代都重新编码一次,形成新的数据;Ⅲ表示前25次迭代重新进行编码,后25次迭代使用最后一次编码得到的数据;Ⅳ与Ⅲ 相反;Ⅴ表示5次迭代使用动态编码,5次迭代使用静态编码,以此类推.
基于分频的最小二乘裂步偏移方法,本文测试了图 2所示5五种不同编码方式不同迭代次数的成像结果.测试的侧重点为:(1)成像过程中混叠数据数据串扰噪声的压制情况;(2)不同编码策略的计算效率;(3)不同编码策略的成像精度.五种编码策略不同迭代次数成像结果如图 3所示:图中水平方向代表五种不同的编码方式,垂直方向结果代表 6种不同迭代次数下的计算结果,从上到下迭代次数分别为5、10、20、30、40、50次.对比图 3结果可知:(1)随着迭代次数的增加,成像结果得到明显改善,串扰噪声也到了有效抑制.SALT模型中的高陡构造和高速盐体盐下构造得到了正确成像,中深部成像保幅性和振幅均衡性较好.(2)从5次迭代的结果可以看到,基于静态编码的成像结果中,含有较为明显的成像串扰噪声,基于动态编码的方式的成像结果在串扰噪声压制、成像效果等方面要优于静态编码方式及混合编码方式.随着迭代次数增加到50次,基于动态编码和混合编码方式的成像效果可以比拟,均优于基于静态编码的成像结果.(3)不同编码策略的50次所需数据量及I/O时间如表 1所示,由表 1结果可以看到,基于静态编码的最小二乘裂步偏移所需要的数据最少,同时I/O也最小,这使得方法较易推广到三维情况.而基于动态编码的最小二乘偏移方法,在迭代过程中需要大量的多炮数据和I/O时间,在实际推广应用,尤其是海量三维实际资料处理过程中,需要综合考虑数据量和存储问题.

|
图 3 各编码策略不同迭代次数时成像结果 图中从左到右每列表示Ⅰ-Ⅴ几种编码方式,从上到下每行分别表示迭代第5、10、20、30、40、50次偏移结果. Figure 3 Different encoding migration results From left to right showⅠ-Ⅴ Encoding and from up to down show 5,10,20,30,50 times the iterative migration results. |
|
|
表 1 各编码方式所用数据及I/O时间 Table 1 Speed time in I/O and using data with different encoding |
为了进一步展示不同编码策略对高陡构造、高速盐体下部成像的差异.本文对成像结果中的典型高陡构图 1b中红色框部分及高速岩体下部构造区域图 1b中绿色框部分进行了放大显示,局部放大图如图 4和图 5所示.从图 4的结果中可以清楚地看到:在典型的高陡构造区域,针对编码策略I,混叠数据的成像串扰噪声较为显著,成像噪声弥散在整个高陡构造区域内.究其原因可能是因为:在迭代过程中采用静态编码策略,在迭代过程中编码数据保持不变,不同炮数据之间的差异性存在但不是很明显;而采用动态编码策略Ⅱ的成像过程中,每次迭代采用不同的编码函数,更为准确的保持了单炮记录本身的运动学和动力学特征,所形成超道集的不同炮的特征差异较为明显,成像串扰噪声得到了较为明显的抑制.如图 3中第二列所示.而采用混合编码方式的Ⅲ、Ⅳ、Ⅴ成像结果的串扰噪声介于纯静态编码和纯动态编码策略之间,在达到较大的迭代次数情况下,成像串扰噪声都得到了较好的抑制,同时三种方式所用数据及I/O也介于完全静态编码和完全动态编码方式之间.不同编码策略需要结合不同的实际计算需求、计算资源、处理目标特点及成像精度要求来综合选择.当地下结构复杂,计算资源比较充足的时候可以采用动态编码策略的方式;当地下结构比较简单的层状构造,静态编码完全可以满足计算需求;当地下结构较为复杂,计算资源有限的时候可以采用动静编码交替使用,既可以节省计算资源也可以较快的收敛到所需要的精度.

|
图 4 各编码策略不同迭代次数时成像结果中红色框区域放大图 图中从左到右每列表示Ⅰ-Ⅴ几种编码方式,从上到下每行分别表示迭代第5、10、20、30、40、50次偏移结果. Figure 4 Different encoding migration resultsforredarea From left to right showⅠ-Ⅴ Encoding and from up to down show 5,10,20,30,50 times the iterative migration results. |

|
图 5 各编码策略不同迭代次数时成像结果中绿色框区域放大图 图中从左到右每列表示Ⅰ-Ⅴ几种编码方式,从上到下每行分别表示迭代第5、10、20、30、40、50次偏移结果. Figure 5 Different encoding migration resultsfor greenarea From left to right showⅠ-Ⅴ Encoding and from up to down show 5,10,20,30,50 times the iterative migration results. |
类似于高陡构造成像结果局部放大图 4,图 5给出了高速盐体下部构造结果放大图.从图中可以得到与图 4较为一致的结论:(1)成像质量上,纯动态编码成像结果要优于纯静态编码成像结果,三种混合编码方式介于二者之间;(2)计算效率和计算存储上,静态编码方式要优于动态编码策略,而三种混合编码方式也介于二者之间;(3)与黄建平等(2014a)研究结果类似,在较大迭代次数情况下,成像更新量主要更新深部构造误差,对于中深部储层保幅构造具有重要意义.为此,在计算资源允许的情况下,较多的成像迭代次数是十分必要的.
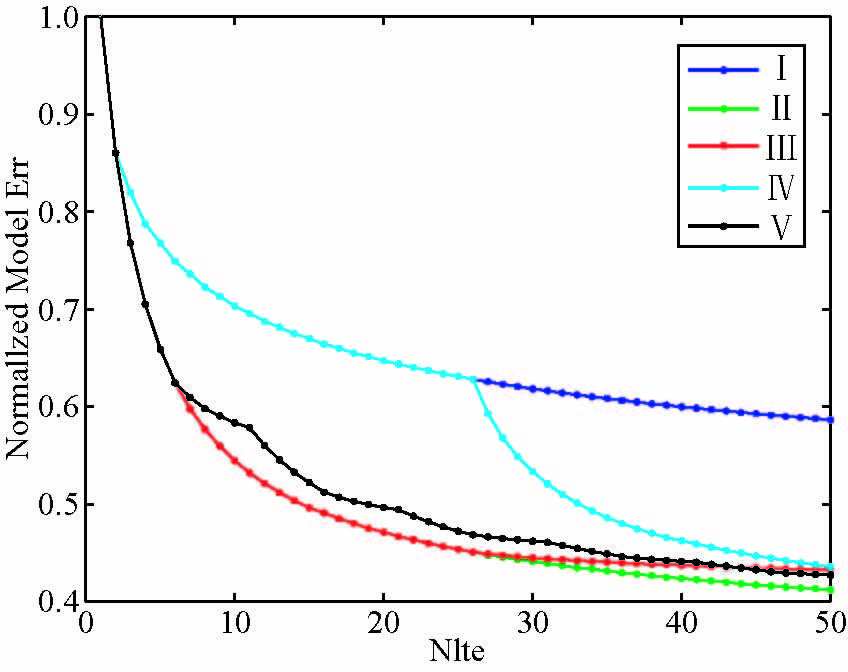
下文给出了最小二乘迭代的误差随迭代次数的变化曲线,其中数据收敛曲线和模型收敛曲线分别如图 6和图 7所示.
|
图 6 各种编码方式模型收敛曲线 Figure 6 The modeldata error of different encoding |
|
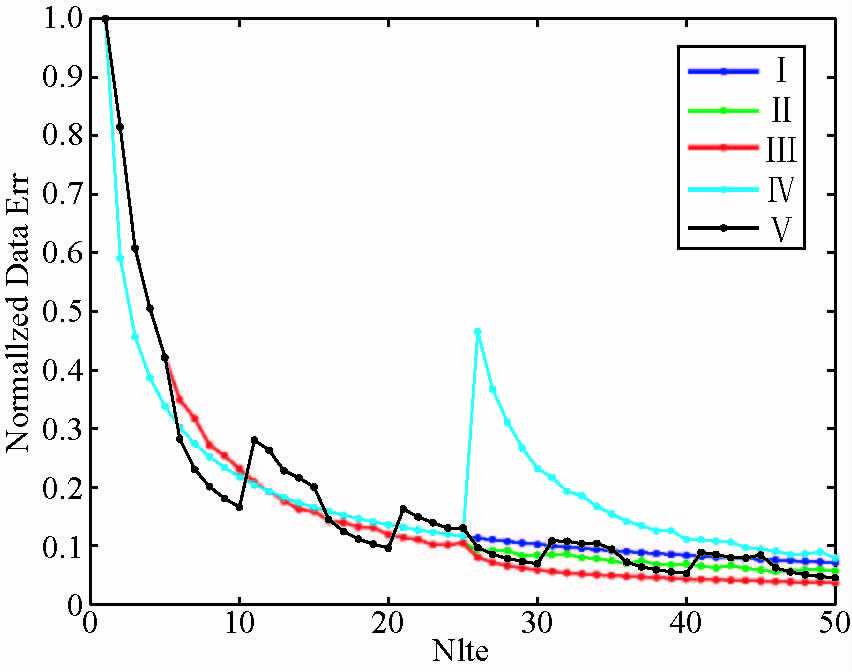
图 7 各种编码方式数据收敛曲线 Figure 7 The data error of different encoding |
从误差收敛结果图 6和图 7可以发现:迭代过程中使用动态编码明显要比静态编码收敛的速度更快,特别是在计算的前半部分.在收敛到一定程度之后,动态编码速度上的优势就不再像迭代初期一样显著.在五种编码方式中,完全使用静态编码的收敛效果最差,且收敛速度最慢(方式I);使用的动态编码次数越多最终收敛的精度越高,完全使用动态编码使模型收敛达到的精度最高(方式Ⅱ);迭代过程中,使用的动态编码的次数相同的情况下,混合使用动态静态编码的方式对模型的收敛效果差异不大(方式Ⅲ,Ⅳ,Ⅴ).
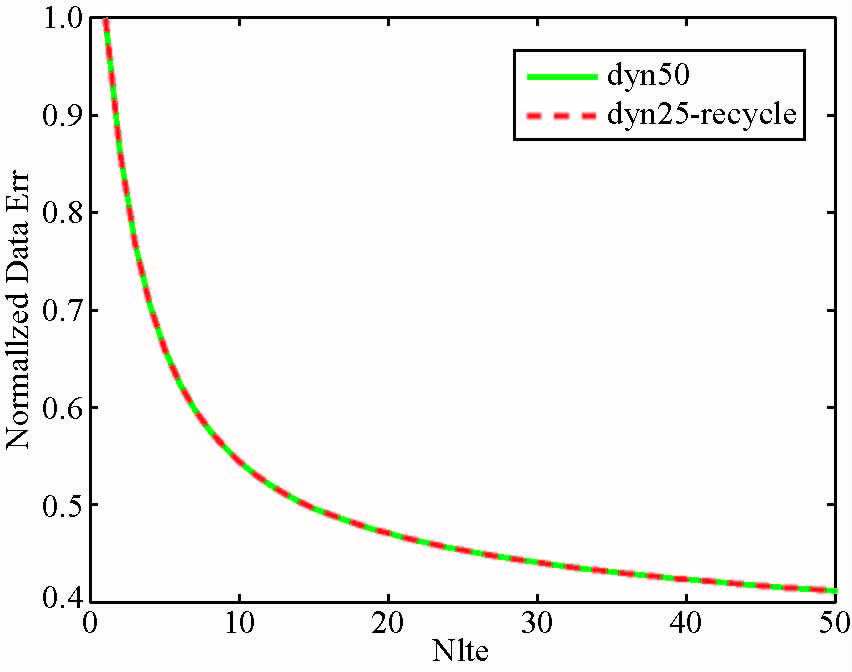
由于动态编码需要利用更多的数据,在得到的多炮数据有限的情况下如何能够得到更高精度的成像剖面,本文测试了如下方法:先使用有限次编码得到的数据进行动态编码的最小二乘迭代,然后循环的使用之前的数据继续做动态编码迭代.结果显示这种方法效果和完全动态编码方式相当.图 8是测试的这两种方式的模型收敛曲线.图 8中绿色曲线表示最小二乘迭代50次,每次都使用一次新的编码(方式Ⅱ);红色曲线表示迭代50次,前25次迭代每次使用新的编码,之后25次迭代循环使用之前的25次编码结果做迭代,这种方式所使用的多炮炮集数量及I/O只是前者的一半.从图 8中我们可以看出使用部分动态编码,再循环使用数据这种方式与完全的动态编码方式对模型的收敛效果几乎相同.
|
图 8 各种编码方式数据收敛曲线 Figure 8 The error of different encoding |
本文在实现分频编码的最小二乘裂步法偏移的基础上,从成像精度、串扰噪声压制、收敛速度及计算内存等方面比较了五种不同编码策略的差异,通过模型试算得到如下几点认识:
(1) 在成像精度方面,从图 7数据误差收敛曲线及图 3成像结果可知,动态编码的误差曲线收敛到更小的误差值,成像结果要明显优于静态编码.混合编码成像精度介于纯动态编码和纯静态编码之间.
(2) 在串扰噪声压制方面,动态编码在每一步迭代过程都对数据进行重新编码,强化了数据之间的差异性,在压制串扰噪声方面要明显要优于纯静态编码,但是动态编码需要较大的计算内存,并且对于算法实现要求更高,所以可以根据地下结构的复杂程度和拥有的计算资源合理地选择编码方式,在地下构造简单的时候,可以采用静态编码.
(3) 在迭代中使用动态编码能够帮助模型更快的收敛,各编码方式中动态编码次数对收敛精度有较大影响,使用的动态编码次数越多收敛达到的精度越高,相同动态编码次数情况下,动静结合的方式对收敛速度影响不大.使用动态编码次数与需要的多炮数据及I/O时间成正比.先使用动态编码然后用之前的数据循环迭代,这种方法不仅能够节省使用的数据量和I/O时间,在模型收敛精度上能达到和完全动态编码相当的水平.
致谢 感谢国家重点基础研究发展计划(973)子课题(2014CB239006,2011CB202402)、国家自然科学基金(41104069,41274124)、中石化课题(KJWX-2014-05)和中央高校科研业务费专项基金(R1401005A)的联合资助.| [] | Godwin J, Sava P. 2010. Blended source imaging by amplitude encoding[C].//2010 SEG Annual Meeting, Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts, 3125-3129. |
| [] | Godwin J, Sava P. 2011. A comparison of shot-encoding schemes for wave-equation migration[C].//2011 SEG Annual Meeting, Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts, 32-36. |
| [] | Huang J P, Li Z C, Kong X, et al .2013a. A study of least-squares migration imaging method for fractured-type carbonate reservoir[J]. Chinese Journal of Geophysics (in Chinese), 56 (5) : 1716–1725. DOI:10.6038/cjg20130529 |
| [] | Huang J P, Li C, Li Q Y, et al .2015. Least-squares reverse time migration with static plane-wave encoding[J]. Chinese Journal of Geophysics (in Chinese), 58 (6) : 2046–2056. DOI:10.6038/cjg20150619 |
| [] | Huang J P, Li Z C, Liu Y J, et al .2013b. The least square pre-stack depth migration on complex media[J]. Progress in Geophysics (in Chinese), 28 (6) : 2977–2983. DOI:10.6038/pg20130619 |
| [] | Huang Y S, Schuster G T .2012. Multisource least-squares migration of marine streamer and land data with frequency-division encoding[J]. Geophysical Prospecting, 60 (4) : 663–680. DOI:10.1111/gpr.2012.60.issue-4 |
| [] | Jing X, Finn C J, Dickens T A, et al. 2000. Encoding multiple shot gathers in prestack migration[C].//2000 SEG Annual Meeting, Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts, 786-789. |
| [] | Krebs J R, Anderson J E, Hinkley D, et al .2009. Fast full-wavefield seismic inversion using encoded sources[J]. Geophysics, 74 (6) : WCC177–WCC188. DOI:10.1190/1.3230502 |
| [] | Liu F Q, Hanson D W, Whitmore N D, et al .2006. Toward a unified analysis for source plane-wave migration[J]. Geophysics, 71 (4) : S129–S139. DOI:10.1190/1.2213933 |
| [] | Morton S A, Ober C C. 1998. Fastershot-record depth migrations using phase encoding[C].//68th Annual International Meeting, Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts, 1131-1134. |
| [] | Rietveld W E A, Berkhout A J .1994. Prestack depth migration by means of controlled illumination[J]. Geophysics, 59 (5) : 801–809. DOI:10.1190/1.1443638 |
| [] | Romero L A, Ghiglia D C, Ober C C, et al .2000. Phase encoding of shot records in prestack migration[J]. Geophysics, 65 (2) : 426–436. DOI:10.1190/1.1444737 |
| [] | Schuster G T, Wang X, Huang Y, et al .2011. Theory of multisource crosstalk reduction by phase-encoded statics[J]. Geophysical Journal International, 184 (3) : 1289–1303. DOI:10.1111/gji.2011.184.issue-3 |
| [] | Shen X J, Liu N C .2012. Split-step least-squares migration[J]. Progress in Geophysics (in Chinese), 27 (2) : 761–770. DOI:10.6038/j.issn.1004-2903.2012.02.044 |
| [] | Soubaras R. 2006. Modulated-shot migration[C].//2006 SEG Annual Meeting, Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts, 2430-2434 |
| [] | Tieman H J .1997. Improving plane-wave decomposition and migration[J]. Geophysics, 62 (1) : 195–205. DOI:10.1190/1.1444119 |
| [] | Wang X W, Yang W Y, Lv B, et al .2013. Grasp of the world geophysical technology development status, to promote seismic data processing and interpretation of technological progress[J]. Progress in Geophysics (in Chinese), 28 (1) : 224–239. DOI:10.6038/pg20130124 |
| [] | Wang Y F .2013. Comparison of interferometric migration and preconditioned regularizing least squares migration inversion methods in seismic imaging[J]. Chinese Journal of Geophysics (in Chinese), 56 (1) : 230–238. DOI:10.6038/cjg20130123 |
| [] | Zhou H M, Chen S C, Ren H R, et al .2014. One-way wave equation least-squares migration based on illumination compensation[J]. Chinese Journal of Geophysics (in Chinese), 57 (8) : 2644–2655. DOI:10.6038/cjg20140823 |
| [] | 黄建平, 曹晓莉, 李振春, 等.2014c. 最小二乘逆时偏移在近地表高精度成像中的应用[J]. 石油地球物理勘探, 49 (1) : 107–112. |
| [] | 黄建平, 李闯, 李庆洋, 等.2015. 一种基于平面波静态编码的最小二乘逆时偏移方法[J]. 地球物理学报, 58 (6) : 2046–2056. DOI:10.6038/cjg20150619 |
| [] | 黄建平, 李振春, 孔雪, 等.2013a. 碳酸盐岩裂缝型储层最小二乘偏移成像方法研究[J]. 地球物理学报, 56 (5) : 1716–1725. DOI:10.6038/cjg20130529 |
| [] | 黄建平, 李振春, 刘玉金, 等.2013b. 复杂介质最小二乘叠前深度偏移成像方法[J]. 地球物理学进展, 28 (6) : 2977–2983. DOI:10.6038/pg20130619 |
| [] | 黄建平, 孙陨松, 李振春, 等.2014a. 一种基于分频编码的最小二乘裂步偏移方法[J]. 石油地球物理勘探, 49 (4) : 702–707. |
| [] | 黄建平, 薛志广, 步长城, 等.2014b. 基于裂步DSR的最小二乘偏移方法[J]. 吉林大学学报(地球科学版), 44 (1) : 369–374. |
| [] | 沈雄君, 刘能超.2012. 裂步法最小二乘偏移[J]. 地球物理学进 展, 27 (2) : 761–770. DOI:10.6038/j.issn.1004-2903.2012.02.044 |
| [] | 王西文, 杨午阳, 吕彬, 等.2013. 把握世界物探技术发展现状, 促进地震资料处理、解释技术进步[J]. 地球物理学进展, 28 (1) : 224–239. DOI:10.6038/pg20130124 |
| [] | 王彦飞.2013. 地震波干涉偏移及预条件正则化最小二乘偏移成像方法对比[J]. 地球物理学报, 56 (1) : 230–238. DOI:10.6038/cjg20130123 |
| [] | 周华敏, 陈生昌, 任浩然, 等.2014. 基于照明补偿的单程波最小二乘偏移[J]. 地球物理学报, 57 (8) : 2644–2655. DOI:10.6038/cjg20140823 |
 2016, Vol. 31
2016, Vol. 31


