2. 三峡大学 土木与建筑学院, 宜昌 443002
2. China Three Gorges University College of civil engineering and architecture, Yichang 443002, China
电阻率法是以地层的导电性差异为物理基础, 通过观测人工建立的地下电流场分布规律解决地质问题的一种电法勘探分支方法(付良魁和李金铭, 1980).该方法具有确定地下异常能力强, 应用领域广的优点, 被广泛应用在环境、工程地质(吴小平和徐果明, 2000)、(Dahlin, 2001)、水文(Wilkinson et al., 2006)、考古(Griffiths et al., 1990)、矿产资源勘察等领域(白登海和于晟, 1995)、(Bauman, 2005).成像范围从微米级至千米级(Storz et al., 2000);除了在地表勘探之外该方法还可以应用到跨孔电阻率(雷旭友等et al., 2009) 、(潘纪顺等, 2010)以及水上勘探中(Loke and Lane Jr, 2004).
随着仪器硬件以及正反演技术的发展, 电阻率法采集方式从两个电极供电两个电极采集发展到现在的两个电极供电多道采集方式;电阻率反演技术从1D、2D(王兴泰等, 1995)、(Song et al., 2015)、2.5D(毛先进和鲍光淑, 1999)、(鲁杏等, 2014)发展到3D反演(吴小平和徐果明, 2000), 针对起伏地形的非结构网格的三维反演(吴小平等, 2015)以及针对特殊工程需求的多同性源阵列电阻率法(李术才等, 2015).不同的电阻率观测系统, 对地下介质的分辨率不同.常规的电阻率法通常采用2个电极供电2个电极采集的方式, 并通过滚动4极的位置以组合成不同观测方式进行测量.多通道采集主要包括超高密度(雷旭友等, 2009)、(潘纪顺, 2010)、三维E-scan(黄俊革等, 2006)、井地密集阵列数据采集(农观海等, 2013)等采集方式, 可提供更丰富的地电信息, 但以上研究都没有对井-井(Arato et al., 2014)、井-地等不同装置的有效分辨能力做出详细讨论, 在实际地质条件下无法预先设计合理的观测方式, 造成施工效率降低或无法满足勘探要求.
全通道采集为除去2个供电电极外其余电极均采集电位场数据并参与成像计算的方式, 极大的增加了观测电位数据的采集量, 例如采用32个电极, 全通道采集得到的电位值数为29760个, 温纳装置采集数据个数为155个.全通道采集数据量为温纳装置采集数据量的192倍.通过采集更多的观测数据来约束电阻率反演使反演结果更趋向于唯一性.
本文首先研究了两个电极供电的电场分布规律以及其差分求解算法, 进而求出理论模型下的观测电位值.电阻率反演中最为关键问题是系数矩阵的求取, 但因其为稠密矩阵, 显式给出会占用较大内存, 本文采用伴随矩阵方式给出(Pidlisecky et al., 2007).迭代反演采用了共轭梯度方法.在此基础上, 比较了多种装置形式及其与常规四极装置的区别以及不同观测方式下对异常的分辨能力.通过本文理论模型正反演研究, 可以更好的指导电阻率法勘探施工设计, 针对不同的工程地质需求选择合适的装置形式, 达到更好的解决实际工程地质问题的目的.
1 方法理论直流电阻率层析成像主要包括正演和反演两个部分.要解决直流反演成像问题, 必须首先实现电阻率正演, 即求解稳定电流场.其次反演问题主要涉及到目标函数选取、搜索方向及步长、迭代方法及终止条件.我们下面主要针对电阻率正反演问题进行讨论.
1.1 2.5D电阻率正演假设在水平y方向上, 地下介质的电阻率不发生变化, 因此可以用水平y方向波数域中的2.5D空间稳定电流场方程表示, 公式为
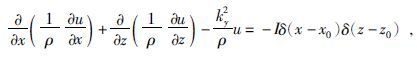
|
(1) |
式中x0、z0为供电电极位置、ρ为电阻率、I为供电电流、u为电位、Ky为y方向的波数变量(潘克家和汤井田, 2013).
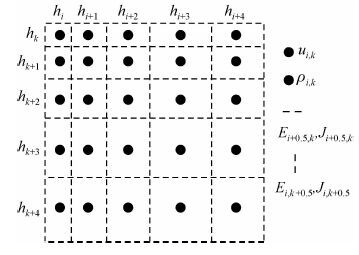
我们采用中心元胞法和正交的空间变网格, 对电位和电阻率进行空间网格离散化.其中电位和电阻率皆位于单位元胞网格的中心处, hi 和hk分别为x方向和z方向空间离散网格步长.电场强度E和电流密度J位于相邻元胞的交界中心处.
相邻元胞分界线或面处的电阻率值可通过面积加权平均计算得到.例如在z方向上第k个网格上, 其边界编号分别为i和i+1, 对应边界点处的电阻率为
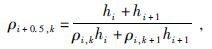
|
(2) |
在图 1所示的空间网格离散方案下, 采用二阶中心差分格式对式(1) 进行离散, 得到:
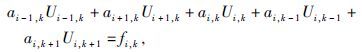
|
(3) |
|
图 1 非均匀元胞和格点用于离散电位、电阻率、电场强度和电流密度示意图.其中电位和电阻率位于元胞中心处的格点, 电场强度和电流密度位于相邻元胞的交界中心处 Figure 1 Distribution of non-uniform cells and nodes for discretizing electrical voltage, resistivity, intensity, and current density. Electrical voltage and resistivity are set at central node of each cell and electrical intensity and current density are located at the central boundary node of neighboring cells |
其中,
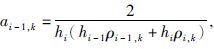
|
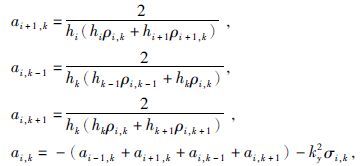
|
式(3) 可用矩阵向量的形式表达, 即:
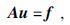
|
(4) |
其中, A为五对角带状系数矩阵, u为待求解网格节点处电位值, f为-Iδ(x-x0)δ(z-z0).在自由地表处, 采用镜像边界条件, 在其他外边界, 采用扩大模型边界区域及施加混合边界条件.同时因供电电极附近电位衰减较迅速, 为更精确求解电位场, 需把地表附近及孔中电极附近位置的网格边长尽量减小.
通过正演计算可以求取空间某一网格点处电位对地下模型网格点上所有电阻率的偏导数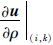
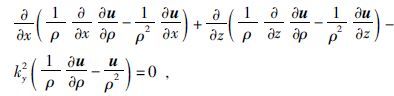
|
(5) |
设uρ=∂u/∂ρ为观测电位对地下介质模型电阻率偏导数, 进一步整理可得:
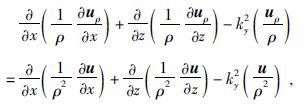
|
(6) |
式(6) 和式(1) 有着相同的方程形式, 对式(6) 进行离散化, 并写成矩阵可得:
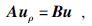
|
(7) |
其中矩阵B为稀疏的五对角矩阵, 具有与矩阵A类似的结构.通过式(7) 求逆可得:
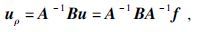
|
(8) |
电位对电导率的偏导数计算步骤是:首先通过式(4) 正演求得电位场向量u;然后将系数矩阵B和向量u相乘得到ψ=Bu, ψ为虚拟场源向量;最后再通过一次正演基于
式(8) 计算得到地下某点处电位对电阻率的偏导数uρ.
1.2 2.5D电阻率反演在利用实际采集到的电位数据值做电阻率层析成像时, 需要对反演模型进行离散化.通常根据观测电极距的大小来确定模型剖分网格间距的大小, 一般选择网格间距为电极距的一半.但实际的供电电极位置及观测数据位置不一定正好落在离散网格节点上, 因此需要将采集到的不规则数据及供电电极位置投影到规则的离散网格上.投影可以通过双线性插值并以投影矩阵Q的方式来实现(Pidlisecky et al., 2007) .公式为
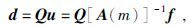
|
(9) |
其中:d为观测数据;Q为投影矩阵;u为供电在所有网格上的电位值, 每一列代表一次供电模型所有网格的电位值, 每一行为同一模型网格在不同次供电产生的电位值(矩阵U列数为供电电极对数、行数为模型总网格数);f为震源函数.
因每一次供电采集位置互不重叠, 所以投影矩阵Q为正交矩阵Q-1=QT, 则投影后的规则网格上分布的电位值数据为
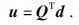
|
(10) |
考虑到模型电阻率不能为负值以及电阻率的数量级可能变化很大, 为了反演稳定, 这里采取将电阻率模型参数取电导率对数的方式可以保证电阻率不为负值, 如下式所示为
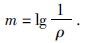
|
(11) |
此时, 在规则网格上的观测电位u对模型m的求导为
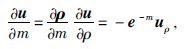
|
(12) |
其中e-m为一主对角矩阵.
定义雅克比矩阵J为观测电位数据d对模型m的求导, 有:
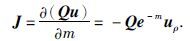
|
(13) |
电阻率成像目标函数φ(m)分为两个部分, 第一部分表示理论数据和观测数据的拟合程度, 第二部分表示反演模型与参考模型的差距.通过目标函数的最小化, 得到的电阻率模型既能较好的拟合观测数据又能靠近参考模型, 具体表示为
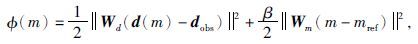
|
(14) |
其中: dobs观测数据值、d(m)模型正演数据值、m为迭代模型、mref为参考模型, Wd为观测数据加权矩阵、Wm为模型约束加权矩阵, β为观测数据拟合和模型约束之间的权重, 其权重大小采用L曲线方式选取, 一定程度同时满足数据拟合残差与模型的光滑度.
对式(14) 所表示的目标函数, 求极值, 并线性化得到:
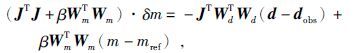
|
(15) |
其中, δm为模型修改量, 设g=JTWdTWd(d-dobs)-βWmTWm(m-mref)为目标函数的梯度, H=JTJ+βWmTWm为近似汉森矩阵.
基于式(13) 的最优化采用高斯-牛顿算法, 初始电阻率模型一般给定一个均匀模型, 采取观测视电阻率的平均值作为初始模型的电阻率值.写成线性方程组形式, 有:
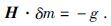
|
(16) |
当通过线性方程组求解器求出δm后, 可以用式(17) 对初始模型进行迭代, 公式为
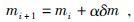
|
(17) |
其中α为模型迭代步长, 可以采用线性搜索方法决定它的大小(Armijo, 1966) , 相应搜索目标函数为
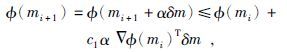
|
(18) |
其中c1为一常数, 通常取10-4.至此, 通过共轭梯度迭代, 对模型进行了更新迭代以满足反演目标函数, 对模型不停迭代修正, 直至满足终止条件.
基于式(16) 的迭代涉及到雅克比矩阵和向量的乘积, 如果先直接计算雅克比矩阵, 则计算耗时和内存需求非常巨大; 为了减少计算量, 雅克比矩阵和任一向量的乘积可以采用以下方式间接计算.例如计算数据的梯度, 公式为
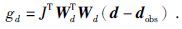
|
(19) |
可以将式(15) 、式(8) 代入式(19) , 整理得:
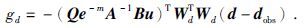
|
(20) |
在上述过程中, 总共用到了两次正演计算, 见步骤1和步骤3.非转置雅克比矩阵与任意向量乘积的方法类似于转置雅克比矩阵与任意向量的乘积.
另外, 直接计算汉森矩阵与任意向量的乘积, 计算量和存储量也非常巨大, 也可以采用间接的办法来计算.H矩阵与任意向量的乘积为
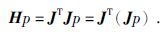
|
(21) |
所谓全通道电阻率成像, 是指在全部电极中任意取2个电极作为正负供电电极, 其余电极全部接收电位值并参与计算的一种成像方式.因此可以实现常规高密度地表采集, 同时可以实现任意观测装置方式采集.现比较其与温纳装置成像效果的不同(图 2).对于图 2所示的两个10 Ω·m低电阻异常, 异常大小为2 m×1 m, 异常之间距离15 m, 距离地面4 m.温纳装置与全通道装置反演结果都可以较好的分辨出异常所在的位置.但比较来说, 全通道电阻率成像能够更好地恢复背景电阻率值, 得到的背景电阻率更平滑均匀, 且低阻异常中心位置与形态收敛的更为准确.
|
图 2 全通道和温纳装置电阻率成像比较 (a) 电阻率模型, 在100 Ω·m的背景电阻率上存在两个10 Ω·m的低电阻异常;(b) 温纳装置视电阻率剖面;(c) 温纳装置反演结果;(d)全通道装置反演结果. Figure 2 Comparison of resistivity tomography by Wenner and full channel survey (a) Resistivity model consisting of 2 low resistivity anomalies of 10 Ω·m embedded on the background resistivity of 100 Ω·m;(b) Apparent resistivity profile with Wenner survey;(c) Inverted model by the Wenner survey;(d)Inveretd resistivity model by full channel survey. |
下面采用全通道采集方式, 分别以井-井、井-地观测方式分析不同观测装置形式下对地下介质成像的特点.
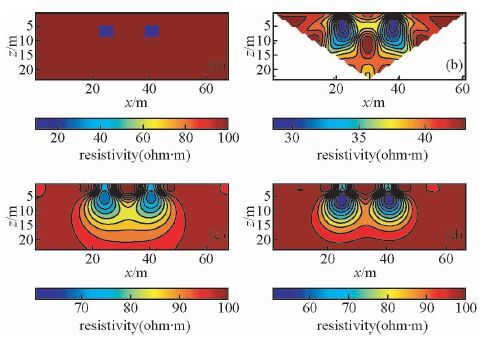
3.1 井-井电阻率层析成像在工程地质勘探有地质勘探钻孔的情况下, 两条大线可分别布置在两个钻孔中, 实现钻孔之间电阻率层析成像(图 3a).这里我们设计了井-井观测模型, 整个观测装置共包含32个电极, 两个井中分别放置16个电极, 极距1 m, 井深16 m, 井距在2~8 m之间变化.
|
图 3 井-井电阻率观测装置(a) 及理论模型(b) .共有32个电极, 每个孔中分别放置16个,电极距1 m.电阻率理论模型存在两个低阻异常体, 长宽均为1 m, 异常间距离4 m Figure 3 Configuration of cross-borehole resistivity survey(a) and resistivity model(b) . There are 32 electrodes and each borehole has 16 electrodes with an interval of 1 m. The model consists of two 1×1 m low resistivity anomalies with a separation of 4 m. |
图 3b为理论模型示意图, 模型背景电阻率值为100 Ω·m, 存在两个低阻异常:大小1 m×1 m、间距4 m、电阻率为10 Ω·m, 异常位于两个井的水平中心位置.
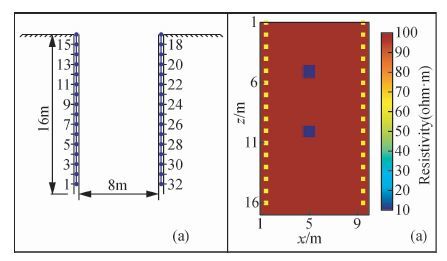
图 4为在不同孔距情况下电阻率反演的结果.从图中可以看出, 在孔距为8 m时能反演出中间的低阻条带, 但是两个异常无法完全区分;当孔距为6 m时, 能在纵向上区分两个低阻异常, 异常中间有一定的低阻过渡;孔距为4 m时两个低阻异常在纵向上分辨的较好.从8 m到4 m的跨孔观测方式都在单个低阻异常周围产生了一定的低阻异常;孔距为2 m时两个低阻异常在水平以及垂直方向上均可以区分, 单个低阻异常的成像分辨率最高.通过对不同孔距的成像结果比较, 可以看出, 跨孔电阻率对两个低阻异常的分辨率随着孔距的减小而增大, 此时异常距离电极距离也由大减小, 这也说明, 跨孔电阻率对靠近钻孔的异常的分辨率较高, 随着异常远离钻孔, 分辨率降低.
|
图 4 不同孔距下电阻率反演结果 (a) 8 m孔距;(b) 6 m孔距;(c) 4 m孔距;(d)2 m孔距.随着孔距的减小对异常的分辨也逐渐增加.从结果可以看出, 跨孔电阻率层析成像能分辨出孔距1/6~1/3大小的异常体. Figure 4 Resistivity inversion results for different distances between two holes (a) 8 m ;(b) 6 m;(c) 4 m;(d)2 m. With the decrease of distance for two holes, the model resolution gradually increases. For the cross hole resistivity tomography, it can distinguish the anomaly with the size of 1/6 to 1/3 cross-hole distance |
在实际工程勘探中, 一般情况下钻孔比较少或者钻孔之间的间距太大, 在使用跨孔电阻率勘探时对孔间地层的分辨率较低.为了解决这个问题, 我们设计了井地观测方式, 并进一步来研究井地观测方式对地下介质异常的分辨能力及分辨区域.图 5为井地观测方式示意图, 电极距1 m, 孔深 16 m, 1-16#电极在孔中布置, 17-32#电极在地表布置.
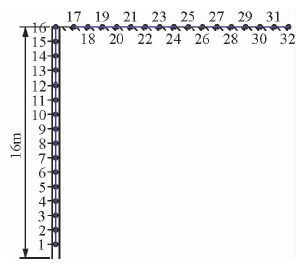
|
图 5 井地观测方式示意图, 1-16#电极在孔中布置, 17-32#电极在地表布置 Figure 5 Configuration of well-surface electrical observation system. Electrode #1-16 is in the borehole and #17-32 electrode is on the surface |
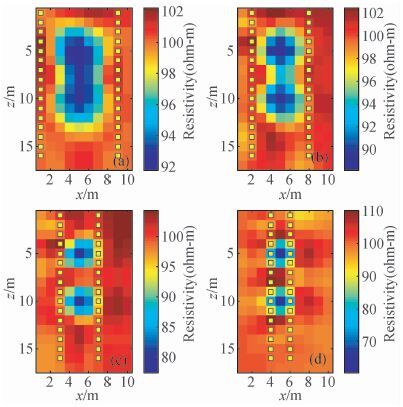
在井地装置形式下分别设计了几种不同的异常模型, 以此研究此种观测方式的分辨能力, 如图 6所示.
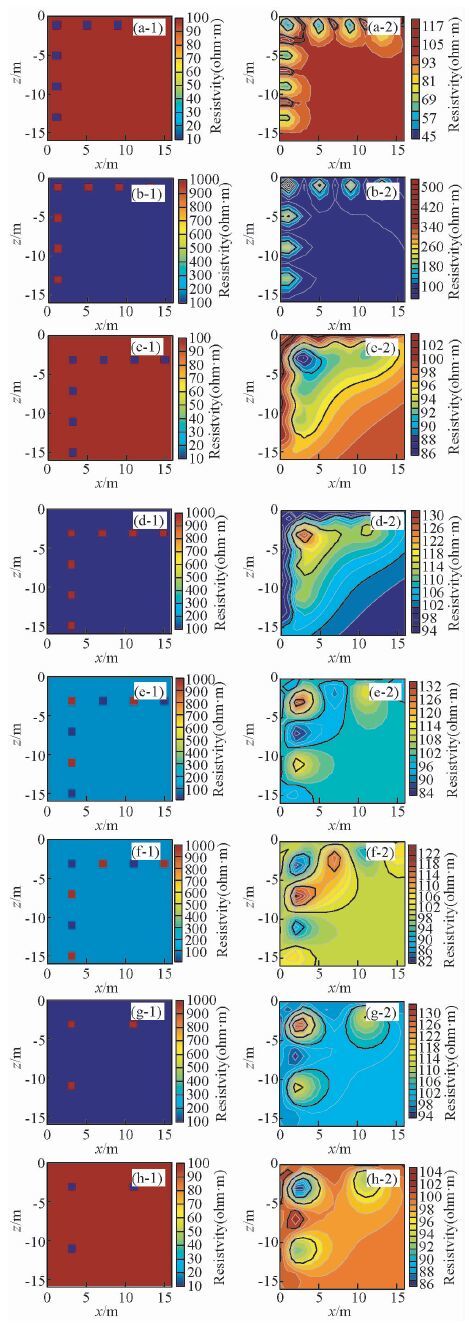
|
图 6 井-地观测系统下对不同电阻率模型的反演结果.所有模型中的电阻率异常大小为1×1 m (a) 10 Ω·m低电阻异常间距3 m, 异常距离地表电极或孔中电极距离均为2 m.(b) 1000 Ω·m高电阻异常间距3 m, 异常距离地表电极或孔中电极距离均为2 m.(c) 和(d)所示的模型与(a) 和(b) 的情况类似, 但是异常距离电极距离变大为4 m.(e)和(f)所示的模型与(d)类似但异常高低相间.(g)和(h)分别显示的模型高电阻和低电阻异常数量减少, 间距从4 m增加为8 m. Figure 6 Test of borehole-surface observation system on resolving different resistivity models. The anomaly size is 1 m by 1 m in all models (a) The separation between low resistivity anomalies of 10 Ω·mis 3 m, which are 2 m away from the surface and borehole electrodes.(b) The same as(a) but for high resistivity anomalies.(c) and(d)are the same as(a) and(b) except that anomalies are 4 m away from the electrodes. The model in(e)and(f)are similar to(d)but low and high anomalies are alternatively distributed. In(g)and h), the number of anomalies is less than the case of(e)and the anomaly separation increases from 4 m to 8 m. |
图 6a、6b为分别布置10 Ω·m低阻异常及1000 Ω·m高阻异常的模型反演.异常大小为1×1 m、相距3 m, 异常距离地表电极或孔中电极距离均为2 m.从图中可以看出, 该观测方式对高阻异常及低阻异常的成像分辨率相同.图 6c、6d与6a、6b的情况类似但是异常距离地表电极或孔中电极距离增加为4 m, 从图中可以看出, 当异常距离测线距离为4 m时, 该观测装置形式对高阻及低阻异常的分辨能量降低, 均无法较好的分辨出各自纵横向边界.图 6e、6f为按照6c、6d异常大小及位置布置, 但异常体是高阻与低阻交替布置.从图中可以看出, 当高低阻异常交替出现时, 该井地观测系统能较好的成像出异常的位置.图 6g、6h所显示的模型中异常体之间距离变为8 m.从图中可以看出, 当异常之间距离为8 m时, 该井地观测装置能较好的成像出异常的位置, 但同时也发现当异常接近地表时, 成像效果相对好于异常位于深部.此分辨率区别是因为地表为半空间, 地表附近电流强度大于孔中全空间电流强度.
通过图 6列举的几种模型的反演结果, 从中可以归纳井地观测装置电阻率勘探的几个主要特点:
1) 同样观测方式电阻率对低阻异常具有更好的分辨能力.
2) 随着异常远离测线, 反演对异常的分辨能力降低.
3) 反演对高低阻异常交替出现的情况的分辨能力高于只有高阻或只有低阻异常.
4) 孔中测线对异常分辨能力小于地表测线对异常分辨能力.此处原因为地表为半空间, 地表附近电流强度大于孔中全空间电流强度.
5) 随着异常间距增大, 反演分离异常的能力增强.
3.3 特殊工程需求观测系统研究根据井-地及井-井观测方式对地质异常分辨能力, 一般可以解决井旁或者是地面测线下伏地层的构造异常.在一些特殊工程地质问题上, 如在探测井底以下一定深度内有无地质构造异常的情况, 需要根据地质目标的需求设计合适的观测系统.例如为了探测井底以下5 m处的低阻异常, 我们设计了一个井-地观测系统, 如图 7a所示.
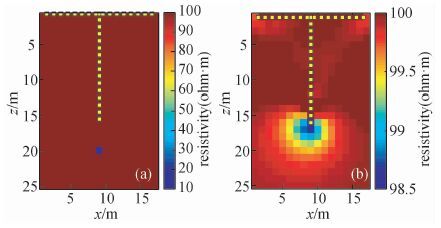
|
图 7 利用T型观测系对一个低电阻异常进行成像 Figure 7 Resistivity tomography of a low resistivity anomaly using a T-shape observation system |
从图 7b成像结果可以看出, 对于井下5 m的一个低阻异常, 利用T字形井地观测系统可以成像出井底以下的低阻异常.但是异常的纵向定位稍有偏移, 横向分辨较好, 低阻异常向浅部移动, 但此观测方式能分辨出井底以下是否存在低阻地质异常, 能部分解决井底以下一定范围的地质构造问题, 为井底以下一定深度范围内勘探提供一种新的装置思路.
4 结论与讨论本文首先研究了直流静电场理论, 根据2.5D点源在Y方向积分选择合适的空间波数, 实现正演计算.在反演迭代过程中着重研究雅克比、汉森矩阵的求取.在此基础上, 通过对比井-井、井-地等不同观测方式下异常模型的反演结果, 分析了多种装置的分辨能力, 以及设计了T型观测方式对井底异常进行探测, 取得了以下几点认识:
(1) 全通道采集数据更丰富, 默认包含了多种装置形式, 与常规四极法相比, 对同样异常具有更好的成像效果, 包括异常归位、背景值恢复.
(2) 井-井电阻率成像能分辨孔距1/6~1/3大小的异常体, 根据实际目标异常大小设计合适的孔距.
(3) 针对特殊的工程地质问题, 设计具有针对性的观测方式, 可以解决常规电法难以解决的问题.
电阻率成像具有体积效应, 同时电场线具有与地震波前面相同的自动愈合性质, 当采集电极距离供电电极较远时异常对采集位置处电位影响较小, 造成对异常难以成像.针对此问题, 一方面可以通过采集更多信息对地下介质模型约束;另一方面对特定问题设计合适的装置形式, 使目标区域在观测位置产生较大的电位异常信息;第三从覆盖角度出发, 尽量使观测位置对目标区域具有更大的方位角覆盖.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Arato A, Godio A, Sambuelli L .2014. Staggered grid inversion of cross hole 2-D resistivity tomography[J]. Journal of Applied Geophysics, 107 : 60–70. DOI:10.1016/j.jappgeo.2014.05.004 |
| [] | Bai D H, Yu S .1995. Theory and methods of resistivity tomography[J]. Progress in Geophysics (in Chinese), 10 (1) : 56–75. |
| [] | Bauman P .2005. 2-D resistivity surveying for hydrocarbons-a primer[J]. Focus, 30 (4) : 25–33. |
| [] | Dahlin T .2001. The development of DC resistivity imaging techniques[J]. Computers & Geosciences, 27 (9) : 1019–1029. |
| [] | Fu L K, Li J M. 1980. Electrical Exploration Tutorial (in Chinese)[M]. Beijing:Geological Publishing House. |
| [] | Griffiths D H, Turnbull J, Olayinka A I .1990. Two-dimensional resistivity mapping with a computer-controlled array[J]. First Break, 8 (4) : 121–129. |
| [] | Huang J G, Wang J L, Ruan B R .2006. A study on FEM modeling of anomalies of 3-D high-density E-SCAN resistivity survey[J]. Chinese Journal of Geophysics (in Chinese), 49 (4) : 1206–1214. DOI:10.3321/j.issn:0001-5733.2006.04.037 |
| [] | Lei X Y, Li Z W, Zhe J P .2009. Applications and research of the high resolution resistivity method in explovation of caves, mined regions and Karst region[J]. Progress in Geophysics (in Chinese), 24 (1) : 340–347. |
| [] | Li S C, Nie L C, Liu B, et al .2015. Advanced detection and physical model test based on multi-electrode sources array resistivity method in tunnel[J]. Chinese Journal of Geophysics (in Chinese), 58 (4) : 1434–1446. DOI:10.6038/cjg20150429 |
| [] | Loke M H, Lane Jr J W .2004. Inversion of data from electrical resistivity imaging surveys in water-covered areas[J]. Exploration Geophysics, 35 (4) : 266–271. DOI:10.1071/EG04266 |
| [] | Lu X, Zhang S Y, Cui X W. 2014. Finite element method for 2.5D resistivity forward modeling based on anomaly electric field[J]. Progress in Geophysics (in Chinese), 29(6):2718-2722, doi:10.6038/pg20140637. |
| [] | Mao X J, Bao G S. 1999. A new technique for 2.5 dimensional resistivity imagery[J]. Geophysical and Geochemical Exploration (in Chinese), 23(2):150-152. |
| [] | Nong G H, Huang J G, Gao W L, et al .2013. Theoretical model in the observation method of borehole-ground dense array 3D resistivity/polarizability[J]. Chinese Journal of Engineering Geophysics (in Chinese), 10 (1) : 29–34. |
| [] | Pan J S, Ge W Z, Zhe J P .2010. High-density electrical resistivity imaging technique of ground/boreholeto-surface/inter-well[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power (in Chinese), 31 (2) : 74–78. |
| [] | Pan K J, Tang J T. 2013. Optimized selection of discrete wavenumbers for inverse Fourier transform in 2.5D DC resistivity modeling[J]. Journal of Central South University (Science and Technology) (in Chinese), 44(7):2819-2826. |
| [] | Pidlisecky A, Haber E, Knight R .2007. RESINVM3D:A 3D resistivity inversion package[J]. Geophysics, 72 (2) : H1–H10. DOI:10.1190/1.2402499 |
| [] | Ruan B Y, Xu S Z. 1996. Rapid inversion of two-dimensional D.C. resistivity sounding curve[J]. Geophysical and Geochemical Exploration (in Chinese), 20(6):455-460. |
| [] | Song X Z, Xu Y B, Dong F .2015. A hybrid regularization method combining Tikhonov with total variation for electrical resistance tomography[J]. Flow Measurement and Instrumentation, 46 : 268–275. DOI:10.1016/j.flowmeasinst.2015.07.001 |
| [] | Storz H, Storz W, Jacobs F .2000. Electrical resistivity tomography to investigate geological structures of the earth's upper crust[J]. Geophysical Prospecting, 48 (3) : 455–471. DOI:10.1046/j.1365-2478.2000.00196.x |
| [] | Wang X T, Wang J S, Li X Q .1995. A new method for the reconstruction of two-dimensional resistivity image[J]. Geophysical and Geochemical Exploration (in Chinese), 19 (1) : 54–59. |
| [] | Wilkinson P B, Meldrum P I, Chambers J E, et al .2006. Improved strategies for the automatic selection of optimized sets of electrical resistivity tomography measurement configurations[J]. Geophysical Journal International, 167 (3) : 1119–1126. DOI:10.1111/gji.2006.167.issue-3 |
| [] | Wu X P, Liu Y, Wang W .2015. 3D resistivity inversion incorporating topography based on unstructured meshes[J]. Chinese Journal of Geophysics (in Chinese), 58 (8) : 2706–2717. DOI:10.6038/cjg20150808 |
| [] | Wu X P, Xu G M .2000. Study on 3-D resistivity inversion using conjugate gradient method[J]. Chinese Journal of Geophysics (in Chinese), 43 (3) : 420–426. DOI:10.3321/j.issn:0001-5733.2000.03.016 |
| [] | 白登海, 于晟.1995. 电阻率层析成象理论和方法[J]. 地球物理学进展, 10 (1) : 56–75. |
| [] | 付良魁, 李金铭. 1980. 电法勘探教程[M]. 北京:地质出版社. |
| [] | 黄俊革, 王家林, 阮百尧.2006. 三维高密度电阻率 E-SCAN 法有限元模拟异常特征研究[J]. 地球物理学报, 49 (4) : 1206–1214. DOI:10.3321/j.issn:0001-5733.2006.04.037 |
| [] | 雷旭友, 李正文, 折京平.2009. 超高密度电阻率法在土洞、煤窑采空区和岩溶勘探中应用研究[J]. 地球物理学进展, 24 (1) : 340–347. |
| [] | 李术才, 聂利超, 刘斌, 等.2015. 多同性源阵列电阻率法隧道超前探测方法与物理模拟试验研究[J]. 地球物理学报, 58 (4) : 1434–1446. DOI:10.6038/cjg20150429 |
| [] | 鲁杏, 张胜业, 崔先文. 2014. 基于异常场的2.5维电阻率有限元正演模拟[J]. 地球物理学进展, 29(6):2718-2722, doi:10.6038/pg20140637. |
| [] | 毛先进, 鲍光淑. 1999. 2.5维电阻率成像的新方法[J]. 物探与化探, 23(2):150-152. |
| [] | 农观海, 黄俊革, 高文立, 等.2013. 井地密集阵列三维电阻率极化率观测方法的理论模型研究[J]. 工程地球物理学报, 10 (1) : 29–34. |
| [] | 潘纪顺, 葛为中, 折京平.2010. 地面/井地/井间超高密度电阻率成像技术[J]. 华北水利水电学院学报, 31 (2) : 74–78. |
| [] | 潘克家, 汤井田. 2013. 2.5维直流电法正演中 Fourier逆变换离散波数的最优化选取[J]. 中南大学学报(自然科学版), 44(7):2819-2826. |
| [] | 阮百尧, 徐世浙.1996. 二维直流电阻率测深曲线的快速反演[J]. 物探与化探, 20 (6) : 455–460. |
| [] | 王兴泰, 王劲松, 李晓芹.1995. 二维电阻率图像重建的一种新方法[J]. 物探与化探, 19 (1) : 54–59. |
| [] | 吴小平, 刘洋, 王威.2015. 基于非结构网格的电阻率三维带地形反演[J]. 地球物理学报, 58 (8) : 2706–2717. DOI:10.6038/cjg20150808 |
| [] | 吴小平, 徐果明.2000. 利用共轭梯度法的电阻率三维反演研究[J]. 地球物理学报, 43 (3) : 420–426. DOI:10.3321/j.issn:0001-5733.2000.03.016 |
 2016, Vol. 31
2016, Vol. 31


