2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
大地电磁测深是在地表上观测具有区域性乃至全球性分布特征的天然交变电磁场来研究地下岩石的电学性质及其分布特征的一种勘探方法(陈乐寿和王光锷,1990).大地电磁测深法的基本假设是入射的电磁波为平面波,在此假设下,电磁场信号在某个频率下的电场分量和磁场分量的关系为
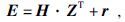
|
(1) |
式中E是水平电场向量,H是水平磁场向量,Z是2×2阻抗张量,r是随机误差.如果r符合高斯分布且E和H都是平稳信号(Wawrzyniak et al., 2013) ,则Z的最小二乘解(LS)为
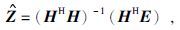
|
(2) |
上标H表示厄尔米特转置,括号内的项分别表示自功率谱和互功率谱.
大量文献表明(Gamble et al., 1979;Egbert and Booker, 1986;Chave et al., 1987;Sutarno and Vozoff, 1989;Egbert and Livelybrooks, 1996;Egbert and Livelybrooks, 1996;Larsen et al., 1996;Chave and Jones, 2012):(2) 式所需的条件通常难以满足,这使得阻抗张量Z及其方差的估计会出现较大偏差.自20个世纪末以来,Gamble等(1979) 提出用远参考道电磁阵列观测方法处理解释变量(水平磁场)中的不相关噪声.Jones和Jödicke(1984) 证实了一种相干筛选法对剔除相干性差的飞点有很好的效果.随后,众多学者先后提出了稳健的M估计方法(Egbert and Booker, 1986;Chave et al., 1987;Sutarno and Vozoff, 1989).尽管稳健M估计方法能削弱甚至剔除飞点(被解释变量中的远离大部分观测数据的观测值,一般对应于较大的回归残差),但其对杠杆点(解释变量中远离大部分观测数据的异常观测值)却非常不敏感(Chave and Thomson, 2004).紧接着多种混合方案被用于提高稳健M估计的性能,其中绝大多数属于预筛选或者预加权的稳健M估计(Egbert and Livelybrooks, 1996;Shalivahan et al., 2006).Smirnov(2003) 提出一种基于重复中值估计的高崩溃点估计方法.Chave和Thomson(2004) 利用帽子矩阵对角线的统计特征发展了一种有界影响估计方法(BI),能使估计结果免受解释变量和被解释变量中飞点的影响,并保持较高的渐近有效性.柳建新等(2003) 针对海洋的特殊环境,提出了基于相关归一Robust方法,以相关系数为参数对阻抗张量元素进行归一,根据相关系数值的变化修正Robust的权系数.严家斌和刘贵忠(2007) 提出了基于各向异性扩散Robust阻抗估计方法,模拟结果表明该方法对噪声或“飞点”具有明显的压制作用,与最小二乘法(LS)及常规的Robust估计方法相比具有更好的稳定性和精度.张刚等(2011) 将基于重复中位数估计的 Robust 算法应用于长周期大地电磁阻抗张量估算中.与传统 Robust 估计(M估计)相比,重复中位数估计求解过程不需要重设参量,并且提高了算法对时间域原始资料中噪声干扰的容限,使算法的理论崩溃值从30%提高到50%,也能得到准确的估算结果.景建恩等(2012) 研究了基于广义S变换的大地电磁测深数据Robust处理方法.汤井田等(2012,2013)比较了最小二乘估计、M回归估计、有界影响估计和重复中值估计等四种大地电磁阻抗估计方法的性能.
然而在极端情况下,BI方法也可能失效.首先,BI估计是一种广义的M估计,其崩溃点理论上是1/N(N为观测值的个数),即在特定的环境下有一个飞点就足以让估计结果远离真实值.第二,BI方法只削弱了高振幅杠杆点对估计结果的影响,而低振幅杠杆点对估计结果的影响保持不变.如果假定环境中电磁波噪声水平和仪器热噪声水平在观测过程中基本保持不变,则振幅明显低于其他观测值的杠杆点更有可能是坏数据(信噪比极低).第三,BI方法中,高振幅的杠杆点无论好坏,其影响都会被削弱.实际上,好的杠杆点可以大大地提高估计结果的统计有效性,其对估计结果的影响不应该被削弱.最后,其对杠杆点的加权是依据帽子矩阵对角线元素非自适应进行的,这种基于经验选取的加权衰减原则会因观测数据的非高斯分布而造成衰减不足或过头.
当地球近表层存在小尺度三维异常体时,会对附近测点的大地电磁阻抗张量的估计造成严重畸变,为了得到准确可靠的解释结果,在对大地电磁进行阻抗张量估计时,需要将阻抗张量中的局部畸变和区域构造响应部分分离.许多学者对阻抗张量分解进行了深入的研究.晋光文等(晋光文等,2003; 晋光文和孔祥儒,2006)对川西—藏东大地电磁资料的阻抗张量畸变进行分解并应用于剖面分析结果.蔡军涛,陈小斌,叶涛等(陈小斌等, 2008,2014; 蔡军涛等,2010; 叶涛等,2013)对大地电磁观测阻抗实施共轭阻抗变换,将观测阻抗中的电场局部畸变与区域阻抗分离.李洋等(2010) 在前人研究基础上,对Groom Bailey(GB)张量分解畸变因子和区域阻抗的求解方法进行了改进.尹曜田等(2012) 提出基于遗传算法的大地电磁阻抗张量分解方法.谢成良(2013) 研究了相位张量分析约束下的大地电磁测深阻抗张量GB分解方法.王书明等(2013) 证明相位张量不仅可以反映一般三维构造信息,亦可有效反映复杂近地表构造下三维区域构造信息,而无须假设区域构造为一维或二维.阮帅等(2015) 采用三维正演技术模拟地形和地表不均匀体的背景响应,对实测数据阻抗相位不变量进行校正.
本文介绍了一种改进的截断最小二乘估计.它不仅可以抵抗被解释变量中飞点、高低杠杆点的干扰,而且崩溃点很高,同时其估计结果还能保持较高的统计有效性,此外该方法的计算效率也很高.我们首先使用稳健马氏距离识别出极差的观测数据并将其剔除,然后通过一种广义的复数LTS估计获取阻抗张量的初始估计值,最后通过重加权最小二乘改善估计结果的统计有效性.另外,文章中还使用了一些加速技术对整个计算过程进行加速.文章内容安排如下:第一部分讨论如何检测和剔除飞点;第二部分详细地介绍复LTS估计方法并提出改进的RLS方法;第三部分给出本文所介绍的改进LTS估计的具体处理流程;第四部分通过一系列MT野外数据试算,把我们提出的改进LTS估计与BI估计以及稳健M估计作了比较,对比结果体现出改进LTS估计的优势;最后一部分指出改进LST估计方法仍然具有一些不足之处并提出下一步改进的建议.
1 飞点的检测和剔除稳健性M估计方法和Chave和Thomson(2004) 提出的BI估计方法实质上都是基于普通最小二乘(OLS)的迭代重加权最小二乘方法,它们对飞点检测的方法都是基于残差的.OLS估计的前提假设是残差严格满足高斯分布且各变量都是平稳的,其估计结果对这一模型假设极其敏感,因此那些远离大多数观测数据的异常观测值会引起OLS估计结果严重畸变.有时OLS估计结果会受到飞点的影响而出现严重畸变,以至于在极端情况下飞点的残差比一些好的观测数据的残差还小.此时,这些飞点会被OLS估计出来的初值所隐藏,这种数量很少但是品质极差的观测数据正是该方法可能会失效的原因.在使用该估计法之前必须先识别出这种品质极差的观测数据并将其剔除.
在简单的单变量回归分析中,我们常使用二维散点图来识别品质极差的观测数据.但当变量数目超过两个,我们就很难从视觉上直观地将飞点识别出来.特别是在MT阻抗张量估计中,所有的变量都是复数,这种直观的方法几乎不具备可行性,我们需要使用高级的统计工具.
实际上,大部分品质极差的观测值都有一个共同的特征,那就是它们远离大部分数据所表现出来的分布趋势.因此,可以通过某观测点远离大部分数据的程度来判断其是否为飞点.在统计学中,这种远离程度可用马氏距离衡量.马氏距离是由Mahalanobis(1936) 提出的,它表示某样本距离总体统计中心的距离.其定义为
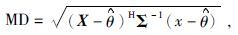
|
(3) |
式中X=[Ex Hx Hy],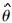
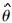
在统计学中,有多种方法可用于估计高维观测数据的统计中心(可用总体期望表征)和离散度(可用总体协方差矩阵Hier表征).其中最小协方差行列式(MCD)和最小体积椭圆方法(MVE)是实际中使用最多的两种方法.MVE方法从n个样本中寻找出h个样本,使得这h个样本张成的高维椭圆体积最小;MCD则是从n个样本中挑选h个样本(这h个样本构成一个样本子集),使得该样本子集的样本协方差矩阵的行列式最小.其中n/2 <h≤n.两种方法的崩溃点都(n-h)/n是,但MCD的高统计有效性和快收敛速度使得它比MVE方法更适合于MT阻抗张量的估计.
本文中我们利用Rousseeuw and Van Driessen(1999) 提出的快速算法来计算统计中心和离散度的MCD估计量,也就是稳健的总体期望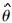
首先,必须对各变量进行标准化处理.在假设时间序列的概率分布函数是高斯型的情况下,傅立叶变换的线性性质使得傅立叶系数的复分布是圆对称的且是复共轭不相关的(Adali et al., 2011),即傅立叶系数变量的实部和虚部相互独立并且有相同的方差.因此,可以用一个实因子对复变量进行标准化.标准化是一种如下的线性映射,公式为
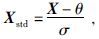
|
(4) |
式中θ和σ分别是总体期望和标准差.实际计算中,θ可以用样本中值代替.MED为
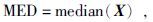
|
(5) |
标准差σ可由下式进行估计(推导过程见附录),公式为
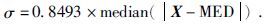
|
(6) |
考虑到实部和虚部的联合概率分布函数比传统的复概率分布函数能给出更多信息,我们把复变量分解成实部和虚部(Schreier and Scharf, 2010) .分解过程可由下列矩阵运算表示,公式为
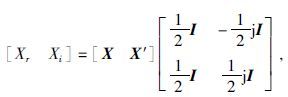
|
(7) |
式中Xr,Xi,X′分别是X的实部,虚部和共轭.I是和X同维度的单位矩阵.
然后,用[Xr Xi]计算出稳健的马氏距离,并将MD偏大的观测值剔除.剔除时,MD的截断值一般设置为自由度为2p的卡方分布的上0.05分位点.
我们通过对频率为317 Hz的MT野外数据处理,详细地介绍用稳健马氏距离检测飞点的过程.首先对该数据作传统的OLS估计并获得标准化残差;然后用MCD方法估计出总体的期望和协方差矩阵并计算稳健的马氏距离;之后取稳健马氏距离实际概率分布的上0.05分位点作为截断值,剔除分位点以上的飞点;最后再对筛选过的数据作传统OLS估计并获得相应的标准化残差.如图 1所示,图 1a是原始资料的标准化残差随稳健马氏距离变化的散点图.横向和纵向的红色实线分别对应标准LS残差和稳健马氏距离的实际概率分布的上0.05分位点.无论是用稳健的马氏距离还是用残差衡量,位于左下区域的观测值均被认为是好的观测值.而位于右上区域的观测值无论以哪种标准衡量都是飞点.位于右下区域的观测值从马氏距离的角度衡量是飞点,但是从标准化残差的角度来看是好的观测值.由图 1我们可以直观地对比稳健马氏距离和标准LS残差检测飞点的能力.有很多观测值从残差的角度会被当作是好的数据,而从稳健的马氏距离来看是飞点.也就是说稳健的马氏距离对飞点更加敏感.换句话说,如果只考虑残差很多飞点会被错误地当作是好的观测值.因此,稳健马氏距离比标准LS残差检测飞点的能力更强.
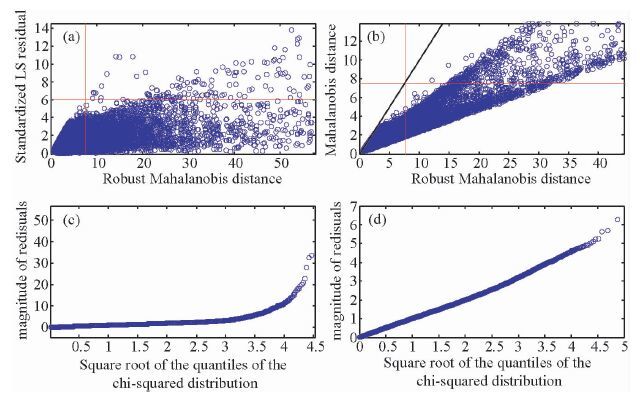
|
图 1 频率为317 Hz的野外大地电磁数据,共101500个观测值.a和b中的红色实线对应各统计量实际概率分布的上0.05分位点.所有的统计量均作了归一化 (a)对比稳健马氏距离和标准OLS残差和的散点图;(b)对比传统马氏距离和稳健马氏距离的散点图;(c)原始数据OLS估计残差的分位数-分位数图;(d)用稳健马氏距离识别并剔除飞点后的OLS估计残差的分位数-分位数图. Figure 1 The 317 Hz data taken from a field MT data, 101500 observations totally. The red line in A and B are cutoff values of the corresponding measurements for 5% outliers. All the measurements are normalized to unit 1 (a)The scatter plot of comparison of standardized OLS residuals with robust Mhalanobis distance;(b)The scatter plot of comparison of classical Mahalanobis distance with robust Mahalanobis distance;(c)The Quantile-Quantile plot for residuals of the OLS estimate of the Original data;(d)The Quantile-Quantile plot for residuals of the OLS estimate after removing the outliers detected by robust Mahalanobis distance. |
在图 1b中Y轴代表传统马氏距离,是通过基于总体期望和协方差的传统范数计算得到的.其中左下角的飞点由于受到了掩蔽作用,传统马氏距离无法将其检测出来,稳健马氏距离却可以识别出这些飞点,从而说明了稳健马氏距离比传统马氏距离对飞点更加敏感.在观测数据满足高斯分布的条件下,标准化残差的范数服从自由度为2的卡方分布(Chave et al., 1987).因此,残差与分位数(符合卡方分布)平方根的分位数-分位数(q-q)图可以用来检测数据是否符合高斯分布.
图 1c是原始数据OLS估计残差的分位数-分位数图,可以看到q-q图有明显地拽尾,可能是由大量的飞点引起.图 1d是用稳健马氏距离识别并剔除飞点后的OLS估计残差的分位数-分位数图.图 1c和图 1d证实了稳健的马氏距离是一种有效的飞点识别工具.
2 LTS估计和RLS改进 2.1 传统LTS估计本文介绍的复LTS估计方法源自统计学中Rousseeuw(1984) 提出的传统LTS估计方法.为了更加清楚地介绍传统LTS估计,我们将模型(1) 表示成标量的形式,公式为
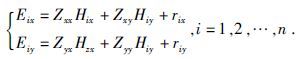
|
(8) |
Zx=[Zxx Zxy]T的最小截断二乘估计(LTS)为
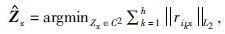
|
(9) |
式中||rikx||L2表示||ri1x||L2 <||ri2x||L2<…<||rikx||L2<… <||rinx||L2
中第k个残差的L2范数,h是截断常数其值满足
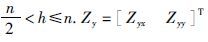
忽略公式(9) 的求和项是L2范数的这一事实,公式(9) 可以看作是Rousseeuw(1984) 表达式的复数广义形式,能够适用于高维回归变量问题.回归模型(公式(9) )给出了该模型h个观测值在L2范数下的残差和的极小值.这意味着其余n-h个观测值在L2范数下的残差和为极大值,并且不包含关于真实模型的有效信息.也就是说,如果我们能够确定h个观测值,其在L2范数下残差和取极小值,则用这h个观测值就足够确定真实的模型.如果假定飞点的总数小于n-h,则将总是存在符合以上描述的h个观测值,因此LTS估计方法既可以不受电场中飞点干扰又能抵抗磁场中杠杆点干扰.
传统LTS估计方法扩展到复数域中具有下列性质(Rousseeuw and Leroy, 1987;Víšek, 2006a,b,c):
(1) LTS估计是回归、线性和仿射同变的,这使得资料的预处理变得容易.如果对电场和磁场采用同样的处理,那么在时间域的滤波和白噪不会对估计结果造成影响,并且傅立叶系数可以在频率域作标准化处理;
(2) LTS方法的崩溃点h=[n/2]+[(p+1) /2],其值等于([(n-p)]/2) /n,式中p是解释变量的个数,在我们的例子中p等于2.所以只要有多于h个未被干扰的观测值,MT阻抗张量就仍然是有界的;
(3) 该方法的收敛速度为n-1/2,比最小中值平方方法(LMS)要快,这是其能够应用于MT大数据量分析的基础;
(4) LTS估计方法具有一致性和渐进正态性,其获得的MT阻抗张量估计值是值得信赖的.
2.2 LTS的计算
从公式(9) 可知如果h=n,则LTS估计和复数普通最小二乘(OLS)估计是一致的,而且对特定h个观测值的复数OLS估计的形式等价于对全部观测值的LTS估计的形式.因此可以通过复数OLS估计获得LTS估计的结果.我们对所有可能的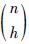
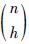
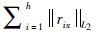
1.给定估计量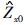
2.计算残差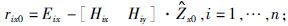
3.将残差的范数按升序排序
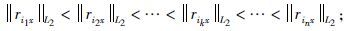
|
4.取h个观测值作为子样本={i1,i2,…,ih};
5.计算基于子样本的OLS估计值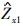
6.如果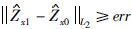
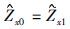
如果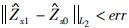
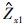
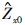
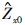
通过以上流程获得的估计量可能是公式(9) 的极小值,但是要想得到全部观测值的最小值的最优近似,必须从全部n个观测值中随机抽取大量的秩为2的子样本,对每一个子样本得到一个阻抗张量的初始估计值,重复以上流程得到一系列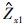
尽管LTS估计有很多优点,但是其有效性并不高,我们在复LTS估计之后再作重加权最小二乘(RLS)以提高LTS估计的有效性.RLS实质是给残差加上适当的权重系数从而使残差的平方和最小,经过重加权改进过的截断最小二乘估计可以大大提高估计的有效性.重加权最小二乘用数学语言表示为
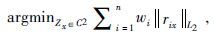
|
(10) |
权重系数取值
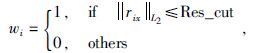
|
(11) |
Res_cut是判定残差是否为飞点的截断值.
||rix||L2服从自由度为2的卡方分布.因此Res_cut可以取卡方分布的上0.05分位点.当残差的L2范数小于截断值时,权重系数取1,该数据点良好;否则,权重系数取0,该数据为飞点.不同的残差加上适当的权重系数,从而使得最后残差的平方和最小.
3 处理流程在对MT阻抗张量作改进LTS估计前,必须先在时间域内对时间序列作预处理.用Smirnov(2003) 提出的AR滤波器移除脉冲、阶跃和饱和的记录,然后用带阻滤波器滤掉工频干扰,最后对时间序列用一阶差分滤波器作预白化处理.利用基于改进各向异性扩散方程的MT时间序列噪声抑制方法(Zhang et al., 2015)可以有效地去除时间序列中的尖峰干扰.
为了得到精确的估计量,原始时间序列被分成了相互重叠的几个部分,高频部分的重叠程度为25%,低频部分为75%,然后再对时间序列作抽取、加窗和傅立叶变换.
假设我们在频率为f时得到了傅立叶系数Nf,即叠加次数是Nf,然后在谱估计和改进LTS估计之前对叠加点作相干性排序.Jones and Jödicke(1984) 提出的“逐点删除”技术虽然有效但计算量很大,尤其是在叠加次数很多且信号的信噪比很低时需要花费大量的计算.我们采用“组删除”技术改进了一种方法,根据叠加点在时间上的相邻程度,把叠加点分成小组,每组的叠加点数量在三到五个之间.由于MT中的电磁噪声是随时间变化的,我们需要计算每个组的局部
相干因子和所有叠加点的全局相干因子,然后删除相干性最差的组,直到剩余叠加点的全局相干因子达到了预设的阈值.该技术比Jones提出的技术要快很多并被证明在消除严重噪化的观测值方面是有效的.实验表明“组删除”技术可以通过只删除35%的观测值就能把全局相干因子从0.2提高到0.75.计算相干因子的公式为
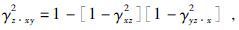
|
(12a) |
式中
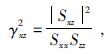
|
(12b) |
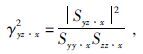
|
(12c) |
分别是全局相干因子和局部相干因子.其中
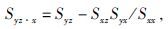
|
(13) |
Sxz、Syz、Sxz、Syx是互谱密度,Sxx、Szz是自谱密度,z代表Ex,x代表Hx,y代表Hy.
在相干性排序后MT的叠加次数通常多达几百万次,因此在作阻抗张量估计之前必须先把叠加点分成若干个子集,子集的个数根据叠加点的数量确定(一般在1~20之间),然后对每个子集按照下列流程处理:
1.用传统方法作谱估计;
2.标准化;
3.把复数分解为实数;
4.在实数域内作稳健统计中心 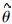
5.计算每个观测值的稳健马氏距离;
6.基于稳健马氏距离剔除飞点;
7.在复数域内对MT阻抗张量作复LTS估计;
8.对估计量作RLS改进;
9.标准化校正.
假设我们从每个子集中得到了一个估计量,则最终的估计量是所有估计量的稳健平均值,其定义如下:
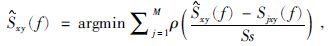
|
(14a) |
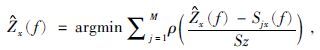
|
(14b) |
式中M是子集的总数,Sjxy(f)是谱(互谱和自谱)估计量,Zjx(f)是从第j个子集中获得的阻抗,ρ(u)是Huber范数,其值为
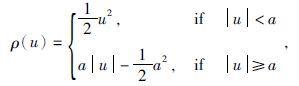
|
(15) |
式中Ss和Sz是比例系数,参数a是飞点的权重系数开始减小的标志,相关细节见(Chave et al., 1987).优化问题(14) 的解决方案已在大量的文献中提到,在此不再赘述.
4 改进LTS估计的性能例一的MT数据是在中国河北省西北部城市张家口获得的.微弱的环境电磁噪声和简单的地质构造使之成为电磁勘探的理想场地.采集数据的接收机由中国科学院地质与地球物理研究所设计,磁感应器件由中国船舶重工集团公司722研究所生产.采样率有三种,高频信号用2.4 kHz,中频信号用150 kHz,低频信号用15 Hz.接收机交替使用2.4 kHz和150 kHz的采样率.在时间域预处理(第4部分)中对每个时间序列作傅立叶变换,然后通过相干筛选剔除低品质的观测值并分成若干个子集.对每一个子集用稳健马氏距离剔除飞点,截断值选用自由度为6的卡方分布的上0.025分位点,然后作广义LTS估计,之后再作RLS估计以改进阻抗张量的有效性,最后得到阻抗张量的稳健平均值.
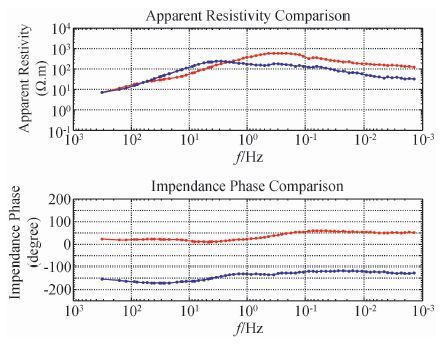
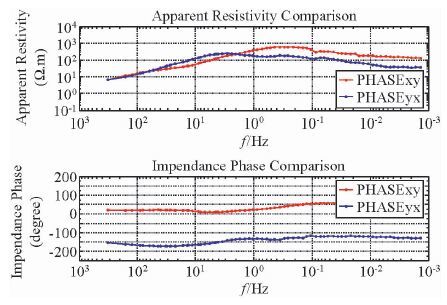
图 2到4分别是对张家口的MT数据用改进LTS估计、有界影响估计和稳健M估计得到的视电阻率和相位.LTS估计和有界影响估计两者都表现出了在宽至317 Hz~0.001 Hz的频带范围内剔除飞点的能力,但是图 2在某些细节方面比图 3更加光滑,这是因为改进LTS估计趋向于将它的估计值置于数据的中心区域且其飞点的权重值为零,而有界影响估计虽然权重在衰减但是不严格为零,因此飞点对有界估计的影响要大于改进LTS估计.稳健M估计没有抵抗杠杆点的能力,即低频中的单个杠杆点就会破坏估计值.而在高频时叠加次数相当大,比如317 Hz时叠加次数多达20000次,飞点和杠杆点的影响会因良好观测值的平均作用而减弱,因而高频时三种方法的效果都很好.
|
图 2 张家口MT数据的改进LTS估计 Figure 2 Improved LTS estimate of Chang-chia-k’ou’s MT field data |
|
图 3 张家口MT数据的有界影响估计 Figure 3 Bounded influence estimate of Chang-chia-k’ou’s MT field data |

|
图 4 张家口MT数据的稳健M估计 Figure 4 Robust M estimate of Chang-chia-k’ou’s MT field data |
例二中的MT数据是在位于北京南面50 km的城市固安获得的.蓬勃的工业、铁路和高速公路网络带来全频带的噪声,使得MT信号的信噪比要比第一个例子低很多.数据的处理过程和第一个例子相似.
图 5至图 7展示了用三种方法计算出固安MT野外数据的视电阻率和阻抗相位.和第一个例子类似,因为改进的LTS方法对飞点的剔除能力更强,所以图 5中的曲线更加光滑.稳健M估计在高频段受到严重的工频干扰,而且在频率为10 Hz附近的相位畸变严重.有界影响估计和稳健M估计由于叠加次数少因而在低频段起伏剧烈.
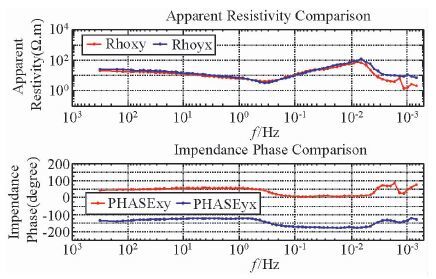
|
图 5 固安MT数据的改进LTS估计 Figure 5 Improved LTS estimate of Gu-An’s MT field data |
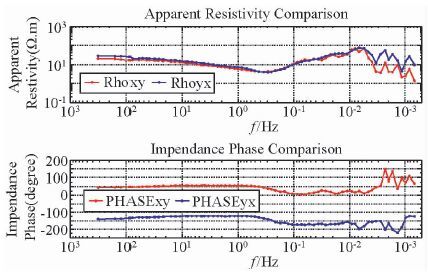
|
图 6 固安MT数据的有界影响估计 Figure 6 Bounded influence estimate of Gu-An’s MT field data |
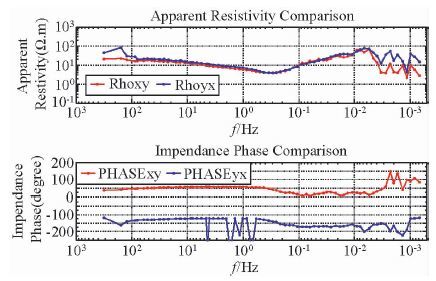
|
图 7 固安MT野外数据的稳健M估计 Figure 7 Robust M estimate of Gu-An’s MT field data |
图 8中比较了不同数量的观测值下三种方法的CPU运行时间,实验是在Intel Core(TM)2 Duo E7500 @2.93 GHz CPU平台上进行.稳健M估计和有界影响估计都是基于迭代算法,因此他们CPU运行时间表现出周期性的波动.改进LTS估计表现为CPU时间和观测值数量之间具有稳定的线性关系.在观测数量很少时,稳健M估计和有界影响估计的CPU时间相对很小并随观测值数量增加线性增长.当观测值个数多于2000时,两种方法的CPU时间急剧增长,特别的是有界影响估计用的计算量最多.不管观测值的数量多少,稳健的M方法总是三种方法中CPU用时较少的算法.我们提出的改进LTS估计显示出在数据量很大时所受影响有限的优势,考虑到本文所用的两个实例仅在317 Hz频率下每24小时的观测值数量就有150000个之多,长周期MT勘探的数据处理需要非常巨大的计算量,因而在这种情况下极力推荐我们的算法.
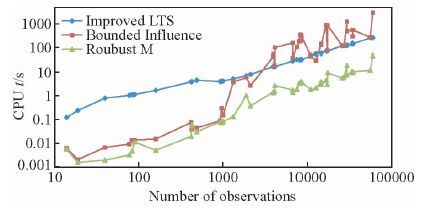
|
图 8 不同数量观测值下三种方法的CPU时间曲线 Figure 8 Comparison of CPU times between three methods under different amount of observations |
本文介绍改进的截断最小二乘估计(LTS)方法.我们首先通过稳健的马氏距离来识别并剔除品质极差的观测数据,然后通过广义的复数截断最小二乘估计出阻抗张量初始值,最后用重加权最小二乘方法(RLS)来改进阻抗张量的统计有效性.野外MT测量数据的试验结果表明,改进的截断最小二乘估计是获得MT阻抗张量的有效方法;它不仅可以抵抗被解释变量中飞点、高低杠杆点的干扰,而且崩溃点很高,同时其估计结果还能保持较高的统计有效性.虽然改进LTS估计的被解释变量和解释变量对飞点都有很强的抵抗性,而且对大数据的计算效率相对较高,但是仍有一些缺点需要克服.首先,同有界影响估计类似,由于稳健马氏距离只提供有限的有效信息,因而LTS估计中的杠杆点不论好坏其权重都在减小.第二,虽然用RLS作了改进,但是统计有效性仍然很低,因为LTS估计方法本质即是如此.
5.2我们为了改进这个问题做了很多努力.首先,利用“两步估计”技术(Chave and Thomson, 2004)把我们的方法推广到有远参考道的观测方式,该技术现在被广泛应用于消除磁场的噪声,但是这种推广会使计算量加倍,因此需要找到精度和计算效率之间的平衡点.除此之外,可以用一步M估计替换RLS以提高统计有效性.为了保持LTS的高崩溃点和M估计的高统计有效性,我们更推荐第二种改进.尽管我们的方法具有高崩溃点,但是为了准确估计高分辨率的频谱并剔除飞点,仍然需要对时间序列进行精心地预处理.只有仔细地完成从数据采集到稳健求平均过程的每一个步骤,我们的方法才会提供一个可信的估计值.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Adali T, Schreier P J, Scharf L L .2011. Complex-valued signal processing:The proper way to deal with impropriety[J]. IEEE Transactions on Signal Processing, 59 (11) : 5101–5125. DOI:10.1109/TSP.2011.2162954 |
| [] | Cai J T, Chen X B .2010. Refined techniques for data processing and two-dimensional inversion in magnetotelluric Ⅱ:Which data polarization mode should be used in 2D inversion[J]. Chinese Journal of Geophysics (in Chinese), 53 (11) : 2703–2714. DOI:10.3969/j.issn.0001-5733.2010.11.018 |
| [] | Cai J T, Chen X B, Zhao G Z .2010. Refined techniques for data processing and two-dimensional inversion in magnetotelluric I:Tensor decomposition and dimensionality analysis[J]. Chinese Journal of Geophysics (in Chinese), 53 (10) : 2516–2526. DOI:10.3969/j.issn.0001-5733.2010.10.025 |
| [] | Chave A D, Jones A G .2012. The Magnetotelluric Method:Theory and Practice[M]. Cambridge: Cambridge University Press . |
| [] | Chave A D, Thomson D J .2004. Bounded influence magnetotelluric response function estimation[J]. Geophysical Journal International, 157 (3) : 988–1006. DOI:10.1111/gji.2004.157.issue-3 |
| [] | Chave A D, Thomson D J, Ander M E .1987. On the robust estimation of power spectra, coherences, and transfer functions[J]. Journal of Geophysical Research, 92 (B1) : 633–648. DOI:10.1029/JB092iB01p00633 |
| [] | Chen X B, Cai J T, Wang L F, et al .2014. Refined techniques for magnetotelluric data processing and two-dimensional inversion (IV):Statistical image method based on multi-site, multi-frequency tensor decomposition[J]. Chinese Journal Geophysics (in Chinese), 57 (6) : 1946–1957. DOI:10.6038/cjg20140625 |
| [] | Chen X B, Zhao G Z, Tang J, et al .2008. Impedance tensor of Network-MT and the influencing factors[J]. Chinese Journal of Geophysics (in Chinese), 51 (1) : 273–279. DOI:10.3321/j.issn:0001-5733.2008.01.034 |
| [] | Egbert G D, Booker J R .1986. Robust estimation of geomagnetic transfer functions[J]. Geophysical Journal International, 87 (1) : 173–194. DOI:10.1111/gji.1986.87.issue-1 |
| [] | Egbert G D, Livelybrooks D W .1996. Single station magnetotelluric impedance estimation:Coherence weighting and the regression M-estimate[J]. Geophysics, 61 (4) : 964–970. DOI:10.1190/1.1444045 |
| [] | Gamble T D, Goubau W M, Clarke J .1979. Magnetotellurics with a remote magnetic reference[J]. Geophysics, 44 (1) : 53–68. DOI:10.1190/1.1440923 |
| [] | Hawkins D M, Olive D J .1999. Improved feasible solution algorithms for high breakdown estimation[J]. Computational Statistics & Data Analysis, 30 (1) : 1–11. |
| [] | Jin G W, Sun J, Bai D H, et al .2003. Impedance tensor distortion decomposition of magnetotelluric data from west Sichuan-east Xizang[J]. Chinese Journal of Geophysics (in Chinese), 46 (4) : 547–552. DOI:10.3321/j.issn:0001-5733.2003.04.018 |
| [] | Jing J E, Wei W B, Chen H Y, et al .2012. Magnetotelluric sounding data processing based on generalized S transformation[J]. Chinese Journal of Geophysics (in Chinese), 55 (12) : 4015–4022. DOI:10.6038/j.issn.0001-5733.2012.12.013 |
| [] | Jones A G, Jödicke H. 1984. Magnetotelluric transfer function estimation improvement by a coherence-based rejection technique[C].//Paper Presented at the 1984 SEG Annual Meeting. Expanded Abstracts, 51-55. |
| [] | Larsen J C, Mackie R L, Manzella A, et al .1996. Robust smooth magnetotelluric transfer functions[J]. Geophysical Journal International, 124 (3) : 801–819. DOI:10.1111/gji.1996.124.issue-3 |
| [] | Li Y, Yu P, Zhang L L, et al .2010. Distortion decomposition of magnetotelluric impedance tensor based on hybrid optimization algorithm[J]. Chinese Journal of Geophysics (in Chinese), 53 (8) : 1924–1930. DOI:10.3969/j.issn.0001-5733.2010.08.018 |
| [] | Liu J X, Yan J B, He J S, et al .2003. Robust estimation method of sea magnetotelluric impedance based on correlative coefficient[J]. Chinese Journal of Geophysics (in Chinese), 46 (2) : 241–245. DOI:10.3321/j.issn:0001-5733.2003.02.018 |
| [] | Mahalanobis P C. 1936. On the generalized distance in statistics[C].//Proceedings of the National Institute of Science. Calcutta, 2:49-55. |
| [] | Rousseeuw P J .1984. Least median of squares regression[J]. Journal of the American Statistical Association, 79 (388) : 871–880. DOI:10.1080/01621459.1984.10477105 |
| [] | Rousseeuw P J, Leroy A M .1987. Robust Regression and Outlier Detection:Wiley Series in Probability and Mathematical Statistics[M]. New York: Wiley : 1 . |
| [] | Rousseeuw P J, Van Driessen K .2006. Computing LTS regression for large data sets[J]. Data Mining and Knowledge Discovery, 12 (1) : 29–45. DOI:10.1007/s10618-005-0024-4 |
| [] | Rousseeuw P J, Van Driessen K .1999. A fast algorithm for the minimum covariance determinant estimator[J]. Technometrics, 41 (3) : 212–223. DOI:10.1080/00401706.1999.10485670 |
| [] | Rousseeuw P J, Van Zomeren B C .1990. Unmasking multivariate outliers and leverage points[J]. Journal of the American Statistical Association, 85 (411) : 633–639. DOI:10.1080/01621459.1990.10474920 |
| [] | Ruan S, Zhang J, Sun Y B, et al .2015. AMT impedance phase invariant correction based on 3D MT modeling technology[J]. Chinese Journal of Geophysics (in Chinese), 58 (2) : 685–696. DOI:10.6038/cjg20150229 |
| [] | Schreier P J, Scharf L L. 2010. Statistical Signal Processing of Complex-valued Data:The Theory of Improper and Noncircular Signals[M]. Cambridge:Cambridge University Press. |
| [] | Shalivahan, Sinharay R K, Bhattacharya B B .2006. Remote reference magnetotelluric impedance estimation of wideband data using hybrid algorithm[J]. Journal of Geophysical Research, 111 (B11) : B11103. |
| [] | Smirnov M Y .2003. Magnetotelluric data processing with a robust statistical procedure having a high breakdown point[J]. Geophysical Journal International, 152 (1) : 1–7. DOI:10.1046/j.1365-246X.2003.01733.x |
| [] | Sutarno D, Vozoff K .1989. Robust M-estimation of magnetotelluric impedance tensors[J]. Exploration Geophysics, 20 (3) : 383–398. DOI:10.1071/EG989383 |
| [] | Tang J T, Li J, Xiao X, et al .2012. Mathematical morphology filtering and noise suppression of magnetotelluric sounding data[J]. Chinese Journal of Geophysics (in Chinese), 55 (5) : 1784–1793. DOI:10.6038/j.issn.0001-5733.2012.05.036 |
| [] | Víšek J á. 2006a. The least trimmed squares. Part Ⅰ:Consistency[J]. Kybernetika, 42(1):1-36. |
| [] | Víšek J á. 2006b. The least trimmed squares. Part Ⅱ:√n-Consistency[J]. Kybernetika, 42(2):181-202. |
| [] | Víšek J á. 2006c. The least trimmed squares. Part Ⅲ:Asymptotic normality[J]. Kybernetika, 42(2):203-224. |
| [] | Wang S M, Li D S, Hu H .2013. Numerical modeling of magnetotelluric phase tensor in the context of 3D/3D formation[J]. Chinese Journal of Geophysics (in Chinese), 56 (5) : 1745–1752. DOI:10.6038/cjg20130532 |
| [] | Wawrzyniak P, Sailhac P, Marquis G .2013. Robust error on magnetotelluric impedance estimates[J]. Geophysical Prospecting, 61 (S1) : 533–546. |
| [] | Xie C L, Wei W B, Jin S, et al .2013. Study of magnetotelluric impedance tensor decomposition under the constraint of analysis of phase tensor[J]. Progress in Geophysics (in Chinese), 28 (3) : 1208–1218. DOI:10.6038/pg20130312 |
| [] | Yan J B, Liu G Z .2007. Robust Impedance estimation method based on anisotropic diffusion[J]. Progress in Geophysics (in Chinese), 22 (5) : 1403–1407. DOI:10.3969/j.issn.1004-2903.2007.05.010 |
| [] | Ye T, Chen X B, Yan L J .2013. Refined techniques for data processing and two-dimensional inversion in magnetotelluric (Ⅲ):using the Impressing Method to construct starting model of 2D magnetotelluric inversion[J]. Chinese Journal of Geophysics (in Chinese), 56 (10) : 3596–3606. DOI:10.6038/cjg20131034 |
| [] | Yin Y T, Wei W B, Ye G F, et al .2012. An improved GB decomposition method based on genetic algorithm[J]. Chinese Journal of Geophysics (in Chinese), 55 (2) : 671–682. DOI:10.6038/j.issn.0001-5733.2012.02.031 |
| [] | Zhang L L, Hao T Y, Xiao Q B, et al .2015. Magnetotelluric investigation of the geothermal anomaly in Hailin, Mudanjiang, northeastern China[J]. Journal of Applied Geophysics, 118 : 47–65. DOI:10.1016/j.jappgeo.2015.04.006 |
| [] | 蔡军涛, 陈小斌.2010. 大地电磁资料精细处理和二维反演解释技术研究(二)——反演数据极化模式选择[J]. 地球物理学报, 53 (11) : 2703–2714. DOI:10.3969/j.issn.0001-5733.2010.11.018 |
| [] | 蔡军涛, 陈小斌, 赵国泽.2010. 大地电磁资料精细处理和二维反演解释技术研究(一)——阻抗张量分解与构造维性分析[J]. 地球物理学报, 53 (10) : 2516–2526. DOI:10.3969/j.issn.0001-5733.2010.10.025 |
| [] | 陈乐寿, 王光锷.1990. 大地电磁测深法[M]. 北京: 地质出版社 . |
| [] | 陈小斌, 蔡军涛, 王立凤, 等.2014. 大地电磁资料精细处理和二维反演解释技术研究(四)——阻抗张量分解的多测点-多频点统计成像分析[J]. 地球物理学报, 57 (6) : 1946–1957. DOI:10.6038/cjg20140625 |
| [] | 陈小斌, 赵国泽, 汤吉, 等.2008. 网式大地电磁阻抗张量及其影响因素分析[J]. 地球物理学报, 51 (1) : 273–279. DOI:10.3321/j.issn:0001-5733.2008.01.034 |
| [] | 晋光文, 孙洁, 白登海, 等.2003. 川西-藏东大地电磁资料的阻抗张量畸变分解[J]. 地球物理学报, 46 (4) : 547–552. DOI:10.3321/j.issn:0001-5733.2003.04.018 |
| [] | 晋光文, 孔祥儒.2006. 大地电磁阻抗张量的畸变与分解[M]. 北京: 地震出版社 . |
| [] | 景建恩, 魏文博, 陈海燕, 等.2012. 基于广义S变换的大地电磁测深数据处理[J]. 地球物理学报, 55 (12) : 4015–4022. DOI:10.6038/j.issn.0001-5733.2012.12.013 |
| [] | 李洋, 于鹏, 张罗磊, 等.2010. 基于混合优化算法的MT阻抗张量畸变分解方法[J]. 地球物理学报, 53 (8) : 1924–1930. DOI:10.3969/j.issn.0001-5733.2010.08.018 |
| [] | 柳建新, 严家斌, 何继善, 等.2003. 基于相关系数的海底大地电磁阻抗Robust估算方法[J]. 地球物理学报, 46 (2) : 241–245. DOI:10.3321/j.issn:0001-5733.2003.02.018 |
| [] | 阮帅, 张炯, 孙远彬, 等.2015. 基于三维正演的音频大地电磁阻抗相位不变量校正技术[J]. 地球物理学报, 58 (2) : 685–696. DOI:10.6038/cjg20150229 |
| [] | 汤井田, 李晋, 肖晓, 等.2012. 数学形态滤波与大地电磁噪声压制[J]. 地球物理学报, 55 (5) : 1784–1793. DOI:10.6038/j.issn.0001-5733.2012.05.036 |
| [] | 汤井田, 张驰, 肖晓, 等.2013. 大地电磁阻抗估计方法对比[J]. 中国有色金属学报, 23 (9) : 2351–2358. |
| [] | 王书明, 李德山, 胡浩.2013. 三维/三维构造下大地电磁相位张量数值模拟[J]. 地球物理学报, 56 (5) : 1745–1752. DOI:10.6038/cjg20130532 |
| [] | 谢成良, 魏文博, 金胜, 等.2013. 相位张量分析约束下的大地电磁测深阻抗张量分解方法研究[J]. 地球物理学进展, 28 (3) : 1208–1218. DOI:10.6038/pg20130312 |
| [] | 严家斌, 刘贵忠.2007. 基于各向异性扩散的ROBUST阻抗估计方法[J]. 地球物理学进展, 22 (5) : 1403–1407. DOI:10.3969/j.issn.1004-2903.2007.05.010 |
| [] | 叶涛, 陈小斌, 严良俊.2013. 大地电磁资料精细处理和二维反演解释技术研究(三)——构建二维反演初始模型的印模法[J]. 地球物理学报, 56 (10) : 3596–3606. DOI:10.6038/cjg20131034 |
| [] | 尹曜田, 魏文博, 叶高峰, 等.2012. 基于遗传算法的大地电磁阻抗张量分解方法研究[J]. 地球物理学报, 55 (2) : 671–682. DOI:10.6038/j.issn.0001-5733.2012.02.031 |
| [] | 张刚, 王绪本, 张伟, 等.2011. 重复中位数估计Robust算法在长周期大地电磁中的应用[J]. 物探和化探, 35 (6) : 813–816. |
 2016, Vol. 31
2016, Vol. 31

