众所周知,地球物理方法是探测地球内部构造和所储藏资源的比较有效的方法,其以地下介质的物理性质和参数的差异为基础,查明地下所储藏的矿物和油气等资源,近几年来随着资源的大量消耗,人们对资源的需求越来越强烈,因此人们不仅仅把目标放在寻找资源上,同时更加关注资源的动态信息,尤其是油气资源的储存和动态监测问题.
大地电磁测深法(Magnetotelluric Sounding,简称MT)是苏联学者Tikhonov(1950)和法国学者Cagniard(1953)于20世纪50年代提出来的.它是利用大地中频率范围很宽10-4~104Hz且广泛分布的天然变化的电磁场进行深部地质构造研究的一种频率域电磁测深法.其优点在于频谱范围丰富,穿透能力强,不受高阻屏蔽且对低阻层反映灵敏,目前该方法在国内外的地质构造探测、地热田的调查、矿产普查和勘探、地壳和上地慢电性结构的研究、地震的预报、海洋地球物理、环境地球物理和地质工程中都发挥着重要的作用,近年来其应用又扩展到考古等领域.
可控源音频大地电磁法(Controlled Source Audio frequency Magnetotelluric,简称CSAMT)是在大地电磁法(MT)和音频大地电磁法(Audio frequency Magnetotelluric,简称AMT)的基础上发展起来的一种人工源频率域测深方法,其利用人工源电磁场通过分析地表观测的电场和磁场数据反洗处理来调查地下电导率的构造.CSAMT和MT的不同之处在于源的EM场,MT依赖于天然场源,这既是MT法的优点也是它的缺点,因为天然场源是不可预测的,并且天然场源的连续谱在1Hz附近的能量较低,从而导致需要很长的时间才能采集该频段较好的数据.由于强人为干扰,通常在油田地区无法采集到高质量的MT数据.为了得到稳定可靠的信号,Goldstein和Strangway(1975)提出利用接地线源代替天然场源,这一技术就是可控源音频大地电磁(CSAMT).自1970年代中期以来CSAMT作为非地震技术勘探的主要手段,已经应用于油气和矿产勘探、地热、地下水、环境调查研究等诸多方面.但是CSAMT反演模拟算法明显滞后于MT方法并缺少有效的解释技术,这大大限制了CSAMT的推广,所以寻找有效的CSAMT反演解释技术成为了现今电磁法勘探的主要研究课题之一.
目前随着海洋勘探的发展,海洋可控源电磁法(marine controlled source electromagnetics method,简称mCSEM)得到一定的重视.海洋CSEM用于近海油气勘探和储层评价,在工业和学术领域中,频率域可控源电磁(CSEM)主要用于近海和航空研究,目前海洋CSEM(mCSEM)也应用于电法自身方法联合反演等.
地震勘探是以研究人工激发的弹性波或者天然地震波在地下的传播为基础,包括多种探测地下结构的方法,因此,地震勘探从源上分为人工源地震勘探和天然场源地震勘探.另外从方法上分为反射波法和折射波法.地震勘探探测深度大,分辨率高,能直观反映地下精细结构,能详细地划分地层,高精度地确定沉积地层的倾角,所以地震勘探被广泛的用于解决地质构造问题,尤其用于寻找石油和天然气藏,也被广泛用于普查煤矿、岩盐及解决各种工程地质问题.
1 联合反演每种地球物理方法都有其局限性,大地电磁测深由于是用天然大地电磁场做场源,因此它的抗干扰能力较弱,特别是在人口稠密地区,如村镇和道路附近等的强干扰地区往往很难采集到高信噪比的数据,其次,受仪器和技术的限制,大地电磁对地层的纵向分辨能力还远远满足不了精细构造研究的需要,另外,由于电磁场强度随深度呈指数规律衰减,其分辨能力也随着深度按指数规律减小,所以它的垂向分辨率和分层能力都比地震低.地震勘探虽然其探测深度大,分辨率高,能直观反映地下精细结构,但是对于地下构造复杂区域,其很难得到可靠的结果,并且不能比较清晰的划分出速度差异小的介质之间的边界,此外,地震勘探中还存在数据采集激发和接收耦合条件不佳,采集的数据存在横向变化剧烈、信噪比低,无明显标志层、多解性严重等问题.综上所述,寻找一种更为有效的方法显得至关重要.近些年来发展起来的更好的探测方法是联合反演方法,其克服了单一方法的局限性,更好的探测地下资源以及对油气进行监测.
联合反演是指在地球物理反演中联合应用多种地球物理方法采集的信息,通过地质体的岩石物性和几何参数之间的相互关系共同反演相同地下地质、地球物理模型的方法,因为调查的对象是同一个地方的岩石层,因此不同的地球物理场的解释应具有兼容性.按照地质解释过程中反演流程和方法的不同,联合反演可分为四类:剥离法反演、顺序反演、伸展法反演和同步反演.根据反演模型的物性特征,即是否基于相同地球物理场,联合反演又可以分为基于相同物性和不同物性的联合反演两大类.其中目前应用较多的是同步联合反演,其利用多种地球物理数据对所有物性参数同时进行反演.
联合反演起源于20世纪70年代,目前为止已经经历30多年的发展,并且随着计算机技术的发展,联合反演也得到了更广泛的研究,尤其随着计算机内存增大和运算速度的加快,联合反演逐渐从一维发展到二维、三维联合反演,由线性和广义的联合反演发展到非线性联合反演,并且随之后来出现不同物性之间的联合反演.早期的联合反演主要是基于相同物性参数,最早是由Vozoff和Jupp(1977)最先提出的,他们用迭代二阶Marquardt阻尼最小二乘法实现了一维直流电测深(DC)和大地电磁测深(MT)资料的联合反演,解决了层状介质中的各向异性问题;还有如:杨文采等(1987)利用阻尼最小二乘法实现均方根速度和反射波走时的联合反演;Vasco(1996)和Wang(1999)研究了地震波走时和振幅联合反演;Grechka等(1999)进行了P波和PS波走时的联合反演等;近几年基于相同物性的联合反演仍然是热门问题,如:Horspool等(2006)实现了接收函数和面波联合反演;Moro等(2007)应用多目标函数的算法进行面波频散曲线和反射波走时之间联合反演;Abubakar等(2009)应用乘法成本函数方法进行MT和CSEM数据联合反演等.
20世纪80年代,随着联合反演的发展,出现了不同物性的联合反演,首先是重力-地震的联合反演并得到迅速发展,如:Sovino等(1981)首次利用地震数据和重力数据进行联合反演研究,通过反演计算得到了上地幔速度和密度结构;冯锐(1985)根据国外的研究结合我国的实际情况,给出了中国速度-密度转换公式,这为重力-地震联合反演提供了方便;之后,科学家又尝试加入更多的方法进行联合反演和更多地球物理方法之间的联合反演,如:Lines等(1987,1988)利用最小二乘原理,联合地震、声波测井、地面和井中重力进行了顺序联合反演研究;李雄(1992)对地震-重力联合反演的不同实现方式进行了全面的总结;于鹏等(2007)引入模拟退火法约束联合反演进行重力和地震资料的联合反演;王新胜等(2012)使用剩余重力异常,采用重震联合反演法得到华北克拉通岩石圈的三维密度结构;Shamsipour等(2012)提出一种基于协同克里金法的随机重力和磁法数据3D联合反演,从而用于评估密度和磁性的评估;Stefano(2012)应用交叉梯度法进行折射层析成像和磁测数据的同时联合反演;Basuyau等(2013)将远震和卫星重力进行联合反演用于喜马拉雅和西藏高原探测;Kumar等(2014)联合自由空间重力异常、大地水准面异常和地形数据进行印度南部地盾岩石密度结构探测.陈晓等(2016)基于非常快速模拟退火(VFSA)算法实现了大地电磁和重力数据的贝叶斯同步联合反演.
2 电磁与地震联合反演基础 2.1 电磁和地震理论相似性根据地震和电磁波动方程公式,可以得到在自然界中不论是交变电磁场还是位移场均遵循波动方程,并且具有相似性.对于反射地震仪器接收的信号是地震子波和介质响应函数的叠加,在电磁法中电磁场场强在传播过程中与介质响应函数有关,在电磁波或弹性波双程传播时间相等的“薄层”中,可得到电磁测深法和地震反射法的复反射函数分别为
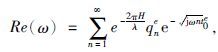
|
(1) |
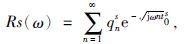
|
(2) |
上面两式中,Re(ω)为电磁频率测深反射函数,Rs(w)为地震反射函数,qne为电磁测深反射系数函数,qns为地震反射法反射系数函数,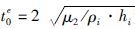
在重力-地震联合反演中,常用的联系重力和地震数据的物性关系是联系密度和速度的Garden公式,然而对于电磁和地震数据之间的联系公式,至今没有确定的普遍适用的公式,目前的公式均是根据实验总结出的经验公式,其中最为著名的电磁和地震数据的联系公式出自地球物理测井,是Faust研究总结出的电阻率-速度公式,也就是著名的Faust公式公式为

|
(3) |
Faust公式表征在深度约束条件下地层电阻率曲线与声波曲线之间具有统计关系,式中v为声波速度,K,C,d为待定系数,H为深度,Rt为岩层电阻率,这个公式可通过岩石物性测量和统计相关得到,它只适用于某些特定地区,对于不同地区,式中的常量是不同的.
2.2.2 间接关系另一种联系地震和电磁数据之间的关系是通过Archie(1942)公式和Gassmann(1951)方程将电磁和地震中参数通过孔隙度和饱和度进行联系,但是这种联系也不是普遍适用的,主要在于Archie公式和Gassmann方程也是经验公式,随着地区的变化而变化,但就目前来看,其也是研究联合反演比较好的联系.
对于这种关系,首先通过Archie公式将电导率σ和孔隙度φ及含水饱和度Sw相联系,其公式为

|
(4) |
其中a是曲折因子,m为孔隙度指数,n为饱和度指数,σw为含盐水结构电导率.
之后通过Gassmann方程将孔隙度φ和油、气、水的饱和度So,Sg,Sw同地震波P波速度VP进行联系,其公式为

|
(5) |
其中

|
β是Biot系数,通常情况下其是孔隙度的函数.
以上我们介绍了电磁和地震数据之间的直接和间接物性关系,目前研究还只用间接关系,直接关系还没有得到应用,因此以后直接应用电磁和地震数据的直接关系还是一个可以考虑的方向.
3 电磁与地震联合反演研究进展及现状较早的电磁和地震的联合反演要从20世纪90年代算起,Dobróka等(1991)采用基于最大频率值(MFV)的加权最小二乘算法对垂直地震剖面(VSP)走时数据和电法数据进行联合反演,这种算法具有估计误差小以及初始模型选择对结果影响小的特点,结果表明联合反演比单一反演结果可靠;周辉等(1994)记录地面地震波场和大地电磁测深地面视电阻率理论记录,并用广义线性联合反演方法反演模型参数,之后与单独方法对比发现联合反演效果更优越;Hering等(1995)提出地电和地震面波数据联合反演方法,其分别进行电法中不同方法和地震中不同方法的联合反演,之后进行地震面波数据和地电数据联合反演;周辉等(1995)又进一步在广义线性联合反演基础上,将联合反演推广到非线性联合反演,并对两种方法进行对比,发现非线性方法更优越;杨振武等(1998)进行了一维大地电磁和地震数据的联合反演,并进行了实验研究,其也应用了新的岩石物理关系Faust公式和Garden公式,将密度、速度和电阻率进行直接联系.
进入21世纪,这种电磁和地震的联合反演逐步向更多方法和更高维度去发展,如2D的联合反演.Gallardo和Meju(2003)发展了结合交叉梯度方法的电阻率和地震走时联合反演用于近地表不均匀介质描述;陈东敬和于鹏(2005)开展了引入模拟退火法约束的大地电磁和地震多参量同步联合反演,较好的建立了物理-地质模型,然后结合重磁资料确定地质体的位置;Nardis等(2005)提出地震和电磁数据的准2D混合联合反演,其中电磁和地震的耦合通过共同边界,边界表面用级数展开进行定义,采用A和B两种策略,一种以间隔交接常数函数作为级数展开函数,另一种则以Chebyshev多项式进行级数展开,同时这篇文章经过一些实验验证该文方法可得到稳定和精确的解;Hoversten等(2006)结合电阻率和地震速度间的岩石物理联系联合地震振幅随入射角变化(AVA)和CSEM数据进行1D模型参数反演,其结果表明联合反演比单一反演得到更好的效果;林剑和敬荣中(2007)针对电性和速度界面不一致的联合反演,提出以地质模型作为速度界面和电性不一致联合反演的统一模型,并采用基于模式识别的联合反演算法,应用神经网络算法进行反演,结果表明地质模型作为联合反演统一模型的可行性.
2007年以后,更多种信息和方法的数据联合反演逐步兴起.Gallardo和Meju(2007)提出一种广义交叉梯度方法,用于近地表P波、S波、DC电阻率和磁法数据的联合反演,从而更精确的进行复杂储层环境描述,同年Gallardo和Meju等联合2D交叉梯度进行大地电磁和地震走时联合反演;Chen等(2007)在海洋地震AVA和CSEM数据联合反演用于油气储藏评估的研究中引入一种贝叶斯模型进行研究;之后Chen和Dickens(2009)结合一种贝叶斯反演结构将AVA和CESM数据联合反演评估储层参数反演之间的不确定性;Colombo等(Colombo and Stefano, 2007; Colombo et al., 2008)和Moorkamp等(2011)描述了3D结构MT、重力和地震折射联合反演的框架,并应用于海洋储层探测;刘远(2008)在自己的硕士论文中进行了地微动探测与大地电磁测深联合反演,将两种均利用天然场源的方法进行联合,从广义线形反演方法和非线性反演方法讨论了两种地球物理数据的联合反演,并从理论上论证了两种方法同一地点联合使用的可能性;Hu等(2009)使用基于交叉梯度结构约束的方法发展了电磁和地震数据联合反演;Moorkamp等(2010)提出应用多目标遗传算法(GA)的大地电磁、接收函数和瑞雷波散布数据联合反演用于1D地球探测;Viriglio等(2010)第一次进行地震和大地电磁数据3D同时联合反演(SJI)并应用于墨西哥湾复杂岩层下深度成像.
近几年来,人们逐渐把重点关注于如何将电磁和地震之间的参数进行更好的联系,从而使联合反演的结果更精确. Muñoz等(2010)在进行大地电磁和地震层析成像联合反演中,为了得到地震和电磁的高相关性,应用统计学观点绘制地震层析-大地电磁剖面去寻找两者之间的高度相关性;陈高等(2010)提出一种改进的大地电磁与地震资料联合反演,其利用基于不同物性参数随机分布共网格模型的大地电磁与地震资料同步联合反演技术,并应用于实际,发现该方法适用于物性剧烈变化的复杂地质模型;Roux等(2011)在各向异性结构中应用长周期大地电磁和面波色散曲线联合反演用于德国中部数据反演,并在反演中应用遗传算法优化结果;陈晓等(2011)用自适应正则化法确定联合反演正则化因子,将正则化思想引入到联合反演中,进行电阻率和速度随机分布的大地电磁和地震联合反演;Gao等(2012)结合岩石物理方法的电磁(EM)数据和声波全波形地震数据进行2D联合反演,之后Abubakar等(2012)将岩石物理中的Archie公式和Gassman方程应用到CSEM和弹性波全波形数据联合反演中,将地震波速度和电阻率等参数联系起来进行频率域联合反演,其同时也提出了基于交叉梯度的应用CSEM和弹性波全波形数据进行频率域结构联合反演.
随着海洋地球物理的发展,联合反演的方法也被应用于海洋地球物理,将海洋地球物理和提高联合反演精度同时发展.Chen和Hoversten(2012)进一步发展海洋地震AVA和CSEM数据联合反演,并使用统计岩石物理发展一种贝叶斯模型以及引入马尔可夫随机场获得储层参数;彭淼等(2012)利用接收函数和大地电磁数据进行联合反演,其中接收函数是采用时间域迭代反褶积技术处理得到的,反演方法采用遗传算法并且通过权衡图分析地震数据和大地电磁数据的兼容性;Mahardika等(2012)提出一种随机地震和电磁图像联合反演,通过使用自适应Mtropolis 算法(AMA)去得到参数的后几率密度函数来描述地震源,经过验证发现波形联合反演在综合自由噪声数据和AMA算法中评估未知参数的真实值是有效的;Karaoulis等(2012)年提出时移联合反演用于交叉井DC电阻率和地震数据,其所用联合方法为交叉梯度和岩石物理关系两种;Bauer等(2012)在地震层析和大地电磁联合反演的模型解释中引入自组织映射(SOMS)技术进行模型解释;Lien(2013)提出基于结构耦合的地震AVO和CSEM数据的联合反演方法,解决了先验信息有限的高度不确定的问题;Molodtsov等(2013)提出一种直接结构约束用于地震走时和大地电磁数据联合反演,所谓直接是指要考虑重构参数梯度间交叉相关信号的先验信息,其发展一种用于2D基于像素的联合反演,其中预先的结构约束也作为目标函数的一项,并且在地震慢度和Levenberg-Marquardt阻尼项的总变化中加入稳定项.文中经过一些实验发现与交叉梯度相比,该方法减少了模型恢复的不确定性;侯征(2013)在其博士论文研究中进行直流电阻率和瑞雷面波联合反演研究,其将电法与地震面波联合反演,也是联合反演的一种突破,对于算法上,其引入人工蜂群智能优化算法,并得到很好的反演效果;彭淼等(2013)以天然地震走时资料三维正反演和大地电磁三维正反演算法为基础,用交叉梯度结构耦合进行约束,实现了共同反演网格,并能同时获得电阻率和速度模型的三维联合反演算法;Giuseppe等(2014)在2D大地电磁和地震剖面综合解释方法中将k均值聚类法应用于反演后单变量电阻率和P波速度模型,用于得到高分辨率剖面;Um等(2014)提出新的耦合地震-电磁反演方法用于克服地震-电磁联合反演中的收敛和病态问题,并将全波形、大地电磁和可控源电磁联合,其在Laplace域中将波动方程离散化从而处理地震和电磁间不同解的性质,使得地震解对于电磁数据可用,之后为了克服收敛问题,其通过交叉梯度唯一反演和电阻率-地震交会图去增强两者结构相似,进而得到更好的图像;Juhojuntti和Kamm(2015)进行折射地震和电阻率数据联合反演,其将该方法应用于近地表地下水的探测引入层状锐边界作为模型边界,地震折射正演中选用射线追踪计算Jacobian矩阵,电阻率正演用有限差分法并用Fréchet导数实现细胞到层的转换,通过综合测试得出该方法的边界很好的匹配测试数据,对于小结构也能很好的反映;Bennington等(2015)在地震和大地电磁数据联合反演中应用归一化交叉梯度进行结构约束,并在反演中应用tomoDDMT和tomoDD代码进行运算,其结果表明通过这种算法可以得到更加精确的结果和地下结构.徐凯军等(2016)基于岩石物理关系,采用模拟退火结合粒子群算法的优化反演方法,进行了一维海洋可控源电磁和地震数据联合反演,直接得到储层孔隙度和饱和度参数.
根据国内外目前的研究现状来看,联合反演通过将不同地球物理方法的数据联合起来进行反演,的确比使用单独某种地球物理资料反演具有优越性.过去的大量工作多集中于一维的地震和电磁测深资料反演,或者假设速度界面和电性界面一致情况下进行电磁反演,要么通过物性参数间的关系进行联系,要么通过结构约束强制两者具有一致的结构.在算法上,目前主要的还是线性迭代的方法,非线性优化计算方法还相对比较少,而且目前研究所用的非线性优化算法还存在许多问题,算法还比较简单;对于模型来说,复杂地质结构的电震联合反演仍然是个难点.因此,未来的联合反演的发展中,如何减少反演多解性,提高计算速度和反演精度等,这些均是电磁与地震联合反演技术发展必须面临的问题.
4 电磁与地震联合反演的未来电磁法反演和地震反演所用到的岩石物性参数不同,其联合反演属于基于不同物性地球物理数据之间的反演,在保证数据精度的前提下,两种方法的联合可以比单一方法更好的确定电性层和速度层以及两者之间的关系,从目前的研究来看,对于两者之间的联系主要有两种方法:岩石物理方法和交叉梯度结构约束法,前者适合于地震波速度界面和电性界面具有一致性的水平层状介质结构,后者适用于速度界面和电性界面不一致的复杂地质结构,但是目前所用到的岩石物理方法中,几乎没有直接将电阻率和速度进行联系的基本公式,所以只能通过饱和度和孔隙度进行联系,也就是说通过Archie公式将电阻率和孔隙度和饱和度进行联系,通过Gaussmann方程将速度和孔隙度及饱和度进行联系,从而建立起速度和电阻率之间的联系,但是目前的岩石物理学中的公式几乎都是经验公式,通过岩石物理实验观测并推导出的公式,因此结合岩石物理学的联合反演的局限在于仅仅在采集所测岩石的地区适用,区域不同则不一定适用;而对于交叉梯度联合反演,其对于两者之间的联系是比较有效的,但是其对于两者之间的约束是强制性的.
综上所述,展望未来电磁和地震联合反演主要有以下几个方面:
(1)层状均匀介质结构需要优化线性迭代技术,改善模型参数化技术和迭代过程的自组织.
(2)对于非线性的复杂地质结构,需要加紧理论向实际的发展,其中目前来看,结构法反演前景看来较开阔,但需要加强与实际资料的结合,计算方法包括交叉梯度算法在内的非线性算法也需要优化,而且对于结构算法来说,其需要寻找不同方法之间的相似性并且其对于不同方法之间的约束是强制的,这就要求联合反演的两种方法间有很好的相似性,否则两者难以很好结合,因此未来的发展中寻找更好的联合不同方法之间的关系和方法也尤为重要.
(3)岩石物理法的结合也是电磁和地震联合的热点,只不过其目前所用的关系式几乎全为经验公式,仅仅在某一地区适用,并且目前的岩石物理学公式中直接联系电磁和地震之间的公式非常少,虽然有Faust公式,但是Faust公式也只是区域性适用,而且Faust公式也没有被广泛的证明与应用,因此未来在岩石物理学方面的发展中,寻找更好的联系公式是重要的,可以通过实验和推导等进一步寻找电磁和地震参数之间联系的岩石物理学公式,更进一步可以引入更多统计学的思想对公式间联系的不确定性进行约束,让经验公式不仅仅只针对某一地区或者层位适用.
(4)对于地震和电磁法而言,目前已经发展出许多勘探方法,如:地震的射线追踪、全波形反演方法、电磁法的大地电磁测深、海洋大地电磁测深、可控源音频大地电磁测深等,因此,对于电磁法和地震的联合反演而言,发展不同地震和电磁法的不同方法的联合也是一个值得考虑的方向,如可发展地震和音频大地电磁的联合反演等;另一方面,随着数学方法和技术的发展,如何找到更好的正演模拟和优化方法,从而提高计算的精度和效率也是有必要加以考虑的,由于联合反演所需的时间和数据存储相对于单一方法要多得多,因此,提高联合反演的精度和速度也是未来的一个发展方向,如:加入并行运算,从而提高计算速度等.
(5)既然联合反演可以更好的反映地下资源和结构构造分布的情况,因此发展更多的方法的联合也是值得考虑的一方面,目前已经出现有重磁电震联合反演的研究,但是总的来说,目前的联合反演仍然处于初级阶段,相对还不是十分成熟,因此,未来的发展中结合更多方法的联合反演也是一个可研究的方向,例如:结合测井数据和方法,结合探地雷达、极化雷达,甚至结合遥感知识等.
(6)随着联合反演被逐步应用于储层监测,所以如何将联合反演从一维提高到二维、三维,甚至四维也是未来联合反演所面临的一大问题和挑战.
(7)地球物理反演中存在不适定的特性,反演解释的正确性取决于反演方法的性质和对研究区的认识程度.所以电磁和地震的联合反演也需要结合岩石物性等先验地质信息,才可得到更好的综合方法和解释结果.
总之,联合反演虽然有十几年的历史,但是电震联合反演的真正发展时间却不太长,因此从目前来看,电震联合反演还处于比较初级的阶段,因此未来电震联合反演发展方向还有很大的空间.
致谢 感谢固体组的老师和同学们的帮助,他们在很多问题上提供了必要的支持与参考意见,并且他们在许多问题上的见解让我受益匪浅,同时也感谢评审专家及编辑部的指导和帮助,感谢你们提出宝贵建议!| [] | Abubakar A, Gao G, Habashy T M, et al .2012. Joint inversion approaches for geophysical electromagnetic and elastic full-waveform data[J]. Inverse Problems, 28 (5) : 055016. DOI:10.1088/0266-5611/28/5/055016 |
| [] | Archie G E .1942. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Transactions of AIME, 146 (1) : 54–62. DOI:10.2118/942054-G |
| [] | Basuyau C, Diament M, Tiberi C, et al .2013. Joint inversion of teleseismic and GOCE gravity data:Application to the Himalayas[J]. Geophysical Journal International, 193 (1) : 149–160. DOI:10.1093/gji/ggs110 |
| [] | Bauer K, Muñoz G, Moeck I .2012. Pattern recognition and lithological interpretation of collocated seismic and magnetotelluric models using self-organizing maps[J]. Geophysical Journal International, 189 (2) : 984–998. DOI:10.1111/gji.2012.189.issue-2 |
| [] | Bennington N L, Zhang H J, Thurber C H, et al .2015. Joint inversion of seismic and magnetotelluric data in the parkfield region of California using the normalized cross-gradient constraint[J]. Pure and Applied Geophysics, 172 (5) : 1033–1052. DOI:10.1007/s00024-014-1002-9 |
| [] | Chen D. J., Yu P. 2005. The integrated application of joint inversion technology of magnetotelluric and seismic in an area of West Asia[J]. Geophysical Prospecting for Petroleum, Vol. 44 (3):251-256. |
| [] | Chen G.H., Wang Y.G. 2005. The application of Faust formula in sonic curve reconstruction[J]. Progress in Exploration Geophysics, Vol. 28 (2):125-128. |
| [] | Chen G., Yu P., Chen X., et al. 2010. The applicability study of joint inversion of modified magnetotelluric and seismic data in the area of the Central Guizhou Uplift[J]. Geophysical Prospecting for Petroleum, Vol. 49 (2):158-197. |
| [] | Chen J S, Hoversten G M, Vasco D, et al .2007. A Bayesian model for gas saturation estimation using marine seismic AVA and CSEM data[J]. Geophysics, 72 (2) . DOI:10.1190/1.2435082 |
| [] | Chen J S, Dickens T A .2009. Effects of uncertainty in rock-physics models on reservoir parameter estimation using seismic amplitude variation with angle and controlled-source electromagnetics data[J]. Geophysical Prospecting, 57 (1) : 61–74. DOI:10.1111/gpr.2008.57.issue-1 |
| [] | Chen J S, Hoversten G M .2012. Joint inversion of marine seismic AVA and CSEM data using statistical rock-physics models and Markov random fields[J]. Geophysics, 77 (1) . DOI:10.1190/GEO2011-0219.1 |
| [] | Chen Q. 2011. Research on the method for inversion of 2.5D CSAMT data[Master Degree Dissertation]. Beijing:China University of Geosciences (Beijing). |
| [] | Chen X., Li W.Q., Guo M., et al. 2016. Bayesian joint inversion of magnetotelluric and gravity data[J]. Science Technology and Engineering, Vol. 16 (15):30-35. |
| [] | Chen X, Yu P, Zhang L L, et al .2011. Adaptive regularized synchronous joint inversion of MT and seismic data[J]. Chinese Journal of Geophysics (in Chinese), 54 (10) : 2673–2681. DOI:10.3969/j.issn.0001-5733.2011.10.024 |
| [] | Colombo D, Mantovani M, Hallinan S, et al. 2008. Sub-basalt depth imaging using simultaneous joint inversion of seismic and electromagnetic(MT) data:A CRB field study[C].//77th Annual International Meeting, SEG Technical Program Expanded Abstracts. Expanded Abstracts, 2674-2678. |
| [] | Colombo D, Stefano M .2007. Geophysical modeling via simultaneous joint inversion of seismic, gravity, and electromagnetic data:Application to prestack depth imaging[J]. The Leading Edge, 26 (3) : 326–331. DOI:10.1190/1.2715057 |
| [] | Constable S .2010. Ten years of marine CSEM for hydrocarbon exploration[J]. Geophysics, 75 (5) : 75A. DOI:10.1190/1.3483451 |
| [] | Constable S, Srnka L J .2007. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration[J]. Geophysics, 72 (2) . DOI:10.1190/1.2432483 |
| [] | Dobróka M, Gyulai á, Ormos T, et al .1991. Joint inversion of seismic and geoelectric data recorded in an underground coal mine[J]. Geophysical Prospecting, 39 (5) : 643–665. DOI:10.1111/gpr.1991.39.issue-5 |
| [] | Feng R. 1985. Crustal thickness and density in the upper mantle beneath China (the results of three dimensional gravity inversion)[J]. Acta Seismologica Sinica, Vol. 7 (2):143-157. |
| [] | He Q.D., Han L.G., Wang D.L.. 2009. Seismic Exploration[M]. Fourth Edition. Beijing:Geological Publishing House. |
| [] | Hou Z. 2013.Nonlinear Joint Inversion Algorithm Research of DC Resistivity and Rayleigh Wave Seismic[Doctoral Degree Dissertation]. Beijing:China University of Geosciences (Beijing). |
| [] | Gallardo L A .2007. Multiple cross-gradient joint inversion for geospectral imaging[J]. Geophysical Research Letters, 34 (19) : L19301. DOI:10.1029/2007GL030409 |
| [] | Gallardo L A, Meju M A .2003. Characterization of heterogeneous near-surface materials by joint 2D inversion of DC resistivity and seismic data[J]. Geophysical Research Letters, 30 (13) : 1658. DOI:10.1029/2003GL017370 |
| [] | Gallardo L A, Meju M A .2007. Joint two-dimensional cross-gradient imaging of magnetotelluric and seismic traveltime data for structural and lithological classification[J]. Geophysical Journal International, 169 (3) : 1261–1272. DOI:10.1111/gji.2007.169.issue-3 |
| [] | Gao G Z, Abubakar A, Habashy T M .2012. Joint petrophysical inversion of electromagnetic and full-waveform seismic data[J]. Geophysics, 77 (3) : WA3–WA18. DOI:10.1190/geo2011.0157.1 |
| [] | Gassmann F .1951. über die Elastizität poröser Medien[J]. Viertel Naturforsch Ges Zürich, 96 : 1–23. |
| [] | Giuseppe M G D, Troiano A, Troise C, et al. 2014. k-Means clustering as tool for multivariate geophysical data analysis. An application to shallow fault zone imaging[J]. Journal of Applied Geophysics, 101:108-115, doi:10.1016/j.jappgeo.2013.12.004. |
| [] | Hering A, Misiek R, Gyulai A, et al .1995. A joint inversion algorithm to process geoelectric and sutface wave seismic data, Part I:Basic ideas[J]. Geophysical Prospecting, 43 (3) : 135–156. |
| [] | Hoversten G M, Cassassuce F, Gasperikova E, et al .2006. Direct reservoir parameter estimation using joint inversion of marine seismic AVA and CSEM data[J]. Geophysics, 71 (3) : C1–C13. DOI:10.1190/1.2194510 |
| [] | Hu W Y, Abubakar A, Habashy T M .2009. Joint electromagnetic and seismic inversion using structural constraints[J]. Geophysics, 74 (6) : R99–R109. DOI:10.1190/1.3246586 |
| [] | Juhojuntti N, Kamm J .2015. Joint inversion of seismic refraction and resistivity data using layered models-Applications to groundwater investigation[J]. Geophysics, 80 (1) : EN43–EN55. DOI:10.1190/GEO2013-0476.1 |
| [] | Karaoulis M, Revil A, Zhang J, et al .2012. Time-lapse joint inversion of crosswell DC resistivity and seismic data:A numerical investigation[J]. Geophysics, 77 (4) : D141–D157. DOI:10.1190/GEO2012-0011.1 |
| [] | Kumar N, Zeyen H, Singh A P .2014. 3D Lithosphere density structure of southern Indian shield from joint inversion of gravity, geoid and topography data[J]. Journal of Asian Earth Sciences, 89 : 98–107. DOI:10.1016/j.jseaes.2014.03.028 |
| [] | Li J.M. 2005. Geoelectric Field and Electrical Exploration (in Chinese)[M]. Beijing:Geological Publishing House. |
| [] | Li X. 1992. Joint inversion of seismic and gravity-different implementation model[J]. Natural Gas Geoscience, Vol. 3 (5):37-42. |
| [] | Lien M. 2013. Simultaneous joint inversion of amplitude-versus-offset and controlled-source electromagnetic data by implicit representation of common parameter structure[J]. Geophysics, 78(4):ID15-ID27, doi:10.1190/GEO2012-0188.1. |
| [] | Lin J., Jing R.Z. 2007. A joint inversion method based on interface inconformity of electrical property and velocity of geologic model[J]. Mineral Resources and Geology, Vol. 21 (6):668-672. |
| [] | Liu Y. 2008. Study of Microtremor and Megnetotelluric Associated Survey[Master Degree Dissertation]. Beijing:China University of Geosciences (Beijing). |
| [] | Liu Y, Lv Q T, Meng G X, et al .2012. Joint electromagnetic and seismic inversion survey:status and prospect[J]. Progress in Geophysics (in Chinese), 27 (6) : 2444–2451. DOI:10.6038/j.issn.1004-2903.2012.06.019 |
| [] | Mahardika H, Revil A, Jardani A .2012. Waveform joint inversion of seismograms and electrograms for moment tensor characterization of fracking events[J]. Geophysics, 77 (5) : ID23–ID39. DOI:10.1190/GEO2012-0019.1 |
| [] | Molodtsov D M, Troyan V N, Roslov Y V, et al .2013. Joint inversion of seismic traveltimes and magnetotelluric data with a directed structural constraint[J]. Geophysical Prospecting, 61 (6) : 1218–1228. DOI:10.1111/gpr.2013.61.issue-6 |
| [] | Moorkamp M, Jones A G, Fishwick S .2010. Joint inversion of receiver functions, surface wave dispersion, and magnetotelluric data[J]. Journal of Geophysical Research, 115 (B4) : B04318. DOI:10.1029/2009JB006369 |
| [] | Moorkamp M, Heincke B, Jegen M, et al .2011. A framework for 3-D joint inversion of MT, gravity and seismic refraction data[J]. Geophysical Journal International, 184 (1) : 477–493. DOI:10.1111/gji.2010.184.issue-1 |
| [] | Muñoz G, Bauer K, Moeck I, et al .2010. Exploring the Groß Schönebeck (Germany) geothermal site using a statistical joint interpretation of magnetotelluric and seismic tomography models[J]. Geothermics, 39 (1) : 35–45. DOI:10.1016/j.geothermics.2009.12.004 |
| [] | Nardis R D, Cardarelli E, Dobroka M .2005. Quasi-2D hybrid joint inversion of seismic and geoelectric data[J]. Geophysical Prospecting, 53 (5) : 705–716. DOI:10.1111/gpr.2005.53.issue-5 |
| [] | Peng M, Tan H D, Jiang M, et al .2012. Joint inversion of receiver functions and magnetotelluric data:Application to crustal and mantle structure beneath central Namche Barwa,eastern Himalayan syntaxis[J]. Chinese Journal of Geophysics (in Chinese), 55 (7) : 2281–2291. DOI:10.6038/j.issn.0001-5733.2012.07.014 |
| [] | Peng M, Tan H D, Jiang M, et al .2013. Three-dimensional joint inversion of magnetotelluric and seismic travel time data with cross-gradient constraints[J]. Chinese Journal of Geophysics (in Chinese), 56 (8) : 2728–2738. DOI:10.6038/cjg.20130821 |
| [] | Qiu G.G. 2010. Three-dimensional Magnetotelluric Inversion Test of MT Sounding Data and Research for Visualization[Master Degree Dissertation]. Beijing:China University of Geosciences (Beijing). |
| [] | Roux E, Moorkamp M, Jones A G, et al .2011. Joint inversion of long-period magnetotelluric data and surface-wave dispersion curves for anisotropic structure:Application to data from Central Germany[J]. Geophysical Research Letters, 38 (5) . DOI:10.1029/2010GL046358 |
| [] | Shamsipour P, Marcotte D, Chouteau M .2012. 3D stochastic joint inversion of gravity and magnetic data[J]. Journal of Applied Geophysics, 79 : 27–37. DOI:10.1016/j.jappgeo.2011.12.012 |
| [] | Stefano M D. 2012. Simultaneous joint inversion of refraction tomography and magnetic data[C].//Progress in Electromagnetics Research Symposium Proceedings. Moscow, Russia, 491-495. |
| [] | Suo K. 2013. Distribution of The Crust and Upper Mantle Density by Joint Inversion of Gravity and Seismic Data[Master Degree Dissertation]. Beijing:China University of Geosicences (Beijing). |
| [] | Tang J T, Li J, Xiao X, et al .2012. Mathematical morphology filtering and noise suppression of magnetotelluric sounding data[J]. Chinese Journal of Geophysics (in Chinese), 55 (5) : 1784–1793. DOI:10.6038/j.issn.0001-5733.2012.05.036 |
| [] | Um E S, Commer M, Newman G A .2014. A strategy for coupled 3D imaging of large-scale seismic and electromagnetic data sets:Application to subsalt imaging[J]. Geophysics, 79 (3) : ID1–ID13. DOI:10.1190/geo2013-0053.1 |
| [] | Viriglio M, Stefano M D, Re S, et al. 2010. Simultaneous joint inversion of seismic and magnetotelluric data for complex sub-salt depth imaging in gulf of Mexico[C].//Progress in Electromagnetics Research Symposium Proceedings. Cambridge, USA, 617-620. |
| [] | Vozoff K, Jupp D L B .1977. Effective search for a buried layer:An approach to experimental design in geophysics[J]. Exploration Geophysics, 8 (1) : 6–15. DOI:10.1071/EG977006 |
| [] | Wang J.Y., Oldenburg D., Levy S., 1985. The pseudo-seismic interpretation of magnetotelluric[J]. Oil Geophysical Prospecting, Vol. 20 (1):66-79. |
| [] | Wang X S, Fang J, Xu H Z, et al .2012. Density structure of the lithosphere beneath North China Craton[J]. Chinese Journal of Geophysics (in Chinese), 55 (4) : 1154–1160. DOI:10.6038/j.issn.0001-5733.2012.04.011 |
| [] | Wiik T, Hokstad K, Ursin B, et al .2013. Joint contrast source inversion of marine magnetotelluric and controlled-source electromagnetic data[J]. Geophysics, 78 (6) . DOI:10.1190/GEO2012-0477.1 |
| [] | Xu K.J., Du R.L., Liu Z. 2016. Joint reservoir parameter inversion of 1D marine controlled source electromagnetic and seismic data[J]. Oil Geophysical Prospecting, Vol. 51 (1):197-203. |
| [] | Yang H, Dai S K, Song H B, et al .2002. Overview of joint inversion of integrated geophysics[J]. Progress in Geophysics (in Chinese), 17 (2) : 262–271. DOI:10.3969/j.issn.1004-2903.2002.02.011 |
| [] | Yang H, Wang J L, Wu J S, et al .2002. Constrained joint inversion of magnetotelluric and seismic data using simulated annealing algorithm[J]. Chinese Journal of Geophysics (in Chinese), 45 (5) : 723–734. DOI:10.3321/j.issn:0001-5733.2002.05.015 |
| [] | Yang W.C. 1997. Theory and methods of geophysical inversion[M]. Beijing:Geological Publishing House. |
| [] | Yang Z.W., Wang J.Y., Zhang S.Y., et al. 1998. Research on joint inversion of 1-D manetotelliuric and seismic data[J]. Oil Geophysical Prospecting, Vol. 33 (1):78-88. |
| [] | Yu P, Wang J L, Wu J S, et al .2007. Comparative analysis of inversion methods of retrieving atmospheric profiles with GPS occultation measurements[J]. Chinese Journal of Geophysics (in Chinese), 50 (2) : 529–538. DOI:10.3321/j.issn:0001-5733.2007.02.026 |
| [] | Zhou H., Liu C., Qu G.X. 1995. Research on non-linear integration inversion of seismic and magnetotelluric data[J]. Journal of Jilin University (Earth Science Edition), Vol. 25 (2):205-211. |
| [] | Zhou H, Yang B J, Liu C .1994. Combined inversion of seismic and magnetotelluric sounding data[J]. Acta Geophysica Sinica (in Chinese), 37 (S1) : 477–485. |
| [] | 陈东敬, 于鹏.2005. 大地电磁与地震联合反演技术在西亚某区的综合应用[J]. 石油物探, 44 (3) : 251–256. |
| [] | 陈高, 于鹏, 陈晓, 等.2010. 改进的大地电磁与地震资料联合反演方法在黔中隆起区的适用性研究[J]. 石油物探, 49 (2) : 158–197. DOI:10.3969/j.issn.1000-1441.2010.02.009 |
| [] | 陈钢花, 王永刚.2005. Faust公式在声波曲线重构中的应用[J]. 勘探地球物理进展, 28 (2) : 125–128. |
| [] | 陈清. 2011. 2.5维可控源电磁测深数据反演方法研究[硕士论文]. 北京:中国地质大学(北京). |
| [] | 陈晓, 于鹏, 张罗磊, 等.2011. 地震与大地电磁测深数据的自适应正则化同步联合反演[J]. 地球物理学报, 54 (10) : 2673–2681. DOI:10.3969/j.issn.0001-5733.2011.10.024 |
| [] | 陈晓, 李文乔, 郭曼, 等.2016. 大地电磁测深和重力数据贝叶斯联合反演[J]. 科学技术与工程, 16 (15) : 30–35. |
| [] | 冯锐.1985. 中国地壳厚度及上地幔密度分布(三维重力反演结果)[J]. 地震学报, 7 (2) : 143–157. |
| [] | 何樵登, 韩立国, 王德利. 2009. 地震勘探[M]. 4版. 北京:地质出版社. |
| [] | 侯征. 2013. 直流电阻率与瑞雷面波非线性联合反演方法研究[博士论文]. 北京:中国地质大学(北京). |
| [] | 李金铭.2005. 地电场与电法勘探[M]. . |
| [] | 李雄.1992. 地震-重力联合反演-不同的实现方式[J]. 天然气地球科学, 3 (5) : 37–42. |
| [] | 林剑, 敬荣中.2007. 一种基于地质模型的电性与速度界面不一致的联合反演方法[J]. 矿产与地质, 21 (6) : 668–672. |
| [] | 刘远. 2008. 地微动探测与大地电磁测深联合使用的研究[硕士论文]. 北京:中国地质大学(北京). |
| [] | 刘彦, 吕庆田, 孟贵祥, 等.2012. 大地电磁与地震联合反演研究现状与展望[J]. 地球物理学报, 27 (6) : 2444–2451. DOI:10.6038/j.issn.1004-2903.2012.06.019 |
| [] | 彭淼, 谭捍东, 姜枚, 等.2012. 利用接收函数和大地电磁数据联合反演南迦巴瓦构造结中部地区壳幔结构[J]. 地球物理学报, 55 (7) : 2281–2291. DOI:10.6038/j.issn.0001-5733.2012.07.014 |
| [] | 彭淼, 谭捍东, 姜枚, 等.2013. 基于交叉梯度耦合的大地电磁与地震走时资料三维联合反演[J]. 地球物理学报, 56 (8) : 2728–2738. DOI:10.6038/cjg.20130821 |
| [] | 仇根根. 2010. 大地电磁测深数据三维反演试算及可视化研究[硕士论文]. 北京:中国地质大学(北京). |
| [] | 索奎. 2013. 重震联合反演地壳上地幔密度结构[硕士论文]. 北京:中国地质大学(北京). |
| [] | 汤井田, 李晋, 肖晓, 等.2012. 数学形态滤波与大地电磁噪声压制[J]. 地球物理学报, 55 (5) : 1784–1793. DOI:10.6038/j.issn.0001-5733.2012.05.036 |
| [] | 王家映.Oldenburg D, LevyS.1985. 大地电磁测深的拟地震解释法[J]. 石油地球物理勘探, 20 (1) : 66–79. |
| [] | 王新胜, 方剑, 许厚泽, 等.2012. 华北克拉通岩石圈三维密度结构[J]. 地球物理学报, 55 (4) : 1154–1160. DOI:10.6038/j.issn.0001-5733.2012.04.011 |
| [] | 徐凯军, 杜润林, 刘展.2016. 海洋可控源电磁与地震一维联合储层参数反演[J]. 石油地球物理勘探, 51 (1) : 197–203. |
| [] | 杨辉, 戴世坤, 宋海斌, 等.2002. 综合地球物理联合反演综述[J]. 地球物理学进展, 17 (2) : 262–271. DOI:10.3969/j.issn.1004-2903.2002.02.011 |
| [] | 杨辉, 王家林, 吴建生, 等.2002. 大地电磁与地震资料仿真退火约束联合反演[J]. 地球物理学报, 45 (5) : 723–734. DOI:10.3321/j.issn:0001-5733.2002.05.015 |
| [] | 杨文采. 1997. 地球物理反演理论与方法[M]. 北京:地质出版社. |
| [] | 杨振武, 王家映, 张胜业, 等.1998. 一维大地电磁和地震数据联合反演方法研究[J]. 石油地球物理勘探, 33 (1) : 78–88. |
| [] | 于鹏, 王家林, 吴健生, 等.2007. 重力与地震资料的模拟退火约束联合反演[J]. 地球物理学报, 50 (2) : 529–538. DOI:10.3321/j.issn:0001-5733.2007.02.026 |
| [] | 周辉, 杨宝俊, 刘财.1994. 地震-大地电磁测深资料综合反演[J]. 地球物理学报, 37 (S1) : 477–485. |
| [] | 周辉, 刘财, 渠广学.1995. 地震-大地电磁数据非线性联合反演方法研究[J]. 长春地质学院学报, 25 (2) : 205–211. |
 2016, Vol. 31
2016, Vol. 31


