2. 中国石油化工股份有限公司西北油田分公司勘探开发研究院, 乌鲁木齐 830011
2. Exploration and Development Research Institute, Sinopec Northwest Oilfield Branch Corporation, Vrümqi 830011, China
地震图像增强(Seismic Image Enhance)不同于常规的地震资料去噪技术,它是指按照某一类应用的要求,对现有地震图像进行加工,以突出地震图像中某些信息,削弱或去除某些不需要的信息,增加特定信息的视觉分辨率,得到对具体应用来说更实用的地震图像,或将原地震图像转换成一种更适合人或机器进行分析处理的形式的处理方法.其宗旨是在不增加数据的内在信息含量的基础上,增加所选择特征的动态范围,以使其容易被检测到.信息特征范围的增大,也是极大地提高后续地震资料的判读、分析、识别、计量结果的准确性,减少地球物理、地质解释中的多解性.
随着高密度三维地震勘探的开展,对勘探精度的要求不断提高,尤其是四川盆地构造解释中小团块结构和成群发育的微小断裂体系研究,要求地震图像有很高的分辨率.同样现代层序地层学中地层层序横向变化研究等等,同样有待于地震图像分辨率的提高.地震纹理分析中,对地震图像分辨率的要求很高,其中微弱地震纹理信号和噪声的分离问题一直是一个难题.所以地震图像增强在很多实际地震资料解释应用场合中都具有必要性,因此一直是地震图像处理领域一个重要的研究课题.Höcker和Fehmers(2002)提出了基于地震图像的地震资料快速构造解释方法,紧接着许多研究者将扩散模型直接引入地震图像处理.Luo等(2002)把保边去噪引入到地震资料解释领域取得了较好的结果.Marfurt(2006)评估了各种滤波算法,得出如果要增强地震信号的细节特征就必须去除混杂在一起的随机噪声.并成功的把图像增强算法应用到各种地震属性提取计算中.
近些年,国内在构造倾向滤波技术这方面取得了长足的进步,包括中值滤波(刘财等,2007;刘洋等,2011;王伟等,2012)、 Kuwahara滤波(Bakker,2002)、扩散滤波等.由于全变分(TV,Total Variation)(Paulsen and Jiang,1996; Lieu and Vese,2008,陈勇等,2010;卢昕婷等,2015)图像去噪模型与偏微分计算的进步,基于全变分理论的偏微分方程进行图像去噪方法由线性扩散到非线性扩散、由简单单一方程实现到多类方程综合实现、由偏微分方程单步实现到多次迭代实现的改进,使其处理结果质量不断提高.孙夕平和杜世通(孙夕平等,2004)等应用相干增强各向异性扩散用于地震资料处理,处理结果品质提高有限,仅能反映大致轮廓,对于细节刻画不准确.陈凤和李金宗等(陈凤等,2004)、王绪松和杨长春(王绪松和杨长春,2006)运用非线性各向异性扩散对地震图像进行增强处理,所得处理结果品质明显提高,但未分别对待边缘区域和细节纹理区域.杨宁和贺振华等(杨宁等,2010)提出利用地震复数道信息来构建结构张量的地震图像增强算法,但该方法尚未推导出三维地震图像增强算法.杨培杰(杨培杰等,2010)提出了方向性边界保持断层增强技术,该技术在保持方向性的基础上提高了断层的自动识别率.钟勇和王山山等(钟勇等,2011)提出了边缘定向的扩撒模型,并讨论了边缘定向参数的选择.(Wen Xiao-Tao和He Zhen-Hua等Wen et al.,2011)提出了基于方向滤波的地质体突出显示方法,并且推导和分析了扩散门限参数选取的原则,但没有讨论结果显示好坏的评价方式.Gao(Gao,2011)分析了地震纹理在储层预测中的应用,并指出新的基于纹理统计分析的地震图像增强方法.在实际应用中构造导向滤波技术有效的压制随机噪声、保护地层边界信息(张尔华等,2010).
本文的核心内容为全变分图像分解模型结合偏微分方程(PDE,Partial Differential Equations)的地震图像增强技术,从新的角度出发把地震图像分解为结构和纹理部分,针对不同的部分“对症下药”,结合构造倾向滤波技术(SOF,Structure-oriented Filter)(Fehmers and Höcker,2003),在不增加数据的内在信息含量的基础上,间接地扩展了频带的动态范围,提高了地震图像的空间分辨率.
1 全变分地震数据分解模型参照Rudin-Osher-Fatemi(ROF)(2002)模型理论,我们把二维地震剖面或三维地震数据体简记为

|
(1) |
其中f为原始地震图像,定义e(原地震数据的近似)为地震数据的结构分量(即地震图像光滑部分).而n也不是原来所称的噪声,被称为地震数据的纹理分量(包含纹理和噪声,即地震图像振荡部分).如果地震数据处理中随机噪声与相干噪声得到有效的压制,那么n则趋近于地震图像的真实纹理.地震图像f分解为e+n是一个逆问题,可通过能量泛函极小化和迭代全变分正则化来实现,其一般形式为

|
(2) |
其中F1(e),F2(n)为非负函数,其中函数或者分布空间X1={e:F1(e)<∞},X2={n:F2(n)<∞}.假设x∈X1+X2,那么常量λ>0为协调参数,用于协调F1(e)与F2(n)之间的权重.通常F1(e),F2(n)为函数空间的范数或半范数(即F1(e)=eX1,F2(n)=nX2),对应的模型称为(X1,X2)模型.
本文的研究重点为TV-L1模型:
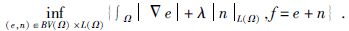
|
(3) |
上式为L1范数的各向异性全变分(L1-based anisotropic TV),虽然该问题为凸,但并不是严格凸的,所以局部最小值不是唯一的,需要在离散化时加入边界条件.
2 TV-L1模型分解算法 2.1 算法原理全变分最小化问题是一个典型的凸优化问题,难点在于目标函数通常为非光滑的函数.为了解决该问题,我们引入Chambolle-Pock算法(Chambolle and Pock,2011).假设X,Y为两个有限维度的实向量空间,并且存在映射K:X→Y 为连续线性算子,同时满足以下范数,公式为
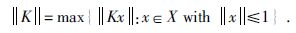
|
(4) |
那么文中的全变分最小化的凸问题即为求取广义鞍点问题,公式为

|
(5) |
这里G:X→[0,+∞),F*:Y→[0,+∞)为真凸、下半连续的函数,F*为下半连续的函数F的凸共轭函数.我们假定这些问题至少有一个解

|
(6) |
其中φF*与φG分别为凸函数F*与G的次梯度.同时假设F与G为“简单”函数,可得到近似算子为

|
(7) |
其中最右边等式为次微分表达式.
2.2 离散化处理TV-L1模型的Chambolle-Pock离散解法可导出原对偶问题,公式为
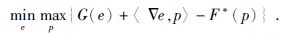
|
(8) |
至此我们可采用Chambolle原对偶算法来解决此凸优化问题,得到近似算子为
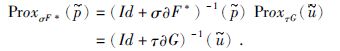
|
(9) |
由于
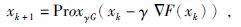
|
(10) |
对分解后的地震数据e(结构分量)与n(纹理分量和高频随机噪声)分别进行分析,针对不同的应用,可对不同的分量进行基于倾向扩散因子的SOF地震图像增强(杨宁等,2010).
首先利用希尔伯特变换求取瞬时频率ω 与瞬时波数k,则瞬时倾向p为
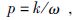
|
(11) |
采用瞬时倾向p与倾角的关系来构造结构张量为
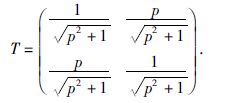
|
(12) |
由各向异性扩散张量D导出基本的扩散方程为
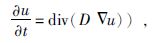
|
(13) |
式中:D为各向异性扩散张量;Δ为梯度算子;u为原始地震信号.代入平滑方程,得到
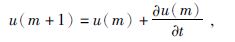
|
(14) |
式中:u(m)为原始地震信号;u(m+1)为扩散算子平滑后信号;m为迭代次数,如果只是去除高频随机噪声,可只对纹理分量进行处理,m取2~4即可;若为图像增强,对结构分量与纹理分量分别进行处理,则m宜取5~20.
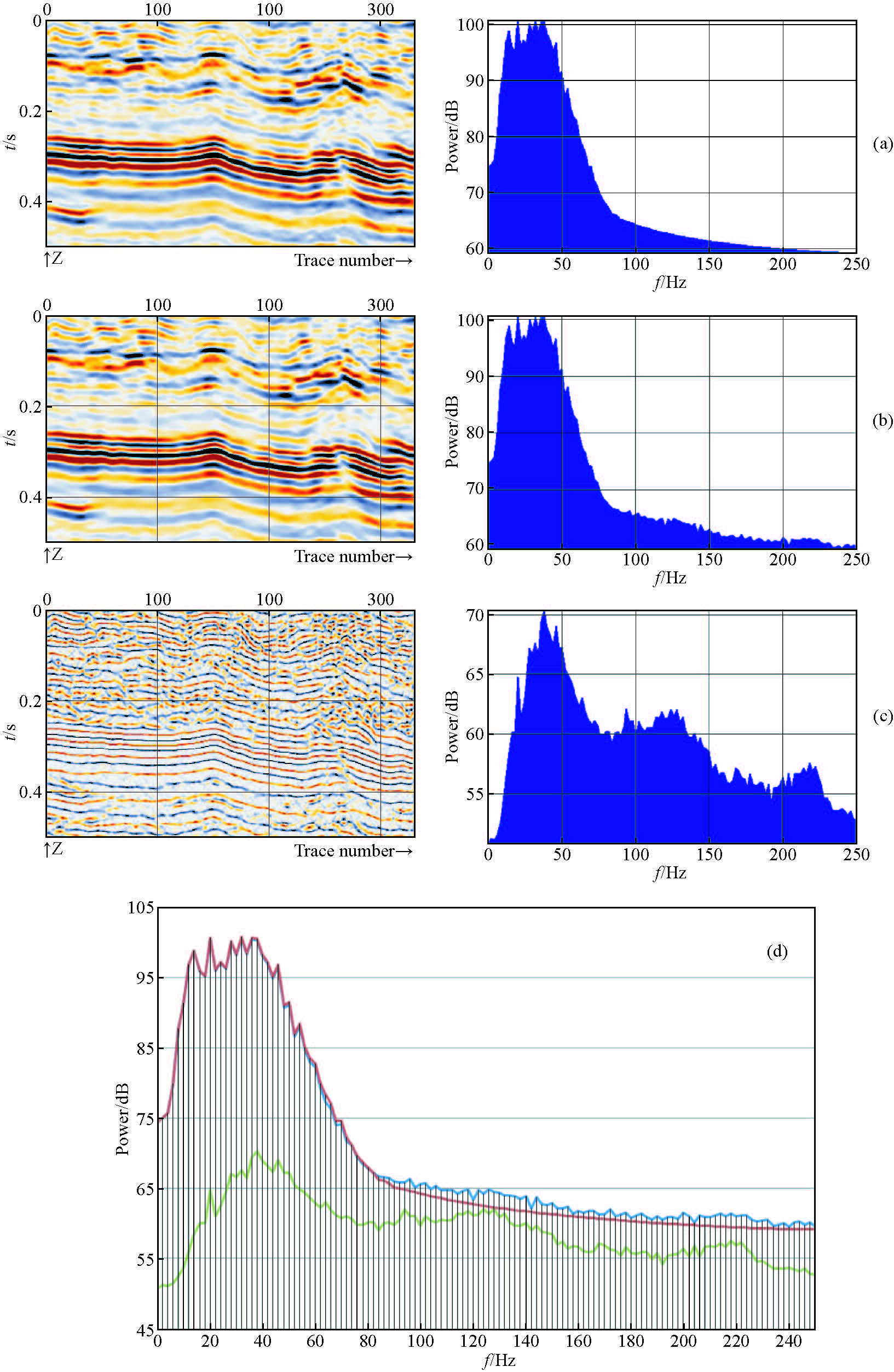
4 算例分析 4.1 TV-L1地震数据分解模型算例1图 1中1a图左为某区叠后地震数据,右为该数据的振幅谱.图 1b为λ=0.001时分解后的结构分量(左图)与振幅谱(右图).结构分量图像接近原始地震图像,其振幅谱(1a右图、1b右图、1d图)的统计分布也是相近的,但是受分解参数以及数值计算的影响,当频率80~250 Hz区间的能量出现些许增强,其包络线形态与原始数据振幅谱包络线是一致的;图 1c为分解后的纹理分量(左图)与振幅谱(右图).纹理分量其主频与原始数据主频不一致、能量较结构分量弱,从振幅谱看出频率80~250 Hz区间内能量得到相对“增强”,近似于起到拓频的作用,间接提高了地震图像的空间分辨率,突出了地质构造的地震响应特征,进而方便地震资料解释人员的研究工作.
|
图 1 地震数据分解与振幅谱 (a)原始地震图像与振幅谱;(b)结构分量地震图像与振幅谱;(c)纹理分量地震图像与振幅谱;(d)红线为原始地震图像振幅谱包络线、蓝线为结构分量地震图像振幅谱包络线、绿线为纹理分量地震图像振幅谱包络线. Figure 1 Seismic data decomposition and amplitude spectrum (a)Original seismic image and Amplitude spectrum;(b)Structural component and Amplitude spectrum;(c)Texture component and Amplitude spectrum;(d)The red line for the original seismic image amplitude spectrum envelope,the blue line for structure component for amplitude spectrum envelope,green line for texture component for amplitude spectrum envelope. |
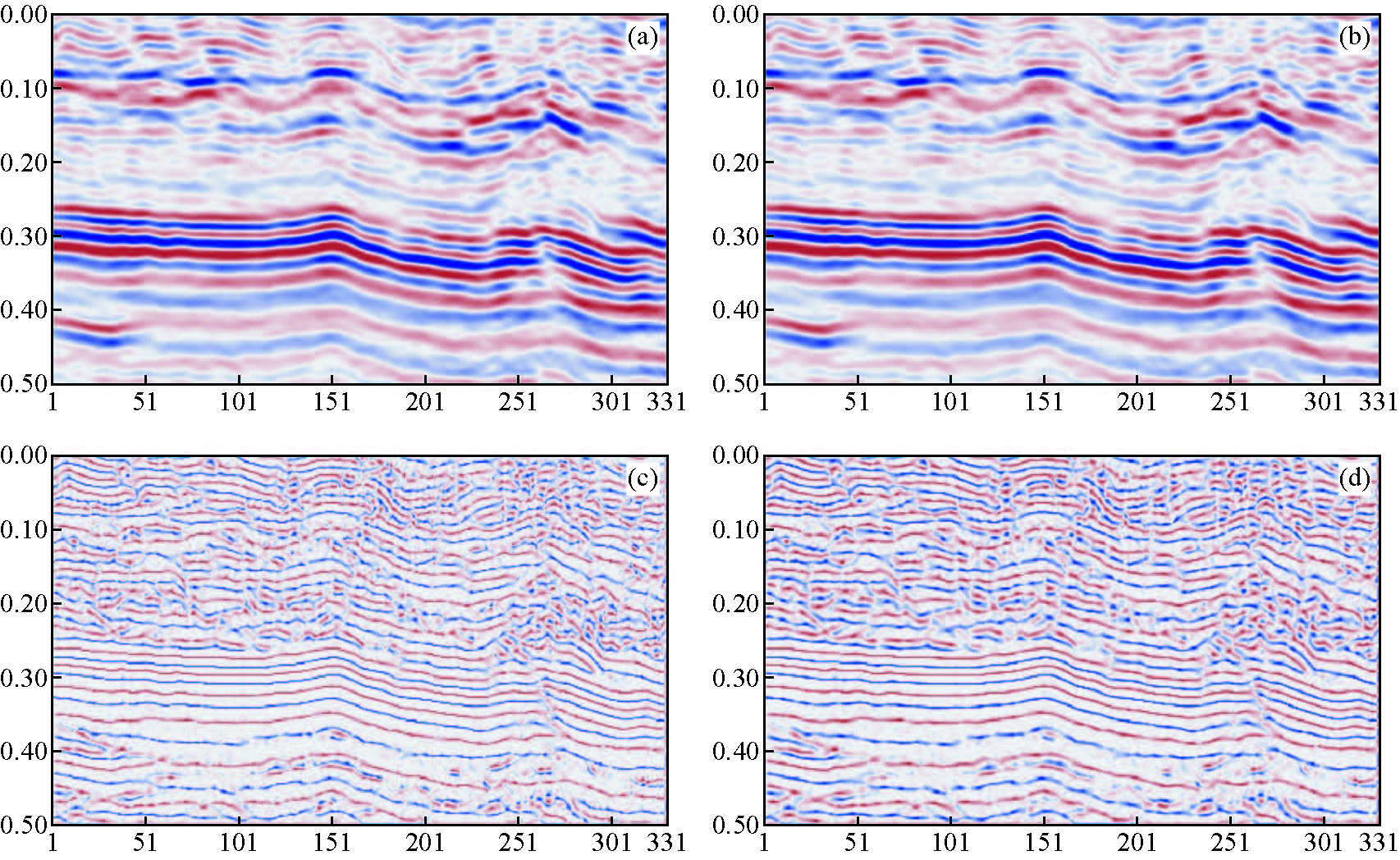
图 2为图 1数据原始数据与纹理分量增强后的结果对比.在构造解释和曲率分析中我们常常采用SOF地震图像增强方法,然而在某些情况下该方法并不能取得较好的结果.2a为原始地震数据,由于该区域目的层反射能量很大,地下构造较为平缓,地震图像增强后(见图 2b)结果对比差距不大,并不能有效地进行反射特征分析.本文采用TV-L1分解模型结合构造倾向地震图像增强方法,仅需对纹理分量进行增强,消除了由于高频噪声与计算噪声带来的平缓部分阶梯状现象(见图 2c、2d中0.3~0.4 s,51~151道区域),是反射特征更加清晰,断层更易于分析,该结果可直接用于层位追踪、曲率分析等等.
|
图 2 TV-L1地震数据分解与增强结果算例 (a)原始地震图像(数据增益2%);(b)原始地震图像增强后结果(数据增益2%); (c)纹理分量结果(数据增益2%);(d)纹理分量做增强后的结果(数据增益2%). Figure 2 Base on TV-L1 model seismic data decomposition and enhancement results (a)Original seismic image(gain 2%);(b)Seismic image enhancement results(gain 2%); (c)Texture component(gain 2%);(d)Texture component enhancement results(gain 2%). |
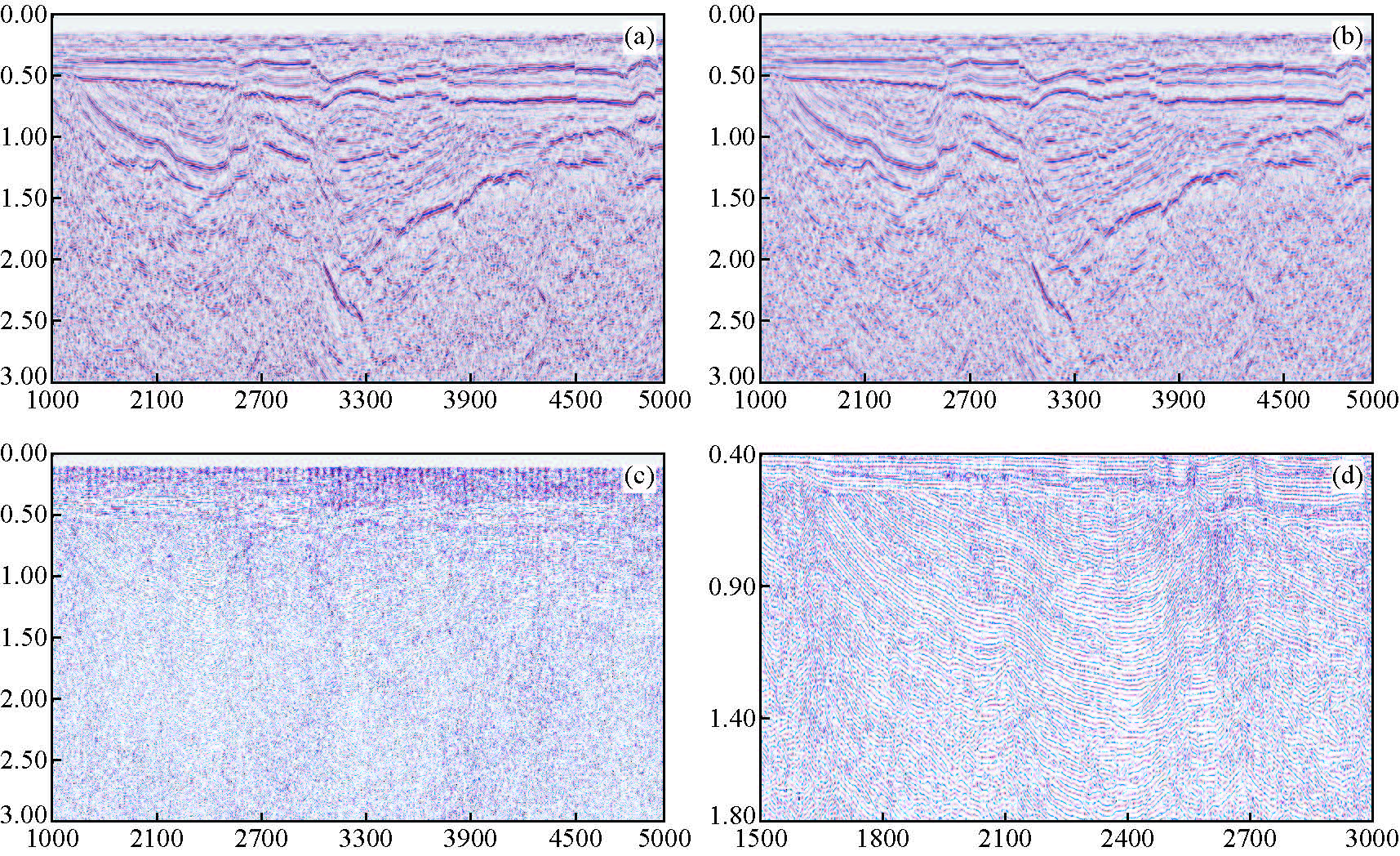
我们选取东北某区地震数据(见图 3a数据为1500~3000道,时间为0~3000 ms,采样率为2 ms),图 3b、图 3c为当λ=0.001时结构与纹理分量的地震图像,其中图 3c、图 3d为进行地震图像增强处理后的纹理分量部分,在0~500 ms区间多为浅层低速带,地震散射现象明显,地震剖面纹理丰富且较杂乱.500 ms后的数据,随着深度增加地震纹理结构越发清晰,其碟状平行地震纹理特征明显,并在边界处伴有断层特征,为典型的盆地坳陷构造.
|
图 3 λ=0.001地震数据分解与增强结果 (a)原始地震图像;(b)结构分量地震图像;(c)纹理分量地震图像; (d)400~1800 ms区间纹理分量地震图像增强结果(某盆地坳陷构造). Figure 3 λ=0.001 seismic data decomposition and enhance results (a)Original seismic image;(b)Structural component results; (c)Texture component results;(d)400~1800 ms texture component enhancement results. |
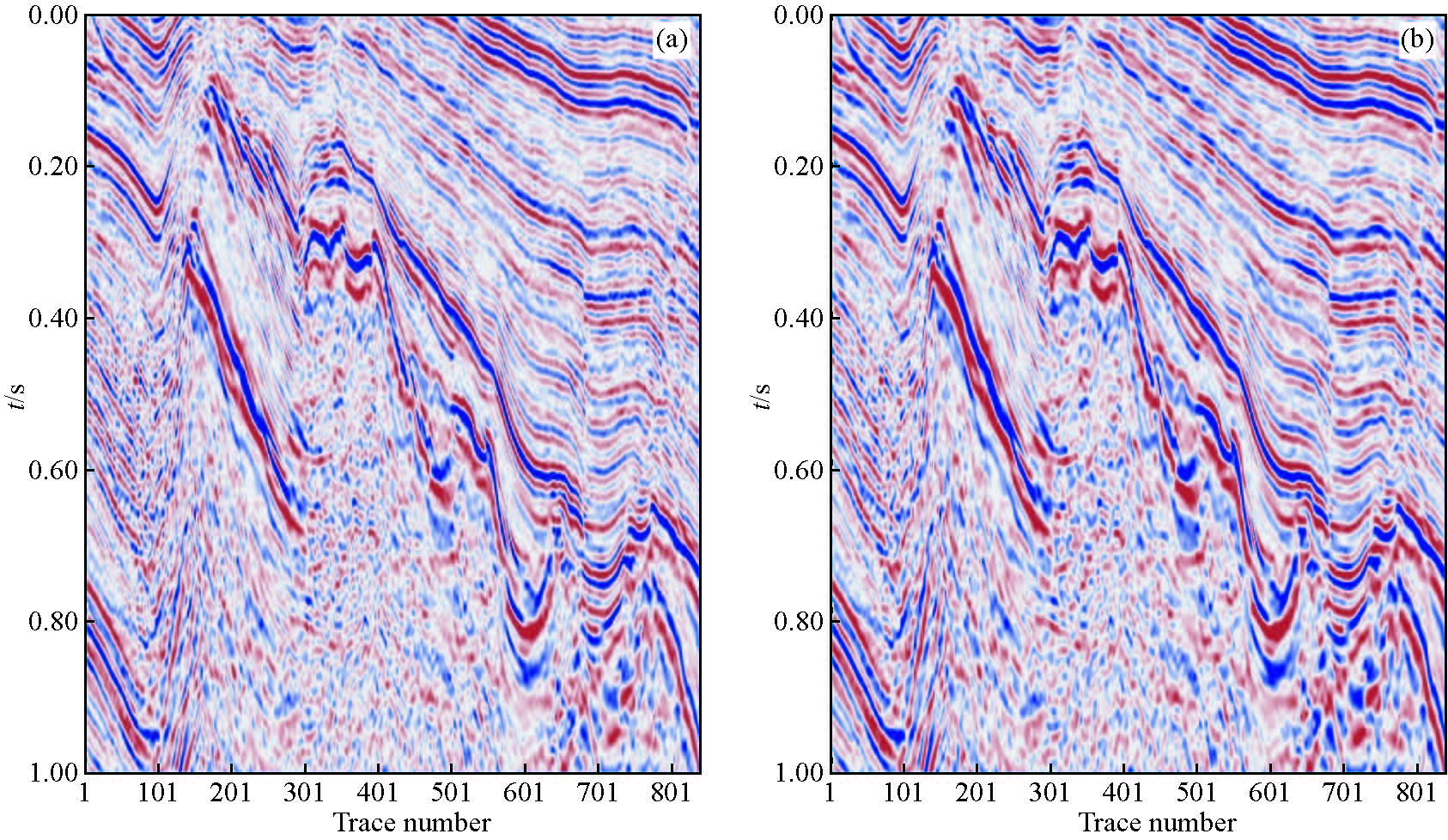
中国西部H地区数据(图 4).该数据信噪比较低,反射同相轴连续性较差.b图为处理后的H地区地震剖面,与a图对比可看出在红色线框圈定范围(时间0.25~0.80 s,CMP号400~650)反射同相轴变得更加平滑,且连续性更好;红色箭头(时间0.4 s,CMP号800)所指处的逆断层比原始剖面更加明显,并且没有破坏其他层位信息.
|
图 4 λ=0.001高陡构造地震反射区增强结果 (a)中国西部H地区较低信噪比原始地震剖面;(b)增强处理后的H地区地震剖面. Figure 4 λ=0.001 High steep structure seismic reflection area enhancement results (a)Original seismic image;(b)Seismic image enhancement results. |
本文把地震振幅属性结合TV-L1地震数据分解理论,建立地震图像结构与纹理分量的数学模型,从理论推导和实际数据验证结果表明TV-L1地震数据分解模型能够较为精确地刻画地震纹理信息,同时结合基于倾向扩散因子的SOF地震图像增强方法分别对两部分进行增强处理.从最终的结果上来看该模型的地震图像增强方法不仅起到近似于起到拓频的作用,同时间接的提高了地震图像空间分辨率,突出了地质构造的地震响应特征,利于地震资料解释人员的研究工作.给予TV-L1地震数据分解模型的地震图像增强方法让我们从整个剖面的振幅特征角度来研究地震数据,不同于常规的单一地震道数据统计分析或后小波基类的地震信号多维数学变换,为刻画地震响应特征的基础性研究工作.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Bakker P. 2002. Image structure analysis for seismic interpretation[Ph. D. thesis]. Delft TU:Delft University of Technology. |
| [] | Chambolle A, Pock T .2011. A first-order primal-dual algorithm for convex problems with applications to imaging[J]. Journal of Mathematical Imaging and Vision, 40 (1) : 120–145. DOI:10.1007/s10851-010-0251-1 |
| [] | Chen F, Li J Z, Chen D D, et al .2004. A model of nonlinear anisotropic diffusion for increasing signal to noise ratio of seismic image[J]. Petroleum Exploration and Development (in Chinese), 31 (2) : 77–80. |
| [] | Chen Y, Han B, Xiao L, et al .2010. Multiscale total variation method and its application on time-lapse seismic[J]. Chinese Journal of Geophysics (in Chinese), 53 (8) : 1883–1892. DOI:10.3969/j.issn.0001-5733.2010.08.014 |
| [] | Fehmers G C, Höcker C F W .2003. Fast structural interpretation with structure-oriented filtering[J]. Geophysics, 68 (4) : 1286–1293. DOI:10.1190/1.1598121 |
| [] | Gao D L .2011. Latest developments in seismic texture analysis for subsurface structure, facies, and reservoir characterization:A review[J]. Geophysics, 76 (2) : W1–W3. DOI:10.1190/1.3553479 |
| [] | Höcker C, Fehmers G .2002. Fast structural interpretation with structure-oriented filtering[J]. The Leading Edge, 21 (3) : 238–243. DOI:10.1190/1.1463775 |
| [] | Lieu L H, Vese L A .2008. Image restoration and decomposition via bounded total variation and negative Hilbert-sobolev spaces[J]. Applied Mathematics and Optimization, 58 (2) : 167. DOI:10.1007/s00245-008-9047-8 |
| [] | Liu C, Li H X, Tao C H, et al .2007. A new fuzzy nesting multilevel median filter and its application to seismic data processing[J]. Chinese Journal of Geophysics (in Chinese), 50 (5) : 1534–1542. DOI:10.3321/j.issn:0001-5733.2007.05.030 |
| [] | Liu Y, Wang D, Liu C, et al .2011. Weighted median filter based on local correlation and its application to poststack random noise attenuation[J]. Chinese Journal of Geophysics (in Chinese), 54 (2) : 358–367. DOI:10.3969/j.issn.0001-5733.2011.02.012 |
| [] | Lu X T, Han L G, Zhang P, et al .2015. Direct migration method of multi-source blended data based on total variation[J]. Chinese Journal of Geophysics (in Chinese), 58 (9) : 3335–3345. DOI:10.6038/cjg20150926 |
| [] | Luo Y, Marhoon M, Al Dossary S, et al .2002. Edge-preserving smoothing and applications[J]. The Leading Edge, 21 (2) : 136–158. DOI:10.1190/1.1452603 |
| [] | Marfurt K J .2006. Robust estimates of 3D reflector dip and azimuth[J]. Geophysics, 71 (4) : P29–P40. DOI:10.1190/1.2213049 |
| [] | Meyer Y. 2002. Oscillating patterns in image processing and nonlinear evolution equations:The fifteenth Dean Jacqueline B. Lewis memorial lectures, University lecture series volume 22[M]. Boston:American Mathematical Society. |
| [] | Paulsen K D, Jiang H B .1996. Enhanced frequency-domain optical image reconstruction in tissues through total-variation minimization[J]. Applied Optics, 35 (19) : 3447–3458. DOI:10.1364/AO.35.003447 |
| [] | Sun X P, Du S T, Tang L .2004. Coherent-enhancing anisotropic diffusion filtering technique[J]. Oil Geophysical Prospecting (in Chinese), 39 (6) : 651–655. |
| [] | Wang X S, Yang C C .2006. An edge-preserving smoothing algorithm of seismic image using nonlinear anisotropic diffusion equation[J]. Progress in Geophysics (in Chinese), 21 (2) : 452–457. DOI:10.3969/j.issn.1004-2903.2006.02.017 |
| [] | Wen X T, He Z H, Huang D J, et al .2011. Highlighting display of geologic bodies based on directivity filtering[J]. Applied Geophysics, 8 (4) : 355–362. DOI:10.1007/s11770-011-0305-1 |
| [] | Yang N, He Z H, Wen X T, et al .2010. SOF seismic image enhancement method based on the dip diffusion factor[J]. Oil Geophysical Prospecting (in Chinese), 45 (6) : 833–835. |
| [] | Yang P J, Mu X, Zhang J C .2010. Orientational edge preserving fault enhance[J]. Chinese Journal of Geophysics (in Chinese), 53 (12) : 2992–2997. DOI:10.3969/j.issn.0001-5733.2010.12.023 |
| [] | Zhang E H, Wang W, Gao J H, et al .2010. Non-linear anisotropic diffusion filtering for 3D seismic noise removal and structure enhancement[J]. Progress in Geophysics (in Chinese), 25 (3) : 866–870. DOI:10.3969/j.issn.1004-2903.2010.03.019 |
| [] | Zhong Y, Wang S S, Chen L .2011. Application of structure enhancement diffusion to seismic data interpretation[J]. Journal of Chengdu University of Technology (Sciences & Technology Edition) (in Chinese), 38 (2) : 121–125. |
| [] | 陈凤, 李金宗, 李冬冬, 等.2004. 提高地震图像信噪比的非线性各向异性扩散算法模型[J]. 石油勘探与开发, 31 (2) : 77–80. |
| [] | 陈勇, 韩波, 肖龙, 等.2010. 多尺度全变分法及其在时移地震中的应用[J]. 地球物理学报, 53 (8) : 1883–1892. DOI:10.3969/j.issn.0001-5733.2010.08.014 |
| [] | 刘财, 李红星, 陶春辉, 等.2007. 模糊嵌套多级中值滤波方法及其在地震数据处理中的应用[J]. 地球物理学报, 50 (5) : 1534–1542. DOI:10.3321/j.issn:0001-5733.2007.05.030 |
| [] | 刘洋, 王典, 刘财, 等.2011. 局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用[J]. 地球物理学报, 54 (2) : 358–367. DOI:10.3969/j.issn.0001-5733.2011.02.012 |
| [] | 卢昕婷, 韩立国, 张盼, 等.2015. 基于全变分原理的多震源混合数据直接偏移方法[J]. 地球物理学报, 58 (9) : 3335–3345. DOI:10.6038/cjg20150926 |
| [] | 孙夕平, 杜世通, 汤磊.2004. 相干增强各向异性扩散滤波技术[J]. 石油地球物理勘探, 39 (6) : 651–655. |
| [] | 王绪松, 杨长春.2006. 对地震图像进行保边滤波的非线性各向异性扩散算法[J]. 地球物理学进展, 21 (2) : 452–457. DOI:10.3969/j.issn.1004-2903.2006.02.017 |
| [] | 杨宁, 贺振华, 文晓涛, 等.2010. 基于倾向扩散因子的SOF地震图像增强方法[J]. 石油地球物理勘探, 45 (6) : 833–835. |
| [] | 杨培杰, 穆星, 张景涛.2010. 方向性边界保持断层增强技术[J]. 地球物理学报, 53 (12) : 2992–2997. DOI:10.3969/j.issn.0001-5733.2010.12.023 |
| [] | 张尔华, 王伟, 高静怀, 等.2010. 非线性各向异性扩散滤波器用于三维地震资料噪声衰减与结构特征增强[J]. 地球物理学进展, 25 (3) : 866–870. DOI:10.3969/j.issn.1004-2903.2010.03.019 |
| [] | 钟勇, 王山山, 陈磊.2011. 结构增强扩散在地震资料构造解释中的应用[J]. 成都理工大学学报(自然科学版), 38 (2) : 121–125. |
 2016, Vol. 31
2016, Vol. 31

