2. 武汉大学测绘遥感信息工程国家重点实验室, 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying、Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
函数逼近问题可归为两大类问题:第一大类问题是根据未知函数的有限数据(通常是观测数据)来构造该函数的逼近,也即数据逼近问题;第二大类问题是根据发生于各种物理过程中的数学模型寻求方程解的问题,通常只有最简单的特定问题,该方程的解才能显式地表达出来,当不能得到方程的显式解,或者显式解的数学表达式非常复杂时,就要采用数值方法,即利用数值方法对方程的解进行逼近(马利敏,2009).重力场逼近的本质就是偏微分方程的求解,属于第二大类函数逼近问题.
利用径向基函数(Radial Basis Function,RBF)求解偏微分方程是近年来受到普遍关注的一种数值方法(陈荣华,2005).径向基函数是一种比较简单的多元函数,或者说是事实上的一元函数,具有形式简单、各向同性、节点配置灵活、精度相对较高、自适应强等优点,可以逼近几乎所有的函数(吴宗敏,2002).近年来,许多学者也将径向基函数方法应用于重力场逼近中,取得一些较好逼近效果( Schmidt et al.,2007; Tenzer and Klees,2008; Antoni et al.,2009; Klees et al.,2009; Wittwer,2009; 吴星等,2009;Weigelt et al.,2010; 吴怿昊等,2016).本文根据径向基函数的基本定义和重力场逼近的基本性质,介绍满足重力场逼近调和函数性质的四种径向基核函数,给出这些核函数在空间直角坐标系和球坐标系下的解析表达式及它们的Legendre级数展开式,并通过规格化比较分析它们的空间特性和频域特性.
1 径向基函数根据E.M. Stein和G. Weiss的定义(Stein and Weiss,1971),径向函数就是满足:如果||x1||=||x2||(||·||是Euclidean范数),那么Ψ(x1)=Ψ(x2)的函数Ψ,即仅依赖于l=||x||的函数.径向基函数是这样的函数空间:给定一个函数Ψ:R+→R,在定义域x∈Rd上,所有形如Ψ(||x,xj||)=Ψ(||x-xj||)及其线性组合张成的函数空间称为由函数Ψ导出的径向基函数空间.在一定条件下,只要取{xj}两两不同,{Ψ||x-xj||}就是线性无关的,从而形成径向基函数空间中某子空间的一组基.当{xj}几乎充满R时,{Ψ||x-xj||}及其线性组合可以逼近几乎任何函数.有的文献中也给径向基函数加上一个形状参数(shape parameter)c,即Ψ(||x-xj||)的形式变为Ψ||(x-xj||,c).可以看出,径向基函数是局部分布、中心径向对称、非负衰减的非线性函数,其函数相应只依赖于相对基函数中心点xj的距离.
径向基函数的研究就是研究形如Ψ(||·-xj||)的函数张成的函数空间及其性质和如何利用这个函数空间来解决一般事物的函数描述问题.许多实际问题进行数学抽象后会成为一个各向同性的问题,这样的问题往往会导出径向基函数的表示(吴宗敏,1998).目前被广泛研究和应用的径向基核函数有Kriging方法的高斯函数、Markov分布函数、Hardy的MultiQuadric(MQ)函数、逆MultiQuadric(IMQ)函数和Duchon的薄板样条函数等.
|
|
表 1 几种常见的径向基核函数 Table 1 Types of radial basis kernel functions |
对于函数逼近中第一类函数逼近问题,利用径向基函数进行逼近即为寻找如下形式的近似函数,公式为
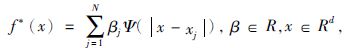
|
(1) |
并且满足条件:
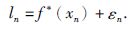
|
(2) |
对于函数逼近中第二类函数逼近问题,利用径向基函数进行逼近即为寻找如下形式的近似函数,公式为
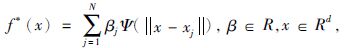
|
(3) |
并且满足条件:
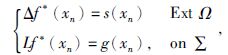
|
(4) |
在确定了某一类形式径向基核函数后,上述函数逼近问题则变为基函数中心{xj}以及参数βj的非线性最优估计问题.
2 重力场逼近中的径向基核函数定义:ΩR={xR∈R3|xR=R}为三维空间中任意一球面,x,y∈R3为空间中两点,其中x={(x1,x2,x3)T|x≥R}为球外部空间点,y={(y1,y2,y3)T|y<R}为球内部空间点,g(xn)为球外部空间的观测场元,则球外部扰动位T(x)可用径向基函数表示为
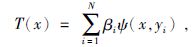
|
(5) |
式中,βi是基函数的系数.T(x)必须满足条件为
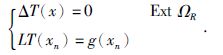
|
(6) |
应用径向基函数进行函数逼近,首先需要解决的是如何根据研究的对象选择和构造合适的径向基核函数.重力场逼近的理论基础是重力边值问题,应用径向基函数进行地球外部重力场逼近,选择和构造的核函数必需满足Laplace方程,也即必需为调和函数.目前常用的满足重力场逼近中调和函数性质的径向基核函数有IMQ核函数、Poisson核函数、径向多级子(Radial multipole)函数、Poisson小波核函数等.
2.1 IMQ核函数IMQ核函数是Hardy(1971)提出的一种逆多面函数,因其强大的逼近性能被广泛应用各种函数逼近中.它的解析表达式为
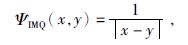
|
(7) |
对于重力场逼近而言,IMQ核函数实际上就是被广泛研究的点质量模型.因为是源于重力位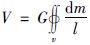
Poisson核函数的解析表达式为(Klees et al.,2008):
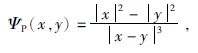
|
(8) |
它源于Poisson积分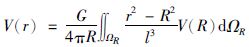
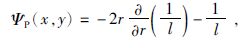
|
(9) |
因为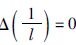
径向多级子核函数的解析表达式为(Marchenko et al.,2001):
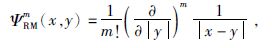
|
(10) |
当m=0时,其就是IMQ核函数.当m=1时,径向多级子核函数为
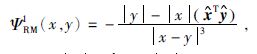
|
(11) |
式中,$\hat{x}=x/|x|$和$\hat{y}=y/|y|$是x,y的单位矢量.
当m≥2时,径向多级子核函数可通过下面公式递归计算:
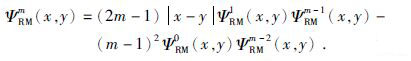
|
(12) |
Poisson小波核函数的解析表达式为(Witter,2009):
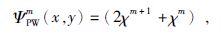
|
(13) |
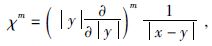
|
(14) |
可以看出,零阶Poisson小波就是Poisson核函数,公式为
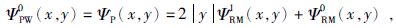
|
(15) |
高阶Poisson小波函数为
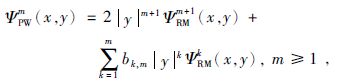
|
(16) |
式中m≤9的系数bk,m见表 2(Tenzer and Klees,2008).
|
|
表 2 Poisson小波函数的系数{bk,m,k=1,…,m;m≤9} Table 2 Coefficients {bk,m,k=1,…,m;m≤9} to compute Poisson wavelets |
球坐标系对于描述地球外部空间更为直观方便,在重力场逼近中,通常采用球坐标来表示,本文给出径向基函数在球坐标下的表示形式.令n:=[cosφ cosλ,cosφsinλ,sinφ]T为球坐标表示的单位矢量,其中φ和λ分别表示地心纬度和经度,则空间两点x,y∈R3在球坐标系下可分别表示为(x,φx,λx),(y,φy,λy).在笛卡尔直角坐标系下,径向基函数表示为与两点间距离相关的函数Ψ(l),距离l可表示为
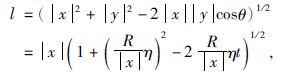
|
(17) |
其中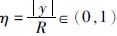
将上式代入径向基核函数Ψ(x,y),则Ψ(x,y)在球坐标下表示为Ψ(x,t,η).再令|x|=R=1,使x变为单位球面上的矢量nx,y为单位球内的矢量ηny,则Ψ(x,t,η)变为在单位球上表示的两点间球心角距和宽度参数相关的函数Ψ(t;η).本文将在单位球上表示的径向基函数也称为球径向基函数(SBF,Spherical basis functions).为便于对径向基函数的空间和频域特性进行分析,下面给出前面四种径向基核函数在单位球面上的表示及其规格化后的形式.
3.1 单位球上的IMQ核函数IMQ径向基核函数在单位球上的形式为
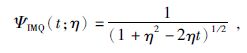
|
(18) |
规格化后的IMQ核函数为
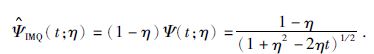
|
(19) |
Poisson核函数在单位球上的形式为
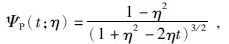
|
(20) |
规格化后的Poisson核函数为
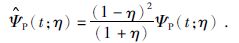
|
(21) |
径向多级子核函数在单位球上的形式为
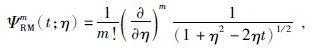
|
(22) |
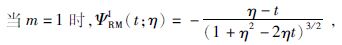
|
(23) |
当m≥2时,径向多级子核函数可通过下面公式递归计算:
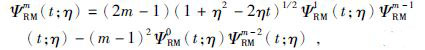
|
(24) |
规格化后的多级子核函数为
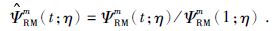
|
(25) |
Poisson小波核函数在单位球上的形式为
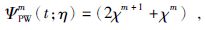
|
(26) |
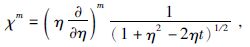
|
(27) |
可以看出,零阶Poisson小波就是Poisson核函数,公式为
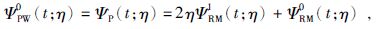
|
(28) |
高阶Poisson小波函数为
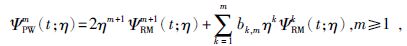
|
(29) |
规格化后的Poisson小波函数为
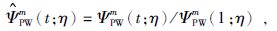
|
(30) |
很容易可以看出,上述径向基函数和球径向基函数之间有如下简单的关系:
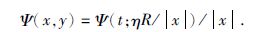
|
(31) |
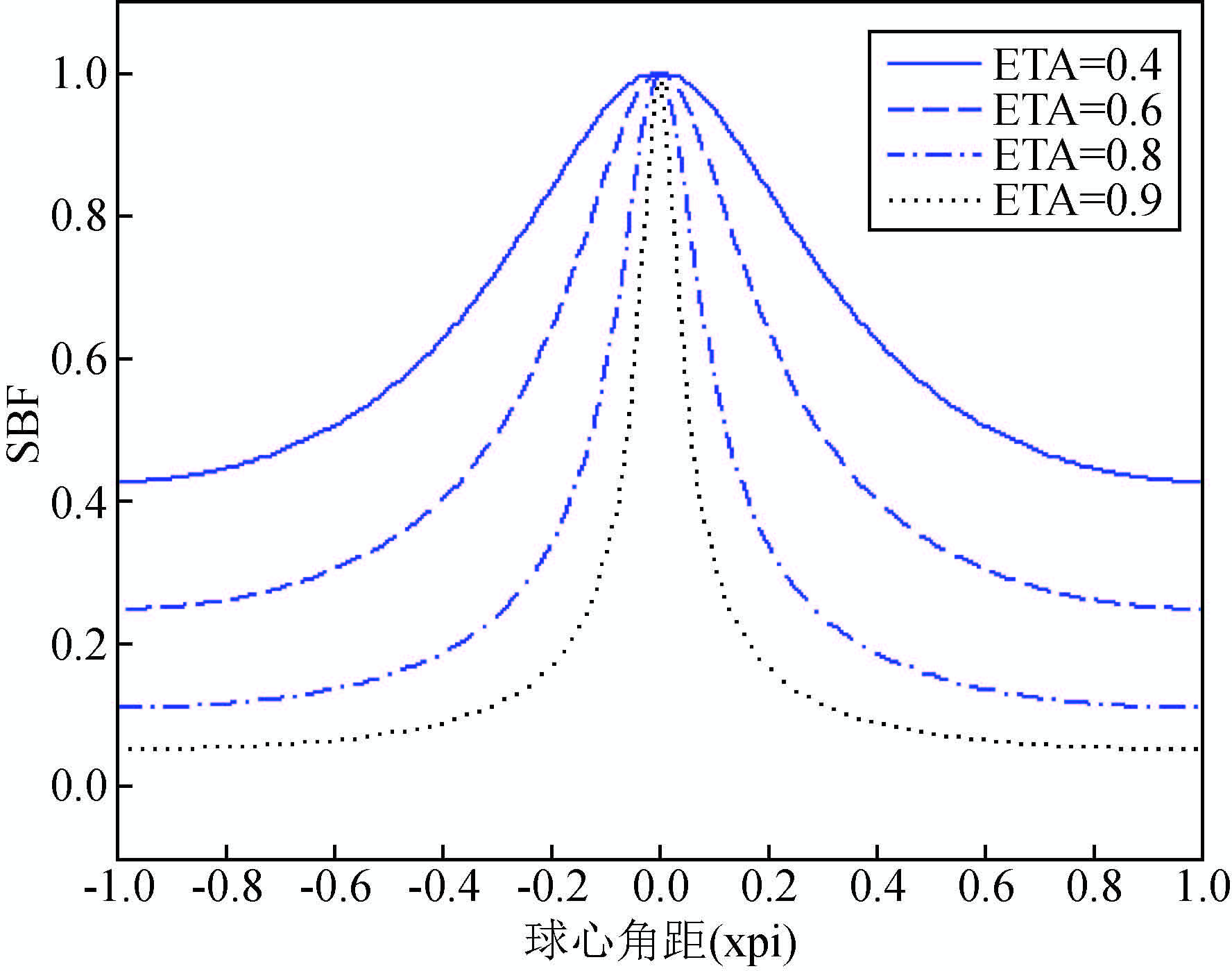
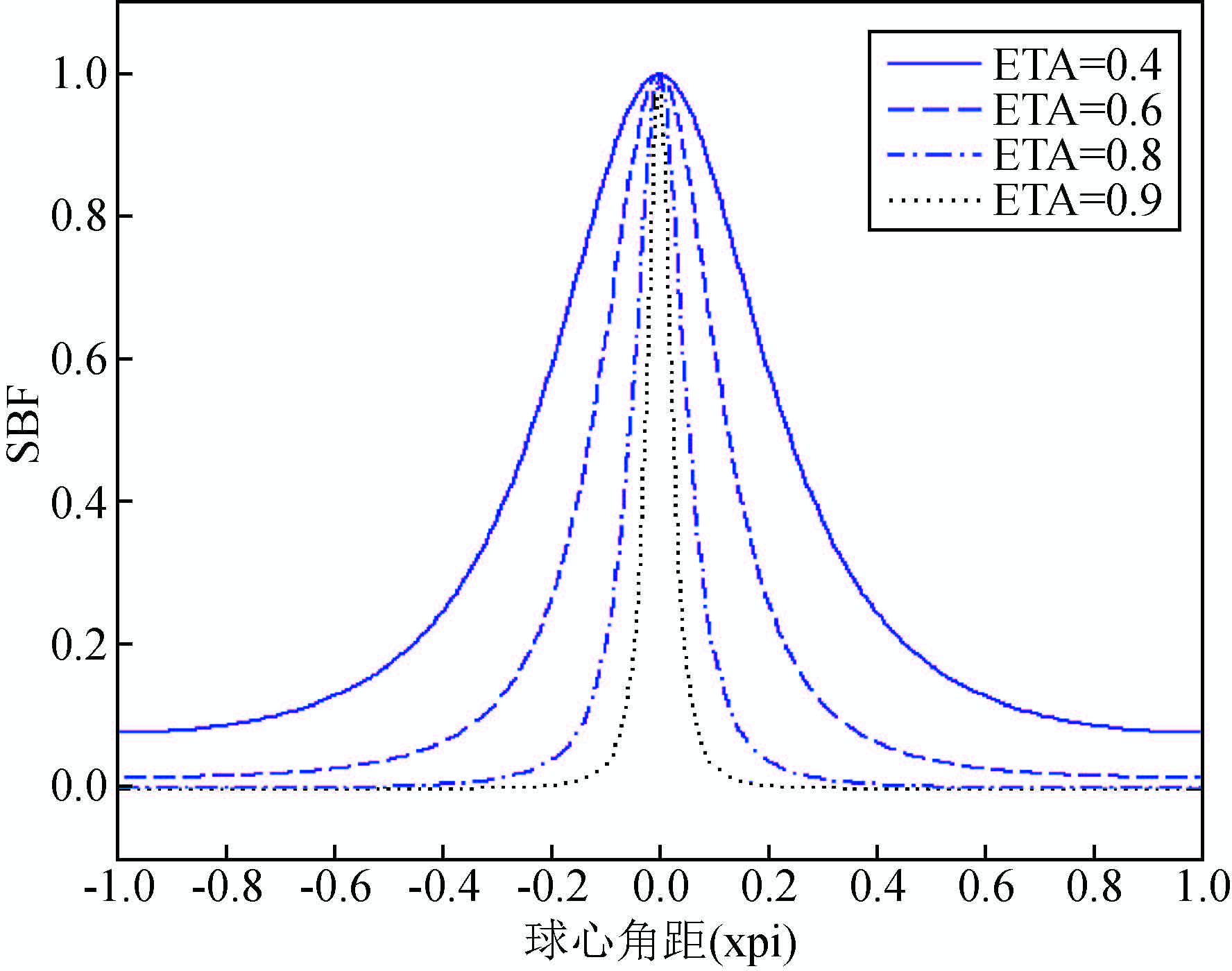
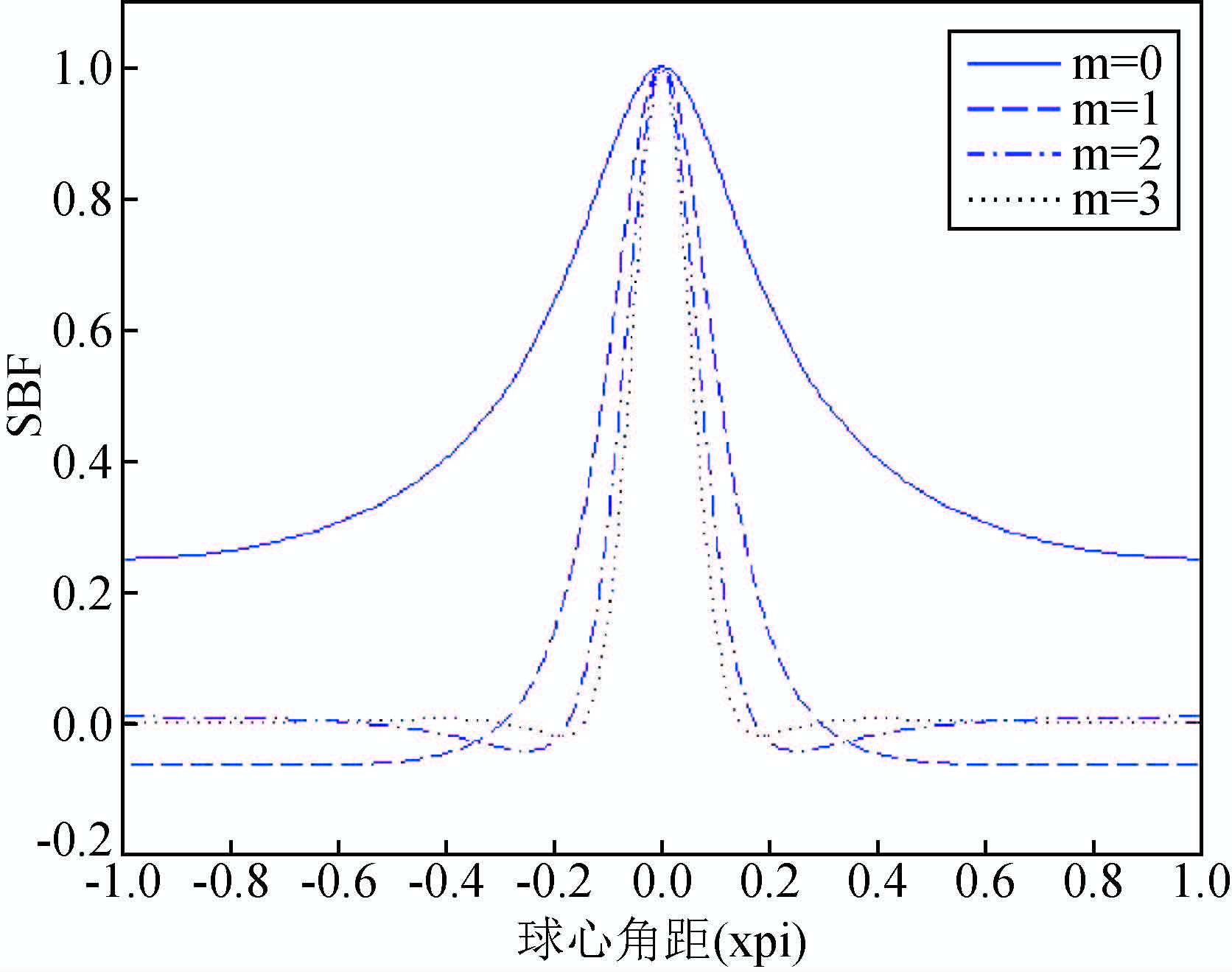
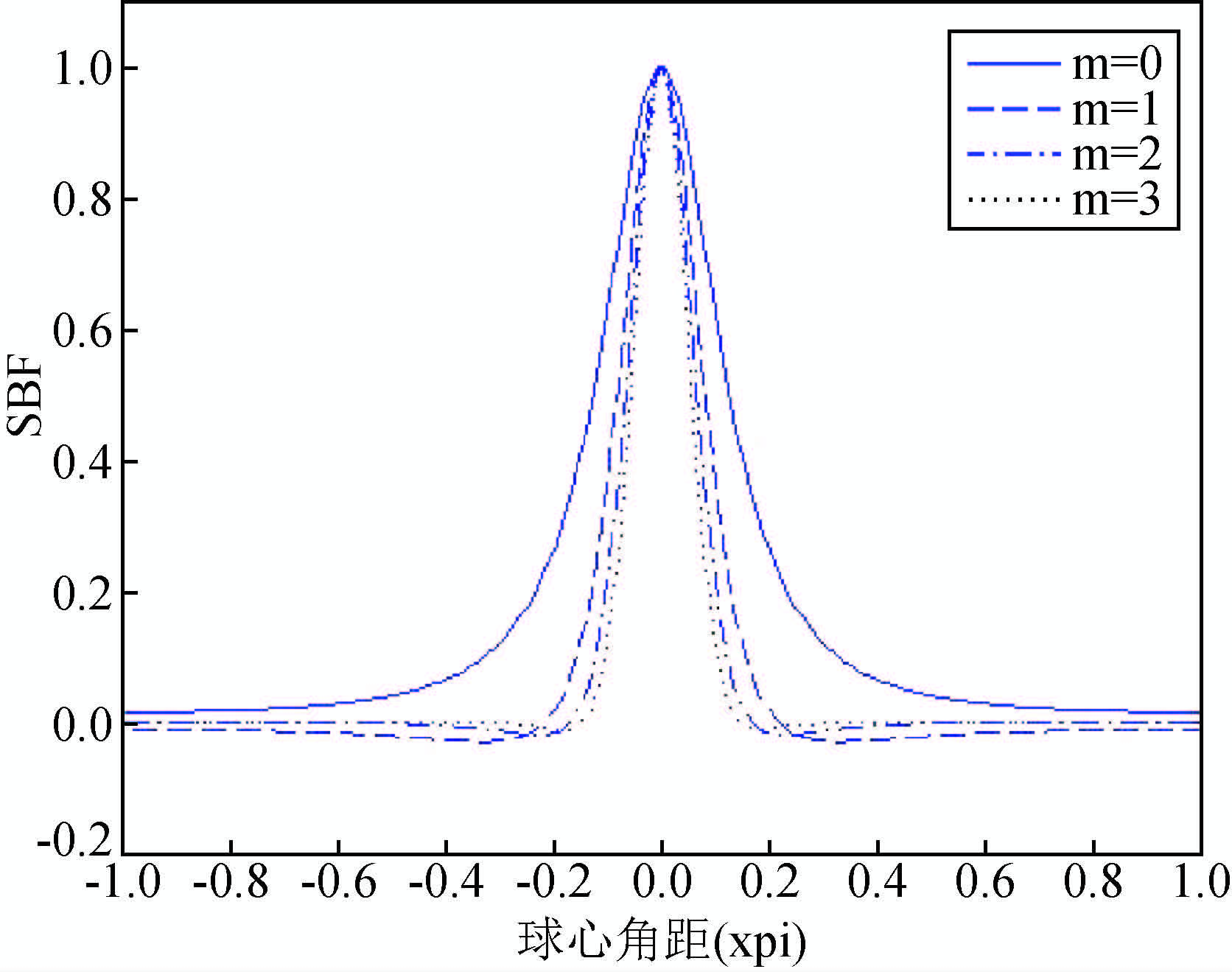
从 图 (1~5)可以看出,上面几个径向基核函数都具有很强的局部特性,且在作用域内都是全支撑的.径向基函数的性能和宽度参数η有很大关系,随着宽度参数η增大,径向基函数在远处的影响越来越小,也即局部特性更强.从图 4和图 6可以看出,高阶多级子和Poisson小波核函数相对低阶核函数具有更强的局部特性,甚至近似为紧支撑的.
|
图 1 ${{\hat{\Psi }}_{\text{IMQ}}}\left( t,\eta \right)$的空间特性 Figure 1 Behaviour of ${{\hat{\Psi }}_{\text{IMQ}}}\left( t,\eta \right)$ in the spatial domain |
|
图 2 ${{\hat{\Psi }}_{P}}\left( t,\eta \right)$的空间特性 Figure 2 Behaviour of ${{\hat{\Psi }}_{P}}\left( t,\eta \right)$ in the spatial domain |
|
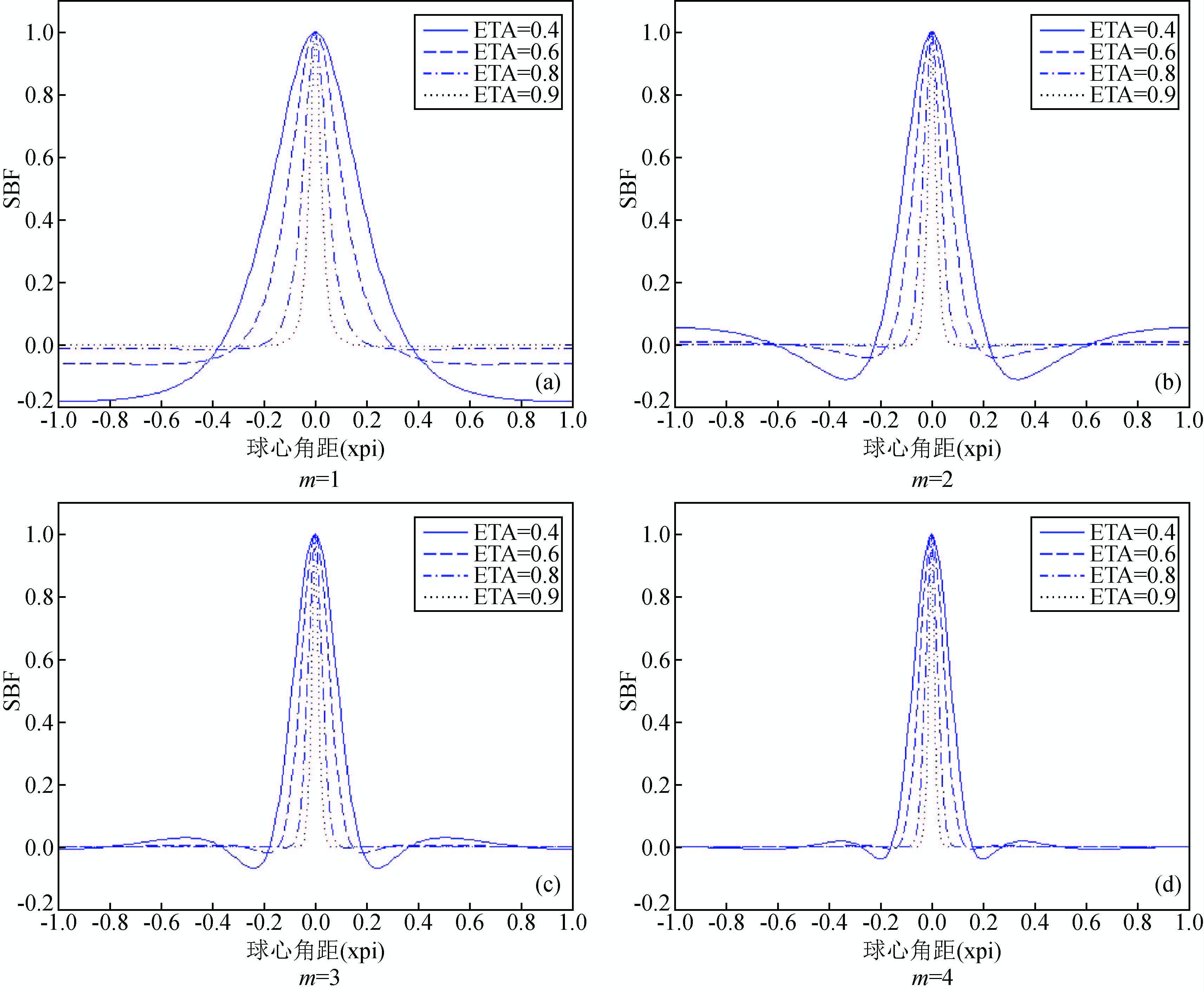
图 3 $\hat{\Psi }_{\text{RM}}^{m}\left( t,\eta \right)$在不同宽度参数下的空间特性 Figure 3 Behaviour of $\hat{\Psi }_{\text{RM}}^{m}\left( t,\eta \right)$ of various orders in the spatial domain |
|
图 4 不同阶$\hat{\Psi }_{\text{RM}}^{m}\left( t,\eta \right)$在相同宽度参数(η=0.6)下的空间特性 Figure 4 Behaviour of $\hat{\Psi }_{\text{RM}}^{m}\left( t,\eta \right)$ of various orders with the same bandwidth parameter(0.6)in the spatial domain |
|
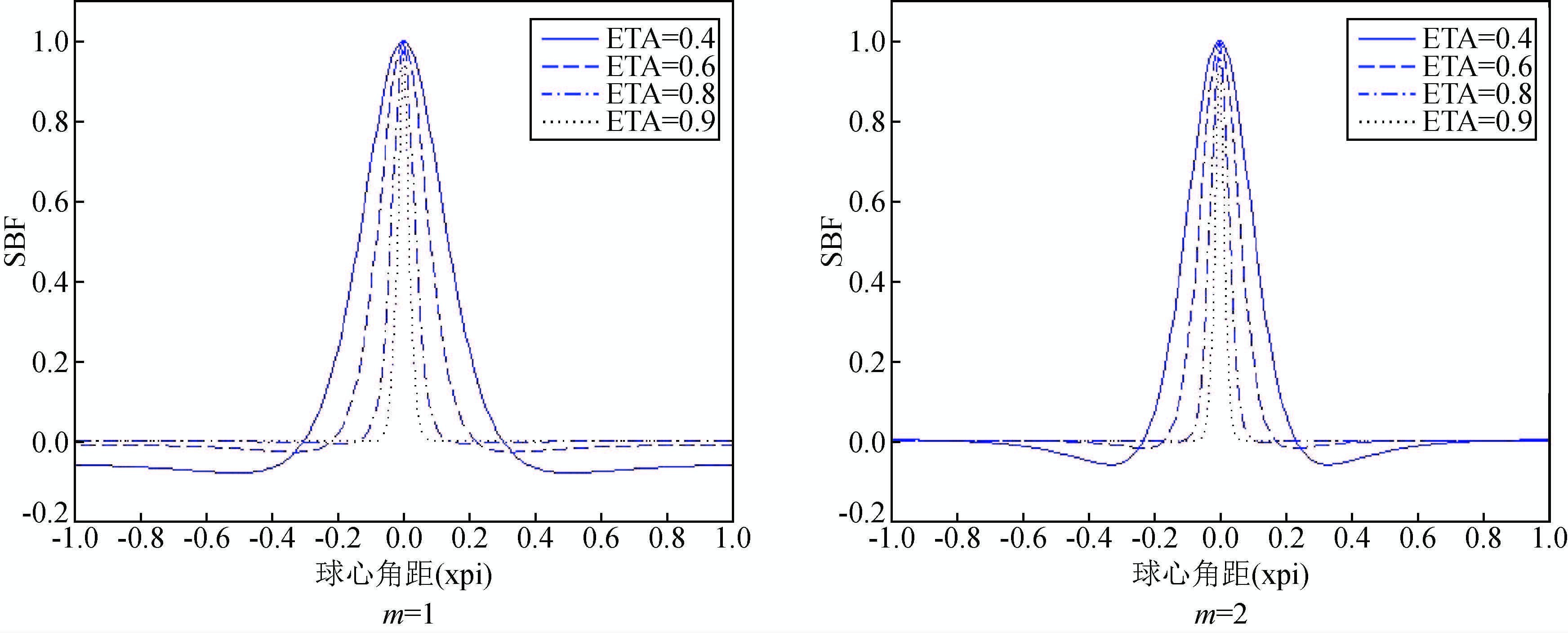
图 5 $\hat{\Psi }_{PW}^{m}\left( t,\eta \right)$在不同宽度参数下(η=0.4,0.6,0.8,0.9)的空间特性 Figure 5 Behaviour of $\hat{\Psi }_{PW}^{m}\left( t,\eta \right)$ with various bandwidth parameter in the spatial domain |
|
图 6 不同阶$\hat{\Psi }_{PW}^{m}\left( t,\eta \right)$在相同宽度参数(η=0.6)下的空间特性 Figure 6 Behaviour of $\hat{\Psi }_{PW}^{m}\left( t,\eta \right)$ of various orders with the same bandwidth parameter(0.6)in the spatial domain |
全球重力场模型通常用球谐级数函数表示,同样,球径向基函数Ψ(t;η)可在单位球面展开成Legendre级数形式,它的一般表示为
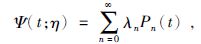
|
(32) |
其中Pn(t)为Legendre函数,λn为Legendre级数系数.
则径向基核函数Ψ(x,y)在空间点x处展开成如下形式:
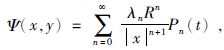
|
(33) |
表 3给出了上面几种径向基核函数Legendre级数展开系数λn的具体形式.
|
|
表 3 不同径向基核函数Legendre级数展开系数λn Table 3 Legendre coefficients λn of different basis function kernel |
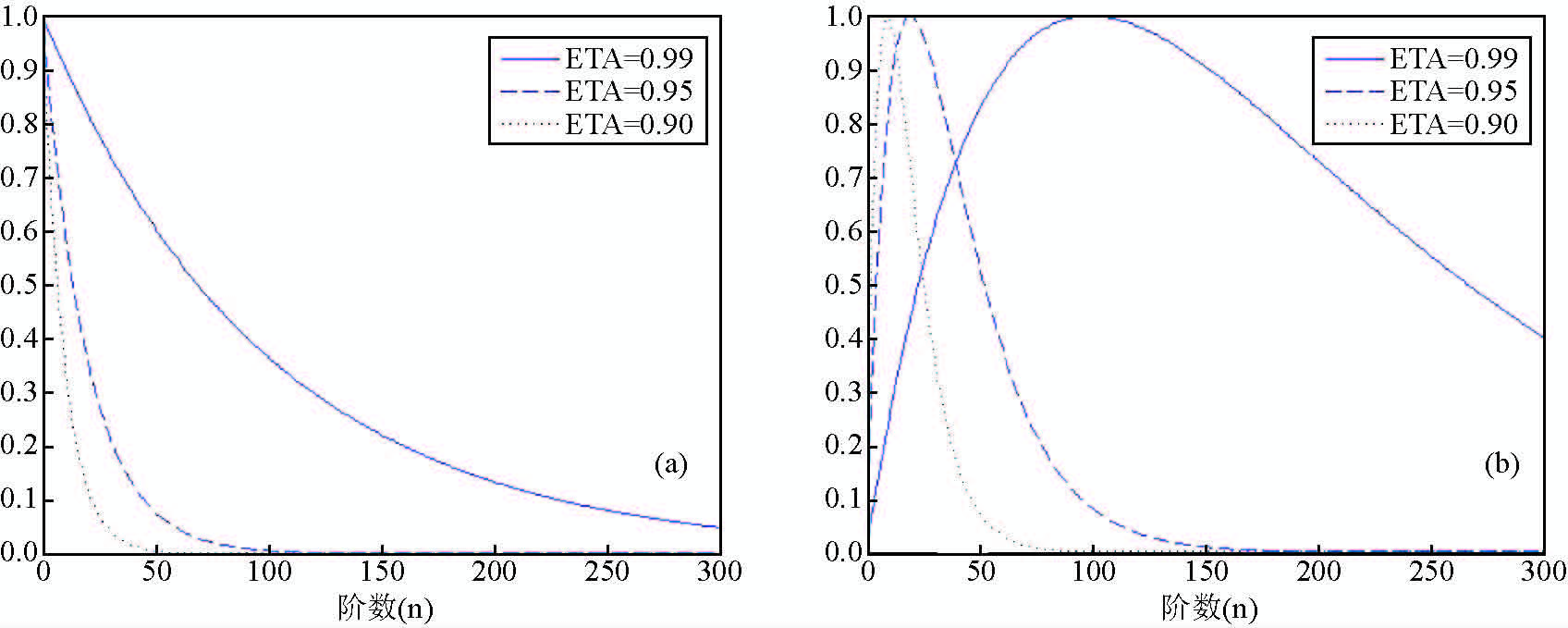
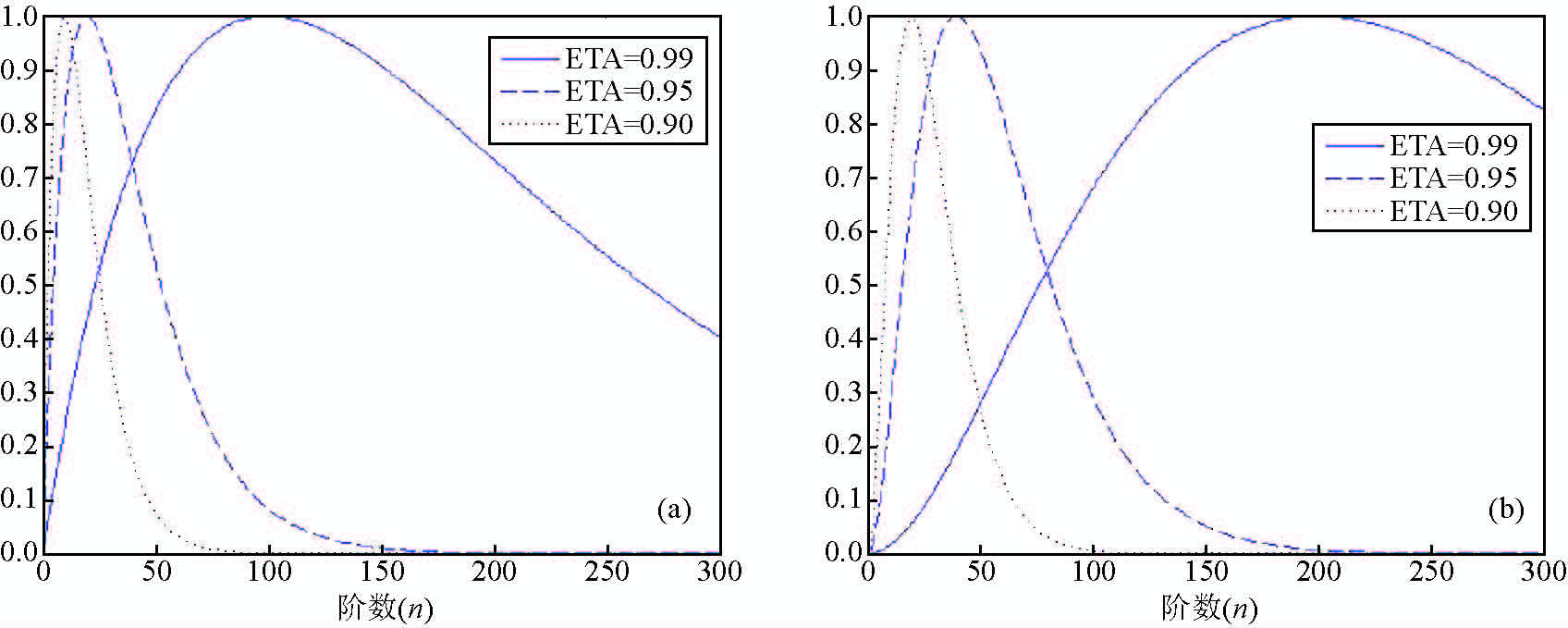
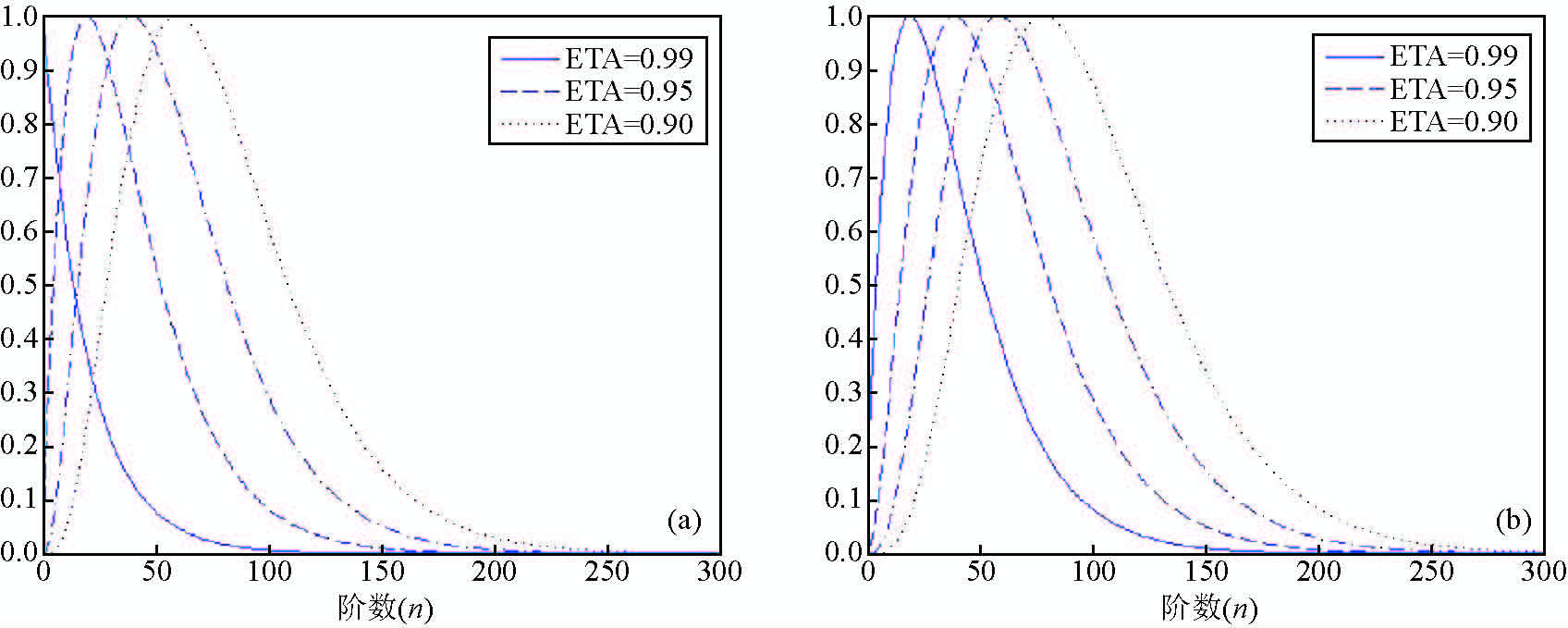
从图(7~9)可以看出,随着宽度参数η增大,径向基函数受高频信号的影响越来越大,其中IMQ核函数类似于低通滤波器(low-pass filter),而其他核函数则类似与带通滤波器(band-pass filter).从图 10也可看出,对于相同的宽度参数,不同阶多级子和Poisson小波核函数受影响的频率信号也不同,阶数越高,受影响频率也越高.
|
图 7 IMQ核(a)和Poisson核(b)的谱特性 Figure 7 Behaviour of IMQ(a)and Poisson(b)in the spectral domain |
|
图 8 多级子核的谱特性(a)m=1;(b)m=2 Figure 8 Behaviour of radial multipole of order 1(a)and order 3(b)in the spectral domain |
|
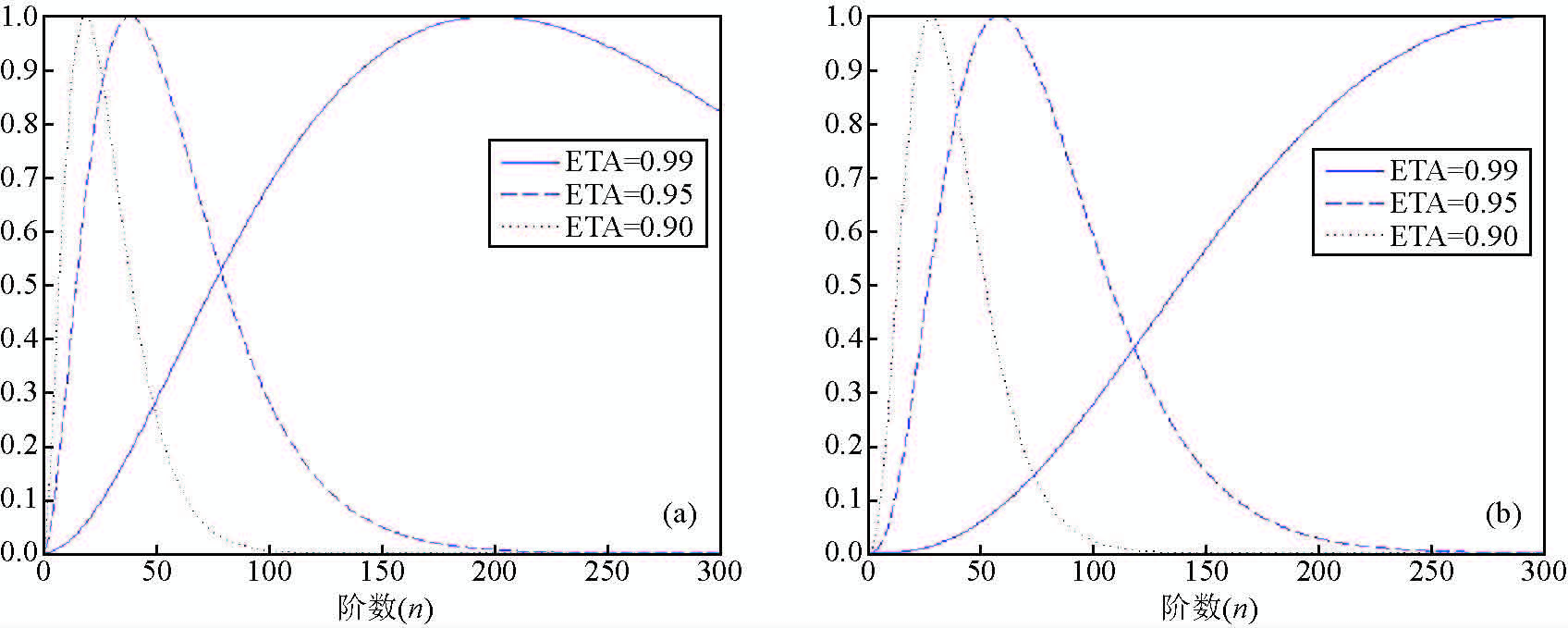
图 9 poisson小波核的谱特性(a)m=1;(b)m=2 Figure 9 Behaviour of poisson wavelet of order 1(left)and order 2(right)in the spectral domain |
|
图 10 不同阶多级子核(a)和Poisson小波核(b)的谱特性(η=0.95) Figure 10 Behaviour of radial multipole(a)and poisson wavelet(b)of various orders with the same bandwidth parameter(0.95)in the spectral domain |
球谐函数展开式是重力场逼近最常采用的表示方法,因为它的展开具有正交性,函数逼近的结果是一组简单的系数值,且在频域空间上是高度局部化的.但球谐函数缺乏空间局部性,任何局部的变化都会导致所有球谐系数发生改变,且在展开到高阶时不得不面对收敛问题和计算复杂度的膨胀,对高频局部重力场信号的表示有极大困难.径向基函数具有空间局部特性,近年来被应用于局部重力场表示.本文介绍了四种满足重力场逼近中调和函数性质的径向基核函数IMQ核函数、Poisson核函数、径向多级子(Radial multipole)函数、Poisson小波核函数,给出了它们在空间直角坐标系和球坐标系下的解析表达式,推导出这几种核函数的Legendre级数展开式,并通过规格化比较分析了它们的空间特性和频域特性.从文中可看出,径向基函数的性能和宽度参数η有很大关系,随着宽度参数η增大,径向基函数在远处的影响越来越小,也即局部特性更强.高阶多级子和Poisson小波核函数相对低阶核函数具有更强的局部特性,甚至近似为紧支撑的.而从频域来看,随着宽度参数η增大,径向基函数则受高频信号的影响越来越大.其中IMQ核函数类似于低通滤波器,而其他核函数则类似与带通滤波器.对于相同的宽度参数,不同阶多级子和Poisson小波核函数受影响的频率信号也不同,阶数越高,受影响频率也越高.因而,不管采用哪种核函数,利用径向基函数逼近局部重力场,提高逼近效果的关键问题之一是如何根据所逼近的重力信号确定合适甚至最优的宽度参数.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Antoni M, Keller W, Weigelt M. 2009. Representation of regional gravity fields by radial base functions[M]//Sideris M G ed. Observing our Changing Earth, International Association of Geodesy Symposia. Volume.133. Berlin Heidelberg:Spinger Verlag, 293-299. |
| [] | Chen R H. 2005. Quasi-interpolation with radial basis function and application to solve partial differential equations[Ph. D. thesis] (in Chinese). Shanghai:Fudan University. |
| [] | Hardy R L .1971. Multiquadric equations of topography and other irregular surfaces[J]. Journal of Geophysical Research Atmospheres, 76 (8) : 1905–1915. DOI:10.1029/JB076i008p01905 |
| [] | Klees R, Tenzer R, Prutkin I, et al .2008. A data-driven approach to local gravity field modelling using spherical radial basis functions[J]. Journal of Geodesy, 82 (8) : 457–471. DOI:10.1007/s00190-007-0196-3 |
| [] | Ma L M. 2009. Some theory, method and application of radial basis function approximation[Ph. D. thesis] (in Chinese). Shanghai:FuDan University. |
| [] | Marchenko A N, Barthelmes F, Meyer U, et al. 2001. Regional geoid determination:An application to airborne gravity data in the Skagerrak[R]. Scientific Technical Report no.01/07. Potsdam:GeoForschungsZentrun. |
| [] | Schmidt M, Fengler M, Mayer-Gürr T, et al .2007. Regional gravity modeling in terms of spherical base functions[J]. Journal of Geodesy, 81 (1) : 17–38. |
| [] | Stein E M, Weiss G .1971. Introduction to Fourier Analysis on Euclidean Spaces[M]. Princeton, New Jersey: Princeton University Press . |
| [] | Tenzer R, Klees R .2008. The choice of the spherical radial basis functions in local gravity field modeling[J]. Studia Geophysica et Geodaetica, 52 (3) : 287–304. DOI:10.1007/s11200-008-0022-2 |
| [] | Weigelt M, Antoni M, Keller W .2010. Regional gravity field recovery from GRACE Using position optimized radial base functions[M]. Gravity, Geoid and Earth Observation, International Association of Geodesy Symposia. Volume. 135. Berlin Heidelberg: Springer . |
| [] | Wittwer T. 2009. Regional gravity field modeling with radial basis functions[Ph. D. thesis]. Netherlands:TU Delft. |
| [] | Wu X, Zhang C D, Zhao D M .2009. Point mass harmonic analysis method based on spherical boundary value problem[J]. Chinese Journal of Geophysics (in Chinese), 52 (12) : 2993–3000. DOI:10.3969/j.issn.0001-5733.2009.12.008 |
| [] | Wu Y H, Luo Z C, Zhou B Y .2016. Regional gravity modeling based on heterogeneous data sets by using Poisson wavelets radial basis functions[J]. Chinese Journal of Geophysics (in Chinese), 59 (3) : 852–864. DOI:10.6038/cjg20160308 |
| [] | Wu Z M .1998. Radial basis functions-a survey[J]. Advances in Mathematics (in Chinese), 27 (3) : 202–208. |
| [] | Wu Z M .2002. Radial basis function scattered data interpolation and the meshless method of numerical solution of PDEs[J]. Journal of Engineering Mathematics (in Chinese), 19 (2) : 1–12. |
| [] | 陈荣华. 2005. 径向基函数拟插值理论及其在微分方程数值解中的应用[博士论文]. 上海:复旦大学. |
| [] | 马利敏. 2009. 径向基函数逼近中的若干理论、方法及其应用[博士论文]. 上海:复旦大学. |
| [] | 吴星, 张传定, 赵东明.2009. 基于球面边值问题的点质量调和分析方法[J]. 地球物理学报, 52 (12) : 2993–3000. DOI:10.3969/j.issn.0001-5733.2009.12.008 |
| [] | 吴宗敏.1998. 函数的径向基表示[J]. 数学进展, 27 (3) : 202–208. |
| [] | 吴宗敏.2002. 径向基函数、散乱数据拟合与无网格偏微分方程数值解[J]. 工程数学学报, 19 (2) : 1–12. |
| [] | 吴怿昊, 罗志才, 周波阳.2016. 基于泊松小波径向基函数融合多源数据的局部重力场建模[J]. 地球物理学报, 59 (3) : 852–864. DOI:10.6038/cjg20160308 |
 2016, Vol. 31
2016, Vol. 31

