成都理工大学, 地球勘探与信息技术教育部重点实验室, 成都 610059
收稿日期: 2016-02-12; 修回日期: 2016-06-29.
基金项目: 国家自然科学基金(41274078)--大地电磁垂直磁场和倾子正反演方法研究资助.
Comprehensive utilization of NLCG and OCCAM in two-dimensional magnetotelluric inversion
Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu 610059, China
0 引言
大地电磁测深法(MT)是一种有效的地球物理勘探方法,20世纪50年代初期由吉洪诺夫和卡尼亚提出并奠定了该方法的基础(Tikhonov,1950;Cagniard,1953);经过这么多年的发展,大地电磁不仅自身的理论体系得到发展完善,而且不断引进其他优秀的数学方法计算机等工具.所以在理论与方法上都得到了很大的发展,在实际油气勘查、金属矿产勘探、地热资源勘探等中得到了广泛的应用.实践证明这是一种经济、有效的地球物理勘探手段(刘国栋和陈乐寿,1984).其中反演解释是MT的最终目的,反演问题的最终形式是求取目标函数的最优化问题,在这个过程中采用的转化手段不同,导致形成的算法也不同.生产研究中常见二维反演方法有NLCG和OCCAM反演等方法.Rody和Mackie在2001年提出了非线性共轭梯度法(NLCG),Constable等(Constable et al.,1987)初次将OCCAM反演这种说法用于一维反演,deGroot-Hedin等(1990)年由OCCAM一维反演方法扩展得到OCCAM二维反演(柳建新等,2012),Siripunvaraporn等(Siripunvaraporn and Egbert, 2000)研究提出了数据空间OCCAM反演方法,并且成功地应用于MT二维、三维反演.他们在数据空间方法中,又结合了CG的优点而研究出了DCGOCC (Siripunvaraporn and Sarakorn, 2011).张罗磊等(张罗磊等,2009)还提出了光滑模型与尖锐边界相结合的反演方法.对OCCAM反演的普遍而详细的论述可见于文献(Constable et al.,1987;Siripunvaraporn and Egbert, 2000;Siripunvaraporn Siripunvaraporn and Sarakorn, 2011)等.
NLCG反演速度较快,但较依赖初始模型和经验参数输入,否则效果较差,所以这具有一定的偶然性和盲目性;OCCAM反演对初始模型和参数的依赖较弱,且效果平滑度、与模型的拟合度较好,但是速度慢、计算消耗大也是制约其广泛应用的主要短板.
本文结合了两种方法,即将NLCG反演的结果作为OCCAM反演的初始模型进行反演(NLCG2OCCAM),对典型模型进行了三种模式(TE、TM、TETM)试算,结果显示了该方法能发挥各自的优势,避免各自的劣势,也就是说两者结合会效果既好收敛速度又较快.
1 理论基础
NLCG (nonlinear conjugate gradients)反演算法是Rodi和Mackie (2001)提出的一种快速、稳定、收敛的二维反演计算方法(柳建新等,2012),其正演模拟方法是基于有限差分法.反演计算的基本策略如下:
反演计算的目标函数表示为
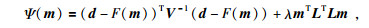
|
(1) |
式中,λ为正则化因子;V是与误差向量e有关的协方差矩阵;L是与模型参数相关的二维微分矩阵.
NLCG反演计算可以简单描述为
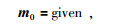
|
(2) |
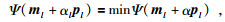
|
(3) |
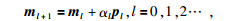
|
(4) |
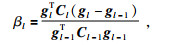
|
(5) |
式中,αl是搜索步长;p l是模型空间的搜索方向,可以采用下面的关系确定,公式为
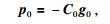
|
(6) |
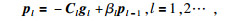
|
(7) |
式中,Cl为预条件矩阵,其表达式为
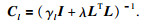
|
(8) |
当预条件信息不存在时,预条件矩阵将变成单位矩阵,即C l=I.
NLCG将CG技术直接应用到非线性目标函数最优化的方法(朱崇利,2013),实践证明,该反演处理方法是比较有效的,反演结果具有较高的分辨率,反演计算具有较快的速度,反演计算只需较小的存储量(Rodi and Mackie, 2001).另外,NLCG反演方法可以进行联合反演,如TE和TM视电阻率和相位的联合.当然,NLCG反演方法的缺点也是有的,比如对初始模型的选择存在依赖性,即反演时上述式(1)等的正则化因子(λ)是固定不变的,所以需凭经验用不同的正则化因子进行试算,然后根据结果来选取合适的正则化因子,这对地球物理工作人员的要求较高,凭经验也具有一定的偶然性和盲目性,并且该反演方法也可能因为正则化因子选择的不合适等原因而容易产生冗余构造.
OCCAM二维反演算法是deGroot-Hedin等(1990)由OCCAM一维反演方法扩展而来的(柳建新等,2012),为了有效的压制迭代过程中产生的冗余构造,并提高解的稳定性(Constable et al., 1987),在目标函数中引入了模型粗糙度,并将粗糙度(R1)定义为
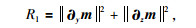
|
(9) |
式中,∂y是模型参数沿横向的粗糙度矩阵,∂z是模型参数沿纵向(深度方向)的粗糙度矩阵.反演计算的目标函数变为
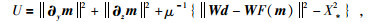
|
(10) |
式中,μ-1为正则化因子或正则化参数.
将非线性函数F(m)进行线性化处理,则有
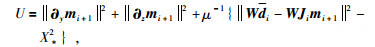
|
(11) |
使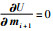 即可,通过求解方程组得到模型的一般解为
即可,通过求解方程组得到模型的一般解为
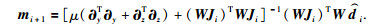
|
(12) |
OCCAM反演是光滑模型的反演,相对NLCG反演来说对初始模型和参数的依赖较弱;不像NLCG反演,OCCAM在反演过程中每次迭代都不断搜索合适的(一般需要10次以上才能搜索到合适的)正则化因子(式(10)等的μ-1),尽管这样使得反演结果较好,但也导致了速度慢、效率低的问题.
所以当把均匀半空间作为NLCG反演的初始模型时,结果可以客观的反映真实数据响应,也结合了NLCG反演速度快、精度高等优势,尽管产生一些冗余构造,但此时再将这个结果作为OCCAM反演的初始模型,进行少量次数的OCCAM反演,由于利用了OCCAM反演冗余构造少、效果平滑等优势,将会减少甚至消除这些冗余构造,OCCAM反演次数的减少,也将提高反演的效率.
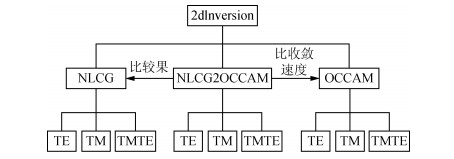
本章先介绍了正演所建立的两个典型模型和反演的流程图,然后再将三种方法(NLCG、NLCG2OCCAM、OCCAM)分别在三种模式(TE、TM、TETM)下的反演结果展示出来,进行分析、总结.反演设置的目标拟合差均为1.3,所用的笔记本电脑配置为:处理器Intel Core i3 390,主频2.67 GHz,内存4 G.
1.1 建立正演模型
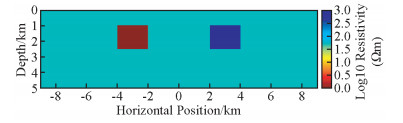
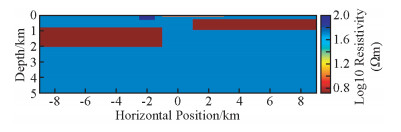
如图 1~2中背景电阻率均为50 Ω·m;图 1为一低(1 Ω·m)一高(1000 Ω·m)两个异常体,长均为2 km,厚均为1.5 km;图 2中模型为经典sasaki模型,靠近地表分别有一高阻体(100 Ω·m)、一低阻体(10 Ω·m),高阻体长1 km、厚0.3 km,低阻体长4 km,厚约0.1 km;另外两个低阻体(均为5 Ω·m),靠左边的低阻体长8 km、厚约1.2 km,靠右边的低阻体长8 km、厚约0.7 km;对于这三个模型均利用趋肤深度来进行网格剖分和划分网格边界(欧东新,2007;万汉平,2010);本次正反演采用的网格均为35×51,横向35个网格,纵向51个;横向,等间距布设30个测点,垂向,在地表附近采用加密网格,中间部分采用均匀网格,深部采用大网格,保证精度的同时减小计算量,采用对数等间距的16个频点(0.01~100 Hz),测量数据为TE、TM两种极化方式的视电阻率和相位(有限单元法).
1.2 反演试算
NLCG反演和OCCAM反演的初始模型为均匀半空间50 Ω·m,NLCG2OCCAM反演方法的初始模型采用NLCG反演的结果,反演的流程如图 3.
1.3 模型一
表 1
(Table 1)

表 1
TE反演结果
Table 1
Inversion result of TE
| counts |
types |
| rms (NLCG) |
rms (NLCG2OCCAM) |
rms (OCCAM) |
| iter0 |
9.347 |
1.611297 |
9.321217 |
| iter1 |
4.958 |
1.299899 |
4.715513 |
| iter2 |
3.871 |
|
2.396590 |
| iter3 |
2.457 |
|
1.299792 |
| iter4 |
2.023 |
|
1.300053 |
| iter5 |
1.487 |
|
1.300241 |
| iter6 |
1.336 |
|
1.300141 |
| iter7 |
1.191 |
|
1.300084 |
|
表 1
TE反演结果
Table 1
Inversion result of TE
|
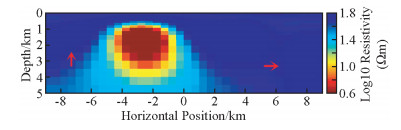
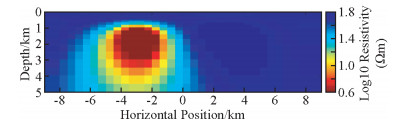
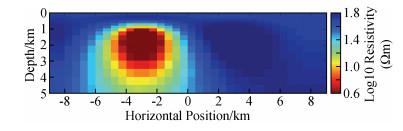
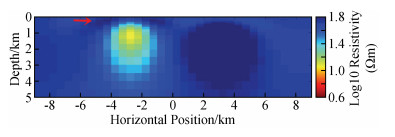
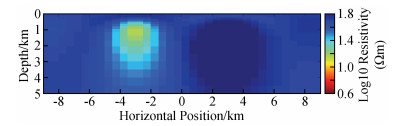
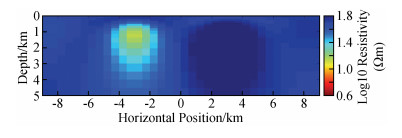
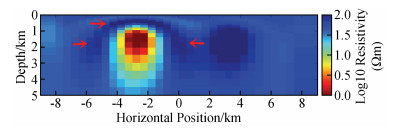
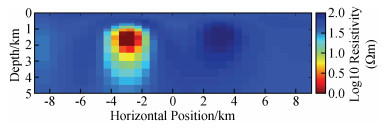
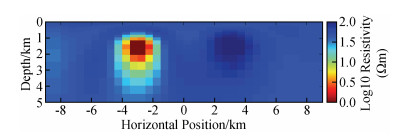
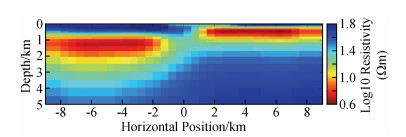
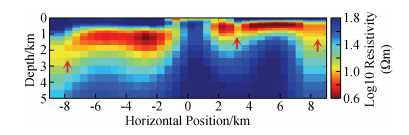
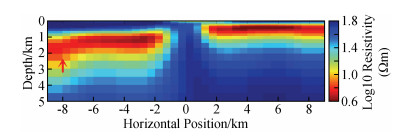
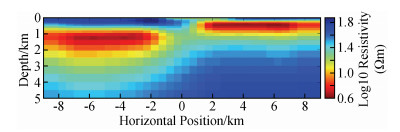
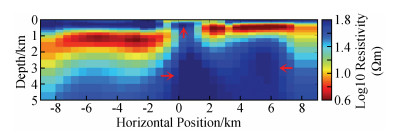
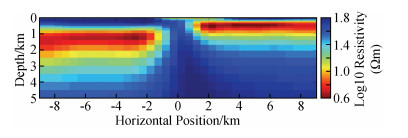
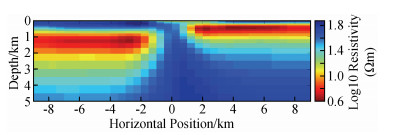
如图 4为NLCG反演第7次迭代的结果,速度快(总用时约34 s),但结果相对来说没那么光滑,其中对高阻异常体的灵敏度相对不是很好,右下角和左上角出现冗余构造(红色箭头标注);NLCG2OCCAM将NLCG第6次迭代结果作为OCCAM反演初始模型来做OCCAM反演,NLCG第6次迭代的rms与NLCG2OCCAM第0次迭代的rms不同,主要是因为二者在反演时所用的正演方式不同造成(下同),如图 5为该反演第1次迭代的结果,反演的结果较为平滑,对高低阻异常体分辨得较NLCG好,冗余构造较少,其中6次NLCG反演用时约31 s,1次OCCAM反演用时约87 s,总用时约118 s;如图 6为OCCAM反演第7次迭代的结果,该结果较为平滑,对高、低阻异常体分辨得较NLCG好,目标体周围的假异常较NLCG2OOCAM反演要少,但耗时长(总用时约403 s).
表 2
(Table 2)

表 2
TM反演结果
Table 2
Inversion result of TM
| counts |
types |
| rms (NLCG) |
rms (NLCG2OCCAM) |
rms (OCCAM) |
| iter0 |
6.003 |
2.330745 |
5.993907 |
| iter1 |
2.175 |
1.300020 |
1.300201 |
| iter2 |
1.503 |
|
1.300029 |
| iter3 |
1.171 |
|
1.299947 |
|
表 2
TM反演结果
Table 2
Inversion result of TM
|
如图 7为NLCG反演第2次迭代的结果,反演速度快(总用时约5 s),但出现一些较明显假异常(红色箭头标注);NLCG2OCCAM将NLCG第2次迭代结果作为OCCAM反演初始模型来做OCCAM反演,如图 8为NLCG2OCCAM反演的第1次迭代结果,该结果较为平滑,其中2次NLCG反演用时约3 s,1次OCCAM反演用时约53 s,总用时约58 s;如图 9为OCCAM反演第3次迭代的结果,该结果较为平滑,但耗时长(总用时约198 s).
表 3
(Table 3)

表 3
TEM反演结果
Table 3
Inversion result of TEM
| counts |
types |
| rms (NLCG) |
rms (NLCG2OCCAM) |
rms (OCCAM) |
| iter0 |
7.855 |
2.661588 |
7.836198 |
| iter1 |
5.039 |
1.299990 |
4.323135 |
| iter2 |
4.046 |
1.300151 |
2.268638 |
| iter3 |
3.287 |
1.300027 |
1.299947 |
| iter4 |
2.295 |
1.299982 |
1.300104 |
| iter5 |
1.763 |
|
1.300085 |
| iter6 |
1.561 |
|
1.299945 |
| iter7 |
1.377 |
|
1.299969 |
| iter8 |
1.229 |
|
1.299964 |
|
表 3
TEM反演结果
Table 3
Inversion result of TEM
|
三种反演方式TMTE模式反演效果较好,由于参与反演的数据量较大,更接近真实地下地质体分布情况;如图 10为NLCG反演第8次迭代的结果,该结果相对来说没那么光滑,速度快(总用时约30 s),但在低阻体周围产生明显冗余构造(红色箭头标示),对异常体的厚度、长度等确定得不是很好;NLCG2OCCAM反演将NLCG反演第4次迭代结果作为OCCAM反演初始模型来做OCCAM反演,如图 11为NLCG2OCCAM反演的第4次迭代结果,NLCG2OCCAM反演的结果较为平滑,目标体周围的假异常较NLCG反演要少,其中4次NLCG反演用时约12 s,4次OCCAM反演用时约348 s,总用时约360 s;如图 12为OCCAM反演第8次迭代的结果,该结果较为平滑,目标体周围的冗余构造较NLCG反演要少,对异常体厚度、长度确定得比NLCG反演和NLCG2OCCAM反演好,但耗时长(总用时约721 s).
1.4 模型二
表 4
(Table 4)

表 4
TE反演结果
Table 4
Inversion result of TE
| counts |
types |
| rms (NLCG) |
rms (NLCG2OCCAM) |
rms (OCCAM) |
| iter0 |
16.022 |
1.873554 |
15.97525 |
| iter1 |
5.366 |
1.299827 |
6.292383 |
| iter2 |
3.220 |
|
2.142821 |
| iter3 |
2.280 |
|
1.299952 |
| iter4 |
1.656 |
|
1.30029 |
| iter5 |
1.207 |
|
1.30000 |
|
表 4
TE反演结果
Table 4
Inversion result of TE
|
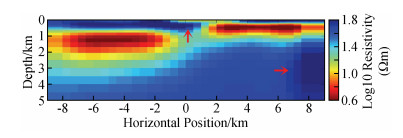
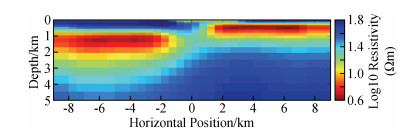
如图 13为NLCG反演第5次迭代的结果,该结果相对来说没那么光滑,速度快(总用时约19 s),但对异常体边界等确定得并不是很好,浅部高阻体的轮廓不清晰,变形,下部两条状低阻体界定得也不是很清晰,右下出现冗余构造;NLCG2OCCAM反演将NLCG反演第4次迭代结果作为OCCAM反演初始模型来做OCCAM反演,如图 14为NLCG2OCCAM反演的第1次迭代结果,该反演结果较为平滑,第1次迭代拟合差就已经达到目标拟合差,其中4次NLCG反演用时约16 s,1次OCCAM反演用时约56 s,总用时约74 s;如图 15为OCCAM反演第5次迭代的结果,该反演结果较为平滑,第3次迭代拟合差才达到目标拟合差,对低阻异常体分辨得较好,耗时长(总用时约285 s).
表 5
(Table 5)

表 5
TM反演结果
Table 5
Inversion result of TM
| counts |
types |
| rms (NLCG) |
rms (NLCG2OCCAM) |
rms (OCCAM) |
| iter0 |
17.003 |
4.890635 |
16.96255 |
| iter1 |
9.423 |
1.300037 |
5.894039 |
| iter2 |
6.881 |
|
2.012065 |
| iter3 |
4.966 |
|
1.299840 |
| iter4 |
4.214 |
|
1.299911 |
| iter5 |
3.292 |
|
1.299910 |
| iter6 |
2.726 |
|
1.299937 |
|
表 5
TM反演结果
Table 5
Inversion result of TM
|
如图 16为NLCG反演第6次迭代的结果,该反演结果相对来说没那么光滑,速度快(总用时约7 s),但对异常体边界等确定得并不是很好,浅部高低阻体的轮廓不清晰,变形,对下部两条状低阻体界定得也不是很清晰,下部出现冗余构造;NLCG2OCCAM反演将NLCG反演第5次迭代结果作为OCCAM反演初始模型来做OCCAM反演,如图 17为NLCG2OCCAM反演的第1次迭代结果,相较于同等迭代次数的NLCG反演,一些变形的情况和冗余构造经过OCCAM一次反演得到了一些纠正,其中5次NLCG反演用时约5 s,1次OCCAM反演用时约94 s,总用时约99 s;如图 18为OCCAM反演第5次迭代的结果,OCCAM反演结果较为平滑,对异常体分辨得较好,目标体周围的假异常较NLCG反演要少,效果也比NLCG2OCCAM反演好,但是耗时长(总用时280 s).
表 6
(Table 6)

表 6
TEM反演结果
Table 6
Inversion result of TEM
| counts |
types |
| rms (NLCG) |
rms (NLCG2OCCAM) |
rms (OCCAM) |
| iter0 |
16.52 |
3.736348 |
16.47630 |
| iter1 |
6.72 |
1.299959 |
6.383521 |
| iter2 |
4.907 |
|
2.270103 |
| iter3 |
3.616 |
|
1.300321 |
| iter4 |
3.009 |
|
1.300209 |
| iter5 |
2.653 |
|
1.300204 |
| iter6 |
2.437 |
|
1.300234 |
|
表 6
TEM反演结果
Table 6
Inversion result of TEM
|
三种反演方式TMTE模式反演效果较好,由于参与反演的数据量较大,更接近真实地下地质体分布情况;如图 19为NLCG第6次迭代的结果,NLCG反演速度快(总用时约41 s),但其结果相对来说没那么光滑,对两个异常体的长度、厚度确定得并不是很好,下部出现冗余构造(红色箭头标注),且靠近地表两个异常体轮廓扭曲,模糊不清;NLCG2OCCAM将NLCG第5次迭代结果作为OCCAM反演初始模型来做OCCAM反演,如图 20为NLCG2OCCAM反演的第1次迭代结果,该反演的结果较为平滑,目标体周围的冗余构造较NLCG反演要少,对异常体界定得较清晰,其中5次NLCG反演用时约35s,1次OCCAM反演用时约147 s,总用时182 s;如图 21为OCCAM反演第6次迭代的结果,OCCAM反演结果较为平滑,目标体周围的冗余构造较NLCG反演要少,对异常体界定得更清晰,但耗时长(总用时约775 s).
2 结论认识
2.1
本文基于对OCCAM反演和NLCG反演的进一步认识,提出了二维NLCG反演结果作二维OCCAM反演初始模型的方法,根据上述试算结果,总的来说,三种模式下,NLCG2OCCAM的反演效果要比单独进行NLCG反演好,收敛速度比单独进行OCCAM快.
2.2
这是因为NLCG反演依赖于初始模型和经验参数输入,经验、初始模型选择存在一定的偶然性、盲目性,一旦选择不合适,效果将会很差,或产生错误的判断;OCCAM反演对初始模型和经验参输入依赖较弱,模型光滑,接近真实解;NLCG2OCCAM综合了OCCAM反演的优点,削弱了由于NLCG反演依赖于初始模型和经验参数输入所带来的影响,所以比NLCG反演效果好;同时综合了NLCG反演快速的优点,收敛快速,解决了OCCAM反演速度慢、时间长、计算消耗大的缺点.
2.3
地下地质情况复杂多变,过于依赖经验来选取反演参数和初始模型,这是带有偶然性、盲目性的,NLCG2OCCAM可以有效削弱这种偶然性、盲目性;而OCCAM反演在达到目标拟合差时,还会继续迭代,追求最光滑的模型,结果表明,求最光滑模型计算得太慢,尤其是在接近收敛的时候,为使得模型光滑更是如此,实际上,最后的结果未必比前几次迭代的结果更接近真实模型,反而可能使得一些构造模糊不清(朴英哲等,2014);所以采用NLCG2OCCAM进行反演时可以将最大迭代次数设置小一些,保证效果的情况下(以拟合差即拟合观测数据为主),既能够加快反演速度,又能避免过于追求最光滑模型.
致谢
感谢审稿专家提出的修改意见和编辑部的大力支持!
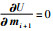
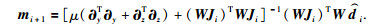
 2016, Vol. 31
2016, Vol. 31


