2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266071
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
地震波速度在地震资料的采集、处理、解释和评价中起着必不可少的作用,同时在油气勘探开发等各个阶段也起着关键的作用,地震波速度求取的准确与否直接影响着地震勘探的最终成果.在地震解释过程中,只有得到准确的速度场,才能精确确定目的层的深度、倾角和倾向,落实井位的可靠性,并进行时深转换,为油气勘探和开发提供准确的各类地质图件,进而确定储层和流体的性质.随着油气勘探程度的不断提高,勘探区域地质条件变得越来越复杂,地下介质非均质性强、速度纵横向变化大、高陡构造发育等问题对高精度速度建模及地质图件的精确时深转换提出了挑战.为此,各种各样的地震速度分析与反演技术应运而生,但大部分方法都是以地震速度转换或以测井速度内插为主,以地震速度为主的速度建模方法主要包括基于叠加速度或偏移速度分析的方法以及基于层析速度反演的方法等;以测井速度为主的速度建模方法主要有克里金估计法以及随机模拟、随机反演法等.在勘探相对成熟的区块测井资料比较丰富,充分结合井震资料各自的优势联合开展速度建模对提高时深转换精度具有十分重要的意义.但由于声波测井与地震勘探在原理、方法上的不同,得到的数据在观测尺度和所处域上都有所差异,因此在开展井震联合速度建模之前需要首先解决测井资料和地震资料之间在尺度与频率匹配等方面的问题.在井震匹配基础上为了提高速度建模的精度,同时还应该考虑井震联合速度建模中的约束条件问题以及不确定性分析等问题.
1 以地震资料为主的速度建模方法 1.1 基于叠加速度分析的建模方法20世纪60年代末,Garotta等(1967)和Cook等(1969)基于水平层状介质假设,根据反射波的双曲线型时距方程,提出了常规叠加速度分析方法.该方法具有较高的计算效率,在地震资料常规处理中起着重要作用,影响着偏移速度分析、层析速度反演建模的精度,同时也是众多时深转换速度求取方法的基础.但该方法不适用于界面倾斜(Hale,1984;Forel et al., 1988)和速度横向变化的情况,为了适应复杂地质条件下反射波时距曲线为非双曲线的情况,提出了高阶动校正优化、非双曲线速度分析技术及基于起伏地表的速度分析等方法(Taner et al., 1969;Al-chalabi,1973;Gausse et al., 2000;薛冈等,2003),这些方法都不同程度地提高了速度分析的精度.
在将叠加速度应用于时深转换方面,国内外一直致力于借助Dix公式将叠加速度转换为层速度或平均速度.Dix公式实现了在水平层状介质下层速度的稳定求取(Dix,1955),但Hubral (1976)指出均方根速度是利用未偏移的地震数据提取的,倾斜构造对速度建模精度的影响非常大.Grechka等(2002)指出在复杂地质构造情况下,层速度的估计方法需要更好地处理强横向变速、陡倾角构造、非均质性以及各向异性等因素的影响.Koren等(2005, 2006)提出了一种由背景速度趋势做约束的Dix反演方法,该方法可以建立更加稳定、合理的速度场,能适应叠加速度质量较差的情况.Buland等(2011)提出了贝叶斯框架下的Dix反演,该反演方法的优点在于能够将估计的不确定性包含在层速度的解中.Dischler等(2013)研究了各向异性介质的贝叶斯Dix反演,分析了各向异性参数对层速度的影响.为解决速度横向变化问题,近年来,地球物理学家结合射线追踪方法,以射线追踪正演走时与待求点叠加速度走时的匹配程度最好为标准,发展了一系列基于叠加速度的反演方法(吴国忱等,2003;易远元,2003;孙武亮等,2008).这些层速度反演方法克服了走时的双曲线假设,一定程度上解决了层速度横向变化的问题,比Dix公式法得到了更高的精度.可见,通过贝叶斯理论框架加入各向异性等因素的影响能够更好地提高Dix公式的转换精度,但仍无法克服水平层状介质的假设,从本质上解决速度横向变化等问题,而基于叠加速度的反演方法则可以在一定程度上解决这个问题.因此,在勘探开发初期对速度模型精度要求不高或地下构造比较简单、无强横向变速的情况下,可以考虑使用这种方法.
1.2 基于偏移速度分析的建模方法偏移成像技术起源于20世纪中叶,经历了Kirchhoff积分偏移、波动方程偏移与逆时偏移等方法的发展历程(叶勇,2003;潘宏勋,2006;刘百红,2013),同时促进了多种以成像质量最优为标准的偏移速度分析方法的发展.常用的有深度聚焦分析(DFA)(Doherty and Claerbout, 1976;Faye et al,1993)、基于共聚焦点的速度分析(CFP)(Kabir et al,1996;Barkhoul,1997;辛可峰等,2005)和剩余曲率分析(RCA)(Al-Yahya,1989;Biondi,1999;李振春,2000)等速度分析方法,这些方法把速度分析与偏移成像紧密结合,物理意义更为明显.但深度聚焦分析受到来自倾斜界面的能量、绕射能量等的干扰,聚焦深度存在不确定性,因此偏移速度分析结果不能保证收敛;基于共聚焦点技术的速度分析方法目前已经和层析反演等方法相结合,提高了速度分析的精度,但仍依赖于叠加剖面和层位解释结果;而剩余曲率方法在一定程度上克服了倾角的限制,是工业上应用最为广泛的一种速度分析方法,但仍需形成更符合速度分析的共成像点道集,建立更为准确的剩余时差与剩余速度关系.
偏移速度分析相比叠加速度分析具有更高的精度.在应用于时深转换方面,Maria Cameron等(2009)基于成像射线理论和旁轴射线追踪理论提出了一种由时间偏移速度来建立层速度场的有效算法.该方法可以看作是Dix公式在横向非均匀介质中的延伸,而且它根据几何扩散因子对速度场进行校正,摆脱了常规处理中利用测井信息进行校正的方法.很多学者在一些构造复杂地区利用偏移速度分析开展时深转换的研究中也取得了较好的效果,如塔里木盆地塔中地区(冯全东,2008)、库车山前的高陡构造地区(杨德兴,2008)以及准葛尔盆地(许海涛,2010)等地区.但偏移速度分析法仍然无法处理速度横向变化剧烈情况下所引起的成像构造扭曲现象.因此该方法与基于叠加速度分析的方法同样,比较适用于构造简单,无强横向变速的区块.
1.3 基于层析反演的速度建模方法地震层析成像是通过对观测到的地震波各种震相的运动学(走时、射线路径)和动力学(波形、振幅、相位、频率)资料的分析,以观测数据与合成数据的逼近误差的方差最小为原则,进而反演地下介质的结构、速度分布及其弹性参数等重要信息的一种地球物理方法.根据地震波的运动学和动力学特征,地震层析成像方法可分为两大类:其一是以运动学特征为基础的射线层析成像;其二是以动力学特征为基础的波动方程层析成像(雷栋,2006).
1.3.1 射线层析反演射线层析反演是利用地震波走时和其传播的射线路径来反演地下介质速度的一种技术,主要包含射线追踪的正演和反演求解两个过程,并在速度建模中得到了广泛的应用.在正演方面,射线追踪方法已相对成熟,主要包含传统方法,如打靶法(Julian et al.1977)、弯曲法(Cerveny,2001)、改进型伪弯曲法(Thurber,1987)等;基于网格单元的波前扩展法,如有限差分法(FD)(John and Vidale, 1990)、最短路径法(SPM)(Moser,1991)等.但这些方法各有优缺点,有待于进一步发展:其中打靶法不能追踪影区的射线,只能找到最小的绝对走时且耗时较大;弯曲法较快一些,但可能会找到局部最小走时;有限差分法计算走时比较精确,但需要较大的运算量;最短路径法随着网格节点的增加,计算效率变慢.就传统方法而言,其未来的发展方向是实现完全非线性的相应算法,而基于网格单元的算法则主要是扩展后续波、多值波前的追踪等功能(李强等,2012).在反演方面,按照反演求解的方法可分为傅氏变换法、滤波反投影法、矩阵反演法和迭代重建法四大类.前两种以积分变换为基础,后两种以解线性方程组为基础.在实际应用中变换法很少使用,主要原因是它们以直射线假设为前提,不适用于震源与检波器排列不规则的情形.矩阵反演法不受震源与检波器排列的限制,但运算量巨大,需要大量的计算机内存.迭代重建法考虑射线弯曲的影响,不仅适用于任意形态的震源与检波器分布,而且没有内存限制(甘利灯,1993).
在实际应用中,通常需要先结合工区的实际情况给定初始速度模型,然后计算正演得到的初至与拾取的初至之差,利用迭代重建等方法不断修改速度模型,直到误差满足精度要求.该方法在琼东南盆地、渤海油田(周东红等,2010)等地区的时深转换中得到了较好的应用.从理论上来说,基于射线层析反演的速度建模精度要高于偏移速度分析和叠加速度分析,但在实际中该方法也受到资料信噪比等诸多因素制约,而且所用的地震信息有限,不能充分地挖掘和利用地震资料中的各种信息.
1.3.2 波形层析反演为了克服射线理论的局限性并能够处理非均匀介质中的成像问题,还需要回归到波形层析反演,也就是全波形反演(FWI).全波形反演是通过解弹性波方程或声波方程来实现的,尽管运算量巨大,但随着计算技术的发展,全波形反演已经逐渐从理论研究走向实际应用.
20世纪80年代,Tarantola (1984, 1986)等人首次提出了广义最小二乘理论的时间域全波形反演方法,并推动了全波形反演的发展.之后,Bunks等(1995)提出了时间域多尺度反演,提高了问题求解的稳定性.20世纪90年代,Pratt等(1990)为提高计算效率,将全波形反演理论推广到频率域,极大推动了全波形反演的实用化进程.但无论是时间域反演还是频率域反演,低频信息的缺失使得常规建模手段难以满足全波形反演对初始模型精度的要求.为了解决实际应用中的这一问题,Shin等(2008)提出了拉普拉斯域全波形反演,但该方法只能恢复模型中的长波长信息,并不能获得像频率域全波形反演那么高的精度.全波形反演在时间域、频率域、拉普拉斯域各有优势与不足,因此也促进了多域之间的联合研究与应用,如Kim等(2013)发展了拉普拉斯域联合频率域的全波形反演.
目前,全波形反演在速度建模中的应用大多数是海洋地震资料.Sirgue等(2010)率先对挪威北海油田(Valhall地区) OBC数据实现了三维全波形反演,这一成果极大地鼓舞了全波形反演的研究热潮,全波形反演对海上三维实际资料的应用陆续出现.但全波形反演在陆上资料的工业化应用还存在很大挑战,主要是很难采集到足够低频的观测数据并提供满足全波形反演要求精度的初始速度模型,Plessix等(2010)在低频大偏移距观测系统下实现了陆上二维资料的全波形反演,证明了陆上资料全波形反演应用的可行性.理论上全波形反演精度比射线层析法高,但是对信噪比、初始模型的建立等方面也提出了更高的要求,而且计算效率比较低.
射线理论忽略了射线路径以外速度结构的影响,无法准确地对非均匀性很强的地质结构进行成像,而全波形反演对初始模型,资料质量要求苛刻,计算效率较低.鉴于这种情况,又发展了有限频率层析成像(Dahlen,2000;Gautier,2008),并在实际应用中取得了较好的效果(Hung et al., 2004;Li et al., 2006).相对速度分析来说,层析速度反演是基于地震资料进行速度建模的最有效途径,在地下构造复杂,对速度模型精度要求高的区域可以优先考虑这种方法.每个速度建模方法都有其针对性,在应用中需要根据实际资料特征选择合适的方法.
2 以测井资料为主的速度建模方法以地震速度为主的建模方法虽然有较高的横向分辨率,但纵向精度差,而测井速度则有较高的纵向分辨率.因此在油气勘探相对成熟,测井资料丰富的区块,利用测井资料进行速度建模有很重要的意义.基于测井资料开展速度建模的核心是地质统计学,地质统计学是20世纪60年代由克里金等人在对南非金矿储量评估的基础上发展起来的.地质统计法以测井速度作为硬数据,综合考虑二维平面的速度趋势,同时在井点处又严格遵循井上的硬数据,即将地震的横向连续性和测井速度的高纵向分辨率有机地结合在一起,从而提高模型精度,降低勘探成本.
2.1 克里金估计一个好的估算方法不只是简单地给出某一区域的估计值,还应给出一个确定的估计精度.地质统计学的克里金估计就是在充分考虑了信息样品的形状、大小及其待估区相互之间的空间分布等几何特征,以及变量的空间结构信息后,为了达到线性无偏差和最小估计方差,而对每个样品值赋予一定权值,利用加权平均值法来对待估区的未知量进行估计的方法,也就是说是一种待定的滑动加权平均.
根据原始数据条件及研究目的的差异,相继产生了各种各样的克里金方法.普通克里金法是在满足随机函数二阶平稳以及期望值在搜寻邻域内稳定但未知假设条件下提出的,是一种基本的克里金方法.指示克里金法是针对非参数和无分布的区域化变量提出的,它可以在不必去掉重要而实际的高值数据条件下,处理各种不同的现象,而且给出一定风险条件下未知量的估计量及空间分布.泛克里金法是主要针对某些区域化变量具有非平稳的特性所提出的一种方法,并考虑了下面两种情况:一是区域化变量整体有变化趋势,但局部可看作平稳;二是区域化变量整体平稳,而局部有变化.协克里金法是一种融合了多变量的克里金法,它主要通过研究主变量与次级变量之间的相互关系,借助次级变量的数据信息以提高对主变量的估计精度.
克里金估计的优势在于它是一种最优估计和无偏估计,反映了变量的空间结构性,而且能给出估计精度,因此在实际中得到了广泛的应用.该方法常用于井资料丰富、地质结构简单的区块,另外在地震速度建模的测井校正中也有一定应用.在地质结构复杂的地区,为提高建模精度,往往使用协克里金法将测井速度作为硬数据,将地震速度或与测井速度相关性较好的其他属性作为软数据来对速度模型进行空间估计(王西文等,2004;Claprood et al., 2011).除了协克里金法,针对某些区域化变量具有非平稳特性的泛克里金法(Hwang et al., 1994;段天友等,1999;Duchesne et al., 2012)、与贝叶斯方法结合的贝叶斯克里金法(谢清惠等,2012)也在实际中也有广泛的应用.但克里金估计也有其局限性,首先是计算效率问题,巨大的计算量始终是制约它进行三维速度建模的一个关键;其次是该方法是一种局部估计,对估计值的整体空间相关性考虑不够;另外克里金估计还是一种光滑内插方法,很容易会把一些有意义的异常带给“光滑”掉.
2.2 随机模拟与随机反演为修正克里金估计的“光滑效应”,随机模拟方法随之发展起来,即以已知井信息为基础,以随机函数为理论产生可选的、等概率的储集层模型的方法.与克里金局部估计、结果唯一的特点不同,随机模拟考虑的是变量的全局空间相关性,且能产生多个结果.随机模拟技术在方法和应用研究上都取得了很好的进展,印兴耀等(2006)研究了基于贝叶斯-序贯高斯模拟的三维储层建模方法,很好地整合了测井和地震数据,提高了模型的纵横向分辨率;Gibson等(2007)将蒙特卡洛模拟用于不确定性分析和地震信息评价;Vidal等(2008)将马尔科夫-贝叶斯模拟用于构造的不确定性估计.在实际应用中,该方法建立的速度模型准确反映了速度空间的变化规律,在阿拉斯加斜坡带(柯宗强,1997)、巴楚夏河(武丽,2006)等工区都取得了较好的实际效果.
随机反演方法则将随机模拟的思想引到地震反演中,以地质信息(包括地震、钻井、测井等)为基础,应用随机函数理论和地质统计学方法(变差函数分析、直方图分析、相关分析等),结合传统的地震反演技术,在每一个地震道(或多个地震道)产生多个可选的等概率反演结果.早在1992年Bortoliand就提出了地质统计学反演方法,此后Dubrule (1998)和Rowbotham (1999)在EAGE和SEG年会上对该方法进行发展.随机反演法兼顾了地震数据的横向分辨率与测井数据的纵向分辨率,能最大限度利用地震、地质及测井等所有资料,使反演结果与己知条件充分吻合,其结果既能反映地震资料的反射特征,又受地质构造框架模型和井点己知资料的三维空间统计规律控制,能更好地反映储层的非均匀性和不确定性(印兴耀,2014;张繁昌,2014;孙瑞莹,2015).但由于该反演方法计算过程复杂、数据量大,计算效率在过去一直制约着随机反演在实际中的应用,近年来随着计算机技术的快速发展,该方法在实践中开始受到越来越多的重视.随机反演已经在弹性参数、物性参数、波阻抗反演中取得了一定的效果(慎国强等,2004;易平等,2005;杨丽兵等,2010),因此通过叠后反演的思路利用随机反演进行速度建模也不失为一种好的选择.以上基于地质统计学的方法由于是以测井资料作为主要数据,因此更加适用于测井资料丰富的区块,尤其是进入油气开发阶段的区块.
3 井震联合速度建模中的关键问题 3.1 井震联合速度建模中的井震跨尺度匹配问题在勘探相对成熟的区块,充分结合井震资料进行时深转换有十分重要的意义.但由于地震勘探与声波测井在原理、方法上不同,得到的数据在观测尺度、波速频率以及所处域上都存在着差异(韩行吉等,1995).因此,在将两者联合进行速度建模和时深转换之前需要先开展声波测井与地震资料之间的匹配,主要包括尺度匹配和频率匹配.
3.1.1 井震尺度匹配由于受井眼扩径及泥岩蚀变等因素的影响,测井资料本身存在一定的误差,因此在进行尺度匹配之前,要先进行环境校正(杨文采,1987).由于声波测井采样间隔远远大于地震资料,因此首先要对测井资料进行粗化,相当于在井震尺度匹配过程中对测井资料进行重采样.但根据shannon采样定理,如果直接对测井资料进行重采样,往往会使得到的结果失真(张白林等,2003).为解决这个问题,通常可以对声波测井资料进行多次中值滤波来有效减弱重采样信号的频率混叠现象,也可以采用Backus平均等方法对测井资料进行尺度粗化(曹丹平,2015),从而达到跨尺度资料之间的有效匹配.
3.1.2 井震频率匹配地震波在地层传播的过程中,会经受地层的吸收而引起振幅衰减(Hamilton,1972;Toksoz et al,1979)和速度频散(Sams et al., 1997;Spencer et al., 1982).振幅衰减使得地震记录的主频降低,有效频带变窄,需对地震资料进行有效的能量补偿,只有波形准确才能确保合成记录与井旁道匹配.速度频散使不同频率的地震波具有不同的传播速度,且高频的声波测井速度往往高于低频的地震波相速度.频率匹配的目的就是将声波测井频率条件下的声波相速度转化为地震主频下的相速度.目前可以通过估计地震子波,利用闭合差校正(易维启等,1994)、基于谐振模型的校正(杨文采,1987)、基于频散公式的外推校正(张元中等,2001)和基于多分辨率技术的匹配(董恩清等,1999)等速度校正技术来准确求取地震频带下的速度,在此基础上制作合成记录,提高合成记录与井旁道的匹配精度,从而实现井震资料在频率上的匹配(罗伟平,2014).
3.2 井震联合速度建模中的约束条件问题 3.2.1 基于地震资料的速度建模中的井校正鉴于地震资料建立的速度场往往与井点的速度不匹配,还需要对建立的速度场进行井校正.但单点的精确校正并不代表全局的合理校正,因此需要对井点处的速度误差进行插值.传统的井校正方法一般是对得到的井点处的误差利用反距离加权法进行插值(冯全东,2008),得到误差平面,将得到的误差平面与之前得到的速度场平面相减,得到最终的速度平面图.但反距离加权法仅考虑了距离的影响因素,忽视了变量之间的空间关系,而且用于插值的井数量有限,得到的结果往往难令人满意.而结合地质统计学方法对井点处误差数据进行插值,可以综合考虑误差的空间分布,从而提高全局误差插值的精度(许晓宏,1997).
3.2.2 基于测井资料的速度建模中的地震约束问题在用地质统计学方法进行速度建模或储层预测时常常存在两方面问题:一是井少,使得作为“硬数据”的测井数据不充足;二是遇到河流相储层时,由于其规模小,横向变化快,难以对其进行定量描述.针对测井数据不足的问题,需要利用能够携带二级变量的克里金方法或随机模拟等方法综合地震属性数据进行计算.由于地震属性本身就是空间变化关系的数据载体,因此选择一个与测井数据相关性好的地震属性做约束(刘文岭,2008),可以有效降低插值和模拟带来的不确定性.针对河流相储层规模小,横向变化快的问题,利用地震层面属性或井震联合绘制的小层沉积相带图等二维数据及平面趋势的方式进行约束(刘文岭,2008;周单,2010),能够更好地提高横向外推的精度.
3.2.3 层速度反演中的测井约束问题在基于叠后地震数据的反演方法中,地震资料的频带宽度、子波的特性以及层位标定结果等都会影响反演结果的精度.除此之外,叠后地震反演一般利用测井信息对反演结果进行约束,测井资料的环境因素以及测井约束条件使用的恰当与否也将严重影响反演结果的准确性,而且不同的反演方法对测井约束条件的需求也存在差异(潘昱洁,2011).实践证明,在叠后地震反演中如果用过多井信息进行插值建立低频模型,由于不同井的真值之间存在差异将会产生“牛眼”假象,最终导致反演结果不准确(凌云等,2009).但对于随机反演而言,最好能有多口井作为约束,因为随机反演是通过随机扰动进行反演,因此,井的信息将作为真值被利用,故井信息越多,随机模拟的结果与真实情况越接近.再进一步结合地震相、沉积相等先验信息,还可以有效降低反演的不确定性,使反演结果有更好的横向连续性和可靠性,在此基础上再开展时深转换可以取得更好的精度.
3.3 时深转换中的不确定性分析在油气田勘探开发过程中,由于地质条件的复杂性以及资料的不完备性,不确定性是固有存在的,厘清不确定性有助于降低勘探开发的风险.以随机函数理论为基础的随机模拟与随机反演法承认井点外的地层参数具有一定的随机性,它们可以生成地质模型的多个等概率实现,是一种可以用于表征储层不确定性特征的建模方法,这在时深转换中有很重要的意义.许多学者也在不确定性分析方面开展了大量工作,O’Brien和Lerche (1988)研究了叠加速度的不确定性;Aabrahamsen等(1991)研究了多层时深转换的不确定性处理方法.Landa等(1991)指出数据的不确定性和模型的不确定性都应该被考虑,提出了一种大尺度速度模型估计的不确定性分析方法;Mlaba等(2003)讨论了确定性方法和随机方法在时深转换中的应用,并对储层体积进行了不确定性分析;Bartel等(2006)讨论了多种平均速度建模方法,他们指出采用不同的方法进行速度建模,不同模型间的差异可以用来量化速度的不确定性;Hosseini等(2012)采用地质统计学方法进行时深转换并描述了不同方法产生的不确定性;Osypov等(2013)提出了与层析速度模型和各向异性有关的地震不确定性分析方法;Fomel和Landa (2014)提出了一种用于定量分析叠前时间偏移造成的地震图像中构造不确定性的方法.在时深转换过程中需要采用不同的速度建模方法进行综合考虑,在不确定性分析的基础之上提高利用井震资料联合开展时深转换的精度和可靠性.
4 实际效果分析以某工区为例,该工区位于渤海湾北部沿海.利用上述方法对该工区东2顶层进行时深转换,参与计算的井数为18口.
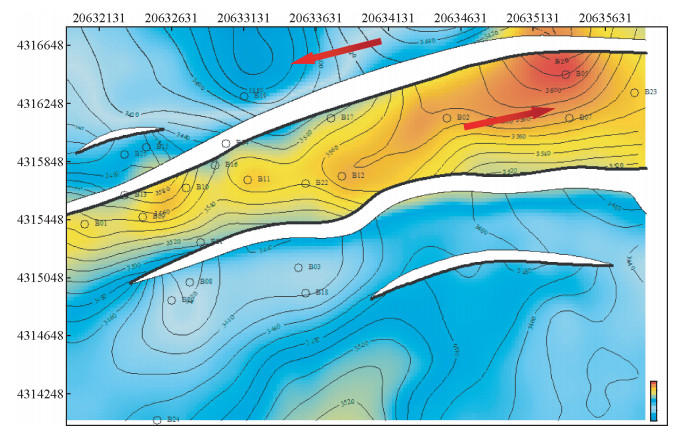
图 1为用基于叠加速度分析的地震方法得到的该工区东2顶层深度域构造图.由于地震数据在平面上分布密度大,所以该方法对构造整体变化趋势的控制较好,但由于地震资料分辨率低,且不适用于地层倾角较大,速度横向变化剧烈的情况,因此得到的深度构造图存在较大误差,有些位置处误差甚至达到上百米.因此针对在地下构造复杂,对速度模型精度要求高的区域可以优先考虑使用精度更高的层析反演法.
|
图 1 利用基于叠加速度分析的方法绘制的深度域构造图 Figure 1 The depth structural map got by the mothod of stacking velocity analysis |
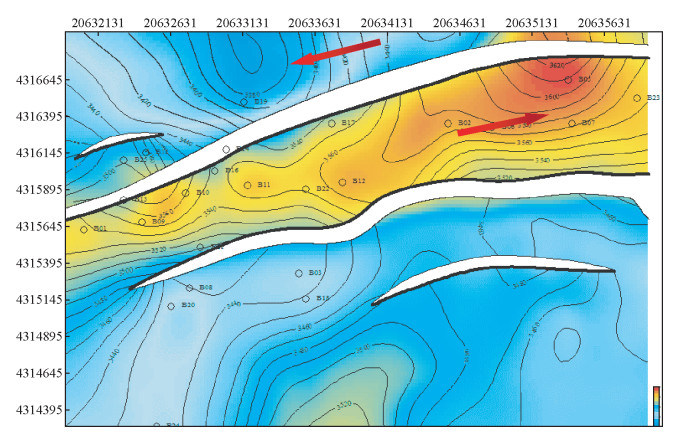
图 2为用普通克里金估计法得到的该工区东2顶层深度域构造图.由于克里金估计在井点位置处完全忠实于观测深度,因此得到的构造图在井点处深度可靠,但用该方法在井间进行内插外推时难以控制构造的变化趋势,在井上或无井位置甚至会出现构造假象,如图 2红色箭头处.因此可通过引入横向连续性好的地震数据作为约束来提高速度建模的精度.
|
图 2 利用普通克里金方法绘制的深度域构造图 Figure 2 The depth structural map got by the method of Ordinary Kriging |
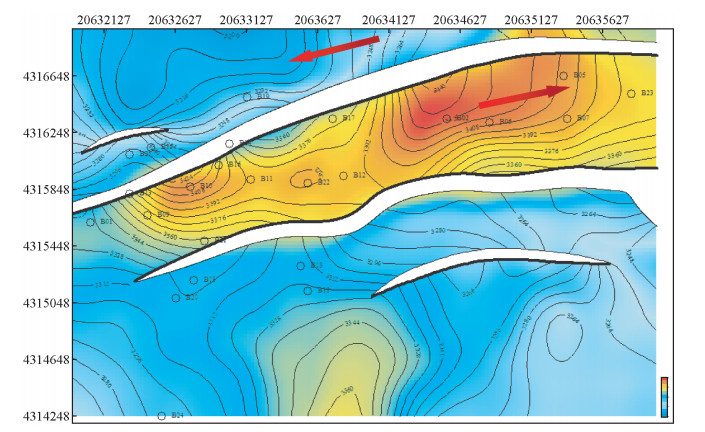
图 3为用井震联合法得到的该工区东2顶层深度域构造图.井震联合法以测井数据作为硬数据,通过协克里金估计法引入与测井速度相关性好的地震数据作为约束数据,即将地震叠加速度的横向连续性和测井速度的高纵向分辨率有机地结合在了一起,得到的深度构造图不仅有较高的预测精度,而且构造变化也符合实际地质情况,如图 3红色箭头处.
|
图 3 利用井震联合方法绘制的深度域构造图 Figure 3 The depth structural map got by the method of well seismic joint |
以地震为主的速度建模方法经过半个多世纪的完善已经从双曲线型叠加速度分析发展到偏移速度分析、层析反演等多种方法,精度获得了不断的提高.但偏移速度分析的稳定性问题、层析速度反演中的数据拾取和计算效率等问题依然需要改善;以测井为主的速度建模方法以测井速度作为硬数据,通过克里金方法引入地震数据作为约束,极大的提高了速度建模的精度,但克里金估计以及随机反演的效率仍有待提高;井震联合速度建模可以充分利用地震资料好的横向连续性和测井资料高的纵向分辨率,融合地震属性、沉积相等作为约束,建立一个高精度的速度模型.但在使用过程中要注意做好井震匹配,选择与测井速度相关性好的约束条件,并与时深转换过程中的不确定性分析相结合,从而提高利用井震联合速度建模开展时深转换的准确性和可靠性.无论哪种方法,都应该既要考虑到对低信噪比资料有一定的适应性,又要具有较高的计算效率才可有效地服务于生产.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Abrahamsen P, Omre H, Lia O .1991. Stochastic Models for Seismic Depth Conversion of Geological Horizons[J]. Proceedings of Offshore Europe . |
| [] | Al-Chalabi M .1973. Series Approximation in Velocity and Traveltime Computations[J]. Geophysical Prospecting, 21 (4) : 783–795. DOI:10.1111/gpr.1973.21.issue-4 |
| [] | Al-Yahya .1989. Velocity Analysis by Iterative Profile Migration[J]. GEOPHYSICS, 54 (6) : 718–729. DOI:10.1190/1.1442699 |
| [] | Amir H, Hosseini, Hong Feng, Abu Yousuf, Tony Kay .2012. Time to depth conversion and uncertainty characterization for SAGD base of pay in the McMurray formation[J]. GeoConvention . |
| [] | Bartel, Busby, Nealon, Zaske J, editors. 2006.Time to Depth Conversion and Uncertainty Assessment Using Average Velocity Modeling. 76th SEG Annual Meeting; |
| [] | Berkhout AJ .1992. Pushing the Limits of Seismic Imaging[J]. Seg Technical Program Expanded Abstracts : p. 1389–1393. |
| [] | Buland, Bayesian .2011. Dix Inversion[J]. GEOPHYSICS, 76 (2) : R15–R22. DOI:10.1190/1.3552596 |
| [] | Bunks C, Saleck FM, Zaleski S, Chavent G .1995. Multiscale Seismic Waveform Inversion[J]. GEOPHYSICS, 60 (5) : 1457–1473. DOI:10.1190/1.1443880 |
| [] | Cao D P .2015. The upscaling method of the well logging data based on Backus equivalence average method[J]. Geophysical Prospecting for Petroleum (01) : 105–111. |
| [] | Causse E, Haugen GU, Rommel BE .2000. Large-Offset Approximation to Seismic Reflection Traveltimes[J]. Geophysical Prospecting, 48 (4) : 763–778. DOI:10.1046/j.1365-2478.2000.00207.x |
| [] | Cerveny V. 2001.Seismic Ray Theory:Cambridge University Press. http://www.oalib.com/references/18992177 |
| [] | Claprood, Duchesne, Gloaguen E .2011. A Geostatistical Approach for Two Dimensional Seismic Velocity Modelling[J]. Geological Survey of Canada . |
| [] | Cook EE, Taner MT .1969. Velocity Spectra and Their Use in Stratigraphic and Lithologic Differentiation[J]. Geophysical Prospecting, 17 (4) : 433–448. DOI:10.1111/gpr.1969.17.issue-4 |
| [] | Cui D, Zhang Y, Hu Y, et al .2014. The review of near surface velocity modeling[J]. Progress in Geophysics (06) : 2635–2641. DOI:10.6038/pg20140625 |
| [] | Dahlen F, Hung S-H, Nolet G .2000. Fréchet Kernels for Finite-Frequency Travel times-I. Theory[J]. Geophysical Journal International, 141 (1) : 157–174. DOI:10.1046/j.1365-246X.2000.00070.x |
| [] | Dischler E, Hokstad K, Buland A .2013. Bayesian Anisotropic Dix Inversion[J]. Seg Technical Program Expanded Abstracts : p4853–4857. |
| [] | Dix CH .1955. Seismic Velocities from Surface Measurements[J]. GEOPHYSICS, 20 (1) : 68–86. DOI:10.1190/1.1438126 |
| [] | Doherty SM, Claerbout JF .1976. Structure Independent Velocity Estimation[J]. GEOPHYSICS, 41 (5) : 850–881. DOI:10.1190/1.1440669 |
| [] | Dong E Q, Liu G Z, Zhang Z P, et al .1999. Resampling of Logging Data and Matching Synthetic Seismogram with Seismic Trace by multiresolution Analysis[J]. WLT, 23 (4) : 264–267. |
| [] | Du X D, Wong B, Liu J R, et al .2008. Migration velocity modeling strategies of TI media[J]. Chinese Journal of Geophysics (02) : 538–545. |
| [] | Duan T Y, Zhu G S .1999. Application of Kriging Technique to Establishing the Database of Average Velocity Field[J]. Journal of Jianghan Petroleum Institute, 21 (4) : 41–44. |
| [] | Dubrule O .1998. Geostatistics in Petroleum Geology[J]. American Association of Petroleum Geologists Tulsa . |
| [] | Duchesne MJ, Claprood M, Gloaguen E .2012. Improving Seismic Velocity Estimation for 2d Poststack Time Migration of Regional Seismic Data Using Kriging with an External Drift[J]. The Leading Edge, 31 (10) : 1156–1166. DOI:10.1190/tle31101156.1 |
| [] | Faye JP, Jeannot JP .1986. Prestack Migration Velocities from Focusing Depth Analysis[J]. Seg Technical Program Expanded Abstracts : p. 438–440. |
| [] | Fomel S, Landa E .2014. Structural Uncertainty of Time-Migrated Seismic Images[J]. Journal of Applied Geophysics, 101 : 27–30. DOI:10.1016/j.jappgeo.2013.11.010 |
| [] | Forel D, Gardner GHF .1988. A Three-Dimensional Perspective on Two-Dimensional Dip Moveout[J]. GEOPHYSICS, 53 (5) : 604–610. DOI:10.1190/1.1442495 |
| [] | Garotta R, Michon D .1967. Continuous Analysis of the Velocity Function and of the Move out Corrections[J]. Geophysical Prospecting, 15 (4) : 584–589. DOI:10.1111/gpr.1967.15.issue-4 |
| [] | Gautier S, Nolet G, Virieux J .2008. Finite-Frequency Tomography in a Crustal Environment:Application to the Western Part of the Gulf of Corinth[J]. Geophysical Prospecting, 56 (4) : 493–503. DOI:10.1111/j.1365-2478.2007.00683.x |
| [] | Gibson R, Bickel JE, MacVay D, Pickering S .2007. Model-Based Uncertainty Quantification and Seismic Information Value[J]. SEG Annual Meeting.2007:Society of Exploration Geophysicists . |
| [] | Grechka V, Pech A, Tsvankin I .2002. Multicomponent Stacking-Velocity Tomography for Transversely Isotropic Media[J]. GEOPHYSICS, 67 (5) : 1564–1574. DOI:10.1190/1.1512802 |
| [] | Han X J, Yang W C, Wu Y G .1995. Seismic and acoustic logging data matching[J]. Oil Geophysical Prospecting, S2 : 27–33. |
| [] | Hung SH, Shen Y, Chiao LY .2004. Imaging Seismic Velocity Structure beneath the Iceland Hot Spot:A Finite Frequency Approach[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 109 (B8) . |
| [] | Hubral P .1976. Interval Velocities from Surface Measurements in the Three-Dimensional Plane Layer Case[J]. GEOPHYSICS, 41 (2) : 233–242. DOI:10.1190/1.1440613 |
| [] | Hwang L-F, McCorkindale D .1994. Troll Field Depth Conversion Using Geostatistically Derived Average Velocities[J]. The Leading Edge, 13 (4) : 262–269. DOI:10.1190/1.1437018 |
| [] | Hale D .1984. Dip-Moveout by Fourier Transform[J]. GEOPHYSICS, 49 (6) : 741–757. DOI:10.1190/1.1441702 |
| [] | Hamilton EL .1972. Compressional-Wave Attenuation in Marine Sediments[J]. Geophysics, 37 (4) : 620–46. DOI:10.1190/1.1440287 |
| [] | Higginbotham JH, Brown MP, Clapp RG .2008. Wave Equation Migration Velocity Focusing Analysis[J]. Seg Technical Program Expanded Abstracts : p. 3083–3087. |
| [] | Koren Z, Ravve I .2005. Constrained Velocity Inversion[J]. Seg Technical Program Expanded Abstracts : p. 2289–2292. DOI:10.1190/SEGEAB.24 |
| [] | Kabir, Verschuur DJ .1996. Migration Velocity Analysis Using the Common Focus Point Technology[J]. Seg Technical Program Expanded Abstracts : P. 407–410. |
| [] | Kim Y, Shin C, Calandra H, Min D-J .2013. An Algorithm for 3d Acoustic Time-Laplace-Fourier-Domain Hybrid Full Waveform Inversion[J]. GEOPHYSICS, 78 (4) : R151–R166. DOI:10.1190/geo2012-0155.1 |
| [] | Koren .2006. Constrained Dix Inversion[J]. GEOPHYSICS, 71 (6) : R113–R130. DOI:10.1190/1.2348763 |
| [] | Lamy P, Swaby P, Rowbotham P, Dubrule O, Haas A .1999. Geostatistical Inversion:Seismic Data to Reservoir Properties[J]. Journal of petroleum technology, 51 (6) : 38–39. DOI:10.2118/0699-0038-JPT |
| [] | Landa E, Thore P, Sorin V, Koren Z .1991. Interpretation of Velocity Estimates from Coherency Inversion[J]. Geophysics, 56 (9) : 1377–1383. DOI:10.1190/1.1443157 |
| [] | Lei D, Hu X Y .2006. Review of Seismic Tomography Methods[J]. Journal of Seismological Research (04) : 418–426. |
| [] | Li C, Vander Hilst RD, Toksöz MN .2006. Constraining P-Wave Velocity Variations in the Upper Mantle beneath Southeast Asia[J]. Physics of the Earth and Planetary Interiors, 154 (2) : 180–195. DOI:10.1016/j.pepi.2005.09.008 |
| [] | Li Q, Bai Y C .2012. Review on seismic wavefront and raytracing in complex media[J]. Progress in Geophysics (01) : 92–104. DOI:10.6038/j.issn.1004-2903.2012.01.011 |
| [] | Li Z C, Wang H Z, Ma Z T .2000. Migration velocity analysis of common mid-point gathers[J]. Geophysical Prospecting for Petroleum (01) : 20–26. |
| [] | Liu A Q, Chen D Y, Fan C W, et al .2014. QDN basin deepwater area of velocity research and velocity modeling thinking[J]. Progress in Geophysics (04) : 1900–1906. DOI:10.6038/pg20140457 |
| [] | Liu B H, Ren Y H, Chen G J .2013. Review on Migration Velocity Analysis and Inversion[J]. Computerized Tomography Theory and Applications[J]. (04) : 727–740. |
| [] | Liu G F, Liu H, Meng X H, et al .2012. Frequency-related factors analysis in frequency domain waveform inversion[J]. Chinese Journal of Geophysics (04) : 1345–1353. DOI:10.6038/j.issn.0001-5733.201204030 |
| [] | Liu W L .2008. Geological modeling technique for reservoir constrained by seismic data[J]. Acta Petrolei Sinica (01) : 64–68. |
| [] | Liu W Q, Wang X W, Liu H, et al .2013. Application of velocity modeling and reverse time migration to subsalt structure[J]. Chinese Journal of Geophysics (02) : 616–625. DOI:10.6038/cjg20130225 |
| [] | Ling Y, Mu X, Sun D S, et al .2009. Analysis on affecting factors of post stack inversion and seismic attribute interpretation of thin reservoir[J]. Geophysical Prospecting for Petroleum, 47 (6) : 531–558. |
| [] | Luo W P, Li H Q, Zhu L P, et al . Research on automatic matching of seismic and well logging data[J]. Oil Geophysical Prospecting (01) : 205–212. |
| [] | Mlaba M, Feddersen J, Young P, editors .2003. Does Stochastic Time-Depth Conversion Give Us So Much More Than a Deterministic Approach[J]. 8th SAGA Biennial Technical Meeting and Exhibition . |
| [] | Moser TJ .1991. Shortest Path Calculation of Seismic Rays[J]. GEOPHYSICS, 56 (1) : 59–67. DOI:10.1190/1.1442958 |
| [] | O'Brien J, Lerche I .1988. Seismic Imaging of Deep Hydrocarbon Reservoirs[J]. Pure and applied geophysics, 127 (1) : 33–61. DOI:10.1007/BF00878689 |
| [] | Osypov K, Nichols D, Yarman C, Qiao F, Woodward M, Ivanova N, et al .2012. Quantitative Analysis of Seismic Uncertainty[J]. Saint Petersburg . |
| [] | Pan H X, Fang W B .2006. Review of seismic velocity analysis methods[J]. Progress in Exploration Geophysics (05) : 305–311. |
| [] | Pan X X, Qin N, Qu Z P, et al .2013. Tomography velocity modeling and application of prestack depth migration[J]. Progress in Geophysics (06) : 3080–3085. DOI:10.6038/pg20130632 |
| [] | Pencer T, Sonnad J, Butler T .1982. Seismic Q-Stratigraphy or Dissipation[J]. Geophysics, 47 (1) : 16–24. DOI:10.1190/1.1441275 |
| [] | Plessix R-E, Perkins C .2010. Thematic Set:Full Waveform Inversion of a Deep Water Ocean Bottom Seismometer Dataset[J]. First Break, 28 (4) . |
| [] | Pratt RG .1990. Frequency-Domain Elastic Wave Modeling by Finite Differences:A Tool for Crosshole Seismic Imaging[J]. GEOPHYSICS, 55 (5) : 626–632. DOI:10.1190/1.1442874 |
| [] | Sams M, Neep J, Worthington M, King M .1997. The Measurement of Velocity Dispersion and Frequency-Dependent Intrinsic Attenuation in Sedimentary Rocks[J]. Geophysics, 62 (5) : 1456–1464. DOI:10.1190/1.1444249 |
| [] | Shin C, Cha YH .2008. Waveform Inversion in the Laplace Domain[J]. Geophysical Journal International, 173 (3) : 922–931. DOI:10.1111/gji.2008.173.issue-3 |
| [] | Sirgue L, Barkved O, Dellinger J, Etgen J, Albertin U, Kommedal J .2010. Thematic Set:Full Waveform Inversion:The Next Leap Forward in Imaging at Valhall[J]. First Break, 28 (4) . |
| [] | Sun R Y, Yin X Y, Wang B L .2015. Stochastic inversion of elastic impedance based on Metropolis sampling algorithm[J]. Geophysical and Geochemical Exploration (01) : 203–210. |
| [] | Tarantola .1986. A Strategy for Nonlinear Elastic Inversion of Seismic Reflection Data[J]. GEOPHYSICS, 51 (10) : 1893–1903. DOI:10.1190/1.1442046 |
| [] | Tarantola A .1984. Inversion of Seismic Reflection Data in the Acoustic Approximatin[J]. GEOPHYSICS, 49 (8) : 1259–1266. DOI:10.1190/1.1441754 |
| [] | Taner MT, Koehler F .1969. Velocity Spectra-Digital Computer Derivation Applications of Velocity Functions[J]. GEOPHYSICS, 34 (6) : 859–881. DOI:10.1190/1.1440058 |
| [] | Toksöz, Johnston D, Timur A .1979. Attenuation of Seismic Waves in Dry and Saturated Rocks:ILaboratory Measurements[J]. Geophysics, 44 (4) : 681–690. DOI:10.1190/1.1440969 |
| [] | Vidale JE .1990. Finite-Difference Calculation of Traveltimes in Three Dimensions[J]. GEOPHYSICS, 55 (5) : 521–526. DOI:10.1190/1.1442863 |
| [] | Vidal MM, Rusic A, Srinivasan S, Sen M, Sil S, editors .2008. Markov Bayes Simulation for Structural Uncertaint Estimation[J]. 2008 SEG Annual Meeting. Society of Exploration Geophysicists . |
| [] | Wei Z F, Gao H W, Zhang J F .2014. Time-domain full waveform inversion based on an irregular-grid acoustic modeling method[J]. Chinese Journal of Geophysics (02) : 586–594. |
| [] | Wu G C, Wang H Z, Ma Z T .2003. Ray tracing with constant velocity gradient and inversion of 2-D interval velocity[J]. Geophysical Prospecting for Petroleum (04) : 434–440. |
| [] | Wu S H, Yang Y Q .2012. Uncertainty and Scientific Methodology in Subsurface Reservoir Characterization[J]. Journal of Earch Sciences and Environment, 34 (2) : 72–80. DOI:10.6038/cjg20140222 |
| [] | Xin K F, Wang H Z, Ma Z T, et al .2005. Interactive Velocity Analysis on CFP Gathers[J]. Oil Geophysical Prospecting (04) : 386–390. |
| [] | Yang L B, Zhang H, Qiao S R, et al .2010. Application of stochastic seismic inversion on reservoir prediction of DY structure in Western Sichuan Depression[J]. Oil Geophysical Prospecting (04) : 373–379. |
| [] | Ye Y, Zheng X .2003. Advances in migration velocity analysis[J]. Progress in Exploration Geophysics (02) : 136–142. |
| [] | Yi Y Y, Jiang J L, Zhao D J .2003. Velocity Research Based on Model Chromatography[J]. Journal of Jianghan Petroleum Institute (01) : 47–49. |
| [] | Yin X Y, He W S, Huang X R .2006. Bayesian sequential Gaussian simulation method[J]. Journal of the University of Petroleum, China (Edition of Natural Science), 29 (5) : 28–32. |
| [] | Yin X Y, Sun R Y, Zhang G Z, et al .2014. Stochastic inversion of reservoir physical property parameters based on high-frequency initial model from fractal and low-frequency prior information[J]. Geophysical Prospecting for Petroleum (05) : 537–544. |
| [] | Zhang J J, Zhang J F .2011. Wave equation based migration velocity estimation:a direct inversion approach[J]. Chinese Journal of Geophysics (03) : 835–841. DOI:10.3969j/.isns.0001-5733.2011.03.024 |
| [] | Zhang Y Z, Chu Z H .2001. An Experimental Study of Acoustic Dispersion of Rock and Extrapolation of the Velocity[J]. Chinese Journal of Geophysics, 44 (1) : 103–111. |
| [] | Zhou Q C, Liu H S, Kondrashkov .2009. Research of dual parameters evolving common reflection point stack and velocity analysis method[J]. Chinese Journal of Geophysics (07) : 1881–1890. DOI:10.3969/1.issn.0001-5733.2009.07.023 |
| [] | 曹丹平.2015. 基于Backus等效平均的测井资料尺度粗化方法研究[J]. 石油物探, 54 (01) : 105–111. |
| [] | 崔栋, 张研, 胡英, 等.2014. 近地表速度建模方法综述[J]. 地球物理学进展, 29 (06) : 2635–2641. DOI:10.6038/pg20140625 |
| [] | 段天友, 朱广生.1999. 克立格方法在建立平均速度场数据库中的应用[J]. 江汉石油学院学报, 21 (4) : 41–44. |
| [] | 董恩清, 刘贵忠, 张宗平, 等.1999. 多分辨分析用于测井资料的重采样及合成记录与地震道的匹配[J]. 测井技术, 23 (4) : 264–267. |
| [] | 杜向东, 翁斌, 刘军荣, 等.2008. TI介质偏移速度建模研究[J]. 地球物理学报, 51 (02) : 538–545. |
| [] | 韩行吉, 杨文采, 吴永刚.1995. 地震与声测井资料的匹配[J]. 石油地球物理勘探, S2 : 27–33. |
| [] | 凌云, 亩心, 孙德胜, 等.2009. 薄储层叠后反演影响因素分析与地震属性解释研究[J]. 石油物探, 47 (6) : 531–558. |
| [] | 罗伟平, 李洪奇, 朱丽萍, 等.2014. 地震与测井资料自动匹配的研究[J]. 石油地球物理勘探, 49 (01) : 205–212. |
| [] | 李振春, 王华忠, 马在田.2000. 共中心点道集偏移速度分析[J]. 石油物探, 39 (01) : 20–26. |
| [] | 刘爱群, 陈殿远, 范彩伟, 等.2014. 琼东南盆地深水区速度研究及速度建模思考[J]. 地球物理学进展 (04) : 1900–1906. DOI:10.6038/pg20140457 |
| [] | 刘百红, 任跃华, 陈国金.2013. 偏移速度分析与速度反演方法评述[J]. CT理论与应用研究, 22 (04) : 727–740. |
| [] | 刘国峰, 刘洪, 孟小红, 等.2012. 频率域波形反演中与频率相关的影响因素分析[J]. 地球物理学报 (04) : 1345–1353. DOI:10.6038/j.issn.0001-5733.201204030 |
| [] | 刘文卿, 王西文, 刘洪, 等.2013. 盐下构造速度建模与逆时偏移成像研究及应用[J]. 地球物理学报, 56 (02) : 616–625. DOI:10.6038/cjg20130225 |
| [] | 刘文岭.2008. 地震约束储层地质建模技术[J]. 石油学报, 29 (01) : 64–68. |
| [] | 雷栋, 胡祥云.2006. 地震层析成像方法综述[J]. 地震研究, 29 (04) : 418–426. |
| [] | 李强, 白超英.2012. 复杂介质中地震波前及射线追踪综述[J]. 地球物理学进展, 27 (01) : 92–104. DOI:10.6038/j.issn.1004-2903.2012.01.011 |
| [] | 潘宏勋, 方伍宝.2006. 地震速度分析方法综述[J]. 勘探地球物理进展, 29 (05) : 305–311. |
| [] | 潘兴祥, 秦宁, 曲志鹏, 等.2013. 叠前深度偏移层析速度建模及应用[J]. 地球物理学进展, 28 (06) : 3080–3085. DOI:10.6038/pg20130632 |
| [] | 慎国强, 孟宪军, 王玉梅, 等.2004. 随机地震反演方法及其在埕北35井区的应用[J]. 石油地球物理勘探, 39 (01) : 75–81. |
| [] | 孙瑞莹, 印兴耀, 王保丽.2015. 基于Metropolis抽样的弹性阻抗随机反演[J]. 物探与化探, 39 (01) : 203–210. |
| [] | 魏哲枫, 高红伟, 张剑锋.2014. 基于非规则网格声波正演的时间域全波形反演[J]. 地球物理学报, 57 (02) . DOI:10.6038/cjg20140222 |
| [] | 武丽, 李剑峰, 施炜, 等.2006. 巴楚夏河工区的三维速度建模方法[J]. 石油地球物理勘探, 41 (1) : 87–92. |
| [] | 吴胜和, 杨延强.2012. 地下储层表征的不确定性及科学思维方法[J]. 地球科学与环境学报, 34 (2) : 72–80. |
| [] | 王西文, 刘全新, 苏明军, 等.2004. 多井约束下的速度建模方法和应用[J]. 石油地球物理勘探, 38 (3) : 263–267. |
| [] | 吴国忱, 王华忠, 马在田.2003. 常速度梯度射线追踪与二维层速度反演[J]. 石油物探, 42 (04) : 434–440. |
| [] | 辛可锋, 王华忠, 马在田, 等.2005. CFP道集交互速度分析[J]. 石油地球物理勘探, 40 (04) : 386–390. |
| [] | 薛冈, 王良书, 胡中平.2003. 大炮检距地震资料动校正方法比较[J]. 石油地球物理勘探, 38 (02) : 151–155. |
| [] | 许晓宏, 黄海平, 马玉柱.1997. 地震层速度的地质统计学处理[J]. 石油与天然气地质, 18 (2) : 103–107. |
| [] | 谢清惠, 赵中平.2012. 贝叶斯-克里金估计方法在变速成图中的应用[J]. 石油物探, 51 (3) : 251–256. |
| [] | 杨丽兵, 张虹, 谯述蓉, 等.2010. 随机地震反演在川西坳陷DY构造储层预测中的应用[J]. 石油物探 (04) : 373–379. |
| [] | 叶勇, 郑雄.2003. 偏移速度分析技术新进展[J]. 勘探地球物理进展, 26 (02) : 136–142. |
| [] | 印兴耀, 孙瑞莹, 张广智, 等.2014. 基于分形高频初始模型和低频先验信息的物性参数随机反演[J]. 石油物探, 53 (05) : 537–544. |
| [] | 印兴耀, 贺维胜, 黄旭日.2006. 贝叶斯-序贯高斯模拟方法[J]. 石油大学学报:自然科学版, 29 (5) : 28–32. |
| [] | 易维启, 宋吉杰.1994. 声波测井资料与地震资料之间的匹配--波速频散校正[J]. 石油地球物理勘探, S1 : 72–75. |
| [] | 杨文采.1987. 岩石的粘弹性谐振Q模型[J]. 地球物理学报, 30 (4) : 399–411. |
| [] | 易平, 林桂康.2005. 随机地震反演技术及在文昌13-1油田的应用[J]. 石油地球物理勘探, 40 (01) : 87–91. |
| [] | 易远元, 姜建莉, 赵殿君.2003. 基于模型层析法的地震速度研究[J]. 江汉石油学院学报, 25 (01) : 47–49. |
| [] | 周东红, 姚以泰, 陈树亮, 王建立, 张洁.2010. 基于射线追踪的CMP相干速度反演技术在渤海油田的应用[J]. 石油地球物理勘探, 45 (03) : 392–397. |
| [] | 张江杰, 张剑锋.2011. 波动方程偏移速度建模:一种直接反演方法[J]. 地球物理学报, 54 (03) : 835–841. DOI:10.3969j/.isns.0001-5733.2011.03.024 |
| [] | 张元中, 楚泽涵.2001. 岩石声频散的实验研究及声波速度的外推[J]. 地球物理学报, 44 (1) : 103–111. |
| [] | 张繁昌, 肖张波, 印兴耀.2014. 地震数据约束下的贝叶斯随机反演[J]. 石油地球物理勘探, 49 (01) : 176–182. |
| [] | 周青春, 刘怀山, Kondrashkov.2009. 双参数展开CRP叠加和速度分析方法研究[J]. 地球物理学报, 52 (07) : 1881–1890. DOI:10.3969/1.issn.0001-5733.2009.07.023 |
 2016, Vol. 31
2016, Vol. 31


